Abstract
Moiré patterns (MPs), arising from the superposition of two lattices with close periods, are tightly related to the physicochemical properties of bilayer nanostructures. Here, we develop the theory of complex MPs emerging in twisted bilayer graphene and planar nets of double-walled nanotubes at significant relative twist and/or deformation of layers. The proposed theory clarifies the physicochemical regularities arising at sorting of single-walled carbon nanotubes (SWCNTs) by organic molecules, which self-assemble in regular coatings on both the tubes and planar graphene. We introduce and consider an outer tubular virtual lattice that is a parent structure for the deposited coating and due to this fact, its existence is crucial for the coating formation. As we show, such outer lattices exist only for successfully sorted SWCNTs and the superposition between the outer lattice and SWCNT forms a specific long-period MP. We explain known experimental results of SWCNT sorting by molecules of flavin group, poly(9,9-dioctylfluorene-2,7-diyl), and poly [(m-phenylenevinylene)-alt-(p-phenylenevinylene)]. Also, our approach points out other organic molecules and polymers suitable for effective carbon nanotube sorting.
Export citation and abstract BibTeX RIS
1. Introduction
The phenomenon of moiré pattens has been known for a long time in extremely diverse systems [1]. It occurs, in the simplest form, when overlaying two planar periodic structures which have close periods and a small relative twist angle between them. As a result, a new superstructure with remarkably larger periodicity appears. The closer the periods of overlaid structures and the smaller the twist angle, the greater the periodicity of the moiré pattern (MP) is. The latter fact is often used to determine the difference between lattice constants of two superimposed periodic structures making the MP an efficient tool for controlling the bilayer sample.
Current significant interest to the purely mathematical theory of MPs is due to the active studies of bilayer carbon and similar nanostructures, which are potentially suitable for various nanotechnological applications [2–7]. The analysis of MPs in planar twisted bilayer graphene (TBLG) makes it easy to determine the twist angle and select an approximate unit cell even in the case when the layers are incommensurate to each other and have no common subgroup of translations [8, 9]. Such a unit cell allows one to model and compare with experiments the electronic and phonon properties of heterogeneous multilayer structures [8–13]. There is a whole series of striking works showing how the TBLG physical properties depend on the twist angle. For example, at certain twist angles, new modes [14] become active in Raman spectra. With a decrease in the twist angle, the group velocity of electrons also decreases, until, at a certain angle, it vanishes because of electronic band flattening [2, 15, 16]. Concurrently, the transverse superconductivity becomes possible, and the phenomenon is widely investigated and discussed [17, 18]. The dependence of the above phenomena on the twist angle once again shows that specific structural relationships in coplanar two-dimensional lattices are critical for inducing unusual physical and physical-chemical effects.
The physical properties of double-walled carbon nanotubes (DWCNTs) also depend on the chiral indices of both nanotubes and the angle between their chirality vectors [6, 7, 19–21]. Certain geometric relationships between the chirality vectors of the comprising nanotubes, on the one hand, affect the type of MP, and on the other hand, induce a strong inter-layer coupling and result in inter-tube optical transitions [22–24]. Nevertheless, the existing consideration of MPs in DWCNTs [23] is overcomplicated and incomplete. In particular, despite the obvious similarity, MPs in planar and tubular bilayer structures were not considered within the framework of a unified formalism.
The only way to visualize the MP in a DWCNT is to consider the unrolled cylindrical bilayer. When constructing the DWCNT net, not only the directions of the chiral vectors P and P' of the inner and outer tubes must coincide, but also their angular lengths (2π) must become equal. Therefore, in the direction perpendicular to the axis of DWCNT, it is necessary to uniformly deform the lattice of at least one of the comprising tubes. Such deformation can be small only in very thick DWCNTs, for which the interlayer distance determined by Van der Waals interaction is much less than the tube radius. In relatively thin DWCNTs, the deformation is not small, which leads to interesting features, in particular, as we show here, to the appearance of two overlapped MPs. We explain this effect in the same manner, as the existence of the aperiodic MP in TBLG with large twist angles. As far as we know, the concurrent existence of two MPs was previously discussed only for cases of trilayer graphene [25] and graphene encapsulated by hexagonal boron nitride [22, 26].
Here we show for the first time that MPs are useful not only for interpreting the physical properties of multilayer structures, but also in search for organic molecules suitable for carbon nanotubes sorting. As is known, the existing methods of synthesis do not provide complete control of the chirality of SWCNTs [27] and do not ensure the production of desired SWCNTs of high purity in sufficient quantities [27–29]. Therefore, to date, many methods have been developed for sorting previously obtained SWCNTs according to their structural parameters [29]. For such sorting, various organic molecules are usually used, including polymers, which, when dissolved in certain solvents, are capable to deposit only on carbon nanotubes with the desired structural parameters. This phenomenon, as we have shown earlier [30], depends on the ability of some molecules to wrap around the certain SWCNT in a commensurate way.
Widely applied for the nanotubes sorting flavin mononucleotide (FMN), as is known, can form a dense double-row coating both on some SWCNTs and on planar graphene [31–36]. Here, using this experimental fact, we first reduce the geometric conditions for successful formation of the coating (and, therefore, successful sorting of SWCNTs by these molecules) to an analysis of commensurability and geometric characteristics of MPs appearing between layers of a specific virtual bilayer nanotube. Its inner layer is the SWCNT being sorted, while the outer one is the parent structure for the considered covering. Then, using poly(9,9-dioctylfluorenyl-2,7-diyl) (PFO) polymer molecules as an example, we generalize the proposed approach and show that it also explains the results of SWCNT sorting by those organic molecules, from which one can construct the coating commensurate with the planar graphene.
2. Results and discussion
2.1. Unusual MPs in bilayer carbon structures
It is well known [9] that the period D of the MP arising in planar TBLG is determined by the twist angle ϕ:

where d is the graphene lattice period. This formula can be obtained in different ways. Below we present a simple but general method that allows us to determine the geometric characteristics of the MP arising not only due to the relative twist, but also when the layers are subjected to different uniform strains. We characterize the layers A and B by the microscopic density functions 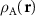 and
and 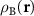 . Obviously, the MP nodes are located in the regions where both structures are similar, which is equivalent to
. Obviously, the MP nodes are located in the regions where both structures are similar, which is equivalent to 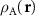 ≈
≈ 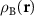 . Instead of two-component radius vector r, it is convenient to use a linearly r dependent two-component quantity (
. Instead of two-component radius vector r, it is convenient to use a linearly r dependent two-component quantity (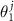 ,
, 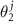 ), where
), where 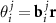 ;
; 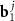 and
and 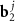 are basis vectors in the reciprocal space of a layer with an index j = A, B. Such a replacement allows us to consider instead of two different density functions the single one, depending on the phase variables
are basis vectors in the reciprocal space of a layer with an index j = A, B. Such a replacement allows us to consider instead of two different density functions the single one, depending on the phase variables 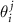 . Accordingly, the positions of the MP nodes are located around the points that satisfy the condition:
. Accordingly, the positions of the MP nodes are located around the points that satisfy the condition:

Since the density function depends periodically on the phase variables, then the obvious particular solution of equation (2), allowing us to find the coordinates r nk , is reduced to the system:

where 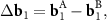
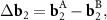 n and m are integer. The system (3) defines the periodic moiré lattice in the direct space. Since there are six vectors in the first coordination circle of the reciprocal space of graphene, and the differences
n and m are integer. The system (3) defines the periodic moiré lattice in the direct space. Since there are six vectors in the first coordination circle of the reciprocal space of graphene, and the differences 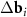 appearing in the right-hand side of equation (3) can be constructed using different pairs of vectors of the first and second layers, the resulting moiré lattice may be not unique. If the layers are not deformed and the twist angle ϕ is less than 30°, then one should simply select two pairs of differences
appearing in the right-hand side of equation (3) can be constructed using different pairs of vectors of the first and second layers, the resulting moiré lattice may be not unique. If the layers are not deformed and the twist angle ϕ is less than 30°, then one should simply select two pairs of differences 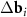 with the smallest equal lengths. In this case |
with the smallest equal lengths. In this case |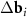 | = 2bsin(ϕ/2), where b is the length of the reciprocal space vectors of the superimposed layers. The latter relation leads to equation (1) in the direct space.
| = 2bsin(ϕ/2), where b is the length of the reciprocal space vectors of the superimposed layers. The latter relation leads to equation (1) in the direct space.
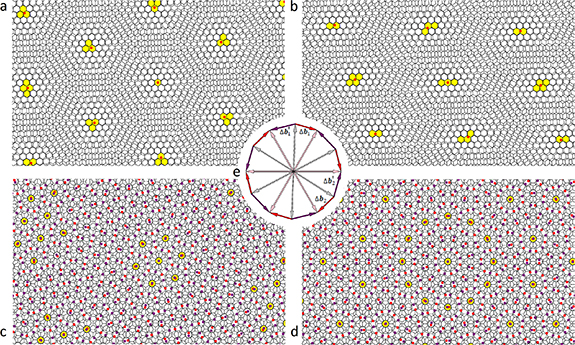
Different cases of MPs in the twisted and strained bilayer honeycomb structure are shown in figure 1. Primitive hexagonal moiré lattices (red and purple circles in figure 1), determined by the system (3), are superimposed on MPs. In the case of small rotation and deformation, the choice of vectors 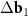 and
and 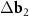 for the constructing moiré lattice is unambiguous (see figures 1(a) and (b)). Nevertheless, if the reciprocal basis vectors of the top and bottom layers are significantly different, the unambiguity in the choice of the vectors
for the constructing moiré lattice is unambiguous (see figures 1(a) and (b)). Nevertheless, if the reciprocal basis vectors of the top and bottom layers are significantly different, the unambiguity in the choice of the vectors 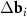 disappears and unusual aperiodic MPs arise. For example, if the twist angle ϕ is close to 30°, then all the differences between the adjacent vectors of the reciprocal space
disappears and unusual aperiodic MPs arise. For example, if the twist angle ϕ is close to 30°, then all the differences between the adjacent vectors of the reciprocal space 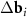 and
and  (figure 1(e)) become close in length and MP loses its visible periodicity (see figure 1(c)). At ϕ = 30°,
(figure 1(e)) become close in length and MP loses its visible periodicity (see figure 1(c)). At ϕ = 30°, 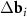 and
and  are equal in length and a quasicrystalline motif appears in the arrangement of the MP nodes [37] (see figure 1(d)). Nevertheless, in the last two considered cases, the lattices determined by the system (3) retain their meaning, since the positions of the MP nodes are determined by two moiré lattices at once (see figures 1(c) and (d)). It is interesting to note that for the aperiodic MP the introduced periodic lattices play approximately the same role as the average periodic lattices [38–40] in the theory of quasicrystalline order.
are equal in length and a quasicrystalline motif appears in the arrangement of the MP nodes [37] (see figure 1(d)). Nevertheless, in the last two considered cases, the lattices determined by the system (3) retain their meaning, since the positions of the MP nodes are determined by two moiré lattices at once (see figures 1(c) and (d)). It is interesting to note that for the aperiodic MP the introduced periodic lattices play approximately the same role as the average periodic lattices [38–40] in the theory of quasicrystalline order.
Figure 1. Moiré patterns of twisted and uniformly deformed bilayer honeycomb lattices. The intersections of overlapped honeycombs are highlighted in yellow if the distance between their centres does not exceed 8% of the hexagon edge. This choice of the cut-off distance between the centers is optimal for better visualization of MPs on all four panels. Red (a)–(d) and purple (c)–(d) dots show the nodes determined by the system (3). (a) Typical MP corresponding to a small twist angle ϕ= 5°. The nodes of the moiré lattice do not always coincide with the centers of the honeycombs. (b) MP corresponding to a small twist angle (ϕ= 5°) and a small deformation ( = 1.05) of the honeycomb lattice. (c) Periodicity in location of the MP nodes is lost when the twist angle (ϕ = 27°) is close to ϕ = 30°; the latter angle value corresponds to the symmetric pattern (d), where the arrangement of the MP nodes becomes quasicrystalline. For the case (c) the reciprocal space vectors (
= 1.05) of the honeycomb lattice. (c) Periodicity in location of the MP nodes is lost when the twist angle (ϕ = 27°) is close to ϕ = 30°; the latter angle value corresponds to the symmetric pattern (d), where the arrangement of the MP nodes becomes quasicrystalline. For the case (c) the reciprocal space vectors (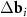 and
and 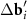 ) of the considered moiré lattices are shown in panel (e). Longer difference vectors
) of the considered moiré lattices are shown in panel (e). Longer difference vectors 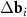 (purple) define the moiré lattice (set of small purple circles) with a shorter period. In panels (c) and (d), the MP nodes lie between the nearest nodes of two considered moiré lattices.
(purple) define the moiré lattice (set of small purple circles) with a shorter period. In panels (c) and (d), the MP nodes lie between the nearest nodes of two considered moiré lattices.
Download figure:
Standard image High-resolution imageAt first glance, it may seem that the MPs arising under uniform deformation of the layers have nothing to do with real carbon structures. Such effective deformations, however, arise in planar nets of DWCNTs (see  (where
(where  is equal to the ratio of nanotube diameters) in the direction perpendicular to the common axis. Since the distance between the tubes is determined by the Van der Waals interaction, the most pronounced uniquely determined MPs can take place in relatively thick DWCNTs (where
is equal to the ratio of nanotube diameters) in the direction perpendicular to the common axis. Since the distance between the tubes is determined by the Van der Waals interaction, the most pronounced uniquely determined MPs can take place in relatively thick DWCNTs (where  is close to 1). Nevertheless, even in relatively thin DWCNTs, depending on the chirality of the comprising layers, a long-period MP may be distinguished. A situation, when it makes sense to consider two moiré lattices concurrently, is also possible. These issues will be considered in more detail in relation to the theory of nanotubes sorting.
is close to 1). Nevertheless, even in relatively thin DWCNTs, depending on the chirality of the comprising layers, a long-period MP may be distinguished. A situation, when it makes sense to consider two moiré lattices concurrently, is also possible. These issues will be considered in more detail in relation to the theory of nanotubes sorting.
2.2. MPs and nanotubes sorting by flavin group molecules
FMN is the phosphorylated form of vitamin B2. It looks like three honeycombs (aromatic isoalloxazine moiety) with a long anionic phosphate tail group (see figure 2) and it wraps around SWCNTs in a helical pattern [31–35]. Flavin group molecules are widely used for both sorting nanotubes and producing graphene nanoribbons [31–36]. When FMN is deposited on graphene, its molecules self-assemble into one-dimensional ribbons, consisting of two FMN rows (with the same structure) linked by hydrogen bonds. According to Yoon et al [36], the FMN aromatic isoalloxazine moieties can be commensurably arranged on the graphene sheet. Namely, they are aligned along the direction of honeycombs dense packing, and adjacent FMN molecules from the same row are translated into each other by the translation S = (0,3) of the honeycomb lattice (figure 2(a)). Usually, several double-row FMN ribbons are deposited on graphene. The arrangement of adjacent FMN ribbons relative to each other is not fixed as rigidly as the arrangement of two FMN rows in one ribbon. This is due to the fact that the dimethyl tail groups of neighboring double-row ribbons can interact only through the Van der Waals interaction, which is weaker than the strong hydrogen bond, and, therefore, does not fix the distance between the ribbons so rigidly.
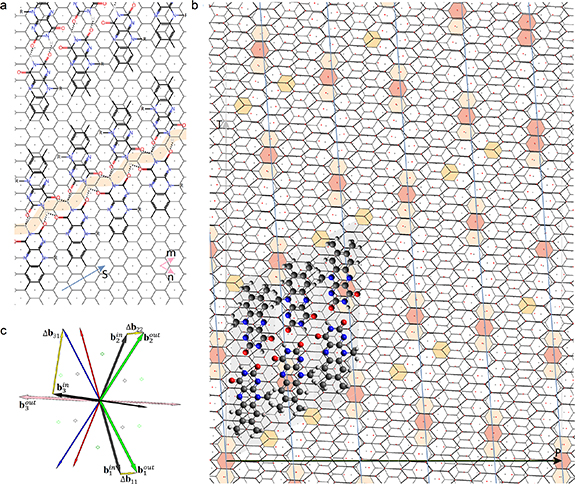
Figure 2. Coatings with FMN molecules: from the planar graphene to SWCNT. (a) Arrangement of FMN on the planar graphene according to Yoon et al [35]. The vector S = (0,3) translating adjacent FMN molecules into each other is shown with a blue arrow. (b) The net of the considered double-walled tube (6,8)@(11,13). The layer corresponding to the inner tube is stretched perpendicular to the tube axis in  ≈ 1.71 times. The inner tube net is shown with black lines. Vertical, slightly oblique blue lines indicate stripes of the main MP. Everywhere in the plotted region the centers of the honeycombs (highlighted in pink) of the top layer are close with the honeycomb centers of the bottom layer. The distance between the nearest centers, however, varies. Thus, a second MP (see the main text) arises. The centers of the yellow cells are translated into each other by the vector S and practically coincide either with the vertices or with the nodes of the inner layer, determining (with the accuracy up to a small uniform deformation) the arrangement of a double-row ribbon of FMN molecules on SWCNT (6,8). Only three molecules in each row are shown. (c) Reciprocal space vectors for the bilayer tube (6,8)@(11,13). Differences between vectors for inner and outer tubes
≈ 1.71 times. The inner tube net is shown with black lines. Vertical, slightly oblique blue lines indicate stripes of the main MP. Everywhere in the plotted region the centers of the honeycombs (highlighted in pink) of the top layer are close with the honeycomb centers of the bottom layer. The distance between the nearest centers, however, varies. Thus, a second MP (see the main text) arises. The centers of the yellow cells are translated into each other by the vector S and practically coincide either with the vertices or with the nodes of the inner layer, determining (with the accuracy up to a small uniform deformation) the arrangement of a double-row ribbon of FMN molecules on SWCNT (6,8). Only three molecules in each row are shown. (c) Reciprocal space vectors for the bilayer tube (6,8)@(11,13). Differences between vectors for inner and outer tubes 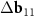 ,
,  correspond to the main MP. The vector
correspond to the main MP. The vector 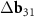 contributes to the formation of the second MP.
contributes to the formation of the second MP.
Download figure:
Standard image High-resolution imageWhen sorting SWCNTs, only one FMN ribbon (or that of FMN-like molecules) wraps around the tube, forming a two-row helical packing that almost completely covers the tube surface. The interlayer gap between the cylinders corresponding to FMN and SWCNT (ΔR ≈ 0.34 nm [31]) is determined by the characteristic length of the Van der Waals interaction. Note that distances between the coating atoms and the distances between their projections on the SWCNT surface can be significantly different, since in order to unroll the tubular structure into a plane sheet (see figure 2(b)), the layer corresponding to the inner tube should be stretched perpendicular to the tube axis by  = (1 + ΔR/R). For SWCNT (6,8)
= (1 + ΔR/R). For SWCNT (6,8)  ≈ 1.71, and therefore the translation between the projections of adjacent FMN molecules on the SWCNT surface cannot be exactly the vector S = (0,3). It is replaced by a close vector S'. The commensurability of the FMN coating with graphene allows us to rigorously find the vector S'. Thus, we reduce the geometric conditions for the successful sorting and formation of the SWCNT coating with FMN group molecules to the analysis of the MP that appears between the layers of specific double-walled nanotubes. In the considered nanotubes, the inner layer is the surface of SWCNT to be sorted, and the outer layer corresponds to a cylindrical honeycomb lattice, on which the arrangement of FMN molecules (typical of the planar case) is projected (figure 2(a)). Precisely, we surround the SWCNT with an external virtual layer, which corresponds to the planar packing of FMN molecules on the honeycomb lattice with translations of the same length as that in graphene.
≈ 1.71, and therefore the translation between the projections of adjacent FMN molecules on the SWCNT surface cannot be exactly the vector S = (0,3). It is replaced by a close vector S'. The commensurability of the FMN coating with graphene allows us to rigorously find the vector S'. Thus, we reduce the geometric conditions for the successful sorting and formation of the SWCNT coating with FMN group molecules to the analysis of the MP that appears between the layers of specific double-walled nanotubes. In the considered nanotubes, the inner layer is the surface of SWCNT to be sorted, and the outer layer corresponds to a cylindrical honeycomb lattice, on which the arrangement of FMN molecules (typical of the planar case) is projected (figure 2(a)). Precisely, we surround the SWCNT with an external virtual layer, which corresponds to the planar packing of FMN molecules on the honeycomb lattice with translations of the same length as that in graphene.
On the tube surface, flavin group molecules tend (if possible) to reproduce a packing as close as possible to the planar one. Therefore, the honeycomb lattice of the inner layer turns out to be as similar as possible to the honeycomb lattice of the outer virtual layer. Within the framework of the theory of MPs, this means that the MP between the cylindrical layers should have maximum periods, and this makes the regions of local similarity between the layers maximally large. Let us recall that the similar phenomenon occurs in the planar case. If ϕ → 0 than, the MP period (see equation (1)) approaches infinity, and the regions of local similarity between the layers grow indefinitely.
The considered long periodicity can be characterized by the area of the MP unit cell, and we select the chirality indices (h, k) of the outer tube in such a way that maximizes the area of this cell. Technically, however, it is more convenient to minimize its inverse value, which is the area of parallelogram, the sides of which are the differences in the basis vectors of the reciprocal spaces of the inner and outer tubes. This minimization (see
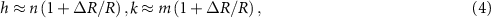
where R is the radius of the inner tube and (n, m) are its chirality indices. Note that, since the integer indices (h, k) specify the radius of the outer nanotube, the use of the relations (4) is not reduced to rounding to the nearest integer: several nearest indices must be considered as well.
FMN group molecules are deposited on three SWCNTs: (6, 8), (6, 5) and (6, 7) [31–35]. For each of these SWCNTs, by enumerating the indices of the outer layer, we have selected three outer tubes that provide the three largest (including the maximal) areas A of the MP cell (see table 1).
Table 1. Selection of the chirality indices of the outer layer. The first column contains chiral indices of the SWCNT under consideration. The 2nd, 5th and 8th columns represent the indices for three possible cases of external virtual tubes; ΔR and A are the interlayer distance and cell area of the corresponding moiré pattern, respectively.
| Inner tube | Tubeout #1 | ΔR, nm | A, nm2 | Tubeout #2 | ΔR, nm | A, nm2 | Tubeout #3 | ΔR, nm | A, nm2 |
|---|---|---|---|---|---|---|---|---|---|
| (6,8) | (11,13) | 0.338 | 56.4 | (10,14) | 0.341 | 355.6 | (9,15) | 0.346 | 17.8 |
| (6,5) | (11,10) | 0.339 | 110.3 | (12,9) | 0.341 | 77.1 | (10,11) | 0.339 | 10.1 |
| (6,7) | (11,12) | 0.339 | 179.8 | (10,13) | 0.341 | 70.6 | (12,11) | 0.339 | 13.85 |
To make the final choice between the selected variants of the outer layer, we note that the projection of the vector S onto the surface of the inner tube must be close to some distinguished point S' that has rational (with a small denominator) coordinates. The distance between FMN molecules in different coatings may lightly vary, and if an energetically favorable commensurate coating is formed on SWCNTs, the end of the vector S exactly coincides with S' point and completely determines the structure of the helical commensurate coating.
Geometric analysis shows that the proximity condition is satisfied only for the coatings from the second column of table 1. For all three inner tubes, the vector S= (0,3) of the outer layer with very good accuracy (|S'− S| < 0.075а, where а is the length of the honeycomb lattice edge) corresponds to vector S' = (−2,7)/3 of the inner layer (see figure 2(b)). The components of the last vector become integer [S' = (1,3)] in the basis of the associated primitive hexagonal lattice (PHL), the nodes of which are both the vertices and the centers of the honeycombs.
Let us discuss in more detail why only the tubes from the tubeout #1 column are suitable as parent structures for the coatings (see table 1). Unlike the other options presented in table 1, for the bilayer structures [(6,8)@(11,13), (6,5)@(11,10) and (6,7)@(11,12)] the approximate equality

is satisfied with very good accuracy. Moreover, in the direction perpendicular to the tube axis, it is fulfilled exactly: n − m= h − k (see explicit expression for the reciprocal space vectors in
It is also useful to consider a case for which the approximate equality (5) is less accurate. For example, from table 1 one can see that for the bilayer structure (6,8)@(10,14) (in which n − m≠ h − k) the area of the MP cell is even larger than in the structure (6,8)@(11,13). At the same time, since the condition (5) is unsatisfied for this tube, the vector S turns out to be quite distant from the nodes and vertices of the honeycomb lattice; therefore, it is simply not possible to associate a certain vector S' with the vector S.
Earlier in the literature [23, 24], DWCNTs, in which points K1 ≡ (b1−b2)/3 of the inner and outer layers are close, have been discussed. Note that this proximity is equivalent to the relation (5). These DWCNTs are interesting since the proximity of K1 points can lead to a strong coupling 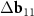 between the layers and the corresponding rearrangement of the electronic spectrum [23, 24]. Koshino et al [23] consider MPs using the nets of similar DWCNTs, but define the reciprocal space vectors of these patterns not as the differences between the basis vectors
between the layers and the corresponding rearrangement of the electronic spectrum [23, 24]. Koshino et al [23] consider MPs using the nets of similar DWCNTs, but define the reciprocal space vectors of these patterns not as the differences between the basis vectors  and
and 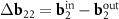 , but as vectors
, but as vectors 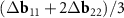 and
and 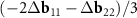 . If K1 points in both layers coincide exactly, then our approach and that of Koshino et al [23] are equivalent. The exact coincidence, however, is possible only in some commensurate DWCNTs. If the coincidence is approximate, then a direct analysis of the MP in the DWCNT nets shows that the approach of Koshino et al [23] leads to inaccurate construction of the moiré lattice. We also note that although the proximity of the points K1 in the reciprocal space of the layers always makes the area of the MP cell large, as we showed above, the general way for maximizing the MP cell area is a choice of double-walled tubes (n, m)@(h, k) for which n/m≈ h/k (see equation (4)).
. If K1 points in both layers coincide exactly, then our approach and that of Koshino et al [23] are equivalent. The exact coincidence, however, is possible only in some commensurate DWCNTs. If the coincidence is approximate, then a direct analysis of the MP in the DWCNT nets shows that the approach of Koshino et al [23] leads to inaccurate construction of the moiré lattice. We also note that although the proximity of the points K1 in the reciprocal space of the layers always makes the area of the MP cell large, as we showed above, the general way for maximizing the MP cell area is a choice of double-walled tubes (n, m)@(h, k) for which n/m≈ h/k (see equation (4)).
Below, we will discuss the general features of MPs in the double-walled tubes (6,8)@(11,13), (6,5)@(11,10) and (6,7)@(11,12), in which the inner layer corresponds to SWCNTs sorted by FMN group molecules and the outer layer is the parent structure of the coating. Since the analysis of the relationships between the inner and outer layers (which is the parent structure for the coating) is similar for all three cases, we consider only the first of them in detail. For a double-walled tube (6,8)@(11,13), the interlayer distance ΔR equals 0.338 nm and, accordingly,  ≈ 1.71. In a planar net of this tube, the end of the vector S = (0,3) of the outer layer practically coincides with the vertex of the stretched honeycomb lattice resulting from the inner tube (see figure 2(b)). For FMN and FMN-like molecules, both the centers of the honeycombs and their vertices are approximately equivalent points of attraction for the deposited molecules [30]. Therefore, one can consider not a honeycomb lattice, but the associated PHL, the nodes of which coincide with both the positions of carbon atoms and with the honeycomb centers.
≈ 1.71. In a planar net of this tube, the end of the vector S = (0,3) of the outer layer practically coincides with the vertex of the stretched honeycomb lattice resulting from the inner tube (see figure 2(b)). For FMN and FMN-like molecules, both the centers of the honeycombs and their vertices are approximately equivalent points of attraction for the deposited molecules [30]. Therefore, one can consider not a honeycomb lattice, but the associated PHL, the nodes of which coincide with both the positions of carbon atoms and with the honeycomb centers.
In the reciprocal space of all three considered double-walled tubes, the differences in the basis vectors approximately coincide: 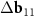 ≈
≈ 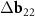 (see figure 2(c); explicit expressions for the reciprocal space basis vectors are given in
(see figure 2(c); explicit expressions for the reciprocal space basis vectors are given in 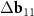 and
and 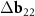 (see figure 2(c)) are small in comparison with the basis vectors themselves, therefore, a long-period MP consisting of long stripes oriented approximately along the tube axis appears in the direct space. In the net of nanotube (6,8)@(11,13) (see figure 2(b)), five such stripes are placed around the tube perimeter, and the moiré lattice edges are parallel to the axis or perimeter of the tube.
(see figure 2(c)) are small in comparison with the basis vectors themselves, therefore, a long-period MP consisting of long stripes oriented approximately along the tube axis appears in the direct space. In the net of nanotube (6,8)@(11,13) (see figure 2(b)), five such stripes are placed around the tube perimeter, and the moiré lattice edges are parallel to the axis or perimeter of the tube.
Another interesting feature of the (6,8)@(11,13) superimposition is the presence of a noticeable second MP, which determines the regions where the centers of the honeycombs of the outer and inner tubes coincide most closely. The difference vector 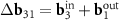 has the third smallest length after vectors
has the third smallest length after vectors 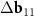 ,
, 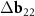 and their trivial linear combination
and their trivial linear combination 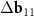 +
+ 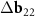 . One can see from direct calculation that the vector
. One can see from direct calculation that the vector 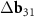 is the basis one for the corresponded MP. As the second basis vector, one can take small (approximately equal) vector
is the basis one for the corresponded MP. As the second basis vector, one can take small (approximately equal) vector 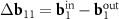 or
or 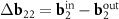 . The difference between the resulting moiré lattices is invisible on the scale of figure 2(c). The nodes of both lattices locate approximately near the centers of the honeycombs that are highlighted in pink. It is also interesting to note that on the scale of the figure, the vectors 3S and 6S practically coincide with the nodes of the moiré lattice corresponding to the second MP. Thus, the emerging MP reflects the closeness of the vectors S and S'.
. The difference between the resulting moiré lattices is invisible on the scale of figure 2(c). The nodes of both lattices locate approximately near the centers of the honeycombs that are highlighted in pink. It is also interesting to note that on the scale of the figure, the vectors 3S and 6S practically coincide with the nodes of the moiré lattice corresponding to the second MP. Thus, the emerging MP reflects the closeness of the vectors S and S'.
This section was mainly devoted to the relationship between the MP theory and the structure of commensurate coatings on SWCNTs that are selected by FMN group molecules. To understand which SWCNTs can in principle be sorted by these molecules, the commensurate vector S' obtained is used. It allows one to calculate the size of the coating unit cells and then check whether the molecules under consideration correspond to these cells. This method was described in detail in [30]. Moreover, if the selection of SWCNTs is carried out by polymer chains, then such an analysis is not needed. While the sidechains of the polymer are not involved in the sorting process and adjacent turns of polymer helices do not overlap, the main selection criterion is associated with the length of the commensurate vector S'. This approach is developed in the next section, where we explore the example of PFO to demonstrate the relationship between the MP theory and the SWCNT sorting by polymer chains.
2.3. SWCNTs sorting using PFO molecules
Using the MP theory, it is possible to draw significant conclusions about the geometric features of the nanotube sorting by polymers. The first polymer used for the sorting was PFO [41, 42]. PFO selectively wraps around certain SWCNTs with small diameter (<1.1 nm) and large chirality angle (>24.5°) [42]. Namely, PFO sorts (7,5), (7,6), (8,6), (8,7), (9,7) and (9,8) SWCNTs dispersed in toluene [41–43].
Currently, the list of polymers utilized for the sorting has expanded significantly [44]. In particular, conjugated polymers are widely used for this purpose. Most of them include a fragment structurally close to PFO molecule (see figure 3 in [44]). Below, basing on the generality of the PFO structural motif, we consider the geometric regularities of the SWCNT sorting by polymers, using the PFO example.
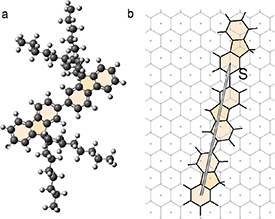
The molecule consists of a polymer backbone that looks like two hexagonal aromatic rings connected through a pentagon (see figure 3(a)) and long alkyl sidechains. In the process of sorting by means of PFO, main polymer chains wrap around the selected SWCNT, and the alkyl sidechains branch away from the nanotube [43]. At a low concentration of PFO molecules in solution, the interactions between the alkyl sidechains can be neglected [45], and this is the case we consider.
Figure 3. Geometrical regularities of SWCNT sorting by PFO molecules. (a) Pair of PFO molecules. The sidechains in the molecule are perpendicular to the aromatic plane. (b) The commensurate superimposition of PFO molecules on planar graphene. In the proposed symmetrized model, the length of a pair of adjacent PFO molecules (1.674 nm) and the orientation of the polymer chain are determined by the vector S = (23, −16) /3; here, it is expressed in the basis of the honeycomb lattice.
Download figure:
Standard image High-resolution imageNote that there is no experimental evidence that PFO molecules (like FMN ones) can form commensurate coatings on the planar graphene. The sidechains of these molecules (figure 3(a)) may block the formation of such coatings. Nevertheless, based on the estimate of the PFO molecule length (≈0.84 nm [46]), we propose a parent commensurate packing of the PFO backbone on the planar graphene (see figure 3(b)). Based on this parent packing, it is easy to adapt the method developed in the previous section to the present case.
As in the previous section, the vector S, translating pairs of molecules into each other, is an integer in the basis of the associated PHL, the vertices of which coincide with both vertices and centers of the honeycombs. This time, however, in contrast to the previous section, in order to construct a theory suitable for explaining the known experimental data, the parent outer tubes (corresponding to PFO molecules) are chosen as rolled up not from the honeycomb lattice, but from the associated PHL. Since for the chirality indices of the outer tubes, we continue to use the basis of the honeycomb lattice, the coefficient 3 may appear in the denominators of these indices. Naturally, to find the outer tubes that lead to the maximum area of the MP cell (see (A6) in
A simple Python program, with the help of which table 2 was filled, is given in supporting information (available online at stacks.iop.org/NANOF/6/015005/mmedia). The algorithm enumerates all left- and right-handed semiconducting SWCNTs with a radius less than 0.75 nm and selects outer parent tubes ensuring a sufficiently large moiré lattice cell. As we checked, in the considered range of radii for each inner SWCNT, there are one or several outer tubes for which ![$|[\Delta {{\mathbf{b}}_1} \times \Delta {{\mathbf{b}}_2}]| < 1$](https://content.cld.iop.org/journals/2399-1984/6/1/015005/revision2/nanofac4a27ieqn46.gif) nm−1 (see
nm−1 (see
Table 2. Modeling of the SWCNT sorting by PFO molecules. The table columns contain, respectively: indices of the sorted SWCNT, tripled indices of the outer parent tube, tripled coordinates of the vector S ' obtained after the projection of the vector S onto the surface of the inner tube, the radius of the inner tube Rin, the interlayer distance ΔR, the length of the vector S ', the angle ϕ between the axis of the SWCNT and the direction of the polymer helix.
| (n, m) | 3(h, k) | 3S' | Rin | ΔR | |S'| | ϕ |
|---|---|---|---|---|---|---|
| (5, 7) | (29, 38) | (22, −17) | 0.409 | 0.351 | 1.667 | 12.894 |
| (6, 8) | (32, 41) | (22, −17) | 0.476 | 0.351 | 1.668 | 13.389 |
| (7, 6) | (36, 33) | (21, −18) | 0.441 | 0.339 | 1.665 | 17.534 |
| (7,8) | (36, 39) | (22, −17) | 0.509 | 0.339 | 1.684 | 16.868 |
| (7, 9) | (35, 44) | (22, −17) | 0.544 | 0.351 | 1.667 | 13.642 |
| (8, 6) | (41, 32) | (22, −17) | 0.476 | 0.351 | 1.685 | 20.745 |
| (8, 9) | (39, 42) | (21, −18) | 0.577 | 0.339 | 1.679 | 16.510 |
| (6, 5) | (35, 29) | (21, −18) | 0.373 | 0.351 | 1.686 | 19.938 |
| (8, 10) | (36, 48) | (22, −17) | 0.611 | 0.341 | 1.665 | 13.632 |
| (8, 10) | (38, 47) | (22, −17) | 0.611 | 0.351 | 1.666 | 13.767 |
| (10, 11) | (45, 48) | (22, −17) | 0.712 | 0.339 | 1.672 | 15.929 |
| (10, 11) | (44, 50) | (22, −17) | 0.712 | 0.351 | 1.673 | 16.100 |
| (10, 12) | (42, 54) | (22, −17) | 0.747 | 0.341 | 1.663 | 13.718 |
| (10, 12) | (44, 53) | (22, −17) | 0.747 | 0.351 | 1.663 | 13.840 |
| (9, 10) | (42, 45) | (22, −17) | 0.644 | 0.339 | 1.675 | 16.200 |
| (9, 11) | (39, 51) | (22, −17) | 0.679 | 0.341 | 1.664 | 13.694 |
| (9, 11) | (41, 50) | (22, −17) | 0.679 | 0.351 | 1.665 | 13.823 |
Note that since the symmetry of plane graphene is C6v and the vector S has trivial symmetry, there are 12 equivalent orientations of this vector. The vectors S and −S, however, define the same helix on the tube surface. Also, since we iterate over both left and right-handed SWCNTs, we restrict ourselves to three symmetrically equivalent orientations S i : S1= (23, −16)/3; S2= (−7, 23)/3 and S3= (−16,7)/3.
For unambiguous definition of S ', the deviation between S and S ' should not exceed a quarter of the distance between the nearest carbon atoms. This accuracy is set in the program (see supporting information). After determining the vector S ', its length |S '| is calculated. It may change slightly due to stretching or contraction of the polymer chain when it wraps around the nanotube. Nanotubes presented in table 2 satisfy the semiempirical condition 1.6 < |S '| < 1.695 nm. In this inequality, the lower limit is the length of two monomer units for the α-conformation of PFO chain [47, 48]. The conjugation length of the highly ordered β-conformation is longer than that of the α phase [47, 48] and the upper limit of the inequality is the maximal estimate of this length obtained using the Avogadro software [49]. The Auto Optimize tool was applied to optimize the SWCNT-PFO geometry through molecular mechanics. In addition, we impose the second condition on possible values of the angle ϕ between the tube axis and the direction of PFO helix: 5° < ϕ< 35°. All the coatings selected by two abovementioned conditions are listed in the table 2 and correspond exclusively to the vector S1= (23, −16)/3.
Refining the second conditions, we note that the β-conformation has an intrachain torsion angle equal to 165°. The corresponding small intrinsic curvature of the polymer chain in this conformation (due to the slight difference between the torsion angle and 180°) does not allow PFO molecules to be located directly along the axis of the tube.
Concurrently, the rigidity of the chain prevents its excessive bending and wrapping around the tube if the angle ϕ is too large. This justifies the second condition, which is rather mild. According to the experimental data [45], at a low concentration of PFO molecules in the toluene solution, the angle ϕ in different SWCNTs can vary from 12° to 22°. Thus, in our opinion, the β-conformation is suitable to sort SWCNTs. In contrast to the β-conformation, the α-one does not sort SWCNTs because of the smaller torsion angle of 35° and, accordingly, the larger intrinsic curvature.
First seven lines of the table 2 correspond to nanotubes experimentally selected by PFO molecules. The next seven lines contain data on four SWCNTs selected by polyfluorene derivatives with extended alkyl sidechains [43]. These 14 lines mentioned above are highlighted in bold. One more argument confirming the model applicability for explaining the results of sorting by PFO molecules is the fact that according to the experimental data [45], the values of the angle ϕ in tubes (7,5), (8,6), and (8,7) are [12, 17 and 14] ±2°, respectively. For the first and last SWCNTs, the discrepancies between the model and the experiment are 1° and 3° (see the last column of the table 2). At the same time, for SWCNTs (6,8) and (8,6) the model predicts the following angle values 13.39° and 20.75°. The experimentally measured value 17° is closer to the first predicted angle with an error of 3.61°.
Although the two last tubes [(9,10) and (9,11)] presented in table 2 satisfy the above-mentioned selection conditions, they are not sorted by PFO molecules or its derivatives in known experiments. Additional conditions leading to a stricter and more correct selection could be of different physicochemical nature and their discussion clearly goes beyond the aim of our work that is mainly devoted to the application of the MP theory for the SWCNT sorting. Note also, that we were unable to adapt the proposed geometric scheme for the selection of SWCNTs by the polyfluorene derivatives with extended alkyl sidechains [43]. This is primarily because our approach does not take into account the effect of interactions between alkyl sidechains on SWCNT sorting. In the next section, we will consider one more example useful for further developing the proposed approach.
2.4. SWCNTs sorting using PmPV molecules
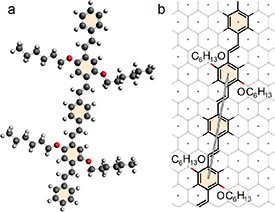
The sorting of SWCNTs by poly [(m-phenylenevinylene)-alt-(p-phenylenevinylene)] (PmPV) was investigated in the work [50]. During this study pure SWNTs were added to the solution of PmPV in tetrahydrofuran, and after that the mixture was sonicated and centrifugated several times. At the end of the processing, it was found that only two semiconductor SWCNTs (11,6) and (11,7) were polymer-wrapped. Note also that the PmPV wrapping can be used not only for the sorting of nanotubes, but also for the fabrication of light-emitting diodes [51]. Like the PFO case, the deposition of this polymer on graphene has never been observed and the reason to discuss this example is a fact that the translation between neighboring molecules in the polymer chain coincides unambiguously with the translation (2,4) of graphene (see figure 4).
Figure 4. Commensurability between graphene and PmPV chain. (a) Pair of PmPV molecules. The sidechains in the molecule are perpendicular to the aromatic plane. (b) The commensurate superimposition of the chain on planar graphene. Translation between adjacent molecules in the PmPV chain coincides with the graphene translation S = (2,4), which is indicated by a long arrow.
Download figure:
Standard image High-resolution imageTo consider the SWCNT sorting by PmPV molecules, we use the method described in detail above. Due to the simple commensurability between graphene and PmPV chain, the outer virtual tubes have the honeycomb lattice, which simplifies their selection (see supporting information). For all possible semiconducting inner SWCNTs with a diameter 2Rin < 1.5 nm table 3 represents all possible outer virtual layers that satisfy the relation (4) (with accuracy 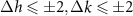 and two additional conditions. First, we limit the interlayer distance ΔR as 0.34 ± 0.05 nm. Second, we suppose that in the net of bilayer structure, translation S (or translation S
i
that is symmetrically equivalent to S) fits a translation S' of the outer layer with an accuracy better than 0.1а0. Note that for bilayer structures represented in table 3, the length S' and value ϕ are not additionally restricted. Thus, the program used to obtain table 3 is a simplified version of the program used to explain the peculiarities of PFO sorting (see both programs in supporting information).
and two additional conditions. First, we limit the interlayer distance ΔR as 0.34 ± 0.05 nm. Second, we suppose that in the net of bilayer structure, translation S (or translation S
i
that is symmetrically equivalent to S) fits a translation S' of the outer layer with an accuracy better than 0.1а0. Note that for bilayer structures represented in table 3, the length S' and value ϕ are not additionally restricted. Thus, the program used to obtain table 3 is a simplified version of the program used to explain the peculiarities of PFO sorting (see both programs in supporting information).
Table 3. Modeling of the SWCNT sorting by PmPV molecules. The table columns are analogous to those of table 2.
| (n, m) | (h, k) | S' | Rin | ΔR | |S'| | ϕ |
|---|---|---|---|---|---|---|
| (8, 3) | (14, 7) | (4, −6) | 0.385 | 0.339 | 1.311 | 8.236 |
| (8, 12) | (13, 17) | (1, 3) | 0.683 | 0.338 | 1.315 | 83.601 |
| (8, 13) | (13, 18) | (1, 3) | 0.719 | 0.337 | 1.295 | 84.345 |
| (9, 11) | (14, 16) | (1, 3) | 0.679 | 0.339 | 1.310 | 81.381 |
| (11, 6) | (16, 11) | (1, 3) | 0.585 | 0.336 | 1.315 | 72.978 |
| (11, 7) | (16, 12) | (1, 3) | 0.615 | 0.337 | 1.308 | 74.374 |
| (11, 9) | (16, 14) | (1, 3) | 0.679 | 0.339 | 1.288 | 76.771 |
| (13, 5) | (19, 9) | (4, −6) | 0.630 | 0.339 | 1.307 | 7.232 |
Let us compare the data from table 3 with the experimental results [50]. The initial solution in the study [50] contained two types of metallic and 19 types of semiconducting tubes. The observed sorting of the metallic tubes (12,6) and (8,8) can occur due to specific electrostatic interactions and here we do not discuss this phenomenon. Among the tubes dispersed in solution, PmPV molecules exhibited a profound affinity only to two semiconducting SWCNTs (11,6), (11,7). These both tubes satisfy the above formulated selection rules and are presented in table 3.
The same table also contains tube (8,3), on which PmPV molecules were deposited initially, but retained worse than on the tubes (11,6) and (11,7). According to [50], the tube (10,3) also has a similar lower affinity. This tube is absent in the table 3 since for this tube ΔR = 0.3474 nm and this value is slightly larger than the chosen upper limit. Its increase up to 0.348 nm, along with the tube (10,3), leads to the selection of three more semiconducting SWCNTs, none of which were dispersed in the solution studied in [50]. Also, it is interesting to note that, within the framework of the proposed model, in tubes (8,3) and (10,3), the polymer chain has a small angle (8.24° and 3.22°, respectively) with the nanotube axis, which is probably less energetically favorable for PmPV molecules.
Concluding this section, we stress that five SWCNTs from table 3 were not dispersed in the solution [50], and it would be interesting to experimentally verify the possibility of PmPV deposition on these tubes. Deposition of PmPV on the SWCNTs (8,12), (9,11), and (13,5) is most probable, since within the framework of our theory resulting bilayer structures would be structurally closest to the experimentally observed wrappings of tubes (11,6) and (11,7).
3. Conclusion
In this work, we discussed previously unknown aspects of the MPs theory and applied the obtained results to explain the experimental data on SWCNT sorting by organic molecules. Using the experimental fact that FMN and FMN-like molecules can form coatings on both planar graphene and nanotubes, we for the first time reduced the conditions of the successful sorting to the analysis of MPs appearing between the layers of certain double-walled nanotubes. In these tubes, the inner layer corresponds to the surface of the SWCNT to be sorted. The outer layer is a honeycomb lattice rolled up into a tube, onto the surface of which the arrangement of FMN molecules (typical of the planar case) can be projected. FMN and FMN-like molecules on the SWCNT surface tend (if they can) to reproduce their planar packing as closely as possible. Therefore, the honeycomb lattice of the inner layer should be as similar as possible to the honeycomb lattice of the outer parent (virtual) layer. Within the framework of the MP theory, this means that the MP formed by superimposition of the layers should have a large period, which makes the regions of local similarity between the inner and outer layers larger. In addition, the projection of the vector S (which translates the molecules of the outer layer) onto the inner one should be close to some distinguished vector S' that has rational coordinates. In the proposed structural models of coatings with FMN-like molecules, the vectors S and S' are very close and approximately commensurate with the translation of the additional, second MP, which emerges in the nets of the double-walled nanotubes under consideration.
We also applied our approach to explain the results of SWCNT sorting by PFO and PmPV molecules. For these cases we hypothesized how the polymer backbone can be located on a planar graphene layer. Then, using the proposed structural model, we explained the experimental results of SWCNT sorting by the considered molecules. Following this way, we predicted several SWCNTs, which can also be sorted by PmPV molecules. Many conjugated polymers (e.g. poly(9,9-dioctylfluorene-alt-benzothiadiazole), poly(9,9-dioctylfluorene-alt-pyridine), copolymer of 9,9-dioctylfluorenyl-2,7-diyl and bipyridine, copolymers containing the carbazole and thiophene units), which are widely used today for the nanotube sorting, contain PFO or structurally similar to PFO molecules [44]. Therefore, the geometric regularities of the SWCNT sorting by PFO molecules can be generalized to a wide range of polymers that form or can form commensurate periodic coatings on planar graphene.
Acknowledgments
Authors acknowledge financial support from the Russian Foundation for Basic Research (Grant No. 18-29-19043 mk). We thank Vladimir Dmitriev and Dmitrii Chalin for useful discussions.
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).
Appendix.: Direct and reciprocal spaces of DWCNT planar projection
Considering SWCNT translational and rotational symmetry, it is convenient to project graphene basis translations a1 and a2 on the surface of a nanotube [52, 53] and calculate the components of these translations along its perimeter and axis. Here, the first component of the translations is the projection on the SWCNT perimeter, while the second one is the longitudinal projection. For a SWCNT with the chiral indices (n, m), one can obtain:

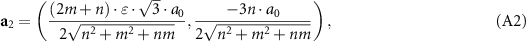
where а0 = 0.142 nm is the distance between the nearest carbon atoms;  = 1 for the outer nanotube and
= 1 for the outer nanotube and  = dout/din for the inner nanotube; dout and din are the outer and inner nanotube diameters. Using the condition
= dout/din for the inner nanotube; dout and din are the outer and inner nanotube diameters. Using the condition 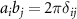 , where
, where 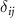 is the Kronecker delta, one can easily obtain the components of the reciprocal lattice vectors b1 and b2:
is the Kronecker delta, one can easily obtain the components of the reciprocal lattice vectors b1 and b2:
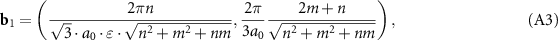

Due to effective stretching perpendicular to the axis of the inner tube, not only the distances change, but also the angles between the directions. In particular, the modified chiral angle can be written as:

In the DWCNT net, the area A of one unit cell of a long-periodic MP (for which the absolute value of the differences 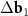 and
and 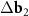 between the basis vectors of the outer and the inner layers are essentially less than their lengths) can be found as
between the basis vectors of the outer and the inner layers are essentially less than their lengths) can be found as

For any inner SWCNT (n, m), maximizing (A6) with a condition imposed on the diameter of the outer tube, one can choose the latter tube with the most similar structure. In the net of the obtained double-walled tube, the basis directions of the honeycomb lattice in different layers turn out to be close. More precisely, if we set the chirality indices (nin, min) of the inner tube, fix the diameter of the outer tube, and assume that the indices of the outer tube (nout, mout) are real (not necessarily integers) numbers, then the problem of (A6) maximization is solved exactly:

The relation (A7) leads to the equation (4) of the main part of the article.