Abstract
Quantum tomography is currently the mainly employed method to characterize a quantum system and therefore plays a fundamental role when trying to characterize the action of a particular channel. Nonetheless, quantum tomography works on the premise of a full characterization and description of the devices preparing the quantum state and realizing the measurements. Such an assumption was recently relaxed in Dall'Arno et al (arXiv:1805.01159) and Dall'Arno et al (2017 Proc. R. Soc. A 473 20160721), where a theoretical framework for the device-independent inference of quantum channels was developed and experimentally implemented with superconducting qubits. Here, based on such a framework, we present a complete experimental test on a photonic setup of two semi-device-independent protocols that can be employed for the validation of the tomographic reconstruction or the characterization of a given quantum channel, not relying on many assumptions on the adopted device. Our implementation paves the way to the development of new experimental methods not relying on the assumptions typically taken for granted in all the previous protocols.
Export citation and abstract BibTeX RIS
Measurements are essential to acquire information about physical systems and its dynamics in any experimental science. In quantum physics, in particular, the importance of measurements is promoted even further since they perturb the quantum system under scrutiny and thus require a new understanding of how to connect observed empirical data with the underlying quantum description of nature. To cope with that, we can rely on quantum tomography [1–3], a general procedure to reconstruct quantum states and channels from the statistics obtained by measurements on ensembles of quantum systems. However, how can one guarantee that the measurement apparatus is measuring what it is supposed to? In practice, experimental errors are unavoidable and such deviations from an ideal scenario not only can lead to the reconstruction of unphysical states [4] but also imply false positives in entanglement detection [5–7] and compromise the security in quantum cryptography protocols [8–11].
Strikingly, with the emergence of quantum information science, a new paradigm has been established for the processing of information. This is the so-called device-independent (di) approach [12–16], a framework where conclusions and hypotheses about the system of interest can be established without the need of a precise knowledge of the measurement apparatus/devices. In some cases, however, some assumptions are needed, for instance imposing a upper bound to the dimension of the Hilbert space of the quantum states, a scenario typically refereed as semi-device-independent (sDI), introduced in [17, 18]. The prototypical example of how the DI reasoning works is given by Bell's theorem [19, 20], which implies experimentally testable inequalities, whose violation certifies the presence of entanglement and provides further information about the quantum state, such as its dimension [21, 22] or fidelity with a maximally entangled state [23]. In other words, even with no information whatsoever about what measurements are being performed, general features of the quantum state can be recovered. A natural question is then whether the di approach can also be adopted within the other pillar of quantum tomography: the reconstruction of quantum channels.
This question was very recently answered on the affirmative by Dall'Arno et al in [24, 25], where a general theoretical framework for the device-independent inference of unknown quantum channels, given as a black-box, was derived and experimentally implemented with superconducting qubits. In this article, based on such a framework, we assume that the dimension of the system under study is 1-qubit and that the quantum channel is D2-covariant. Considering the Bloch sphere representation, a 1-qubit D2-covariant channel maps the sphere into an ellipsoid, translated along one of its symmetry axes, as shown in figure 1. This symmetry restriction, about which we will give an insight later, includes however many frequently studied and implemented quantum channels, as the amplitude damping and Pauli channels.
Figure 1. Bloch sphere representation of the action of a general qubit dihedrally-covariant channel. The Bloch sphere is mapped into an ellipsoid with semi-axis d1, d2, and d3, which is translated along one of its own axis (d3, in the figure) by a distance c3.
Download figure:
Standard image High-resolution imageHence, the semi-device-independent feature of protocols we are going to present, i.e. semi-device-independent tomography validation (sDI–TV) and semi-device-independent channel characterization (sDI–CC).
The first protocol is schematically represented in figure 2(a) and can be performed after a usual tomography. If the results given by the QPT are not compatible with the semi-device-independent reconstruction, the tomography is falsified. On the other hand, if the sDI–TV gives no evidence of incorrectness of the tomography results, we cannot undoubtedly conclude that the reconstruction of the QPT is correct, but the compatibility of the two algorithms' results strengthens the confidence about the validity of the reconstruction. Therefore, we propose, as a further step, an algorithm to quantify the compatibility of the results of the two approaches. Following the sDI–TV, we implement a second protocol, depicted in figure 2(b): a semi-device-independent channel characterization (sDI–CC), where we have no information about the nature of the channel and, by preparing random quantum states and measuring random observables, we can determine the equivalence class of channels that are compatible with the measurement data and as little else as possible. Such a minimal compatibility criterion will be explained in what follows. The two protocols, as mentioned, are semi-device-independent, since they require an assumption about the dimensionality of the system under study and about its simmetry, being restricted to 1-qubit D2-covariant quantum channels. However, the performed measurements can be completely non characterized and acting on a Hilbert space of arbitrary dimension, provided that the registered outcome is relative to the subspace of the qubit that has gone through the channel, and there is no need to assume independence between the state preparation and measurement stage. In this work, we apply the proposed protocols on two different types of quantum channels, the amplitude damping and the dephased amplitude damping channels, by exploiting a photonic setup and using a qubit encoded in the photons' polarization degree of freedom.
Figure 2. Summary of the sDI tests. (a) sDI–TV (semi-device-independent tomography validation): we first perform a standard quantum process tomography (QPT) on the channel, using maximum likelihood estimation [26, 27]. We then find the set of correlations compatible with the reconstructed channel and perform additional measurements, obtaining correlations  that can invalidate the QPT if they do not belong to the expected set. (b) sDI–CC (semi-device-independent channel characterization): in this case we do not perform the QPT, instead we collect a fixed number of correlations
that can invalidate the QPT if they do not belong to the expected set. (b) sDI–CC (semi-device-independent channel characterization): in this case we do not perform the QPT, instead we collect a fixed number of correlations  , spanning uniformly the Bloch sphere with the states ρi and measurements πj (but, as opposed to QPT, without any assumption on their actual physical implementation). Then we find the channel parameters (see [24, 25] and supplementary material) that best fit the set of experimentally found correlations.
, spanning uniformly the Bloch sphere with the states ρi and measurements πj (but, as opposed to QPT, without any assumption on their actual physical implementation). Then we find the channel parameters (see [24, 25] and supplementary material) that best fit the set of experimentally found correlations.
Download figure:
Standard image High-resolution imageThe scenario of interest is depicted in figure 3. In order to characterize an unknown quantum channel  via tomography, we prepare a number of known quantum states ρi that evolve as
via tomography, we prepare a number of known quantum states ρi that evolve as  and that are then measured according to a measurement operator πj associated with outcome j. For example, for a single qubit, quantum process tomography (QPT) [28] requires the preparation of the states
and that are then measured according to a measurement operator πj associated with outcome j. For example, for a single qubit, quantum process tomography (QPT) [28] requires the preparation of the states  ,
,  ,
,  ,
,  and the projection onto the eigenstates of the Pauli matrices
and the projection onto the eigenstates of the Pauli matrices  , σy and σz. By the Born's rule we associate the observed statistics with the state and measurements via
, σy and σz. By the Born's rule we associate the observed statistics with the state and measurements via ![${p}_{j| i}=\mathrm{Tr}\left[{\pi }_{j}{ \mathcal X }({\rho }_{i})\right]$](https://content.cld.iop.org/journals/2058-9565/4/3/035004/revision2/qstab19f2ieqn10.gif) and, if we know ρi and πj, this equation can be inverted to find the expression for the channel
and, if we know ρi and πj, this equation can be inverted to find the expression for the channel  . However, if we have no information (or trust) about the states and measurements, what kind of relevant information can be extracted from the observed statistics
. However, if we have no information (or trust) about the states and measurements, what kind of relevant information can be extracted from the observed statistics  ? A given quantum channel defines a convex set of m- input/
? A given quantum channel defines a convex set of m- input/  output correlations
output correlations  that are compatible with it (
that are compatible with it ( ). Thus, as noticed in [24, 25], if the experiment produces a point
). Thus, as noticed in [24, 25], if the experiment produces a point  outside the boundary of the correlation set of a channel, taken as hypothesis (for example arising from the quantum process tomography), we can unambiguously exclude this channel as potential candidate for our reconstruction. Alternatively, if the measured correlation points
outside the boundary of the correlation set of a channel, taken as hypothesis (for example arising from the quantum process tomography), we can unambiguously exclude this channel as potential candidate for our reconstruction. Alternatively, if the measured correlation points  fall within the set, the hypothesis is not falsified and one can move further, searching for a confidence range within which the QPT and the semi-device-independent reconstruction are compatible. Moreover, overlooking any device-dependent channel reconstruction, one can find the best quantum channel fitting the data, as the 'minimal surviving hypothesis', that is, the channel
fall within the set, the hypothesis is not falsified and one can move further, searching for a confidence range within which the QPT and the semi-device-independent reconstruction are compatible. Moreover, overlooking any device-dependent channel reconstruction, one can find the best quantum channel fitting the data, as the 'minimal surviving hypothesis', that is, the channel  whose boundary contains all the observed correlations set, but minimizing the surrounded volume, as first proposed in [24, 25]. Note that this protocol cannot unambiguously determine all of the characterizing parameters of the quantum channel, so it actually enables to single out the equivalence class to which it belongs (see supplementary material of [24]. Considering the case where i, j = 0, 1, that is two possible state preparations and a dichotomic measurement, as mentioned before, we restrict to the class of 1-qubit quantum channels, which are invariant under the dihedral group D2. Indeed, given that
whose boundary contains all the observed correlations set, but minimizing the surrounded volume, as first proposed in [24, 25]. Note that this protocol cannot unambiguously determine all of the characterizing parameters of the quantum channel, so it actually enables to single out the equivalence class to which it belongs (see supplementary material of [24]. Considering the case where i, j = 0, 1, that is two possible state preparations and a dichotomic measurement, as mentioned before, we restrict to the class of 1-qubit quantum channels, which are invariant under the dihedral group D2. Indeed, given that  is convex, according to the hyperplane separation theorem [29, 30],
is convex, according to the hyperplane separation theorem [29, 30],  if and only if there exists a m × n matrix ω such that
if and only if there exists a m × n matrix ω such that
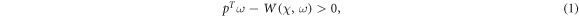
where  and
and  where ω is a channel witness and W its treshold, for channel χ. Depending on the ω witness, we are able to exclude some correlations but, finding the optimal witness, to exclude all the incompatible correlations, also for a 1-qubit channel, would involve a NP-hard optimization problem, which becomes feasible for specific symmetries, as the dihedral group [24, 25]. These channels, for which the boundary of the set of correlations was recently characterized [24, 25], can be represented by four real numbers
where ω is a channel witness and W its treshold, for channel χ. Depending on the ω witness, we are able to exclude some correlations but, finding the optimal witness, to exclude all the incompatible correlations, also for a 1-qubit channel, would involve a NP-hard optimization problem, which becomes feasible for specific symmetries, as the dihedral group [24, 25]. These channels, for which the boundary of the set of correlations was recently characterized [24, 25], can be represented by four real numbers  and, as already mentioned, map the Bloch sphere into an ellipsoid translated along one of its own axis. This transformation is pictorially represented in figure 1 (see supplementary material, available at stacks.iop.org/QST/4/035004/mmedia for further details), which shows that geometrically d1, d2 and d3 represent the ellipsoid's axes, and c3 the translation along the z axis.
and, as already mentioned, map the Bloch sphere into an ellipsoid translated along one of its own axis. This transformation is pictorially represented in figure 1 (see supplementary material, available at stacks.iop.org/QST/4/035004/mmedia for further details), which shows that geometrically d1, d2 and d3 represent the ellipsoid's axes, and c3 the translation along the z axis.
Figure 3. Schematic representation of a measurement process. A state ρi is prepared and sent through the unknown channel, after which we perform a measurement πj. Repeating the process for different combinations of states and measurements we get the correlations  .
.
Download figure:
Standard image High-resolution imageSemi-device-independent tomography validation. Now, let us consider the goal of characterizing an implemented quantum channel through a tomography, however without trusting our apparatus and therefore requiring a device-independent validation to state its correct functioning. Sticking to the hypothesis of D2 covariance, we perform the QPT, restricting to the hypothesis of dihedral covariance (see supplementary material), and find the four parameters (d1, d2, d3, c3) that identify our channel. This restriction is fully supported by our experimental evidence, indeed the fidelity between the general and the D2-covariance restricted quantum process tomographies, performed on all the implemented channels, has been found to be always higher than 0.99. As following step, we are able to reconstruct the hypothetical channel's boundary of the set of input/output correlations [24, 25]. The tomographic experiment is considered compatible to the results given by the semi-device-independent reconstruction if, uniformly spanning the whole set of correlations, all the observed data fall within the boundary. Otherwise, the quantum process tomography is falsified (for a numerical example, see supplementary material). In principle, it is possible to exploit the same data set, both for the quantum process tomography and the DI validation. Indeed, in the latter case, the data would be interpreted as bare correlations, without any assumptions about states and measurements. Clearly, however, a better validation includes additional experimental data probing the boundary of the set defined by the channel being validated. After a tomographic reconstruction is validated, we need to quantify the compatibility between our tomographic reconstruction and the semi-device-independently obtained results, since, if the boundary lies too far from the observed points, the hypothesis, although in principle validated, would not be really supported by the data. In other words, a good hypothesis is an 'almost falsified one': its boundaries should enclose all the observed correlations, but not much more [24].
This protocol was applied to experimental data, in order to validate quantum process tomography on 1-qubit quantum channels. The implementation, as well as the characterization of the channels, was performed exploiting the photonic platform in figure 4. The setup can be seen as made of three parts: (i) photonic state preparation, (ii) quantum channel, (iii) measurement station. In part (i), the desired state is prepared encoding one qubit in the polarization degree of freedom of a photon which goes through an apparatus made of a polarizing beam splitter (PBS1), followed by a quarter- and half- wave plate (G1 and G2). The photon is generated by a heralded photon source making use of a spontaneous parametric down-conversion (SPDC) process, where the second photon of the pair is used as a trigger. In part (ii), our quantum channel is made of two birefringent calcite crystals (C1 and C2), followed by a beam splitter, and has the aim of introducing a desired amount λ of decoherence between path a and b, depending on the rotation of the half-wave plate H2. The measurement station in part (iii) allows to perform projective measurements, through the sequence of a quarter- and a half- wave plate (M1 and M2), followed by a PBS2 (see supplementary material).
Figure 4. Experimental apparatus. In the preparation stage a couple of photons is generated by a spontaneous parametric down-conversion (SPDC) process in a nonlinear crystal. Photon 1 will act as a trigger while photon 2's polarization encodes the particular qubit to be analyzed. The state preparation is performed by a polarizing beam splitter (PBS1), a quarter-wave plate (G1) and a half-wave plate (G2), which rotates the horizontal polarization of incoming photons in order to generate  +
+  . After the preparation of the state, photon 2 is sent to the amplitude damping channel section (yellow stage) composed by a first calcite crystal (C1), two half-wave plates (H1 and H2) one for each generated path and another calcite crystal (C2) to recombine the paths. Setting the angle of H1 at 45o we are able to close the calcite interferometer thus sending the photons to the output 'a'. Conversely, when H1 is at 0°, photon 2 comes out in path 'b' projected onto the vertical polarization
. After the preparation of the state, photon 2 is sent to the amplitude damping channel section (yellow stage) composed by a first calcite crystal (C1), two half-wave plates (H1 and H2) one for each generated path and another calcite crystal (C2) to recombine the paths. Setting the angle of H1 at 45o we are able to close the calcite interferometer thus sending the photons to the output 'a'. Conversely, when H1 is at 0°, photon 2 comes out in path 'b' projected onto the vertical polarization  . The two paths 'a' and 'b' are incoherently recombined at the beam splitter (BS). Intermediate angles between 0° and 45o for H2 and H1 allow to tune the contribution
. The two paths 'a' and 'b' are incoherently recombined at the beam splitter (BS). Intermediate angles between 0° and 45o for H2 and H1 allow to tune the contribution  and
and  to be recombined in the BS. The measurement stage is composed by a quarter-wave plate (M1), a half-wave plate (M2) and a PBS, after which the photons are coupled into single-mode (SM) fibers connected to single photon detectors.
to be recombined in the BS. The measurement stage is composed by a quarter-wave plate (M1), a half-wave plate (M2) and a PBS, after which the photons are coupled into single-mode (SM) fibers connected to single photon detectors.
Download figure:
Standard image High-resolution imageBy exploiting the aforementioned apparatus, we implemented an amplitude damping channel  acting as
acting as
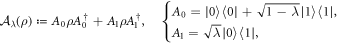
with varying efficiency (i.e. the amount of noise) of the channel as quantified by a parameter λ. First, we performed a QPT over this channel, whose estimated action on the Bloch sphere is depicted in blue, in figures 5(a) and (b). The noise corresponds to deformations of the Bloch sphere: the size of the blue ellipsoid is inversely proportional to the noise strength λ. Through the QPT, we evaluated the four characteristic parameters (d1, d2, d3, c3), reported in table 1. Using the results of [24, 25] we could then compute the boundary of the set of input/output correlations and the states and measurements allowing us to probe this boundary (see supplementary material). To validate the QPT hypothesis, we prepared 29 different pairs of orthogonal states and projected each of these couples onto 29 pairs of orthogonal directions, in order to span a significant part of correlations set, using in total 841 combinations of states and measurements for each plot.
Figure 5. Semi-device-independent test of a quantum process tomography (QPT). From a QPT on two channels, imposing D2 covariance, we evaluate the four characteristic parameters (d1, d2, d3 and c3). The action of the channels on the Bloch sphere is shown on the left, where the blue ellipsoid represents the deformation of the original unit sphere, in blue. The correlations set is surrounded by the red curve. To certificate the QPT, we feed our channel with orthogonal pure states belonging to the XZ plane of the Bloch sphere. In order to cover a significant part of the correlations set, we test all possible combinations of states and measurements. The blank corners within the curves, which are trivial for our analysis (can be obtained by a convex combination of the other points), are not covered, since the channel was fed only with orthogonal states and only orthogonal projection measurements were performed.
Download figure:
Standard image High-resolution imageTable 1. Semi-device-independent tomography validation. Characteristic parameters (d1, d2, d3, c3) obtained for the two channels A and B. The confidence level indicators given by tomography validation are in the right two columns: the parameters' variation range within which the QPT would still be validated, and the Δ, which quantifies the relative difference between the two area of the correlations sets. In the last column on the right we report the μ parameters, which define the equivalence class to which each of the two channels belongs.
| (d1, d2, d3, c3) | Parameters' variation range | Δ | μ | |
|---|---|---|---|---|
| A | (0.719, 0.791, 0.596, 0.397) | (−, −), (−0.025, +0.051), (−0.038, +0.023), (−0.028, +0.034) | 0.004 | 0.692 |
| B | (0.815, 0.877, 0.791, 0.231) | (−, −), (−0.010, +0.020), (−0.025, +0.014), (−0.012, +0.029) | 0.005 | 0.763 |
Both tomographies were validated, since, within 2σ, taking into account the Poissonian distribution of the collected coincidence counts, all the points lie inside the boundary, as it is shown in the plots in figures 5(a), (b). The confidence level was estimated in two ways. First, as proposed in [24], by evaluating the relative difference between the union and the intersection of the two correlation sets (Δ). The obtained values were respectively 0.004 (A) and 0.005 (B). A second evaluated quantity was the variation range associated to each of the parameters (d2, d3, c3) for each channel, reported in table 1. This is the range of values within which the characterizing parameters would still allow to validate the QPT. This kind of uncertainty was achieved imposing the two following conditions: for every parameter set in the given range, the QPT boundary strictly surrounds all the experimental points (within 1σ), and the Δ parameter cannot be larger than 2 times its original value. As mentioned before, our semi-device-independent procedure cannot determine all of the four parameters (d1, d2, d3, c3), specifically, it is insensitive to either d1 or d2 (see [24]). We choose d1 as the parameter that the procedure is insensitive to, so its uncertainty is not reported. Adopting this protocol, with no assumptions on the implementation nor on the state measurement execution, we were able to recognize the equivalence class of our channel, making only assumptions on the dimensionality of the system and its invariance under the dihedral group. Indeed, the device-independent boundary reconstruction can be the same for different quantum channels, and such an equivalence class was characterized in [24]. Using such a characterization, we define the following quantity:  this parameter specifies the equivalence class to which the reconstructed quantum channel belongs. In our case, for both the implemented quantum channels, 0 ≤ μ ≤ 1, as reported in table 1. Within this regime, two semi-device-independent reconstructions
this parameter specifies the equivalence class to which the reconstructed quantum channel belongs. In our case, for both the implemented quantum channels, 0 ≤ μ ≤ 1, as reported in table 1. Within this regime, two semi-device-independent reconstructions  and
and  are indistinguishable when
are indistinguishable when  . This allows to recognize whether our apparatus is working correctly, generating the correct states and performing the required measurements. As pointed out above, the most plausible hypothesis describing a set of correlations is the one whose boundary encloses all the correlation points while being as close as possible to them.
. This allows to recognize whether our apparatus is working correctly, generating the correct states and performing the required measurements. As pointed out above, the most plausible hypothesis describing a set of correlations is the one whose boundary encloses all the correlation points while being as close as possible to them.
Semi-device-independent channel characterization The second implemented protocol, the semi-device-independent Channel Characterization (sDI–CC), naturally arises if the above insight is lifted to the level of a guiding principle to choose the most plausible hypothesis compatible with the observed data, as discussed in [24]. The idea here is to single out the 'minimal surviving hypothesis', that is the channel  whose boundary encloses the smallest volume
whose boundary encloses the smallest volume  in correlation space but still contains all the observed correlations set
in correlation space but still contains all the observed correlations set  . According to this idea [24], the best candidate channel is given by
. According to this idea [24], the best candidate channel is given by
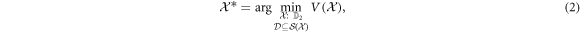
where  is the set of correlations associated with the channel
is the set of correlations associated with the channel  . This set can be spanned sending states and performing projections which are uniformly distributed over the Bloch sphere.
. This set can be spanned sending states and performing projections which are uniformly distributed over the Bloch sphere.
In the experiment, we covered a significant part of this set, through 841 pairs of state/measurement combinations, as in the previous case. Here, the aim is to characterize the implemented channel without relying on any device-dependent procedure. After the parametrization of the experimental data, the boundary of the correlation set is obtained through a minimization algorithm, based on sequential quadratic programming [31], with the aim of finding the minimum area which contains all the correlation set, compatible with the constraints imposed by the dihedral covariance of the channel (see the supplementary material). Exploiting this protocol we can identify the equivalence class to which our channel belongs (using the characterization of such an equivalence class provided in [24]), through three of the four characterizing parameters (d2, d3, c3, again d1 is chosen as the parameter that the procedure is insensitive to). This procedure effectively extracts from our measurements as much information as we are allowed to, without assuming anything about the measuring device. We test the sDI–CC protocol using the experimental setup described in the previous paragraph, setting five different λ parameters and also introducing an additional dephasing by carefully tuning the position of the calcite crystals. The results for the d2, d3, c3 parameters of the five different channels are shown in table 2, while in figure 6 we show the correlation set, along with the optimal boundary, for channels A, C, D, and E. To evaluate the reliability of this protocol we compare the results with the ones obtained using standard tomographic techniques (see supplementary material), using again the relative difference between the union and intersection areas of the correlation sets, which is shown in table 2 as Δ. In figure 6, the gray boundaries are those estimated by the QPT on the channels, whose actions on the Bloch sphere is shown on the left side of each plot. The experimental data are shown in purple and the boundaries evaluated through the optimization algorithm are drawn in green. Figure 6(c) corresponds to the channel in which the additional dephasing factor is present. There is good agreement between the sDI–CC's and the QPT's boundaries, indeed the Δ parameters are all below 3%.
Figure 6. Semi-device-independent channel characterization (DI-CC) of input–output correlations (DI-CC). Characterization of three channels, implemented with different λ parameters. The purple dots are obtained feeding orthogonal pure states belonging to the XZ plane of the Bloch sphere to our channel. The green curves surround the correlations of the sDI–CC while the blue ones are those obtained by the QPT, imposing D2 covariance. For each plot, the action on the Bloch sphere given by the QPT is shown in blue on the left. In the plot the empty sectors can be trivially obtained using non orthogonal states and projectors and are not necessary for our analysis.
Download figure:
Standard image High-resolution imageTable 2. Semi-device-independent channel characterization. Characteristic parameters (d1, d2, d3, c3) with their statistical uncertainties obtained using the sDI–CC protocol for five different channels A–E. In channel E an artificial dephasing factor was added. In the last column on the right we report the μ parameters of each semi-device-independent channel characterization, which define their equivalence class.
| (d2, d3, c3) | Δ | μ | |
|---|---|---|---|
| A | (0.735, 0.606, 0.394) | 0.018 | 0.723 |
| B | (0.875, 0.789, 0.210) | 0.009 | 0.865 |
| C | (0.612, 0.415, 0.585) | 0.027 | 0.833 |
| D | (0.823, 0.784, 0.215) | 0.009 | 0.372 |
| E | (0.696, 0.675, 0.325) | 0.001 | 0.131 |
As noted before, the sDI–CC protocol does not identify the quantum channel unambiguously [24]: indeed, for each minimization problem, there is an equivalence class of quantum channels, which optimizes equation (2), specified by the parameter μ. In this case, all the implemented quantum channels have 0 ≤ μ ≤ 1, as reported in table 2. This regime, which is the same that was mentioned in the previous paragraph, brings two device-independent reconstructions  and
and  to be indistinguishable when
to be indistinguishable when  , as proved in [24].
, as proved in [24].
Discussion
In conclusion, our work provides a strong experimental insight into results recently derived and experimentally implemented with superconducting qubits by Dall'Arno et al in [24, 25]. We apply those results to a photonic experimental implementation, and we introduce an algorithm for the estimation of the confidence level, in addition to that introduced in [24]. Indeed, we apply two semi-device-independent protocols (semi-device-independent tomography validation, sDI–TV, and semi-device-independent channel characterization, sDI–CC) to two types of dihedrally covariant quantum channels (amplitude damping channel and dephased amplitude damping channel), implemented on a photonic platform. These protocols are based only on the set of input/output correlations which can be observed by an experimenter, with the only assumptions about the dimensionality of the system under study and its simmetry, since we are restricting to 1-qubit D2-covariant quantum channels. Through the aforementioned procedures, we were able to validate the implemented channel reconstruction of a quantum process tomography and to extract the maximum amount of information from the observed correlation set, in a semi-device-independent fashion. This study, therefore, gives new experimental tools which can be adopted to test whether the experimental apparatus is correctly functioning, but free from the vicious circle affecting device-dependent procedures like QPT, which require the apparatus to be trusted in the preparation of probe states and on the realization of specific projective measurements and we believe our results pave the way for future experimental implementations along this direction.
Acknowledgments
This work was supported by the ERC-Starting Grant 3D-QUEST (3D-Quantum Integrated Optical Simulation; Grant Agreement No. 307783): http://www.3dquest.eu and the John Templeton Foundation via the grant Q-CAUSAL No. 61084. R C acknowledges the Brazilian ministries MCTIC, MEC and the CNPq (PQ Grant No. 307172/2017 − 1 and INCT-IQ) and the Serrapilheira Institute (Grant No. Serra-1708-15763). G C thanks Becas Chile and Conicyt. F B was supported by JSPS KAKENHI, Grant No. 17K17796. M D acknowledges support from the National Research Fund and the the Ministry of Education, Singapore, under the Research Centres of Excellence programme.







