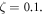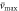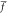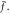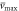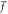Abstract
In order to study the intrinsic size-effects, the stress gradient theory is implemented to a nano-scale beam model in nonlinear flexure. The nonlocal integral elasticity model is considered as a suitable counterpart to examine the softening behavior of nano-beams. Reissner variational principle is extended consistent with the stress gradient theory and applied to establish the differential, constitutive and boundary conditions of a nano-sized beam in nonlinear flexure. The nonlinear integro-differential and boundary conditions of inflected beams in the framework of the nonlocal integral elasticity are determined utilizing the total elastic strain energy formulation. A practical series solution approach in terms of Chebyshev polynomials is introduced to appropriately estimate the kinematic and kinetic field variables. A softening structural behavior is observed in the flexure of the stress gradient and the nonlocal beam in terms of the characteristic parameter and the smaller-is-softer phenomenon is, therefore, confirmed. The flexural response associated with the stress gradient theory is demonstrated to be in excellent agreement with the counterpart results of the nonlocal elasticity model equipped with the Helmholtz kernel function. The nonlocal elasticity theory endowed with the Error kernel function is illustrated to underestimate the flexural results of the stress gradient beam model. Detected numerical benchmark can be efficiently exploited for structural design and optimization of pioneering nano-engineering devices broadly utilized in advanced nano-electro-mechanical systems.

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
New opportunities have emerged in the design of nano/micro-electro-mechanical systems (NEMS/MEMS) as a result of introducing nano-structured materials possessing prominent thermo-electrical [1–4] and mechanical [5–8] characteristics at nano-scale. Extensive implementation of nano-materials in modern NEMS devices, such as nano/micro-sensors [9–11], -scanners [12, 13], -resonators [14–16] and -wires [17–19], has motivated significant research interest in nano-mechanics problems. The elasticity theory, in its classical scheme, is inadequate to precisely describe the mechanical behavior of nano-structures. Various size-dependent elasticity theories, supplemented with suitable intrinsic length scales, are accordingly introduced in the recent literature to realize the size-effect phenomenon. The size-dependent elasticity models can be categorized into the frameworks of the gradient elasticity theory [20–25], the nonlocal elasticity model [26–34] and the unified nonlocal gradient theory [35–43], where recent reviews are tackled in [44, 45].
As a proper counterpart of the strain gradient elasticity model, the stress gradient theory of elasticity is proposed by Forest and Sab [46] and independently elaborated by Polizzotto [47]. Consistent with the stress gradient elasticity theory, the material response at a reference point is dependent on the stress field and the stress gradients of higher-order [48]. A decisive fact stands in favor of the stress gradient theory; it leads to well-posed boundary value problem with associated existence and uniqueness theorems [49]. The stress gradient theory demonstrates the smaller-is-softer response, i.e. the structural stiffness decreases as the characteristic length scale increases. This remarkable feature of the stress gradient elasticity, predicting the softening structural response, is in agreement with the experimental results reported in the materials science [50–52]. Recent advances in the stress gradient elasticity theory are discussed in [53–57]. The softening phenomenon can be alternatively realized applying the nonlocal elasticity approach. To simulate long-range nonlocality, the local strain field at a reference point produces a nonlocal stress field as a function of the source point in addition to all other adjacent points in the continuum with a magnitude rapidly decreasing with the distance [58]. Addressing the nonlocal elasticity through the Helmholtz differential equation as the constitutive law, however, yields in anomalous structural response [59, 60]. To avoid the peculiar anomalies, the nonlocal elasticity theory can be appropriately modified to incorporate the effects of the surface elasticity [61, 62] or the higher-order gradients [63–65]. Nevertheless, the smaller-is-softer phenomenon at nano-scale can be advantageously realized via implementing the nonlocal elasticity theory in its original integral scheme.
Due to remarkable properties of nano-structured materials, they have found a broad range of applications in a variety of new-generation devices, as recently addressed in [33, 34]. Nevertheless, sensitive nano-engineering systems are typically subject to large applied forces which can lead to significant nonlinear structural characteristics. To simulate the nonlinear behavior of structures, effects of mid-plane stretching during the transverse deflection should be appropriately taken into consideration. It is acknowledged that neglecting the nonlinearity issue has undeniable consequences on the elastostatic analysis of nano-structures. Accordingly, the main aim of the present study is to conceive a viable approach to rigorously analyze the nonlinear flexure of nano-scale beams. The stress gradient theory and the nonlocal integral elasticity model are applied to capture the softening structural behavior. The plan of the paper is therefore as follows. The extended form of the Reissner variational principle is presented in section 2 to determine the governing equations and associated constitutive and boundary conditions of the stress gradient beam in flexure. The integro-differential and boundary conditions of equilibrium of a nonlocal nonlinear beam is derived in section 3 utilizing the minimum total elastic strain energy principle. A series solution methodology is introduced to detect the kinematic and kinetic field variables in the nonlinear flexure of nano-beams where its accuracy is assured through comparison with analogous results from the literature. Effects of the nonlocal kernel function on the softening structural response of a nonlocal nano-beam are examined and compared with the counterpart results of the stress gradient beam. Numerical results of the nonlinear bending of a nano-sized beam are graphically illustrated, discussed and tabulated in section 4, followed by the conclusion drawn in section 5.
2. Stress gradient theory of elasticity
A straight beam of elasticity modulus E, length with rectangular cross-section of width w and height h is considered, as illustrated in figure 1. The beam is referred to orthogonal co-ordinates with x coinciding with the beam longitudinal axis, y along the beam height and z in the width direction. The plane x–y, accordingly, identifies with the plane of flexure. The beam ends, at and are restrained preventing any rigid-body motion. Founded on the Saint-Venant elasticity solution [66, 67], the displacement field of the flexure problem consistent with the Euler–Bernoulli beam model writes as
where and designate the components of the displacement field correspondingly along the x−, y− and z− directions together with v denoting the centroid transverse displacement. The shear deformation and warping of the cross-section are well-established to be disregarded in the classical beam model [67, 68], and therefore, the only non-zero component of the von Kármán nonlinear strain field is expressed by
Let M and N respectively represent the bending moment field and the axial force field along with f denoting the distributed transverse load. The Reissner variational functional for the stress gradient beam in nonlinear flexure is introduced as
where the bending stiffness is defined by the second moment of elastic area weighted with the scalar field of elasticity modulus about the z axis and the axial elastic stiffness is defined by the elastic cross-sectional area weighted with the scalar field of elasticity modulus. The stress gradient characteristic length is also introduced to establish the significance of the first-order stress gradient field. Assuming the transverse displacement field, bending moment and axial force field to be subject to variation, the first-order variation of the Reissner functional while integrating by parts writes as
As a result of prescribing stationarity of the Reissner functional, the differential and boundary conditions of equilibrium of a stress gradient beam is detected as
where the last two Neumann conditions represent the extra gradient-induced boundary conditions. The non-classical boundary conditions in the stress gradient elasticity framework, introduced by Forest and Sab [46] and extended by Polizzotto [47], may be heuristically demonstrated to be released for beam-type structures [48]. As expected in implementation of the Reissner variational principle, the desired constitutive laws cast as differential equations and the bending moment and the axial force fields can be determined as
Since the in-plane inertia term is assumed to be insignificant, the fast dynamics can be neglected, and therefore, the axial force field takes the form of [69]
The boundary value problem governing the nonlinear flexure of the stress gradient elastic beam is determined in terms of the transverse displacement field as
A variety of solution approach exists in the literature to deal with the nonlinear governing equations wherein the kinetic fields [70–72] or the kinematic variables [73–75] are assumed to have a series solution form. We, nevertheless, take particular advantage of the Reissner variational principle to introduce independent series solutions for the transverse displacement and the bending moment field as
where and are unknown coefficients yet to be determined. The kinematic and kinetic coordinate functions are to be selected later based on the geometric and static boundary conditions of the inflected beam. The introduced series solutions are thus substituted in the Reissner functional equation (4) rather than the nonlinear equilibrium conditions equation (8). The first-order variation of the Reissner functional, by virtue of equation (7), writes as
Figure 1. Coordinate system and configuration of the beam in flexure.
Download figure:
Standard image High-resolution imageSince and are arbitrary and linearly independent, the system of equations governing the nonlinear flexure of the stress gradient elastic beam is obtained
The resulted system of nonlinear algebraic equations can be numerically solved to obtain the unknown coefficients and
In order to examine the linear flexural response of nano-beams consistent with the stress gradient elasticity theory, it is sufficient to conveniently overlook the geometrical nonlinearity in equation (11).
3. Nonlocal integral elasticity theory
To investigate the nonlinear flexural response of a nano-sized beam consistent with the nonlocal integral elasticity theory, the nonlocal axial force and the nonlocal bending moment fields are formulated as
where the nonlocal stress resultants at a point x are dependent on the corresponding kinematic fields at all points in the domain through the kernel function α. The nonlocal scale-effects are taken into account through expressing the kernel function in terms of the dimensionless characteristic parameter The nonlocal kernel should also meet the specific properties of positivity, parity, symmetry, normalization and limit impulsivity. The mathematical form of the kernel function is well-established to significantly influence the size-effects. Two broadly adopted kernel functions in literature are the Helmholtz and the Error kernel functions given by
with denoting the intrinsic length of the nonlocal integral elasticity theory. The difference between the distribution of the Helmholtz and the Error kernels is demonstrated in figure 2 for two values of the nonlocal characteristic parameter
Figure 2. Comparison of the Helmholtz and the Error kernel functions.
Download figure:
Standard image High-resolution imageTo determine the integro-differential and boundary conditions of equilibrium of a nonlocal beam in nonlinear flexure, the total elastic strain energy in terms of the kinematic field is given by
The first-order variation of the total elastic strain energy is therefore given by
The corresponding integro-differential and boundary conditions of the nonlocal nonlinear Euler–Bernoulli beam are detected by employing the principle of minimum total potential energy and integration by parts as
The governing equation and the pertinent boundary conditions regarding the linear kinematics of the nano-beam can be readily restored by disregarding the source of geometrical nonlinearity.
The exact solution of the boundary value problem governing the nonlinear flexure of the nonlocal beam is too intricate to be found. An analytical series solution of the kinematic field can properly estimate the transverse deflection of inflected nano-sized beams. In place of directly dealing with the integro-differential condition of equilibrium, we avail the first-order variation of the total elastic strain energy associated with the nonlocal nonlinear beam. Exploiting the series solution of the transverse displacement field as equation (9)1 in equation (15), therefore, leads to
As are assumed to be arbitrary and linearly independent, the system of nonlinear equations to be solved in order to examine the nonlinear flexural response of the nonlocal nano-beam writes as
The unknown coefficients can be obtained by means of the numerical solution of the aforementioned system of nonlinear algebraic equations. To investigate the linear flexure of the nonlocal nano-sized beam, the geometrical nonlinearity should be ignored in equation (18).
4. Numerical results and discussions
To illustrate the softening structural response of inflected nano-beams consistent with the stress gradient theory and the nonlocal integral elasticity, a nano-sized beam with simply supported boundary conditions subject to a uniformly distributed transverse load is considered. To fulfill the geometric and static boundary conditions of zero deflection and zero moment at the beam ends, both the kinematic and kinetic coordinate functions are selected as [76]
where denotes the Chebyshev polynomials of the first kind. The following non-dimensional variables: characteristic parameter transverse displacement and load parameter are introduced for the sake of consistency
The non-dimensional characteristic parameter correspondingly associated with the stress gradient and the nonlocal integral theory is obtained via utilizing the stress gradient intrinsic length and the nonlocal characteristic length Such an assumption is merely feasible for positive values of the nonlocal characteristic length. In fact, as it is possible to set the stress gradient characteristic length the nonlocal kernel functions equation (13) are not defined when the nonlocal characteristic length is vanishing; a limit evaluation as is merely allowable.
Effects of the size-dependent elasticity models to capture the smaller-is-softer phenomenon along with the influences of the characteristic parameter, nonlocal kernel function and geometrical nonlinearity on the flexural response of nano-sized beams are examined here. In all illustrations, numerical results of the linear and nonlinear flexure of the nano-scale beam are respectively determined applying and terms of the series solution in equation (9).
To examine the accuracy of the proposed solution approach, the linear flexural response of the stress gradient and nonlocal nano-beam is compared with the counterpart results presented by Fernández-Sáez et al [77]. The maximum dimensionless transverse displacement of a simply-supported nano-beam under uniformly distributed load is accordingly exhibited in figure 3. The characteristic parameter is assumed to range in the interval and the Helmholtz function is applied as the nonlocal kernel for the consistency.
Figure 3. Linear flexure of the stress gradient and nonlocal nano-beam in comparison with Fernández-Sáez et al [77].
Download figure:
Standard image High-resolution imageBoth the stress gradient theory and the nonlocal integral elasticity indicate a softening structural behavior in terms of the characteristic parameter which is in excellent agreement with the counterpart numerical results detected by Fernández-Sáez et al [77]. While the linear flexural response consistent with the stress gradient theory coincides with the corresponding counterpart results, the maximum relative error of the nonlocal integral approach at is less than 0.02% with reference to the numerical results of Fernández-Sáez et al [77]. Table 1 summarizes the numerical results of the maximum transverse displacement in the linear flexure of the nano-sized beam for different values of the characteristic parameter.
Table 1. Linear flexure of the stress gradient and nonlocal beam.
| Nonlocal integral elasticity | Stress gradient theory | Fernández-Sáez et al [77] | |
|---|---|---|---|
| 0.01 | 0.013033 | 0.013033 | 0.013033 |
| 0.02 | 0.013070 | 0.013071 | 0.013071 |
| 0.03 | 0.013132 | 0.013133 | 0.013133 |
| 0.04 | 0.013219 | 0.013221 | 0.013221 |
| 0.05 | 0.013330 | 0.013333 | 0.013333 |
The nonlinear and linear responses of the nano-scale beam associated with the stress gradient theory and the nonlocal integral elasticity are, respectively, demonstrated in figures 4 and 5, wherein the effect of altering the nonlocal kernel function is also studied. As the characteristic parameter is ranging in the interval the non-dimensional load parameter is set The nonlinear flexural response of the nano-sized beam is also independent of the slenderness ratio in view of applying the special non-dimensional variables as equation (20).
Figure 4. Nonlinear maximum transverse displacement of the inflected nano-beam: versus
Download figure:
Standard image High-resolution imageFigure 5. Linear maximum transverse displacement of the inflected nano-beam: versus
Download figure:
Standard image High-resolution imageIt is noticeably inferred from the illustrative results in figures 4 and 5 that the structural response associated with the stress gradient and nonlocal integral models are softer than the local beam model in both the linear and nonlinear flexure analyses. The characteristic parameter therefore has the effect of increasing the transverse deflection of the beam, that is a larger involves a larger deflection The smaller-is-softer phenomenon can be effectively realized in both frameworks of the stress gradient and the nonlocal integral theory. The flexural response of the stress gradient beam is in excellent agreement with the results of the nonlocal elasticity model equipped with the Helmholtz kernel function. The transverse displacement of the beam consistent with the nonlocal integral model endowed with the Error kernel function, however, underestimates the counterpart results of the stress gradient theory. The Helmholtz kernel, hence, exposes a more softening behavior in comparison with the Error kernel. It is realized in view of the illustrations made in figure 2 that the Helmholtz kernel has a lower decay rate in contrast to the Error kernel, and consequently, more number of adjacent points in the domain contributes to the nonlocality. The softening structural behavior is more pronounced in the nonlocal integral elasticity equipped with the Helmholtz kernel leading to the higher transverse deflections in comparison with the nonlocal elasticity model endowed with the Error kernel. The discrepancy between the flexural responses of the stress gradient theory and the nonlocal elasticity model, employing the Error kernel, is enhanced by increasing the value of the characteristic parameter in both the linear and nonlinear analysis. The local linear and nonlinear flexure results are detected by making use of the presented series solution methodology while utilizing the limit impulsivity property of the kernel function. Both the size-dependent elasticity models accordingly provide the deflection result of the local beam theory for vanishing of the characteristic parameter. Numerical values of the non-dimensional transverse displacements of nano-sized beams in the nonlinear and linear flexural analyses are correspondingly tabulated in tables 2 and 3 for the stress gradient and the nonlocal elasticity theory in terms of the characteristic parameter.
Table 2. Nonlinear maximum transverse displacement of the inflected nano-beam: versus
| Nonlocal integral elasticity | |||
|---|---|---|---|
| Helmholtz kernel | Error kernel | Stress gradient theory | |
| 0+ | 0.013011 | 0.013011 | 0.013011 |
| 0.01 | 0.013024 | 0.013014 | 0.013027 |
| 0.02 | 0.013061 | 0.013024 | 0.013064 |
| 0.03 | 0.013123 | 0.013040 | 0.013126 |
| 0.04 | 0.013208 | 0.013063 | 0.013214 |
| 0.05 | 0.013317 | 0.013092 | 0.013326 |
| 0.06 | 0.013450 | 0.013128 | 0.013463 |
| 0.07 | 0.013607 | 0.013171 | 0.013625 |
| 0.08 | 0.013788 | 0.013223 | 0.013812 |
| 0.09 | 0.013992 | 0.013283 | 0.014024 |
| 0.1 | 0.014221 | 0.013352 | 0.014261 |
Table 3. Linear maximum transverse displacement of the inflected nano-beam: versus
| Nonlocal integral elasticity | |||
|---|---|---|---|
| Helmholtz kernel | Error kernel | Stress gradient theory | |
| 0+ | 0.013021 | 0.013021 | 0.013021 |
| 0.01 | 0.013033 | 0.013024 | 0.013033 |
| 0.02 | 0.013070 | 0.013033 | 0.013071 |
| 0.03 | 0.013132 | 0.013050 | 0.013133 |
| 0.04 | 0.013219 | 0.013075 | 0.013221 |
| 0.05 | 0.013330 | 0.013109 | 0.013333 |
| 0.06 | 0.013466 | 0.013156 | 0.013471 |
| 0.07 | 0.013627 | 0.013211 | 0.013633 |
| 0.08 | 0.013813 | 0.013283 | 0.013821 |
| 0.09 | 0.014022 | 0.013380 | 0.014033 |
| 0.1 | 0.014256 | 0.013504 | 0.014271 |
Influence of geometrical nonlinearity on the transverse deflection of the inflected nano-beam in both frameworks of the stress gradient and the nonlocal elasticity theory is demonstrated in figure 6 wherein the effect of altering the nonlocal kernel function is also investigated. While the non-dimensional load parameter is ranging in the interval the value of the characteristic parameter is assumed as
Figure 6. Nonlinear and linear flexural response of the nano-beam: versus (solid and dashed curves respectively denote the results of the nonlinear and linear analysis).
Download figure:
Standard image High-resolution imageReferring to figure 6, it is deduced that the nonlinear flexural response of the nano-scale beam is noticeably smaller than its linear counterpart in both the stress gradient and the nonlocal integral approaches. The intrinsic stiffening effect in the nonlinear analysis is justified by stretching of the centroidal axis of the beam. Applying the nonlinear von Kármán strains in the kinematics of the beam model inevitably results in smaller values of the transverse displacement in comparison with the corresponding linear flexural results. For small enough values of the non-dimensional load parameter, the nonlinear flexural response of the nano-beam exhibits an asymptotic behavior to the transverse deflections detected in the linear analysis. Once more, both the nonlinear and linear deflections of the stress gradient beam are in excellent agreement with the result of the nonlocal integral model utilizing the Helmholtz kernel while overestimating the flexural response associated with the nonlocal model equipped with the Error kernel. Table 4 collects the non-dimensional maximum transverse displacement of the stress gradient and the nonlocal beam determined in the nonlinear and linear flexural analyses for different values of the non-dimensional load parameter.
Table 4. Nonlinear and linear flexural response of the nano-beam: versus
| Nonlocal integral elasticity | ||||||
|---|---|---|---|---|---|---|
| Helmholtz kernel | Error kernel | Stress gradient theory | ||||
| Nonlinear | Linear | Nonlinear | Linear | Nonlinear | Linear | |
| 10 | 0.133853 | 0.142558 | 0.125917 | 0.135037 | 0.134529 | 0.142708 |
| 20 | 0.237566 | 0.285122 | 0.224072 | 0.270076 | 0.239296 | 0.285417 |
| 30 | 0.316370 | 0.427677 | 0.298940 | 0.405109 | 0.318823 | 0.428125 |
| 40 | 0.379435 | 0.570251 | 0.358969 | 0.540147 | 0.382187 | 0.570833 |
| 50 | 0.432232 | 0.712804 | 0.409281 | 0.675192 | 0.434959 | 0.713542 |
5. Conclusion
The stress gradient theory and the nonlocal integral elasticity with reference to the nonlinear flexure problem are implemented to rigorously study the softening behavior of structures at nano-scale. The geometrical nonlinearity, attributable to the stretching effect of the centroidal axis of the beam, is applied through the von Kármán nonlinear strain field. The extended form of the Reissner variational principle consistent with the stress gradient theory is introduced and the differential, constitutive and boundary conditions of a nano-sized beam in flexure are determined. The integro-differential and boundary conditions of equilibrium of an inflected beam in the framework of the nonlocal integral elasticity are also established by a formal application of the principle of minimum total potential energy. A series solution methodology is introduced for nanoscopic study of the field quantities in the nonlinear flexure of beams. Taking advantage of the Reissner variational principle, independent series solutions are introduced for the kinematic and kinetic field variables in the nonlinear flexure of the stress gradient beam. The transverse deflection of the nonlocal nonlinear beam is alternatively expanded in a series form. Both the series solutions are proposed in terms of Chebyshev polynomials satisfying the required geometric and static boundary conditions. The series solution approach is invoked to obtain a system of nonlinear algebraic equations which are numerically solved.
Application to a simply supported elastic beam under a uniform static load is performed and detected flexural results are graphically elucidated and commented upon. The transverse displacement of the nano-scale beam in nonlinear flexure is demonstrated to increase as the characteristic parameter increases. Therefore, both the stress gradient and the nonlocal elasticity theory can noticeably capture the smaller-is-softer phenomenon. The influence of the nonlocal kernel function on the nonlinear flexural behavior of the nonlocal beam is also investigated and compared with the corresponding results of the stress gradient beam. The flexural response of the stress gradient theory is realized to be in excellent agreement with the results of the nonlocal elasticity model equipped with the Helmholtz kernel while overestimating the flexural result associated with the nonlocal model endowed with the Error kernel. This issue can be justified through examination of the mathematical form of the nonlocal kernel functions where the Helmholtz kernel indicates a lower decay rate in comparison with the Error kernel, and accordingly, more adjacent points of the continuum domain contribute to the nonlocality. As a limiting response, the flexure of the nano-beam is examined while the characteristic parameter tends to zero and the deflection result of the local beam model is effectively restored. The nonlinear flexural responses of the stress gradient and nonlocal beams are demonstrated to have an asymptotic behavior to the linear flexure results for small enough values of the transverse loading. The presented nonlinear flexural analysis of nano-scale elastic beams can be advantageously exploited in the design and optimization of structural components of advanced nano-devices in view of their considerable nonlinear characteristics in practical nano-engineering applications.
Declarations
The authors declared no potential conflicts of interest. This research did not receive any specific grant-based funding.


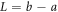
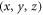


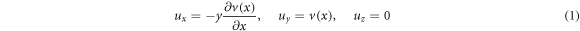


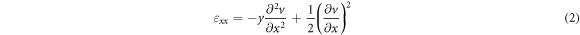
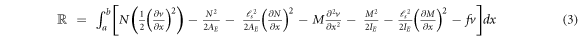
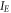



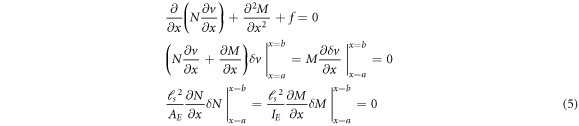

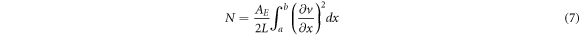
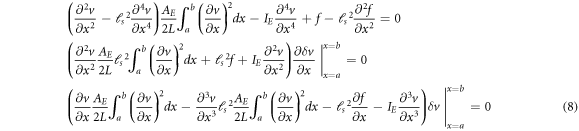
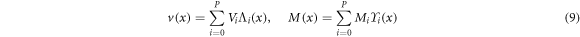
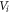




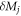
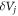
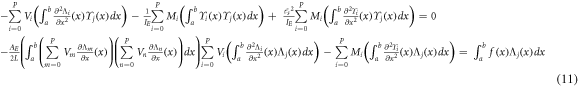
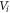
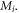
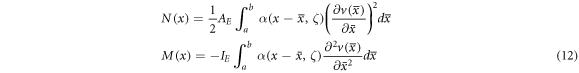
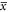
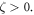
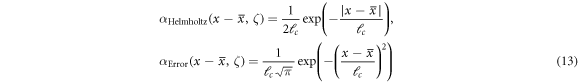
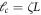
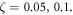

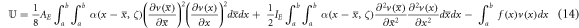
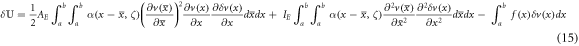
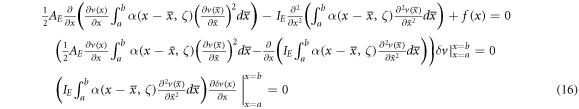
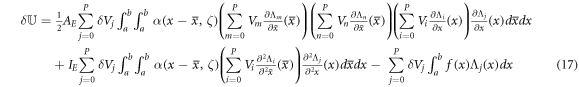

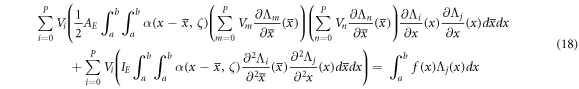
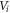




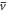
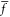

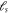
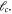
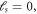
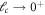
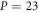
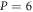

![$\left[0.01,0.05\right]$](https://content.cld.iop.org/journals/2053-1591/8/3/035011/revision2/mrxabe3c6ieqn35.gif)

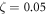

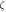

![$\left]0,0.1\right],$](https://content.cld.iop.org/journals/2053-1591/8/3/035011/revision2/mrxabe3c6ieqn40.gif)



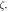







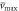
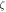
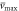


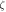
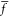
![$\left[0,50\right],$](https://content.cld.iop.org/journals/2053-1591/8/3/035011/revision2/mrxabe3c6ieqn57.gif)