Abstract
We derive a material-realistic real-space many-body Hamiltonian for twisted bilayer graphene from first principles, including both single-particle hopping terms for pz electrons and their long-range Coulomb interaction. By disentangling low- and high-energy subspaces of the electronic dispersion, we are able to utilize state-of-the-art constrained random phase approximation calculations to reliably describe the non-local background screening from the high-energy s, px, and py electron states which we find to be independent of the bilayer stacking and thus of the twisting angle. The twist-dependent low-energy screening from pz states is subsequently added to obtain a full screening model. We use this modeling scheme to study plasmons in electron-doped twisted bilayer graphene supercells. We find that the finite system size yields discretized plasmonic levels, which are controlled by the system size, doping level, and twisting angle. This tunability together with atomic-like charge distributions of some of the excitations renders these plasmonic excitations remarkably similar to the electronic states in electronic quantum dots. To emphasize this analogy in the following we refer to these supercells as plasmonic quantum dots. Based on a careful comparison to pristine AB-stacked bilayer graphene plasmons, we show that two kinds of plasmonic excitations arise, which differ in their layer polarization. Depending on this layer polarization the resulting plasmonic quantum dot states are either significantly or barely dependent on the twisting angle. Due to their tunability and their coupling to light, these plasmonic quantum dots form a versatile and promising platform for tailored light-matter interactions.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Layered materials with weak interlayer van der Waals interactions allow for precise control of the interlayer twisting angle. The resulting moiré potential has been shown to yield fascinating effects. For example, for twisted bilayer graphene a small 'magic angle' has been theoretically predicted, at which ultra-flat bands form [1, 2]. Together with sizable Coulomb interaction this allows for possibly strong correlation effects. Both, the characteristics of ultra-flat bands [3] as well as correlation effects have been experimentally verified in the form of insulating and superconducting gaps as well as in the form of ferromagnetic behavior controlled by doping [4–7]. For twisted semiconducting layered materials, such as transition metal dichalcogenides (TMDCs), the effects of the moiré potential on the excitonic properties have been theoretically [8–12] and experimentally [13–15] studied. In these cases, a finite twisting angle can yield superlattices with periodicities of the order of the excitonic radii, which can again yield flat electronic dispersions [16, 17] and can effectively trap exciton complexes [11, 14].
For both, correlation effects in twisted bilayer graphene as well as for the formation of moiré excitons in twisted TMDCs, the Coulomb interaction plays a major role. While single-particle properties of these twisted materials have been studied in great detail, including the ab initio derivation of the moiré potentials, the Coulomb interaction has so far been treated with less care. For twisted bilayer graphene various models have been utilized ranging from purely local Coulomb interaction [4], to non-local interaction taking the effective thickness and/or the dielectric environment into account [18–21], and to models treating the low-energy pz screening on the level of (constrained) random phase approximation (RPA) [22, 23]. To describe the Coulomb interaction in twisted bilayer TMDCs, various models have been suggested and used including models resolving the intra- and interlayer Coulomb interactions based on ab initio estimates for the relevant dielectric properties [9, 11, 12].
Here, we go beyond these effective Coulomb descriptions by deriving an interacting low-energy model for twisted bilayer graphene including both single-particle and Coulomb interaction matrix elements via state-of-the-art down folding of ab initio calculations. With this we especially aim to consistently describe the screening from both low-energy pz orbitals and remaining bands, i.e. from sp2 and all other higher-energy states. Although our model remains valid for infinite twisted bilayer graphene structures, we explicitly focus on finite-size supercells and their correlation effects in real space. These finite-size twisted bilayer graphene supercells have been studied in terms of their single-particle properties and optical properties estimated from Fermi's golden rule [24, 25]. Here, we calculate plasmonic excitations in real space for electron-doped finite-size samples at moderate and large twisting angles. So far, plasmons in twisted bilayer graphene have been mostly investigated with a focus on small ('magic') angles [26–30] with the exception of [31]. Our focus on larger angles comes with a major methodological advantage, which is the circumvention of the screening from extremely flat bands and thus large density of states (DOS), as it is in the latter situation still not entirely clear whether the RPA is applicable [32–34]. Additionally, the interlayer hopping model for large twist angles is less delicate than for small angles. In the latter case one needs to take into account atomic relaxations, either numerically [35] or at the model level by introducing a family of topological defects [36], both of which make the calculations more challenging. For moderate to large twist angles, atomic relaxation effects turn out to be negligible as was shown in [37] using atomistic simulations with realistic carbon potentials. The use of a nominal, purely geometric moiré structure is therefore justified for larger twist angles.
Within the outlined framework, circumventing common modeling issues, we are able to reliably describe real-space plasmonic excitations from first principles at various doping levels and for moderate to large twisting angles. We find that finite-size supercells naturally yield a discretization of the plasmonic spectrum, which shows well defined and separated plasmonic levels. These plasmonic levels are efficiently tunable by the system size, doping level, and twisting angle. Based on this and in analogy to electronic quantum dots, we refer to these plasmonic systems formed in twisted bilayer graphene supercells as plasmonic quantum dots, although their formation is very different to the one of electronic quantum dots. We discuss in detail the real-space charge distribution of these plasmonic excitations in terms of their in-plane shapes and layer polarization. We find that the latter controls the dependence of the corresponding plasmonic quantum dot state on the twisting angle.
2. Modeling approach
2.1. Hamiltonian and plasmonic properties
We aim to study finite-size twisted bilayer graphene supercells as depicted in figure 1. These are constructed such that for zero twist angle ( ) we get an AB (Bernal) stacking. The rotation axis is centered at the upper A sublattice (lower B sublattice), as indicated in the inset of figure 1. The outer boundaries are chosen to be of armchair type. We describe these supercells with a low-energy Hamiltonian for the pz
states,
) we get an AB (Bernal) stacking. The rotation axis is centered at the upper A sublattice (lower B sublattice), as indicated in the inset of figure 1. The outer boundaries are chosen to be of armchair type. We describe these supercells with a low-energy Hamiltonian for the pz
states,
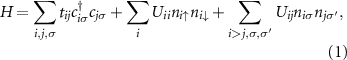
with i and j labeling atomic site positions of (twisted) bilayer graphene.  (
( ) and
) and  are pz
-orbital annihilation (creation) and orbital occupation number operators, respectively, at site i with spin σ. tij
and Uij
are hopping and density-density Coulomb interaction matrix elements, respectively, which we derive in the following section from ab initio calculations. At this stage we do not explicitly differentiate between the upper and lower layer: i and j label lattice sites in both layers.
are pz
-orbital annihilation (creation) and orbital occupation number operators, respectively, at site i with spin σ. tij
and Uij
are hopping and density-density Coulomb interaction matrix elements, respectively, which we derive in the following section from ab initio calculations. At this stage we do not explicitly differentiate between the upper and lower layer: i and j label lattice sites in both layers.
Figure 1. Sketch of a twisted bilayer supercell with 3252 atoms, armchair edges, and at  . The rotation axis is marked in dark grey in the inset and is centered on the A (B) sublattice of the upper (lower) layer.
. The rotation axis is marked in dark grey in the inset and is centered on the A (B) sublattice of the upper (lower) layer.
Download figure:
Standard image High-resolution imageTo study plasmonic properties we utilize a real-space version of the RPA [38–42] to calculate the electron energy loss spectra (EELS). We start with the eigen decomposition of  :
:
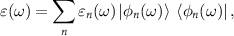
where we order the eigenvalues εn
according to ![$-\operatorname{Im}[1 / \varepsilon_n(\omega)]$](https://content.cld.iop.org/journals/2053-1583/9/1/014004/revision2/tdmac38caieqn6.gif) . ε1 is the eigenvalue with the largest
. ε1 is the eigenvalue with the largest ![$-\operatorname{Im}[1 / \varepsilon_n(\omega)]$](https://content.cld.iop.org/journals/2053-1583/9/1/014004/revision2/tdmac38caieqn7.gif) and we call it 'leading'. EELS is defined by:
and we call it 'leading'. EELS is defined by:
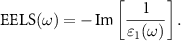
 is the corresponding eigenvector in real space which renders the plasmonic excitation pattern. Within a real-space tight-binding approximation, the RPA dielectric matrix is given by:
is the corresponding eigenvector in real space which renders the plasmonic excitation pattern. Within a real-space tight-binding approximation, the RPA dielectric matrix is given by:
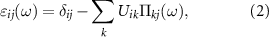
with the Coulomb interaction Uik
entering the Hamiltonian (1) and the polarizability function  given by:
given by:
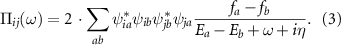
Here Ea
,  and
and  are eigenvalues, eigenvectors and corresponding Fermi–Dirac distribution functions obtained upon diagonalization of the single-particle tight-binding Hamiltonian. i, j, and k label site indices while a and b label eigenstates of the Hamiltonian. η is a small positive constant which we set to
are eigenvalues, eigenvectors and corresponding Fermi–Dirac distribution functions obtained upon diagonalization of the single-particle tight-binding Hamiltonian. i, j, and k label site indices while a and b label eigenstates of the Hamiltonian. η is a small positive constant which we set to  meV in our calculations. More details on the implementation can be found in [41]. In appendix
meV in our calculations. More details on the implementation can be found in [41]. In appendix
2.2. Ab initio down folding
In order to derive all model parameters for arbitrary twist angles via down folding of first principles calculations we have to make one well justified approximation: only the pz states will experience the moiré potential and thus the twist angle θ. To stress the validity of this assumption we show in figure 2(a) the sp2-projected density functional theory (DFT) DOS of pristine AA-stacked (blue) and AB-stacked (orange) bilayer graphene. Their difference is nearly invisible so that we can readily assume that the relative layer rotation does not affect these electronic states. This, of course, does not hold for the pz states, as is obvious from pz -projected DOS shown in figure 2(b).
Figure 2. (a) sp2 and (b) pz
projected ab initio density of states (DOS) of AB-stacked (orange) and AA-stacked (blue) bilayer graphene.  eV corresponds to the Fermi energy.
eV corresponds to the Fermi energy.
Download figure:
Standard image High-resolution imageBased on this assumption we can derive the single-particle hopping matrix elements tij
for the pz
states via a Wannier construction based on DFT calculations for the AB-stacked bilayer graphene (see appendix

for the untwisted ( ) geometry and using the DFT Hamiltonian together with the pz
-like ab initio Wannier functions
) geometry and using the DFT Hamiltonian together with the pz
-like ab initio Wannier functions  . In table 1 we list the resulting intralayer and interlayer hopping matrix elements for an interlayer distance of
. In table 1 we list the resulting intralayer and interlayer hopping matrix elements for an interlayer distance of  Å. To account for finite twisting angles on the single-particle level, we utilize a Slater-Koster based interlayer hopping model [43]
Å. To account for finite twisting angles on the single-particle level, we utilize a Slater-Koster based interlayer hopping model [43] ![$t_\perp(r) = \gamma_0~\operatorname{exp}[-\alpha (r-r_0)]$](https://content.cld.iop.org/journals/2053-1583/9/1/014004/revision2/tdmac38caieqn18.gif) , which we fit to the interlayer hopping matrix elements from table 1 to obtain
, which we fit to the interlayer hopping matrix elements from table 1 to obtain  eV and
eV and  . As mentioned above, for small twist angles one would additionally need to account for modulations in the interlayer distance [35–37], but here we are interested in moderate to large twist angles such that the assumption of a purely nominal twisting is adequate.
. As mentioned above, for small twist angles one would additionally need to account for modulations in the interlayer distance [35–37], but here we are interested in moderate to large twist angles such that the assumption of a purely nominal twisting is adequate.
Table 1. Intra- and interlayer hopping matrix elements for the pz Wannier orbitals in AB-stacked bilayer graphene. Due to the four sublattices we get two different values for the next-nearest-neighbor interlayer hopping.
| Intralayer | Interlayer | ||
|---|---|---|---|
| r, Å | tij , eV | r, Å | tij , eV |
| 0 | −0.991 | 3.35 | +0.290 |
| 1.42 | −2.857 | 3.64 | +0.118 |
| 2.47 | +0.244 | 3.64 | +0.067 |
| 2.85 | −0.258 | ||
| 3.77 | +0.024 | ||
| 4.28 | +0.052 | ||
| 4.94 | −0.021 | ||
| 5.14 | −0.014 | ||
| 5.70 | −0.022 | ||
The description of fully screened, retarded and θ-dependent Coulomb interaction  requires more attention.
requires more attention.  is defined by:
is defined by:
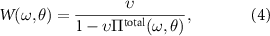
where v is the bare Coulomb interaction.  renders all possible screening processes at a given rotation angle θ which can be separated into two terms:
renders all possible screening processes at a given rotation angle θ which can be separated into two terms:
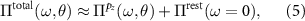
with  being the partial polarizability resulting from virtual excitations within the low-energy pz
sub-space. It can be evaluated using equation (3). The rest polarizability
being the partial polarizability resulting from virtual excitations within the low-energy pz
sub-space. It can be evaluated using equation (3). The rest polarizability  describes in principle instantaneous screening processes from virtual excitations from, to, and between non-pz
states (such as sp2 and others). Due to the orthogonality of pz
and sp2 states, the cross-polarization terms between pz
and non-pz
orbitals can be safely neglected [44]. This way,
describes in principle instantaneous screening processes from virtual excitations from, to, and between non-pz
states (such as sp2 and others). Due to the orthogonality of pz
and sp2 states, the cross-polarization terms between pz
and non-pz
orbitals can be safely neglected [44]. This way,  effectively describes the screening of a semiconductor with a gap of about
effectively describes the screening of a semiconductor with a gap of about  eV (see figure 2(a)), which renders the instantaneous approximation valid. Importantly, this renders the background (or rest) polarizability independent of the twist angle. Equation (4) now reads:
eV (see figure 2(a)), which renders the instantaneous approximation valid. Importantly, this renders the background (or rest) polarizability independent of the twist angle. Equation (4) now reads:
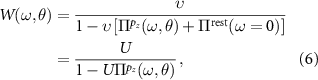
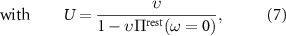
being the θ-independent background-screened Coulomb interaction, as needed for the evaluation of equation (2). We calculate U within the constrained RPA [45] based on ab initio calculations for AB-stacked bilayer graphene (see appendix  . For the evaluation of equation (2) we, however, need to evaluate Uij
at other positions resulting from the finite twisting angle θ. To this end, we map the discretized Uij
to a continuous model
. For the evaluation of equation (2) we, however, need to evaluate Uij
at other positions resulting from the finite twisting angle θ. To this end, we map the discretized Uij
to a continuous model  . For the latter we choose the analytic image-charge model for the potential within a dielectric slab of height d reading [42, 46–48]:
. For the latter we choose the analytic image-charge model for the potential within a dielectric slab of height d reading [42, 46–48]:
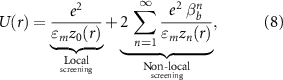
with e being the elementary charge, εm
the dielectric constant of the slab,  , and
, and  . An additional parameter δ allows us to also fit the on-site potential
. An additional parameter δ allows us to also fit the on-site potential  . In figure 3 we show the ab initio cRPA data together with the fit using equation (8), the locally-screened interaction
. In figure 3 we show the ab initio cRPA data together with the fit using equation (8), the locally-screened interaction  (
( ), and the fully-screened interaction
), and the fully-screened interaction  . For the fit we fixed
. For the fit we fixed  (twice the interlayer distance) and find
(twice the interlayer distance) and find  (in good agreement with similar fits in momentum space [49]) and
(in good agreement with similar fits in momentum space [49]) and  , which evidently interpolate the ab initio data well. From the comparison to the locally-screened interaction we see that the background screening, as described by the second term in equation (8), acts differently at each r due to its non-local character. The fully-screened interaction
, which evidently interpolate the ab initio data well. From the comparison to the locally-screened interaction we see that the background screening, as described by the second term in equation (8), acts differently at each r due to its non-local character. The fully-screened interaction  behaves as expected from Thomas-Fermi screening theory in two dimensions [50] which predicts a strongly decaying potential with a r−3 asymptotic behavior, but in our calculations we also find a finite offset c. This offset c decays with the supercell size and vanishes in the infinite-size limit (not shown). We attribute this behavior to finite-size/boundary effects. In detail, although the polarization function
behaves as expected from Thomas-Fermi screening theory in two dimensions [50] which predicts a strongly decaying potential with a r−3 asymptotic behavior, but in our calculations we also find a finite offset c. This offset c decays with the supercell size and vanishes in the infinite-size limit (not shown). We attribute this behavior to finite-size/boundary effects. In detail, although the polarization function  is rather localized, as shown in figure 3, it still has some non-vanishing oscillating tails due to the finite Fermi surface. These tails in r are partially missing if
is rather localized, as shown in figure 3, it still has some non-vanishing oscillating tails due to the finite Fermi surface. These tails in r are partially missing if  is fixed to an edge side, which likely induces the finite offset c.
is fixed to an edge side, which likely induces the finite offset c.
Figure 3. AB-stacked bilayer graphene Coulomb matrix elements. Orange circles depict cRPA results. The blue line is obtained by fitting equation (8) to the cRPA data. In green we show the locally-screened Coulomb interaction (i.e. the first term in equation (8)). Pink diamonds show fully-screened Coulomb interaction  .
.
Download figure:
Standard image High-resolution imageEquipped with the continuous representation of the background-screened Coulomb interaction U(r) and the tight-binding model described by the hopping matrix elements from table 1 we can evaluate the dielectric function from equation (2) and thus plasmonic properties for arbitrary twist angles θ. At this point it is important to note the limits of our material-realistic Coulomb modeling approach. In the 'low-energy' range ( eV) we are mostly describing virtual excitations (i.e. screening processes) solely within the pz
manifold. For larger excitation energies transitions involving the rest space would become important, which we do not fully render here. Thus, we restrict our plasmon considerations to energies below
eV) we are mostly describing virtual excitations (i.e. screening processes) solely within the pz
manifold. For larger excitation energies transitions involving the rest space would become important, which we do not fully render here. Thus, we restrict our plasmon considerations to energies below  eV.
eV.
3. Plasmonic excitations in bilayer graphene
3.1. From continuous plasmon dispersions to discrete plasmonic quantum dot levels
The momentum resolved EELS( ) of pristine doped bilayer graphene is dominated by two plasmonic branches,
) of pristine doped bilayer graphene is dominated by two plasmonic branches,  and
and  , sketched in figure 4(a). The
, sketched in figure 4(a). The  branch is higher in energy with
branch is higher in energy with  in the long-wavelength limit, while the
in the long-wavelength limit, while the  branch is linear in this limit,
branch is linear in this limit,  [51–53]. The upper branch does not show any layer polarization with charge modulations only within the bilayer plane. Classically the corresponding plasmon can thus be understood as interacting charge monopoles governed by conventional monopole Coulomb interaction terms so that the usual
[51–53]. The upper branch does not show any layer polarization with charge modulations only within the bilayer plane. Classically the corresponding plasmon can thus be understood as interacting charge monopoles governed by conventional monopole Coulomb interaction terms so that the usual  dispersion is expected. The lower branch describes plasmons with a layer polarization, which hence forms interacting charge dipoles in the bilayer plane. In contrast to the monopole interactions, the resulting dipole interactions yield a linear plasmonic dispersion. These long-wavelength-limit dispersion relations are indicated as dashed lines in the sketch of figure 4(a). For intermediate q we see that these trends are modified. The
dispersion is expected. The lower branch describes plasmons with a layer polarization, which hence forms interacting charge dipoles in the bilayer plane. In contrast to the monopole interactions, the resulting dipole interactions yield a linear plasmonic dispersion. These long-wavelength-limit dispersion relations are indicated as dashed lines in the sketch of figure 4(a). For intermediate q we see that these trends are modified. The  dispersion of the
dispersion of the  branch is significantly reduced (flattened) due to the non-local background screening from the sp2 states (and, in reality, also due to substrate screening) [42, 54]. The
branch is significantly reduced (flattened) due to the non-local background screening from the sp2 states (and, in reality, also due to substrate screening) [42, 54]. The  is also affected, but rather mildly. For pristine infinite systems, the resulting full spectral functions of these plasmonic branches are indicated in figure 4(b). They are continuous functions attaining their maxima before entering the inter-band continuum.
is also affected, but rather mildly. For pristine infinite systems, the resulting full spectral functions of these plasmonic branches are indicated in figure 4(b). They are continuous functions attaining their maxima before entering the inter-band continuum.
Figure 4. Sketches of the qualitative plasmonic dispersion in pristine bilayer graphene (a) together with the resulting plasmonic spectral functions (b). The lower and upper grey triangles in (a) represent the intra- and inter-band polarization continua. In (c) and (d) we sketch the same situation but for a finite-size system in which the momentum q is discretized.
Download figure:
Standard image High-resolution imageIn the finite-size bilayer graphene supercells under consideration here, these plasmonic properties are modified as sketched in figure 4(c). The finite diameter of the hexagonal supercells defines an upper plasmonic wavelength λmax and a minimal wave vector  . Below this
. Below this  the system cannot host any of the plasmonic excitations of the
the system cannot host any of the plasmonic excitations of the  branches. Furthermore, the finite system size also discretizes the allowed momenta in multiples of this
branches. Furthermore, the finite system size also discretizes the allowed momenta in multiples of this  . As a result the plasmonic dispersions become gapped between these q values and the full plasmonic spectrum becomes discretized as well, as sketched in figures 4(c) and (d). The previously continuous plasmonic spectrum now shows well defined discretized levels.
. As a result the plasmonic dispersions become gapped between these q values and the full plasmonic spectrum becomes discretized as well, as sketched in figures 4(c) and (d). The previously continuous plasmonic spectrum now shows well defined discretized levels.
This is in full analogy to the formation of electronic quantum dot states: the finite system size discretizes the continuous electronic spectrum into well defined electronic quantum dot states. Based on this analogy, we call the resulting plasmonic states in the finite-size cells plasmonic quantum dot states. Their tunability is, however, much richer than in the case of electronic quantum dots. The energies of the plasmonic quantum dot states are controlled by (a) the system size as this affects  , (b) the doping level and substrate screening as these control the energies of the underlying continuous branches
, (b) the doping level and substrate screening as these control the energies of the underlying continuous branches  , as well as by (c) the twisting angle, as we will discuss in more detail in the following. Also the discretization of the linear
, as well as by (c) the twisting angle, as we will discuss in more detail in the following. Also the discretization of the linear  branch yields a very different level spacing than the discretized
branch yields a very different level spacing than the discretized  branch as indicated in figure 4(d).
branch as indicated in figure 4(d).
In the following sections we discuss how this scheme is realized in full real-space RPA calculations for finite AB-stacked (and twisted) bilayer graphene supercells.
3.2. Plasmonic quantum dots in AB stacked graphene supercells
We start our discussion with comparing EELS( ) for different finite-size supercells of untwisted AB-stacked bilayer graphene, which is defined by:
) for different finite-size supercells of untwisted AB-stacked bilayer graphene, which is defined by:
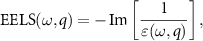
where  is the diagonal of the formal Fourier transform of
is the diagonal of the formal Fourier transform of  . In figures 5(a) and (b) we show EELS(
. In figures 5(a) and (b) we show EELS( ) for hexagonal supercells of diameter
) for hexagonal supercells of diameter  (11 028 atoms) and
(11 028 atoms) and  (3252 atoms), respectively. In both cases the electron doping is about
(3252 atoms), respectively. In both cases the electron doping is about  cm
cm (µ = 1.34 eV), which is around the maximum of what is achievable with double sided ionic-liquid gating techniques [55]. In both of these panels we can clearly identify the
(µ = 1.34 eV), which is around the maximum of what is achievable with double sided ionic-liquid gating techniques [55]. In both of these panels we can clearly identify the  branches. In the case of the larger supercell we find a nearly continuous
branches. In the case of the larger supercell we find a nearly continuous  branch, which starts to deviate from the
branch, which starts to deviate from the  form around
form around  showing the characteristic flattening. The lower
showing the characteristic flattening. The lower  branch shows its approximate linear dispersion. For
branch shows its approximate linear dispersion. For  (above
(above  eV) both branches smear out due to strong Landau damping induced by the particle-hole continuum. Also note that the approximate plasmonic energies are similar to the ones observed in highly doped graphene monolayers [56]. Hence, the overall characteristics of these plasmonic branches are fully in line with the expectations as discussed in section 3.1, underlining the appropriateness of our modeling scheme. For the larger supercell only the lower branch shows first signs of discretization, which becomes more evident for the smaller cell in figure 5(b). In this case we find clear gaps in both branches, which is also reflected in the discrete peaks in the full EELS(ω) depicted in figure 5(c).
eV) both branches smear out due to strong Landau damping induced by the particle-hole continuum. Also note that the approximate plasmonic energies are similar to the ones observed in highly doped graphene monolayers [56]. Hence, the overall characteristics of these plasmonic branches are fully in line with the expectations as discussed in section 3.1, underlining the appropriateness of our modeling scheme. For the larger supercell only the lower branch shows first signs of discretization, which becomes more evident for the smaller cell in figure 5(b). In this case we find clear gaps in both branches, which is also reflected in the discrete peaks in the full EELS(ω) depicted in figure 5(c).
Figure 5. (a) Plasmonic dispersion for a supercell with diameter  (11 028 atoms). (b), (c) Plasmonic dispersion for a supercell with diameter
(11 028 atoms). (b), (c) Plasmonic dispersion for a supercell with diameter  (3252 atoms) together with full EELS(ω). Annotations in panel (c) refer to subplots of figure 6.
(3252 atoms) together with full EELS(ω). Annotations in panel (c) refer to subplots of figure 6.
Download figure:
Standard image High-resolution imageFrom the comparison between the momentum resolved EELS( ) with the plasmonic levels in the full EELS(ω), we can identify the origin of the specific plasmonic states. Starting at the lowest level with
) with the plasmonic levels in the full EELS(ω), we can identify the origin of the specific plasmonic states. Starting at the lowest level with  eV (barely visible in figure 5(c)) we see that this mode arises from the layer polarized
eV (barely visible in figure 5(c)) we see that this mode arises from the layer polarized  branch (black doted line in figures 5(b) and (c)). The corresponding layer-resolved real-space representation of that mode (the eigenvector
branch (black doted line in figures 5(b) and (c)). The corresponding layer-resolved real-space representation of that mode (the eigenvector  eV) of the dielectric function) is shown in figure 6(a). As expected, we find a layer-polarized excitation with a homogeneous charge distribution within each layer. The next plasmonic level at
eV) of the dielectric function) is shown in figure 6(a). As expected, we find a layer-polarized excitation with a homogeneous charge distribution within each layer. The next plasmonic level at  eV is again resulting from the
eV is again resulting from the  branch, which accordingly shows the layer polarization, see figure 6(c). However, the charge distribution within each layer is not homogeneous anymore and this mode is best described as a layer-polarized dipole excitation. It is accompanied at the same q by a plasmonic excitation with
branch, which accordingly shows the layer polarization, see figure 6(c). However, the charge distribution within each layer is not homogeneous anymore and this mode is best described as a layer-polarized dipole excitation. It is accompanied at the same q by a plasmonic excitation with  eV, which originates from the upper
eV, which originates from the upper  branch (blue dashed lines in figures 5(b) and (c)). Accordingly, this mode does not show a layer polarization (figure 6(c)), but is otherwise also of dipole character. The plasmonic mode at
branch (blue dashed lines in figures 5(b) and (c)). Accordingly, this mode does not show a layer polarization (figure 6(c)), but is otherwise also of dipole character. The plasmonic mode at  eV is again originating from the layer polarized branch, as is also evident from its real-space representation depicted in figure 6(e). This mode has a circular charge distribution, which is vastly reminiscent of a 1s atomic wave function. This mode is as well accompanied at the same q by a 1s-like plasmonic state at
eV is again originating from the layer polarized branch, as is also evident from its real-space representation depicted in figure 6(e). This mode has a circular charge distribution, which is vastly reminiscent of a 1s atomic wave function. This mode is as well accompanied at the same q by a 1s-like plasmonic state at  eV from the upper branch (orange dashed-doted line in figures 5(b) and (c)), which does not show any layer polarization. Finally, we find another layer-polarized plasmonic excitation around
eV from the upper branch (orange dashed-doted line in figures 5(b) and (c)), which does not show any layer polarization. Finally, we find another layer-polarized plasmonic excitation around  eV which hosts a p-like state (see figure 6(f)) which is again reminiscent of the atomic-like wave functions of electronic quantum dots. For this mode, we were however not able to identify the accompanying mode from the upper plasmonic branch, which we attribute to smaller energy separation of plasmonic states at higher energies, as also indicated in the sketches in figure 4.
eV which hosts a p-like state (see figure 6(f)) which is again reminiscent of the atomic-like wave functions of electronic quantum dots. For this mode, we were however not able to identify the accompanying mode from the upper plasmonic branch, which we attribute to smaller energy separation of plasmonic states at higher energies, as also indicated in the sketches in figure 4.
Figure 6. Plasmonic eigenmodes in real space for a supercell with 3252 atoms. Depicted modes correspond to the highlighted excitation energies in figure 5(c).
Download figure:
Standard image High-resolution imageThus, next to the finite-size induced discrete energy levels and tunability, these plasmonic charge distributions can also resemble atomic-like wave functions of electronic quantum dots, which further underlines their identification as plasmonic quantum dots. In the following we proceed with the twist-angle dependence, focusing on the dipole and 1s-like modes.
3.3. Twist angle dependence
From the previous discussion, the dependence of the plasmonic quantum dot energies on doping level and system size are already clear. In the following we thus focus on the twist angle dependence. To this end we present in figure 7 the 'dark' and 'bright' dipole and 1s modes for  . Modes are called 'dark' or 'bright' when they originate from
. Modes are called 'dark' or 'bright' when they originate from  or
or  branches, respectively.
branches, respectively.
Figure 7. Plasmonic eigenmodes in real space for various twisting angles  . Columns show evolution of different modes: (a) 'dark' dipole, (b) 'bright' dipole, (c) 'dark' 1s, (d) 'bright' 1s.
. Columns show evolution of different modes: (a) 'dark' dipole, (b) 'bright' dipole, (c) 'dark' 1s, (d) 'bright' 1s.
Download figure:
Standard image High-resolution imageFigure 8. Excitation energies of all modes from figure 7 as a function of θ.
Download figure:
Standard image High-resolution imageFor the bright dipole modes, shown in figure 7(b), we observe that the boundary separating the differently charged areas is rotating when we adjust θ, synchronously in the lower and upper layer, however, only with  . The latter can be readily understood by overlaying the rotated dipole patterns and by remembering that the charge distributions in the two layers are not independent. The missing overlap at the corners of the hexagons additionally yields enhanced charge accumulations in the two opposite corners of each layer. The dark dipole mode, shown in figure 7(a), behaves similarly. The charge separation line again rotates with
. The latter can be readily understood by overlaying the rotated dipole patterns and by remembering that the charge distributions in the two layers are not independent. The missing overlap at the corners of the hexagons additionally yields enhanced charge accumulations in the two opposite corners of each layer. The dark dipole mode, shown in figure 7(a), behaves similarly. The charge separation line again rotates with  , but we observe a smearing of it, such that the charge separation is not as sharp as in the bright dipole mode. Note that rotated dark dipole modes are additionally rotated by 90∘ compared to
, but we observe a smearing of it, such that the charge separation is not as sharp as in the bright dipole mode. Note that rotated dark dipole modes are additionally rotated by 90∘ compared to  case. This, however, does not affect any of the drawn conclusions as these unrotated dipole modes have nearly the same excitation energies, see figure 9 for more details.
case. This, however, does not affect any of the drawn conclusions as these unrotated dipole modes have nearly the same excitation energies, see figure 9 for more details.
Figure 9. Plasmonic modes in real-space for  together with their excitation energies at reduced doping (µ = 0.2 eV). Panels (a) and (b) depict 'bright' and 'dark' modes respectively. Modes in panel (b) are half-transparent to indicate that they are not real plasmonic eigenmodes (the condition
together with their excitation energies at reduced doping (µ = 0.2 eV). Panels (a) and (b) depict 'bright' and 'dark' modes respectively. Modes in panel (b) are half-transparent to indicate that they are not real plasmonic eigenmodes (the condition ![$\mathrm{Re}[\varepsilon(\omega)] = 0$](https://content.cld.iop.org/journals/2053-1583/9/1/014004/revision2/tdmac38caieqn114.gif) is not satisfied).
is not satisfied).
Download figure:
Standard image High-resolution imageIn figures 7(c) and (d) we depict patterns of the 1s quantum dot mode. Except for a slight deformation of the initial hexagonal shape we do not see any major changes to the bright excitation upon twisting. Its dark counterpart also does not show any significant changes in its excitation pattern, except for a smearing of the clear charge separation.
In fact, the most important changes to these plasmonic states are their excitation energy shifts. In figure 8 we plot the excitation energies for all modes as a function of θ. We see that within the given accuracy, the excitation energies of the bright modes do not dependent on the rotation angle. The dark modes, however, do. We see for both the dark dipole and the dark 1s mode that the energy is significantly decreased upon 10 degree twist. Afterwards, these modes just mildly dependent on further rotation towards  . The initial symmetry breaking between 0∘ and 10∘ thus leaves the strongest footprint in the plasmonic energies, while the larger rotation angles do not change it too drastically anymore.
. The initial symmetry breaking between 0∘ and 10∘ thus leaves the strongest footprint in the plasmonic energies, while the larger rotation angles do not change it too drastically anymore.
We attribute this different impact of the rotation to the bright and dark modes to the single-particle properties. In figure 4, the original continuous 'bright' plasmonic branch  is clearly detached from the particle-hole continuum (shown in grey), while the 'dark'
is clearly detached from the particle-hole continuum (shown in grey), while the 'dark'  branch is in its close vicinity. Thus, the dark states are much more prone to Landau damping and to changes in the particle-hole continuum due to modifications of the the single-particle electronic states.
branch is in its close vicinity. Thus, the dark states are much more prone to Landau damping and to changes in the particle-hole continuum due to modifications of the the single-particle electronic states.
To verify this hypothesis we calculated EELS(ω) from
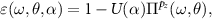
where θ and α are both referring to the twist angle, but now separated in the rotation in the polarizability (θ) and the Coulomb interaction (α) matrices. For all previous calculations we have set  . From the resulting spectra in figure 11 we see that the rotation in the Coulomb interaction matrix, i.e. changes to α, barely affect the energy of the dark 1s mode, whereas the rotation in the polarizability matrix (changes to θ), strongly affect it. Thus, indeed the single-particle properties as reflected by the polarizability affect the dark states the most. If we additionally remember that the approximate morié lattice constant λ is inversely proportional to
. From the resulting spectra in figure 11 we see that the rotation in the Coulomb interaction matrix, i.e. changes to α, barely affect the energy of the dark 1s mode, whereas the rotation in the polarizability matrix (changes to θ), strongly affect it. Thus, indeed the single-particle properties as reflected by the polarizability affect the dark states the most. If we additionally remember that the approximate morié lattice constant λ is inversely proportional to  , yielding
, yielding  ,
,  , and
, and  , we understand that the changes to the lattice structure are the largest when going from
, we understand that the changes to the lattice structure are the largest when going from  to
to  , while increasing θ further modifies λ only slightly. Under the reasonable assumption that changes to the lattice structure are also imprinted on the electronic structure, we can qualitatively understand why the excitation energy of the dark modes is affected the most upon the initial twist by
, while increasing θ further modifies λ only slightly. Under the reasonable assumption that changes to the lattice structure are also imprinted on the electronic structure, we can qualitatively understand why the excitation energy of the dark modes is affected the most upon the initial twist by  .
.
Figure 10. Static polarizability  for two different choices of
for two different choices of  . The color bar is clamped to a small range to highlight the oscillating tails.
. The color bar is clamped to a small range to highlight the oscillating tails.
Download figure:
Standard image High-resolution imageFigure 11. EELS(ω) around the unrotated and 10∘-rotated dark 1s mode energies for individual rotations of the involved Coulomb (α) and polarizability (θ) matrices.
Download figure:
Standard image High-resolution image4. Conclusions and outlook
We have presented an ab initio derived twisted bilayer graphene many-body model including a consistent description of the kinetic (hopping) and Coulomb matrix elements. Upon separating the different screening channels into the low-energy pz and residual background screening, we were able to map the twisting dependence of the total polarizability to the low-energy screening channels only. This allowed us to calculate the background-screened Coulomb interaction from first principles using constrained RPA and to fit the resulting partially-screened interaction with a lightweighted continuous model. All rotation dependencies were subsequently handled within the low-energy pz subspace only.
Based on this model we studied low-energy plasmonic excitations in real space in electron-doped twisted bilayer graphene supercells. We found that the system-size-induced discretization of the plasmonic spectrum gives rise to plasmonic quantum dot states, which can be tuned by the doping level, system size, and, as we have discussed in detail, by the twisting angle. In fact, we showed that two different types of plasmonic quantum dot states arise from the two plasmonic branches of pristine bilayer graphene. These differ in their layer polarization. Layer-polarized states are strongly affected by twisting, whereas their in-phase counterparts are almost completely twist-independent.
Since plasmonic quantum dot modes are highly inhomogeneous due to their real-space confinement as well as due to their different in- and out-of-plane structures (dipole-, 1s-, 1p-like) they can couple to external electromagnetic fields [57, 58]. In combination with a high degree of tunability, this allows for very promising light-matter engineering routes within sensors, diodes, or photovoltaic applications. In this respect, we would like to emphasize that for the chosen system size and doping levels, the plasmonic energies already lie in the visible / near-infrared range.
For the characterization of these plasmonic quantum dot modes, we imagine scanning near-field optical microscopy measurements [59, 60] as most promising, as they allow spatial mapping of charge distributions.
We thus expect that this initial study forms the ground for further material-specific quantitative real-space plasmonics studies of twisted bilayer graphene and similar systems.
Acknowledgments
We thank Merzuk Kaltak for sharing his cRPA implementation with us. The work of MIK and TW was supported by European Research Council via Synergy Grant 854843-FASTCORR. Numerical simulations in this work were carried out on the Dutch national e-infrastructure with the support of SURF Cooperative.
Data availability statement
The data that support the findings of this study are available upon reasonable request from the authors.
Appendix A.: Doping dependence
In figure 9 we present a few plasmonic excitation patterns for a smaller electron doping of  (µ = 0.2 eV) and the same supercell as before. In this case we can again clearly identify a variety of bright modes. The dark modes are, however, not well defined anymore. Although we find some plasmonic eigenvectors which resemble the corresponding dark modes at lower excitation energies, these are not well defined plasmonic excitations since the real parts of their dielectric functions do not fulfill the necessary requirement
(µ = 0.2 eV) and the same supercell as before. In this case we can again clearly identify a variety of bright modes. The dark modes are, however, not well defined anymore. Although we find some plasmonic eigenvectors which resemble the corresponding dark modes at lower excitation energies, these are not well defined plasmonic excitations since the real parts of their dielectric functions do not fulfill the necessary requirement ![$\operatorname{Re}\left[ \varepsilon(\omega) \right] = 0$](https://content.cld.iop.org/journals/2053-1583/9/1/014004/revision2/tdmac38caieqn111.gif) . The excitation energies of the bright dipole and 1s modes are strongly reduced compared to the corresponding mode at high electron doping. These observations are in line with the expected behavior of the previously mentioned
. The excitation energies of the bright dipole and 1s modes are strongly reduced compared to the corresponding mode at high electron doping. These observations are in line with the expected behavior of the previously mentioned  modes [52, 53, 61]. The vanishing/fading of the dark modes is thus a result of their close vicinity to the electron–hole continuum.
modes [52, 53, 61]. The vanishing/fading of the dark modes is thus a result of their close vicinity to the electron–hole continuum.
Appendix B.: Ab initio details
Our ab initio calculations were performed within DFT utilizing the projected augmented wave (PAW) formalism [62, 63] as implemented in the Vienna ab initio simulation package (vasp) [64, 65]. Exchange-correlation effects were considered using the generalized gradient approximation (GGA) [66]. A 517 eV energy cut-off for the plane-waves and a convergence threshold of  eV were used in the calculations. The Brillouin zone was sampled by a (
eV were used in the calculations. The Brillouin zone was sampled by a ( ) k-point mesh. The in-plane lattice constant was set to 2.468
) k-point mesh. The in-plane lattice constant was set to 2.468  and the out-of-plane distance between the two layers was
and the out-of-plane distance between the two layers was  . A
. A  thick super-cell was used in the direction orthogonal to the 2D plane in order to reduce spurious interactions between supercell images. The Wannier functions and the tight-binding Hamiltonian were calculated within the scheme of maximal localization [67, 68] using the wannier90 package [69]. Therefore, we used an inner (frozen) wannierization window of about
thick super-cell was used in the direction orthogonal to the 2D plane in order to reduce spurious interactions between supercell images. The Wannier functions and the tight-binding Hamiltonian were calculated within the scheme of maximal localization [67, 68] using the wannier90 package [69]. Therefore, we used an inner (frozen) wannierization window of about  eV around the Fermi level. This way the Wannier-interpolated band structure perfectly reproduces the Kohn–Sham states within this window and shows only minor deviations away from it.
eV around the Fermi level. This way the Wannier-interpolated band structure perfectly reproduces the Kohn–Sham states within this window and shows only minor deviations away from it.
The Coulomb interaction was evaluated using the maximally-localized Wannier functions within the constrained random phase approximation (cRPA) [70, 71] as  , where U was the partially-screened Coulomb interaction defined by
, where U was the partially-screened Coulomb interaction defined by  with v the bare Coulomb interaction,
with v the bare Coulomb interaction,  the cRPA polarizability, and wi
the Wannier function at lattice site i. The polarizability operator
the cRPA polarizability, and wi
the Wannier function at lattice site i. The polarizability operator  describes screening from all electronic states except those given by the tight-binding Hamiltonian in the Wannier basis. For these calculations, we used a recent cRPA implementation by Kaltak within vasp [71]. To converge the cRPA polarization with respect to the number of empty states we used in total 208 bands.
describes screening from all electronic states except those given by the tight-binding Hamiltonian in the Wannier basis. For these calculations, we used a recent cRPA implementation by Kaltak within vasp [71]. To converge the cRPA polarization with respect to the number of empty states we used in total 208 bands.
Appendix C.: RPA details
The screening from the low-energy pz
orbitals is calculated using the real-space random phase approximation code from [41]. This code evaluates equation (3) for a given single-particle Hamiltonian at a given temperature T and damping η. In all our calculations, the temperature was set to  eV and damping was η = 0.001 eV. Compared to [41] we applied two notable optimizations. First of all, we reduced the computational load by taking the sparsity of equation (2) at finite temperatures into account. This reduced the effective algorithmic complexity from
eV and damping was η = 0.001 eV. Compared to [41] we applied two notable optimizations. First of all, we reduced the computational load by taking the sparsity of equation (2) at finite temperatures into account. This reduced the effective algorithmic complexity from  to
to  where N was the number of lattice sites. Furthermore, we run the computations on GPUs which are much better at dense linear algebra than CPUs. All together, we could evaluate equation (3) for a given ω in less than 30 seconds on an NVIDIA V100, whereas for a comparable system size it took more than 24 hours in [41], thus achieving ×3000 speedup.
where N was the number of lattice sites. Furthermore, we run the computations on GPUs which are much better at dense linear algebra than CPUs. All together, we could evaluate equation (3) for a given ω in less than 30 seconds on an NVIDIA V100, whereas for a comparable system size it took more than 24 hours in [41], thus achieving ×3000 speedup.
An example of a resulting polarizability function in real space is depicted in figure (10).
Appendix D.: Rotation details
In figure (11) we show EELS(ω) around the unrotated and 10∘-rotated dark 1s mode energies for individual rotations of the involved Coulomb (α) and polarizability (θ) matrices. From this, it is evident that the rotation of the polarizability matrix affects EELS the most.











