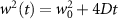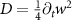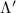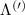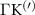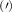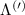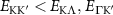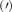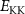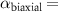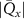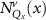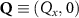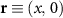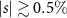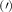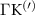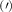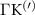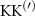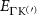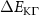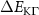Abstract
Monolayers of transition metal dichalcogenides have a remarkable excitonic landscape with deeply bound bright and dark exciton states. Their properties are strongly affected by lattice distortions that can be created in a controlled way via strain. Here, we perform a joint theory-experiment study investigating exciton diffusion in strained tungsten disulfide (WS2) monolayers. We reveal a non-trivial and non-monotonic influence of strain. Lattice deformations give rise to different energy shifts for bright and dark excitons changing the excitonic landscape, the efficiency of intervalley scattering channels and the weight of single exciton species to the overall exciton diffusion. We predict a minimal diffusion coefficient in unstrained WS2 followed by a steep speed-up by a factor of 3 for tensile biaxial strain at about 0.6% strain—in excellent agreement with our experiments. The obtained microscopic insights on the impact of strain on exciton diffusion are applicable to a broad class of multi-valley 2D materials.

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
Transition metal dichalcogenides (TMDs) and related van der Waals heterostructures have attracted much attention in current research due to their remarkable excitonic landscape including bright, spin- and momentum-dark and spatially separated exciton states [1–9] Optical properties of TMDs are strongly sensitive to lattice distortions, as shown for spatially-homogenous [10–17] and spatially-inhomogeneous strain [18–25]. Strain-induced lattice deformations (see figure 1(a)) induce changes in the energy and in the effective mass of electronic valleys [12, 26–29] resulting in a qualitative change of the excitonic landscape and efficiency of exciton-phonon scattering channels (figure 1(b)) [15, 28, 29].
Figure 1. Strain-dependent exciton diffusion. Biaxial strain implies (a) lattice deformations, which modify (b) the excitonic landscape by different spectral shifts of the bright KK and momentum-dark KΛ and KK excitons. This can introduce strain-dependent phonon bottlenecks for intervalley scattering. (c) As a result, an initial spatially-localized exciton occupation diffuses slower or faster depending on the applied strain.
Download figure:
Standard image High-resolution imageStrain is expected to have an important impact also on transport in TMDs, e.g. spatially inhomogenous strain acts as a driving force for exciton/carrier funneling [23, 25, 30], similarly to bias fields for charged particles [31, 32] or gauge potentials for interlayer excitons in van der Waals heterostructures [33]. Even in the absence of additional driving forces, an initial spatially-localized excitonic occupation spreads in space due to the occupation gradient resulting eventually in a conventional exciton diffusion [34], as sketched in figure 1(c). While in the presence of one single valley the diffusion is expected to be only quantitatively altered by strain through e.g. changes in the effective masses, the multi-valley exciton landscape in TMDs promises interesting strain effects. The diffusion is expected to be dominated by the most populated, energetically lowest exciton valley [34–36], which might vary as a function of strain due to the strongly valley-dependent energy shifts (figure 1(b)). Since different valleys have different valley-intrinsic diffusion coefficients [34], this leads to strain-induced changes of the overall diffusion, see figure 1(c). Furthermore, strain-induced energy shifts also change the possibility for phonon-induced intervalley scattering channels and may even result in phonon bottlenecks at specific strain values (figure 1(b)). This has also a direct impact on the efficiency of exciton diffusion.
Based on a fully quantum-mechanical approach and supported by experimental measurements, our work provides microscopic insights into the interplay of exciton diffusion and strain in the WS2 monolayer as an exemplary TMD material. We microscopically address the evolution of optically excited, spatially localized excitons resolved in time, momentum and space. We take into account bright and momentum-dark excitonic states obtained by solving the Wannier equation under strain [28, 29]. We predict non-trivial dependence of the diffusion on strain, showing a non-monotonic behaviour, where the overall diffusion is either dominated by specific dark excitons or determined by intervalley scattering. This leads to a steep speed-up of the diffusion upon small tensile strain values—in excellent agreement with our spatiotemporal photoluminescence experiments.
1. Results
Theoretical approach: Starting with the unstrained single-particle dispersion [37], we implement the strain-induced variations of effective masses and band extrema Ev [28]. For each strain value we then solve the Wannier Equation [38–41] with a non-local Coulomb screening [42] to obtain a set of excitonic states labelled by the excitonic valley v and the center-of-mass momentum . These states have the energy , which depends on strain largely via changes in Ev [28] [see also figure 1(b)], but also via changes in the total mass Mv . Due to considerable energetic separations to higher excitonic states, we restrict our investigations to the ground 1 s exciton, however taking into account all relevant electronic valleys and the resulting bright KK as well as momentum-dark KK, KΛ, K, ΓK and ΓK excitons [3]. Here, the first and the second letter denote the location of the Coulomb-bound hole and electron, respectively. We neglect all other states that are considerably higher in energy () than the energetically lowest one. Furthermore, we have not considered spin-dark states [43, 44] due to the less efficient spin-flipping processes [45], as has been recently observed in the slower formation of phonon sidebands from spin-dark states in low-temperature PL [46, 47].
Now, we introduce the excitonic intravalley Wigner function , which summed over provides the intravalley spatial density [34]. At the spatial and temporal scales considered here, can be directly interpreted as probability of finding excitons with momentum in position and valley v. An equation of motion for the spatiotemporal dynamics of excitons can be introduced by exploiting the Heisenberg equation and the many-particle Hamilton operator [38, 48]. The derived equation can then be transformed into Wigner representation [49, 50] and reads in the low excitation regime [34]
The first term indicates the free evolution of excitons, while the second term takes into account the losses due to the radiative recombination γ within the light cone () [39–41, 46].
The first contribution in the second line of equation (1) describes the formation of incoherent excitons due to phonon-driven transfer from the excitonic polarization . The process is driven by exciton-phonon scattering rates describing scattering from the state to via interaction with phonons [40, 41]. The last term in equation (1) describes the scattering contribution , which is dominated by exciton-phonon scattering in the considered low-excitation regime. It gives rise to a redistribution of the Wigner function in momentum toward a local equilibrium distribution, cf the supplementary material (stacks.iop.org/2DM/8/015030/mmedia) for more details. Importantly, exciton-phonon scattering depends crucially on strain, mostly via the energies of the involved initial and final exciton states, while the variations of phonon energies or electron-phonon scattering are typically less relevant and are thus not considered here [28, 51]. In particular, strain-induced energy shifts can lead to drastic changes in intervalley scattering via opening or closing of scattering channels [see phonon bottleneck in figure 1(b)]. In contrast, intravalley scattering is only slightly influenced by strain via changes in the effective mass Mv [28, 52, 53]. Note that strain could in principle also change the surface mass density of the monolayer as well as the phonon dispersion [11, 28, 54], however both variations are small for the considered strain values and have been neglected here.
In the steady-state regime the interplay between scattering-free propagation and scattering mechanisms implies that the spatial distribution evolves at first approximation according to the Fick's law , where decaying mechanisms have been omitted [55, 56]. Here, is the diffusion coefficient with denoting the momentum-dependent relaxation times. We have introduced the expectation value . Under the assumption of constant relaxation times the well-known steady-state relation can be recovered. The overall diffusion of the total excitonic spatial density can be affected by strain in two major ways: (i) Strain changes the relative occupation weight Nv /N of each valley. The overall diffusion will be dominated by the most populated valley and its own valley-intrinsic diffusion [34]. (ii) Strain changes the efficiency of the scattering channels through shifting the energies of initial and final scattering states, which crucially determine the velocity of exciton diffusion.
Strain-dependent exciton diffusion: Exploiting equation (1), we have a microscopic access to the spatially and temporally resolved dynamics of excitons in strained TMDs. In the main manuscript, we focus on the exemplary case of WS2 monolayers on a SiO2 substrate. In supplementary material, we also discuss the exciton diffusion in strained WSe2, MoSe2 and MoS2 monolayers. Figures 2(a)–(b) illustrate the strain dependent spatial evolution of the exciton density soon after the optical excitation [t = 2 ps in (a)] and at a later time [t = 40 ps in (b)]. We consider a pulsed optical excitation around t = 0 resonant to the bright exciton X0 and with a Gaussian spatial confinement corresponding to a full-width-half-maximum of 800 nm in amplitude and a temporal duration of 200 fs. This generates an initial strain-independent excitonic distribution, cf. figure 2(a). After few tens of picoseconds, the spatial distribution becomes broader and the width is strongly strain dependent, cf. figure 2(b). We find in particular a faster spatial spreading for given strain values s, e.g. s ≈ 0.6%. The differences in exciton diffusion are not monotonic in strain: Increasing the strain from negative (compressive) to positive (tensile) values, the diffusion initially becomes slower from −1% to 0% strain, then it speeds up steeply as the strain increases to 0.6% and finally it slows down again for larger strain values.
Figure 2. Spatiotemporal evolution under strain. Strain-dependent spatial evolution of the exciton density N in a WS2 monolayer on SiO2 after a pulsed spatially-localized optical excitation. The spatial evolution is shown along the x axis at the fixed time of (a) 2 ps soon after the optical excitation and after (b) 40 ps. For given strain values, we show the evolution of the corresponding (c) squared spatial width w2 and the (d) associated effective diffusion coefficient D.
Download figure:
Standard image High-resolution imageThe spatial broadening of the exciton density N can be quantified introducing a width w whose squared modulus is proportional to the variance . According to Fick's law, confined spatial distributions behave as with [57–59], where w0 is the initial width. It follows that also in the microscopic case when evaluating equation (1) one can define an effective diffusion coefficient (also called diffusivity) , i.e. as slope of the temporal evolution of the squared width w2. In figures 2(c) and (d) we plot the temporal evolution of squared width w2 and the associated effective diffusion coefficient for three different values of strain. The squared width w2 shows quickly a linear evolution for all strain values, although the slope varies crucially with strain indicating a strong strain-dependence of the exciton diffusion. We find that after an initial steep increase, the diffusion coefficient D(t) reaches a stationary value after a few ps. This corresponds to the transition from a ballistic regime, i.e. scattering-free evolution with a quadratic w2 and linear D, to the conventional diffusive regime with a linear w2 and stationary D(t)≡D [34]. Both strain-induced quicker ballistic-to-diffusive transition and smaller D values are signatures of more efficient scattering channels, as seen e.g. at 0% strain. Due to the very short ballistic-to-diffusive transition, it is the stationary diffusion coefficient D that determines the exciton diffusion in figure 2(b).
Now, we investigate the strain-dependence of the stationary diffusion coefficient covering a larger range of compressive to tensile biaxial strain values, cf figure 3(a). We find saturation values for the diffusion coefficient of 2.2 and 0.4 cm2 s−1 for compressive strain around −1% and tensile strain above +1.6%, respectively. Furthermore, we predict a strongly non-monotonic strain-dependence including a relative minimum in the unstrained material (0% strain) and a maximum at about 0.6% tensile strain. This can be understood by decomposing the valley-dependent contribution to the overall exciton diffusion. Thin lines in figure 3(a) show the diffusion coefficient obtained considering a reduced excitonic valley landscape. In all cases we have taken into account the optically excited KK excitons together with only KK (purple line) or KΛ and K (i.e. K, orange line) or ΓK (green line) excitons, respectively. These thin lines reflect the scenario of valley-intrinsic diffusion, where the overall diffusion is dominated by the considered specific valley and the corresponding valley-specific diffusion determined by its total mass and intravalley scattering [34]. We find immediately that the saturation value of the diffusion at compressive (tensile) strain is determined by KΛ (ΓK) excitons, while the maximum in diffusion is governed by the contribution of KK excitons.
Figure 3. Strain-dependent stationary diffusion. (a) Diffusion coefficient plotted as a function of biaxial strain in WS2 containing a direct comparison between theoretically predicted (red solid line) and experimentally measured (blue line with error bars) values. Note that the experiment was performed with uniaxial strain that has been projected to equivalent biaxial strain values (cf supplementary material). The thin lines show the gedanken experiment where only KK (blue), K (orange) and (green) excitons are taken into account (besides the optically excited KK states). (b) Strain-dependent energy shifts of the minima of KK, K and K excitons. The dashed lines indicate the case with electrons located in equivalent primed exciton valleys. The vertical dashed line marks the strain at which giving rise to a minimum in the diffusion coefficient, while the vertical solid line indicates the maximum of the diffusion.
Download figure:
Standard image High-resolution imageTo better understand the valley-specific contribution to the overall diffusion, we show the strain dependent energy of the involved exciton valley minima in figure 3(b) [28]. We find that at larger compressive (tensile) strain values, KΛ (ΓK excitons are the energetically lowest and thus most occupied states. The same applies to KK excitons for strain values around 0.5%. As shown in our previous work [34], efficient intervalley scattering gives rise to one joint diffusion coefficient, however the weight of each valley is determined by its relative occupation. The latter depends crucially on the position of the bottom of the valley Ev as well as on degeneracy (3 times larger for K) or total mass (smaller total mass leads to smaller population): This explains why KΛ or the very massive ΓK excitons still contribute even when [see e.g. vertical solid line in figure 3(a)]. At very strong compressive strain it is KΛ which dominates the diffusion. Since at these strain values, the KΛ valley is already by far the energetically lowest state, the diffusion coefficient is not affected anymore by further strain-induced energetic changes resulting in a stationary value. The same also applies to the situation at high tensile strain, where the valley when low enough becomes dominant also due to its large effective mass and high exciton occupation.
The predicted maximum in the exciton diffusion at about 0.6% is formed when moving from the strain regime, where KK excitons are energetically lowest states toward the regime governed by ΓK states. The latter exhibit a considerably slower diffusion due to a much larger effective mass. The dip toward the unstrained case cannot be explained by just considering valley-intrinsic diffusion and is due to intervalley scattering, which will be discussed separately in the next section. Note that the abrupt increase in the diffusion coefficient in the considered hypothetical two-valley system dominated by ΓK (thin green line) and KΛ (thin orange line) excitons for strain values around 0.5% is due to the increasing impact of KK excitons exhibiting a much smaller effective mass and thus a much larger diffusion coefficient [34]. The thin purple line does not show this steep increase, since KK and KK excitons have a very similar dependence on strain modifying their separation by only approximately 5 meV per percentage of biaxial strain (cf. solid and dashed purple line in figure 3(b)).
We compare our microscopic results with measurements of the exciton diffusion in an uniaxially strained WS2 monolayer. To this end, the monolayer is placed on a flexible PMMA substrate and a homogeneous, uniaxial, tensile strain from 0 % to 1 % is applied via the bending method [10, 15]. The similar optical properties between PMMA and SiO2 make a comparison of experiment and theory possible. Since we apply uniaxial strain, the experimentally determined strain values are related to the biaxial ones of theory by comparing the energy shifts of KK excitons. Both uni- and biaxial strain lead to a linear decrease of , although with different gauge factors [28, 60] (see also supplementary material). Here, we theoretically predict a decrease rate of 113 meV/% for biaxial strain, cf the solid purple line in figure 3(b). At the same time, we observe experimentally that uniaxial deformation leads to a decrease rate 50 meV/% [15]. This allows us to fix a relation between uni- and biaxial strain. Note that the maximum experimentally accessible uniaxial strain of s ≈ 1% corresponds to slightly less than 0.5% biaxial strain.
The exciton diffusion is measured by space- and time-resolved photoluminescence after applying a spatially localized optical excitation at 2.10 eV (see supplementary information for details). We find an excellent agreement between theoretically predicted and experimentally measured diffusion coefficients in the experimentally accessible strain region, cf figure 3(a). We see an increase in the diffusion coefficient from approximately 0.6 to 2.2 cm2 s−1 when varying the strain from 0 to 0.5%. The slope of this increase strongly depends on the formation of the minimum in the diffusion coefficient D appearing approximately for the unstrained case.
Impact of intervalley scattering: While the overall diffusion discussed so far was dominated by one exciton valley with the lowest energy and largest occupation (valley-intrinsic diffusion), there are strain regions where multiple valleys have similar energies, cf figure 3(b). This occurs e.g. at small compressive strain values, where KΛ (solid orange) and KK excitons (dashed purple) cross, cf the vertical dashed line. Here, intervalley scattering turns out to play a crucial role resulting in a minimum in the exciton diffusion, cf figure 3(a).
Now, we investigate the origin of the predicted dip in the diffusion coefficient for the unstrained WS2 monolayer, cf figure 3(a). In particular, we study the role of intervalley scattering between KK and KΛ excitons, whose energies are the lowest and cross in the strain region, where the minimum appears, cf figure 3(b). The intervalley scattering between KK and KΛ excitons is driven by absorption or emission of high-momentum M phonons. These phonons can be approximated as nearly dispersion-free including two acoustic modes with the energies of 16.5 and 22.7 meV. The corresponding optical M phonons have larger energies between 40 and 50 meV [61]. When the strain-induced separation between valleys becomes larger than these phonon energies, excitons from the energetically lowest states cannot scatter any longer out of these states, cf figure 1(b). To better visualize the condition for this phonon bottleneck, we show the Wigner function for the KK excitons for three different strain values, where KK are the energetically lowest states, cf figures 4(a)–(c). Here, the thin horizontal lines show the minimum momentum required for the absorption of acoustic M phonons. In the unstrained case (figure 4(a)), the two momentum-dark exciton valleys are aligned (figure 3(b)), thus all intervalley channels into KΛ states are possible. The situation changes at 0.25% strain (figure 4(b)), where the energetic misalignment is already large enough that only a small portion of the most occupied excitons is able to scatter into KΛ states. At 0.5% strain (figure 4(c)), there are almost no occupied states fulfilling the condition for intervalley scattering resulting in a phonon bottleneck.
Figure 4. Impact of intervalley scattering. (a)–(c) Wigner function is shown in dependence on and at 40 ps for the lowest v = KK valley and three different values of strain. Thin horizontal lines indicate the minimum wave-vector required for intervalley scattering via TA phonons. (d) Comparison of the full simulation (dark-red) with the cases in which only acoustic (dark-blue) or optical (orange) phonons are switched off.
Download figure:
Standard image High-resolution imageNow we address the impact of this phonon bottleneck for the strain-dependent evolution of the exciton diffusion. In figure 4(d), we compare the full calculation (also shown in figure 3(a)) with the case, where the KK-KΛ intervalley scattering via acoustic or optical phonons is switched off, respectively. We see that optical phonons have in general a minor effect, since their energy is relatively high resulting in a small phonon occupation and thus a negligbly small phonon absorption. We also find that scattering with acoustic phonons does not play a role for strain values . The reason is the phonon bottleneck illustrated in figure 4(c). However, in the strain region , switching off scattering with acoustic phonons suppresses the appearance of the dip in the exciton diffusion. This illustrates the crucial role of intervalley scattering with acoustic phonons for the formation of the predicted minimal exciton diffusion in unstrained WS2 monolayers.
Note that the scattering with M phonons connecting KK and KΛ excitons is particularly strong according to DFT calculations [61]. In contrast, the corresponding phonon-induced intervalley scattering connecting ΓK and KK excitons is much weaker. This together with the much larger effective mass and smaller diffusion coefficient in the valley does not lead to a similar dip in the exciton diffusion around 1.5% strain, where KK- and states are energetically lowest and cross (figure 3(b)). Note that the efficiency of the KK-KΛ intervalley scattering together with the small energy of acoustic M phonon leads to a persistence of the dip also at smaller temperatures, as shown in the supplementary material.
Finally, we briefly discuss the strain-dependence of exciton diffusion in other TMD materials. More details can be found in the supplementary material. In WSe2, the diffusion behaviour with compressive or small tensile strain is qualitatively similar to WS2, in particular showing a dip at s ≈ 0%. However, much higher values of strain are necessary to enter in the regime dominated by ΓK excitons due to a larger energetic separation between and excitons compared to the case of WS2. While the physical mechanisms are the same, in Mo-based monolayers one needs a larger tensile or compressive strain to reach the multi-valley features discussed for WS2. In particular, in unstrained MoSe2 the diffusion is dominated by KK excitons, while large tensile (s ≈ 2%) or compressive strain values (s ≈ −1%) are needed to approach the saturation points dominated by ΓK and K excitons, respectively. The situation in MoS2 is more involved due to the initial excitonic landscape in the unstrained case, where the position of strongly depends on the relative distance of the valence-band maxima located in K and Γ. The latter is still being controversially discussed in literature [28, 37, 62, 63]. We predict a qualitatively different strain-dependent exciton diffusion in MoS2 depending on , cf the supplementary material. An experimental study of exciton diffusion in MoS2 could thus provide a better understanding of the relative position of the bright KK and the dark ΓK excitons.
2. Discussion
In conclusion, the presented joint theory-experiment study provides new microscopic insights into strain-dependent exciton diffusion in TMD monolayers. We find that the diffusion becomes faster or slower with strain in a non-trivial and non-monotonic way. This is a result of the interplay between lattice-distortions and the remarkable multi-valley excitonic landscape in TMDs. Strain-induced shifts of exciton energies change the relative energy separations in the excitonic landscape of bright and momentum-dark excitons. This has an immediate impact on which state is dominant and governs the overall diffusion coefficient. In particular, we predict a dip in the diffusion for unstrained WS2 monolayers that we microscopically ascribe to intervalley scattering with acoustic phonons. This dip is followed by a large increase of exciton diffusion by a factor of 3 for tensile biaxial strain of up to 0.6%. The theoretical prediction is found to be in excellent agreement with spatiotemporal photoluminescence experiments. Overall, our study provides microscopic insights into the impact of strain on exciton diffusion in technologically promising 2D materials and uncovers the underlying fundamental intra- and intervalley scattering processes involving bright and momentum-dark excitons.
Acknowledgments
The authors thank Zahra Khatibi and Maja Feierabend for fruitful discussions. This project has received funding from the Swedish Research Council (VR, project number 2018-00734) and the European Union's Horizon 2020 research and innovation programme under grant agreement no. 881603 (Graphene Flagship). The computations were enabled by resources provided by the Swedish National Infrastructure for Computing (SNIC) at C3SE partially funded by the Swedish Research Council through grant agreement no. 2016-07213.




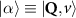
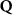
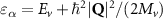



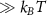
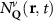
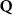
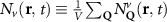
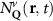
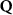

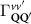


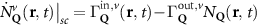
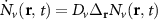
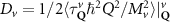
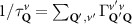

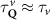
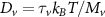
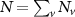
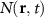

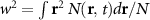
![$N(\mathbf{r},t)\propto \exp\left[-r^2/w^2(t)\right]$](https://content.cld.iop.org/journals/2053-1583/8/1/015030/revision3/tdmabbd51ieqn30.gif)