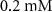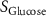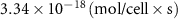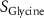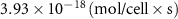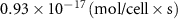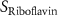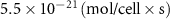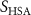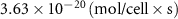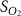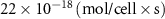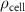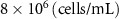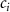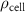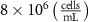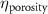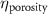Abstract
Vascularization is an indispensable requirement for fabricating large solid tissues and organs. The natural vasculature derived from medical imaging modalities for large tissues and organs are highly complex and convoluted. However, the present bioprinting capabilities limit the fabrication of such complex natural vascular networks. Simplified bioprinted vascular networks, on the other hand, lack the capability to sustain large solid tissues. This work proposes a generalized and adaptable numerical model to design the vasculature by utilizing the tissue/organ anatomy. Starting with processing the patient's medical images, organ structure, tissue-specific cues, and key vasculature tethers are determined. An open-source abdomen magnetic resonance image dataset was used in this work. The extracted properties and cues are then used in a mathematical model for guiding the vascular network formation comprising arterial and venous networks. Next, the generated three-dimensional networks are used to simulate the nutrient transport and consumption within the organ over time and the regions deprived of the nutrients are identified. These regions provide cues to evolve and optimize the vasculature in an iterative manner to ensure the availability of the nutrient transport throughout the bioprinted scaffolds. The mass transport of six components of cell culture media—glucose, glycine, glutamine, riboflavin, human serum albumin, and oxygen was studied within the organ with designed vasculature. As the vascular structure underwent iterations, the organ regions deprived of these key components decreased significantly highlighting the increase in structural complexity and efficacy of the designed vasculature. The numerical method presented in this work offers a valuable tool for designing vascular scaffolds to guide the cell growth and maturation of the bioprinted tissues for faster regeneration post bioprinting.

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Developing successful heterogeneous tissue structures requires that tissue scaffolds be carefully designed to incorporate vasculature that resembles native tissues while also demonstrating the structural, populational, and functional characteristics. A scaffold must be designed with a precise tuning of parameters (e.g. degradation rate, porosity, strength, etc) and a well-connected vascular network [1–3]. Medical imaging modalities such as computed tomography (CT), magnetic resonance imaging (MRI), and ultrasound provide angiography (i.e. images of the vessels) that acts as a starting point for scaffold design [4, 5]. In order to yield anatomically correct 3D models that eliminate noise from the medical images, segmentation methods can be used to delineate vessels from other tissues.
Various segmentation methods that are based on image intensity, such as histogram, edge-based, region-based, edge relaxation, border detection, and Hough transform, and texture-based features like statistical, structural and spectral, have been used to optimize the process. Gargiulo et al combined images retrieved from CT and MR imaging scans with those retrieved from diffusion tensor imaging, a tool that makes it possible to reconstruct nerve fibers in the brain [6]. This model was then used to create a 3D model of a patient's skull base, tumor and fiber tracts that were 3D printed. This anatomically realistic model of a patient's head was intended to aid surgeons in planning complicated surgeries; however, such technology is also making inroads into personalized tissue engineering. Recently, Lee et al described the production of collagen-based cardiac structures that were based on models reconstructed from MRI scans [7]. Additionally, vascular structures were integrated into the model via a separate computational model that used heat-map data based on the distance of blood vessels from the coronary artery. The Voronoi space-filling algorithm was then extended to the rest of the structure in order to generate 3D microvasculature. Such integration of vascular networks within models for bioprinting could aid in creating functional heterogeneous tissues. Additionally, in order to eliminate noise from 3D images that can result from variations in radiation doses and patient comfort, novel tools in deep learning like generative adversarial networks (GANs) can be applied [8–10]. The method makes use of two neural networks, one that is trained to generate an image and the other to discriminate. In this process, an image can be assessed for its authenticity due to which accurate 3D organ models could be enabled. This blend of the latest imaging technologies, in combination with bioprinting technologies will make it possible to advance the state of tissue-engineered constructs and enable a personalized therapeutic approach that is tailor-made, considering the patient's physiology and their clinical condition.
Various tissues and organs in the body fail and lose their functionality with ageing or after tissue damage. In such cases, large and thick tissues or full-size organs are needed to replace the damaged tissues or organs through transplant. However, this approach is limited by the scarcity of suitable tissues or organs available for transplants as well as the challenge of immunorejection. Bioprinting presents the capability to fabricate large tissue and organ analogues using the patient derived cells, anatomy and scaffold materials engineered to circumvent immunorejection [11]. The bioprinting methods use bioinks comprising living cells, biomaterials and additives (e.g. growth factors, nanomaterials and drugs) to construct the cell-laden hydrogel scaffolds. Recent studies have demonstrated evolved biofabrication capabilities to produce high-resolution, multi-material and structurally complex scaffolds [2, 12]. These advanced biofabrication processes have also been used to fabricate thick tissues and full-scale organ models [13, 14]. However, vascularization is an indispensable requirement for fabricating large solid tissues and remains a challenge. Lack of vasculature limits the size as well as complexity of the fabricated scaffolds by hindering the cell growth [15]. To address this, a few studies have attempted to fabricate perfusable scaffolds using sacrificial materials [2, 16–19]. In most of these works, simple hollow channels have been used as the vasculature. Kinstlinger et al attempted to create a bifurcating branched network, however, it was modeled as a geometrically simple closed network [19]. The modelled network was designed considering a cuboidal tissue geometry without any structural heterogeneity. These networks included a single inlet and outlet with branches bifurcating between the inlet and outlet. The fluid flow was examined within these networks with the aim of examining the flow velocities and pressure within the branches and bifurcation nodes. Further, Skylar-Scott et al presented an improved biomanufacturing model using organ building blocks and sacrificial writing into functional tissue to create more complex vascular tissues with high cellular density [20]. However, when compared with the natural vasculature in various organs, these bioprinted networks pose a problem of blood flow shunting as they are designed to allow unrestricted perfusion through a lumen network [21]. The bioprinted vasculature is required to include higher complexity in their architecture to mimic the natural vasculature. Therefore, a more complex and biomimetic vasculature needs to be designed. Further, the performance of the designed vasculature should be examined to ensure the nutrients are transported to the entire tissue. Beyond the vasculature design, the current bioprinting capabilities and bioink properties limit the fabrication of highly complex vasculature [22]. Medical imaging modalities can provide a detailed anatomy of the patient specific vasculature, however, structural complexity of such models cannot be captured by current bioprinting techniques. To mimic the natural tissues and vasculature, the microarchitecture of the scaffold also needs to be carefully controlled. These considerations are guided by the bioink properties like processing strategy (photocrosslinking, ionic crosslinking, thermal crosslinking etc.), rheological behavior, post-printing strength and porosity [23, 24]. Further, these bioink characteristics drive the biofabrication process. For instance, the varying branch thickness in the vasculature requires an adaptive control of extrusion rate and crosslinking intensity/duration in extrusion and light-based bioprinting respectively [25]. Post-fabrication, the hydrogel scaffolds can undergo swelling when immersed in cell growth medium and lead to deformation of the scaffold and, in turn, skewing the scaffold maturation. Such artifacts are remedied by either modifying the bioprinting process or bioink compositions [26]. The vascular scaffold design, therefore, should be constrained by the bioprinting and bioink limitations and necessary simplifications in the scaffold model and improvements in the bioprinting process should be introduced.
The vascular networks in the human body differ among the organs and tissues. In a typical network, the blood flows into the tissues through arteries that sub-divide into arterioles. The arterioles sub-divide to form capillaries that participate in exchanging nutrients and waste through diffusive mass transport [27, 28]. Further, the capillaries merge to form venules which, in turn, combine to form the veins for outflow of the blood from the tissue. When a scaffold with embedded vasculature is fabricated, the bioprinter capability limits the fabrication of small capillaries [29, 30]. Such vascular scaffolds rely on the vasculogenesis by the embedded hollow channels post fabrication and are currently designed to form connected vascular channels to allow perfusion through the scaffold. As the bioprinted scaffolds mature over time, angiogenesis is expected to evolve the vasculature and increase its complexity to sustain the entire scaffold [31]. However, the presence of a vascular network with unrestricted perfusion capability can skew the angiogenesis process and result in a tissue with uneven cell growth. Therefore, an initially fabricated vasculature should be bioinspired, simplified to meet bioprinting capabilities and sufficiently complex to provide diffusive nutrient transport to the entire scaffold during tissue/organ maturation. Since porous biocompatible hydrogels are used for fabricating these vascular scaffolds, the diffusive mass transport from the vasculature walls can take place until the endothelial lumens are formed completely. The surrounding cells rely on this diffusive mass transport from vasculogenesis until the capillaries are formed by angiogenesis.
Some recent studies have attempted to utilize the leaf vein networks for fabricating vascular tissues by decellularizing leaves and seeding with mammalian cells [32, 33]. Earlier, a leaf venation algorithm was presented which could mimic 2D vein networks in plant leaves [34]. This was further extended to mimic the 3D network of the tree branches [35]. We adapt this leaf venation model to develop a numerical model for designing the vasculature network that is inspired by the vein network present in the plant leaves. This work presents a framework to design the vasculature for a bioprinted tissue or organ while being driven by the organ or tissue structure and physical properties and concurrently being constrained by bioprinting limitations. First, the patient MR image processing is described to obtain organ structure and tissue-specific cues for guiding the vasculature design. Next, the vasculature generation numerical model is described in detail elaborating the steps involved in formation of branched arterial and venous networks. Further, the diffusive nutrient transport model considering the tissue properties and cellular consumption is described. Finally, an iterative way of optimizing the designed vasculature is presented which utilizes the outcomes of the diffusive nutrient transport model. Following this framework, the organ structure and relative tissue porosity could be estimated and utilized to generate open branched arterial and venous vasculature. As the vasculature evolved through various iterations, an increment in the fraction of scaffold volume receiving required nutrition for the cells was observed. Overall, this closed-loop design framework allowed extracting patient-specific tissue information and designing a personalized vasculature which can be bioprinted.
2. Theoretical model
2.1. Medical image processing
The vasculature network generation model proposed in this study comprises four major steps—medical image processing, vascular network generation, mass transport modeling and new tether points generation, as shown in figure 1. The process commences with medical image processing and segmentation to obtain the 3D structure of the target tissue or organ. The medical images in the form of a stack of slice images representing the cross-section structure of the tissue/organ at different depths were used in this study. The target tissue/organ regions were segmented in each slice image and stitched to form a point cloud representation of the tissue/organ volume. This point cloud was then translated into a 3D model of the tissue.
Figure 1. Sequence of steps involved in iterative vasculature generation and optimization. Four key steps are involved in the workflow—MR image segmentation to extract tissue/organ structure, estimate local tissue properties and identify vasculature tethers; vasculature generation constrained to the tissue/organ anatomy; nutrient transport modeling to characterize the effectiveness of the generated vascular network; and new tether points estimation to improve the designed vascular network.
Download figure:
Standard image High-resolution imageThis study used an open-source dataset of abdomen MRI with the liver as the target organ for designing the vasculature. The MRI dataset was retrieved from The Cancer Imaging Archive (TCIA, www.cancerimagingarchive.net/). Characteristics of the MRI dataset used to generate the liver 3D model are listed in table 1. We agree that variability among datasets can exist due to variations in the MRI scanners, scan parameters, patients, scanned organs and the type of imaging sequence. We believe the selected dataset provides a suitable representative case to demonstrate the proposed design framework. The selected open-source database TCIA is a well-curated database providing essential and reliable resources for medical imaging research. We aimed to demonstrate our method on a thick and dense organ with indispensable vasculature requirement and selected the abdomen MRI dataset owing to its completeness and high quality. Moreover, MR image dataset provides information about tissue water content which can be used to infer various tissue properties. Different MR modes can simplify the segmentation of the target tissue/organ structure from the images. However, the vasculature design method developed in this study is kept generic to allow the use of other imaging modalities. Further, MR elastography data can be used to include tissue viscoelastic properties in guiding the vascular network generation. Different image modes of the MRI dataset images are shown in figure 2(A). T1- and T2-weighted images with and without gadolinium contrast agents were recorded.
Figure 2. (A) Representative images from MRI dataset showing liver tissue in different imaging modes—T1-weighted, T2-weighted, T1-weighted with contrast agent (T1-contrast), and T2-weighted with contrast agent (T2-contrast). (B) Detailed sequence of steps in MR image segmentation for liver 3D model generation, tissue equivalent porosity parameter estimation and tether point generation. Input is marked in green; outputs are marked in orange and stored information of interest is enclosed in red boxes.
Download figure:
Standard image High-resolution imageTable 1. Liver MRI dataset specifications.
| Property | Value |
|---|---|
| Procedure | MRI ABDOMEN W + WO CONTRAST |
| Device | Philips Imaging DD 001 |
| Patient information (sex, age, weight) | M, 61Y, 127 kg |
| Magnetic field strength | 1.5 T |
| Echo numbers | 1 |
| Echo time | 1.954 s (T1) |
| Slice thickness | 4 mm |
| Spacing between slices | 2 mm |
| Pixel spacing | 0.98 mm |
| Number of phase encoding steps | 258 |
| Contrast medium | Gadolinium |
The MR slice images were segmented based on intensity thresholding to isolate the liver region represented by higher pixel intensity (gray level value). The threshold value was determined manually, however, other improved medical image segmentation methods can be applied. The segmented sections of the MR images were stitched to form a 3D point cloud dataset which was further filtered by applying a point clustering operation. Euclidean distance between the points was used as the clustering criteria. Small sub-clusters and points lying away from the clusters were removed to form an initial 3D liver model. It should be highlighted that the MRI images contain several regions of similar signal intensity that hamper intensity-based segmentation approaches and outputs point cloud data with undesired noise levels. Therefore, manual segmentation of target tissue/organ from the slice images by marking the tissue outlines can be used as an alternative approach. The 3D model achieved from the filtered point cloud was then converted to a 3D solid mesh comprising tetragonal elements. Since the mesh includes several defects that prevent its use in numerical simulations, mesh smoothing and repair steps were applied to improve the mesh quality. The final liver 3D model was then sliced to obtain a stack of binary images showing the cross-section at different depths. The slice spacing parameters specified in the MR image dataset (table 1) were utilized in this step. In this study, the segmented images were manually examined by an expert user, however, to further improve the accuracy and clinical relevance, the segmented images and the obtained organ 3D model can be rechecked by medical experts. The obtained slice images were used as digital masks and superimposed with the corresponding input MR images to extract the MR image data in the superimposed regions. A stack of segmented MR images was obtained with this step to provide gray-level intensity at each voxel of the generated liver 3D mesh. Next, the intensity data from T2 mode images from the segmented slice images was used for estimating a porosity equivalent parameter . The T2 mode images specifically selected as the pixel gray level intensity in T2 mode are proportional to the tissue water content. Since the designed scaffolds are intended for biofabrication with porous hydrogels, the approximate porosity of gelatin methacrylate (GelMA) hydrogels was used in this study. GelMA hydrogels have been reported to exhibit a porosity in the range of 80% to 90% [36, 37] in the literature which was used to define a linear variation as shown in equation (1)
where represents the voxel intensity at (x,y,z) coordinates from the liver volume formed by T2 mode images and represents the volume maximum intensity.
The histogram of the voxel gray level intensity of the liver volume formed by T2 mode images was obtained, corresponding to the distribution of the voxel water content in the liver. A threshold was applied to identify high water content regions (i.e. regions with high . These regions were then filtered from the liver volume and converted to a point cloud on which a point clustering step was performed to form multiple sub-clusters using Euclidean distance criteria. Centroids of these sub-clusters were identified as an initial set of tether (attraction) points for guiding the vascular network formation. A pair of initiation node points was also identified on the liver 3D model surface to initiate the vascular network formation. The described sequence of steps in the MR image processing with dependencies and outputs is graphically represented in figure 2(B).
2.2. Vascular network generation
The tether points and initiation points extracted from MR image processing were transferred to a custom venation program created in MATLAB™. Figure 3 shows a graphical representation of the different mathematical steps involved in the venation algorithm. The algorithm commences by computing the distance between the first node (initiation points or and the tether points (figure 3(A)). Several tissues and organs can include a cavity or other heterogeneous components (e.g. bones where the designed vasculature cannot be directly printed); therefore, a domain crossing restriction was introduced to restrict the vasculature within the feasible domain of the tissue/organ. To implement this, the lines connecting a node with all available and feasible tether points were formed and examined for intersection with the boundaries of the tissue/organ 3D structure. Any intersection led to the removal of the corresponding tether from the set of feasible tether points for the current node and was considered to not attract the growing vasculature network towards it. This criterion was re-evaluated as the vascular network evolved and presented as a possibility of the network moving around the cavity or bone volumes. A list was populated containing pairs of all the tether points attracting the current node to advance the vasculature. A bi-directional approach was used in determining such pairs where a node was attracted by all feasible tether points, but a tether point was only able to influence the geometrically closest node. The intersection of these sets provided the required tether-node pairs. Using the respective coordinates of the node and the tether points, the unit vectors at the current node were obtained pointing towards the attracting nodes. All the vectors were combined to compute a resultant vector that provided the stepping direction for the growing vasculature and the location of subsequent node. It should be highlighted that the stepping step can be evolved to scale the respective unit vectors and prioritize the attracting tether points based on the tissue physical characteristics as their location. This capability can aid the vasculature design process in various complex tissues where several factors (e.g. presence of different cell types, tissue composition with high fat content) affect the vasculature. The computed resultant stepping vector was then used to place a new node or . The new node was added to the growing vascular network and the line joining the new node and the previous node (or ) integrated with the growing branch as shown in figure 3(B). With the updated vascular network, the pair of feasible attracting tether points for each node were determined again with the methodology described earlier.
Figure 3. Detailed graphical representation of venation algorithm. (A) Initiation of the vascular network. (B) Propagation of the network by formation of new nodes. (C) Branching in the network. (D) Tether termination by approached branches. (E) Steps in determining the nodes in the relative neighborhood of a tether.
Download figure:
Standard image High-resolution imageAs the branches grew towards the tethers, the influence of the tether points was limited to the geometrically closest nodes combined with an additional criterion described later. For example, the node was closer to several tether point as compared to , which resulted in omission of those tether points when determining the feasible attracting tether points for node . This exclusion was determined by examining the relative neighborhood graph of the tether points as explained later in this section. Considering subsequent steps when the network had further evolved and included the nodes , , and as shown in figure 3(C). At this stage, the tether-node pairs were determined for all the nodes and only the tether was found to be an eligible attracting tether point for the node . This resulted in the sprouting of a new branch at the node approaching the tether and created a bifurcation in the growing vascular network (figure 3(C)). As the vasculature branches get closer to a tether point, a termination criterion was applied such that if the separation between a node and the tether point is less than or equal to the defined kill distance, the tether and the node were joined and terminated. Termination of the tether inactivates its influence over any nodes in further computation and the terminated nodes mark the end of the growing vasculature branch. When the branches from nodes and approached the tethers and and entered within the kill distance, the tethers and and the nodes and were terminated (figure 3(D)). On the other hand, all the branches approaching a tether point were tracked when a closed vascular network was sought. When a node was placed within the kill distance of the tether point, it was inactivated. However, the tether point was inactivated only when all the approaching branches had been terminated or the approaching branch nodes fell out of the tether point's relative neighborhood and were excluded from its influence in attracting the branch. The geometric interpretation of the various computation steps involved in determining the relative neighborhood of the tether S are shown graphically in figure 3(E). In this illustration, a scenario is considered when four branches approach the tether S along different directions. The leading nodes of these approaching branches were designated as nodes , , and , respectively. The blue circle marks the locus of a point located at a distance of (i.e. the distance between S and ) is indicated by a blue circle. When the leading nodes approaching the tether lie within the same quadrant, the node geometrically closer to the tether lies in the relative neighborhood of the tether and the other nodes are omitted. However, when the leading nodes on the approaching branches lie on different quadrants, the geometrical proximity is not the sole criteria for determining the nodes in the relative neighborhood of the tether. In such a scenario, a node was considered to be in the relative neighborhood of the tether S if the separation between the tether S and any other node was less than the separation between S and but the separation between and S was less than the separation between and [34]. A generalized form of this criterion is mathematically represented by equation (2).
After applying this definition of relative neighborhood, the nodes , and were included in the relative neighborhood of the tether S while the node was omitted because . Intrinsically, this criterion forced a geometric constraint that multiple branches in the vasculature can simultaneously approach a tether only if the lines joining the leading nodes of these branches and the approached tether point are at obtuse angles with respect to each other (i.e. the angle between two branches approaching the same tether cannot be less than ). This geometric constraint also imposes a limit on the vasculature density. Therefore, we revised this constraint in order to generate denser vascular networks and equation (2) was improved to include a parameter (equation (3)). For instance, if is set to , multiple vasculature branches could simultaneously approach the tether point with a minimum angle of between them and output a denser vascular network. On the other hand, increasing beyond will result in the formation of a sparser vasculature.
where
Once the vascular network was generated from the venation algorithm, a cleaning operation was performed to remove short branches that included less than two nodes and did not connect to a tether. While designing a closed vascular network, the cleaning operation identified and removed all the open branches (i.e. not connected to other branches directly or at tethers) in the vascular network. The tethers that were connected to a single branch were also removed in this process along with the branch. As the vasculature comprised of several splits where the parent branch divided into multiple child branches, the Murray's Law with was applied to determine the thickness of the respective branches (equation (4)).
The thickness of the primary branch of the vasculature at the initiation nodes was defined manually, and the thickness of subsequent child branches was computed with equation (4). When determining the branch thickness in closed vascular networks, Murray's Law poses an ill-defined problem with no solution. Therefore, an additional constraint was applied by restricting the minimum branch thickness to the dimensions of the smallest features that can be fabricated by the bioprinting system that will be used subsequently for fabricating the designed vascular tissues. The entire vasculature was a connected network of nodes which were points in a 3D cartesian space. The branch thickness was applied by placing concentric circles of determined diameter at and between the connected nodes. After applying the branch thickness to the entire vasculature, a point cloud was formed that was transformed into a 3D mesh object to be used in subsequent steps or for biofabrication.
The obtained vasculature point clouds for both artery and vein were imported into MeshLab, an open-source meshing software. Point normals were computed for the point clouds, followed by screened Poisson surface reconstruction to generate watertight surfaces. Parameters such as reconstruction depth, interpolation weight and Gauss Seidel relaxations were adjusted to create a smooth surface for the artery and vein 3D models. The resulting surface mesh was imported into Autodesk Meshmixer and converted into a solid tetragonal mesh. Artery and vein mesh, when assembled, were found to intersect at a few points that were readjusted to create a combined intersection free mesh. As these meshes consist of approximately 50,000 faces, intersecting faces and inward point facing normals occur frequently resulting in mesh with poor quality. Thus, several smoothing and remeshing operations are recommended before proceeding with further simulation steps.
Current studies model and fabricate networks that have arteries and veins connected together (i.e. closed vasculature) without the presence of capillaries, which creates a shunted blood flow [18, 19, 21, 38]. Although these veins and arteries pass through the fabricated tissue, the diffusion rate of nutrients from the walls of such networks is significantly slower than the fluid flow within the network. In the present model, the veins and arteries are not directly connected (i.e. open vasculature). Instead, nutrient transport occurs through the porous hydrogel between the arteries and veins. Nutrient transport through these pores crudely mimics a cluster of tiny capillaries. The described venation algorithm was tested to design a closed shunted vasculature forming around the brain, as shown in figure S1(A). The capability to design an open vascular architecture was also demonstrated by designing a combination of arterial and venous networks inside a liver (figure S1(B)).
2.3. Diffusion-based vasculature optimization
The processed 3D mesh combining the artery and vein structure and the 3D model of the liver generated from the MR image processing was imported into COMSOL to simulate the mass transport of various cell growth media components. We focused on the mass transport characteristics of six components—glucose, glycine, glutamine, riboflavin, human serum albumin (HSA) and oxygen. These components represented the classes of sugar, amino acid, vitamin, protein, and gas, respectively. The designed 3D liver structure and the vascular network are intended to be bioprinted with porous hydrogels. Therefore, the surface of the artery and vein network within the liver was defined as an internally permeable wall allowing the diffusion of cell growth media components. The vascular networks were defined as hollow domains filled with cell growth media. The vascular network's primary branches beginning at the initiation nodes are, by design, located within the tissue domain, which makes them inaccessible to apply required boundary conditions. Therefore, the primary initiation branches were extended to protrude out of the liver volume. The extended protruded parts in the arterial and venous vascular networks were defined as hollow tubular structures for the inlet and outlet of the cell growth media (figure 4(A)). Next, we defined the liver body as a porous medium saturated with an aqueous solution, and the initial concentration of various cell growth media components was set as zero. Since a porous hydrogel will be utilized to fabricate the liver scaffold, it is expected to allow diffusion of various chemical species through the outer surface. However, an epithelial cell layer forms the outer surface of the organs and prevents such diffusive mass transport and limits the mass transport contribution to the vasculature. Therefore, we modeled the external wall of the liver body to be surrounded by mucous, which prevents a diffusive mass transport by applying a no flux boundary condition. The local porosity within the liver body was defined using the porosity equivalent parameter determined earlier from the MR images. The spatial porosity variation in y-z and x-y cross-sectional planes is shown in figures 4(B)–(D). The diffusive mass transport in the liver domain was modelled using equation (5) by considering a saturated porous media.
The diffusive flux was defined by equation (6) using an effective diffusivity , considering a negligible contribution in mass transport from dispersion.
Figure 4. Model definitions for cell growth media transport simulation. (A) Description of domains properties, inlet and outlet. (B) Perspective view of equivalent porosity parameter variation. Cross-sectional plane showing local variations in the equivalent porosity parameter within the liver body on (C) y-z plane and (D) x-y plane.
Download figure:
Standard image High-resolution imageThe effective diffusivity , in turn, was computed using equation (7) by using Millington and Quirk model. This model defines the fluid tortuosity as a function of media porosity , and represents the diffusion coefficient of the various cell growth media components in the aqueous medium
The thin permeable vasculature walls allowed a diffusive mass transport with nutrient diffusion flux given by equation (8), where the concentration of various components in the liver domain and the vasculature domain are denoted by and , respectively, and represents the thickness of the thin permeable outer wall of the vasculature.
Convective mass transport was not included in this model as the growth media flows through the vasculature and the diffusion of various chemical species occurs through the permeable wall of the vasculature channels and beyond the vasculature. The species transport is not influenced by the growth media flow. Although the cell growth medium comprises numerous components, for simplicity, five components were considered, and their respective concentrations and diffusion coefficients were obtained from previous experimental investigations (table 2). The entire liver scaffold was considered to encapsulate the hepatocytes as a bioprinted construct. As the cell media components diffused through the liver, they were also consumed by the encapsulated cells with the consumption rates listed in table 2. The local consumption rate of these components was computed by equation (9),
Table 2. Diffusive mass transport modelling parameters.
| Parameter | Value | Description | References |
|---|---|---|---|
| Diffusion coefficient of glucose in water | [39] | ||
| Diffusion coefficient of glycine in water | [40, 41] | ||
| Diffusion coefficient of glutamine in water | [42] | ||
| Diffusion coefficient of riboflavin in water | [43] | ||
| Diffusion coefficient of human serum albumin in water | [44] | ||
| Diffusion coefficient of oxygen in water | [45] | ||
| Initial concentration of glucose in growth medium | [46, 47] | ||
| Initial concentration of glycine in growth medium | [46, 47] | ||
| Initial concentration of glutamine in growth medium | [46, 47] | ||
| Initial concentration of riboflavin in growth medium | [46, 47] | ||
| Initial concentration of human serum albumin in growth medium | [48] | ||
| Initial concentration of oxygen in growth medium | [49, 50] | ||
| Estimated glucose consumption rate | [51] | ||
| Estimated glycine consumption rate | [52] | ||
| Estimated glutamine consumption rate | [53] | ||
| Estimated riboflavin consumption rate of glucose | [54] | ||
| Estimated human serum albumin consumption rate | [55] | ||
| Estimated oxygen consumption rate | [56] | ||
| Initial cell encapsulation density in scaffold | [15, 57] |
where denotes the molar consumption rate of by a single cell per second and represents the population density of the cells in the scaffold. The cell density was kept as based on previous bioprinting studies [15]. The glycine and albumin secretion as a result of the cell metabolic processes was not included in this study for simplification.
The diffusive mass transport in the liver scaffold was simulated up to a duration of 300 min (5 h). Although the cells can survive starvation periods for up to several hours, an upper bound for the starvation period is required in the vasculature design process to constrain the complexity of the vascular networks. This upper bound should be defined by considering the target tissue/organ and the metabolic activity of the constituent cells. In this study, the maximum starvation period was defined as 60 min to impose a stringent condition to drive the branching of the vascular network. The regions in the liver domain without a positive concentration of the cell growth media components at the end of the starvation period were designated as 'starvation' regions. A point cloud dataset was populated with a list of coordinates representing the 3D liver volume and the corresponding concentration of cell growth media components. The starvation regions were then filtered from this dataset, and a point clustering operation with Euclidean distance between the points as the clustering criteria was applied to segment the filtered point cloud dataset. The centroids of the segment clustered were selected as the new tethers for venation. The final list of tethers included the new tethers as well as the previous set of tethers used to generate the vasculature. New tethers in close proximity to the old tethers were removed, and the set of updated tethers was provided as input for the next iteration of the venation to improve the vascular network.
3. Results and discussion
3.1. Liver 3D model generation
The liver 3D model was obtained from an open-source MR image dataset by applying the methodology described above (section 2.1). The MR images were first segmented by applying an intensity threshold on the T1-contrast images (figure 5(A)) to remove dark regions surrounding the liver tissue. The segmented slice images were then individually converted to a 2D point cloud dataset and were further refined by applying a point clustering operation. Post filtering, the slice images were stacked to obtain a 3D point cloud by applying the voxel scaling parameters from table 1 and then the point cloud was converted to a 3D mesh by applying triangulation operations, as shown in figure 5(D). The generated 3D liver model had a rugged topography with sharp vertices and disconnected faces due to the low resolution across the MRI dataset slices and error in the segmentation of exact liver boundaries. Mesh smoothing and mesh repair operations were performed on the 3D liver model to obtain a smooth surface topography, as shown in figure 5(E). The generated model included the aorta along with the liver tissue, which was removed manually to obtain the final liver 3D model (figure 5(F)). Mesh smoothing and repair operations resulted in slight deformation in the overall 3D liver model and introduced a volume shrinkage of 6% when compared to the rugged topography 3D model shown in figure 5(D). The smoothed liver 3D model was sliced again with the same slicing parameters as the input MRI dataset to generate the binary cross-section images at different heights (figure 5(B)). The corresponding slice images of the liver 3D models before and after the mesh smoothing and repair operations (figures 5(D) and (E)) were compared to compute the reconstruction error introduced in each slice due to various mesh manipulations (figure 5(G)). The cross-section area reconstruction error was maintained below 10% in the majority of the slices. However, the liver cross-section in the inferior slices (i.e. slices at the bottom part of the liver) suffered comparatively large distortion (15%–18%). As this study emphasizes the development of a process workflow, a simple segmentation and 3D organ reconstruction approach is used. However, the accuracy of the image segmentation and organ reconstruction can be improved using previously reported methods along with the inclusion of machine learning models [8–10, 58].
Figure 5. MR image processing and 3D model generation. (A) Representative T1-contrast mode slice image. (B) Slice image representing the cross-section of smoothed 3D liver model. (C) MR image segmented by applying cross-section slice image (B) as binary mask. (D) Rough 3D liver model generated from filtered point cloud. (E) 3D liver model after applying smoothing operations. (F) Smoothed 3D liver model after removing aorta. (G) Reconstruction error due to smoothing represented as error in slice area.
Download figure:
Standard image High-resolution imageThe slice images were superimposed from the smooth 3D liver model without aorta on all the image modes in the input MRI dataset (i.e. T1, T2, T1-enhanced and T2-enhanced) and segmented the superimposed regions, as shown in figure 5(C). These images included the intensity variation at each voxel of the liver volume which was subsequently used to evaluate the local tissue's physical properties. figures 6(A)–(D) show 3D volume plots demonstrating the image signal intensity variation in the liver volume for different MRI modes (T1, T2, T1-enhanced and T2-enhanced). The maximum and minimum grayscale intensity values in the 8-bit input MR images correspond to 255 and 0 and are represented by red and blue, respectively, in a rainbow color map. Further, the histogram for these volumetric data was generated to show the distribution of the faction of voxels at different grayscale intensities, as shown in figure 6(E). The T1-contrast and T2-contrast mode images with gadolinium contrast agent provided a nearly overlapping voxel intensity distribution; however, they had subtle differences. This can also be observed when comparing the T1-contrast and T2-contrast enhanced slice images (figure 2(B)), where the intensity of the liver tissue is comparable. However, a clear difference in the intensity of the vasculature can be observed. The T1 and T2 mode images, on the other hand, show a clearly distinguishable voxel intensity distribution. The narrow voxel intensity distribution in the 3D volume formed by the respective image modes implied relatively uniform tissue characteristics in the liver with slight variations. It should be noted that some tissues/organs (e.g. Kidney) have highly heterogeneous architecture and tissue characteristics and need to be approached with a refined strategy for extracting tissue/organ structure and tissue properties. The 3D point cloud formed by the segmented T2 mode images was further used to compute the porosity equivalent parameter (figures 4(B)–(D)) at each voxel, as well as to identify the initial tether points for initiating the venation algorithm.
Figure 6. Volume intensity plots showing the intensity variations in (A) T1-weighted, (B) T2-weighted, (C) T1-weighted with contrast agent and (D) T2-weighted with contrast agent datasets. (E) Histogram representation of voxel distribution at various intensity.
Download figure:
Standard image High-resolution imageFigure 7. Vascular network generation using venation algorithm. (A) 3D spatial distribution of tether points for vein network generation. (B) Partially formed vein network. (D) 3D models of combined artery (red) and vein (blue) networks. (D) 3D rendering of the generated vascular networks enclosed in the liver body.
Download figure:
Standard image High-resolution image3.2. Vasculature generation
A combination of two distinct vascular networks (arterial and venous) was used to represent the overall liver vasculature, and the porous hydrogel matrix between the two networks mimicked a capillary bed as described above (section 2.2). Using the 3D point cloud volume data of derived from the T2 images, two distinct sets of tether points were obtained for generating the arterial and venous vascular networks, respectively, as described previously. The initiation tether points for arterial and venous networks were also defined separately and coincided with the position of the primary artery and vein near the surface. Figure 7(A) shows the obtained initial set of tether points for the venous network generation along with the lower half of the liver body for reference. Figure 7(B) shows a partially formed vein network following the venation computation steps described earlier. Once the arterial and venous vascular networks were generated, they were processed to remove very short branches (i.e. comprising less than two nodes) and apply the respective branch thickness at each node computed using the Murray's Law. Upon applying the branch thickness, the finalized vascular networks were transformed to 3D point clouds and then converted to 3D mesh objects. The generated 3D mesh objects of arterial and venous networks are collectively shown in figure 7(C). The arterial network is shown in red color and the venous network is shown in blue color for clear demarcation. The 3D meshes were then combined with the liver 3D model and a rendered image mimicking the physical appearance of a 3D bioprinted liver was generated utilizing the optical properties of a typical hydrogel (e.g. GelMA) as shown in figure 7(D).
3.3. Growth media transport
The 3D models of the liver, artery and vein network were imported and combined in COMSOL, and the diffusive mass transport was simulated using the methodology described earlier. Figure 8 shows the isosurface plots representing the concentration of glucose diffused within the liver body from the vasculatures designed in Iteration 1 and Iteration 2. To demonstrate the availability of glucose for the cells and the starvation regions within the liver body, representative isosurface plots at 6, 30, 60 and 300 min, respectively, are shown. A concentration gradient of the diffused species also exists within the isosurface envelope (figure 8 inset image). The extent of diffusion for other species in the cell growth media—glycine, glutamine, riboflavin, human serum albumin and oxygen are also shown in figures S2–S6. The portion of the liver volume covered with the diffused cell growth media components is shown in figure 9(A). The glucose diffusing from the vasculature designed in Iteration 1 covered 56.7% of the liver volume at 5 h while including cellular consumption. On the other hand, 86.8% of liver volume was covered by glucose diffusion in absence of cellular consumption.
Figure 8. Glucose distribution in liver by diffusive mass transport simulation. Concentration isosurface plots in the liver body at 6, 30, 60 and 300 min due to the diffusive mass transport from vasculature obtained in iteration 1 and iteration 2. Inset: Gradient in the glucose concentration distribution.
Download figure:
Standard image High-resolution imageFigure 9. (A) Time series plot of portion of liver volume covered with various cell growth media components with vasculature from iteration 1 and 2 including cellular consumption. (B) Temporal variation of average cellular consumption rates of various chemical species in the liver volume for vasculature design iterations 1 and 2.
Download figure:
Standard image High-resolution imageConversely, the vasculature designed in Iteration 2 exhibited improved coverage due to a denser network and covered 64.4% of the liver volume at the end of 5 h in presence of cellular consumption (table S1). However, in absence of cellular consumption, the glucose diffusion from the vasculature designed in Iteration 2 covered 86.5% of liver volume. Further iterations are expected to increase the complexity of the vasculature and achieve complete coverage of the liver volume in the designated maximum starvation duration of 5 h. As various chemical species become available to the encapsulated cells, they begin the uptake of the respective chemical species; however, this uptake is not consistent throughout the liver scaffold and is adaptive in nature, relying on the distribution of the species. The presented model accounts for such adaptive cellular consumption of the growth media components, as demonstrated by figure 9(B), which shows the average consumption rate of various species within the liver scaffold. HSA and riboflavin are present in the cell culture media at very low concentrations and have very low diffusivity in an aqueous medium due to their large molecular size. Concurrently, their cellular consumption rates are very low as compared to other chemical species that result in a similar portion of the liver being covered by albumin and riboflavin as compared to smaller molecules like glutamine and glycine. The adaptive nature of species consumption by the cells, in turn, contributes to the diffusive transport of various species that cause fluctuations in the total portion of liver volume covered (figure 9(A)) in the initial period. We also examined the diffusive transport of various chemical species in the absence of cellular consumption. As shown in figure S7, the vasculature designed in Iteration 2 was suitable to cover a major portion of the liver scaffold with glucose for 5 h.
An often-overlooked pitfall is the differential diffusion of various cell growth media components within the bioprinted constructs. Such differences are neglected in small scaffolds and current studies in which the bioprinted scaffolds are submerged in cell culture media. However, the differences in the diffusivity of various growth media components can lead to significant differences in the composition of unit volume at different regions in large scaffolds. This will be further convoluted by implementing a more physiologically relevant constraint of relying solely on the vasculature rather than submerging the entire scaffold in the cell growth media. This is clearly highlighted in figure 9(A), where the differences in the concentration and molecular size of various species in the cell growth media resulted in striking differences in the coverage portion of the liver body, thus, altering the chemical composition of each voxel.
Although the hepatocytes can sustain starvation periods extending beyond 5 h, we imposed a stricter criterion for increasing the complexity of the designed vasculature in Iteration 2 and beyond by considering the glucose availability at 60 min (figure 10(A)). Such a criterion identifies a larger portion of the liver body as the starved region. The concentration distribution of glucose within the liver body was used to identify the starvation region using a custom MATLAB script and is represented as a point cloud in figure 10(B). These point clouds were further processed by applying a Euclidean distance-based point clustering operation as described in earlier sections. The centroids of these point clusters were then identified and compared with the previous set of vasculature tether points to determine the new set of tether points for designing a vasculature evolved from the previous iteration. The set of tether points obtained for arterial (red) and venous (green) network generation at the end of Iterations 1 and 2 are shown in figures 10(Ci) and (Cii), respectively. The second iteration of the venation algorithm generated a denser network, which in turn led to broader nutrient coverage in the liver body, as shown in figure 8.
Figure 10. (A) Glucose covered portions of liver volume at 60 min in (i) iteration 1 and (ii) iteration 2. (B) Point cloud representation of nutrient starvation region in (i) iteration 1 and (ii) iteration 2. (C)(i-ii) Distribution of tether points for next iterations of venation.
Download figure:
Standard image High-resolution imageA vasculature network architecture ideally consists of branched arterial and venous networks and these two networks are connected by a dense capillary bed. Such structure is capable of perfusion under a pressure gradient to generate bulk or interstitial flow of cell growth media. Although arterial and venous networks can be designed, the design of capillary bed poses a challenge. This challenge arises from the different length scales of arteries/veins and capillaries as well as from determining the spatial location of the capillaries. Inclusion of such capillary designs can be achieved by performing multiscale modeling at significantly higher computational complexity. On the other hand, the absence of the capillaries limits the capability to model convective mass transport. In this study, a simplification has been introduced considering that if a bioprinted scaffold is perfused with the cell growth medium, the fluid flows through the connected vasculature and the vasculature walls restrict the flow beyond the vasculature. This leads to a diffusive mass transport occurring from the vasculature walls to the bulk tissue whereas the convective mass transport within the vasculature is significantly larger. Therefore, the cell growth media at any unit volume of the vasculature is replenished quickly and appears to be a constant composition at the diffusive mass transport timescale. This has been modelled in the present study by considering a constant composition of growth media in the vasculature branches and simulating the diffusive mass transport within the bulk tissue. Further, the bulk tissue is modelled as a porous material in which the interconnected pores approximate the presence of a capillary bed. However, including a multiscale model of capillaries can further improve the presented model and provide better insights into angiogenesis and tissue maturation. Moreover, the designed vasculature with simplified architecture is intended to ensure adequate nutrient availability to the encapsulated cells in the entire scaffold in the early stages of maturation after bioprinting. As the vascular scaffold matures, the formation of capillaries will lead to a perfusable vascular network.
The vascular networks generated from the three iterations in this study are shown in figure 11. The perspective views of the network 3D models are shown in figures 11(Ai), (Bi) and (Ci), top views are shown in, (ii), (Bii) and (Cii) and the rendered 3D models are shown in, (iii), (Biii) and (Ciii), respectively. Typically, 4-5 iterations are expected to achieve a volume coverage greater than 80%. Although the presented model captures the consumption of various chemical species, modelling the production of various metabolites by the cells can improve this model. Adaptive cellular consumption rates have been modelled in the presented system; however, such cellular consumption processes can be coupled with known metabolic pathways to define how the cellular consumption kinetics will vary. Moreover, the growth of cells and migration using agent-based models [59, 60] and angiogenesis [61] can also be implemented for a more realistic perspective on the maturation of the fabricated vascularized tissues. The migration and growth of the cells within the scaffold will be governed by the degradation of the biomaterial scaffold which can be implemented in the presented model to improve it. The local physical properties and their variation in the hydrogel scaffold can be predicted based on the bioprinting conditions [62] which, in turn, can be used to predict scaffold degradation as the scaffold matures under the physiological conditions [63] in the extension of the presented study.
Figure 11. Generated liver vascular networks from venation algorithm and guided by MR images. (A) Vasculature generated in iteration 1–(i) perspective view, (ii) top view and (iii) 3D rendering image with liver body. (B) Vasculature generated in iteration 2–(i) perspective view, (ii) top view and (iii) 3D rendering image with liver body. (C) Vasculature generated in iteration 3–(i) perspective view, (ii) top view and (iii) 3D rendering image with liver body.
Download figure:
Standard image High-resolution imageThe scaffold remodeling by encapsulated cells during maturation should include various cell-biomaterial interactions as well as multiple cell types [64, 65]. A suggested pathway can include modeling the enzyme and extracellular matrix secretion by the cells followed by enzymatic degradation of the scaffold hydrogel [66, 67]. These processes can lead to changes in the hydrogel porosity which can be integrated with an angiogenesis model in simulation the diffusive and convective mass transport from a capillary bed between the arteries and veins. Concurrently, the designed vasculature should be experimentally validated. The fabrication of scaffolds with high structural complexity has been demonstrated by evolved biofabrication methods such as embedded 3D bioprinting of hydrogels in a biocompatible gel bath with multiple bioinks, high-resolution stereolithography, or volumetric bioprinting [12, 20, 68, 69]. However, these biofabrication approaches still have specific limitations which can limit their suitability in fabricating the vascular structures designed in this study. We propose a hybrid bioprinting approach combining embedded 3D bioprinting of hydrogels and volumetric bioprinting can potentially achieve the biofabrication of the designed vascular scaffolds. In such hybrid bioprinting approach, the embedded 3D bioprinting of hydrogels can be used to fabricate the vascular network followed by the surrounding tissue fabrication by volumetric bioprinting. For detailed in vitro characterization, small vascular tissues with comparable anatomical complexity can be fabricated with the hybrid bioprinting method. These scaffolds can be subjected to similar physiological conditions in the numerical modeling and the mass transport of various growth media components and local cell growth can be experimentally measured and compared with the simulated values.
4. Conclusion
In this study, a closed-loop method of vasculature design is presented. The liver was selected as the target organ due to being a solid organ with the high metabolic activity of the constituent cells and, therefore, the requirement of a highly complex vasculature. First, a methodology to process MR images was presented. The MR images were segmented to form point clouds representing the liver volume. The liver 3D model was created from these point clouds by applying various refining and smoothing operations. The generated liver model was again coupled with the MR images to derive volumetric tissue specifications. These derived properties were used with a venation algorithm to guide the vascular network formation. Several modifications in the venation were made to arrive at a bioinspired vasculature design. The resulting vasculature from the first iteration was quite simplified and could not achieve nutrient transport to the entire liver volume. The outcome of the diffusive mass transport simulation was then used to identify the nutrient deficit (starved) regions which were used as feedback for the subsequent vasculature evolution. Through the iterations, increased complexity in the vascular network was observed along with increased nutrient-covered liver volume. The framework presented in this work also presents a potential tool for predicting the cell growth within the scaffold volume. The volumetric distribution of various chemokines can also be predicted and controlled in the scaffold to potentially guide cell growth. Moreover, if coupled with the predictive hydrogel formation models, cell growth models and angiogenesis models, this framework can be used to customize the scaffolds to guide the maturation of fabricated tissue over time.
Acknowledgments
This work was supported by the Science and Engineering Research Board (SERB, India) Overseas Doctoral Fellowship and the Natural Sciences and Engineering Research Council of Canada (NSERC) Discovery Grant (RGPIN-2020-04559). This research was enabled in part with support provided by (SHARCNET, Calcul Québec, and WestGrid) (www.sharcnet.ca) and Compute Canada (www.computecanada.ca). The authors would like to thank Dr Sudhir Kamle (IIT Kanpur) and Mr Brij Mohan (IIT Kanpur) for their valuable advice in refining the numerical model.
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files)
Conflict of interest
The authors declare no conflict of interest.





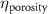
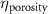
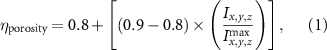
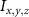
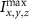

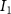

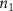
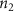
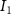
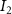

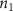
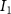
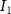
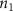
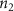
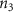
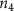
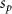
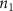
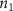
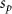
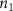
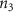
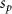
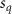
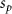

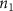
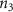

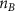
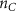
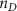
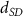
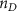
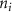
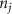
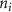
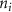
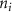
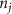
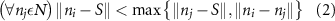
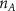
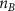
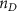
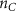
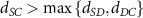
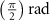
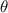
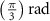
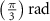
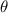
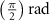
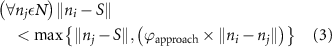
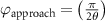
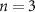
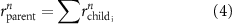
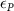
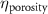
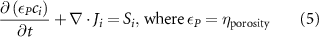
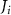
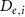


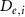
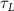
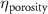
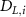


![${[{c_i}]_{{\text{liver}}}}$](https://content.cld.iop.org/journals/1758-5090/15/2/024104/revision2/bfacb73cieqn66.gif)
![${\left[ {{c_i}} \right]_{{\text{vasculature}}}}$](https://content.cld.iop.org/journals/1758-5090/15/2/024104/revision2/bfacb73cieqn67.gif)

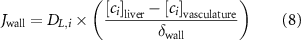
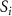

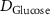
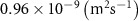
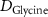
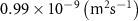
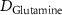
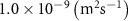
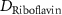

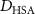
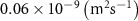
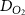
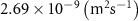
![${\left[ {{C_{{\text{Glucose}}}}} \right]_o}$](https://content.cld.iop.org/journals/1758-5090/15/2/024104/revision2/bfacb73cieqn81.gif)
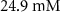
![${\left[ {{C_{{\text{Glycine}}}}} \right]_o}$](https://content.cld.iop.org/journals/1758-5090/15/2/024104/revision2/bfacb73cieqn83.gif)
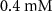
![${\left[ {{C_{{\text{Glutamine}}}}} \right]_o}$](https://content.cld.iop.org/journals/1758-5090/15/2/024104/revision2/bfacb73cieqn85.gif)
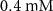
![${\left[ {{C_{{\text{Riboflavin}}}}} \right]_o}$](https://content.cld.iop.org/journals/1758-5090/15/2/024104/revision2/bfacb73cieqn87.gif)
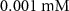
![${\left[ {{C_{{\text{HSA}}}}} \right]_o}$](https://content.cld.iop.org/journals/1758-5090/15/2/024104/revision2/bfacb73cieqn89.gif)
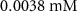
![${\left[ {{C_{{O_2}}}} \right]_o}$](https://content.cld.iop.org/journals/1758-5090/15/2/024104/revision2/bfacb73cieqn91.gif)