Abstract
Carbon nanotube with electric fluxes confined in one dimension is studied. We show that a Coulomb interaction 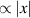 leads to a confinement phase with many properties similar to QCD in 4D. Low-energy physics is described by the massive Schwinger model with multi-species fermions labeled by the band and valley indices. We propose two means to detect this state. One is through an optical measurement of the exciton spectrum, which has been calculated via the 't Hooft–Berknoff equation with the light-front field theory. We show that the Gell–Mann−Oakes−Renner relation is satisfied by a dark exciton. The second is the nonlinear transport which is related to Coleman's 'half-asymptotic' state.
leads to a confinement phase with many properties similar to QCD in 4D. Low-energy physics is described by the massive Schwinger model with multi-species fermions labeled by the band and valley indices. We propose two means to detect this state. One is through an optical measurement of the exciton spectrum, which has been calculated via the 't Hooft–Berknoff equation with the light-front field theory. We show that the Gell–Mann−Oakes−Renner relation is satisfied by a dark exciton. The second is the nonlinear transport which is related to Coleman's 'half-asymptotic' state.
Export citation and abstract BibTeX RIS
Even after two decades from its discovery, fascination continues with the carbon nanotube [1]. One line of research is motivated by its possible application as opto-electronic devices. Another is more academic, in which possibilities are explored to realize new states of matter. In low dimensions quantum fluctuations are enhanced, which makes the nanotube an ideal host for strongly correlated and clean quantum systems. One monumental result along this line is the Tomonaga–Luttinger liquid in single-wall metallic nanotubes [2–4]. In the present work, we theoretically predict a realization of yet another interesting state, namely the confinement phase (CP), in nanotubes. In this state, charged particles cannot exist as free asymptotic states where all the excitations are neutral bound states (i.e. excitons in the present case).
A most famous realization of the CP is the hadronic system where the effective quantum field theory is quantum chromodynamics (QCD) in (3+1)D. By contrast, a carbon nanotube is a one-dimensional object, and no dynamical nonabelian gauge field exists. Nonetheless, we propose here a CP may exist; A key is the dimensionality. In a seminal paper by Schwinger, a (1+1)D version of quantum electrodynamics (QED), i.e. the Schwinger model, was studied [5]. In this model, Dirac particles interact through a one-dimensional Coulomb potential ( ). The long-range interaction mimics the confinement potential, and the groundstate is indeed in a CP. The Schwinger model and its extensions were studied as a toy model of (3+1)D QCD to understand non-perturbative aspects of the CP [6–12]. However, up to now, no physical realization of this model is known. Our claim here is that the low-energy effective model for electrons in a nanotube can be, in certain situations, modeled by an extended massive Schwinger model. It is well known that a multi-species Dirac spectrum is realized in the band structure of nanotube within the effective mass approximation. In order to realize the one-dimensional Coulomb potential, the electric fluxes must be confined along the tube. The situation with shielded 1D electric flux can possibly be realized in (a) multi-wall nanotubes with metallic outer tubes, (b) a tube surrounded by metallic tubes, or (c) tubes embedded in a superconductor. While one may wonder if such shielding can really take place, there is a prominent example in two-dimensional (2D) organic crystals studied by Yamaguchi et al [13]. They have experimentally shown that a layered structure with a large difference in the dielectric constants leads to confinement of electric fluxes in the 2D plane where the Coulomb potential becomes logarithmic. In this experiment, the long-range Coulomb interaction leads to a power-law current–electric field (J–E) characteristics with a temperature dependent power. This gives us a strong motivation to study nanotube with a 1D Coulomb potential. The properties of the CP is reflected in the excitation spectrum. In order to explore this, we propose two observable properties, one optical and another transport.
). The long-range interaction mimics the confinement potential, and the groundstate is indeed in a CP. The Schwinger model and its extensions were studied as a toy model of (3+1)D QCD to understand non-perturbative aspects of the CP [6–12]. However, up to now, no physical realization of this model is known. Our claim here is that the low-energy effective model for electrons in a nanotube can be, in certain situations, modeled by an extended massive Schwinger model. It is well known that a multi-species Dirac spectrum is realized in the band structure of nanotube within the effective mass approximation. In order to realize the one-dimensional Coulomb potential, the electric fluxes must be confined along the tube. The situation with shielded 1D electric flux can possibly be realized in (a) multi-wall nanotubes with metallic outer tubes, (b) a tube surrounded by metallic tubes, or (c) tubes embedded in a superconductor. While one may wonder if such shielding can really take place, there is a prominent example in two-dimensional (2D) organic crystals studied by Yamaguchi et al [13]. They have experimentally shown that a layered structure with a large difference in the dielectric constants leads to confinement of electric fluxes in the 2D plane where the Coulomb potential becomes logarithmic. In this experiment, the long-range Coulomb interaction leads to a power-law current–electric field (J–E) characteristics with a temperature dependent power. This gives us a strong motivation to study nanotube with a 1D Coulomb potential. The properties of the CP is reflected in the excitation spectrum. In order to explore this, we propose two observable properties, one optical and another transport.
1. Model
We study nanotubes within the effective-mass formalism. There are infinitely many bands corresponding to different modes along the circumference of the tube, which we label with 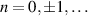 . The way in which the tube is wound is characterized by an index
. The way in which the tube is wound is characterized by an index  , which in turn specifies whether a discrete set of momenta along the tube circumference intersect the two Dirac cones at
, which in turn specifies whether a discrete set of momenta along the tube circumference intersect the two Dirac cones at 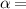 K, Kʹ points in the graphene Brillouin zone (ν = 0; the '(semi)metallic' case), or not (
K, Kʹ points in the graphene Brillouin zone (ν = 0; the '(semi)metallic' case), or not ( ; the 'semiconducting'), for the half-filled band. In addition there is the spin degeneracy for
; the 'semiconducting'), for the half-filled band. In addition there is the spin degeneracy for  with the Zeeman effect neglected here. Each band is characterized by a mass
with the Zeeman effect neglected here. Each band is characterized by a mass  , where
, where  and
and 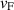 the Fermi velocity in graphene [14]. We take
the Fermi velocity in graphene [14]. We take 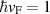 to be the unit of energy. Here we have introduced a magnetic field whose flux passing through the tube is ϕ in units of the flux quantum
to be the unit of energy. Here we have introduced a magnetic field whose flux passing through the tube is ϕ in units of the flux quantum  , which acts to shift the discrete set of momenta. Assuming 1D electromagnetic fields, the system is described by the extended massive Schwinger model with a Lagrangian
, which acts to shift the discrete set of momenta. Assuming 1D electromagnetic fields, the system is described by the extended massive Schwinger model with a Lagrangian
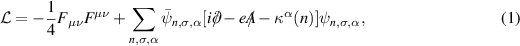
where  is the electromagnetic field tensor,
is the electromagnetic field tensor,  the fermion field with
the fermion field with 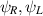 the left and right moving components,
the left and right moving components, 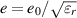 the screened charge with a dielectric constant εr
, and we use the relativistic convention
the screened charge with a dielectric constant εr
, and we use the relativistic convention  with
with  and
and  . The model has a spin SU(2) symmetry, which is enlarged to SU(4) if K and K' are degenerate. However, perturbations can break this into SU(2) × SU(2). When the electric fluxes are confined in 1D, the inter-electron potential is
. The model has a spin SU(2) symmetry, which is enlarged to SU(4) if K and K' are degenerate. However, perturbations can break this into SU(2) × SU(2). When the electric fluxes are confined in 1D, the inter-electron potential is  , which enforces confinement of charges. The coupling strength is
, which enforces confinement of charges. The coupling strength is  determined by the screening factor εr
(see e.g. [15]).
determined by the screening factor εr
(see e.g. [15]).
2. Exciton spectrum
Excitons are of central importance in understanding the optical properties of carbon-nanotubes [16–20]. Specifically, Kishida et al have observed not only the bright excitons, but also the dark excitons [19], while Wang et al observed excitons in metallic nanotubes [20]. In the CP, the optical spectrum is dominated by excitons, and no two-particle continuum exists. Since there is a possibility that the lightest fermion mass vanishes, the conventional weak-coupling approaches cannot be used, and strong-coupling methods are required. Two powerful methods are applicable; One is the light-front quantization scheme [9–11], and the other is bosonization [6–8]. For studying the crossover from metallic to semiconducting tubes, we employ the former, since bosonization for a massive model is still an open problem [8]. With the light-cone coordinates  we can eliminate the dynamical variables except for the right-fermionic components ψiR
(with a shorthand
we can eliminate the dynamical variables except for the right-fermionic components ψiR
(with a shorthand  ) by means of the equation of motion. The Lagrangian reads
) by means of the equation of motion. The Lagrangian reads
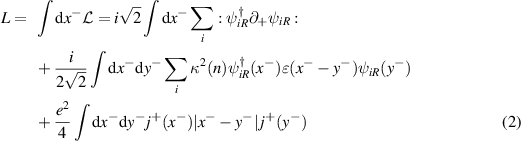
with the U(1) current  . The index i runs over infinite number of modes with the mass term depending on n, which contrasts with the standard SU(N) massive Schwinger model where the mass is common to all i's. The free-field expansion is
. The index i runs over infinite number of modes with the mass term depending on n, which contrasts with the standard SU(N) massive Schwinger model where the mass is common to all i's. The free-field expansion is ![$\psi_{iR}(x^-) = \frac{1}{2^{1/4}}\int_0^\infty\frac{\mathrm{d}k^+}{2\pi\sqrt{k^+}}[b_i(k^+)e^{-ik^+x^-}+d_i^\dagger (k^+)e^{ik^+x^-}]$](https://content.cld.iop.org/journals/1751-8121/55/50/504001/revision2/aaca7e5ieqn25.gif) , where
, where  creating electrons and
creating electrons and  holes satisfy a canonical commutation,
holes satisfy a canonical commutation,  . The virtue of using the light-front formalism is that the groundstate, which is a CP, is described by the Fock vacuum
. The virtue of using the light-front formalism is that the groundstate, which is a CP, is described by the Fock vacuum 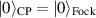 (with
(with 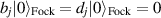 ).
).
Now let us look at the two-particle excitation, i.e. an exciton with a wave function
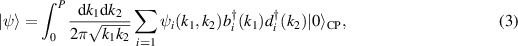
where the integral is restricted to  . From the Lorentz invariance, the exciton wave function satisfies the Einstein–Schrödinger equation,
. From the Lorentz invariance, the exciton wave function satisfies the Einstein–Schrödinger equation,  , where
, where  is the light-cone Hamiltonian,
is the light-cone Hamiltonian,  the momentum operator for the center of mass momentum P with
the momentum operator for the center of mass momentum P with  , and M the excitation energy ('mass') of the boundstate. With the light-cone operators, the Einstein–Schrödinger equation for the wave function is given explicitly as
, and M the excitation energy ('mass') of the boundstate. With the light-cone operators, the Einstein–Schrödinger equation for the wave function is given explicitly as
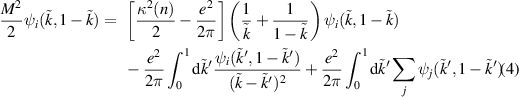
with re-scaled momenta  [21]. This is an extension of the 't Hooft–Bergknoff equation [9, 22], here possessing infinite number of modes labeled by i. The last term is the anomaly term, which physically corresponds to a virtual process of exciton pair-annihilated into a photon and then regenerated as an exciton. The process is intimately related to the photon-exciton coupling, and for bright excitons this term is nonzero. By contrast, the term disappears for dark excitons with
[21]. This is an extension of the 't Hooft–Bergknoff equation [9, 22], here possessing infinite number of modes labeled by i. The last term is the anomaly term, which physically corresponds to a virtual process of exciton pair-annihilated into a photon and then regenerated as an exciton. The process is intimately related to the photon-exciton coupling, and for bright excitons this term is nonzero. By contrast, the term disappears for dark excitons with  , and equation (4) reduces to the 't Hooft equation for planar QCD [22]. For the optical activity the bright excitons must satisfy the condition that
, and equation (4) reduces to the 't Hooft equation for planar QCD [22]. For the optical activity the bright excitons must satisfy the condition that  to be a SU(2) spin singlet (note
to be a SU(2) spin singlet (note  creates a hole with spin
creates a hole with spin  ), and, when K and Kʹ are degenerate, an additional condition
), and, when K and Kʹ are degenerate, an additional condition  is imposed to make it a SU(2) valley singlet. We note that in equation (4) the effect of vacuum polarization and self-energy corrections due to 'meson' propagators [12] are neglected for simplicity. We solve [23] the 't Hooft–Bergknoff equation using the basis-function method [10, 11].
is imposed to make it a SU(2) valley singlet. We note that in equation (4) the effect of vacuum polarization and self-energy corrections due to 'meson' propagators [12] are neglected for simplicity. We solve [23] the 't Hooft–Bergknoff equation using the basis-function method [10, 11].
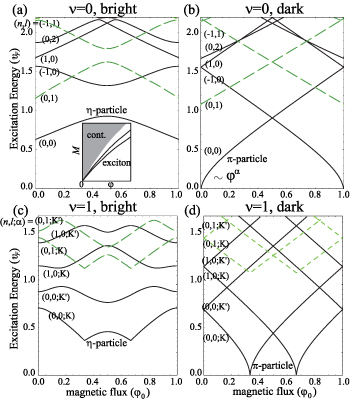
Let us first look at the excitation spectrum (exciton energy M) against the magnetic field for a metallic nanotube with ν = 0 in figure 1. We immediately notice that the system is no longer metallic due to charge confinement, namely, the spectrum for the bright exciton has a gap, and an excitation continuum does not exist, either. This is in sharp contrast with the case for the conventional weak-coupling picture with a  potential (inset of (a)), where a continuum exists down to zero energy at ϕ = 0. The spectrum has a periodicity with a period ϕ = 1, which originates from the mass structure of the fermion modes. We label each exciton mode with
potential (inset of (a)), where a continuum exists down to zero energy at ϕ = 0. The spectrum has a periodicity with a period ϕ = 1, which originates from the mass structure of the fermion modes. We label each exciton mode with  , where
, where  K,Kʹ is the dominant valley character near ϕ = 0, and
K,Kʹ is the dominant valley character near ϕ = 0, and  the exciton quantum number that labels the bound state in a trapping potential (see figure 3(c)). Odd-l states are parity odd and one-photon allowed, while even-l states are only two-photon accessible. For ν = 0 the
the exciton quantum number that labels the bound state in a trapping potential (see figure 3(c)). Odd-l states are parity odd and one-photon allowed, while even-l states are only two-photon accessible. For ν = 0 the  and
and  excitons are degenerate due to the valley symmetry, so we can omit α from the index.
excitons are degenerate due to the valley symmetry, so we can omit α from the index.
Figure 1. Two-body excitation spectrum against magnetic field for bright (a), (c) or dark (b), (d) excitons for metallic (a,b; ν = 0) or semiconducting ((c), (d); ν = 1) nanotubes with  . Solid (dashed) lines correspond to states with even (odd) l. Inset in (a) is a schematic spectrum for a system with
. Solid (dashed) lines correspond to states with even (odd) l. Inset in (a) is a schematic spectrum for a system with  potential near ϕ = 0.
potential near ϕ = 0.
Download figure:
Standard image High-resolution imageWhat can we learn more about the spectrum? Comparison with the meson spectrum in QCD becomes interesting. In fact, the bright and dark excitons with lowest energies (figure 1) have many aspects shared by the η and π (pion) particles, respectively, in QCD [7]. Interestingly, the η and π boundstates behave differently in the strong-coupling limit; As the fermion mass goes to zero, the π mass vanishes, while the η mass remains finite due to a U(1) anomaly. For QCD there is the Gell–Mann−Oakes−Renner relation [24], which is a relation,  , between the pion and quark masses. When translated into the present problem, the relation applies to the lightest dark exciton. For example, as shown in figures 1(b) and (d), the energy of the lightest dark exciton, i.e. pion in the QCD context, goes to zero at
, between the pion and quark masses. When translated into the present problem, the relation applies to the lightest dark exciton. For example, as shown in figures 1(b) and (d), the energy of the lightest dark exciton, i.e. pion in the QCD context, goes to zero at  in metallic nanotubes and at
in metallic nanotubes and at  in semiconducting ones. However, the exciton energy behaves as
in semiconducting ones. However, the exciton energy behaves as  with a power
with a power  and, since the fermion mass is proportional to
and, since the fermion mass is proportional to  , we can regard this as a manifestation of the Gell–Mann−Oakes−Renner relation in nanotubes, which holds even in 1+1D systems where chiral symmetry is 'almost' broken [25].
, we can regard this as a manifestation of the Gell–Mann−Oakes−Renner relation in nanotubes, which holds even in 1+1D systems where chiral symmetry is 'almost' broken [25].
The situation is even more interesting for the lightest bright excitons ( -particles), since they remain massive even though the fermions are massless. This can be seen in the
-particles), since they remain massive even though the fermions are massless. This can be seen in the  and
and  states in figures 1(a) and (c), which have nonzero minima at
states in figures 1(a) and (c), which have nonzero minima at  . This is due to a U(1) anomaly coming from the pair creation-annihilation process, i.e. the last term in equation (4). The physical picture is the following. In an exciton, electrons and holes are continuously created and annihilated when the fermion mass is small, and a cloud of photon is formed. The electromagnetic energy of the photon cloud is finite, and contributes to the exciton energy. This process is not restricted to the 1D Coulomb potential, and similar effect may take place in metallic single-wall nanotubes where excitons with finite binding energy were observed [20].
. This is due to a U(1) anomaly coming from the pair creation-annihilation process, i.e. the last term in equation (4). The physical picture is the following. In an exciton, electrons and holes are continuously created and annihilated when the fermion mass is small, and a cloud of photon is formed. The electromagnetic energy of the photon cloud is finite, and contributes to the exciton energy. This process is not restricted to the 1D Coulomb potential, and similar effect may take place in metallic single-wall nanotubes where excitons with finite binding energy were observed [20].
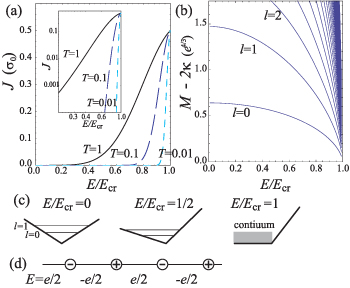
In experiments it often happens that the nanotubes have random circumference L. In figures 2(a) and (c), we plot the dependence of the exciton energy on the circumference. The mixing between different modes n is small when L is small, since the energy difference between modes is  , and in the limit L → 0, the system approaches to the pure SU(N) massless Schwinger model [7]. In this limit, the lightest bright exciton (η-particle) mass is given by
, and in the limit L → 0, the system approaches to the pure SU(N) massless Schwinger model [7]. In this limit, the lightest bright exciton (η-particle) mass is given by  , which amounts to
, which amounts to  in metallic (ν = 0, SU(4)) nanotubes and
in metallic (ν = 0, SU(4)) nanotubes and  in semiconducting (ν = 1, SU(2)) ones for
in semiconducting (ν = 1, SU(2)) ones for  . The mixing of modes lowers the exciton energy as shown in figures 2(a) and (c). This is because the mixing reduces the anomaly term, where the
. The mixing of modes lowers the exciton energy as shown in figures 2(a) and (c). This is because the mixing reduces the anomaly term, where the  mode converges to the dark mode in the SU(
mode converges to the dark mode in the SU( ) massless Schwinger model. In figures 2(b) and (d), we plot the dependence of the spectrum on the screened interaction parameter e2. Starting from 2κ (weak-coupling limit), the exciton energy increases as the interaction becomes stronger, where the increase is larger for larger quantum number l.
) massless Schwinger model. In figures 2(b) and (d), we plot the dependence of the spectrum on the screened interaction parameter e2. Starting from 2κ (weak-coupling limit), the exciton energy increases as the interaction becomes stronger, where the increase is larger for larger quantum number l.
Figure 2. Two-body excitation spectrum in zero magnetic field against circumference L ((a), (c); with  ) or against coupling strength (b,d; with L = 10) for metallic ((a), (b); ν = 0) or semiconducting ((c), (d); ν = 1) nanotubes. Solid (dashed) lines correspond to states with even (odd) l.
) or against coupling strength (b,d; with L = 10) for metallic ((a), (b); ν = 0) or semiconducting ((c), (d); ν = 1) nanotubes. Solid (dashed) lines correspond to states with even (odd) l.
Download figure:
Standard image High-resolution image3. Nonlinear transport and half-asymptotic state
Nonlinear transport in correlated systems is attracting considerable interests (see e.g. [26]), and in nanotubes it serves as a powerful probe in experimentally detecting new states of matter [2]. Here let us show that the semiconducting nanotubes with 1D interaction should exhibit a power-law J-E characteristics in external electric fields, as in the 2D organic systems [13]. Unlike the 2D case, however, the carriers in the field-induced metallic state are only 'half-free'. We explain how this has to do with the half-asymptotic state predicted by Coleman [7].
Let us look at a semiconducting nanotube with a finite fermion mass κ in a strong electric field. Since the strong-coupling analysis in finite electric fields is still an open issue, here we focus on a weak-coupling approach where the U(1) anomaly does not contribute with the bright and dark excitons becoming nearly degenerate. In the nonrelativistic approximation, Dirac particles becomes nonrelativistic fermions with quadratic kinetic terms ( ), and the exciton binding problem in an electric field E is reduced to solving a 1D Schrödinger equation (cf equation (4.1) in [7]),
), and the exciton binding problem in an electric field E is reduced to solving a 1D Schrödinger equation (cf equation (4.1) in [7]),
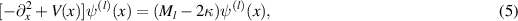

where Ml is the exciton energy, V(x) the trapping potential, and we have introduced an exponential damping factor with a cutoff ξ. We plot the J–E characteristics in figure 3(a) for various values of temperature, where the nonlinear current is seen to behave like

as in [13]. with  the activation energy. The current follows a power-law until the conductivity reaches a peak at a critical field
the activation energy. The current follows a power-law until the conductivity reaches a peak at a critical field  . The power of the conductivity is proportional to T−1 as in [13] but there is also a cutoff ξ dependence. At the critical field, one side of the trapping potential for a test charge becomes flat as depicted in figure 3(c). Then a continuum spectrum emerges, as seen in figure 3(b) where we plot the eigenenergies of the Hamiltonian (equation (5)) obtained by gluing two Airy functions. There, Coleman's half-asymptotic state—a configuration with alternating charges but possibly random displacements (figure 3(d)) – has the lowest energy, where the external field and the force from surrounding charges balance with each other. Strictly speaking, carriers with opposite charges must switch their position in order for the current to flow, and this violates the half-asymptotic state condition, which may modify the simple relation equation (7) for the nonlinear current. This is out of the scope of the present work, but will merit further studies.
. The power of the conductivity is proportional to T−1 as in [13] but there is also a cutoff ξ dependence. At the critical field, one side of the trapping potential for a test charge becomes flat as depicted in figure 3(c). Then a continuum spectrum emerges, as seen in figure 3(b) where we plot the eigenenergies of the Hamiltonian (equation (5)) obtained by gluing two Airy functions. There, Coleman's half-asymptotic state—a configuration with alternating charges but possibly random displacements (figure 3(d)) – has the lowest energy, where the external field and the force from surrounding charges balance with each other. Strictly speaking, carriers with opposite charges must switch their position in order for the current to flow, and this violates the half-asymptotic state condition, which may modify the simple relation equation (7) for the nonlinear current. This is out of the scope of the present work, but will merit further studies.
Figure 3.
J-E characteristics (a) with a logarithmic plot in the inset, and exciton levels (b) for semiconducting nanotubes (for ξ = 100) in the weak-coupling, nonrelativistic limit. (c) Schematic trapping potential V(x) and eigenstates for various values of the electric field. (d) Coleman's half asymptotic state when the external field is  .
.
Download figure:
Standard image High-resolution imageAcknowledgment
T O wishes to thank Kazuhiro Kuroki and Hideo Aoki for valuable discussions, and was supported by JST CREST Grant No. JPMJCR19T3, Japan.
Data availability statement
The data generated and/or analysed during the current study are not publicly available for legal/ethical reasons but are available from the corresponding author on reasonable request.