Abstract
We study a supersymmetric fermion lattice model defined by Hermann Nicolai. We show that its infinitely many classical supersymmetric ground states are associated to breakdown of hidden local supersymmetries.
Export citation and abstract BibTeX RIS
1. Introduction
A supersymmetric fermion lattice model defined by Nicolai [Ni] is a pioneering work on (non-relativistic) supersymmetric quantum mechanics. This model, which we call Nicolai model, even predates Witten's supersymmetric quantum mechanical model [Wi], see [J1] [J2] for some historical remarks. It has been shown that the Nicolai model has highly degenerate supersymmetric ground states [M1] [LScSh] which give rise to interesting dynamical properties. The aim of this paper is to discuss the degeneracy of supersymmetric ground states of the Nicolai model from the viewpoint of symmetry breakdown. Based on our previous findings [M1] we will classify all classical supersymmetric ground states in terms of breakdown of local fermionic symmetries (supersymmetries) hidden in the model.
1.1. Supersymmetric fermion lattice model by Nicolai
We introduce a spinless fermion lattice model on one-dimensional integer lattice  given by Nicolai [Ni]. For each site
given by Nicolai [Ni]. For each site 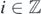 let ci
and
let ci
and  denote the annihilation and the creation of a spinless fermion at i. They obey the canonical anticommutation relations: for all
denote the annihilation and the creation of a spinless fermion at i. They obey the canonical anticommutation relations: for all 

For each site  the fermion number operator is defined by
the fermion number operator is defined by

A formal infinite sum 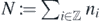 will denote the total fermion number operator. Let
will denote the total fermion number operator. Let

We see that Q and its adjoint Q* are fermion operators in the sense that
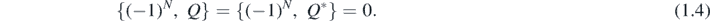
It is essential that the nilpotent property is satisfied:

The supersymmetric Hamiltonian is given by

The pair of supercharges Q, Q* and the supersymmetric Hamiltonian H satisfy the  supersymmetry relation [We], although there is no boson in the model.
supersymmetry relation [We], although there is no boson in the model.
The explicit form of H can be easily computed as

The Nicolai model has some obvious symmetries. The global U(1)-symmetry group γθ (θ ∈ [0, 2π]) is defined by

The particle–hole transformation is given by the  action:
action:

Let σ denote the shift-translation automorphism group defined by
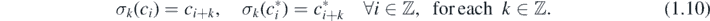
The Hamiltonian H (1.7) is invariant under γθ
(θ ∈ [0, 2π]), so it has the global U(1)-symmetry. It has particle–hole symmetry as ρ(H) = H, which follows from ρ(Q) = −Q* and ρ(Q*) = −Q. Finally, H is invariant under translation by two sites, as σ2k
(H) = H for any 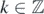 , whereas the full translation symmetry is explicitly broken as σ2k+1(H) ≠ H. We will see in section 2 that the Nicolai model has other local symmetries.
, whereas the full translation symmetry is explicitly broken as σ2k+1(H) ≠ H. We will see in section 2 that the Nicolai model has other local symmetries.
1.2. Mathematical preliminary
In this subsection, we introduce some basic notations. We refer to [M2] that gives a general framework of supersymmetric fermion lattice systems. Although it is not absolutely necessary, the C*-algebraic formulation is helpful to formulate our pertinent problem and gives a clue to solve it.
For each finite  ,
,  denotes the finite-dimensional algebra generated by
denotes the finite-dimensional algebra generated by  , where the notation '
, where the notation ' ' means that
' means that 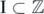 and the number of sites |I| in I is finite. The union of all these
and the number of sites |I| in I is finite. The union of all these 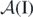 defines the local algebra:
defines the local algebra:

The norm completion of the local algebra  gives a C*-system
gives a C*-system  called the CAR algebra.
called the CAR algebra.
Let Θ denote the fermion grading automorphism on  given as:
given as:

The fermion system  is decomposed into the even part
is decomposed into the even part  and the odd part
and the odd part 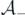 as
as

Any element of  is a linear sum of even monomials of fermion field operators, while that of
is a linear sum of even monomials of fermion field operators, while that of  is a linear sum of odd monomials of fermion field operators. Similarly, for each
is a linear sum of odd monomials of fermion field operators. Similarly, for each  ,
,
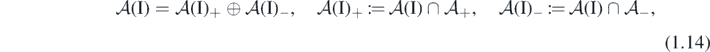
and for the local algebra

Define the graded commutator [ , ]Θ on  by the mixture of the commutator [ , ] and the anti-commutator { , } as
by the mixture of the commutator [ , ] and the anti-commutator { , } as
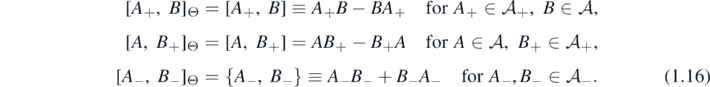
Consider the superderivation generated by the nilpotent supercharge Q:

We see that δQ is a linear map that anticommutes with the grading:

and that the graded Leibniz rule holds:

A state (i.e. normalized positive linear functional on 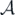 ) is called a supersymmetric (ground) state if and only if it is invariant under the superderivation δQ
, equivalently its state vector (determined by the GNS representation) is annihilated by both the supercharge Q and its adjoint Q*. In this paper, we deal with only pure states on finite systems that are always associated with normalized vectors. For a supersymmetric model, if there is a supersymmetric state, then the supersymmetry is unbroken. If there exists no supersymmetric state, then the supersymmetry is spontaneously broken. The Nicolai model has many supersymmetric states as we will see later. Hence its supersymmetry is unbroken.
) is called a supersymmetric (ground) state if and only if it is invariant under the superderivation δQ
, equivalently its state vector (determined by the GNS representation) is annihilated by both the supercharge Q and its adjoint Q*. In this paper, we deal with only pure states on finite systems that are always associated with normalized vectors. For a supersymmetric model, if there is a supersymmetric state, then the supersymmetry is unbroken. If there exists no supersymmetric state, then the supersymmetry is spontaneously broken. The Nicolai model has many supersymmetric states as we will see later. Hence its supersymmetry is unbroken.
1.3. Classical supersymmetric ground states of the Nicolai model
In this paper, we focus on classical supersymmetric ground states which will be stated below. This subsection is indebted to [M1].
Let |1⟩i
and |0⟩i
denote the occupied and empty vectors of the spinless fermion at site i, respectively. For each 

When there is no fear of confusion, we will omit the subscript and write simply |1⟩ and |0⟩.
We identify general (not necessarily supersymmetric) classical states on the fermion lattice system by classical configurations on  .
.
Definition 1.1. Let g(n) denote an arbitrary {0, 1}-valued function over  . It is called a classical configuration over
. It is called a classical configuration over  . For any classical configuration g(n) define
. For any classical configuration g(n) define

This infinite product vector determines a state ψg(n) on the fermion system  which will be called the classical state associated to the configuration g(n) over
which will be called the classical state associated to the configuration g(n) over  . Let
. Let  . Then
. Then

The above Ω0 is called the Fock vector, and its associated translation-invariant state ψ0 on  is called the Fock state. Similarly let
is called the Fock state. Similarly let 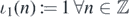 . Then
. Then

The above Ω1 is called the fully-occupied vector, and its associated translation-invariant state ψ1 on 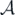 is called the fully-occupied state.
is called the fully-occupied state.
To each classical configuration over  we assign an operator by the following rule.
we assign an operator by the following rule.
Definition 1.2. For each  let
let 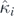 denote the map from {0, 1} into
denote the map from {0, 1} into  given as
given as

For each classical configuration g(n) over  define the infinite-product of fermion field operators:
define the infinite-product of fermion field operators:

where the multiplication is taken in the increasing order of  . If g(n) has a compact support, then
. If g(n) has a compact support, then

Otherwise  denotes a formal operator which does not belong to
denotes a formal operator which does not belong to  .
.
We have the following obvious correspondence between product vectors given in definition 1.1 and product operators given in definition 1.2 via the Fock representation.
Proposition 1.3. Let Ω0 denote the Fock vector given in (1.22). For any classical configuration g(n) over  , the following identity holds:
, the following identity holds:

Proof. The desired identity directly follows from definitions 1.1 and 1.2.□
It is easy to see that the Fock state ψ0 and the fully-occupied state ψ1 are supersymmetric ground state for the Nicolai model. We would like to give all classical supersymmetric ground states of the Nicolai model. For this purpose, we introduce the following class of classical configurations.
Definition 1.4. Consider three consecutive sites {2i − 1, 2i, 2i + 1} centered at an even site 2i ( ). There are 23 configurations (i.e. eight {0, 1}-valued functions) on {2i − 1, 2i, 2i + 1}. Let '0, 1, 0' and '1, 0, 1' be called forbidden triplets. If a classical configuration
). There are 23 configurations (i.e. eight {0, 1}-valued functions) on {2i − 1, 2i, 2i + 1}. Let '0, 1, 0' and '1, 0, 1' be called forbidden triplets. If a classical configuration 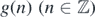 does not include any of such forbidden triplets over
does not include any of such forbidden triplets over  , then it is called a ground-state configuration over
, then it is called a ground-state configuration over 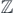 (for the Nicolai model). The set of all ground-state configurations over
(for the Nicolai model). The set of all ground-state configurations over  is denoted by ϒ. The set of all ground-state configurations whose supports are included in some finite region is denoted by ϒ◦. The set of all ground-state configurations whose supports are included in a finite region
is denoted by ϒ. The set of all ground-state configurations whose supports are included in some finite region is denoted by ϒ◦. The set of all ground-state configurations whose supports are included in a finite region  is denoted by ϒI.
is denoted by ϒI.
The following proposition classifies all the classical supersymmetric ground states in terms of classical configurations justifying our nomenclature 'ground-state configurations' of definition 1.4. It is based on the following fact that can be easily checked by using (1.20): the product vector |g(2i − 1)⟩2i−1 ⊗ |g(2i)⟩2i
⊗ |g(2i + 1)⟩2i+1 is annihilated by both q2i
and  unless those are |0⟩2i−1 ⊗ |1⟩2i
⊗ |0⟩2i+1 or |1⟩2i−1 ⊗ |0⟩2i
⊗ |1⟩2i+1 which correspond to the forbidden triplets, {g(2i − 1) = 0, g(2i) = 1, g(2i + 1) = 0} and {g(2i − 1) = 1, g(2i) = 0, g(2i + 1) = 1}, respectively. Theorem 2 [M1] established that if there appears no forbidden triplet in the sequence of
unless those are |0⟩2i−1 ⊗ |1⟩2i
⊗ |0⟩2i+1 or |1⟩2i−1 ⊗ |0⟩2i
⊗ |1⟩2i+1 which correspond to the forbidden triplets, {g(2i − 1) = 0, g(2i) = 1, g(2i + 1) = 0} and {g(2i − 1) = 1, g(2i) = 0, g(2i + 1) = 1}, respectively. Theorem 2 [M1] established that if there appears no forbidden triplet in the sequence of  at all, then the corresponding product vector
at all, then the corresponding product vector  is annihilated by both Q and Q*, hence it is a supersymmetric ground state, whereas if there is at least one forbidden triplet in the sequence of
is annihilated by both Q and Q*, hence it is a supersymmetric ground state, whereas if there is at least one forbidden triplet in the sequence of 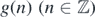 , then either Q or Q*, or both do not annihilate
, then either Q or Q*, or both do not annihilate  and so it is not supersymmetric. See [M1] for the detail.
and so it is not supersymmetric. See [M1] for the detail.
Proposition 1.5. A classical state on the fermion lattice system  is supersymmetric for the Nicolai model if and only if its associated configuration g(n) over
is supersymmetric for the Nicolai model if and only if its associated configuration g(n) over  is a ground-state configuration for the Nicolai model as stated in definition 1.4, namely g(n) ∈ ϒ.
is a ground-state configuration for the Nicolai model as stated in definition 1.4, namely g(n) ∈ ϒ.
1.4. Supersymmetric ground states on subsystems
We shall discuss supersymmetric ground states on finite subsystems. First, we specify finite regions that we will consider. Second, we specify the meaning of 'supersymmetric ground states' upon finite regions, as it is not so obvious due to the boundary.
To deal with the Nicolai model which has period-2 translational symmetry not full translation symmetry, rather than, it is convenient to consider the special finite intervals of  whose edges are both even, see proposition 4.1 given later. Namely for
whose edges are both even, see proposition 4.1 given later. Namely for  (k < l) we take
(k < l) we take

We see that |Ik,l | is 2(l − k) + 1.
Now we give the precise definition of supersymmetric ground states on the finite interval Ik,l .
Definition 1.6. Consider any finite interval ![${\text{I}}_{k,l}\equiv \left[2k,\enspace 2k+1,\enspace 2\left(k+1\right),\dots ,2\left(l-1\right),\enspace 2l-1,\enspace 2l\right]\quad \left(k,l\in \mathbb{Z}\enspace k{< }l\right)$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn61.gif) . Let
. Let
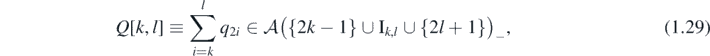
where  as defined in (1.3). A state on
as defined in (1.3). A state on  is called a free-boundary supersymmetric ground state if its arbitrary state-extension to
is called a free-boundary supersymmetric ground state if its arbitrary state-extension to  is invariant under the superderivation δQ[k,l] associated to the local supercharge Q[k, l], equivalently its associated vector is annihilated by both Q[k, l] and Q[k,l]*.
is invariant under the superderivation δQ[k,l] associated to the local supercharge Q[k, l], equivalently its associated vector is annihilated by both Q[k, l] and Q[k,l]*.
First note that

where 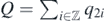 as in (1.3). Namely, upon the subsystem
as in (1.3). Namely, upon the subsystem  , finite supercharge Q[k, l] sitting on a slightly larger region {2k − 1} ∪ Ik,l
∪ {2l + 1} gives the same action as of the total supercharge Q. Second, we address what 'its arbitrary state-extension' exactly means. According to [ArM], for every classical state on the given local system, any state-extension of it to a larger system is also a classical state (or mixture of such). In the present case it is described as follows. By proposition 1.3 any classical state of
, finite supercharge Q[k, l] sitting on a slightly larger region {2k − 1} ∪ Ik,l
∪ {2l + 1} gives the same action as of the total supercharge Q. Second, we address what 'its arbitrary state-extension' exactly means. According to [ArM], for every classical state on the given local system, any state-extension of it to a larger system is also a classical state (or mixture of such). In the present case it is described as follows. By proposition 1.3 any classical state of  is determined by a {0, 1}-valued function g(n) on Ik,l
. Any state-extension of it to
is determined by a {0, 1}-valued function g(n) on Ik,l
. Any state-extension of it to  is determined by
is determined by  on {2k − 1} ∪ Ik,l
∪ {2l + 1} satisfying that
on {2k − 1} ∪ Ik,l
∪ {2l + 1} satisfying that

Due to the choice of the marginal points {2k − 1, 2l + 1} there are four possibilities.
To find configurations associated to definition 1.6, we introduce a subclass of ϒ◦ given in definition 1.4 requiring certain boundary conditions as follows.
Definition 1.7. Let Ik,l
≡ [2k, 2k + 1, 2(k + 1), ..., 2(l − 1), 2l − 1, 2l] (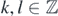 s.t. k < l) as before. The set of all
s.t. k < l) as before. The set of all  satisfying the following boundary conditions
satisfying the following boundary conditions

will be denoted by  .
.
In proposition 1.5 we gave one-to-one correspondence between classical supersymmetric ground states and ground-state configurations over 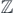 . We can see analogous correspondence on finite regions Ik,l
as follows.
. We can see analogous correspondence on finite regions Ik,l
as follows.
Proposition 1.8. A classical state on the finite system  is free-boundary supersymmetric (definition 1.6) if and only if its associated configuration g(n) on Ik,l
belongs to
is free-boundary supersymmetric (definition 1.6) if and only if its associated configuration g(n) on Ik,l
belongs to 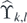 (definition 1.7).
(definition 1.7).
Proof. We will see the if part as follows. For all i ∈ {k + 1, k + 2, ..., l − 1} both q2i
and  annihilate any product vector corresponding to g(n) ∈ ϒk,l
. So we only have to see the marginal points k and l. For any given
annihilate any product vector corresponding to g(n) ∈ ϒk,l
. So we only have to see the marginal points k and l. For any given  its extension to {2k − 1} ∪ Ik,l
∪ {2l + 1} will be denoted as
its extension to {2k − 1} ∪ Ik,l
∪ {2l + 1} will be denoted as  . We see that
. We see that  is arbitrary,
is arbitrary,  ,
,  , and
, and 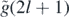 is arbitrary. So there is no forbidden sequence on {2k − 1, 2k, 2k + 1}. Thus both q2k
and
is arbitrary. So there is no forbidden sequence on {2k − 1, 2k, 2k + 1}. Thus both q2k
and  annihilate any product vector corresponding to
annihilate any product vector corresponding to  . Similarly, both q2l
and
. Similarly, both q2l
and  annihilate the product vector corresponding to
annihilate the product vector corresponding to  . The only if part can be shown as in theorem 2 [M1].□
. The only if part can be shown as in theorem 2 [M1].□
2. Hidden local fermionic symmetries
We will show that there are infinitely many local fermionic symmetries hidden in the Nicolai model. To this end, we need some preparation.
Definition 2.1. Take any finite interval Ik,l
defined in (1.28). Let f be a {−1, +1}-valued sequence on Ik,l
. For any consecutive triplet {2i − 1, 2i, 2i + 1} ⊂ Ik,l
( ) assume that neither
) assume that neither

nor

holds. Furthermore assume that f is constant on the left-end pair sites {2k, 2k + 1} and on the right-end pair sites {2l − 1, 2l}:

and

The set of all {−1, +1}-valued sequences on Ik,l
satisfying the above conditions is denoted by 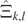 . The union of
. The union of  over all
over all  (k < l) is denoted by
(k < l) is denoted by  :
:

Take any  . Let
. Let

Each 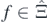 is called a local {−1, +1}-sequence of conservation for the Nicolai model.
is called a local {−1, +1}-sequence of conservation for the Nicolai model.
Remark 2.2. The requirements (2.3) and (2.4) on the edges of Ik,l are essential to make conservation laws for the Nicolai model.
Remark 2.3. By crude estimate we can see that the number of local {−1, +1}-sequences of conservation in  is roughly
is roughly  , where m = 2(l − k) denotes approximately the size of the system (i.e. the number of sites in Ik,l
).
, where m = 2(l − k) denotes approximately the size of the system (i.e. the number of sites in Ik,l
).
It is convenient to consider the following subclasses of  .
.
Definition 2.4. For each 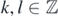 (k < l) let
(k < l) let ![${r}_{\left[2k,2l\right]}^{+}\in {\hat{{\Xi}}}_{k,l}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn98.gif) and
and ![${r}_{\left[2k,2l\right]}^{-}\in {\hat{{\Xi}}}_{k,l}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn99.gif) denote the constants over Ik,l
as
denote the constants over Ik,l
as

The set ![$\left\{{r}_{\left[2k,2l\right]}^{+}\right\}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn100.gif) over all
over all  (k < l) will be denoted as
(k < l) will be denoted as  , and the set
, and the set ![$\left\{{r}_{\left[2k,2l\right]}^{-}\right\}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn103.gif) over all
over all  (k < l) will be denoted as
(k < l) will be denoted as  . Let
. Let  .
.
We shall give a rule to assign a local fermion operator for every local {−1, +1}-sequence of conservation of definition 2.1.
Definition 2.5. For each  let ζi
denote the assignment from {−1, +1} into the fermion field at i given as
let ζi
denote the assignment from {−1, +1} into the fermion field at i given as

Take any pair of integers  such that k < l. For each
such that k < l. For each  , set
, set

where the multiplication is taken in the increasing order as above. The formulas (2.9) for all 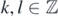 (k < l) yield a unique assignment
(k < l) yield a unique assignment  from
from 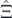 to
to 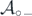 .
.
By definition 2.5 the following local fermion operators are assigned to ±-characters supported on the segment Ik,l
of definition 2.4. For 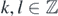 (k < l)
(k < l)

The following is the main result of this section.

where H denotes the Hamiltonian of the Nicolai model over  .
.
Proof. This theorem is established in [M1]. Because of its importance and the reader's convenience, we will provide its more formal derivation below. It suffices to show that

and that

as the former implies ![$\left[H,\enspace \mathcal{Q}\left(f\right)\right]=0$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn117.gif) and the latter implies
and the latter implies ![$\left[H,\enspace \mathcal{Q}{\left(f\right)}^{{\ast}}\right]=0$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn118.gif) by the graded Leibniz rule of superderivations (1.19). Recall
by the graded Leibniz rule of superderivations (1.19). Recall 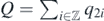 and
and 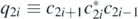 defined in (1.3). By definitions 2.1 and 2.5, we have
defined in (1.3). By definitions 2.1 and 2.5, we have

From the above we obtain (2.12) and (2.13).□
Theorem 2.6 says that the Nicolai model has infinitely many local fermionic constants. Those generate local fermionic symmetries.
Definition 2.7. For each local {−1, +1}-sequence of conservation 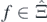 ,
,  is called the local fermionic constant of motion associated to f, and the pair
is called the local fermionic constant of motion associated to f, and the pair  is called the local fermionic charge associated to f.
is called the local fermionic charge associated to f.
Remark 2.8. Fermionic symmetry satisfying the supersymmetry relation other than the dynamical supersymmetry is sometimes called kinematical supersymmetry. See e.g. [NSakY]. Hence the local fermionic charge  for any
for any  gives a local kinematical supersymmetry.
gives a local kinematical supersymmetry.
Remark 2.9. Any operator of the algebra generated by  is a local constant of motion. There exist many such self-adjoint bosonic operators that generate (bosonic) symmetries for the Nicolai model. For example, we obtain a bosonic constant
is a local constant of motion. There exist many such self-adjoint bosonic operators that generate (bosonic) symmetries for the Nicolai model. For example, we obtain a bosonic constant  from the product
from the product ![$\mathcal{Q}\left({r}_{\left[2k,2l\right]}^{+}\right)\enspace \enspace \text{and}\enspace \enspace \mathcal{Q}\left({r}_{\left[2k,2l\right]}^{-}\right)$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn128.gif) .
.
3. Degenerate classical supersymmetric ground states and broken local fermionic symmetries
In this section we will relate the high degeneracy of ground states shown in section 1.3 to the existence of many local fermionic symmetries shown in section 2. In particular, we will show that every classical supersymmetric ground state can be constructed from (broken) local fermionic symmetries.
Theorem 3.1. Take any segment Ik,l
indexed by  (k < l) as in (1.28). Any classical free-boundary supersymmetric ground state on
(k < l) as in (1.28). Any classical free-boundary supersymmetric ground state on 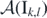 (definition 1.6) can be constructed by some finitely many applications of operators
(definition 1.6) can be constructed by some finitely many applications of operators  (and
(and  ) with
) with  (definition 2.1) to the Fock vector Ω0 (1.22), similarly, to the fully-occupied vector Ω1 (1.23).
(definition 2.1) to the Fock vector Ω0 (1.22), similarly, to the fully-occupied vector Ω1 (1.23).
By definition 1.1 we can identify every classical supersymmetric ground state ψg(n) on  with its corresponding classical configuration g(n) over
with its corresponding classical configuration g(n) over  , and vice versa. By proposition 1.8 we can identify the set of all classical free-boundary supersymmetric ground states on
, and vice versa. By proposition 1.8 we can identify the set of all classical free-boundary supersymmetric ground states on  (definition 1.6) with
(definition 1.6) with 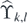 (definition 1.7). We will frequently use those identifications in what follows.
(definition 1.7). We will frequently use those identifications in what follows.
The following lemma implies that the latter part (using Ω1) of theorem 3.1 holds once the former part (using Ω0) is proved. Also it will be used frequently in the proof.
Lemma 3.2. For any  , if
, if  can be constructed by some finitely many applications of local fermionic charges within I0,n
to the Fock vector Ω0. Then it can be constructed by some applications of local fermionic charges within I0,n
to the fully-occupied state Ω1.
can be constructed by some finitely many applications of local fermionic charges within I0,n
to the Fock vector Ω0. Then it can be constructed by some applications of local fermionic charges within I0,n
to the fully-occupied state Ω1.
Proof. For any  ,
,  by definition. From (2.9) in definition 2.5
by definition. From (2.9) in definition 2.5

where ρ is the particle–hole transformation defined in (1.9). Thus by using the particle–hole transformation, we can use Ω0 and Ω1 interchangeably.□
Obviously it is enough to show theorem 3.1 by setting k = 0 and 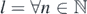 by shift-translations. Thus we will prove the following.
by shift-translations. Thus we will prove the following.
Proposition 3.3. For any  , every
, every  can be constructed by some applications of local fermionic charges within I0,n
:
can be constructed by some applications of local fermionic charges within I0,n
:

to the Fock vector Ω0 (1.22).
Proof. We need concrete forms of elements in 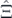 which are listed in appendix
which are listed in appendix
First, let us consider the case n = 1. 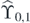 consists of the following two sequences on I0,1:
consists of the following two sequences on I0,1:

|
0 | 1 | 2 |
|---|---|---|---|
![${g}_{\left[0,2\right]}^{{\circ}}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn148.gif)
|
0 | 0 | 0 |
![${g}_{\left[0,2\right]}^{{\bullet}}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn149.gif)
|
1 | 1 | 1 |
The classical configuration ![${g}_{\left[0,2\right]}^{{\circ}}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn150.gif) corresponds to the Fock vector Ω0 (restricted to the local region [0, 1, 2]). We shall write simply
corresponds to the Fock vector Ω0 (restricted to the local region [0, 1, 2]). We shall write simply ![${g}_{\left[0,2\right]}^{{\circ}}={{\Omega}}_{0}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn151.gif) , and this identification will be used hereafter. On the other hand,
, and this identification will be used hereafter. On the other hand, ![${g}_{\left[0,2\right]}^{{\bullet}}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn152.gif) corresponds to
corresponds to ![$\mathcal{Q}\left({r}_{\left[0,2\right]}^{+}\right){{\Omega}}_{0}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn153.gif) which is the fully-occupied state on I0,1, where
which is the fully-occupied state on I0,1, where ![${r}_{\left[0,2\right]}^{+}\in {\hat{{\Xi}}}_{0,1}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn154.gif) . Thus we obtain
. Thus we obtain ![${g}_{\left[0,2\right]}^{{\bullet}}={r}_{\left[0,2\right]}^{+}{{\Omega}}_{0}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn155.gif) which is the desired formula.
which is the desired formula.
Second, let us consider the case n = 2. 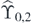 consists of the following six sequences on I0,2:
consists of the following six sequences on I0,2:
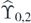
|
0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
![${g}_{\left[0,4\right]}^{{\circ}}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn158.gif)
|
0 | 0 | 0 | 0 | 0 |
![${g}_{\left[0,4\right]}^{1}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn159.gif)
|
0 | 0 | 0 | 1 | 1 |
![${g}_{\left[0,4\right]}^{2}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn160.gif)
|
0 | 0 | 1 | 1 | 1 |
![${g}_{\left[0,4\right]}^{3}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn161.gif)
|
1 | 1 | 1 | 0 | 0 |
![${g}_{\left[0,4\right]}^{4}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn162.gif)
|
1 | 1 | 0 | 0 | 0 |
![${g}_{\left[0,4\right]}^{{\bullet}}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn163.gif)
|
1 | 1 | 1 | 1 | 1 |
We have ![${g}_{\left[0,4\right]}^{{\circ}}={{\Omega}}_{0}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn164.gif) and
and ![${g}_{\left[0,4\right]}^{{\bullet}}={r}_{\left[0,4\right]}^{+}{{\Omega}}_{0}={c}_{0}^{{\ast}}{c}_{1}^{{\ast}}{c}_{2}^{{\ast}}{c}_{3}^{{\ast}}{c}_{4}^{{\ast}}{{\Omega}}_{0}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn165.gif) (the fully-occupied state on I0,2) according to (A.3). We have
(the fully-occupied state on I0,2) according to (A.3). We have

To get ![${g}_{\left[0,4\right]}^{1}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn166.gif) and
and ![${g}_{\left[0,4\right]}^{4}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn167.gif) we use 'double' actions as
we use 'double' actions as

and similarly

We have derived all the elements of 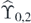 and accordingly all the classical free-boundary supersymmetric ground states on
and accordingly all the classical free-boundary supersymmetric ground states on  from the Fock vector Ω0. Let us note that
from the Fock vector Ω0. Let us note that ![${g}_{\left[0,4\right]}^{1}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn170.gif) and
and ![${g}_{\left[0,4\right]}^{3}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn171.gif) are mapped to each other by the particle–hole transformation, and so are
are mapped to each other by the particle–hole transformation, and so are ![${g}_{\left[0,4\right]}^{2}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn172.gif) and
and ![${g}_{\left[0,4\right]}^{4}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn173.gif) . However, as shown above, we do not need to use the particle–hole transformation.
. However, as shown above, we do not need to use the particle–hole transformation.
In an analogous manner, we can get all the elements of 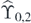 (all the classical free-boundary supersymmetric ground states on
(all the classical free-boundary supersymmetric ground states on  ) from the fully-occupied vector Ω1 in place of Ω0. This fact is important.
) from the fully-occupied vector Ω1 in place of Ω0. This fact is important.
Let us consider the case n = 3.  consists of the following 18 sequences on I0,3:
consists of the following 18 sequences on I0,3:
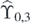
|
0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
![${g}_{\left[0,6\right]}^{{\circ}}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn178.gif)
|
0 | 0 | 0 | 0 | 0 | 0 | 0 |
![${g}_{\left[0,6\right]}^{1}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn179.gif)
|
0 | 0 | 0 | 1 | 1 | 0 | 0 |
![${g}_{\left[0,6\right]}^{2}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn180.gif)
|
0 | 0 | 1 | 1 | 0 | 0 | 0 |
![${g}_{\left[0,6\right]}^{3}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn181.gif)
|
0 | 0 | 0 | 1 | 0 | 0 | 0 |
![${g}_{\left[0,6\right]}^{4}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn182.gif)
|
0 | 0 | 1 | 1 | 1 | 0 | 0 |
![${g}_{\left[0,6\right]}^{5}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn183.gif)
|
0 | 0 | 0 | 0 | 0 | 1 | 1 |
![${g}_{\left[0,6\right]}^{6}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn184.gif)
|
0 | 0 | 0 | 0 | 1 | 1 | 1 |
![${g}_{\left[0,6\right]}^{7}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn185.gif)
|
0 | 0 | 0 | 1 | 1 | 1 | 1 |
![${g}_{\left[0,6\right]}^{8}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn186.gif)
|
0 | 0 | 1 | 1 | 1 | 1 | 1 |
![${g}_{\left[0,6\right]}^{9}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn187.gif)
|
1 | 1 | 1 | 1 | 1 | 0 | 0 |
![${g}_{\left[0,6\right]}^{10}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn188.gif)
|
1 | 1 | 1 | 1 | 0 | 0 | 0 |
![${g}_{\left[0,6\right]}^{11}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn189.gif)
|
1 | 1 | 1 | 0 | 0 | 0 | 0 |
![${g}_{\left[0,6\right]}^{12}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn190.gif)
|
1 | 1 | 0 | 0 | 0 | 0 | 0 |
![${g}_{\left[0,6\right]}^{{\bullet}}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn191.gif)
|
1 | 1 | 1 | 1 | 1 | 1 | 1 |
![${g}_{\left[0,6\right]}^{13}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn192.gif)
|
1 | 1 | 1 | 0 | 0 | 1 | 1 |
![${g}_{\left[0,6\right]}^{14}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn193.gif)
|
1 | 1 | 0 | 0 | 1 | 1 | 1 |
![${g}_{\left[0,6\right]}^{15}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn194.gif)
|
1 | 1 | 1 | 0 | 1 | 1 | 1 |
![${g}_{\left[0,6\right]}^{16}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn195.gif)
|
1 | 1 | 0 | 0 | 0 | 1 | 1 |
We will generate all the above ![${g}_{\left[0,6\right]}^{{\ast}}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn196.gif) . Obviously
. Obviously ![${g}_{\left[0,6\right]}^{{\circ}}={{\Omega}}_{0}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn197.gif) , and
, and ![${g}_{\left[0,6\right]}^{{\bullet}}={r}_{\left[0,6\right]}^{+}{{\Omega}}_{0}={c}_{0}^{{\ast}}{c}_{1}^{{\ast}}{c}_{2}^{{\ast}}{c}_{3}^{{\ast}}{c}_{4}^{{\ast}}{c}_{5}^{{\ast}}{c}_{6}^{{\ast}}{{\Omega}}_{0}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn198.gif) which is the fully-occupied vector Ω1 restricted to I0,3.
which is the fully-occupied vector Ω1 restricted to I0,3.
The restriction of ![${g}_{\left[0,6\right]}^{1}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn199.gif) to [0, 4] is
to [0, 4] is ![${g}_{\left[0,4\right]}^{1}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn200.gif) , and the restriction of
, and the restriction of ![${g}_{\left[0,6\right]}^{4}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn201.gif) to [0, 4] is
to [0, 4] is ![${g}_{\left[0,4\right]}^{2}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn202.gif) . The restriction of
. The restriction of ![${g}_{\left[0,6\right]}^{2}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn203.gif) to [2, 6] is
to [2, 6] is ![${g}_{\left[2,6\right]}^{4}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn204.gif) , which is the translation of
, which is the translation of ![${g}_{\left[0,4\right]}^{4}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn205.gif) used before. Thus each of
used before. Thus each of ![${g}_{\left[0,6\right]}^{1}\enspace {g}_{\left[0,6\right]}^{4}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn206.gif) and
and ![${g}_{\left[0,6\right]}^{2}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn207.gif) can be given as in the case n = 2.
can be given as in the case n = 2.
The restriction of ![${g}_{\left[0,6\right]}^{13}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn208.gif) to [0, 4] is
to [0, 4] is ![${g}_{\left[0,4\right]}^{3}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn209.gif) , the restriction of
, the restriction of ![${g}_{\left[0,6\right]}^{14}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn210.gif) to [2, 6] is
to [2, 6] is ![${g}_{\left[2,6\right]}^{2}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn211.gif) , the restriction of
, the restriction of ![${g}_{\left[0,6\right]}^{16}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn212.gif) to [0, 4] is
to [0, 4] is ![${g}_{\left[0,4\right]}^{4}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn213.gif) (also the restriction of
(also the restriction of ![${g}_{\left[0,6\right]}^{16}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn214.gif) to [2, 6] is
to [2, 6] is ![${g}_{\left[2,6\right]}^{4}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn215.gif) ). Hence each of
). Hence each of ![${g}_{\left[0,6\right]}^{13}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn216.gif) ,
, ![${g}_{\left[0,6\right]}^{14}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn217.gif) and
and ![${g}_{\left[0,6\right]}^{16}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn218.gif) can be given as in the case n = 2. Note that
can be given as in the case n = 2. Note that ![${{\Omega}}_{1}{\vert }_{\left[0,6\right]}={r}_{\left[0,6\right]}^{+}{{\Omega}}_{0}{\vert }_{\left[0,6\right]}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn219.gif) with
with ![${r}_{\left[0,6\right]}^{+}\in \mathcal{A}\left({\text{I}}_{0,3}\right)$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn220.gif) . Therefore each of
. Therefore each of ![${g}_{\left[0,6\right]}^{13}\enspace {g}_{\left[0,6\right]}^{14}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn221.gif) and
and ![${g}_{\left[0,6\right]}^{16}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn222.gif) can be generated by local supercharges in [0, 6] applied to Ω0.
can be generated by local supercharges in [0, 6] applied to Ω0.
We have

and
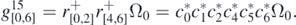
We have

and similarly

We have now derived all the sequences of  , i.e. all the classical free-boundary supersymmetric ground states on
, i.e. all the classical free-boundary supersymmetric ground states on  .
.
We will start the argument of induction. We have verified the statement for n = 1, 2, 3. Now let us assume that the statement holds for any integer from  up to
up to  . We are going to show that the statement holds for
. We are going to show that the statement holds for  . Concretely, we will construct
. Concretely, we will construct  from
from  (0 ⩽ p < q ⩽ n + 1) where 0 < p or q < n + 1.
(0 ⩽ p < q ⩽ n + 1) where 0 < p or q < n + 1.
We divide  into four cases (case I–IV) as below. We shall indicate how the induction argument can be applied to each of them.
into four cases (case I–IV) as below. We shall indicate how the induction argument can be applied to each of them.
Case I: We deal with all  whose left and right ends are
whose left and right ends are


|
0 | 1 | 2 | 3 | ⋯ | ⋯ | ⋯ | 2n − 1 | 2n | 2n + 1 | 2(n + 1) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| I-1 | 0 | 0 | 0 | 0 | ∗∗∗ | ∗∗∗ | ∗∗∗ | 0 | 0 | 0 | 0 |
| I-2 | 0 | 0 | 0 | 0 | ∗∗∗ | ∗∗∗ | ∗∗∗ | 1 | 1 | 0 | 0 |
| I-3 | 0 | 0 | 0 | 0 | ∗∗∗ | ∗∗∗ | ∗∗∗ | 1 | 0 | 0 | 0 |
| I-4 | 0 | 0 | 1 | 1 | ∗∗∗ | ∗∗∗ | ∗∗∗ | 0 | 0 | 0 | 0 |
| I-5 | 0 | 0 | 1 | 1 | ∗∗∗ | ∗∗∗ | ∗∗∗ | 1 | 1 | 0 | 0 |
| I-6 | 0 | 0 | 1 | 1 | ∗∗∗ | ∗∗∗ | ∗∗∗ | 1 | 0 | 0 | 0 |
| I-7 | 0 | 0 | 0 | 1 | ∗∗∗ | ∗∗∗ | ∗∗∗ | 0 | 0 | 0 | 0 |
| I-8 | 0 | 0 | 0 | 1 | ∗∗∗ | ∗∗∗ | ∗∗∗ | 1 | 1 | 0 | 0 |
| I-9 | 0 | 0 | 0 | 1 | ∗∗∗ | ∗∗∗ | ∗∗∗ | 1 | 0 | 0 | 0 |
Note that '∗∗∗'s in the middle mean some appropriate sequences of 0, 1 so that the sequence belongs to  , not being arbitrary.
, not being arbitrary.
All the above elements in  except I-9 belong to
except I-9 belong to  or to
or to  when being restricted to [2, 2(n + 1)] or to [0, 2n], respectively. By applying
when being restricted to [2, 2(n + 1)] or to [0, 2n], respectively. By applying ![${r}_{\left[0,2\right]}^{+}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn237.gif) to the vector of I-9, we get
to the vector of I-9, we get
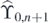
|
0 | 1 | 2 | 3 | ⋯ | ⋯ | ⋯ | 2n − 1 | 2n | 2n + 1 | 2(n + 1) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| New I-9 | 1 | 1 | 1 | 1 | ∗∗∗ | ∗∗∗ | ∗∗∗ | 1 | 0 | 0 | 0 |
'New I-9' above belongs to  when being restricted to [2, 2(n + 1)]. Therefore we can obtain new I-9 by applying some local supercharges in [2, 2(n + 1)] to Ω1 (not Ω0 here). Note that
when being restricted to [2, 2(n + 1)]. Therefore we can obtain new I-9 by applying some local supercharges in [2, 2(n + 1)] to Ω1 (not Ω0 here). Note that ![${{\Omega}}_{1}={r}_{\left[0,2\left(n+1\right)\right]}^{+}{{\Omega}}_{0}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn240.gif) on the segment [0, 2(n + 1)] as noted in lemma 3.2. Hence we can construct I-9 by applying some local supercharges in [0, 2(n + 1)] to Ω0. In this way we have made all the configurations of case I by the specified rule.
on the segment [0, 2(n + 1)] as noted in lemma 3.2. Hence we can construct I-9 by applying some local supercharges in [0, 2(n + 1)] to Ω0. In this way we have made all the configurations of case I by the specified rule.
By applying ![${r}_{\left[2n,2\left(n+1\right)\right]}^{+}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn241.gif) to the vector of I-9, we get
to the vector of I-9, we get

|
0 | 1 | 2 | 3 | ⋯ | ⋯ | ⋯ | 2n − 1 | 2n | 2n + 1 | 2(n + 1) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| New I-9(2) | 0 | 0 | 0 | 1 | ∗∗∗ | ∗∗∗ | ∗∗∗ | 1 | 1 | 1 | 1 |
'New I-9(2)' above belongs to  when being restricted to [0, 2n]. Therefore we can obtain New I-9(2) by applying some local supercharges in [0, 2n] to Ω1 (not Ω0 here). By noting lemma 3.2 we can construct I-9 by applying some local supercharges in [0, 2(n + 1)] to Ω0.
when being restricted to [0, 2n]. Therefore we can obtain New I-9(2) by applying some local supercharges in [0, 2n] to Ω1 (not Ω0 here). By noting lemma 3.2 we can construct I-9 by applying some local supercharges in [0, 2(n + 1)] to Ω0.
Case II:
We deal with all  whose left and right ends are
whose left and right ends are

The proof for case II can be done in the same way as done for case I.
Case III:
We deal with all  whose left and right ends are
whose left and right ends are

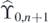
|
0 | 1 | 2 | 3 | ⋯ | ⋯ | ⋯ | 2n − 1 | 2n | 2n + 1 | 2(n + 1) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| III-1 | 0 | 0 | 0 | 0 | ∗∗∗ | ∗∗∗ | ∗∗∗ | 0 | 0 | 1 | 1 |
| III-2 | 0 | 0 | 0 | 0 | ∗∗∗ | ∗∗∗ | ∗∗∗ | 1 | 1 | 1 | 1 |
| III-3 | 0 | 0 | 0 | 0 | ∗∗∗ | ∗∗∗ | ∗∗∗ | 0 | 1 | 1 | 1 |
| III-4 | 0 | 0 | 1 | 1 | ∗∗∗ | ∗∗∗ | ∗∗∗ | 0 | 0 | 1 | 1 |
| III-5 | 0 | 0 | 1 | 1 | ∗∗∗ | ∗∗∗ | ∗∗∗ | 1 | 1 | 1 | 1 |
| III-6 | 0 | 0 | 1 | 1 | ∗∗∗ | ∗∗∗ | ∗∗∗ | 0 | 1 | 1 | 1 |
| III-7 | 0 | 0 | 0 | 1 | ∗∗∗ | ∗∗∗ | ∗∗∗ | 0 | 0 | 1 | 1 |
| III-8 | 0 | 0 | 0 | 1 | ∗∗∗ | ∗∗∗ | ∗∗∗ | 1 | 1 | 1 | 1 |
| III-9 | 0 | 0 | 0 | 1 | ∗∗∗ | ∗∗∗ | ∗∗∗ | 0 | 1 | 1 | 1 |
All the above elements in  except III-9 belong to
except III-9 belong to  or to
or to  when being restricted to [2, 2(n + 1)] or to [0, 2n], respectively. By applying
when being restricted to [2, 2(n + 1)] or to [0, 2n], respectively. By applying ![${r}_{\left[0,2\right]}^{+}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn250.gif) to the vector of III-9, we get
to the vector of III-9, we get

|
0 | 1 | 2 | 3 | ⋯ | ⋯ | ⋯ | 2n − 1 | 2n | 2n + 1 | 2(n + 1) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| New III-9 | 1 | 1 | 1 | 1 | ∗∗∗ | ∗∗∗ | ∗∗∗ | 0 | 1 | 1 | 1 |
'New III-9' above belongs to  when being restricted to [2, 2(n + 1)]. Therefore we can obtain New III-9 by applying some local supercharges in [2, 2(n + 1)] to Ω1 (not Ω0 here). Note that Ω1 can be constructed from Ω0 on [0, 2(n + 1)] by using local supercharges on [0, 2(n + 1)]. Thus we can construct I-9 by applying some local supercharges in [0, 2(n + 1)] to Ω0. We have completed the assertion for case III.
when being restricted to [2, 2(n + 1)]. Therefore we can obtain New III-9 by applying some local supercharges in [2, 2(n + 1)] to Ω1 (not Ω0 here). Note that Ω1 can be constructed from Ω0 on [0, 2(n + 1)] by using local supercharges on [0, 2(n + 1)]. Thus we can construct I-9 by applying some local supercharges in [0, 2(n + 1)] to Ω0. We have completed the assertion for case III.
Case IV:
We deal with all  whose left and right ends are
whose left and right ends are

The proof for case IV is similar to that for case III given above.
In conclusion, for all the cases (Case I–IV) we have generated all the elements of  from
from  and
and  . Hence by the induction, we have shown the statement.□
. Hence by the induction, we have shown the statement.□
The number of classical supersymmetric ground states can be computed explicitly.
Proposition 3.4. The number of classical free-boundary supersymmetric ground states on I0,n
( ) is 2 ⋅ 3n−1.
) is 2 ⋅ 3n−1.
Proof. This computation is given by the transfer-matrix method. We first divide I0,n into n-sequential pairs as
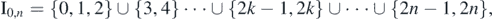
where the first group exceptionally consists of three sites {0, 1, 2}. On each {2k − 1, 2k} all classical configurations are possible. However, to connect {2k − 1, 2k} and {2k + 1, 2(k + 1)} we have to avoid the forbidden triplets: {0, 1, 0} {1, 0, 1} on {2k − 1, 2k, 2k + 1}. So the transfer matrix should be

By taking the edge condition (1.32) into account, the possible configurations are any of
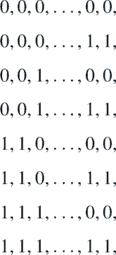
which correspond to (1, 1), (1, 4), (2, 1), (2, 4), (3, 1), (3, 4), (4, 1) and (4, 4) elements of Tn−1, respectively. Those amount to 2 ⋅ 3n−1.□
4. Discussion
We determined all classical supersymmetric ground states of the Nicolai supersymmetric fermion lattice model, and explained the high degeneracy of ground states by breakdown of its infinitely many local fermionic symmetries. The above finding may recall other supersymmetric models with many ground states such as the supersymmetric fermion lattice model by Fendley–Schoutens–de Boer–Nienhuis [FScdB] [FScNi] on two-dimensional lattice [vE], and some Wess–Zumino supersymmetry quantum mechanical model [A].
In [LScSh] the exact number of ground states on finite systems of the Nicolai model is shown, but the precise form of these states is not specified. In this paper, we consider only classical ground states. To determine all the ground states (furthermore all eigenstates) we need more detailed spectral property of the Hamiltonian and its symmetries (including bosonic ones).
In [SanKN] [M3] an extended version of Nicolai model that breaks its dynamical supersymmetry is studied. As we have seen, the (original) Nicolai model does not break its dynamical supersymmetry. However, it will break its hidden supersymmetries for some ground states. It would be interesting to discuss breakdown of these hidden fermionic symmetries.
The final comment is concerned with some technical point. We have chosen special subregions (Ik,l ) and the boundary conditions (the free-boundary supersymmetric condition) which seem artificial. However, as long as we consider classical states only, there is no loss of generality with this choice as follows.
Proposition 4.1. Given any finite subset Λ of  . Any classical supersymmetric state on Λ can be given by restriction of some classical free-boundary supersymmetric ground states on some larger Ik,l
that includes Λ.
. Any classical supersymmetric state on Λ can be given by restriction of some classical free-boundary supersymmetric ground states on some larger Ik,l
that includes Λ.
Proof. First recall the one-to-one correspondence between the set of classical supersymmetric ground states on Λ and ϒΛ by proposition 1.5. Recall the one-to-one correspondence between the set of classical free-boundary supersymmetric ground states on Ik,l
and 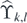 by proposition 1.8. Thus any classical supersymmetric ground state on Λ can be extended to at least one classical free-boundary supersymmetric ground state on Ik,l
that includes Λ.□
by proposition 1.8. Thus any classical supersymmetric ground state on Λ can be extended to at least one classical free-boundary supersymmetric ground state on Ik,l
that includes Λ.□
Acknowledgments
HK was supported in part by JSPS Grant-in-Aid for Scientic Research on Innovative Areas No. JP18H04478 and JP20H04630, and JSPS KAKENHI Grant No. 18K03445. HM would like to thank Prof Arai and Dr Huijse for helpful discussion. HM acknowledges Riyu-1 group of Kanazawa University for encouragement.
A : Appendix
A.1. Forms of 
We will give concrete examples for local {−1, +1}-sequences of conservation of definition 2.1 and their associated local fermion operators of definition 2.5. First we see that  on I0,1 ≡ [0, 1, 2] consists of two ±-characters only.
on I0,1 ≡ [0, 1, 2] consists of two ±-characters only.
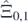
|
0 | 1 | 2 |
|---|---|---|---|
![${r}_{\left[0,2\right]}^{-}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn263.gif)
|
−1 | −1 | −1 |
![${r}_{\left[0,2\right]}^{+}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn264.gif)
|
+1 | +1 | +1 |
By (2.9) of definition 2.5 the corresponding local fermion operators are

We consider a next smallest segment I0,2 ≡ [0, 1, 2, 3, 4] by setting k = 0 and l = 2. The space  on I0,2 consists of the following five {−1, +1}-sequences:
on I0,2 consists of the following five {−1, +1}-sequences:
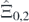
|
0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
![${r}_{\left[0,4\right]}^{-}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn267.gif)
|
−1 | −1 | −1 | −1 | −1 |
![${u}_{\left[0,4\right]}^{\mathrm{i}}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn268.gif)
|
−1 | −1 | −1 | +1 | +1 |
![${u}_{\left[0,4\right]}^{\text{ii}}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn269.gif)
|
−1 | −1 | +1 | +1 | +1 |
![${v}_{\left[0,4\right]}^{\mathrm{i}}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn270.gif)
|
+1 | +1 | +1 | −1 | −1 |
![${v}_{\left[0,4\right]}^{\text{ii}}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn271.gif)
|
+1 | +1 | −1 | −1 | −1 |
![${r}_{\left[0,4\right]}^{+}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn272.gif)
|
+1 | +1 | +1 | +1 | +1 |
Note that

By (2.9) of definition 2.5 we have

We then consider the segment I0,3 ≡ [0, 1, 2, 3, 4, 5, 6] taking k = 0 and l = 3. By definition it consists of 5 + 4 + 4 + 5 = 18 {−1, +1}-sequences:

|
0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
![${s}_{\left[0,6\right]}^{{\circ}}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn274.gif)
|
−1 | −1 | −1 | −1 | −1 | −1 | −1 |
![${s}_{\left[0,6\right]}^{\mathrm{i}}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn275.gif)
|
−1 | −1 | −1 | +1 | +1 | −1 | −1 |
![${s}_{\left[0,6\right]}^{\text{ii}}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn276.gif)
|
−1 | −1 | +1 | +1 | −1 | −1 | −1 |
![${s}_{\left[0,6\right]}^{\text{iii}}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn277.gif)
|
−1 | −1 | −1 | +1 | −1 | −1 | −1 |
![${s}_{\left[0,6\right]}^{\text{iv}}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn278.gif)
|
−1 | −1 | +1 | +1 | +1 | −1 | −1 |
![${u}_{\left[0,6\right]}^{\mathrm{i}}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn279.gif)
|
−1 | −1 | −1 | −1 | −1 | +1 | +1 |
![${u}_{\left[0,6\right]}^{\text{ii}}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn280.gif)
|
−1 | −1 | −1 | −1 | +1 | +1 | +1 |
![${u}_{\left[0,6\right]}^{\text{iii}}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn281.gif)
|
−1 | −1 | −1 | +1 | +1 | +1 | +1 |
![${u}_{\left[0,6\right]}^{\text{iv}}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn282.gif)
|
−1 | −1 | +1 | +1 | +1 | +1 | +1 |
![${v}_{\left[0,6\right]}^{\mathrm{i}}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn283.gif)
|
+1 | +1 | +1 | +1 | +1 | −1 | −1 |
![${v}_{\left[0,6\right]}^{\text{ii}}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn284.gif)
|
+1 | +1 | +1 | +1 | −1 | −1 | −1 |
![${v}_{\left[0,6\right]}^{\text{iii}}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn285.gif)
|
+1 | +1 | +1 | −1 | −1 | −1 | −1 |
![${v}_{\left[0,6\right]}^{\text{iv}}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn286.gif)
|
+1 | +1 | −1 | −1 | −1 | −1 | −1 |
![${t}_{\left[0,6\right]}^{{\bullet}}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn287.gif)
|
+1 | +1 | +1 | +1 | +1 | +1 | +1 |
![${t}_{\left[0,6\right]}^{\mathrm{i}}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn288.gif)
|
+1 | +1 | +1 | −1 | −1 | +1 | +1 |
![${t}_{\left[0,6\right]}^{\text{ii}}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn289.gif)
|
+1 | +1 | −1 | −1 | +1 | +1 | +1 |
![${t}_{\left[0,6\right]}^{\text{iii}}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn290.gif)
|
+1 | +1 | +1 | −1 | +1 | +1 | +1 |
![${t}_{\left[0,6\right]}^{\text{iv}}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn291.gif)
|
+1 | +1 | −1 | −1 | −1 | +1 | +1 |
Note that ![${s}_{\left[0,6\right]}^{{\circ}}\equiv {r}_{\left[0,6\right]}^{-}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn292.gif) and
and ![${t}_{\left[0,6\right]}^{{\bullet}}\equiv {r}_{\left[0,6\right]}^{+}$](https://content.cld.iop.org/journals/1751-8121/53/38/385003/revision2/aab9916ieqn293.gif) and that
and that

Using the rule we obtain the following list of 18 fermion operators associated to 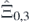 :
:




