Abstract
Deffner and Lutz (2013 J. Phys. A: Math. Theor. 46 335302) extended the Margolus–Levitin bound to time-dependent closed system. We point out that thier analysis is incorrect. The Margolus–Levitin bound has not yet been established in time-dependent quantum systems, except for the adiabatic case.
Export citation and abstract BibTeX RIS
The quantum speed limit (QSL) gives the fundamental speed limit to quantum time evolution. In time-independent quantum systems, the minimal evolution time 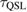 needed for the state to rotate orthogonally is given by
needed for the state to rotate orthogonally is given by

where 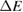 , E and E0 are the energy variance, mean energy and ground-state energy, respectively. The first bound is called the Mandelstam–Tamm (MT) bound [1] and the second bound is called the Margolus–Levitin (ML) bound [2]. We emphasize that the MT and ML bounds are characterized by the energy variance and mean energy, respectively.
, E and E0 are the energy variance, mean energy and ground-state energy, respectively. The first bound is called the Mandelstam–Tamm (MT) bound [1] and the second bound is called the Margolus–Levitin (ML) bound [2]. We emphasize that the MT and ML bounds are characterized by the energy variance and mean energy, respectively.
Recently, Deffner and Lutz derived the two ML bounds in time-dependent closed systems [3]. Furthermore, in [4], they derived the MT bound and the ML bound for non-Markovian dynamics. As a result, they concluded that the ML bound is tighter than the MT bound in non-Markovian systems.
In this comment, we point out the following: (i) the derivation of one ML bound for unitary dynamics in [3] is incorrect. (ii) Another ML bound for unitary dynamics in [3] appears to have no direct physical meaning. (iii) The ML bound has not yet been established in time-dependent quantum systems, except for the adiabatic case [5].
In [3], the authors used the following relation

where they defined that 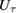 denotes the time evolution operator and
denotes the time evolution operator and 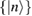 is the set of its instantaneous eigen states, with
is the set of its instantaneous eigen states, with

Using equation (2), the authors obtained the ML bound for time-dependent closed systems

where  and
and 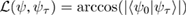 .
.
However, equation (3) does not hold clearly. The authors identified  with
with 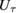 and ignored the time ordered product of
and ignored the time ordered product of 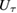 , which is never justified, except for the special case that
, which is never justified, except for the special case that ![$[H_t , H_{t'}]=0$](https://content.cld.iop.org/journals/1751-8121/51/31/318001/revision2/aaacb90ieqn010.gif) for any time. In order to correctly realize their idea, we must use the Magnus expansion [6]:
for any time. In order to correctly realize their idea, we must use the Magnus expansion [6]:

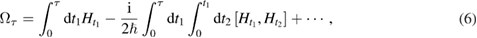

where  is the set of instantaneous eigenstates of
is the set of instantaneous eigenstates of  . Then, we can identify
. Then, we can identify 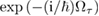 with
with 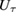 and equation (4) is modified to
and equation (4) is modified to

Although the derivation of equation (8) is correct, it is a formidable task to estimate the value of  via Ht in general.
via Ht in general.
In addition, the authors derived also another ML bound in appendix of [3]

where 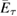 is given by
is given by  . Although the derivation of equation (9) is correct, the value of
. Although the derivation of equation (9) is correct, the value of  cannot be limited only from the eigenvalues of Ht. Therefore, equations (8) and (9) are mathematically correct but appear to have no direct physical meaning. The authors failed to obtain the meaningful ML bound for time-dependent closed systems in [3].
cannot be limited only from the eigenvalues of Ht. Therefore, equations (8) and (9) are mathematically correct but appear to have no direct physical meaning. The authors failed to obtain the meaningful ML bound for time-dependent closed systems in [3].
In summary, the ML bound is limited only to time-independent systems and has not yet been established in time-dependent systems except for the adiabatic case [5]. The derivation of the ML bound is based on spectrum expansion and, when we extend it straightforwardly, we obtain equation (8) which makes no sense physically. In addition, we mention that, for the classical Liouville equation, the classical ML-type bound is looser than the classical MT-type bound even in time-independent systems [7, 8]. It is also noted that the derivation of the ML bound for non-Markovian dynamics in [4] is incorrect [9]. These results might imply that the ML bound is a peculiar phenomenon to time-independent (or adiabatic) systems and not a universal property in time evolution.
Acknowledgments
The authors thank Ryo Takahashi for useful discussions. M Okuyama was supported by JSPS KAKENHI Grant No. 17J10198. M Ohzeki was supported by ImPACT Program of Council for Science, Technology and Innovation (Cabinet Office, Government of Japan) and JSPS KAKENHI No. 16K13849, No. 16H04382, and the Inamori Foundation.
