Abstract
The reduced dynamics of the system S, interacting with the environment E, is not given by a linear map, in general. However, if it is given by a linear map, then this map is also Hermitian. In order that the reduced dynamics of the system is given by a linear Hermitian map, there must be some restrictions on the set of possible initial states of the system-environment or on the possible unitary evolutions of the whole SE. In this paper, adding an ancillary reference space R, we assign to each convex set of possible initial states of the system-environment  , for which the reduced dynamics is Hermitian, a tripartite state
, for which the reduced dynamics is Hermitian, a tripartite state  , which we call the reference state, such that the set
, which we call the reference state, such that the set 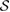 is given as the steered states from the reference state
is given as the steered states from the reference state 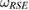 . The set of possible initial states of the system is also given as the steered set from a bipartite reference state
. The set of possible initial states of the system is also given as the steered set from a bipartite reference state 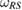 . The relation between these two reference states is as
. The relation between these two reference states is as  , where
, where  is the identity map on R and
is the identity map on R and  is a Hermitian assignment map, from S to SE. As an important consequence of introducing the reference state
is a Hermitian assignment map, from S to SE. As an important consequence of introducing the reference state 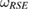 , we generalize the result of Buscemi (2014 Phys. Rev. Lett. 113 140502): we show that, for a U-consistent subspace, the reduced dynamics of the system is completely positive, for arbitrary unitary evolution of the whole system-environment U, if and only if the reference state
, we generalize the result of Buscemi (2014 Phys. Rev. Lett. 113 140502): we show that, for a U-consistent subspace, the reduced dynamics of the system is completely positive, for arbitrary unitary evolution of the whole system-environment U, if and only if the reference state 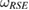 is a Markov state. In addition, we show that the evolution of the set of system-environment (system) states is determined by the evolution of the reference state
is a Markov state. In addition, we show that the evolution of the set of system-environment (system) states is determined by the evolution of the reference state 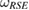 (
(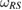 ).
).
Export citation and abstract BibTeX RIS
1. Introduction
Consider a closed finite dimensional quantum system which evolves as

where ρ and 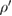 are the initial and final states (density operators) of the system, respectively, and U is a unitary operator (
are the initial and final states (density operators) of the system, respectively, and U is a unitary operator ( , where I is the identity operator).
, where I is the identity operator).
In general, the system is not closed and interacts with its environment. We can consider the whole system-environment as a closed quantum system which evolves as equation (1). So the reduced state of the system after the evolution is given by
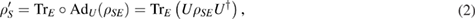
where  is the initial state of the combined system-environment quantum system and U acts on the whole Hilbert space of the system-environment.
is the initial state of the combined system-environment quantum system and U acts on the whole Hilbert space of the system-environment.
In general, the relation between the initial state of the system 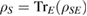 and its final state
and its final state 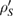 is not given by a map [1, 2]. Even if it is given by a map, then, in general, this map is not a linear map [3, 4]. In order that equation (2) leads to a linear map from
is not given by a map [1, 2]. Even if it is given by a map, then, in general, this map is not a linear map [3, 4]. In order that equation (2) leads to a linear map from 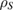 to
to  , there must be some restrictions on the set of possible initial states of the system-environment
, there must be some restrictions on the set of possible initial states of the system-environment 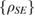 or on the possible unitary evolutions U [2, 5].
or on the possible unitary evolutions U [2, 5].
However, if the reduced dynamics of the system from 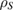 to
to  can be given by a linear map Ψ, then this Ψ is also Hermitian, i.e. maps each Hermitian operator to a Hermitian operator. Now, an important result is that for each linear trace-preserving Hermitian map from
can be given by a linear map Ψ, then this Ψ is also Hermitian, i.e. maps each Hermitian operator to a Hermitian operator. Now, an important result is that for each linear trace-preserving Hermitian map from 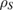 to
to 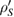 , there exists an operator sum representation in the following form:
, there exists an operator sum representation in the following form:
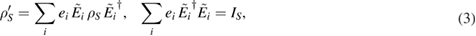
where  are linear operators and ei are real coefficients [2, 6, 7]. For the special case that all of the coefficients ei in equation (3) are positive, then we call the map completely positive (CP) [8] and rewrite equation (3) in the following form:
are linear operators and ei are real coefficients [2, 6, 7]. For the special case that all of the coefficients ei in equation (3) are positive, then we call the map completely positive (CP) [8] and rewrite equation (3) in the following form:

where  .
.
A general framework for linear trace-preserving Hermitian maps, arisen from equation (2), when both the system and the environment are finite dimensional, has been developed in [2]. The starting point of this framework is to consider a convex set of initial states  , for the whole system-environment, i.e. if
, for the whole system-environment, i.e. if  , then
, then 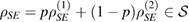 , for
, for  .
.
As we will see in the next section, an straightforward way to construct a convex  is to consider the set of steered states from performing measurements on the part R of a fixed tripartite state
is to consider the set of steered states from performing measurements on the part R of a fixed tripartite state 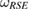 , which is a state on the Hilbert space of the reference-system-environment
, which is a state on the Hilbert space of the reference-system-environment  .
.
We call 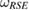 the reference state and we will show that if it can be written as equation (7) below, then the reduced dynamics of the system is Hermitian. Interestingly, this result includes all the previously found sets
the reference state and we will show that if it can be written as equation (7) below, then the reduced dynamics of the system is Hermitian. Interestingly, this result includes all the previously found sets  , in [9–14], for which the reduced dynamics of the system is CP.
, in [9–14], for which the reduced dynamics of the system is CP.
Then, we question whether it is possible to find such reference state  for arbitrary convex set
for arbitrary convex set 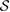 , for which the reduced dynamics is Hermitian. Fortunately, this is the case as we will show in section 3. The possibility of introducing the reference state
, for which the reduced dynamics is Hermitian. Fortunately, this is the case as we will show in section 3. The possibility of introducing the reference state  , for arbitrary
, for arbitrary 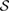 , has an important consequence: in section 4, we generalize the result of [13], i.e. we show that, for arbitrary
, has an important consequence: in section 4, we generalize the result of [13], i.e. we show that, for arbitrary  , when
, when 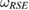 is not a so-called Markov state, then the the reduced dynamics of the system, for at least one U, is not CP.
is not a so-called Markov state, then the the reduced dynamics of the system, for at least one U, is not CP.
Sections 3 and 4 are on the case that there is a one to one correspondence between the members of  and the members of
and the members of  . The general case, where there is no such correspondence, is given in section 5.
. The general case, where there is no such correspondence, is given in section 5.
In section 6, we consider the case studied in [4], as an example, to illustrate (a part of) our results, and finally, we will end this paper in section 7, with a summary of our results.
2. Reduced dynamics for a steered set
Assume that, for each 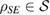 , the reduced dynamics of the system is given by a map Ψ. So, for each
, the reduced dynamics of the system is given by a map Ψ. So, for each 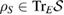 , we have:
, we have:

The first obvious requirement that such a map Ψ can be defined, is the U-consistency of the 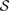 [2], i.e. if for two states
[2], i.e. if for two states 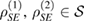 , we have
, we have 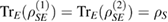 , then we must have
, then we must have  .
.
Interestingly, if  is convex and U-consistent, then the reduced dynamics of the system is given by a (linear trace-preserving) Hermitian map [2].
is convex and U-consistent, then the reduced dynamics of the system is given by a (linear trace-preserving) Hermitian map [2].
An straightforward way to construct a convex 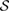 is to consider the set of steered states from performing measurements on the part R of a reference state
is to consider the set of steered states from performing measurements on the part R of a reference state 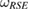 [13, 15]:
[13, 15]:

where PR is arbitrary positive operator on  such that
such that ![${\rm Tr}[(P_{R}\otimes I_{SE})\omega_{RSE}]>0$](https://content.cld.iop.org/journals/1751-8121/51/31/315301/revision2/aaacaaaieqn054.gif) and ISE is the identity operator on
and ISE is the identity operator on 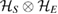 . Note that, up to a positive factor, PR can be considered as an element of a POVM.
. Note that, up to a positive factor, PR can be considered as an element of a POVM.
It can be shown simply that the set of initial states of the system-environment  , in equation (6), is convex. So, if, in addition, it be a U-consistent set, then the reduced dynamics of the system, for all
, in equation (6), is convex. So, if, in addition, it be a U-consistent set, then the reduced dynamics of the system, for all  (
(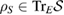 ), is given by a Hermitian map, as equation (3).
), is given by a Hermitian map, as equation (3).
Note that if there is a one to one correspondence between the members of  and the members of
and the members of  , then, trivially, the U-consistency condition is satisfied. In other words, if, for each
, then, trivially, the U-consistency condition is satisfied. In other words, if, for each 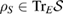 , there is only one
, there is only one  such that
such that 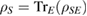 , then the set
, then the set 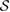 is U-consistent, for any arbitrary unitary evolution of the whole system-environment U.
is U-consistent, for any arbitrary unitary evolution of the whole system-environment U.
Now, let us consider the case that the reference state 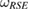 can be written as
can be written as

where  ,
,  is the identity map on
is the identity map on 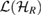 and
and 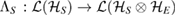 is a Hermitian map. (
is a Hermitian map. ( is the space of linear operators on
is the space of linear operators on  .) So, each
.) So, each  , in equation (6), can be written as
, in equation (6), can be written as

where, the map 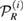 on
on  is defined as
is defined as  , for each
, for each 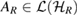 . In addition, without loss of generality, we have considered only those
. In addition, without loss of generality, we have considered only those  , in equation (6), for which we have
, in equation (6), for which we have ![${\rm Tr}[(P_{R}^{(i)}\otimes I_{SE})\omega_{RSE}]=1$](https://content.cld.iop.org/journals/1751-8121/51/31/315301/revision2/aaacaaaieqn078.gif) . Therefore
. Therefore

where, in the fourth line, we have used this fact that, according to equation (7), we have = {{\rm Tr}_{E}}[{\rm i}{d}_{R}\otimes\Lambda_{S}(\omega_{RS})]={{\rm Tr}_{E}}(\omega_{RSE})=\omega_{RS}$](https://content.cld.iop.org/journals/1751-8121/51/31/315301/revision2/aaacaaaieqn079.gif) .
.
Next, assume that  is an orthonormal basis (according to the Hilbert–Schmidt inner product [8]) for
is an orthonormal basis (according to the Hilbert–Schmidt inner product [8]) for 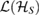 . So, we can decompose
. So, we can decompose  as
as

where Rj are linear operators in 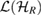 . Therefore, from equation (9), we have
. Therefore, from equation (9), we have

where  . From equations (7) and (10), we have
. From equations (7) and (10), we have

So, from From equations (8) and (11), we get

Now, if  , then, at least for one j, we have
, then, at least for one j, we have 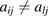 . So, from equation (11), we conclude that
. So, from equation (11), we conclude that 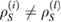 . Therefore, there is a one to one correspondence between the members of
. Therefore, there is a one to one correspondence between the members of  and the members of
and the members of  , and so, the U-consistency condition is satisfied for the set
, and so, the U-consistency condition is satisfied for the set 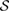 , steered from the
, steered from the  in equation (7).
in equation (7).
In summary, we have proved the following proposition:
Proposition 1. If the set of possible initial states of the whole system-environment is given by the set of steered states from the tripartite reference state  in equation (7), then the reduced dynamics of the system, for arbitrary unitary evolution of the whole system-environment U, is given by a (linear trace-preserving) Hermitian map.
in equation (7), then the reduced dynamics of the system, for arbitrary unitary evolution of the whole system-environment U, is given by a (linear trace-preserving) Hermitian map.
For the special case that  in equation (7) is a CP map,
in equation (7) is a CP map, 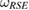 is called a Markov state [16], and the reduced dynamics of the system, for arbitrary U, is, therefore, CP [13]. In fact, the reverse is also true. In summary, we have [13]:
is called a Markov state [16], and the reduced dynamics of the system, for arbitrary U, is, therefore, CP [13]. In fact, the reverse is also true. In summary, we have [13]:
Theorem 1. For a set of steered states, from a tripartite reference state 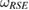 , as equation (6), the reduced dynamics of the system, for arbitrary U, is CP if and only if
, as equation (6), the reduced dynamics of the system, for arbitrary U, is CP if and only if  is a Markov state.
is a Markov state.
Remark 1. During the proof of theorem 1 in [13], it has been assumed that, in general, the dimensions of  and
and 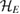 can vary during the evolution, while the dimension of
can vary during the evolution, while the dimension of 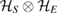 remains unchanged.
remains unchanged.
Interestingly, all the previous results, in this context, are special cases of the above result: all the previously found sets of the system-environment initial states in [9–12], for which the reduced dynamics of the system, for arbitrary U, is CP, can be written as steered sets, from Markov states 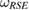 [14].
[14].
This fact that equation (7), for the special case of completely positive 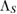 , gives such interesting general results, leads us to this conjecture that equation (7), for the general case of Hermitian
, gives such interesting general results, leads us to this conjecture that equation (7), for the general case of Hermitian 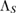 , can also yield general interesting results. In fact, as we will prove in the following section, for arbitrary convex set of system-environment initial states
, can also yield general interesting results. In fact, as we will prove in the following section, for arbitrary convex set of system-environment initial states  , which leads to Hermitian reduced dynamics, we can assign a tripartite reference state
, which leads to Hermitian reduced dynamics, we can assign a tripartite reference state 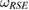 , as equation (7).
, as equation (7).
3. Reference state for a U-consistent subspace
Let us denote the convex set of possible initial states of the system-environment as  , and so, the convex set of possible initial states of the system as
, and so, the convex set of possible initial states of the system as  . Since the Hilbert space of the system
. Since the Hilbert space of the system  is finite dimensional, one can find a set
is finite dimensional, one can find a set  including a finite number of
including a finite number of 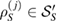 which are linearly independent and other states in
which are linearly independent and other states in 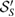 can be decomposed as linear combinations of them:
can be decomposed as linear combinations of them:  , where m is an integer and
, where m is an integer and 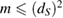 (dS is the dimension of
(dS is the dimension of 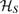 , so
, so 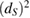 is the dimension of
is the dimension of  ), and, for each
), and, for each  , we have
, we have 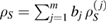 with real bj.
with real bj.
Consider the set 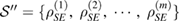 , where
, where  . So,
. So, 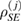 are also linearly independent. Now, there is a one to one correspondence between the members of
are also linearly independent. Now, there is a one to one correspondence between the members of 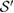 and the members of
and the members of 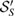 if and only if each
if and only if each  can be decomposed as a linear combination of
can be decomposed as a linear combination of  :
: 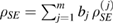 . (Note that the coefficients bj in the decomposition of
. (Note that the coefficients bj in the decomposition of  are the same as bj in the decomposition of
are the same as bj in the decomposition of 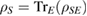 .)
.)
So, if the set 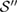 constructs a basis for the convex set
constructs a basis for the convex set 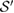 , then
, then 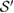 is, in addition, U-consistent for arbitrary U, and, as we will see in the following, the reduced dynamics of the system is Hermitian.
is, in addition, U-consistent for arbitrary U, and, as we will see in the following, the reduced dynamics of the system is Hermitian.
Now, we can define the linear trace-preserving Hermitian map 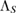 as
as  , where
, where  and so
and so  . Therefore, for each
. Therefore, for each  , we have
, we have
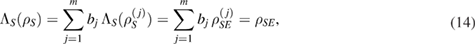
where  such that
such that  . The Hermitian map
. The Hermitian map  is called the assignment map [2, 17]. So, from equation (14), for arbitrary unitary evolution U for the whole system-environment, we have
is called the assignment map [2, 17]. So, from equation (14), for arbitrary unitary evolution U for the whole system-environment, we have

where  is a Hermitian map on
is a Hermitian map on  , since
, since  and
and 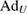 are completely positive [8] and
are completely positive [8] and  is Hermitian.
is Hermitian.
Now, our question is as follows: can we assign to the above convex U-consistent 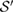 a tripartite reference state
a tripartite reference state 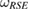 , such that
, such that 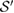 is the set of steered states from this
is the set of steered states from this  ?
?
Without loss of generality, as we will show in the following, we consider a restricted set 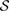 , instead of
, instead of  , such that each
, such that each  can be decomposed as
can be decomposed as  , with
, with 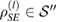 , where
, where 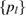 is a probability distribution (
is a probability distribution (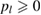 and
and 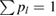 ). As
). As 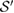 , the set
, the set 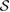 is convex (and U-consistent) and so the set
is convex (and U-consistent) and so the set 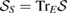 is also convex.
is also convex.
First, we define the bipartite state

where 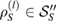 and
and 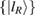 is an orthonormal basis for the reference Hilbert space
is an orthonormal basis for the reference Hilbert space 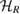 . So, using the assignment map
. So, using the assignment map  in equation (14), we have
in equation (14), we have
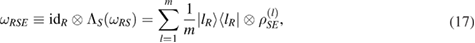
where 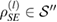 such that
such that 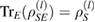 . Therefore, using equation (6), we can write the set
. Therefore, using equation (6), we can write the set  as the steered set from the tripartite reference state
as the steered set from the tripartite reference state 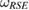 , given in equation (17). It can be done, e.g. by considering the positive operators PR in equation (6) as
, given in equation (17). It can be done, e.g. by considering the positive operators PR in equation (6) as  . Note that
. Note that  , in equation (17), is in the form of equation (7), with the Hermitian assignment map
, in equation (17), is in the form of equation (7), with the Hermitian assignment map  .
.
In summary, we have proved the following theorem:
Theorem 2. Consider a set of linearly independent states 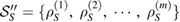 . So, the set
. So, the set  , such that
, such that  (for each
(for each  ), is also linearly independent. The set
), is also linearly independent. The set 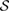 of the convex combinations of
of the convex combinations of 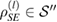 is convex and U-consistent, for arbitrary unitary evolution of the whole system-environment. Therefore, if the set of possible initial states of the system-environment is given by
is convex and U-consistent, for arbitrary unitary evolution of the whole system-environment. Therefore, if the set of possible initial states of the system-environment is given by  , then the reduced dynamics of the system is given by a Hermitian map
, then the reduced dynamics of the system is given by a Hermitian map 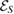 . In addition,
. In addition, 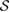 can be written as the steered set from a tripartite reference state
can be written as the steered set from a tripartite reference state 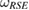 , given in equation (17), which is in the form of equation (7), with the Hermitian assignment map
, given in equation (17), which is in the form of equation (7), with the Hermitian assignment map 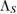 .
.
Next, let us define  as the subspace spanned by the states
as the subspace spanned by the states 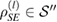 ; i.e. for each
; i.e. for each  , we have
, we have 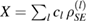 with unique complex coefficients cl. Obviously
with unique complex coefficients cl. Obviously  .
.
So, the subspace 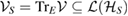 is spanned by the states
is spanned by the states 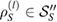 : for each
: for each 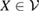 , we have
, we have 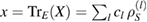 with the same coefficients cl as in the decomposition of X.
with the same coefficients cl as in the decomposition of X.
Note that, since there is a one to one correspondence between the  and the
and the 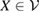 , the whole subspace
, the whole subspace 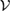 is U-consistent, for arbitrary U.
is U-consistent, for arbitrary U.
In addition, we can write the subspace 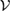 as
as
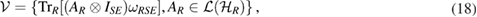
where AR is arbitrary linear operator in 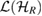 and
and  is the reference state, given in equation (17). We will call the above set the generalized steered set from the reference state
is the reference state, given in equation (17). We will call the above set the generalized steered set from the reference state  . Using this fact that if the subspace
. Using this fact that if the subspace 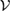 is U-consistent, for arbitrary U, then there is a one to one correspondence between the
is U-consistent, for arbitrary U, then there is a one to one correspondence between the 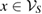 and the
and the 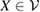 [2], we can write the above result in the following form:
[2], we can write the above result in the following form:
Corollary 1. Consider the subspace 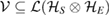 , which is spanned by states. If
, which is spanned by states. If  is U-consistent, for arbitrary U, then it can be written as the generalized steered set from the reference state
is U-consistent, for arbitrary U, then it can be written as the generalized steered set from the reference state  , as equation (18).
, as equation (18).
Note that, since 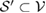 ,
, 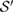 can be written as (a subset of) equation (18). In our discussion, leading to the reference state
can be written as (a subset of) equation (18). In our discussion, leading to the reference state 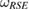 in equation (17), we have restricted ourselves to the set
in equation (17), we have restricted ourselves to the set  , instead of
, instead of  . Now, as stated before, we see that this restriction does not lose the generality of our discussion.
. Now, as stated before, we see that this restriction does not lose the generality of our discussion.
The next observation is that the evolution of the system subspace  and the whole system-environment subspace
and the whole system-environment subspace  can be given from the evolution of
can be given from the evolution of 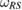 in equation (16), and
in equation (16), and  in equation (17), respectively. So, we can call
in equation (17), respectively. So, we can call 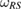 as the reference state of the system and
as the reference state of the system and  as the reference state of the whole system-environment. Note that these two reference states are related to each other as equation (7).
as the reference state of the whole system-environment. Note that these two reference states are related to each other as equation (7).
Assume that the unitary time evolution of the whole system-environment, from the initial instant to the time t, is given by 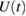 . So,
. So, 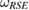 evolves as
evolves as

where  is given in equation (17). As stated before, each
is given in equation (17). As stated before, each 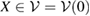 can be written as
can be written as ![$X=X(0)=\sum_{l}c_{l}\, \rho_{SE}^{(l)}={{\rm Tr}_{R}}[(A_{R}\otimes I_{SE})\omega_{RSE}(0)]$](https://content.cld.iop.org/journals/1751-8121/51/31/315301/revision2/aaacaaaieqn218.gif) . So,
. So,  and therefore
and therefore
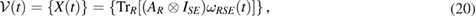
where AR is arbitrary linear operator in 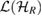 and
and  is the reference state of the system-environment, given in equation (19).
is the reference state of the system-environment, given in equation (19).
Similarly, 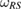 evolves as
evolves as

where  is given in equation (16) and
is given in equation (16) and  is a Hermitian map on
is a Hermitian map on  . Each
. Each  can be decomposed as
can be decomposed as 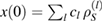 . So,
. So, 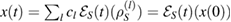 and therefore
and therefore

where AR is arbitrary linear operator in 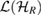 and
and 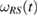 is the reference state of the system, given in equation (21).
is the reference state of the system, given in equation (21).
In summary,
Corollary 2. Consider the subspace  , which is spanned by states. If
, which is spanned by states. If  is U-consistent, for arbitrary U, then
is U-consistent, for arbitrary U, then  and
and 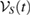 can be written as the generalized steered sets, from the reference states
can be written as the generalized steered sets, from the reference states 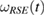 , in equation (19), and
, in equation (19), and  , in equation (21), respectively.
, in equation (21), respectively.
In general, there are more than one possible assignment maps  . So, it may be possible, by choosing an appropriate
. So, it may be possible, by choosing an appropriate 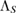 , to write the reduced dynamics of the system S as a CP map. Note that, from equations (16) and (21), we have
, to write the reduced dynamics of the system S as a CP map. Note that, from equations (16) and (21), we have

Now, if the time evolution of the system can be written as a CP map, then, since 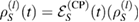 , where
, where  is a CP map on
is a CP map on 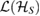 , we have
, we have

i.e. even if we have used a  which leads to equation (21), with a non-CP map
which leads to equation (21), with a non-CP map 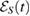 ,
,  can be written as equation (24) too.
can be written as equation (24) too.
Reversely, if 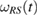 , in equation (23), can be written as equation (24), then, using this fact that
, in equation (23), can be written as equation (24), then, using this fact that  , we, simply, conclude that
, we, simply, conclude that 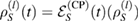 , and so, the reduced dynamics of the system is given by the CP map
, and so, the reduced dynamics of the system is given by the CP map 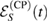 . In summary,
. In summary,
Theorem 3. The reduced dynamics of the system can be written as a CP map if and only if the reference state 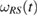 , in equation (23), evolves as equation (24), with a CP map
, in equation (23), evolves as equation (24), with a CP map 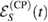 .
.
4. Markovianity of the reference state and the complete positivity of the reduced dynamics
Theorem 1 states the relation between the Markovianity of the reference state  and the CP-ness of the reduced dynamics, for a steered set as equation (6). In the previous section, we have seen that, for an arbitrary U-consistent subspace
and the CP-ness of the reduced dynamics, for a steered set as equation (6). In the previous section, we have seen that, for an arbitrary U-consistent subspace  , we can also introduce a reference state as equation (17), such that
, we can also introduce a reference state as equation (17), such that 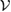 can be written as the generalized steered set from it. Therefore, we conjecture that theorem 1 can be generalized to arbitrary U-consistent subspace
can be written as the generalized steered set from it. Therefore, we conjecture that theorem 1 can be generalized to arbitrary U-consistent subspace  . Fortunately, this is the case, as we will show in this section.
. Fortunately, this is the case, as we will show in this section.
A tripartite state 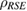 is called a Markov state if it can be written as
is called a Markov state if it can be written as 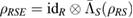 , where
, where 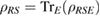 , and
, and 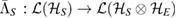 is a CP assignment map [16]. Now, it has been shown in [16] that if
is a CP assignment map [16]. Now, it has been shown in [16] that if  is a Markov state, then there exists a decomposition of the Hilbert space of the system S as
is a Markov state, then there exists a decomposition of the Hilbert space of the system S as 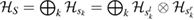 such that
such that

where 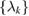 is a probability distribution,
is a probability distribution, 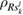 is a state on
is a state on 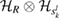 , and
, and 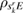 is a state on
is a state on  .
.
Consider a set  which spans the subspace
which spans the subspace 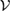 . In general, we can consider different assignment maps
. In general, we can consider different assignment maps  such that, for all of them,
such that, for all of them, 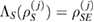 , where
, where 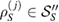 and
and  , and so, we can write equation (14), for all of them. Different assignment maps
, and so, we can write equation (14), for all of them. Different assignment maps 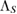 can lead to different reduced dynamics
can lead to different reduced dynamics  , in equation (15).
, in equation (15).
Therefore, it is possible that we choose a Hermitian (non-CP) assignment map  to construct the reference state
to construct the reference state  in equation (17), while there is another CP assignment map which could be used instead. So, the reduced dynamics could be written as a CP map, while we write it as a non-CP map. How can we avoid such inappropriate choosing?
in equation (17), while there is another CP assignment map which could be used instead. So, the reduced dynamics could be written as a CP map, while we write it as a non-CP map. How can we avoid such inappropriate choosing?
Note that if there is a CP assignment map  , such that, for all
, such that, for all  , we have
, we have  , then
, then 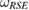 in equation (17) is a Markov state, even if we have used a non-CP assignment map
in equation (17) is a Markov state, even if we have used a non-CP assignment map  to construct it. So, we can check whether
to construct it. So, we can check whether  can be written as equation (25), or not. If it can be written so, then the reference state
can be written as equation (25), or not. If it can be written so, then the reference state 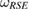 is a Markov state, and the reduced dynamics is CP, for arbitrary U.
is a Markov state, and the reduced dynamics is CP, for arbitrary U.
But if  cannot be written as equation (25), then we conclude that there is no CP assignment map which can map all
cannot be written as equation (25), then we conclude that there is no CP assignment map which can map all 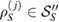 to
to  . In other words, though there may be more than one possible assignment maps
. In other words, though there may be more than one possible assignment maps 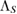 , but none of them is CP.
, but none of them is CP.
Also note that, for the subspace  , we can construct different reference states
, we can construct different reference states  as equation (17), in general: by choosing a different set
as equation (17), in general: by choosing a different set 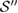 , which also spans
, which also spans 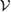 , we can construct a different
, we can construct a different  . Interestingly, if the previously constructed reference state is non-Markovian, this new reference state is not a Markov state, too; otherwise, there is a CP assignment map which maps all
. Interestingly, if the previously constructed reference state is non-Markovian, this new reference state is not a Markov state, too; otherwise, there is a CP assignment map which maps all 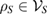 to
to 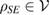 .
.
In summary, we have proved the following theorem:
Theorem 4. Consider the subspace 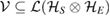 , which is spanned by states and is U-consistent, for arbitrary U. One can find, at least, one CP assignment map
, which is spanned by states and is U-consistent, for arbitrary U. One can find, at least, one CP assignment map 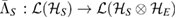 , which maps
, which maps 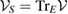 to
to 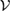 , if and only if any reference state
, if and only if any reference state 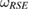 , which is constructed as equation (17), is a Markov state, as equation (25).
, which is constructed as equation (17), is a Markov state, as equation (25).
Next, consider the case that the reference state 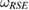 , in equation (17), is not a Markov state. Construct the set of steered states from
, in equation (17), is not a Markov state. Construct the set of steered states from 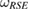 , i.e. the set
, i.e. the set 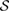 in theorem 2. Using theorem 1, we conclude that the reduced dynamics of the system is non-CP, for at least one U. Since
in theorem 2. Using theorem 1, we conclude that the reduced dynamics of the system is non-CP, for at least one U. Since  , the non-CP-ness of the reduced dynamics for
, the non-CP-ness of the reduced dynamics for 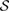 results in the non-CP-ness of the reduced dynamics for
results in the non-CP-ness of the reduced dynamics for  . In other words,
. In other words,
Theorem 5. Consider the subspace  , which is U-consistent, for arbitrary U, and can be written as the generalized steered set, from the reference state
, which is U-consistent, for arbitrary U, and can be written as the generalized steered set, from the reference state  , in equation (17). When
, in equation (17). When  is not a Markov state as equation (25), then the reduced dynamics of the system, for at least one U, is non-CP.
is not a Markov state as equation (25), then the reduced dynamics of the system, for at least one U, is non-CP.
The above theorem, states that, not only for a steered set of initial states of the system-environment as equation (6), but also, for any arbitrary subspace  , which is U-consistent for all U, the reduced dynamics of the system, for arbitrary U, is CP if and only if the reference state
, which is U-consistent for all U, the reduced dynamics of the system, for arbitrary U, is CP if and only if the reference state 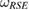 is a Markov state. This is the generalization of theorem 1, to arbitrary U-consistent subspace
is a Markov state. This is the generalization of theorem 1, to arbitrary U-consistent subspace  .
.
The following point is also worth noting:
Corollary 3. Theorems 4 and 5 state that the impossibility of a CP assignment map is equivalent to non-CP-ness of the reduced dynamics, for at least one U.
5. Generalization to arbitrary  -consistent subspace
-consistent subspace
Until now, our discussion was restricted to the case that there is a one to one correspondence between the members of  and
and  . We can generalize our discussion to include the general case (with no such correspondence), straightforwardly.
. We can generalize our discussion to include the general case (with no such correspondence), straightforwardly.
Consider the subspace 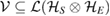 , which is spanned by states. If there is not a one to one correspondence between the members of
, which is spanned by states. If there is not a one to one correspondence between the members of 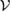 and the members of
and the members of  , then
, then 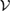 is U-consistent only for a restricted set
is U-consistent only for a restricted set 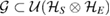 (
( , is the set of all unitary
, is the set of all unitary  ) [2]. In such case, the subspace
) [2]. In such case, the subspace 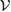 is called a
is called a 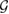 -consistent subspace.
-consistent subspace.
Assume that the set of linearly independent states  , where M is an integer such that
, where M is an integer such that 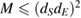 (dS and dE are the dimensions of
(dS and dE are the dimensions of  and
and  , respectively), spans the subspace
, respectively), spans the subspace  . Without loss of generality, we can assume that only
. Without loss of generality, we can assume that only  , for
, for  (where the integer
(where the integer 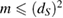 is, in addition, less than M), are linearly independent. So, the subspace
is, in addition, less than M), are linearly independent. So, the subspace  is spanned by the set of states
is spanned by the set of states 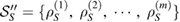 .
.
As before, we can define the (linear trace-preserving) Hermitian assignment map 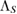 as
as  , where
, where 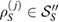 ,
, 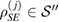 and
and  , and so, we can write a similar relation as equation (14), for each
, and so, we can write a similar relation as equation (14), for each 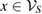 . Therefore, the assignment map
. Therefore, the assignment map  maps
maps  to a subspace
to a subspace 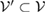 , which is spanned by
, which is spanned by  .
.
Note that

where, for each 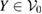 , we have
, we have  . So, the most general possible assignment map is as
. So, the most general possible assignment map is as

where  denotes arbitrary
denotes arbitrary 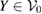 .
.
Each  maps
maps 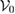 to
to 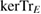 , the set of all
, the set of all  for which we have
for which we have 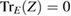 , and so,
, and so, 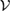 is U-consistent under all
is U-consistent under all 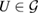 [2]. Therefore, for a unitary time evolution
[2]. Therefore, for a unitary time evolution 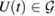 , from equation (26), we have
, from equation (26), we have

where 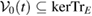 and
and 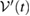 is given as equation (20), i.e. as the generalized steered set from the reference state
is given as equation (20), i.e. as the generalized steered set from the reference state  in equation (19).
in equation (19).
In addition, for each  and each
and each  , we have
, we have =[{{\rm Tr}}_{E}\circ {\rm Ad}_{U(t)}\circ \Lambda_{S}](x)=\mathcal{E}_{S}(t)(x)$](https://content.cld.iop.org/journals/1751-8121/51/31/315301/revision2/aaacaaaieqn360.gif) . Therefore, as before,
. Therefore, as before, 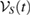 can be written as equation (22), i.e. as the generalized steered set from the reference state
can be written as equation (22), i.e. as the generalized steered set from the reference state 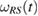 in equation (21).
in equation (21).
So, we have proved the following proposition:
Proposition 2. Consider the 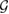 -consistent subspace
-consistent subspace  , which is spanned by states. For each
, which is spanned by states. For each 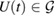 ,
,  , even simply, can be written as the generalized steered set, from the reference state
, even simply, can be written as the generalized steered set, from the reference state 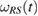 in equation (21). In addition,
in equation (21). In addition, 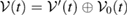 , where
, where 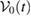 is a subset of
is a subset of  and
and 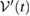 can be written as the generalized steered set, from the reference state
can be written as the generalized steered set, from the reference state 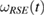 in equation (19).
in equation (19).
Note that theorem 3 is valid for a 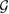 -consistent subspace, too, since, even simply, the reduced dynamics of the system is determined by the evolution of the reference state
-consistent subspace, too, since, even simply, the reduced dynamics of the system is determined by the evolution of the reference state  .
.
In the following, we discuss about the generalization of the results given in the previous section, to a 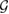 -consistent subspace
-consistent subspace 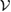 . First, theorem 4 is changed as below:
. First, theorem 4 is changed as below:
Theorem 4'. Consider a 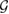 -consistent subspace
-consistent subspace  , which is spanned by states. There exists, at least, one CP assignment map
, which is spanned by states. There exists, at least, one CP assignment map 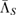 if and only if, at least, one reference state
if and only if, at least, one reference state 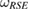 , as equation (17), is a Markov state, as equation (25).
, as equation (17), is a Markov state, as equation (25).
Note that when there exists a CP assignment map 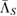 , then using this
, then using this 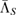 in equation (17), we can construct a Markov reference state
in equation (17), we can construct a Markov reference state  . But, from the CP-ness of
. But, from the CP-ness of  , we cannot, in general, conclude that
, we cannot, in general, conclude that  is also CP. So, in general, one can construct other reference states which are not Markov states. However, if, for our
is also CP. So, in general, one can construct other reference states which are not Markov states. However, if, for our 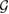 -consistent subspace
-consistent subspace 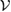 , we can find a reference state
, we can find a reference state 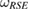 , as equation (17), which is a Markov state, as equation (25), then the reduced dynamics of the system is CP, for any arbitrary
, as equation (17), which is a Markov state, as equation (25), then the reduced dynamics of the system is CP, for any arbitrary  .
.
Unfortunately, theorem 5 cannot be generalized to a  -consistent subspace
-consistent subspace  , in general. Assume that the reduced dynamics of the system
, in general. Assume that the reduced dynamics of the system 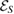 is CP, for any arbitrary
is CP, for any arbitrary  . The CP-ness of the reduced dynamics, for any
. The CP-ness of the reduced dynamics, for any 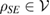 , results in the CP-ness of the reduced dynamics, for any convex set of initial states
, results in the CP-ness of the reduced dynamics, for any convex set of initial states 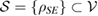 . Therefore, for the steered set
. Therefore, for the steered set  , from any reference state
, from any reference state 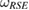 , constructed as equation (17), the reduced dynamics is CP, for any arbitrary
, constructed as equation (17), the reduced dynamics is CP, for any arbitrary 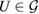 . But, from this result, we cannot (in general) conclude that
. But, from this result, we cannot (in general) conclude that  is a Markov state, unless
is a Markov state, unless 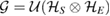 , which is the case considered in the previous section. In fact, as we will see in the next section, the reduced dynamics can be CP, for some (but not all) U, even though
, which is the case considered in the previous section. In fact, as we will see in the next section, the reduced dynamics can be CP, for some (but not all) U, even though 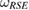 is not a Markov state.
is not a Markov state.
6. Example
In [4], a two-qubit case, one as the system S and the other as the environment E, has been considered. First, note that an arbitrary state of the system can be written as

where 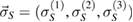 ,
, 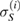 are the Pauli operators, and the Bloch vector
are the Pauli operators, and the Bloch vector  is a real 3D vector such that
is a real 3D vector such that 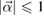 [8].
[8].
Consider the following (linear trace-preserving) Hermitian assignment map 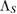 :
:
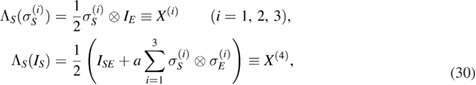
where a is a fixed real constant. For the special case that a = 0, we have  , for each
, for each  , i.e.
, i.e.  is a CP map, in the form first introduced by Pechukas [6, 17]. We denote this special case of
is a CP map, in the form first introduced by Pechukas [6, 17]. We denote this special case of 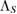 as
as  . But, for
. But, for 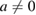 ,
, 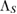 is not CP. We have
is not CP. We have
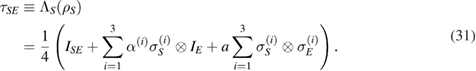
When  ,
, 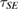 is positive for
is positive for 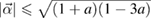 , and when
, and when 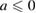 ,
, 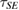 is positive for
is positive for  [2, 4]. Therefore, for
[2, 4]. Therefore, for 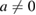 ,
, 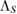 is not even a positive map and, consequently, it is not a CP map.
is not even a positive map and, consequently, it is not a CP map.
Within the positivity domain of  , i.e.
, i.e. 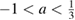 , we can apply the framework of [2]. we can construct
, we can apply the framework of [2]. we can construct 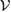 as [2]
as [2]

i.e. each 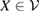 can be decomposed as
can be decomposed as  , with complex coefficients ci. (Out of the positivity domain,
, with complex coefficients ci. (Out of the positivity domain,  , in equation (31), is not a state. In other words,
, in equation (31), is not a state. In other words,  does not contain any state, and so, is not spanned by states.) Therefore,
does not contain any state, and so, is not spanned by states.) Therefore,

From equations (32) and (33), we see that there is a one to one correspondence between the members of  and the members of
and the members of 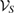 . Therefore,
. Therefore,  is a U-consistent subspace, for arbitrary unitary evolution of the whole system-environment U, and so, the reduced dynamics of the system, from equation (2) (when
is a U-consistent subspace, for arbitrary unitary evolution of the whole system-environment U, and so, the reduced dynamics of the system, from equation (2) (when 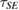 , in equation (31), is positive), is given by
, in equation (31), is positive), is given by

Since  is Hermitian (and not CP), we expect that the reduced dynamics
is Hermitian (and not CP), we expect that the reduced dynamics 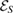 be so, in general. But, interestingly, when U commutes with
be so, in general. But, interestingly, when U commutes with 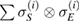 ,
,  is CP [4]. For such U, we have
is CP [4]. For such U, we have

which is a CP map. An interesting question is whether this result can be generalized to other U or whether we can find at least one U, for which the reduced dynamics  is not CP.
is not CP.
This question can be answered simply, using theorem 5. For an a within the positivity domain 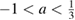 , we, first, choose four states
, we, first, choose four states 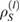 , which can span
, which can span 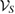 :
:

where  is an arbitrary real constant such that, for
is an arbitrary real constant such that, for 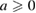 ,
,  , and for
, and for 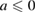 ,
,  . Therefore, from equation (16), we can construct the reference state
. Therefore, from equation (16), we can construct the reference state 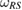 as
as

Next, using equations (31) and (36), we can construct four states 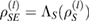 , which span
, which span  :
:

So, from equation (17), the reference state 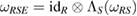 is
is

Third, we will show that the 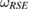 , in the above equation, is not a Markov state, as equation (25). For our case, where S is a qubit, there are only three possibilities for decomposing
, in the above equation, is not a Markov state, as equation (25). For our case, where S is a qubit, there are only three possibilities for decomposing 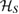 :
:  ,
, 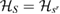 , and
, and  , where
, where  and
and  are 1D. Therefore, a tripartite state
are 1D. Therefore, a tripartite state 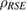 is a Markov state if it can be written as
is a Markov state if it can be written as  , where
, where 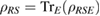 and
and  , or as
, or as 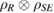 , where
, where 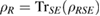 and
and 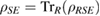 , or as
, or as

where 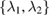 is a probability distribution,
is a probability distribution, 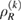 are states on
are states on 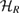 ,
, 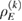 are states on
are states on 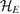 , and
, and 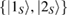 is an orthonormal basis for
is an orthonormal basis for 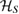 .
.
Now, from equation (39), we can verify simply that, for 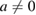 ,
,  can not be written as
can not be written as 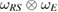 or
or  . (For a = 0, from equations (37) and (39), we see that
. (For a = 0, from equations (37) and (39), we see that 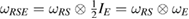 , i.e.
, i.e.  is a Markov state.)
is a Markov state.)
In addition, we cannot write  as equation (40). For a
as equation (40). For a  , which can be written as equation (40), we have
, which can be written as equation (40), we have
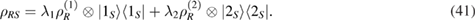
From equation (37), we see that 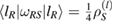 . On the other hand, if
. On the other hand, if 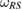 can be written as equation (41), we have
can be written as equation (41), we have
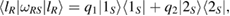
where 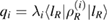 . So, all
. So, all 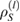 must commute with each other. But, from equation (36), we see that this is not the case. Therefore,
must commute with each other. But, from equation (36), we see that this is not the case. Therefore,  cannot be written as equation (40). Finally, we conclude that, for
cannot be written as equation (40). Finally, we conclude that, for 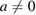 , the reference state
, the reference state  , in equation (39), is not a Markov state, as equation (25).
, in equation (39), is not a Markov state, as equation (25).
Theorem 5 states that the non-Markovianity of  leads to the non-CP-ness of the reduced dynamics, for, at least, one U. This is in agreement with the result of [2, 4]. In [4], a class of unitary operators as
leads to the non-CP-ness of the reduced dynamics, for, at least, one U. This is in agreement with the result of [2, 4]. In [4], a class of unitary operators as
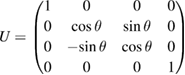
has been introduced, where, for some values of θ, the reduced dynamics of the system is non-CP [2, 4]. Note that, even if one shows that the non-CP-ness of the reduced dynamics, for the above U, is due to inappropriate choosing the assignment map  as equation (30), theorem 5 assures that there exists, at least, one other U, for which the reduced dynamics is non-CP, with any possible assignment map
as equation (30), theorem 5 assures that there exists, at least, one other U, for which the reduced dynamics is non-CP, with any possible assignment map 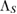 (with any possible reference state
(with any possible reference state  ).
).
It is also worth noting that the above example shows that, even when the reference state  is not a Markov state, the reduced dynamics can be CP for some (but not all) U, in our case, at least, all U which commute with
is not a Markov state, the reduced dynamics can be CP for some (but not all) U, in our case, at least, all U which commute with 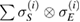 .
.
7. Summary
An straightforward way to construct a convex set of initial states of the system-environment 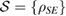 is to consider the set of steered states, from a reference state
is to consider the set of steered states, from a reference state 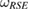 . In section 2, we have shown that if
. In section 2, we have shown that if 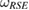 can be written as equation (7), then the reduced dynamics of the system is Hermitian. For the special case that the assignment map
can be written as equation (7), then the reduced dynamics of the system is Hermitian. For the special case that the assignment map 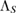 , in equation (7), is CP, the reduced dynamics is so CP. Interestingly, this includes all the previous results in this context, in [9–14].
, in equation (7), is CP, the reduced dynamics is so CP. Interestingly, this includes all the previous results in this context, in [9–14].
The convex set of initial states  is the starting point of the framework introduced in [2]. From this
is the starting point of the framework introduced in [2]. From this 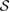 , we can construct the subspace
, we can construct the subspace  . Now, in section 3 (section 5), we have shown that
. Now, in section 3 (section 5), we have shown that 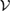 (
(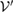 ) and
) and  can be written as the generalized steered sets, from the reference states
can be written as the generalized steered sets, from the reference states  and
and 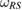 , in equations (16) and (17), respectively. The relation between
, in equations (16) and (17), respectively. The relation between 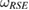 and
and 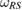 is as equation (7). Therefore, the steered set, from a reference state as equation (7), gives us the most general set (within the framework of [2]) for which the reduced dynamics is Hermitian.
is as equation (7). Therefore, the steered set, from a reference state as equation (7), gives us the most general set (within the framework of [2]) for which the reduced dynamics is Hermitian.
In addition, the evolution of the system-environment (system) states is given by the evolution of the reference state, in equation (19) (equation (21)). Interestingly, for a unitary evolution of the system-environment U, the reduced dynamics of the system is CP if and only if  can be written as equation (24), with a CP map
can be written as equation (24), with a CP map  .
.
This fact that we can construct reference state 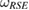 , for arbitrary U-consistent subspace, leads us to an important result, i.e. the generalization of the result of [13], to arbitrary
, for arbitrary U-consistent subspace, leads us to an important result, i.e. the generalization of the result of [13], to arbitrary  -consistent
-consistent 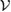 : the reduced dynamics of the system, for arbitrary system-environment unitary evolution U, is CP if and only if the reference state
: the reduced dynamics of the system, for arbitrary system-environment unitary evolution U, is CP if and only if the reference state 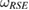 , in equation (17), is a Markov state, as equation (25).
, in equation (17), is a Markov state, as equation (25).
Finally, in section 6, we have considered the case studied in [4]. This example illustrates this result that when the reference state  is not a Markov state, then the reduced dynamics is non-CP, for at least one U. In addition, this example shows that, even when
is not a Markov state, then the reduced dynamics is non-CP, for at least one U. In addition, this example shows that, even when  is not a Markov state, the CP-ness of the reduced dynamics, for some (but not all) U, is possible.
is not a Markov state, the CP-ness of the reduced dynamics, for some (but not all) U, is possible.