The integral of complex variables on three defined contours

Complex variables have aroused strong interest in the community of mathematics in the past few decades. Our aim is to obtain the integral results of a particular equation $\begin{eqnarray}&&\begin{array}{ccc}{\rm{f}}({\rm{Z}})=\frac{{{\rm{z}}}^{3}+(1+2{{\rm{i}}){\rm{z}}}^{2}-7{\rm{z}}+1-2{\rm{i}}}{{{\rm{z}}}^{4}-1},\end{array}\end{eqnarray}$ in three defined contours. To determine the value of integral, the information we need to find is the residue values ABCD on four specific points and find out what residue values each contour includes. After finding the residue values and analysing four contours, we should use Cauchy integral formula to find the integral value. Firstly, by using the partial fraction to separate the equation into four independent parts, we obtain four values on each of the four fractions are the value of integral. Thus we can find exactly the four residue values, which are -1 on (1,0), 3 on (0,i), -2 on (-1.0) and 1 on (-I,0) as shown in the following expression.

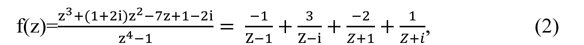$\begin{eqnarray}&&\begin{array}{ccc}{\rm{f(Z)=}}\frac{{{\rm{z}}}^{3}+(1+2{{\rm{i)z}}}^{2}-7{\rm{z+1}}-2{\rm{i}}}{{{\rm{z}}}^{4}-1}=\frac{-1}{{\rm{Z}}-1}+\frac{3}{{\rm{Z}}-{\rm{i}}}+\frac{-2}{Z+1}+\frac{1}{Z+i},\end{array}\end{eqnarray}$ and then we must analyse each contour and find out the residue values they include. By drawing a diagram of each of the three contours. We find that contour 1 contains A, contour 2 contains A and D, and contour 3 contains ABCD. The final step to obtaining the value of residue is to use Cauchy integral formula 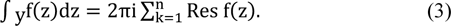$\begin{eqnarray}&&\displaystyle \int {}_{{\rm{y}}}{\rm{f}}({\rm{z}}){\rm{d}}{\rm{z}}=2\pi {\rm{i}}\displaystyle {\sum }_{{\rm{k}}=1}^{{\rm{n}}}{\rm{Res}}\,{\rm{f}}({\rm{z}})\begin{array}{ccc}.\end{array}\end{eqnarray}$ According to Cauchy integral formula, the value of integral of the equation on a specific contour is obtained by multiplying the sum of the residue values included in that contour by 2πi, the value of integral of the equation can be found as we now have all the necessary information. For the first contour 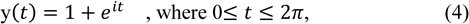$\begin{eqnarray}&&\begin{array}{ccc}{\rm{y}}(t)=1+{e}^{it}\,\,\,\,,\,{\rm{where}}\,0\le t\le 2\pi,\end{array}\end{eqnarray}$ the value of integral is calculated by using 2πi multiply by -1. We can get the result -2πi. For the second contour 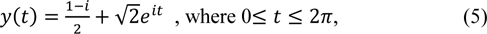$\begin{eqnarray}&&\begin{array}{ccc}y(t)=\frac{1-i}{2}+\sqrt{2}{e}^{it}\,\,,\,{\rm{where}}\,0\le t\le 2\pi,\end{array}\end{eqnarray}$ the value of integral is calculated by using 2πi multiply by the sum of -1 and 1. As we can see, the sum is 0. We can get the result 0. For the third contour 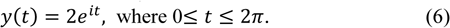$\begin{eqnarray}&&\begin{array}{ccc}y(t)=2{e}^{it},\,\,{\rm{where}}\,0\le t\le 2\pi,\end{array}\end{eqnarray}$ the value of integral is calculated by using 2πi multiply by the sum of -1,3, -2, and 1.

As we can see, the sum of these residue values 1. We can get the result 2πi. Hence all of the values of integral of the equation 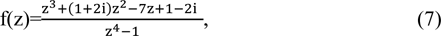$\begin{eqnarray}&&\begin{array}{ccc}{\rm{f}}({\rm{z}})=\frac{{{\rm{z}}}^{3}+(1+2{{\rm{i)z}}}^{2}-7{\rm{z}}+1-2{\rm{i}}}{{{\rm{z}}}^{4}-1},\end{array}\end{eqnarray}$ is found.