Statistical aspects of interface adhesion and detachment of hierarchically patterned structures

Our aim is the introduction of a hierarchical fuse network (HFN) model, inspired by hierarchical fiber bundle structures encountered in problems of biological material adhesion, for instance in the case of the gecko pad, where setae of lengths in the millimeter range are split into several encapsulated levels of microscopic and sub-microscopic spatulae, which effectively increase the adhesion surface area, specifically when contact with heterogeneous substrates is sought. While adhesion mechanisms ultimately reduce to the chemical nature of van der Waals interactions, which benefit from the increased surface area, it was noted in the past that the sparsity of contact patterns arising from the hierarchical organization plays a mechanical role in altering patterns of stress redistribution and arresting crack propagation [12]. This phenomenon has already been explored in network models of bulk fracture. The unique fracture behavior of those systems was found to originate from their hierarchical structure, and in particular from the fact that this structure entails structural gaps between hierarchically nested modules [9]. Unlike random, non-hierarchical structures, where gaps are exponentially distributed in size and thus characterized by minor fluctuations, in hierarchical structures gap size distributions are power-laws, as a result of the self-similar, multi-scale organization of the structure.

Following these lines, we build a 3D HFN model for adhesion as follows (figure 1). The N nodes in the network are distributed in three dimensional space as those of a cubic lattice of N = N_x × N_y × N_z nodes, with N_x = N_y = 2^H and N_z = 2 + H where H defines the number of hierarchical levels. Starting from the node layout, edges are added as a subset of all the possible edges in a perfect cubic lattice. In particular we refer to edges in the z direction as LC, as the load will be applied along that direction, while we define edges in the x and y directions as cross linking (CL). While all LC edges of a cubic lattice are retained, CL edges are selectively cut out depending on the distance from the interface, in order to mimic hierarchical contact and to produce a power-law size distribution of gaps. Our construction method for CL edges is shown in figure 1. Starting at level l = 0 (i.e. at the interface), no CL edges are present and LC edges effectively model adhesion forces. For levels l > 0 up, edges model cohesive interactions. Hierarchical organization is induced by cross-linking the edges at level l into bundles comprising 4^l nodes. At l = 1 + H the system is fully cross linked, while l = 2 + H identifies the top boundary. The resulting network is encoded by the adjacency matrix A, with generic element A_ij = 1 if there is an edge between nodes i and j, and A_ij = 0 otherwise. As discussed for similar 2D models, any form of reshuffling of LC edges that preserves the power-law distribution of gap sizes leads to similar mechanical behavior. For this reason, we restrict ourselves to the study of the deterministic variant introduced here and we compare its behavior to that of random reference non-hierarchical structures (RRN) of the same size where the LC edges are unchanged, while the CL edges of the hierarchical structure are randomly re-distributed across the system. For all systems, periodic boundary conditions are imposed in the x and y directions.

Zoom In Zoom Out Reset image size

We notice that our hierarchical network structure bears some similarity with hierarchical constructions, which have been proposed in the past with the aim of discretizing the Green's influence function of an isotropic, non-hierarchical elastic continuum, in the context of fiber-bundle models [30, 31]. In our case, instead, the hierarchical organization is a microstructural trait of the system.

To model adhesion and detachment properties, we consider the simple case in which the system is already in contact with the interface (l = 0) and is being peeled by a force acting on the top boundary. We model the elastic response of the system and its failure in the RFM framework. Each node i has a displacement-like variable V_i and each edge ij between nodes i and j carries a force-like variable I_ij . Since elastic variables are envisaged as scalars, elastic behavior is enforced by a scalar Hooke's law of the form

$$\begin{equation}{V}_{i}-{V}_{j}=r{I}_{ij},\end{equation} \tag{ 1 }$$

where the resistivity r > 0 corresponds to an elastic compliance of the edge connecting nodes i and j, and elastic equilibrium at each node i is imposed through the system of algebraic equations

$$\begin{equation}\sum\limits _{i=1}^{N}{A}_{ij}({V}_{i}-{V}_{j})=0,\end{equation} \tag{ 2 }$$

where we recall that N is the number of nodes and A_ij is the ij element of the adjacency matrix introduced above. In accordance with the literature, we refer to the displacement-like variables V_i as voltages, and to the force-like variables I_ij as currents, noting that the equations at hand also describe a network of resistors/fuses, subject to continuous electric loads. External loads in our uni-axial geometry can be applied in the form of voltages/displacements, e.g. applying V = 0 at the lower boundary and V = V* > 0 at the upper boundary, or in the form of currents/forces, by choosing V* such that the total current through any load perpendicular cross section of the systems equals a prescribed I*.

The elastic limit of each fuse ij is given by its current threshold t_ij and an extremal failure criterion, stating that ij is removed as soon as it carries a current I_ij > t_ij . Each network realization is characterized by a set of t_ij , extracted from a given threshold distribution P(t). We use different functional forms of P(t) in order to parametrize heterogeneity in the strength of the constituents of our system. In particular, we resort to Weibull distributions of the form

$$\begin{equation}P(t)=\frac{\beta }{\eta }{\left(\frac{t}{\eta }\right)}^{\beta -1}\mathrm{exp}\left[-{\left(\frac{t}{\eta }\right)}^{\beta }\right],\end{equation} \tag{ 3 }$$

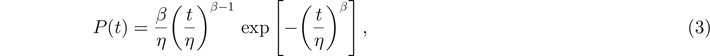
where we choose the scale variable η to control the average of P(t), and vary the shape parameter β in order to model systems of varying degrees of heterogeneity, with larger β corresponding to narrower distributions and less heterogeneity. For comparison with results available in the literature, we also consider the case of a uniform P(t) in the 0 < t < 1 range, which describes systems of high heterogeneity. While a uniform distribution of threshold presents some similarities with the β ≈ 1 case as both allow large fluctuations, it also differs substantially from it because such fluctuations have an upper bound in t = 1.

Since we are interested in the adhesion properties of our model materials, we observe that edges at the interface (i.e. connecting nodes at l = 0 to nodes at l = 1) and in the bulk have substantially different physical origins and may thus be characterized by different choices of P(t). In particular, for interface edges the average of β controls the average adhesive force, while in the bulk it rather controls average material strength. Similarly, low values of β at the interface express high degrees of interface heterogeneity, whereas in the bulk they point to high degrees of randomness within the material. Given the exploratory nature of our study, we make the following modeling assumptions, which allow for the smallest number of free parameters:

• Since we are interested in adhesion properties, characteristic thresholds in the bulk are considered to be significantly higher than at the interface, so that edges in the bulk do not fail;
• Since failure is limited to the interface, we can choose η such that the average of P(t) is 1 without loss of generality; the only free parameter is thus the parameter β which controls the scatter of failure thresholds of interface edges, i.e. the interface heterogeneity.

We run different sets of simulations for different systems (HFN and RRN) and different choices of P(i) (figure 2). We choose the standard quasi-static simulation procedure, where a constant voltage difference ΔV = 1 is applied between the top and bottom boundaries. At every step, equations (2) are solved, edge-wise currents are computed, the edge carrying the maximum ρ_max = max_i,j (I_ij /t_ij ) is identified as the weakest and removed. The global I and V are rescaled by the factor ρ_max, thus setting the current to the precise value when the weakest edge fails. While this method describes an idealized protocol, where at every step I and V are adjusted to the minimum values allowing for the removal of the weakest link, more realistic protocols in which V is controlled can be obtained by enveloping the resulting I–V curves, producing the equivalent of stress–strain curves in displacement- or force controlled experiments. The highest value of I in an I–V curve is the peak load (or peak current) I_p. We denote its corresponding voltage as V_p.

Zoom In Zoom Out Reset image size

Unless otherwise specified, we consider systems of size N_x = 128, resulting in E ≈ 3 × 10⁵ edges, ${N}_{x}^{2}=16\enspace 384$ of which are subject to our failure criterion (i.e. breakable). This choice allows for reasonable run-times at the supercomputing facilities at our institution, ensuring at least 800 realizations for each system/parameter choice.

We use our simulation results to characterize failure of hierarchical materials at interfaces of varying heterogeneity, in comparison to equivalent, non-hierarchical systems. We focus on two specific aspects of failure, namely material strength and crack morphology.

To quantify strength, we look at the peak current I_p, averaged over all realizations of a specific set of parameters, and the work of failure W_f, i.e. the average area below the V-control envelope of each of the I–V curves. I_p points to the maximum load that a structure can carry and provides an adequate strength descriptor for very brittle materials with little post-peak resistance. W_f on the other hand quantifies the energy that is necessary to reach failure, including the post-peak regime.

Regarding crack morphology, we note that under our assumptions cracks are constrained to the interface plane l = 0. An interface crack can then be envisaged as a connected cluster of failed edges in the interface plane. To identify the failure mode for every system, we analyze the statistics of crack sizes s, measured as connected component sizes, using a breadth-first algorithm. In systems where failure occurs by nucleation and propagation of a critical crack, we expect the system to display traits of scale invariance when approaching I_p. In analogy with similar scale invariant traits in avalanche size statistics [16, 32], we expect that in voltage controlled simulations for V < V_p crack areas s are distributed according to truncated power-laws of the form

$$\begin{equation}P(s)=\mathcal{N}{s}^{-\tau }\enspace \mathrm{exp}\left[-\frac{s}{{s}_{0}}{\left(1-\frac{V}{{V}_{\mathrm{p}}}\right)}^{\frac{1}{\sigma }}\right],\end{equation} \tag{ 4 }$$

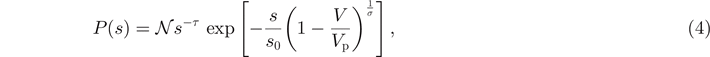
where τ is the exponent of the power-law distribution, 1/σ controls the exponential cutoff, s₀ is a scale factor, and 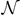$\mathcal{N}$ is a normalization constant. In a system exhibiting this behavior, for V > V_p a single giant crack takes over the failure process, driven by the stress concentrations in the fracture process zone. This critical-like scenario is also identifiable by looking at the sizes of the largest and second largest crack, s₁(f) and s₂(f), as functions of the fraction f of removed links. If a critical crack emerges at f_p corresponding to I_p, s₁(f_p) exhibits a rapid increase, while s₂(f_p) displays a peak. If failure is instead dominated by crack nucleation, a behavior displayed for instance by non-hierarchical systems with low interface disorder (β ≫ 1), systems break upon sudden expansion of an individual crack exceeding a threshold size. In that case, once the critical crack is formed, its size s₁(f) increases in direct proportion with the fraction f of removed links since the other cracks cease to grow.

Figure 3 shows interface voltage patterns in typical simulations of HFN and RRN structures, with uniform threshold distributions and same number of removed edges. The HFN patterns correspond to a configuration encountered at peak load I_p. The RRN patterns are those obtained at a loading stage where the number of removed edges is the same as that of the HFN case. For comparison purposes, voltages are measured in units of the respective applied voltages, so that V = 1 is their upper bound. Brighter colors indicate higher voltages and detached areas. Unlike random reference structures (RRN), HFN prevent the formation of a single critical crack. This type of behavior, which we can define as distributed damage, is also observed in 2D models of bulk fracture [9]. Our aim here is to explore how general this behavior is in the case of adhesion, and how it is affected by variations in interface heterogeneity.

Zoom In Zoom Out Reset image size

A first quantitative look at the effects of the hierarchical network structure on the properties of adhesion is provided by figure 2, where we show typical single-realization I–V curves for varying degrees of interface heterogeneity. We denote by V_p the voltage where I_p is attained. In a voltage control scenario, where the I–V curve is given by the envelope of the quasi-static simulation data (thick lines in figure 2), HFN display significant post-peak activity, while RRN fail immediately at I_p—or after a minor post-peak regime, as for β = 1.5. For low interface heterogeneity (bottom row), by contrast, there are only minor differences in the voltage-control envelopes of HFN and RRN, although the distribution of points below the enveloping curve points to a radically different failure mode, which is borne out by the differences in crack morphology.

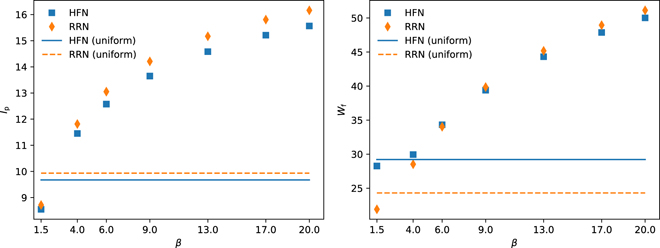
The effects of post-peak activity on HFN adhesion are evident in figure 4, where we show the peak current I_p and the work of failure W_f for different degrees of heterogeneity. For high interface disorder, HFN systematically exhibit higher W_f than their RRN counterparts. As expected from figure 2, this effect disappears at low disorder. For comparison, we show the same results, this time for I_p, and in this case the differences are minimal and slightly in favor of the non-hierarchical case, especially for low levels of interface disorder. The most significant differences between the two cases, at least in voltage-control simulations that sample the area of the I–V curve, occur because of the post-peak regime, which only the hierarchical systems display.

Zoom In Zoom Out Reset image size

We now investigate the effects of the hierarchical structure on the statistics of interface crack sizes, as a way to quantify the observation of distributed damage and relate it to the degree of interface disorder. Figure 5 shows the dependency of the areas of the two largest cracks, give in units of system size, on the fraction of removed edges (damage fraction). We first discuss the behavior of the RRN seen in figure 5 (right). Here we observe see two qualitatively different types of behavior: at low disorder (threshold distributions with β = 4 and β = 9), we see a nucleation-and-growth scenario where the behavior of the system is entirely dominated by the largest crack. After a short initial interval of diffuse damage accumulation which becomes shorter with decreasing disorder, the largest crack becomes critical and its growth attracts all the newly failing edges, leading to a linear dependency of the largest crack size s₁ on the failed-edge fraction. At the same time, the size s₂ of the second largest crack is, in comparison, negligible. At high disorder (β = 1.5 and uniform threshold distribution), on the other hand, we find a percolation-like scenario where, at a critical damage fraction, the size s₁ of the largest crack increases rapidly while the size s₂ of the second-largest crack reaches a maximum (i.e. it first increases, then decreases because of coalescence with the largest crack).

Zoom In Zoom Out Reset image size

In HFN, on the other side, the nucleation-and-growth scenario is entirely absent. Here we see for all degrees of disorder a percolation-like scenario: the largest crack exhibits nonlinear growth behavior where an acceleration of growth coincides with a peak in the size of the second-largest crack.

We next investigate how the different behavior of HFN and RRN is reflected in the crack size distributions and their evolution. At high disorder (β = 1.5 and uniform distribution), differences in crack area statistics of HFN and RRN appear to be minor. Both types of structures seem to follow a critical-like scenario where the crack size distribution is well described by equation (4) with crack size exponent τ = 2 and 1/σ ≈ 1.4...1.7. In the systems showing appreciable post-peak activity (HFN and RRN with β = 1.5), the scale-free distribution persists without discernible cut-off into the post-peak regime. This is illustrated in figures 6 and 7, which also show typical damage patterns immediately past the peak load.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

The main difference between the uniform and the β = 1.5 Weibull distributions shows in the post-peak regime. In this regime, the damage patterns and crack size distributions in HFN are insensitive to the threshold distribution, whereas the failure mode of RRN depends on the high-strength tail of the threshold distribution. For a uniform distribution, there is a maximum strength and the failure mode of RRN is by crack nucleation-and-growth. For a Weibull distribution of low exponent, on the other hand, fuses with high local failure thresholds in the distribution tail act as pins that promote crack arrest, and failure therefore proceeds by diffuse damage accumulation. We see that this behavior has, despite the apparent similarities, different causes in RRN and HFN: in the non hierarchical structures, crack arrest is dependent on the strength tail asymptotics, whereas in the hierarchical networks it represents a generic structural feature that does not depend at all on the statistics of local strength.

As expected from connected components analysis, the behavior of HFN in the low disorder limit differs strongly from their RRN counterparts (figures 8 and 9). RRN display extremely narrow crack area distributions, in agreement with the expectation of failure by crack nucleation-and-growth. The behavior in the approach to failure can be fitted by equation (4) but the scaling regimes are very limited and the distributions approach pure exponentials. HFN, instead, seem to induce scale free fracture patterns even below the peak load. These self similar patterns appear as power-law crack area distributions with continuously varying exponents that decrease towards the peak load—a behavior also observed in bulk failure of HFN [9]. While the system does possess structural network heterogeneity in the bulk, the interface initially has no structural heterogeneity and very low fluctuations in the local thresholds. The fact that broad distributions of crack areas emerge regardless thus points to a novel mechanism where crack patterns are mediated exclusively by the mechanism of stress redistribution in the bulk.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size