Emergence of clones in sexual populations

Sexual reproduction mixes the genetic material from two parents and thereby produces new genotypes from existing genetic variation. To account for recombination, we modify the equation describing the evolution of genotypes as follows:

$$\begin{eqnarray} &&\dot {n}(g)=(F(g)-\langle F\rangle )n(g)+r\left [{N}^{-1}\mathop{\sum }\limits _{{g}^{\prime},{g}^{\prime\prime}}K(g\vert {g}^{\prime},{g}^{\prime\prime})n({g}^{\prime})n({g}^{\prime\prime})-n(g)\right ] \end{eqnarray} \tag{ 5 }$$

where n(g) is the number of individuals with genome g, and K(g|g',g'') accounts for the probability that genotype g is assembled by recombination from the parental genotypes g' and g''. In the absence of recombination, the only relevant characteristic of a genotype is its fitness, and we could study the evolution of the population along the fitness coordinate instead of on the hypercube of possible genotypes. To achieve a similar simplification with recombination we need to know how the fitness of recombinant offspring relates to that of the parents to map equation (5). The correlation between parental and offspring traits is known as heritability and depends on the underlying genetic architecture. If a trait depends on many loci in the genome in an additive manner, i.e., different loci make independent contributions to the trait, the trait value of offspring will be approximately Gaussian distributed around the parental mean. Such traits are called highly heritable since the correlation between trait values of parents and offspring is high. Conversely, if a trait depends on specific combinations of alleles at many loci (epistasis), these combinations will be disrupted with high probability in sexual reproduction. Such traits have a low heritability in sexual reproduction since the correlation between parents and offspring is low.

The trait we are mainly interested in here is fitness, which in general involves many phenotypes and depends on the environment. We shall set aside the issues associated with fluctuating environment and possible time dependence of selection, and focus on how fitness depends on the genotype. As already noted, the genotype space is a high dimensional hypercube, g = (s₁,...,s_L), and for present purposes, the fitness is a complicated (but fixed) function of the genotype parameterized as

$$\begin{eqnarray} &&F(g)={f}_{0}+\mathop{\sum }\limits _{i}{f}_{i}{\mathbf{s}}_{i}+\mathop{\sum }\limits _{i\lt j}{f}_{i j}{\mathbf{s}}_{i}{\mathbf{s}}_{j}+\cdots , \end{eqnarray} \tag{ 6 }$$

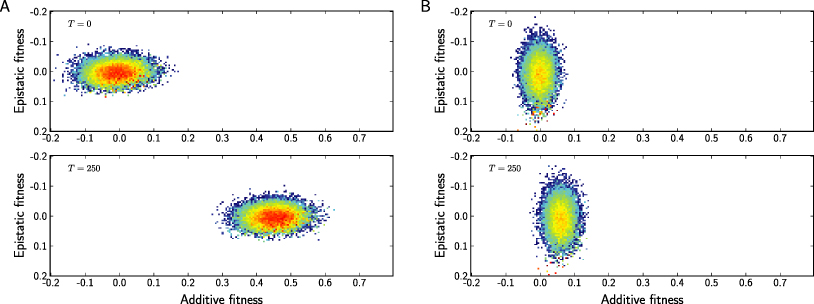
where the terms f_is_i define the additive contribution of locus i to fitness, while higher order terms correspond to epistatic interactions. The relation of the fitness of an offspring relative to that of its parents and the density of states, i.e., the distribution of fitness over all possible genomes, is illustrated in figure 2.

Zoom In Zoom Out Reset image size

The higher the order of the interactions, the less likely it is that a particular set of loci that contributes to one parent is inherited uninterrupted. As a consequence, the heritability of interaction terms goes down with increasing order. Interaction terms of high order are essentially independent of the parents. This is reminiscent of high order spin-glass models, where the energies of any two configurations that differ at a macroscopic number of spins are uncorrelated. The large p limit of such p-spin glasses is the random energy model, where the energy of each configuration is an independent draw from a Gaussian distribution [8, 13].

At large r, this model admits a factorized solution P(A,E) = ϑ(A,t)ω(E) with

$$\begin{eqnarray} &&\vartheta (A,t)=\frac{{\mathrm{e}}^{-(A-{\sigma }_{A}t)^{2}/2{\sigma }_{A}^{2}}}{\sqrt{2 \pi {\sigma }_{A}^{2}}}\tqs \mathrm{and}\tqs \omega (E)=\frac{r}{r-\langle E\rangle -E}\frac{{\mathrm{e}}^{-{E}^{2}/2{\sigma }_{E}^{2}}}{\sqrt{2 \pi {\sigma }_{E}^{2}}} \end{eqnarray} \tag{ 10 }$$

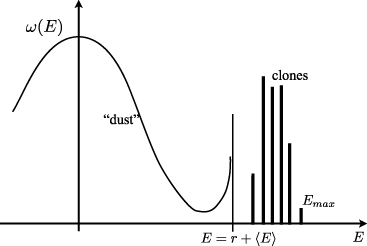
derived in [29]. This solution travels towards higher additive fitness with a velocity equal to the variance of the additive fitness of recombinant offspring, while the epistatic fitness has a steady distribution, where 〈E〉 adjusts itself to normalize the distribution. This factorization is a hallmark of quasi-linkage equilibrium [17, 27, 43], where additive components evolve independently, while epistatic components are in a quasi-steady balance between selection and recombination. However, this factorized solution breaks down as soon as there are individuals with epistatic fitness larger than r + 〈E〉. In that case this solution is no longer normalizable, and additive and epistatic components cease to be independent.

Figure 5 illustrates this condensation behavior. The smooth distribution ω(E) is a deformed Gaussian which diverges at E = r + 〈E〉. Beyond r + 〈E〉, the population consists of growing clones whose size depends on when and where they were seeded.

Zoom In Zoom Out Reset image size

In the following we will characterize the population structure and study how the velocity in the direction of increasing additive fitness depends on parameters. We will begin by studying the purely epistatic case with recombination, which extends the REM by continuous seeding of novel recombinant genotypes. We will then study the condensation phenomenon in the presence of additive fitness, where the population forms a traveling pulse in fitness.

Suppose we start with a diverse sample of size N from the distribution of epistatic fitness and inject new recombinant genotypes with rate Nr. After a time t, the population consists of N initial clones and a Poisson distributed number of new clones. A clone of age τ_i and fitness F_i = E_i will have approximately size

$$\begin{eqnarray} &&{n}_{i}(t)={\mathrm{e}}^{({E}_{i}-r){\tau }_{i}+\int \nolimits _{t-{\tau }_{i}}^{t}\mathrm{d}{t}^{\prime}\hspace{0.167em} \langle E\rangle _{{t}^{\prime}}}, \end{eqnarray} \tag{ 11 }$$

where the mean fitness 〈E〉_t' can be thought of as a Lagrange parameter that keeps the overall population size constant. To calculate 〈Y_t(r,h)〉 we have to average over the fitness of the N initial clones and over the fitnesses and seeding times of all subsequently produced recombinant genotypes:

$$\begin{eqnarray} &&\fl \langle {Y}_{t}(r,h)\rangle =\int \mathrm{d}z\;z\left [N{B}_{0}(z)+\sum _{k=1}^{\infty }\frac{{\mathrm{e}}^{-N r t}}{k !}k{B}_{r}(z)\right ][1-{C}_{0}(z)]^{N}{C}_{r}(z)^{k-1}, \end{eqnarray} \tag{ 12 }$$

where B₀(z) is the average of ${n}_{i}^{2}(t)\hspace{0.167em} {\mathrm{e}}^{-z{n}_{i}(t)}$ over the E_i of initial genotypes (note that 'initial' means that τ_i = t). B_r(z) is the corresponding average over recombinant clones, which in addition are averaged over their age τ_i; see appendix A for derivation. Similarly, C₀(z) and C_r(z) are averages of e^−zn_i(t) over the E_i and τ_i. The sum over k—the number of recombinants generated in time t—can be performed easily. These integrals are evaluated in the appendix B in the limit of large N. One obtains an approximation

$$\begin{eqnarray} &&\langle {Y}_{t}(r,0)\rangle \approx \exp [-N \hspace{0.167em} {\mathrm{e}}^{-\sqrt{2\log N}[1-(r/{r}_{\mathrm{c}})]t \sigma }] \end{eqnarray} \tag{ 13 }$$

valid for r ∼ r_c, with

$$\begin{eqnarray} &&{r}_{\mathrm{c}}\approx \sigma \sqrt{2\log N}. \end{eqnarray} \tag{ 14 }$$

We observe that the participation ratio substantially deviates from zero only for r < r_c and only upon reaching t > t_c(r), where for r ≈ r_c

$$\begin{eqnarray} &&{t}_{\mathrm{c}}(r)={\sigma }^{-1}\frac{\sqrt{\frac{1}{2}\log N}}{1-\frac{r}{{r}_{\mathrm{c}}}}=\frac{{t}_{\mathrm{c}}(0)}{2}\frac{{r}_{\mathrm{c}}}{{r}_{\mathrm{c}}-r}. \end{eqnarray} \tag{ 15 }$$

This provides us with estimates of the critical time of condensation t_c(r) and the critical r_c below which condensation occurs. Condensation is delayed compared to the case of r = 0 and the critical time (analogous to inverse critical temperature) diverges as the recombination rate approaches its critical value r_c. Of course, this divergence only occurs in the limit of $\sqrt{\log N}$ going to infinity. In practice, with realistic population sizes N, one observes not a transition, but merely a crossover between different regimes of behavior. More elaborate expressions for t_c and r_c at finite N can be found in appendix B. Note that the values of t_c and r_c themselves scale with the square root of the logarithm of N.

〈Y_t(r,0)〉 is shown in figure 6(A) for different recombination rates. With increasing recombination rate, the early plateau of 〈Y_t(r,0)〉 is reduced and condensation is delayed. Each individual run condenses rapidly once the dominant clone is large enough that it often recombines with itself, which leaves the genotype intact. Also, the lack of condensation for r > r_c is clearly seen. Figure 6(B) shows the inverse time to condensation for different recombination rates and population sizes, confirming equation (15) for r ≈ r_c. This transition with increasing r was identified in [29]. Intuitively, the divergence of the time to condensation is due to the fact that the growth rate of best genotypes decreases with increasing recombination load r. As soon as E − r is smaller than zero for all existing genotypes, all clones are short lived and no condensation can occur. Similar behavior has been observed in populations with heterozygote advantage or disadvantage [1, 11].

Zoom In Zoom Out Reset image size

Population dynamics for r < r_c, including t > t_c, has the nature of a 'records process' [20, 40]. As time progresses, more and more genotypes are sampled from the density of states and tested by selection. As a consequence, the population will come across fitter and fitter genotypes, resulting in a record process with Nrt trials. Even if initially no genotype with E − r > 0 is present, such a genotype will eventually be found and result in condensation. On the other hand, any finite population will eventually reach a final 'record' (with fitness E_f), giving rise to the clone that will eventually take over the whole population. This is because a clone rapidly fixates once it is large enough to frequently recombine with itself. To prevent its fixation a new record would have to be created with the fitness advantage ΔE > τ(E_f−r)²/logN within the time delay of τ, which is very unlikely beyond a certain E_f.

In the opposite limit when h² = 1, the population moves towards higher fitness with a velocity that is given by the additive variance $v={\sigma }_{A}^{2}$ for sufficiently large r. It will be useful to parameterize the ratio between the velocity v and the scale of selection σ² as γ = v/σ². At high recombination rates, we have γ = h², while we generally expect γ < h² at low recombination rates. In contrast to the case h² = 0, no aging dynamics is observed for h² > 0. Instead, old genotypes are constantly replaced, and dominant genotypes in the population have a finite characteristic age. Hence the initial genotypes are rapidly forgotten and we can restrict the analysis to recombinant genotypes.

Genotypes seeded at the high fitness nose of the population distribution can grow large and dominate the participation ratio 〈Y〉. Since 〈Y〉 is closely related to the rate of coalescence, it is instructive to calculate 〈Y〉 explicitly assuming v = σ² before considering the case v < σ² at low r or h² < 0.

In the steady state, a clone is specified by its age τ_j and its initial fitness A_j. Assuming v = σ², we then find

$$\begin{eqnarray} &&{n}_{j}=\exp \left [({A}_{j}-r){\tau }_{j}-\frac{v{\tau }_{j}^{2}}{2}\right ]. \end{eqnarray} \tag{ 16 }$$

To evaluate 〈Y(r,1)〉, we have to evaluate the integrals B_r(z) and C_r(z) that appear in equation (12) and are defined in the appendix A, see equation (A.9). The integrals involve averaging over the initial fitness A_i and all possible ages τ_i. For h² = γ = 1, one finds C_r(z) ≈ z because relatively young and small clones dominate. In contrast, B_r(z) has a significant contribution from rare old clones, which dominate because of their large size (through the ${n}_{i}^{2}$ factor). The evaluation of the integrals is detailed in appendix C with the result equation (C.5). We obtain

$$\begin{eqnarray} &&{B}_{r}(z)\approx \alpha +{z}^{-1}\hspace{0.167em} \exp \left [-\frac{r}{\sigma }\sqrt{2\log {z}^{-1}}-\frac{{r}^{2}}{2{\sigma }^{2}}\right ]\Gamma \left (-\frac{r}{\sigma \sqrt{2\log {z}^{-1}}}\right ). \end{eqnarray} \tag{ 17 }$$

The first term is of order 1 and corresponds to the contribution of young clones. Its exact value depends on the details of the stochastic dynamics, such as the offspring distribution. The second term is the contribution from old large clones. The participation ratio therefore becomes

$$\begin{eqnarray} \fl \langle Y(r,1)\rangle &\approx &N\int \nolimits _{0}^{\infty }\mathrm{d}z\;{B}_{r}(z)\hspace{0.167em} {\mathrm{e}}^{-N z}\nonumber\\ \fl &\sim &\left \{ \begin{array}{@{}ll@{}} \displaystyle \alpha {N}^{-1}\tqs &\displaystyle r/\sigma \gt (\sqrt{2}-1)\sqrt{2\log N \sigma }\\ \displaystyle \exp \left [-\frac{r}{\sigma }\sqrt{2\log N \sigma }-\frac{{r}^{2}}{2{\sigma }^{2}}\right ]\tqs &\displaystyle r/\sigma \lt (\sqrt{2}-1)\sqrt{2\log N \sigma }~. \end{array}\right. \end{eqnarray} \tag{ 18 }$$

For small r, 〈Y(r,1)〉 does not scale as N⁻¹. In other words, the larger the population is, the larger are the clones it is composed of, and those largest clones dominate 〈Y〉. This result is in agreement with arguments made for rapid coalescence in facultatively sexual populations in [30, 36, 37]. Figure 7(A) shows 〈NY(r)〉 as a function of $r/\sqrt{2{\sigma }^{2}\log N \sigma }$. As soon as $r/\sqrt{2{\sigma }^{2}\log N \sigma }\lt 0.4$, Y(r) increases and no longer scales with N, as predicted by the mean field calculation above. The figure also shows the explicit expression in equation (18) as dashed lines. Note, however, that the calculation of 〈Y(r,1)〉 involved several approximations where $\sqrt{2\log N}$ was assumed large. As a result, the accuracy of the prefactor is low, and we have dropped all non-exponential parts, while enforcing 〈Y(r,1)〉 = 1/N at the crossover.

Zoom In Zoom Out Reset image size

The derivation above is valid for $r{\sigma }^{-1}\sqrt{2\log N \sigma }\gt 1$. For smaller r, the velocity drops below the high recombination limit, γ = 1, and the fitness distribution in the population stops being Gaussian. In this regime, the velocity has to be calculated self-consistently by matching the rate of production of new extremely fit clones to the overall velocity of the population. This problem has been studied by Rouzine and Coffin [35, 37] in the context of HIV evolution.

A simplified version of the arguments of Rouzine and Coffin [35] is given in appendix D. With γ = v/σ², we find

$$\begin{eqnarray} &&1-\gamma =\frac{\log [\frac{\sigma }{r}\sqrt{2(1-\gamma )}]}{\log [\frac{\sigma }{r}\sqrt{2(1-\gamma )}]+\log [{\gamma }^{-1}r N]}. \end{eqnarray} \tag{ 19 }$$

This implicit equation for γ can either be solved numerically or, in the case of very small r, iteratively. The result is similar to that obtained by Rouzine and Coffin [35]; differences are due to the difference in the model used. The numerical solution is compared to simulation data in figure 7(B). Convergence with increasing N is slow and equation (19) has a solution only for small r, for which we have little data.

The velocity of the traveling wave falls below σ² as soon as a few large clones dominate the population. In this case, not only B_r(z,h) but also C_r(z,h) are dominated by those large clones, and 〈Y(r,h)〉 behaves differently. We show in the appendix that 〈Y(r,h)〉 ∼ 1 − γ is of order 1 (see equation (C.7)). This is in agreement with [35], who found that the typical number of large clones is ∼logrNσ ∼ Y(r,h)⁻¹.

In the high recombination limit, the population moves towards higher fitness with velocity $v={\sigma }_{A}^{2}$ regardless of any epistatic fitness contributions. However, we have seen above that a clonal structure can emerge even in the absence of epistasis if recombination rates are low enough. Intuition and the simulation in figure 4 show us that this clonal structure is more pronounced in the presence of epistasis and persists at high recombination rates.

The reason for this behavior is the fact that the fitness variance of the recombinant offspring is larger than the velocity $v={\sigma }_{A}^{2}\lt {\sigma }^{2}$. In this case, fit genotypes grow above the traveling Gaussian envelope and generate macroscopic clones.

Figure 4 shows that, at low recombination rate and heritability, the population is always dominated by a few large clones with high non-heritable fitness components, which produce a large number of (on average) non-fit offspring. Rarely, such offspring are very fit, and replace their predecessors. The probability that offspring are fitter than their parents, and with it the velocity, increases dramatically with h² and r. Conversely, the size of the fit clones and the participation fraction decreases with h² and r. Simulation results for Y and v in the steady state are shown in figure 8 for different values of h² and r. In the following, we will rationalize and quantify the observed behavior. To begin with, we will assume a constant velocity and calculate Y. Again, these calculations are detailed in appendix C.

Zoom In Zoom Out Reset image size

After successful establishment, a clone will grow approximately deterministically according to

$$\begin{eqnarray} &&\frac{{\dot {n}}_{j}}{{n}_{j}}={F}_{j}-r-v{\tau }_{j}-\langle E\rangle \end{eqnarray} \tag{ 20 }$$

where F_j = A_j + E_j is the sum of the additive fitness A_j, measured relative to vt when the clone was born, and E_j is the epistatic fitness. The advancing mean additive fitness is accounted for by vτ_j, while 〈E〉 is the mean epistatic fitness. The size of the clone peaks at age ${\tau }_{j}^{\ast }=({F}_{j}-\tilde {r})/v$ (where we have defined $\tilde {r}=r+\langle E\rangle$) and then decreases until the clone disappears. The maximal size of the clone is ${n}_{j}^{\max }\sim {\mathrm{e}}^{-({F}_{j}-\tilde {r})^{2}/2 v}$. Since the fittest genotypes in the population have a fitness $\sqrt{2\log N}$ above the mean, they grow larger than N if

$$\begin{eqnarray} &&\tilde {r}\lt {r}^{\ast }=\sigma (1-\sqrt{\gamma })\sqrt{2\log N \sigma }~, \end{eqnarray} \tag{ 21 }$$

which gives us a first indication of the breakdown of the mean field solution, where $v={\sigma }_{A}^{2}$. We confirm this again by calculating the integrals C_r(z,v) and B_r(z,v) in appendix C; see equation (C.4).

Furthermore, we calculate 〈Y(r,h²)〉 in appendix C and find that 〈Y(r,h²)〉 starts to be larger than N⁻¹ as soon as

$$\begin{eqnarray} &&\tilde {r}\lt {r}_{\mathrm{c}}=\sigma (\sqrt{2}-\sqrt{\gamma })\sqrt{2\log N \sigma }. \end{eqnarray} \tag{ 22 }$$

These two conditions on $\tilde {r}$ define two critical recombination rates r_c and r* at which different features of the mean field solution break down. Note, however, that this expression is not valid close to v = 0, since we have assumed a traveling wave with clones of finite lifetime.

Both of these two lines seem to play an important role in the behavior of the population. Between the two lines, we observe a coexistence between condensed populations and non-condensed populations, which results in large fluctuations of Y(t). An example trajectory of Y(t) is shown in figure 9. For a limited amount of time, the population is condensed with large Y and does not move in the additive direction. It then becomes unstuck and adapts for a while before getting stuck again. The time average of Y is dominated by these intermittent condensates in this meta-stable region and is larger than N⁻¹ as soon as $r\lt {r}_{\mathrm{c}}=\sigma (\sqrt{2}-\sqrt{\gamma })\sqrt{2\log N}$. Good simulation evidence for the different transition lines, however, is difficult to obtain because of substantial sub-leading corrections.

To investigate the model in the absence of this stick–slip behavior, we simulated a variant of the model where additive fitness is drawn from a distribution that steadily moves towards higher fitness with velocity v, as is assumed in the calculations. The time averaged 〈Y(r,h)〉 is shown in figure 9(B) and compared to the predicted onset of condensation by equation (C.7) (black lines).

Zoom In Zoom Out Reset image size

Correlations between different parts of the genome are usually referred to as linkage disequilibrium, suggesting that due to genetic linkage, i.e., a high probability of coinheritance, the allele frequencies at different loci are not independent. Here, we have used a different measure to characterize correlations in the population. Instead of looking at correlations between individual loci, we have characterized the distribution of clone sizes, or equivalently haplotype frequencies, in adapting populations. Our analysis is not restricted to additive fitness functions, but we have also analyzed a simple model where fitness is partly heritable and partly random.

While macroscopic condensation, 〈Y_∞〉 ∼ (1), sets in only for $r\lt \sigma /\sqrt{2\log N \sigma }$ in the absence of epistasis, we observe condensation of the population at recombination rates of order σ in presence of epistasis. Here, σ is the standard deviation in fitness and sets the strength of selection. The reason for this behavior is the fact that the velocity at which the population adapts is smaller than the fitness variance of the recombinant offspring. The additional epistatic variance allows the seeding of new clones far ahead of the population mean, which is only slowly catching up. Hence fit clones can out-grow any traveling Gaussian. At the same time, condensed clones cause the average epistatic fitness to be significantly greater than 0. Since this epistatic fitness is lost upon outcrossing, the population has a tendency to partition into a few fit clones with high epistatic fitness and a large number of recombinant genotypes with random epistatic fitness. This coexistence between 'condensed' and 'dust' phases is seen in figure 4 in the panels on the right. As long as the heritability, i.e., the fraction of additive variance, is larger than zero, the population seeds new clones even at low recombination rates and the rate of coalescence will be given by 〈Y〉 times the characteristic turn-over rate of clones.

In the absence of any additive variance, the observed behavior is quite different. In this case, the fitness function is completely random (a.k.a. House-of-cards model [18], or random epistasis/energy model [8, 29]). The only way the population adapts is by sampling fitter and fitter individuals from the same distribution. In other words, the population dynamics amounts to a record process where the total number of samples taken increases as N(1 + rt). Records establish and grow with the rate E − 〈E〉 − r. One additional complication that is of particular importance in the case h² = 0 is the fact that whenever a clone recombines with itself, it does not generate a novel genotype. This has the tendency to shut off recombination and stabilize clones as soon as they grow large, resulting in a rapid loss of genetic diversity. In a previous publication [29], some of us have studied the onset of condensation in a more descriptive manner. Here, we have extended this work by explicitly calculating Y, both during an initial transient as well as in a steady state where variance is maintained.

The model we have used is extremely simplistic, and one might wonder about its relation to real world populations. Nevertheless, it accounts for a number of features of real populations such as heritabilities between 0 and 1, outcrossing, and mimics a large number of loci in the sense of quantitative genetics. These features give rise to qualitatively different dynamical regimes, which will also be observable in more realistic models. Some facultatively sexual populations are in fact remarkably close to this simple 'E and A' model. Many plants and microbial populations are facultative outcrossers. In the event of outcrossing, a large number of crossovers on many chromosomes produces many independently inherited genomic segments. HIV, for example, recombines via template switching following coinfection at an outcrossing rate of a few per cent [3, 28]. In each of these outcrossing events, roughly 10 crossovers are observed [21]. If populations are polymorphic at many loci, the resulting offspring distribution is approximately described by equation (7). We have made a further simplification by assuming that the fitness of a recombinant offspring is independent of its parents and simply drawn from a comoving distribution. This assumption is expected to approximate recombination processes where the offspring and parent fitness decorrelate rapidly over a few outcrossing events, as for example in equation (7) [32]. Note, however, that loci close together on the chromosome decorrelate only slowly.

The other dramatic simplification made above was the partitioning of fitness into additive and random components corresponding to high order epistatic interactions. More generally we expect to find epistatic interactions of various orders, which are heritable to different extents. However, the 'E and A' model should not be thought of as a parameterization of the genotype fitness map, but rather as a partitioning into variance that can be explained by the best fitting additive model, and the remaining variance [10, 27]. The best fitting additive model is in general time dependent, and the heritability can change as the allele frequencies change [44]. We know rather little about the genetic architecture of fitness, which justifies the use of such simple models. In specific scenarios where the genotype–phenotype map is known, more detailed modeling should be guided by the general conclusions drawn from the 'E and A' model.

The variation that we assume is always present among the recombinant offspring, it is ultimately fueled by mutations. The balance between the influx of beneficial mutations and selection in facultatively sexual populations has been investigated in [7, 32]. Even in sexual populations, the dynamics of mutation can be strongly affected by the selection through the clonal structure of the population.

The participation ratio, Y, is exactly the probability for two individuals to be genetically identical. Therefore, it immediately gives a measure of the clonal structure of the population. If the two genotypes are identical, they have had a common ancestor in the recent past. Hence, 〈Y〉 is proportional to the rate of coalescence, and as soon as 〈Y〉 is no longer proportional to N⁻¹, coalescence is greatly accelerated relative to a neutral model. It is well known that selection accelerates coalescence since fit individuals have more offspring and dominate future generations. Recombination tends to reduce the effects of linked selection since it decouples different regions of the genome. We have calculated the rate of coalescence in our model, which is set by a balance between selection and recombination. We have shown that there is a critical recombination rate, where recombination is overwhelmed by selection and the population structure changes qualitatively.

In the case of additive fitness functions, we have found that $\langle Y\rangle \sim \exp \left [-(r/\sigma )\sqrt{2\log N \sigma }-{r}^{2}/2{\sigma }^{2}\right ]$, which is in agreement with earlier work [30, 37]. In this case, the population consists of clones apparent as little 'bubbles" in the representation of figure 4. Any such bubble originates from a common ancestor $\sim {\sigma }^{-1}\sqrt{2\log N \sigma }$ generations in the past, and 〈Y〉 is the probability that two individuals belong to the same 'bubble'. This bubble coalescent is similar to ideas developed for structured populations [33] or the fitness class coalescent [45]. Note, however, that the clone size distribution is very long tailed and the bubble coalescent is not in the universality class of the Kingman coalescent [19], but possibly of Bolthausen–Sznitman type [4, 25, 30].

Genetic identity between some of the individuals reduces the effect of outcrossing, since identical parents produce identical offspring. Since the probability of such an occurrence is equal to Y, the effective rate of recombination in the partly clonal population is r_eff = r(1 − Y(r_eff,h)). Hence, strictly speaking our calculations of Y(r,h) deep in the clonal condensation regime must be taken through a self-consistency step, which replaces r that was hereto an independent variable by a dependent variable r_eff. This however would not change our estimates for r_c(h) and t_c(r,h), which are defined by the point of first emergence of clones (when Y rises above O(1/N)). Going beyond the MFT description of recombination, one may define a participation ratio density ϒ(F) in terms of which Y = ∫dF ϒ(F), which picks up the fitness dependence of Y: individuals with relatively high fitness are much more likely to be clonally related.

The significance of Y is not limited to the case of exact genetic identity within clones. In particular, mutations would introduce additional polymorphic loci into the 'clones' that were the focus of our study. Yet the genetic structure of the population introduced by clonal condensation still survives: one only needs to distinguish between high-frequency polymorphisms, which are being reshuffled by recombination as approximated by our model, and the low-frequency new polymorphisms due to recent (on the time scale of clonal growth) mutations. The latter would appear on the background that is clonal with respect to the high-frequency alleles. Thus the 'clones' emerging at low r should be thought of as haplotypes [22] and the 'clonal condensation' is the process that suppresses the number of haplotypes on small length scales.

The participation ratio can be readily generalized to allow for a degree of genetic distance within a pair of individuals. As currently defined Y = 〈δ(||g − g'||)〉 (where ||g − g'|| stands for the genetic distance between g and g'). This is immediately recognizable as a special case of the Parisi order parameter q(x) = 〈δ(||g − g'|| − x)〉 [23]. The latter therefore provides an interesting representation of the haplotypic structure of populations. It would be interesting to understand whether more realistic models of fitness landscapes (with low order, rather than random epistasis) would generate a more complex hierarchical structure of q(x) than the simple 'dust/clone' dichotomy found in our simply model. The relation between the REM and Sherrington–Kirkpatrick models of spin glasses [39] could provide useful guidance and ultimately yield better understanding of haplotype distributions and recombinant coalescents [16, 26, 41].

The analysis of 'clonal condensation' presented above can and should be extended in several ways. Within the confines of the model considered, one may want to obtain a better understanding of the 'mixed phase' lying between the two transition lines identified in figure 8. This phase is characterized by large fluctuations in clone size distribution, and hence in Y, even in the approximation imposing a fixed traveling wave velocity v. In reality, the population sets its own instantaneous rate of change of average fitness, which depends sensitively on the fitness of the leading clones and changes with time as new fitness 'records' are established by fresh recombinants. We have already described in figure 9 the 'stick–slip' dynamics, which is characteristic of the mixed phase regime. (Needless to say, the existence of the mixed phase region corresponds to the 1st order nature of the clonal condensation transition for h ≠ 0,1.) A fully quantitative description of this behavior would require going beyond MFT. So far, attempts to describe fluctuations in the dynamics of adaptation have been few and far apart [4, 14, 31]: a quantitative description of the 'stick–slip' progress of adaptation would represent a major step forward.

Another necessary extension of the model involves mutational influx. A non-zero mutation rate would provide an influx of genetic variation and define true statistically stationary states corresponding to adaptive traveling waves [6, 9, 32, 38, 42] or, in the presence of both deleterious and beneficial mutations, to a dynamic mutation selection balance [12]. In that case, emergent clones become 'fuzzy' as they accumulate mutations, and the participation ratio should be replaced by a more general Parisi order parameter as explained above. The result should provide interesting quantitative insight into the expected genetic structure of facultatively sexual populations.

Perhaps the most interesting and important extension of the present work would involve a generalization of the model and its analysis to linear genomes and obligatory sexual populations. In contrast to the current model where recombination freely re-assorts the loci, a more realistic linear chromosome model would describe recombination in terms of relatively infrequent crossover. This would naturally tie the frequency of recombination to the length of the segment considered. We expect that on sufficiently short scales, where recombination is infrequent, a tendency for haplotype condensation would be manifest if the population is diverse enough. Whether epistasis plays a significant role in the condensation process will depend on the distribution of epistatic interactions along the genome [27]. If there is a strong tendency of mutations to interact with mutations nearby [5], the heritability decreases as smaller and smaller segments are considered. This could result in condensation of mutations into 'super-alleles'. However, the embedding of the haplotype in question into a larger genome gives rise to complications related to Hill–Robertson interference [2, 15, 16]. Transient associations with other genomic regions will either boost (the hitch-hiking process) or suppress (background selection) the spread of a haplotype in the population. This reduces the efficacy of selection and gives rise to a stochastic dynamics with rather different properties than genetic drift [30]. Bridging the different scales and resulting dynamical regimes represent an important challenge for the future.

In conclusion, we stress the distinction between the QLE and 'clonal condensation' regimes. In the QLE regime, recombination is sufficiently rapid to overwhelm any clonal amplification due to selection, and correlations between alleles at different loci are relatively weak. In this regime, the correlations between loci are well described by linkage disequilibrium, which measures population averaged pair correlation of loci. By contrast, clonal condensation is a non-perturbative, large deviation from linkage equilibrium (under which loci are completely uncorrelated), which in particular results in a stratification of the population depending on its fitness: clones appear predominantly in the upper reaches of the fitness distribution. Strong heterogeneity among individuals along the fitness axis is not captured by measuring linkage disequilibrium and other traditional approaches. Understanding strong interactions in multi-locus systems requires new ideas and tools. We have found simple models such as the REM to be a very useful source of insight into these non-trivial aspects of population genetics.

In the additive case with v = 1, the cutoff C_r(z,v) is dominated by the young clones for any recombination rate. Its second derivative, however, is dominated by the contribution from old clones if $r\lt (\sqrt{2}-1)\sqrt{2\log N}$. In this regime, we find

$$\begin{eqnarray} \fl \langle Y(r,1)\rangle &\approx &N\int \nolimits _{0}^{\infty }\mathrm{d}z \hspace{0.167em} \frac{r \hspace{0.167em} \exp \left [-r\sqrt{2\log {z}^{-1}}-{r}^{2}/2\right ]}{\sqrt{2\log {z}^{-1}}}\Gamma \left (1-\frac{r}{\sqrt{2\log {z}^{-1}}}\right ){\mathrm{e}}^{-N z}\nonumber\\ &\sim &\exp \left [-\frac{r}{\sigma }\sqrt{2\log N \sigma }-\frac{{r}^{2}}{2{\sigma }^{2}}\right ].\nonumber\\ \end{eqnarray} \tag{ C.6 }$$

In the last step, we have dropped all preexponential factors and reinstantiated σ. This correction approximately accounts for the fact that only a fraction σ of the clones that are seeded are successful.

For larger r, even the B_r(z,h) term is dominated by young clones, and Y ∼ N⁻¹. This behavior holds while the recombination rate is larger than $1/\sqrt{2\log N}$. For smaller r, the velocity starts to deviate from 1. In this case, C_r(z,h) is dominated by old clones. For large enough populations, the powers of z vary much more quickly than all other terms, which we denote collectively by A(z), and we can approximate the integral as

$$\begin{eqnarray} &&\fl \langle Y(r,h)\rangle =-\int \nolimits _{0}^{\infty }\mathrm{d}z \hspace{0.167em} {z}^{v-1}A(z)\Gamma \left (2-\frac{v({\theta }^{\ast }+r)}{{\theta }^{\ast }}\right ){\mathrm{e}}^{{z}^{v}A(z)\Gamma (-v({\theta }^{\ast }+r)/{\theta }^{\ast })}\nonumber\\ &&=~-{v}^{-1}\frac{\Gamma (2-v({\theta }^{\ast }+r)/{\theta }^{\ast })}{\Gamma (-v({\theta }^{\ast }+r)/{\theta }^{\ast })}=\frac{{\theta }^{\ast }+r}{{\theta }^{\ast }}\left (1-\frac{v({\theta }^{\ast }+r)}{{\theta }^{\ast }}\right )\approx 1-v=1-\gamma ,\nonumber\\ \end{eqnarray} \tag{ C.7 }$$

where in the last step we reintroduced σ by replacing v with γ = v/σ². Along the way, we have assumed $r\ll \sigma \sqrt{2\log N \sigma }$, which is consistent with the assumption of small r made above.

In cases with heritabilities 0 < h² < 1, we generally have v < 1 and can be in a regime where C_r(z,v) ≈ z, while B_r(z,v) is dominated by old clones. In this case, we have

$$\begin{eqnarray} &&\fl \langle Y(r,h)\rangle \approx N\int \nolimits _{0}^{\infty }\mathrm{d}z \hspace{0.167em} {z}^{v-1}\frac{r \hspace{0.167em} {\mathrm{e}}^{-r\sqrt{2 v\log {z}^{-1}}-{r}^{2}/2}}{\sqrt{2 v\log {z}^{-1}}}\hspace{0.167em} {\mathrm{e}}^{-N z}\sim {N}^{1-\gamma }\hspace{0.167em} {\mathrm{e}}^{-r/\sigma \sqrt{2 v\log N \sigma }-{r}^{2}/2{\sigma }^{2}}. \end{eqnarray} \tag{ C.8 }$$

This starts to be of order N⁻¹ as soon as $\tilde {r}\lt \sigma (\sqrt{2}-\gamma )\sqrt{2\log N \sigma }$. This is similar to the condition identified in [29] based on the factorization of the mean field solution. Note, however, that this expression does not hold near the v = 0 line, since it is derived assuming a steady traveling wave.