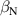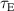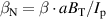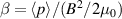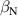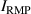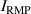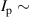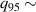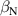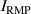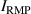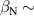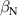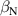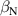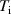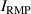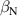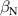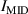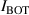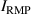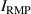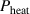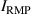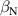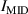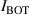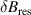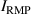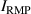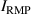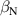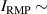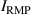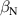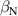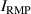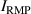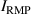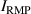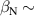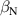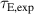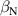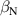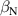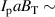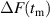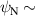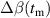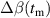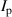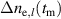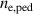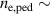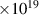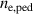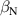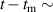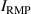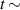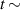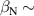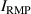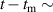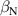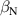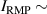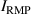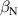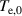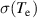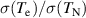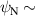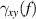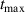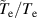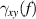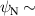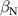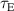Abstract
The integrated Resonant Magnetic Perturbation (RMP)-based Edge-Localized Mode (ELM)-crash-control process aims to enhance the plasma performance during the RMP-driven ELM crash suppression, where the RMP induces an unwanted confinement degradation. In this study, the normalized beta () is introduced as a metric for plasma performance. The integrated process incorporates the latest achievements in the RMP technique to enhance efficiently. The integrated process triggers the n = 1 Edge-localized RMP (ERMP) at the L–H transition timing using the real-time Machine Learning (ML) classifier. The pre-emptive RMP onset can reduce the required external heating power for achieving the same by over 10% compared to the conventional onset. During the RMP phase, the adaptive feedback RMP ELM controller, demonstrating its performance in previous experiments, plays a crucial role in maximizing during the suppression phase and sustaining the -enhanced suppression state by optimizing the RMP strength. The integrated process achieves up to ∼2.65 during the suppression phase, which is ∼10% higher than the previous KSTAR record but ∼6% lower than the target of the K-DEMO first phase ( = 2.8), and maintains the suppression phase above the lower limit of target (= 2.4) for ∼4 s (∼60). In addition to enhancement, the integrated process demonstrates quicker restoration of the suppression phase and recovery of compared to the adaptive control with the n = 1 Conventional RMP (CRMP). The post-analysis of the experiment shows the localized effect of the ERMP spectrum in radial and the close relationship between the evolution of and the electron temperature.

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The steep pressure gradient and the high current density at the edge of High-Performance Mode (H-mode) plasma drive quasi-periodic pedestal relaxation, the so-called Edge-Localized Mode (ELM) crash. The ELM crash generates heat and particle flux onto Plasma-Facing Components (PFC), which can threaten machine safety in ITER [1] and post-ITER tokamaks. An applying external magnetic perturbation resonant at the rational surface(s), called Resonant Magnetic Perturbation (RMP), is proposed to control ELM crashes [2, 3]. Various tokamaks realize the RMP-driven ELM crash suppression, allowing tokamak machines to relieve the mechanical stress: KSTAR [4–6], DIII-D [2, 7–9], ASDEX Upgrade [10, 11], and EAST [12]. However, the RMP technique is associated with an unwanted plasma performance degradation primarily caused by RMP-induced density pump-out, which is experimentally observed in multiple machines, including KSTAR [13–15], DIII-D [16–19], ASDEX Upgrade [11, 20], MAST [21, 22], and EAST [23, 24], and reproduced by simulations [25–27].
Despite the performance degradation induced by the RMP, the RMP spectra reliably suppress ELM crashes within the suppression window. KSTAR can produce various external magnetic perturbation spectra using three rows of in-vessel coils in the poloidal direction and four window-pane-like coils at each row in the toroidal direction [28]. Among many different combinations of coil current in each row and phasing (phase difference of lower-row coil to adjacent upper-row coil), the Non-Resonant Magnetic Perturbation (NRMP), almost orthogonal to the helical field lines, brakes the plasma rotation only without obvious density pump out [29–31]. The Quasi-Symmetric Magnetic Perturbation (QSMP), restoring quasi-symmetry of perturbed particle orbit, has little effect on plasma density and rotation [30]. However, neither NRMP nor QSMP suppresses ELM crashes. Moreover, according to an analysis of DIII-D plasmas without ELM crashes, the RMP plasmas can have advantages over other operating regimes, such as enhanced Dα H-mode (EDA-H), improved energy confinement mode (I-mode), and quiescent H-mode (QH-mode), in terms of the plasma performance [32]. This paper focuses specifically on enhancing plasma performance during the RMP-driven ELM-crash-suppression phase. In order to adopt the RMP technique in ITER and future fusion devices, it is required to recover and enhance the plasma performance during the suppression phase.
A database for KSTAR RMP-driven ELM-crash-control experiments is constructed to investigate experimental conditions favorable to the plasma performance enhancement in the ELM-crash-suppression phase. Here, the normalized beta () represents the plasma performance, where , and . The of performance-enhanced plasmas can be compared to whether it approaches the target of a demonstration fusion power plant (DEMO) design (2.8 in the K-DEMO first phase [33], 2.6 and 3.8 in the EU DEMO1 and DEMO2 design options [34], and 3.4 in the JA DEMO steady-state plasma [35]). The database analysis indicates that the auxiliary heating power () and the RMP coil current () are the two most relevant factors determining during the RMP-driven suppression phase. The basic approach to enhancement is to increase to the maximum available value and to reduce to around the suppression threshold. However, for an efficient and stable -enhanced suppression phase, it is necessary to introduce the latest achievements related to the RMP technique. The pre-emptive RMP onset based on the real-time Machine Learning (ML) classifier [36], which automatically triggers RMP before the first ELM after the L–H transition, can obtain a higher ion temperature at the plasma core region compared to the conventional pre-set RMP onset [37]. The interactive control by the adaptive feedback RMP ELM controller balances enhancement and ELM crash suppression by optimizing [15, 38, 39], in contrast to the conventional pre-set control. The optimization of not only for the RMP strength but also the RMP spectrum can contribute favorably to plasma confinement. The Edge-localized RMP (ERMP) spectrum has a high enough edge resonant magnetic field to suppress ELM crashes while reducing the resonant field in the core region compared to the Conventional RMP (CRMP) spectrum [40, 41]. The accomplishments mentioned above are combined into the integrated RMP-based ELM-crash-control process. The main body of the paper will provide a detailed description and achievements of the integrated process.
The outline of this paper is as follows. Section 2 analyzes the database for KSTAR RMP-driven ELM-crash-control experiments. Section 3 describes the experimental plan for efficient enhancement during the suppression phase. Section 4 reports the achievement of the integrated RMP-based ELM-crash-control process in enhancing and the post-analysis results. Section 5 presents a plan for expanding the integrated process to plasma performance-enhanced long-pulse ELM-less operation. Finally, section 6 gives a summary of this paper.
2. N database for KSTAR RMP-driven ELM-crash-control experiments
KSTAR demonstrates robust and reproducible RMP-driven ELM crash suppression [4, 13, 14, 42–44], thereby contributing to understanding the suppression mechanism [5, 45] and expecting the suppression window in the RMP coil phase-space [46]. Based on this reliability of the RMP-driven suppression in KSTAR, a database for KSTAR RMP-driven ELM-crash-control experiments is constructed to study the plasma performance during the RMP phase, where represents the plasma confinement performance and all the discharges are in a Lower Single Null (LSN) configuration. The database tabulates the following information: (toroidal magnetic field strength at the geometrical axis), plasma current (), RMP configuration [toroidal harmonic number (n), RMP coil phasing, and coil current ()], magnetic EFIT data [47] [safety factor at 95% of normalized toroidal magnetic flux (), plasma elongation (κ), plasma triangularity (δu , and δl ), , and ], line-averaged density () from mm-wave interferometry [48] and two-color interferometry (TCI) [49], total Neutral Beam Injection (NBI) power (), and total electron cyclotron heating (ECH) power (). The RMP configuration of the discharges included in the database is categorized into two groups: static n = 1, +90∘ phasing [4] (207 shots) and static n = 2, +90∘ phasing [6] (76 shots). For reference, in KSTAR, the four window-pane-like RMP coils in the toroidal direction can generate magnetic perturbation up to n = 2. The database includes 283 RMP-driven ELM-crash-control discharges and 2067 data sets, of which 169 are ELM-crash-suppression discharges (119 cases for n = 1 RMP, and 50 cases for n = 2 RMP) and 557 are the suppression data sets (387 cases for n = 1 RMP, and 170 cases for n = 2 RMP). Each data set comprises a collection of time-averaged values for the parameters listed above. The time of interest is selected based on three criteria: 1) Within the time-averaging period of ±0.1 s around the chosen time point, the ELM crash patterns affected by the RMP remain stable, regardless of whether the RMP entirely suppresses ELM crashes. 2) The plasma equilibrium has no unintended perturbations during this period. 3) The measurement data is reliable and free of excessive noise. The database excludes the rotating RMP configuration, where the relative phase to the laboratory frame changes in time. This is because the rotating RMP perturbs equilibrium conditions despite constant RMP strength and phasing [43].
The suppression data sets provide the relationship between and parameters listed in the database during the ELM-crash-suppression period. As shown in figure 1(a), in the n = 1 RMPs, positively correlates with the total auxiliary heating power ( = + ). In the n = 2 RMPs (figure 1(b)), it seems that is insensitive to . However, the n = 2 RMP experiments are conducted in a wide range different from the n = 1 RMP experiments (figure 2). Since is inversely proportional to by definition, it is necessary to decouple the effect on to investigate the relationship between and in the n = 2 RMPs. In both two majority ranges of the n = 2 RMPs (550 620 kA, and 730 800 kA), increases as increases (figure 3). For reference, the NBI in co- direction and the ECH are the main heating sources in KSTAR, but about 91% (153 shots) of the suppression discharges in the database use the NBI only.
Figure 1. in the ELM-crash-suppression phase versus in static n = 1 RMP configuration (a) and static n = 2 RMP configuration (b). The dotted straight lines indicate linear regression lines.
Download figure:
Standard image High-resolution imageFigure 2. Data distributions of ELM crash suppression on (safety factor at 95% of normalized toroidal magnetic flux) and (plasma current) parameter space with histograms of (top) and (right): (a) static n = 1 RMP and (b) static n = 2 RMP configurations.
Download figure:
Standard image High-resolution imageFigure 3. versus for the n = 2 RMP suppression data sets in two majority ranges: 550 620 kA (green) and 730 800 kA (red). The 'Other' label indicates data outside of these two ranges. Dotted straight lines represent linear regression lines for each range, with the same color convention.
Download figure:
Standard image High-resolution imageIn this study, represents the strength of the resonant magnetic field (). However, can vary at the same due to the plasma response to external magnetic perturbation, which is influenced by plasma conditions such as magnetic shear, temperature, and density profiles. Although the precise calculations considering the plasma response can provide exact resonant magnetic field () spectra, such calculations are not available for all the cases in the database. In both n = 1 and n = 2 RMP configurations, an increase in tends to decrease (figure 4), although the effects of (especially n = 2 RMPs) and on are not decoupled from that of . In the n = 1 RMPs, the reduction slope is steeper than the n = 2 RMPs. The observed trend appears to be due to the differences in spectra, such as the penetration depth into the plasma core, between n = 1 and n = 2 RMPs. However, it is not possible to directly compare spectra or of n = 1 and n = 2 RMPs using .
Figure 4. in the ELM-crash-suppression phase versus in static n = 1 RMP configuration (a) and static n = 2 RMP configuration (b). The dotted straight lines indicate linear regression lines.
Download figure:
Standard image High-resolution imageThe database analysis shows that and are the most influential parameters on of the suppression phase. In contrast to and , other parameters, such as , δu , δl , and κ, do not show a clear relationship with during the suppression phase. These results are consistent with intuitive predictions that the additional and the lower can enhance the plasma performance during the suppression phase.
3. Experimental design to achieve N-enhanced ELM crash suppression
3.1. Experimental conditions favorable to > 2.4 ELM crash suppression
As shown figures 1 and 4, is below 2.4 in almost all cases of ELM crash suppression. Therefore, > 2.4 becomes a goal for plasma performance enhancement during the RMP-driven ELM-crash-suppression phase in KSTAR.
The database analysis results indicate that and are the two main actuators to enhance during the suppression phase. All available NBI sources are used to maximize . However, only one ECH source of ∼0.6 MW power is utilized since this power level is optimal for achieving robust ELM crash suppression, considering the ECH effect on the plasma rotation. The ECH injection can change the toroidal rotation profile [50, 51]; in the co- NBI heated discharges of KSTAR, ECH reduces the co- plasma rotation [51]. When the ECH lowers the rotation below the threshold, the ECH-induced rotation drop terminates the suppression phase, as in the DIII-D experiments in which the NBI mix controls the torque affecting the plasma rotation [9]. Additionally, increases step-by-step to avoid failure in plasma control due to abrupt changes in plasma conditions. should be as low as possible but above the suppression threshold level. The scan is necessary to obtain the optimal level since the threshold is sensitive to plasma conditions, such as pressure profile [25], plasm shape [52], [53], RMP configuration [46], etc.
The data distribution in section 2 shows that the n = 1 RMPs obtain higher during the ELM crash suppression than the n = 2 RMPs. Since by definition, the n = 1 RMP-driven suppression at 5 suppression window, with lower as shown in figure 2 ( 490–540 kA when = 1.8 T), has an advantageous over n = 2 RMP-driven suppression in 3.4, 3.8, and 4.4 windows ( 560–800 kA when = 1.8 T) in achieving higher . Moreover, the n = 1 RMP-driven suppression at 5 is more reproducible, as evidenced by the number of cases. Therefore, the n = 1 RMP is more effective in achieving > 2.4 ELM crash suppression. This study uses as a metric for evaluating plasma performance to enable prompt comparison, which makes n = 1 RMP of lower a better option for achieving high . However, it is important to note that the metric should eventually be changed to absolute parameters relevant to the fusion performance.
Other conditions, except the major parameters affecting , are set to be highly reproducible to the n = 1 RMP-driven ELM crash suppression: = 1.8 T, 0.57 ( 0.32 and 0.82), and 1.72.
3.2. RMP onset by real-time ML classifier
A real-time ML classifier [36], providing the current plasma state, such as L-mode, H-mode, and ELMy phase, is introduced for efficient plasma performance enhancement. The RMP application can be connected to the ML classifier results. For example, by synchronizing the RMP onset timing with the L-H transition timing, the RMP can be fired according to the pre-set target and ramp-up rate before the first ELM crash in the H-mode.
Figure 5 compares experiments for enhancement during the RMP-driven ELM crash suppression in two different RMP triggering methods. Preliminary experiments provide the threshold and determine the optimal heating configuration for enhancement and stable plasma control. In the case of the conventional pre-set RMP onset (#28 756), the maximum during the RMP phase is ∼5.76 MW ( 5.3 MW and 0.45 MW), as shown in figure 5(a), and rises during the H-mode phase according to the pre-set control parameter (figure 5(b)). In the case of the ML-classifier-based RMP onset (#29 367), the maximum is ∼5.14 MW ( 4.5 MW and 0.63 MW), and the onset, determined by the ML classifier output, occurs ∼10 ms after the L–H transition accompanied by the increase in shown in figure 5(d). In the conventional case, increases up to ∼2.47 under RMP, but the suppression phase appears transiently (figure 5(c)). The ML-based pre-emptive RMP onset achieves up to 2.56 during the stable ELM crash suppression (figure 5(d)) despite ∼11% lower than the conventional case. around the maximum (indicated by vertical dotted lines in figure 5) is similar in the two cases: ∼1.67 kA/turn in the conventional method (#28 756, 8.95 s) and ∼1.71 kA t−1 in the ML-based RMP onset (#29 367, 6 s).
Figure 5. Comparison of experiments for enhancement during the RMP-driven ELM-crash-suppression phase in KSTAR: RMP onset by conventional pre-set parameters (#28 756, black) and ML classifier (#29 367, red). (a) Total auxiliary heating power. (b) RMP coil current. Time traces of with Dα (cyan) signal for (c) #28 756 and (d) #29 367.
Download figure:
Standard image High-resolution imageThe ML-classifier-based RMP onset, originally designed for the pre-emptive ELM crash control, offers an advantage in enhancing compared to the conventional pre-set RMP onset. This enhancement in the pre-emptive RMP onset is primarily due to higher ion temperature in the plasma core region relative to that in the conventional RMP onset [37]. A turbulence and transport analysis in progress will provide a physics understanding of the increased core in the RMP onset coincident with the L–H transition.
3.3. Interactive control by adaptive feedback RMP ELM controller
In the ML-classifier-based enhancement experiment shown in figure 5, gradually decreases to increase under the given . However, ELM crashes reappear when is below ∼1.68 kA t−1, and finally, the ELM-crash-suppression phase turns into the ELM-crash-mitigation phase after 8.8 s. Despite the need for an increase in to suppress the ELM crash reappearing, continues to decrease according to the pre-set waveform.
The adaptive feedback RMP ELM controller [15, 38, 39] is introduced to compensate for the limitations of the conventional pre-set control through an interactive control. The adaptive controller optimizes based on a built-in real-time ELM crash frequency monitor. During the suppression phase, the adaptive controller reduces to recover plasma confinement, taking into account a hysteresis effect that lowers the suppression threshold [15]. If the ELM crash frequency monitor detects ELM crashes during the reduction, the controller updates the suppression threshold and increases until ELM crashes disappear on the ELM crash monitor. Once the suppression phase is restored, decreases again. This iterative adjustment of can optimize the RMP strength to recover the plasma confinement while maintaining the ELM-crash-suppression phase. More details about the structure and process of the adaptive feedback algorithm can be found in [38, 39].
The previous KSTAR experiments demonstrate that the adaptive controller can recover the plasma performance up to ∼90% of the non-RMP phase: recovered in the suppression phase is ∼1.91, and in the non-RMP phase is ∼2.13 [15]. Therefore, in this study on > 2.4 ELM crash suppression, the adaptive controller is crucial in enhancing the plasma performance during the suppression phase and sustaining the performance-enhanced suppression state. For reference, the , discussed in section 3.1, is higher than in the previous experiments proving the performance of the adaptive controller ( 3 MW).
3.4. Reduced core resonant magnetic field by ERMP
In order to maximize the enhancement under the given experimental conditions, it is necessary to optimize the RMP spectrum in favor of the plasma confinement, as well as to adjust . The RMP configuration of n = 1, +90∘ phasing ( = = and = = 90∘, where is the RMP coil current of each row and is the phase difference between rows) has a finite resonant magnetic field strength near the plasma core [31, 40, 42], which can degrade the plasma confinement. The systematic approach by core-null space projection considering RMP coil constraints, such as coil geometry, location, and maximum current, provides the ERMP [40, 41]. The ERMP spectrum has a reduced resonant component in the core region, compared to the conventional n = 1, +90∘ phasing RMP (n = 1 CRMP) spectrum, while maintaining the edge component above the suppression threshold. The original goal of optimizing RMP spectra for ELM crash control is to avoid disruptive MHD instability driven by core resonant fields, such as locked modes [54]. In this study, it is anticipated that a reduced core component in the ERMP spectrum will enhance the plasma confinement.
4. Integrated RMP-based ELM-crash-control process
4.1. Experimental validation of the integrated process
The integrated RMP-based ELM-crash-control process incorporates the latest achievements described in section 3, such as the real-time ML classifier, the adaptive feedback RMP ELM controller, and the ERMP spectrum, for efficient enhancement during the ELM-crash-suppression phase. The integrated process unfolds as follows: first, the ERMP spectrum is triggered based on real-time ML classifier output. Next, the control authority of the ML classifier is transferred to the adaptive controller. Finally, the adaptive controller optimizes to achieve enhanced during the suppression phase.
The performance of the integrated process is validated by comparing during the suppression phase in different control methods and n = 1 RMP spectra (figure 6). The comparisons include 1) n = 1 CRMP with a constant of 1.9 kA t−1 (#31 185), 2) n = 1 CRMP with adaptive control (#31 184), and 3) n = 1 ERMP with adaptive control (integrated process, #31 189). In all cases, the RMP onset timing is when the real-time ML classifier indicates the L–H transition. During the RMP phase, = 1.8 T, 0.57, 1.72, 490 kA, and 5.1. As shown in figure 6(a), increases step-by-step to avoid failure in plasma control, and the maximum is ∼5.4 MW ( 4.8 MW and 0.58 MW). Figures 6(b)–(d) show that , representing the top coil current among three-row RMP coils, in the ERMP spectrum is consistently larger than the CRMP spectrum throughout the discharge. However, in the ERMP spectrum, the top and bottom coil currents are ∼23.8 times larger than the mid coil current (i.e. = = ∼23.8), resulting in a resonant magnetic field lower than expected from the alone. The Ideal Perturbed Equilibrium Code (IPEC) [55] calculations, shown in figure 7, indicate that the ERMP spectrum (red line) applied in the integrated process produces ∼14% lower near the core region ( 0.48) than CRMP (blue line) when around the pedestal top ( 0.94) is the suppression threshold, based on the assumption that the suppression threshold is similar across different RMP spectra [46].
Figure 6. Comparison of during the n = 1 RMP-driven ELM crash control. (a) Total auxiliary heating power. Time traces of , Dα (cyan), and RMP coil current (black) in (b) the CRMP with pre-set constant (#31 185), (c) the CRMP with adaptive feedback control (#31 184), and (d) the ERMP with adaptive feedback control (#31 189). (e) H-factor. In (b)–(d), is the top coil current among three-row RMP coils (TOP, MIDdle, and BOTtom) in KSTAR. In CRMP, = = , while in ERMP, = > .
Download figure:
Standard image High-resolution imageFigure 7. Comparison of resonant magnetic field () spectra. CRMP is the conventional n = 1, +90∘ phasing RMP applied in #31 184 and #31 185. ERMP is the n = 1 edge-localized RMP for #31 189.
Download figure:
Standard image High-resolution imageOne technical challenge in combining the ML classifier and the adaptive controller is ensuring a smooth transition of control authority. In both discharges (#31 184 and #31 189), where the adaptive feedback control algorithm is activated 3 s and 4 s after the RMP onset, respectively, the adaptive controller takes over control authority from the ML classifier without any issues. For reference, the pre-set parameters for adaptive control are as follows: the ramp-up rate is 0.6 kA t−1 s−1, the ramp-down rate is 0.3 kA t−1 s−1 in #31 184 and 0.5 kA t−1 s−1 in #31 189, and the waiting time for adjustment after the restoration of the suppression phase is 400 ms.
In the reference case (n = 1 CRMP with constant , i.e. #31 185), the maximum during the suppression phase is ∼2.49 (figure 6(b)). Compared to the previous ML-classifier-based RMP onset case (#29 367 in figure 5), the maximum is ∼3% lower despite ∼5% higher . About 11% higher in #31 185 (1.9 kA t−1) could be the main reason for the lower , but it contributes to the stable > 2.4 suppression phase lasting over 6 s (∼2.8 s duration in #29 367).
In #31 184 (figure 6(c)), the adaptive controller reduces three times to enhance the plasma performance. At the first attempt, increases up to ∼2.61 ( 1.43 kA t−1), but ELM crashes reappear soon. The adaptive controller restores the suppression phase in ∼0.55 s by increasing to ∼1.74 kA t−1. The second attempt starts after the pre-set waiting time of 400 ms following the recovery of the suppression phase. The reduction in during the second attempt stops at 1.44 kA t−1, which corresponds to the lower limit of determined by the adaptive controller based on the results of the first attempt. 2.6 suppression phase is maintained for ∼0.6 s, a longer duration than the first attempt, and then the suppression phase transits to the ELM-crash-mitigation phase. The controller achieves the suppression phase recovery in ∼0.48 s by increasing to ∼1.73 kA t−1, similar to the first recovery. During the last attempt, the flat-top ends at 10.5 s.
In the integrated process (#31 189, figure 6(d)), the ERMP spectrum is applied instead of the CRMP spectrum in the previous two cases. The adaptive control with ERMP (i.e. integrated process) achieves a higher than the adaptive control with CRMP. During the RMP phase, the maximum is ∼2.69 around 7.9 s, but sparse ELM crashes appear then. The maximum of the stable suppression phase is ∼2.65 around 8.1 s (∼2.61 in #31 184). The duration of > 2.6 suppression is ∼1.4 s, ∼2.3 times longer than the adaptive control with CRMP. Moreover, the suppression in above 2.4 (the lower limit of target ) is sustained for ∼4 s (∼60), while the duration of > 2.4 suppression is ∼2.1 s (∼31) in #31 184. Like #31 184, the mitigation phase follows the 2.6 suppression phase. The drop in the mitigation phase is about two times larger than observed in the CRMP (#31 184). However, the restoration time for the suppression phase (∼0.30 s and ∼0.21 s) is ∼38% – 62% shorter than that of #31 184 (∼0.55 s and ∼0.48 s). The shorter restoration time means that a smaller change in is sufficient to recover the suppression since the pre-set ramp-up rate for the adaptive control is 0.6 kA t−1 s−1 for both ERMP and CRMP cases. Similarly, the recovery time for 2.6 suppression (∼0.70 s) is ∼51% shorter than #31 184 (∼1.43 s). The reduced inside the edge region in the ERMP is the most likely reason for the quicker recovery.
In two adaptive control cases (#31 184 and #31 189), the pattern of change is consistent with the optimization process described in section 3.3, except for one case that requires explanation. In the integrated process (#31 189), the adaptive controller halts the decrease in at ∼7.76 s when an ELM crash occurs. However, these sporadic ELM crashes do not trigger the mitigation phase. Consequently, the adaptive controller suspends the decision of ramp-up, in contrast to the immediate ramp-up responding to the mitigation phase (for example, ∼8.9 s in #31 189). After a delay of ∼400 ms, the controller triggers a jump in of ∼0.06 kA t−1 (determined by the internal process) at ∼8.17 s to achieve stable suppression and maintains as the updated lower limit of . This increase in can reinforce the reduction of after the peak at ∼7.9 s.
In conclusion, the integrated RMP-based ELM-crash-control process sets a new record for during the RMP-driven ELM crash suppression in KSTAR, reaching 2.65. The adaptive feedback control algorithm achieves higher during the suppression [ 2.65 in the ERMP spectrum (i.e. integrated process) and 2.61 in the CRMP spectrum] than the conventional pre-set operations ( 2.49 in #31 185). The attempts to achieve above the target value of 2.4 during the suppression phase extend the accessible range of the suppression in KSTAR to > 2.4 regions. The H-factor ( = /, where is the energy confinement time from experiments and is the energy confinement time derived from a multi-machine scaling [56]) confirms the plasma confinement enhancement (figure 6(e)). In this analysis, the injected is used to calculate . In #31 189 (integrated process) and #31 184 (CRMP with adaptive control), increases up to ∼1.99 and ∼1.92, respectively, coincident with the timing of maximum . In the reference case (#31 185), the maximum at 5.4 MW is ∼1.84.
2.6 ELM crash suppression is comparable to the target of the EU DEMO1 design option ( = 2.6 [34]) but 5%–7% lower than the target of the K-DEMO first phase ( = 2.8 [33]). Compared to the DIII-D (similar size to KSTAR) record dataset of RMP-driven ELM crash suppression ( 2.5, > 7 MW, 1.2 MA [32]), KSTAR achieves higher during the suppression phase with lower (∼5.4 MW). However, in this comparison, the relatively low in the KSTAR 2.65 case ( 0.49 MA) is favorable for obtaining higher than the DIII-D record. As mentioned in section 3.1, is an insufficient metric to describe the absolute plasma performance. For example, the product is a simple metric for fusion performance [57]. While 1.05 in the DIII-D record [32], in the KSTAR case, 0.41 (with a minor radius of 0.46 m) despite its higher . This study that enhances the plasma performance during the suppression phase will be extended to increase the absolute plasma performance by introducing a metric relevant to the fusion performance.
4.2. recovery after the mitigation phase onset
During the adaptive control in both the ERMP and the CRMP cases, the mitigation phase, accompanied by drop, occurs after the 2.6 suppression phase (figures 6(c) and (d)). This section investigates the recovery after the onset of the mitigation phase. It is worth noting that other MHD instabilities are unlikely to contribute to the rapid reduction observed in the mitigation phases since there are no measurable instability events during the RMP phase except the mitigated ELM crashes.
Figure 8 shows the relative change in the parameters of interest compared to their value at the onset of the mitigation phase. The relative change of variable F can be written by , where denotes the time of the mitigation phase onset. To focus on the temporal change of , time-averaged values for (from TCI) and [from electron cylotron emission (ECE) radiometry [58]] are obtained for each 10 ms time window. The relative change in (, figure 8(b)) exhibits a similar pattern to on 0.2 (figure 8(c)) and 0.8 (figure 8(d)). The evolution of spans a wide radial range, and has a similar level with , except for changes supposed to be attributed to the mitigated ELM crashes. The similarity between and increases as close to the plasma core. The relationship between and is not as obvious as the relationship between and (figure 8(e)). The above observations indicate that predominantly influences the drop or recovery of .
Figure 8. Comparison of the time evolution in electron density and temperature. (a) RMP coil current (green) and Dα signal (grey) in #31 184 (CRMP spectrum with adaptive control). The relative change to the value at the onset of the mitigation phase: (b) , (c) electron temperature () on 0.2, (d) on 0.8, and (e) line-averaged electron density. (f) (red) and Dα (grey) in #31 189 (integrated process). In (b)–(e), green corresponds to #31 184, and red does #31 189. Vertical dotted lines indicate the onset and end of the mitigation phase in #31 184 and #31 189 and the end of the flat-top in #31 189. and denote the time of the mitigation phase onset and the end of the flat-top, respectively.
Download figure:
Standard image High-resolution imageAn interesting observation regarding is that becomes larger than zero at the onset of the mitigation phase in both the ERMP and the CRMP cases. During the suppression phase, . This behavior is similar to the suppression threshold in electron density observed in DIII-D [9] and ASDEX upgrade [11]. The electron density on the pedestal top () at the onset of the mitigation phase (in #31 184, 2.71 and ∼2.57 m−3, while in #31 189, 2.65 and ∼2.69 m−3) is higher than the maximum observed during the suppression phase so far in KSTAR (∼2.5 m−3 [14]). However, further exploration of the high region is necessary to confirm the density threshold in the KSTAR [14].
The increase in independent of the change in is observed in both the ERMP and CRMP cases. During the ramp-up to restore the ELM crash suppression, is recovered by ∼4.3% in the ERMP case ( 0.26–0.38 s) and ∼5.4% in the CRMP case ( 0.11–0.46 s). During the constant due to the waiting time in the adaptive control, increases by ∼3.4% in the ERMP case ( 0.38–0.78 s) and ∼1% in the CRMP case ( 0.6–0.95 s). The plausible explanation for this recovery, not influenced by , is that the plasma can naturally restore to a certain extent without relying on a decrease in if the mitigated ELM crashes excessively degrade below the level anticipated by the RMP strength and auxiliary heating power. For example, in the ERMP case, during the period of constant (∼3.96 kA t−1), increases from ∼2.46 ( 0.38 s, or 9.26 s) to ∼2.55 ( 0.78 s, or 9.66 s). Considering that 2.58 at 7.16 s under similar and conditions (figure 6(d)), it suggests that the plasma at 0.38 s has the potential to recover . In the CRMP case, the restoration of the suppression phase leads to a transient drop in . This drop can be attributed to the higher ( 2.53 at 1.73 kA t−1) just before the suppression restoration ( 0.54 s) than 2.5 under similar and conditions in the previous time ( 5.61 s, figure 6(c)). However, in this drop of the CRMP case, further investigation is required to explain the overshoot in recovery and the sustainment of higher levels during the mitigation phase.
During the ramp-down after the waiting time in the adaptive control, the evident acceleration in recovery is observed in the CRMP case, whereas it is unclear in the ERMP case. This absence of accelerated recovery in the ERMP can be attributed to the quick restoration of the suppression phase. In the ERMP, during the ramp-up to restore the suppression phase, increases by ∼5.8%, while ∼21% in the CRMP. Furthermore, at the end of the waiting time ( 0.78 s), reaches ∼98% of the value at the onset of the mitigation phase and ∼97% of the maximum during the stable suppression phase. In the ERMP, the impact of change in on cannot be as significant as in the CRMP.
Figure 9 shows the repetition frequency of ELM crashes () during the mitigation phase. In the CRMP case (figures 9(a) and (b)), the onset of recovery (indicated by black dotted lines) occurs ∼30 ms before the increase in to above ∼60 Hz (indicated by magenta dotted lines), while in the ERMP case (figures 9(c) and (d)), it occurs ∼20 ms after. Since the stored energy loss driven by ELM crash becomes lower in a higher [59], a higher can cause the recovery of . However, further investigation is required to clarify the causality between the onset of recovery and the increase in , and figure out the threshold for recovery if is related to recovery. A comprehensive simulation can address this matter, but such an investigation is beyond the scope of this paper.
Figure 9. The relative change of to its value at the onset of the mitigation phase in #31 184 (CRMP) (a) and in #31 189 (ERMP) (c). The repetition frequency of ELM crash in #31 184 (CRMP) (b) and in #31 189 (ERMP) (d). Black dotted line: the onset time of recovery. Magenta: the time of the increase to above ∼60 Hz. Green (#31 184) and red (#31 189): the end time of the mitigation phase.
Download figure:
Standard image High-resolution image4.3. Turbulent fluctuation in the suppression phase of ERMP and CRMP spectra
The KSTAR Electron Cyclotron Emission Imaging (ECEI) system [60] is introduced to analyze turbulent fluctuations in the ERMP and CRMP discharges. Among 24 (vertical) × 8 (radial) ECEI channels in a two-dimensional space on the poloidal cross-section, the vertically adjacent two channels are employed to obtain the coherence () spectrum and the relative fluctuation of electron temperature () through correlation analysis. can be derived from the relation [61], where is the video bandwidth (300 kHz for ECEI), is the Intermediate Frequency (IF) bandwidth (700 MHz for ECEI), is the cross-correlation coefficient at zero lag time. However, the ECEI view windows only cover the Low Field Side (LFS) edge in #31 184 (CRMP) and #31 189 (ERMP). For analyzing fluctuations inside the edge of the plasma, the ECE radiometry is utilized. The ECE radiometry channels are distributed radially along the mid-plane, but the distance between adjacent channels is not sufficiently close for correlation analysis. Alternatively, the standard deviation (σ) of for a specific time period represents the fluctuation level during that period. Total can be expressed as = + , where and represent the steady and fluctuation part of electron temperature, respectively. Based on the assumption that ( denotes the time-averaged ) within the time window of interest, can be a reliable proxy for quantifying the magnitude of fluctuations, since is the square root of the expected value of .
Figure 10 shows fluctuation levels of the electron temperature in different radial positions. The ECEI analysis calculates and in non-overlapping 50 ms time segments. Within this time segment, the sensitivity of , determined by [62], is ∼0.2%, where the independent sample number (N) is 25 000 at a 500 kHz sampling rate of ECEI. The ECE analysis obtains for each non-overlapping 50 ms time window, corresponding to the time segment length used in ECEI analysis. In the time of interest, > 2.9, where is the thermal noise temperature of the system. For reference, the sampling rate of ECE radiometry is 500 kHz in the discharge of interest. The resonant positions of ECE and ECEI channels are determined by considering the poloidal magnetic field and relativistic broadening [63]. Due to the potential decrease in correlation analysis accuracy and the possibility of overestimating caused by the frequent ELM crashes, the discussion on fluctuation level does not focus on the period of the ELM-crash-mitigation phase, indicated by magenta dotted lines.
Figure 10. Comparison of electron temperature fluctuation. (a) and (e): Time traces of , Dα (cyan), and RMP coil current (black). (b) and (f): Coherence spectra from two vertically adjacent ECEI channels on low-field side mid-plane ( 0.95). (c) and (g): Relative fluctuation level measured by ECEI channels on 0.95. (d) and (h): Standard deviation of from the ECE radiometry channel on 0.8. (a)–(d) for #31 184 (adaptive control with n = 1 CRMP spectrum) and (e)–(h) for #31 189 (integrated process). The maximum at the stable suppression is indicated by .
Download figure:
Standard image High-resolution imageThe ERMP and the CRMP exhibit a similar trend in turbulent fluctuations on the plasma edge ( 0.95) during the suppression phase since the ERMP is designed to have the same spectrum as the CRMP at the plasma edge. In both suppression phases under the ERMP and CRMP spectra, as decreases (or increases), the coherence spectra on 0.95 get broadened, increases in the frequency range f < 25 kHz (figures 10(b) and (f)), and the relative fluctuation level () at the plasma edge increases (figures 10(c) and (g)). This trend is more evident in the CRMP case. In the ERMP, during the period when decrease by ∼2% after reaching the maximum of the stable suppression phase (indicated by the vertical line labeled ), slightly increases and in f > 25 kHz becomes strong. When decreases, the reduction in can weaken the RMP-induced classical quasi-linear transport [25, 64] or stabilize turbulent fluctuations driven by the anisotropic E×B shearing rate in a magnetic island [65]. However, the expected gradient steepening due to the enhancement, associated with reducing the quasi-linear transport coefficient or the RMP-driven turbulence, can linearly drive additional turbulent fluctuations. Thus, it follows that the observed increase in turbulent fluctuations might be originated from the linear drive of turbulence fluctuations due to the gradually enhanced pedestal with the decrease in RMP strength, which suggests that on the plasma edge in the present experiments, the driving mechanism is more dominant than the turbulence stabilization mechanism when decreases. On the other hand, further analysis is required to tell whether the elevated fluctuation level is related to the onset of the mitigation phase.
In the CRMP case, the fluctuation level () increases in the region of 0.8 as decreases (or increases) if disregarding bumps that coincide with sporadic bursts of the Dα signal around 5.4 s (figure 10(d)). On the other hand, in the ERMP, there are no significant changes in the fluctuation level, except for fluctuations driven by sporadic ELM crashes (figure 10(h)). Supposing that the observed fluctuation level on 0.8 is governed by the same mechanism as the plasma edge explained above, the impact of on the magnitude of the relevant turbulence on 0.8 may be insignificant in the ERMP. This can be attributed to a smaller magnitude of on 0.8 in the ERMP compared to the CRMP, as shown in figure 7, which implies that the applied in the ERMP may not penetrate into the resonant surface near 0.8. It is well-known that only when the applied resonant field penetrates into the resonant surface, the ambient magnetic topologies can be reorganized. Consequently, this change in the magnetic topology can increase particle or heat transport, affecting instability/fluctuation. Thus, the comparison of the fluctuation level on 0.8 suggests that the ERMP spectrum affects the radially narrower regions localized to the plasma edge, compared to the CRMP spectrum.
5. Plans for expanding the integrated process to long-pulse ELM-less operation
This section explores the expansion of the integrated RMP-based ELM-crash-control process, excluding the matter of a metric for evaluating plasma performance. The integrated process needs to consider issues related to long pulse and ELM-less operation for further improvement, although it already demonstrates the ability to enhance plasma performance during the ELM-crash-suppression phase.
Figure 6(d) shows that the integrated process does allow for the reappearance of ELM crashes when enhancing in the suppression phase. While enhancing the plasma performance in the ELM-crash-suppression plasmas, it is crucial to avoid any single ELM crash, which can threaten machine safety in ITER and future fusion devices. The latest version of the adaptive feedback RMP ELM controller incorporates a real-time detector for a precursor to ELM-crash-suppression loss [39], which can pre-emptively control to prevent the ending of the suppression phase. By integrating this update, the integrated process can move closer to achieving the plasma performance-enhanced RMP-based ELM-less operation. However, before deployment, the precursor detector should be optimized for experimental conditions favorable to the plasma performance enhancement.
KSTAR, equipped with superconducting magnets, is an ideal testbed for expanding the integrated process to the long-pulse ELM-less operation. To consider the long-pulse issue, the integrated process can incorporate any long-pulse-relevant actuators compatible with the plasma performance-enhanced RMP-driven ELM crash suppression, even if they are unrelated to the RMP technique. One of the potential candidates is the KSTAR divertor plasma detachment control based on the simplified real-time modeling [66], reducing the heat load on PFCs. However, the impurity seeding, the primary actuator of the detachment control, has a side effect on core plasma performance [67] and affects conditions to access ELM crash suppression by changing electron density and recycling conditions [68, 69]. Therefore, incorporating the detachment control requires upgrading the integrated process to balance plasma detachment, ELM crash suppression, and plasma performance enhancement.
6. Summary
The RMP technique is a promising method to control the ELM crash. However, the RMP-driven ELM crash control is accompanied by an unwanted degradation in plasma performance. Based on the reliability of the RMP-driven ELM crash suppression in KSTAR, the database for KSTAR RMP-driven ELM-crash-control experiments is constructed to investigate the plasma performance during the ELM-crash-suppression phase and identify experimental conditions favorable to enhancement. In this database, is a metric for the plasma confinement performance. Among the 283 discharges included in the database, the data sets from 169 ELM-crash-suppression discharges indicate that 1) the auxiliary heating power () and the RMP coil current () are the two main parameters influencing during the suppression phase, 2) in KSTAR, the lower conditions for the n = 1 RMP suppression have an advantage over the n = 2 RMP suppression in achieving higher , and 3) other parameters, such as line-averaged electron density () and plasma shape, have little correlation with . In almost all KSTAR suppression cases in the database, is below 2.4. Therefore, the lower limit of target for plasma performance enhancement is set at 2.4.
For efficient enhancement, the integrated RMP-based ELM-crash-control process incorporates the latest achievements related to the RMP technique. The integrated process applies the ERMP, favorable to the plasma confinement due to the reduced resonant components inside the edge region while maintaining the edge component above the suppression threshold, at the time of L–H transition using the real-time ML classifier. The ML-based pre-emptive RMP onset, triggering RMP before the first ELM crash of H-mode, reduces the external heating power required to achieve the same by over 10% compared to the conventional RMP onset according to the pre-set control parameter. After taking over control authority from the ML classifier, the adaptive feedback RMP ELM controller optimizes the level to enhance during the suppression phase and sustain the -enhanced suppression state. The performance of the integrated process is experimentally validated. The integrated process maintains the > 2.4 suppression phase for ∼4 s (∼60) and achieves up to ∼2.65 during the suppression phase, which is ∼10% higher than the previous KSTAR record, but ∼6% lower than the target of K-DEMO first phase. Furthermore, the integrated process confirms the additional advantage of the ERMP spectrum on top of its contribution to the enhancement. During the adaptive control, the restoration time for the suppression phase and the recovery time for 2.6 suppression are reduced by ∼38%–62% and ∼51%, respectively, in the ERMP compared to the CRMP when the ELM-crash-mitigation phase accompanied by a drop in occurs.
A series of post-analyses provide several findings that 1) the evolution of is predominantly influenced by electron temperature, 2) the onset of recovery after the mitigation phase accompanied by a temporary drop may be related to the repetition frequency of mitigated ELM crashes, and 3) the impact of the ERMP spectrum is more radially localized to the edge of the plasma compared to the CRMP spectrum.
Acknowledgments
The authors thank all the KSTAR team members for their support. This research was supported by the R&D Program of 'KSTAR Experimental Collaboration and Fusion Plasmas Research (EN2301-14)' through the Korea Institute of Fusion Energy (KFE) funded by Government funds, and by the KOREA HYDRO & NUCLEAR POWER CO., LTD (No. 2019-Tech-G19IO16). This material was supported by the U.S. Department of Energy under Awards DE-SC0020372. This work was also supported by the U.S. Department of Energy under contract number DEAC02-09CH11466 (Princeton Plasma Physics Laboratory).