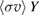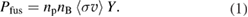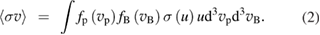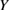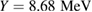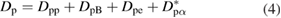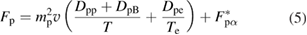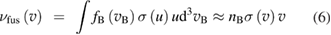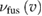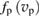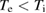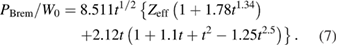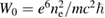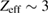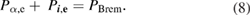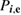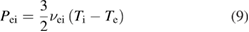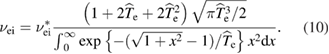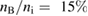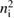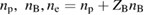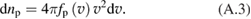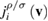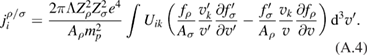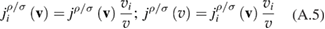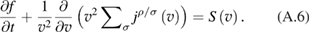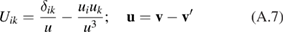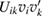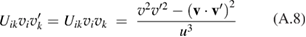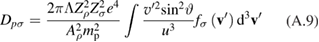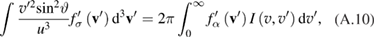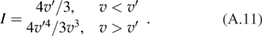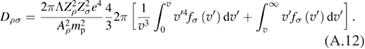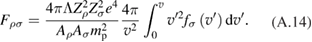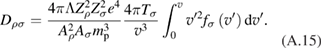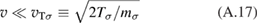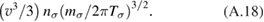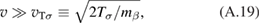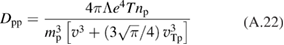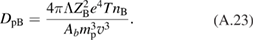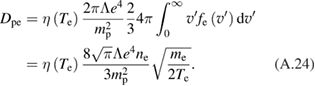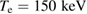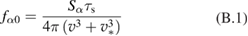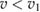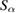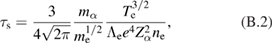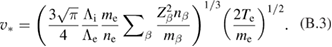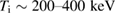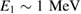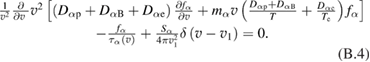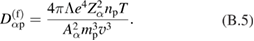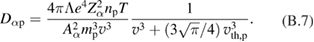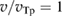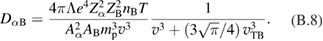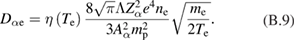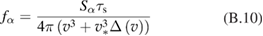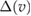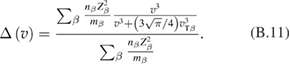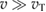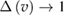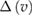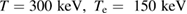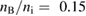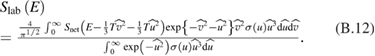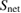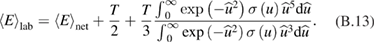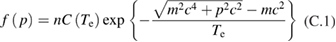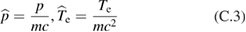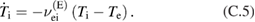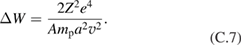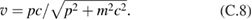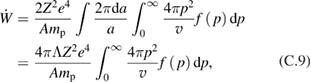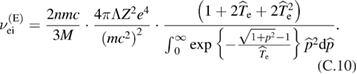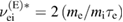Fusion reactivity of the pB¹¹ plasma revisited

The fusion systems with pB¹¹ fuel have significant advantages over the systems based on DT or DD fuels in that the neutron production in the former is orders of magnitude lower than in the latter two. In addition, the fuel components, p and B¹¹, are readily available and no breeding of the reaction components is needed. One more fuel with a low neutron flux is DHe³. However, even though the neutron flux is reduced compared to the DT fuel, it remains significant due to DD reactions and secondary DT reactions. Moreover, terrestrial resources of He³ are scarce and it may have to be transported from the Moon, where it is present in the surface layers of regolith [1]. This explains a continuing interest to the magnetic confinement schemes based on the pB¹¹ fuel [2, 3], notwithstanding difficulties associated with this approach and briefly mentioned later in section 2.

There is a widely shared opinion that pB¹¹ fuel is not useful because of low reactivity. This is, however, a misconception: reactivity of pB¹¹ fuel, although being by a factor of a few lower than that for DT, is still higher than that for DD and DHe³. If comparing the parameter $\left\langle \sigma v \right\rangle Y$ (with $\left\langle \sigma v \right\rangle$ being a reaction rate averaged over the Maxwellian distribution and Y being a fusion reaction yield), the result becomes even more favorable for pB¹¹. This is illustrated in figure 1 that compares fusion reactivities of Maxwellian plasmas times the energy yield Y of fusion reactions.

Zoom In Zoom Out Reset image size

The main difficulty for the pB¹¹ fuel is actually related to high ion temperatures needed to reach this high reactivity. The electrons then become also quite hot, leading to intense bremsstrahlung radiation. This circumstance has led the authors of earlier analyses (e.g. [4–6]) of the power balance in pB¹¹ plasma to rather pessimistic evaluation of the prospects of this fuel. In particular, it has been concluded in [5] that 'Bremsstrahlung radiation prevents ignition in p-B¹¹'.

This conclusion has been reached on the basis of the cross-sectional data that were available at the time of publications. Since then, a progress in the instrumentation, together with a correct identification of the orbital momentum of the primary alpha-particle as l  =  3 [7–9] have led to a re-evaluation of the cross-sectional data. These new data yielded about 20 percent higher reactivity for Maxwellian plasmas in the relevant temperature range, 300–400 keV, see figure 5 in [9]. In our paper these improved data will be folded into analysis. In particular, the curve for p¹¹B in figure 1 was obtained based on these new data.

Furthermore, we shall account for the fact that the proton distribution may deviate from the Maxwellian in the energy range that makes the main contribution to reactivity. We shall calculate fusion yield by using a proton distribution found from solution of the kinetic equation. The Boron distribution is considered to be very close to Maxwellian because the cross-section for BB collisions scales as Z⁴ and is 625 times larger than that of protons.

In addition to ion kinetic effects we have accounted for relativistic corrections to the collisional processes involving electrons, as the latter typically have temperatures of 100–200 keV in pB¹¹ plasmas. These corrections contribute to enhanced ion–electron energy exchange and thereby to a slight increase of Bremsstrahlung radiation.

We emphasize that our paper is oriented toward magnetic confinement fusion. Accordingly, we assume that the plasma is in a steady state maintained by continuous plasma heating and fueling, balanced against fusion product exhaust. The pB¹¹ reactions are of interest also for high-energy density systems driven by intense pulsed lasers, e.g. [10]. A significant number of alpha particles have been detected at high laser intensities [11–13]; the knock-on collisions of just born alphas with protons and Borons have been identified as a factor that increases the yield [14].

The paper is organized as follows. In section 2.1 the fusion power is evaluated accounting for the aforementioned kinetic corrections; in section 2.2 bremsstrahlung radiation is assessed; in section 2.3 the results of calculations presented in the previous two sections are combined to evaluate the plasma energy balance and conclusion is drawn that ignition and high-Q operation are feasible. Section 3 contains summary and discussion. The details of kinetic calculations are presented in the series of appendices.

In this section we shall repeat the analysis of [5, 6] with the new cross sections [9] and with account for kinetic effects. The proton distribution function for the lower energies is close to Maxwellian and can therefore be characterized by the temperature. The proton 'tail' that makes significant contribution to the reactivity deviates from the Maxwellian distribution. These deviations depend on the temperature of the bulk ions. Following [5], we shall use this bulk ion temperature as a parameter and evaluate fusion power, calculated with account for kinetic modification of the ion tail, and compare the result with Bremsstrahlung radiation. Electron temperature shall be estimated self-consistently from power balance for electrons. As in [5], we neglect other loss channels such as particle losses and synchrotron radiation which are device specific. We thereby check only the necessary condition for ignition in pB¹¹ fuel. This allows us to make direct comparison of our reactivity calculations with those of [5]. This also provides a basis for formulating specifications of the confinement device.

2.1. Fusion power density

The fusion power density is

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle {{P}_{{\rm fus}}}={{n}_{{\rm p}}}{{n}_{{\rm B}}}\left\langle \sigma v \right\rangle Y.\nonumber \end{align} \tag{ 1 }$$

Here

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \left\langle \sigma v \right\rangle ~=~\int{{{f}_{{\rm p}}}\left({{v}_{{\rm p}}} \right){{f}_{{\rm B}}}\left({{v}_{{\rm B}}} \right)\sigma \left(u \right)u{{{\rm d}}^{3}}{{v}_{{\rm p}}}{{{\rm d}}^{3}}{{v}_{{\rm B}}}}.\nonumber \end{align} \tag{ 2 }$$

$u=\left| {{\boldsymbol{v}}_{{\bf p}}}-{{\boldsymbol{v}}_{{\bf B}}} \right|$ and $Y$ is fusion yield, $Y=8.68\ {\rm MeV}$ for pB¹¹. We shall use the new cross section [7–9] shown in figure 2. Error bars of the new measurements are ~3% [9]. Equation (1) contains only a nuclear energy release, but the reacting proton and Boron transfer to reaction products also their initial kinetic energy ~1 MeV which is more than ten percent of the fusion energy release. In our analysis we assume that fusion alphas are confined long enough to transfer this additional energy to both protons and electrons, i.e. the kinetic energy returns back to the reacting plasma and thus does not affect the overall power balance.

Zoom In Zoom Out Reset image size

The peak in the cross section lies in the suprathermal tail of the proton distribution function, ${{f}_{{\rm p}}}\left(v \right)$. When considering kinetic effects in this energy range, one can neglect collisions of the tail particles with each other, and account only for their collisions with the thermal particles. In other words, we consider the energetic ions as 'test particles' in the sea of 'field particles', which include thermal protons, Borons, energetic alpha-particles, and electrons. We assume that thermalized alphas are efficiently removed from the system. We include also collisions with fast alpha-particles, which cause 'lift' of the proton tail. Within this approximation, the kinetic equation for the proton distribution function is:

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \frac{1}{{{v}^{2}}}\frac{\partial}{\partial v}{{v}^{2}}\left[{{D}_{{\rm p}}}\frac{\partial {{f}_{{\rm p}}}}{\partial v}+\frac{{{F}_{{\rm p}}}}{{{m}_{{\rm p}}}}{{f}_{{\rm p}}} \right]-{{\nu}_{{\rm fus}}}\left(v \right){{f}_{{\rm p}}}+S\left(v \right)=0\nonumber \end{align} \tag{ 3 }$$

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle {{D}_{{\rm p}}}={{D}_{{\rm pp}}}+{{D}_{{\rm pB}}}+{{D}_{{\rm pe}}}+D_{{\rm p}\alpha}^{{\rm *}}\nonumber \end{align} \tag{ 4 }$$

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle {{F}_{{\rm p}}}=m_{{\rm p}}^{2}v\left(\frac{{{D}_{{\rm pp}}}+{{D}_{{\rm pB}}}}{T}+\frac{{{D}_{{\rm pe}}}}{{{T}_{{\rm e}}}} \right)+F{{_{{\rm p}\alpha}^{{\rm *}}}_{~}}\nonumber \end{align} \tag{ 5 }$$

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle {{\nu}_{{\rm fus}}}\left(v \right) ~ = ~ \int{{{f}_{{\rm B}}}\left({{v}_{{\rm B}}} \right)\sigma \left(u \right)u{{{\rm d}}^{3}}{{v}_{{\rm B}}}}\approx {{n}_{{\rm B}}}\sigma \left(v \right)v\nonumber \end{align} \tag{ 6 }$$

where the symbols D and F stand for the diffusion and dynamic friction. ${{\nu}_{{\rm fus}}}\left(v \right)$ is the rate of proton burnout (proton loss in fusion reactions), and $S(v)$ is net source of protons (including fueling and loss from the system).

Note that Maxwellian field particles produce diffusion coefficient and dynamic friction that are related by the detailed balance principle. For the collisions with the non-Maxwellian particles (in our case, fast alphas) this relation does not hold. We use an asterisk to distinguish the contribution of the non-thermal alphas. Diffusion coefficients and dynamic frictions are evaluated in appendix A. We consider all the plasma species as isotropic.

Three kinetic effects are important in estimates of deviation of ${{f}_{{\rm p}}}\left({{v}_{{\rm p}}} \right)$ from the Maxwellian and thus must be taken into account.

• The first one is depletion of proton energy tail by cooling on colder electrons (${{T}_{{\rm e}}}<{{T}_{{\rm i}}}$). This effect leads to a reduction of reactivity.
• The second effect is heating of the tail by energetic alpha particles resulting in an increase of tail density and thus the reactivity.
• The third one is depletion of proton energy tail by burnout at maximum cross section. The burnout leads to a small reduction of reactivity.

All these effects are encapsulated in equations (3)–(6) and the distribution function f _p is found with the corresponding corrections included. With regard to the first two effects the net result (suppressing or enhancing of the ion tail) depends on the parameters of the system. For the typical parameters considered in this paper, the net effect is positive and adds ~10% to the reactivity on top of 20% increase related to new cross-section data.

2.2. Bremsstrahlung radiation and ion–electron energy exchange

For the power density of bremsstrahlung radiation we shall use fitting formula from [15] which describes with accuracy better than 1% the quantum mechanical calculations [16] in a wide range of electron temperature and Z_eff.

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle {{P}_{{\rm Brem}}}/{{W}_{0}}=&~8.511{{t}^{1/2}}\left\{{{Z}_{{\rm eff}}}\left(1+1.78{{t}^{1.34}} \right)\right.\nonumber \\ &\left.+2.12t\left(1+1.1t+{{t}^{2}}-1.25{{t}^{2.5}} \right) \right\}.\nonumber \end{align} \tag{ 7 }$$

Here $t={{T}_{{\rm e}}}/m{{c}^{2}}$, ${{W}_{0}}={{e}^{6}}n_{{\rm e}}^{2}/m{{c}^{2}}\hbar$. The popular Rider's formula [17] used in the paper [5] does not give accurate dependence on Z_eff (although, accidentally, it gives a good fit with ${{T}_{{\rm e}}}$ at ${{Z}_{{\rm eff}}}\sim 3$ as in pB¹¹ plasmas!).

Electron temperature in equation (4) is evaluated self-consistently from power balance equation for electrons retaining only the main and unavoidable terms (as in [5])

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle {{P}_{\alpha ,{\rm e}}}+~{{P}_{\boldsymbol{i},{\bf e}}}={{P}_{{\rm Brem}}}.\nonumber \end{align} \tag{ 8 }$$

Here ${{P}_{\alpha ,{\rm e}}}$ is electron heating by the slowing-down alphas, and ${{P}_{\boldsymbol{i},{\bf e}}}$ is electron heating by thermal protons and Borons. We neglect electron energy losses by synchrotron radiation and conduction energy losses assuming that magnetic confinement device is designed to make them low. Only about 10% of initial alpha particle energy is deposited to electrons at ${{T}_{{\rm e}}}=100{{\rm \text {--}}}200\ {\rm keV}$. The rest is going to the ion components. For more accurate calculations of ${{P}_{\alpha ,{\rm e}}}$ we have to account for additional energy in alpha particle source due to finite kinetic energy of reacting protons and Borons (appendix B)

Energy exchange rate between electron and thermal ions corrected for relativistic effects (appendix C) is:

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle {{P}_{{\rm ei}}}=\frac{3}{2}{{\nu}_{{\rm ei}}}\left({{T}_{{\rm i}}}-{{T}_{{\rm e}}} \right)\nonumber \end{align} \tag{ 9 }$$

with

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle {{\nu}_{{\rm ei}}}=\nu _{{\rm ei}}^{*}\frac{\left(1+2{{\widehat{T}}_{{\rm e}}}+2\widehat{T}_{{\rm e}}^{2} \right)\sqrt{\pi \widehat{T}_{{\rm e}}^{3}/2}}{\int_{0}^{\infty}{\rm exp}\left\{-(\sqrt{1+{{x}^{2}}}-1)/{{\widehat{T}}_{{\rm e}}} \right\}{{x}^{2}}{\rm d}x}.\nonumber \end{align} \tag{ 10 }$$

Here $\nu _{{\rm ei}}^{*}$ is classical, non-relativistic exchange rate ([18], equation (2.17)), and ${{\widehat{T}}_{{\rm e}}}={{T}_{{\rm e}}}/m{{c}^{2}}$. The corrected energy exchange is about 10% higher than the classical one (figure 3) and results in somewhat higher electron temperature and thus higher Bremsstrahlung radiation.

Zoom In Zoom Out Reset image size

2.3. Results of calculations

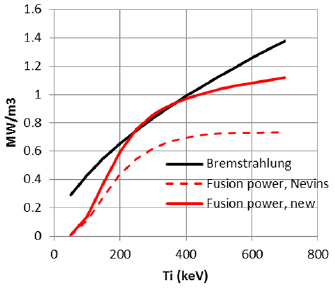
Distribution function of suprathermal protons had been evaluated from equation (3) and used in equation (2) to calculate fusion power. Figure 4 shows comparison of Bremsstrahlung radiation with fusion power as a function of ion temperature. For each ion temperature the electron temperature has been evaluated by equation (8). Calculations are done for optimum Boron concentration, ${{n}_{{\rm B}}}/{{n}_{{\rm i}}}=~15\%$. As in [5], we did not account for He impurity in the ion mix. Increase of fusion reactivity shown in figure 4 is mostly due to higher cross section (~20%). Kinetic effects contribute additional ~10%. The effect of depletion of the ion tail by the burnout effect is less than 1% at the optimum ion temperature T ~ $300~\ {\rm keV}$. As can be seen Bremstrahlung radiation does not preclude ignition in pB¹¹ plasmas.

Zoom In Zoom Out Reset image size

In any steady-state fusion system, an auxiliary power ${{P}_{{\rm aux}}}$ has to be delivered to the plasma for the plasma control, fueling, and compensation of additional losses not included in our model. The relative significance of these external sources can be characterized by the parameter Q defined as

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle Q~=\frac{{{P}_{{\rm fus}}}}{{{P}_{aux}}}.~\nonumber \end{align} \tag{ 11 }$$

Although ignition in pB¹¹ plasma is marginal, a high Q operation can be reached in a broad range of temperatures. The fusion energy release in our case comes out of the system in the form of Bremsstrahlung radiation.

A re-assessment of the basic features of the hot pB¹¹ plasmas leads us to a more optimistic prediction on the feasibility of the pB¹¹ fusion reactor than the earlier analyses, e.g. [4–6]. The main reasons for more optimistic conclusions are two-fold. First, the appearance of the new, more accurate, measurements of the pB¹¹ reaction cross-sections [8, 9] which result in ~20% higher reactivity in a relevant energy range than those used in [5, 6]. The second favorable effect is the kinetic modification of the proton distribution function at energies significantly contributing to the fusion yield. Combined, these factors bring us to a conclusion that, under the same assumption about the plasma confinement as those of [5, 6], the pB¹¹ plasma can come close to the sustained burn and, certainly, can operate as a high-Q system.

One should not of course underestimate the difficulties of reaching an almost perfect plasma confinement assumed both in [5, 6] and in the present paper. However, this belongs with reactor study and should be addressed elsewhere. Here we see that the necessary conditions required for reaching a high-Q performance of the pB¹¹ plasma and even its ignition can be satisfied.

Authors are grateful to Dan Barnes, Erik Trusk, and Michel Tuszewski for helpful comments.

We used assumptions identical to those made by Nevins and Swain [5, 6]: isotropic distribution functions for all species; Maxwellian distributions at thermal energies; equal temperatures of the protons, Borons, and slowed-down alphas:

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle {{T}_{{\rm p}}}={{T}_{{\rm B}}}\equiv T\nonumber \end{align} \tag{ A.1 }$$

different (and lower) self-consistently calculated electron temperature:

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle {{T}_{{\rm e}}}<T.\nonumber \end{align} \tag{ A.2 }$$

Densities: ${{n}_{{\rm p}}},~{{n}_{{\rm B}}},{{n}_{{\rm e}}}={{n}_{{\rm p}}}+{{Z}_{{\rm B}}}{{n}_{{\rm B}}}$. No spatial dependences are considered.

In difference to Nevins and Swain we include into consideration inherently present kinetic effects of proton up-scattering on the non-thermal alpha-particles, and higher-energy proton down-draft by colder electrons. These processes can both increase or decrease the fusion yield by ~10%, depending on the details.

The steady-state kinetic equation for the protons is given by equation (3) in section 2. The normalization of the distribution functions is as follows:

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle {\rm d}{{n}_{{\rm p}}}=4\pi {{f}_{{\rm p}}}\left(v \right){{v}^{2}}{\rm d}v.\nonumber \end{align} \tag{ A.3 }$$

The normalization has the same form for the other components as well.

To find the modification of the proton distribution with respect to Maxwellian, we have to find the diffusion coefficients on the Maxwellian ions for the tail ions; we have also to find contributions from the slowing-down alpha-particles. To do the latter (the most difficult part of the problem), we have to find distribution of the non-thermal alphas and expressions for $D_{{\rm p}\alpha}^{*}$ and $F_{{\rm p}\alpha}^{*}$.

To evaluate the coefficients in equation (3) we use Landau collision integral as presented in a review paper by Trubnikov [19]. The particle flux in the velocity space, $j_{i}^{\rho /\sigma}\left({\bf v} \right)$, is (see equation (11.8) in [19]):

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle j_{i}^{\rho /\sigma}=\frac{2\pi \Lambda Z_{\rho}^{2}Z_{\sigma}^{2}{{e}^{4}}}{{{A}_{\rho}}m_{p}^{2}}\int{{{U}_{ik}}\left(\frac{{{f}_{\rho}}}{{{A}_{\sigma}}}\frac{v_{k}^{\prime}}{{{v}^{\prime}}}\frac{\partial f_{\sigma}^{\prime}}{\partial {{v}^{\prime}}}-\frac{f_{\sigma}^{\prime}}{{{A}_{\rho}}}\frac{{{v}_{k}}}{v}\frac{\partial {{f}_{\rho}}}{\partial v} \right){{{\rm d}}^{3}}{{v}^{\prime}}}.\nonumber \end{align} \tag{ A.4 }$$

The test (field) particles are marked by $\rho ~$ and $\sigma$, respectively, and their velocities by v and v'; we depart from the traditional notation to save the marker 'α' to denote the quantities related to alpha particles.

In the isotropic case the flux is collinear to the velocity vector,

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle j_{i}^{\rho /\sigma}\left({\bf v} \right)={{j}^{\rho /\sigma}}\left({\bf v} \right)\frac{{{v}_{i}}}{v}; ~ {{j}^{\rho /\sigma}}\left(v \right)=j_{i}^{\rho /\sigma}\left({\bf v} \right)\frac{{{v}_{i}}}{v}\nonumber \end{align} \tag{ A.5 }$$

and the kinetic equation becomes:

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \frac{\partial f}{\partial t}+\frac{1}{{{v}^{2}}}\frac{\partial}{\partial v}\left({{v}^{2}}\sum\nolimits_{\sigma}{{{j}^{\rho /\sigma}}\left(v \right)} \right)=S\left(v \right).\nonumber \end{align} \tag{ A.6 }$$

Then, inspecting equations (A.4) and (A.6), one sees that the tensor

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle {{U}_{ik}}=\frac{{{\delta}_{ik}}}{u}-\frac{{{u}_{i}}{{u}_{k}}}{{{u}^{3}}};\quad {\bf u}={\bf v}-{{{\bf v}}^{\prime}}\nonumber \end{align} \tag{ A.7 }$$

enters equation (A.4) only in the form of convolutions ${{U}_{ik}}{{v}_{i}}{{v}_{k~}}$ and ${{U}_{ik}}{{v}_{i}}v_{k}^{\prime}$. Simple algebra shows that

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle {{U}_{ik}}{{v}_{i}}v_{k}^{\prime}={{U}_{ik}}{{v}_{i}}{{v}_{k ~}}= ~ \frac{{{v}^{2}}{{v}^{\prime 2}}-{{\left({\bf v}\cdot {{{\bf v}}^{\prime}} \right)}^{2}}}{{{u}^{3}}}\nonumber \end{align} \tag{ A.8 }$$

which yields the following expression for the diffusion coefficient

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle D_{p\sigma}=\frac{2\pi \Lambda Z_{\rho}^{2}Z_{\sigma}^{2}{{e}^{4}}}{A_{\rho}^{2}m_{{\rm p}}^{2}}\int{\frac{{{v}^{\prime 2}}{\rm si}{{{\rm n}}^{2}}\vartheta}{{{u}^{3}}}{{f}_{\sigma}}\left({{{\bf v}}^{\prime}} \right){{{\rm d}}^{3}}{{{\bf v}}^{\prime}}}~\nonumber \end{align} \tag{ A.9 }$$

where $\vartheta$ is an angle between v and v'.

At this point we note that the integration over v' in equation (A.9) can be represented as

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \mathop{\int}^{}\frac{{{v}^{\prime 2}}{\rm si}{{{\rm n}}^{2}}\vartheta}{{{u}^{3}}}f_{\sigma}^{\prime}\left({{{\bf v}}^{\prime}} \right){{{\rm d}}^{3}}{{{\bf v}}^{\prime}}=2\pi \int_{0}^{\infty}{f_{\alpha}^{\prime}\left({{{\bf v}}^{\prime}} \right)I\left(v,{{v}^{\prime}} \right){\rm d}{{v}^{\prime}}},\nonumber \end{align} \tag{ A.10 }$$

where I is the Rosenbluth–McDonald–Judd ('electrostatic') integral [20]:

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle I=\begin{array}{@{}cccccccccccccccccccc@{}} 4{{v}^{\prime}}/3, & v<{{v}^{\prime}} \nonumber \\ 4{{v}^{\prime 4}}/3{{v}^{3}}, & v>{{v}^{\prime}} \nonumber \\ \end{array}.\nonumber \end{align} \tag{ A.11 }$$

We are now prepared to evaluate the coefficients in equation (3). Using equations (A.9) and (A.11) we find that

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle {{D}_{\rho \sigma}}=\frac{2\pi \Lambda Z_{\rho}^{2}Z_{\sigma}^{2}{{e}^{4}}}{A_{\rho}^{2}m_{{\rm p}}^{2}}\frac{4}{3}2\pi \left[\frac{1}{{{v}^{3}}}\int_{0}^{v}{{{v}^{\prime 4}}{{f}_{\sigma}}\left({{v}^{\prime}} \right){\rm d}{{v}^{\prime}}}+\int_{v}^{\infty}{{{v}^{\prime}}{{f}_{\sigma}}\left({{v}^{\prime}} \right){\rm d}{{v}^{\prime}}} \right].\nonumber \end{align} \tag{ A.12 }$$

This general expression is manageable for the arbitrary velocities of the test particles, but for the first assessment we will use sometime either an appropriate limiting case, or an extrapolation between the two limiting cases.

Analogously, equations (A.4) and (A.6) yield:

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle {{F}_{\rho \sigma}}=&\,-\frac{2\pi \Lambda Z_{\rho}^{2}Z_{\sigma}^{2}{{e}^{4}}}{A_{\rho}^{2}m_{{\rm p}}^{2}}\frac{4}{3}2\pi \left[\frac{1}{{{v}^{2}}}\int_{0}^{v}{{{v}^{\prime 3}}\frac{\partial {{f}_{\sigma}}\left({{v}^{\prime}} \right)}{\partial {{v}^{\prime}}}{\rm d}{{v}^{\prime}}}\right.\nonumber \\ &\left.+v\int_{v}^{\infty}{\frac{\partial {{f}_{\sigma}}\left({{v}^{\prime}} \right)}{\partial {{v}^{\prime}}}{\rm d}{{v}^{\prime}}} \right].\nonumber \end{align} \tag{ A.13 }$$

If the field particles all have velocity higher than velocity of the test particle, then both integrals are obviously zero. In other words, only those field particles that are slower than the test particles contribute to the dynamic force (A.13).

Another representation of the dynamic force can be obtained by the integration by part in equation (A.13). It yields:

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle {{F}_{\rho \sigma}}=\frac{4\pi \Lambda Z_{\rho}^{2}Z_{\sigma}^{2}{{e}^{4}}}{{{A}_{\rho}}{{A}_{\sigma}}m_{{\rm p}}^{2}}\frac{4\pi}{{{v}^{2}}}\int_{0}^{v}{{{v}^{\prime 2}}{{f}_{\sigma}}\left({{v}^{\prime}} \right){\rm d}{{v}^{\prime}}}.\nonumber \end{align} \tag{ A.14 }$$

This representation shows even more clearly that only those of the field particles whose velocity is slower than that of the test particles contribute to the drag force. Another interesting point is that for the Maxwellian distribution of the field particles one can reduce equation (A.12) to a more compact form:

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle {{D}_{\rho \sigma}}=\frac{4\pi \Lambda Z_{\rho}^{2}Z_{\sigma}^{2}{{e}^{4}}}{A_{\rho}^{2}{{A}_{\sigma}}m_{{\rm p}}^{3}}\frac{4\pi {{T}_{\sigma}}}{{{v}^{3}}}\int_{0}^{v}{{{v}^{\prime 2}}{{f}_{\sigma}}\left({{v}^{\prime}} \right){\rm d}{{v}^{\prime}}}.\nonumber \end{align} \tag{ A.15 }$$

In some of the equations below this diffusion coefficient enters in the combination ${{v}^{3}}D$. This combination is proportional to

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \int_{0}^{v}{{{v}^{\prime 2}}{{f}_{\sigma}}\left({{v}^{\prime}} \right){\rm d}{{v}^{\prime}}},\nonumber \end{align} \tag{ A.16 }$$

where subscript $\beta$ refers to the Maxwellian distribution of the particle of the type $\beta$. If the velocity of the test particle is much smaller than the thermal velocity of the field particle,

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle v\ll {{v}_{{\rm T}\sigma}}\equiv \sqrt{2{{T}_{\sigma}}/{{m}_{\sigma}}}\nonumber \end{align} \tag{ A.17 }$$

then the integral (A.16) is approximately equal to

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \left({{v}^{3}}/3 \right){{n}_{\sigma}}{{\left({{m}_{\sigma}}/2\pi {{T}_{\sigma}} \right)}^{3/2}}.\nonumber \end{align} \tag{ A.18 }$$

Conversely, for

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle v\gg {{v}_{{\rm T}\sigma}}\equiv \sqrt{2{{T}_{\sigma}}/{{m}_{\beta}}},\nonumber \end{align} \tag{ A.19 }$$

one can extend integration in the integral (A.16) to infinity and obtain the following expression for this integral:

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle {{n}_{\sigma}}/4\pi .\nonumber \end{align} \tag{ A.20 }$$

One can combine both limits by a simple interpolation:

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \int_{0}^{v}{{{v}^{\prime 2}}{{f}_{\sigma}}\left({{v}^{\prime}} \right){\rm d}{{v}^{\prime}}}\cong \frac{{{n}_{\sigma}}}{4\pi}\frac{{{v}^{3}}}{{{v}^{3}}+\left(3\sqrt{\pi}/4 \right)v_{{\rm T}\sigma}^{3}}.\nonumber \end{align} \tag{ A.21 }$$

We could use an exact value of the integral, but approximation (A.21) has already an accuracy of better than 2%–3% for the relevant velocities.

For the collisions of the suprathermal protons with thermal protons, Borons, and alphas, one has $v~\gg ~{{v}^{\prime}}$, and we obtain the following expressions for the diffusivities:

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle {{D}_{{\rm pp}}}=\frac{4\pi \Lambda {{e}^{4}}T{{n}_{{\rm p}}}}{m_{{\rm p}}^{3}\left[{{v}^{3}}+\left(3\sqrt{\pi}/4 \right)v_{{\rm Tp}}^{3} \right]}\nonumber \end{align} \tag{ A.22 }$$

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle {{D}_{{\rm pB}}}=\frac{4\pi \Lambda Z_{{\rm B}}^{2}{{e}^{4}}T{{n}_{{\rm B}}}}{{{A}_{b}}m_{{\rm p}}^{3}{{v}^{3}}}.\nonumber \end{align} \tag{ A.23 }$$

In equation (A.22) we retain a term accounting for the finite thermal velocity of thermal protons (see definition of the thermal velocity in equation (A.17)). For the proton collisions with the Borons and thermal alpha particles, the corresponding term (accounting for the thermal spread of the Borons and alphas, equation (A.21)) is much smaller and we neglect it.

For collisions with the electrons, the situation is opposite, ${{v}^{\prime}}\gg ~v$, and we get from equation (A.15):

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle {{D}_{{\rm pe}}}&=\eta \left({{T}_{{\rm e}}} \right)\frac{2\pi \Lambda {{e}^{4}}}{m_{{\rm p}}^{2}}\frac{2}{3}4\pi \int_{0}^{\infty}{{{v}^{\prime}}{{f}_{{\rm e}}}\left({{v}^{\prime}} \right){\rm d}{{v}^{\prime}}}\nonumber \\ &=\eta \left({{T}_{{\rm e}}} \right)\frac{8\sqrt{\pi}\Lambda {{e}^{4}}{{n}_{{\rm e}}}}{3m_{{\rm p}}^{2}}\sqrt{\frac{{{m}_{{\rm e}}}}{2{{T}_{{\rm e}}}}}.\nonumber \end{align} \tag{ A.24 }$$

We have introduced here a correction factor $\newcommand{\e}{{\rm e}} \eta \left({{T}_{{\rm e}}} \right)$ related to relativistic effects in the electron distribution functions and in electron–ion collision rates and evaluated in appendix C. For our reference temperature of ${{T}_{{\rm e}}}=150\ {\rm keV}$ it is $\newcommand{\e}{{\rm e}} ~\eta \approx$ 1.1.

Usually the distribution function of high energy alpha particles is evaluated assuming that they are born with the same initial energy (as in DT plasmas) and that their velocity is much higher than ion velocity but lower than electron velocity as in DT plasmas. The slowing down distribution of alpha particles in this approximation is usually expressed as:

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle f_{\alpha 0}=\frac{{{S}_{\alpha}}{{\tau}_{{\rm s}}}}{4\pi \left({{v}^{3}}+v_{*}^{3} \right)}\nonumber \end{align} \tag{ B.1 }$$

at $v<{{v}_{1}}$ and $f_{\alpha 0}=0$ at $v>{{v}_{1}}$, where v₁ is the birth velocity of the alpha particles (see for example [21]). Here ${{S}_{\alpha}}$ is source density, ${{\tau}_{{\rm s}}}$ is slowing down time of alphas on electrons

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle {{\tau}_{{\rm s}}}=\frac{3}{4\sqrt{2\pi}}\frac{{{m}_{\alpha}}}{m_{{\rm e}}^{1/2}}\frac{T_{{\rm e}}^{3/2}}{{{\Lambda}_{{\rm e}}}{{e}^{4}}Z_{\alpha}^{2}{{n}_{{\rm e}}}},\nonumber \end{align} \tag{ B.2 }$$

and

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle {{v}_{{\rm *}}}={{\left(\frac{3\sqrt{\pi}}{4}\frac{{{\Lambda}_{{\rm i}}}}{{{\Lambda}_{{\rm e}}}}\frac{{{m}_{{\rm e}}}}{{{n}_{{\rm e}}}}\sum\nolimits_{\beta}{\frac{Z_{\beta}^{2}{{n}_{\beta}}}{{{m}_{\beta}}}} \right)}^{1/3}}{{\left(\frac{2{{T}_{{\rm e}}}}{{{m}_{{\rm e}}}} \right)}^{1/2}}{\rm .}\nonumber \end{align} \tag{ B.3 }$$

In pB¹¹ plasmas with three alpha particles born in a single reaction event their source spectrum is broad [7–9]. In addition, at ion temperature ${{T}_{{\rm i}}}\sim 200{{\rm \text {--}}}400\ {\rm keV}$ proton velocity can be comparable with velocity of alpha particle with energy of few MeV. Thus equation (B.1) must be corrected.

The just born alpha-particles have a velocity higher than the proton velocity, but at the energy of ${{E}_{1}}\sim 1\ {\rm MeV}$ the situation is reversed, and the protons become faster than alphas. The electrons are much faster than alphas in the whole range of energies. The Borons are universally slower than alpha particles.

In the steady state, the alpha-particle distribution function satisfies the equation:

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \begin{array}{@{}cccccccccccccccccccc@{}} & \frac{1}{{{v}^{2}}}\frac{\partial}{\partial v~}{{v}^{2}}\left[\left({{D}_{\alpha {\rm p}}}+{{D}_{\alpha {\rm B}}}+{{D}_{\alpha {\rm e}}} \right)\frac{\partial {{f}_{\alpha}}}{\partial v}+{{m}_{\alpha}}v\left(\frac{{{D}_{\alpha {\rm p}}}+{{D}_{\alpha {\rm B}}}}{T}+\frac{{{D}_{\alpha {\rm e}}}}{{{T}_{{\rm e}}}} \right){{f}_{\alpha}} \right] \nonumber \\ & -\frac{{{f}_{\alpha}}}{{{\tau}_{\alpha}}\left(v \right)}+\frac{{{S}_{\alpha}}}{4\pi v_{1}^{2}}\delta \left(v-{{v}_{1}} \right)=0. \end{array}\nonumber \end{align} \tag{ B.4 }$$

Here ${{v}_{1}}$ is defined by equation ${{m}_{\alpha}}v_{1}^{2}/2={{E}_{\alpha}}$, and ${{S}_{\alpha}}({{v}_{1}})$ is alpha particle source per unit volume with initial velocity ${{v}_{1}}$.

The second-to-last term in the l.h.s. of equation (B.4) describes alpha-particle losses (without this term they would be accumulated in the system). One can anticipate development of techniques that would allow removal of only slowed-down alphas, so that most of energy released in them would go to plasma heating, and only a small fraction of the fusion yield would be lost by the removal of slow alphas.

Because of low density and high energy of energetic alpha particles we have not included collisions between energetic alpha-particles in equation (B.4).

Using equations of appendix A, we find the following expression for the alpha-particle diffusivity for the fast alpha particles:

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle D_{\alpha {\rm p}}^{\left({\rm f} \right)}=\frac{4\pi \Lambda {{e}^{4}}Z_{\alpha}^{2}{{n}_{{\rm p}}}T}{A_{\alpha}^{2}m_{{\rm p}}^{3}{{v}^{3}}}.\nonumber \end{align} \tag{ B.5 }$$

This expression describes diffusion of alpha particles with velocities exceeding the ion thermal velocity, i.e. the alphas with the energy exceeding roughly 1 MeV (the superscript 'f ' means 'fast'.

When the alphas slow down below this energy limit, their further diffusion is described by the expression:

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle D_{\alpha {\rm p}}^{\left({\rm s} \right)}=\frac{8\sqrt{\pi} \Lambda Z_{\alpha}^{2}{{e}^{4}}{{n}_{{\rm p}}}}{3A_{\alpha}^{2}m_{{\rm p}}^{2}}\sqrt{\frac{{{m}_{{\rm p}}}}{2T}}.\nonumber \end{align} \tag{ B.6 }$$

One can combine equations (B.5) and (B.6) into one equation that covers both the case of fast and slow alphas. The interpolation formula is:

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle {{D}_{\alpha {\rm p}}}=\frac{4\pi \Lambda {{e}^{4}}Z_{\alpha}^{2}{{n}_{{\rm p}}}T}{A_{\alpha}^{2}m_{{\rm p}}^{3}{{v}^{3}}}\frac{1}{{{v}^{3}}+\left(3\sqrt{\pi}/4 \right)v_{{\rm th},{\rm p}}^{3}}.\nonumber \end{align} \tag{ B.7 }$$

The thermal velocity of protons is ${{v}_{{\rm Tp}}}=\sqrt{2T/{{m}_{{\rm p}}}}$. Note also that $v/{{v}_{{\rm Tp}}}=1$ corresponds to the alpha-particle energy of 4T.

A similar diffusion coefficient can be adopted for Borons, although correction for finite Boron velocity is small as noted above

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle {{D}_{\alpha {\rm B}}}=\frac{4\pi \Lambda {{e}^{4}}Z_{\alpha}^{2}Z_{{\rm B}}^{2}{{n}_{{\rm B}}}T}{A_{\alpha}^{2}{{A}_{{\rm B}}}m_{{\rm p}}^{3}{{v}^{3}}}\frac{1}{{{v}^{3}}+\left(3\sqrt{\pi}/4 \right)v_{{\rm TB}}^{3}}.\nonumber \end{align} \tag{ B.8 }$$

Diffusion on the electrons occurs with a coefficient (see appendix A)

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle {{D}_{\alpha {\rm e}}}=\eta \left({{T}_{{\rm e}}} \right)\frac{8\sqrt{\pi} \Lambda Z_{\alpha}^{2}{{e}^{4}}{{n}_{{\rm e}}}}{3A_{\alpha}^{2}m_{{\rm p}}^{2}}\sqrt{\frac{{{m}_{{\rm e}}}}{2{{T}_{{\rm e}}}}}.\nonumber \end{align} \tag{ B.9 }$$

Now we can turn to solving equation (B.4). We note that the loss rate $\propto 1/\tau$ is small in comparison with slowing down rate $\propto 1/{{\tau}_{{\rm s}}}$ by collisional processes and it can be neglected. For the highly suprathermal alpha-particles one can drop the diffusive term in this equation and retain only dynamic friction. This yields a corrected slowing-down distribution in the familiar form:

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle {{f}_{\alpha}}=\frac{{{S}_{\alpha}}{{\tau}_{{\rm s}}}}{4\pi \left({{v}^{3}}+v_{{\rm *}}^{3} \Delta \left(v \right) \right)}\nonumber \end{align} \tag{ B.10 }$$

where correction factor $\Delta (v)$ is

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \Delta \left(v \right)=\frac{\sum\nolimits_{\beta}\frac{{{n}_{\beta}}Z_{\beta}^{2}}{{{m}_{\beta}}}\frac{{{v}^{3}}}{{{v}^{3}}+\left(3\sqrt{\pi}/4 \right)v_{{\rm T}\beta}^{3}}}{\sum\nolimits_{\beta}\frac{{{n}_{\beta}}Z_{\beta}^{2}}{{{m}_{\beta}}}}.\nonumber \end{align} \tag{ B.11 }$$

At $v\gg {{v}_{{\rm T}}}$ we have $\Delta \left(v \right)\to 1$ and equation (B.10) becomes equation (B.1). The correction for finite thermal ion velocity is important only for protons.

Figure B1 shows correction factor, $\Delta \left(v \right)$, and ratio of corrected distribution function, equation (B.10), to the one given by equation (B.1). The calculations are done for $T=300\ {\rm keV},~{{T}_{{\rm e}}}=~150 ~{\rm keV}$, initial alpha particle energy 4 MeV, and Boron concentration ${{n}_{{\rm B}}}/{{n}_{{\rm i}}}=~0.15$. One can see that the effect of finite proton velocity is significant. Note, however, that the power transferred by the alphas to protons and electrons contains an integration of the alpha distribution function with the weight v², so that the effect of the lower alpha velocities is suppressed, and the net heating power of either electrons or ions is still determined by v/v₁ in the range of 0.7–1, where the correction is modest. The net effect is a roughly ten percent increase of the proton and electron heating (a favorable effect).

Zoom In Zoom Out Reset image size

Expression (B.10) should be considered as a Green function and the slowing down distribution can be evaluated by integrating distribution function (B.10) with the energy spectrum of the alpha particle source in the laboratory frame. The energy spectrum of the source can be evaluated using the alpha particle source presented in [9], ${{S}_{{\rm net}}}\left(E \right)$, with account of the gain by alpha particles as an additional kinetic energy from colliding protons and Borons which are assumed at the moment to be Maxwellian with temperatures T. This kinetic addition is sizeable at the high energy where cross section has its peak. Using relative velocity, u, and velocity of CM of colliding particles, v, the source spectrum in the lab frame can be defined as:

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \begin{array}{@{}llcccccccccccccccccc@{}} & {{S}_{{\rm lab}}}\left(E \right) \nonumber \\ & =\frac{\frac{4}{{{\pi}^{1/2}}}\int_{0}^{\infty}{{S}_{{\rm net}}}\left(E-\frac{1}{3}T{{\widehat{v}}^{2}}-\frac{1}{3}T{{\widehat{u}}^{2}} \right){\rm exp}\left\{-{{\widehat{v}}^{2}}-{{\widehat{u}}^{2}} \right\}{{\widehat{v}}^{2}}\sigma \left(u \right){{\widehat{u}}^{3}}{\rm d}\widehat{u}{\rm d}\widehat{v}}{\int_{0}^{\infty}{\rm exp}\left(-{{\widehat{u}}^{2}} \right)\sigma \left(u \right){{\widehat{u}}^{3}}{\rm d}\widehat{u}}. \end{array}\nonumber \end{align} \tag{ B.12 }$$

We have normalized all velocities on their thermal velocities. If ${{S}_{{\rm net}}}$ is normalized as $\int{{{S}_{{\rm net}}}{\rm d}E}=1$ then ${{S}_{{\rm lab}}}$ is also normalized on 1. The average energy of alpha particle accounting for finite temperature of reagents will be

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle {{\left\langle E \right\rangle}_{{\rm lab}}}={{\left\langle E \right\rangle}_{{\rm net}}}+\frac{T}{2}+\frac{T}{3}\frac{\int_{0}^{\infty}\exp \left(-{{\widehat{u}}^{2}} \right)\sigma \left(u \right){{\widehat{u}}^{5}}{\rm d}\widehat{u}}{\int_{0}^{\infty}{\rm exp}\left(-{{\widehat{u}}^{2}} \right)\sigma \left(u \right){{\widehat{u}}^{3}}{\rm d}\widehat{u}}.\nonumber \end{align} \tag{ B.13 }$$

The three alphas get additional 3T/2 from Doppler shift (second term) and energy of relative motion weighted by cross section.

Figure B2 compares the alpha particle spectrum at T  =  325 keV with the one based on the data presented in [9] (T  =  0).

Zoom In Zoom Out Reset image size

To get the slowing down distribution function we integrated equation (B.10) with the spectrum equation (B.12),

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle {{f}_{\alpha}}=\int_{m{{v}^{2}}/2}^{\infty}{\frac{{{S}_{{\rm lab}}}\left(E \right){{\tau}_{{\rm s}}}{\rm d}E}{4\pi \left({{v}^{3}}+v_{*}^{3}\Delta \left(v \right) \right)}}.\nonumber \end{align}$$

This appendix is concerned with the energy exchange rate between the heavy non-relativistic ions and sub-relativistic electrons. The electron temperature anticipated for the pB¹¹ reactors is ${{T}_{{\rm e}}}=150\ {\rm keV}$, so that a part of an electron Maxwellian distribution occupies energies exceeding 500 keV. The significance of this effect has been pointed out to us by Barnes (private communication).

The relativistic Maxwellian momentum distribution is:

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle f\left(\,p \right)=nC\left({{T}_{{\rm e}}} \right){\rm exp}\left\{-\frac{\sqrt{{{m}^{2}}{{c}^{4}}+{{p}^{2}}{{c}^{2}}}-m{{c}^{2}}}{{{T}_{{\rm e}}}} \right\}\nonumber \end{align} \tag{ C.1 }$$

where p  is a momentum and C(T_e) is a normalization factor determined from the following condition:

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \int{f{{{\rm d}}^{3}}\boldsymbol{p}}=n.\nonumber \end{align} \tag{ C.2 }$$

The last term mc² in the exponent of equation (C.1) is introduced to make the distribution function matching both non-relativistic and ultra-relativistic limits.

In normalized variables

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \widehat{p}=\frac{p}{mc},{{\widehat{T}}_{{\rm e}}}=\frac{{{T}_{{\rm e}}}}{m{{c}^{2}}}\nonumber \end{align} \tag{ C.3 }$$

the normalization constant becomes:

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle C&={{\left(mc \right)}^{-3}}{{\left[4\pi \int_{0}^{\infty}{{{\widehat{p}}^{2}}{\rm exp}\left\{-\frac{\sqrt{1+{{\widehat{p}}^{2}}}-1}{{{\widehat{T}}_{{\rm e}}}} \right\}{\rm d}\widehat{p}} \right]}^{-1}}\nonumber \\ &={{\left(mc \right)}^{-3}}\widehat{C}\left({{\widehat{T}}_{{\rm e}}} \right).\nonumber \end{align} \tag{ C.4 }$$

We are going to evaluate the energy exchange rate between the ions and electrons which is described by the equation

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle {{\dot{T}}_{{\rm i}}}=-\nu _{{\rm ei}}^{\left({\rm E} \right)}\left({{T}_{{\rm i}}}-{{T}_{{\rm e}}} \right).\nonumber \end{align} \tag{ C.5 }$$

The first term comes from the dynamic friction of the ions versus electrons, whereas the second one comes from the ion diffusion produced by random electron 'kicks'. The structure of this equation is consistent with the detailed balance principle. To find the parameter $\nu _{{\rm ei}}^{\left({\rm E} \right)}$ it is sufficient to assess one of the two processes (dynamic friction and scattering). Below we evaluate the second term.

The ion velocity is small compared to the electron velocity. The energy transfer to the ion can then be evaluated for the resting ion. We use a technique described in [22]. It is based on the fact that the main contribution to the electron scattering on the Coulomb center comes from the large impact parameter and small scattering angles. For large impact parameters the electron deflection can be found perturbatively. The momentum p _i acquired by the ion is

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle {{p}_{{\rm i}}}=\frac{2Z{{e}^{2}}}{av}\nonumber \end{align} \tag{ C.6 }$$

where v is the electron velocity and a is impact parameter. Accordingly, the energy acquired by the ion with atomic mass A is

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle ~\Delta W=\frac{2{{Z}^{2}}{{e}^{4}}}{A{{m}_{{\rm p}}}{{a}^{2}}{{v}^{2}}}.\nonumber \end{align} \tag{ C.7 }$$

The velocity v is related to the electron momentum by:

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle v=pc/\sqrt{{{p}^{2}}+{{m}^{2}}{{c}^{2}}}.\nonumber \end{align} \tag{ C.8 }$$

Integrating by the impact parameters and electron distribution function, we find the rate of the ion energy increase:

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle ~\dot{W}&=\frac{2{{Z}^{2}}{{e}^{4}}}{A{{m}_{{\rm p}}}}\int{\frac{2\pi {\rm d}a}{a}}\int_{0}^{\infty}{\frac{4\pi {{p}^{2}}}{v}f\left(\,p \right){\rm d}p}\nonumber \\ &=\frac{4\pi \Lambda {{Z}^{2}}{{e}^{4}}}{A{{m}_{{\rm p}}}}\int_{0}^{\infty}{\frac{4\pi {{p}^{2}}}{v}f\left(\,p \right){\rm d}p},\nonumber \end{align} \tag{ C.9 }$$

where $\Lambda$ is the Coulomb logarithm. Then, noting that for Maxwellian ions ${{\dot{T}}_{{\rm i}}}=\left(2/3 \right)\dot{W}$, and using expression (C.1) for the distribution function, we find after some algebra:

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \nu _{{\rm ei}}^{\left({\rm E} \right)}=\frac{2nmc}{3M}\cdot \frac{4\pi \Lambda {{Z}^{2}}{{e}^{4}}}{{{\left(m{{c}^{2}} \right)}^{2}}}\cdot \frac{\left(1+2{{\widehat{T}}_{{\rm e}}}+2\widehat{T}_{{\rm e}}^{2} \right)}{\int_{0}^{\infty}{\rm exp}\left\{-\frac{\sqrt{1+{{p}^{2}}}-1}{{{\widehat{T}}_{{\rm e}}}} \right\}{{\widehat{p}}^{2}}{\rm d}\widehat{p}}.\nonumber \end{align} \tag{ C.10 }$$

In the non-relativistic limit the exchange rate (we will use a notation $\nu _{{\rm ei}}^{\left({\rm E} \right)*}$ for it) coincides with well-known results presented in Braginski's review [18]. In Braginski's notation we have $\nu _{{\rm ei}}^{\left({\rm E} \right)*}=2\left({{m}_{{\rm e}}}/{{m}_{{\rm i}}}{{\tau}_{{\rm e}}} \right)$, see equations (4.5) and (4.8) in [18]. The ratio $\nu _{{\rm ei}}^{\left({\rm E} \right)}/\nu _{{\rm ei}}^{\left({\rm E} \right)*}$ is used in equation (9) in section 2.2.