Abstract
The two-plasmon decay (TPD) instability of the backscattered light of the simulated Raman scattering (SRS) is first investigated with the help of one-dimensional (1D) and two-dimensional (2D) particle-in-cell (PIC) simulations. The 2D PIC simulation results show that the backscattered light of the SRS does excite TPD instability. Further, the comparison between 1D and 2D PIC simulation results shows that the backward SRS is suppressed by the excitation of TPD instability, which means the TPD instability of the scattered light could be a saturation scheme of SRS. It is also shown that, after the excitation of TPD, the electrons could experience a two-stage or even three-stage acceleration and their energy may reach to or even exceed 100 KeV, which means the TPD instability of the backscattered light could be a source of super-hot electrons.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Laser plasma instabilities (LPIs) have been hot topics because they have great influences on the inertial confinement fusion (ICF). Although there are several means of achieving ICF, such as the direct-drive [1], the indirect-drive [2] and the newly proposed hybrid-drive [3, 4], LPIs still cannot be avoided. In the ICF process, LPIs such as backward stimulated Raman scattering (BSRS), forward stimulated Raman scattering (FSRS) or the two-plasmon decay instability could be detrimental effects during the laser propagation [5] and implosion processes [6, 7]; thus, it is very important to study the properties of LPIs and find out ways to suppress LPIs. Even though significant progress in LPI studies have been achieved in recent decades [8–11], there are still many unexplained phenomena in ICF experiments [7, 12, 13, 14], because many LPIs are sensitive to plasma densities and temperatures which are too complex and uncontrollable in experiments. For example, SRS instability only happens below the quarter critical density of the laser, simulated Brillouin scattering (SBS) only occurs below the critical density of the laser and TPD instability near the quarter critical density of the laser [15]. As a result, studies regarding TPD instability are mainly concentrated in direct-drive ICF and shock ignition ICF [16–21], because in these two ignition schemes the laser has opportunities to propagate in the plasma with quarter critical density. In indirect-drive ICF, the plasma density in the hohlraum is usually under the quarter critical density [1, 12, 22], so it is difficult to observe TPD instability of the laser; as a result, the TPD instability is usually ignored in indirect-drive ICF.
Although it is difficult for the laser itself to decay into a couple of electron plasma waves (EPWs) by TPD in the hohlraum, it is possible for its scattered lights to do this because scattered light usually has a lower critical density. Once the TPD instability of the scattered light of BSRS or FSRS occurs, the EPWs generated by TPD may trap electrons to generate super-hot electrons. In [23], it is shown that, in the indirect-drive experiment [12], the super-hot electron with energies exceeding 100 KeV may be generated by rescattering SRS. Essentially, TPD instability of BSRS or FSRS could also be an explanation for the generation of these electrons. Besides, when the scattered light has decayed, the BSRS or FSRS may be suppressed, so the TPD instability may also be a saturation scheme of BSRS or FSRS. Therefore, it is important and necessary to discuss the TPD instability of the scattered light of BSRS or FSRS. However, to the best of our knowledge, on one has ever investigated the TPD instability of scattered light in BSRS or FSRS; this will be the discussion of this paper. We investigate the TPD instability of backscattered light of SRS with the help of 1D and 2D PIC simulations [24]. Since TPD is a 2D instability, it is difficult to simulate the TPD process of the backscattered light of SRS with whole 2D PIC codes or other 2D codes, because the excitation of SRS will take a long simulation time, especially when the laser intensity is low. So, to save simulation time, we need a 1D PIC simulation to investigate the excitation of SRS and the electron heating only by SRS at first, and then give an estimation of the total simulation time of the 2D PIC simulation. The results of the 1D PIC simulation shows that both BSRS and FSRS occur during the laserâ€"plasma interaction. However, the spectrum of BSRS will be broadened because of the excitation of electron beam acoustic modes (BAMs) [25] at a later time. The BAM is caused by the electron trapping effects. However, even if some electrons are trapped by the EPW of the BSRS and their energy is raised, they still cannot be trapped again by the EPW of the FSRS; this is because the phase velocity of the EPW of FSRS is still too far away from the electron thermal velocity. Therefore, it is difficult to generate super-hot electrons only by SRS. However, the results of the 2D PIC simulation show that a new couple of EPWs are generated by TDP. At this time, the phase velocities of these EPWs are no longer too far away from the thermal velocity of the preheated electrons, so it is possible to generate super-hot electrons with the energy exceeds 100 KeV according to the formula  [23], where
[23], where  is the maximum energy of the trapped electrons, me is the electron mass,
is the maximum energy of the trapped electrons, me is the electron mass, 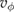 is the phase velocity of the EPW, e is the electron charge and
is the phase velocity of the EPW, e is the electron charge and 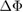 is the difference between the maximum and minimum value of EPW. The 2D PIC simulation also shows that none of the EPWs have the maximum growth rate
is the difference between the maximum and minimum value of EPW. The 2D PIC simulation also shows that none of the EPWs have the maximum growth rate  , where k0 is the laser wave number and vos is the electron's quiver velocity. Instead, the grow rate is about 99.67
, where k0 is the laser wave number and vos is the electron's quiver velocity. Instead, the grow rate is about 99.67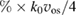 . The comparison between the 1D and 2D PIC simulations also shows that the BSRS is suppressed by the TPD instability.
. The comparison between the 1D and 2D PIC simulations also shows that the BSRS is suppressed by the TPD instability.
The paper is arranged as follows. In section 2, we theoretically discuss the possibility of TPD instability on the backscattered light of BSRS. In section 3 we show the results of the 1D PIC simulation and in section 4, we discuss the results of the 2D PIC simulation. The last two sections are the conclusion and acknowledgments.
2. Possibility of the TPD instability of the scattered light of BSRS
As is well known, TPD instability happens only near the quarter critical density, i.e. only when a laser with the frequency 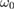 propagates in a plasma with the electron density
propagates in a plasma with the electron density  , where
, where  is the critical density, the TPD instability may be excited. To discuss the TPD instability of the backscattered light of BSRS, we should begin with the matching conditions of BSRS:
is the critical density, the TPD instability may be excited. To discuss the TPD instability of the backscattered light of BSRS, we should begin with the matching conditions of BSRS:





where k0, ks and kL are the wave numbers of the laser, the backscattered light and the EPW, respectively,  and
and 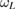 are the frequencies of the backscattered light and the EPW, respectively,
are the frequencies of the backscattered light and the EPW, respectively, 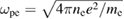 is the plasma frequency and vte is the thermal velocity of the electrons. If TPD can be excited by the backscattered light, we have
is the plasma frequency and vte is the thermal velocity of the electrons. If TPD can be excited by the backscattered light, we have  . Substituting
. Substituting  into the three wave matching condition, we have
into the three wave matching condition, we have 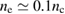 . So it is possible for TPD to be excited by the backscattered light of BSRS in the same plasma, only if the plasma density is near
. So it is possible for TPD to be excited by the backscattered light of BSRS in the same plasma, only if the plasma density is near 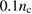 .
.
To further discuss the possibility of the TPD instability of the backscattered light, we also need to discuss the threshold of this kind of instability. As is known that the linear growth rate of TPD is:
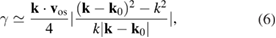
where  is the wave number of the EPW, k is the length of
is the wave number of the EPW, k is the length of  ,
, 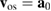 is the quivering velocity of the electrons and
is the quivering velocity of the electrons and 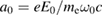 is the normalized vector potential. With the matching condition
is the normalized vector potential. With the matching condition  , it is easy to know from equation (6) that the two EPWs generated by TPD have the same growth rate. Suppose
, it is easy to know from equation (6) that the two EPWs generated by TPD have the same growth rate. Suppose 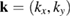 , then the maximum growth rate is on the hyperbola curve [11]:
, then the maximum growth rate is on the hyperbola curve [11]:
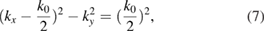
and the maximum growth rate is 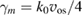 . The threshold of TPD is
. The threshold of TPD is  , where
, where  and
and  are damping rates of the two EPWs. Since we do not consider the collisional effects (as the characteristic electronâ€"ion collision time is much larger than the growth time of the instabilities [17] here) and nonlinear effects,
are damping rates of the two EPWs. Since we do not consider the collisional effects (as the characteristic electronâ€"ion collision time is much larger than the growth time of the instabilities [17] here) and nonlinear effects, 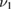 and
and 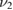 are considered as the linear Landau damping rates, which are decided by the formula:
are considered as the linear Landau damping rates, which are decided by the formula:
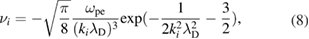
where 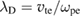 is the Debye length and ki (
is the Debye length and ki ( ) is the wave number of the ith EPW generated by TPD. When
) is the wave number of the ith EPW generated by TPD. When 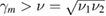 , TPD is possible to be excited. Suppose
, TPD is possible to be excited. Suppose  is the wave vector of the EPW on the maximum growth rate curve and the angle between
is the wave vector of the EPW on the maximum growth rate curve and the angle between  and
and  is θ (
is θ ( ), then we have
), then we have  . Substituting
. Substituting  into equation (7), we have
into equation (7), we have  . Then from
. Then from  we have
we have 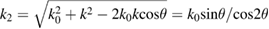 . Substituting k and k2 into equation (8), we obtain the relationship between θ and ν. Then from the matching condition of TPD together with the dispersion relations of the EPW and the laser, we also know that, for an EPW generated by TPD, the wave number
. Substituting k and k2 into equation (8), we obtain the relationship between θ and ν. Then from the matching condition of TPD together with the dispersion relations of the EPW and the laser, we also know that, for an EPW generated by TPD, the wave number  should be on the cycle:
should be on the cycle:
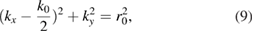
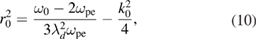
where  is the Debye length of the plasma. Substituting
is the Debye length of the plasma. Substituting  into equation (9), we have
into equation (9), we have  , where
, where  . Since
. Since  , we have
, we have  . Substituting
. Substituting  into equation (10), it is easy to know that, if TPD occurs with the maximum growth rate, the electron density and the thermal velocity will satisfy the following inequation:
into equation (10), it is easy to know that, if TPD occurs with the maximum growth rate, the electron density and the thermal velocity will satisfy the following inequation:

where vte is normalized by the light velocity and ne is normalized by the critical density. The possible electron density and temperature region for TPD instability is noted in figure 1(a). It should be mentioned that when equation (11) is applied to the scattered lights (both backward and forward) of SRS, one can easily get the electron density range for scattered lights of SRS to excited TPD instability, it is 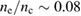 –0.11. Thus, the applicability of this mechanism is not very broad. From
–0.11. Thus, the applicability of this mechanism is not very broad. From 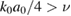 ,
,  ,
,  and
and  , we also get the threshold for different electron densities and temperatures, which is shown in figure 1(b). From figure 1 we can find that, when the electron density and temperature are proper, the threshold of TPD is pretty low, especially when k is small. For a laser whose intensity is
, we also get the threshold for different electron densities and temperatures, which is shown in figure 1(b). From figure 1 we can find that, when the electron density and temperature are proper, the threshold of TPD is pretty low, especially when k is small. For a laser whose intensity is  W cm−2
W cm−2 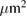 , even if only 1% (corresponding
, even if only 1% (corresponding 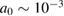 ) of the laser is backscattered (or forward scattered), the intensity of the scattered lights will reach the threshold of TPD. To be more realistic, the threshold caused by the plasma density gradient should also be discussed because the plasma density is no longer uniform after the excitation of SRS. The TPD threshold in nonuniform plasmas is
) of the laser is backscattered (or forward scattered), the intensity of the scattered lights will reach the threshold of TPD. To be more realistic, the threshold caused by the plasma density gradient should also be discussed because the plasma density is no longer uniform after the excitation of SRS. The TPD threshold in nonuniform plasmas is 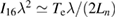 [17, 29, 30], where
[17, 29, 30], where 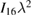 is the laser intensity in units of 1016 W cm−2
is the laser intensity in units of 1016 W cm−2 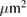 , λ is the laser wave length in units of microns, Te is in units of KeV and the density scale length
, λ is the laser wave length in units of microns, Te is in units of KeV and the density scale length  is also in units of microns. To get the scale length after the excitation of SRS, we suppose the plasma density is perturbed from n0 to
is also in units of microns. To get the scale length after the excitation of SRS, we suppose the plasma density is perturbed from n0 to  , where kL is the wave number of the EPW of SRS, then the scale length is
, where kL is the wave number of the EPW of SRS, then the scale length is ![$L_n\simeq (n_0/\delta n)[{{\rm sec}}(k_Lx)/k_L]$](https://content.cld.iop.org/journals/0029-5515/58/9/096035/revision2/nfaad059ieqn063.gif) . It can be deduced that the smaller
. It can be deduced that the smaller 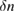 is (or the weaker the EPW is), the lower the threshold is. Also, for the region near
is (or the weaker the EPW is), the lower the threshold is. Also, for the region near  , the scale length will approximate infinity, which means the threshold will approximate to zero. Therefore, this kind of instability is possible and easily observed in indirect-driven ICF. It is also necessary to be mentioned that, in a gas-filled hohlraum in indirect-driven ICF, hydrodynamics will naturally impose gradients in plasma density even if the gas fill is initially uniform. The gradients in plasma density caused by this means should also be considered, because it will also affect the TPD threshold. At this time, the density scale length could not be too large and the threshold will be larger, so more scattered energy is needed for the excitation of TPD.
, the scale length will approximate infinity, which means the threshold will approximate to zero. Therefore, this kind of instability is possible and easily observed in indirect-driven ICF. It is also necessary to be mentioned that, in a gas-filled hohlraum in indirect-driven ICF, hydrodynamics will naturally impose gradients in plasma density even if the gas fill is initially uniform. The gradients in plasma density caused by this means should also be considered, because it will also affect the TPD threshold. At this time, the density scale length could not be too large and the threshold will be larger, so more scattered energy is needed for the excitation of TPD.
Figure 1. Conditions and threshold of TPD instability. (a) Distribution of the function  , where Te is normalized by
, where Te is normalized by  and ne is normalized by ne. When f < 0, TPD is possible to happen, which is the region under the white line shown in the figure. (b) The threshold of TPD instability for different electron densities in different temperatures. When
and ne is normalized by ne. When f < 0, TPD is possible to happen, which is the region under the white line shown in the figure. (b) The threshold of TPD instability for different electron densities in different temperatures. When 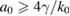 , TPD is possible.
, TPD is possible.
Download figure:
Standard image High-resolution image3. Results of 1D PIC simulation
To estimate the total simulation time of the 2D PIC simulation and investigate the suppression of the BSRS instability, we will first use a 1D PIC simulation to investigate the evolution of the SRS instability (including BSRS and FSRS) and the electron heating by the EPWs of SRS. The simulation parameters are as follows. In the 1D simulation, the laser is a plane wave with an infinite duration. The normalized vector potential of the laser is a0 = 0.02 and the wavelength is  nm, which means the laser intensity is
nm, which means the laser intensity is  W cm−2. The higher the laser intensity is, the faster the SRS grows. To shorten the simulation time, the laser intensity used here is higher than that used in indirect-driven ICF but close to that used in shock ignition, so this kind of instability may also be observed in shock ignition regime. Actually, in SGIII facilities [26], this intensity is nearly reachable in the indirect-driven ICF experiments [27]. The electron density is
W cm−2. The higher the laser intensity is, the faster the SRS grows. To shorten the simulation time, the laser intensity used here is higher than that used in indirect-driven ICF but close to that used in shock ignition, so this kind of instability may also be observed in shock ignition regime. Actually, in SGIII facilities [26], this intensity is nearly reachable in the indirect-driven ICF experiments [27]. The electron density is 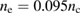 and the ions are fixed in the simulation to exclude the SBS and Langmuir decay instability (LDI) [28]. The electron temperature is
and the ions are fixed in the simulation to exclude the SBS and Langmuir decay instability (LDI) [28]. The electron temperature is 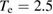 KeV and the ion temperature is Ti = 100 eV. For this electron density and temperature, the critical density of the scattered lights of FSRS and BSRS are
KeV and the ion temperature is Ti = 100 eV. For this electron density and temperature, the critical density of the scattered lights of FSRS and BSRS are 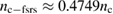 and
and 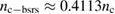 , which means
, which means  and
and  . From figure 1 we know that TPD is possibly excited by both scattered lights, however, the scattered light of BSRS will excite TPD more easily because the threshold is much lower. The simulation box is located between x = 0 to
. From figure 1 we know that TPD is possibly excited by both scattered lights, however, the scattered light of BSRS will excite TPD more easily because the threshold is much lower. The simulation box is located between x = 0 to  along x axis and the plasma is located between
along x axis and the plasma is located between 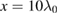 to
to  . For such a short distance, the plasma density is possible to be uniform especially in a gas-filled hohlraum in an ICF experiment. The grid step of the simulation box is
. For such a short distance, the plasma density is possible to be uniform especially in a gas-filled hohlraum in an ICF experiment. The grid step of the simulation box is 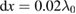 and there are 2000 particles in each cell. The total simulation time is 3 ps and the simulation results are shown in figure 2.
and there are 2000 particles in each cell. The total simulation time is 3 ps and the simulation results are shown in figure 2.
Figure 2. (a) The wave number spectra of the transverse electric field Ey for different moments. The wave numbers of the backward and forward scattered lights are noted by the green lines. (b) The wave number spectra of the longitudinal electric field Ex for different moments. (c) The electron phase space  and the corresponding distribution function
and the corresponding distribution function  at t = 1000T0, when BSRS is very weak. Both functions are in arbitrary units. (d) The electron phase space
at t = 1000T0, when BSRS is very weak. Both functions are in arbitrary units. (d) The electron phase space  and the corresponding distribution function
and the corresponding distribution function 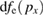 at t = 1300T0, when BSRS becomes nonlinear.
at t = 1300T0, when BSRS becomes nonlinear.
Download figure:
Standard image High-resolution imageFigures 2(a) and (b) show wave number spectra of the electromagnetic (E.M.) field Ey and the electrostatic field Ex at four different moments, which are t = 1000T0, t = 1300T0, t = 1600T0 and t = 1900T0, where 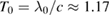 fs is the laser cycle. It is shown that both FSRS and BSRS are excited during the laserâ€"plasma interaction. FSRS seems to be excited earlier, as shown by the blue solid lines in figures 2(a) and (b). It is shown that, at t = 1000T0, both the scattered light and the EPW of FSRS are more intense, especially, the EPW of BSRS is nearly zero. However, BSRS grows much faster, it is shown that at
fs is the laser cycle. It is shown that both FSRS and BSRS are excited during the laserâ€"plasma interaction. FSRS seems to be excited earlier, as shown by the blue solid lines in figures 2(a) and (b). It is shown that, at t = 1000T0, both the scattered light and the EPW of FSRS are more intense, especially, the EPW of BSRS is nearly zero. However, BSRS grows much faster, it is shown that at 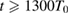 , the intensity of BSRS grows much higher than FSRS. Since the phase velocity of the EPW of BSRS (which is
, the intensity of BSRS grows much higher than FSRS. Since the phase velocity of the EPW of BSRS (which is  ) is much closer to the electron thermal velocity (which is
) is much closer to the electron thermal velocity (which is 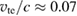 ), the EPW of BSRS will trap electrons more easily. As time goes on, more and more electrons are trapped into the EPW of BSRS, which will cause the generation of electron beam acoustic modes (BAMs) [25]. As a result, we can see that the spectra of both the scattered light and the EPW of the BSRS are broadened. As to FSRS, it is easy to see from figure 2(b) that its phase velocity of EPW
), the EPW of BSRS will trap electrons more easily. As time goes on, more and more electrons are trapped into the EPW of BSRS, which will cause the generation of electron beam acoustic modes (BAMs) [25]. As a result, we can see that the spectra of both the scattered light and the EPW of the BSRS are broadened. As to FSRS, it is easy to see from figure 2(b) that its phase velocity of EPW  is much larger than thermal velocity, so it is more difficult for the EPW of FSRS to trap electrons. As a result, the FSRS grows more linearly, we see no broadened spectra for both the scattered light and the EPW of FSRS. To show the electron trapping effect, we give the phase spaces px − x of the electrons at t = 1000T0 (before BSRS excited) and t = 1300T0 (after the nonlinearity happens) in figures 2(c) and (d). It is obviously shown that, before the BSRS is excited or when it is very weak, the electrons are Maxwell distributed. However, when the EPW of BSRS grows larger, a number of electrons are trapped in the EPW of BSRS, resulting in the trapping structure shown in figure 2(d). The maximum px is just near the phase velocity of the EPW of BSRS. After the trapping effect happens, the distribution function of the electrons will be flattened near the phase velocity
is much larger than thermal velocity, so it is more difficult for the EPW of FSRS to trap electrons. As a result, the FSRS grows more linearly, we see no broadened spectra for both the scattered light and the EPW of FSRS. To show the electron trapping effect, we give the phase spaces px − x of the electrons at t = 1000T0 (before BSRS excited) and t = 1300T0 (after the nonlinearity happens) in figures 2(c) and (d). It is obviously shown that, before the BSRS is excited or when it is very weak, the electrons are Maxwell distributed. However, when the EPW of BSRS grows larger, a number of electrons are trapped in the EPW of BSRS, resulting in the trapping structure shown in figure 2(d). The maximum px is just near the phase velocity of the EPW of BSRS. After the trapping effect happens, the distribution function of the electrons will be flattened near the phase velocity 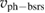 and then causes the excitation of BAMs, which will result in the broadening of the BSRS spectra shown in figures 2(a) and (b). However, even if some electrons have velocities near 0.2c, the velocities are still far away from the phase velocity of the EPW of FSRS 0.9c, so the electrons will not experience a two-step acceleration and the electron energy will always be below 100 KeV.
and then causes the excitation of BAMs, which will result in the broadening of the BSRS spectra shown in figures 2(a) and (b). However, even if some electrons have velocities near 0.2c, the velocities are still far away from the phase velocity of the EPW of FSRS 0.9c, so the electrons will not experience a two-step acceleration and the electron energy will always be below 100 KeV.
4. Results of 2D PIC simulation
As is discussed above, it is difficult for the EPW of FSRS to trap hot electrons to generate super-hot electrons. However, if the TPD instability of scattered lights occurs, two new EPWs will be generated. If one or two of the EPWs have a phase velocity that is close to 0.2c, the electron could experience two-step or even four-step acceleration, then it is possible to generate super-hot electrons with the energy exceeding 100 KeV. To examine the TPD instability of the scattered lights of SRS, we continue to perform a 2D PIC simulation. In the 2D simulation, the laser and the plasma are the same as the 1D simulation. The simulation box is 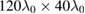 in
in  directions and the plasma is located in
directions and the plasma is located in 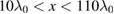 and
and 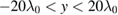 . The total simulation box is located in
. The total simulation box is located in  and
and  . The grid step in both the x and y direction is
. The grid step in both the x and y direction is  and there are 200 particles in each cell. The total simulation time is also 3 ps. The simulation results are shown in figures 3 and 4.
and there are 200 particles in each cell. The total simulation time is also 3 ps. The simulation results are shown in figures 3 and 4.
Figure 3. (a) The wave number spectrum of the longitudinal electric field  at t = 2200T0. The colour bar is in arbitrary unit. (b) The wave number spectrum of the averaged longitudinal electric field
at t = 2200T0. The colour bar is in arbitrary unit. (b) The wave number spectrum of the averaged longitudinal electric field  for different moments, where
for different moments, where  is Ex(x,y) averaged along the y axis. The wave numbers of the FSRS and BSRS are noted in the figure.
is Ex(x,y) averaged along the y axis. The wave numbers of the FSRS and BSRS are noted in the figure.
Download figure:
Standard image High-resolution imageFigure 4. (a) The electron phase space 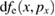 at t = 2200T0. (b) The electron phase space
at t = 2200T0. (b) The electron phase space 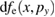 at t = 2200T0. (c) The electron distribution functions
at t = 2200T0. (c) The electron distribution functions 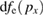 in logarithmic scale for different moments. (d) The electron distribution functions
in logarithmic scale for different moments. (d) The electron distribution functions  in logarithmic scale for different moments. In figures 4(c) and (d), EPW0 is the EPW of the SRS, EPW1 represents the EPW with the wave number k1 and EPW2 represents the EPW with the wave number k2.
in logarithmic scale for different moments. In figures 4(c) and (d), EPW0 is the EPW of the SRS, EPW1 represents the EPW with the wave number k1 and EPW2 represents the EPW with the wave number k2.
Download figure:
Standard image High-resolution imageFigure 3(a) shows the wave number spectrum of the longitudinal electric field Ex at t = 2200T0. This figure shows that there is a new couple of EPWs generated and the wave numbers of this two EPWs satisfy the wave number matching condition 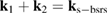 , where
, where 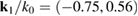 and
and  are the wave numbers of the two new EPWs and
are the wave numbers of the two new EPWs and 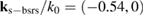 is the wave number of the backscattered light in plasma. And it is calculated by
is the wave number of the backscattered light in plasma. And it is calculated by  that their phase velocities are about
that their phase velocities are about 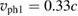 and
and  , respectively. As is discussed above, the wave vectors of the EPWs generated by TPD are on the cycle in equation (9), so we also plot the cycle for the backscattered light in figure 3(a). As is shown that the wave numbers of the two new EPWs are both on the cycle. We also plot the growth rate curve according to equation (6). We find that the wave numbers of the two new EPWs are not exactly on the curve
, respectively. As is discussed above, the wave vectors of the EPWs generated by TPD are on the cycle in equation (9), so we also plot the cycle for the backscattered light in figure 3(a). As is shown that the wave numbers of the two new EPWs are both on the cycle. We also plot the growth rate curve according to equation (6). We find that the wave numbers of the two new EPWs are not exactly on the curve 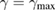 (i.e. the hyperbola curve), instead, they are on the curve
(i.e. the hyperbola curve), instead, they are on the curve 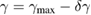 , where
, where 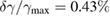 . The curve is named 'Growth Curve', which is the red curve shown in figure 3(a). From the above analysis, we can conclude that TPD instability is excited by the backscattered light of SRS. Then, from the theoretical analysis we can also deduce that even if the laser intensity is decreased in the simulation, TPD could also be excited by the scattered light of SRS as long as the scattered light grows to a certain intensity that exceeds the threshold of TPD. However, it will take more time. To make a comparison with the 1D PIC simulation, in figure 3(b), we plot the wave number spectra of the averaged longitudinal electric field
. The curve is named 'Growth Curve', which is the red curve shown in figure 3(a). From the above analysis, we can conclude that TPD instability is excited by the backscattered light of SRS. Then, from the theoretical analysis we can also deduce that even if the laser intensity is decreased in the simulation, TPD could also be excited by the scattered light of SRS as long as the scattered light grows to a certain intensity that exceeds the threshold of TPD. However, it will take more time. To make a comparison with the 1D PIC simulation, in figure 3(b), we plot the wave number spectra of the averaged longitudinal electric field 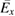 for different moments, where
for different moments, where 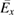 is the electric Ex averaged along y axis. From this figure, we find that the EPW of FSRS keeps growing as time goes on, which is the same as the 1D PIC simulation. However, BSRS keeps the same level as time goes on, and is strongly suppressed compared to the 1D simulation and when broadening of its spectrum does not happen. As a result, we can conclude that the TPD instability of the scattered could be a saturation scheme of BSRS.
is the electric Ex averaged along y axis. From this figure, we find that the EPW of FSRS keeps growing as time goes on, which is the same as the 1D PIC simulation. However, BSRS keeps the same level as time goes on, and is strongly suppressed compared to the 1D simulation and when broadening of its spectrum does not happen. As a result, we can conclude that the TPD instability of the scattered could be a saturation scheme of BSRS.
As is mentioned, the TPD instability of the scattered light of SRS could be a source of super-hot electrons whose energy exceeds 100 KeV. To study this, we give the phase spaces and distribution functions of the electrons for different moments in figure 4. In figures 4(a) and (b), we give the phase spaces of the electron's longitudinal momentum px and transverse momentum py versus the longitudinal space x at t = 2200T0. From figure 4(a) it is seen that, after the excitation of the TPD instability, there are more than one trapping structure. For the first trapping structure, the maximum 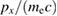 is about 0.28, which is near the phase velocity (about 0.2c) of the EPW of BSRS. The second trapping structure has the maximum
is about 0.28, which is near the phase velocity (about 0.2c) of the EPW of BSRS. The second trapping structure has the maximum 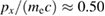 , which is also near the longitudinal component of the phase velocity
, which is also near the longitudinal component of the phase velocity  , where
, where 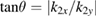 . The two trapping structures implies that the electrons will at least experience a two-step acceleration, which is corresponds to our above analysis. In figure 4(b), the trapping structure is not obvious. It seems that the electrons are still Maxwell distributed versus py. As a result, we plot the distribution functions of the electrons versus px (
. The two trapping structures implies that the electrons will at least experience a two-step acceleration, which is corresponds to our above analysis. In figure 4(b), the trapping structure is not obvious. It seems that the electrons are still Maxwell distributed versus py. As a result, we plot the distribution functions of the electrons versus px ( ) and py (
) and py ( ) for different moments in figures 4(c) and (d), respectively. It is shown that
) for different moments in figures 4(c) and (d), respectively. It is shown that  and
and  are both Maxwell distribution functions initially. At t = 1700T0, when BSRS is excited for a long time, the EPW of BSRS begins to trap electrons, so we see a platform in
are both Maxwell distribution functions initially. At t = 1700T0, when BSRS is excited for a long time, the EPW of BSRS begins to trap electrons, so we see a platform in  near the phase velocity
near the phase velocity 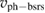 . The distribution function
. The distribution function  keeps a Maxwell distribution at t = 1700T0, which further proves that the first trapping structure is caused by the EPW of BSRS. At t = 2500T0, the TPD instability of BSRS is also excited for a long time. At this time, the EPW of TPD, which obliquely propagates, begins to trap electrons which are preheated by the EPW of BSRS, as a result, we see platforms in both
keeps a Maxwell distribution at t = 1700T0, which further proves that the first trapping structure is caused by the EPW of BSRS. At t = 2500T0, the TPD instability of BSRS is also excited for a long time. At this time, the EPW of TPD, which obliquely propagates, begins to trap electrons which are preheated by the EPW of BSRS, as a result, we see platforms in both 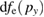 and
and  near the phase velocity of the EPW generated by TPD instability, as is shown in the black dash-dot lines in figures 4(c) and (d). Then we can deduce that super-hot electrons with the energy near to or over 100 KeV could be generated according to the formula
near the phase velocity of the EPW generated by TPD instability, as is shown in the black dash-dot lines in figures 4(c) and (d). Then we can deduce that super-hot electrons with the energy near to or over 100 KeV could be generated according to the formula 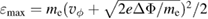 . The formula also explains why the trapping structures have larger maximum velocities than the phase velocities of the EPWs. It is also worth mentioning that the EPW with the wave vector
. The formula also explains why the trapping structures have larger maximum velocities than the phase velocities of the EPWs. It is also worth mentioning that the EPW with the wave vector 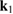 also traps electrons (although weak), the trapping structures are noted in both figures 4(c) and (d). Since the two newly excited EPWs go in opposite directions in the x and y direction, we see an asymmetry in the positive and negative directions for the trapping structures of the two EPWs in figures 4(c) and (d), which means figure 4 is well corresponding to figure 3(a).
also traps electrons (although weak), the trapping structures are noted in both figures 4(c) and (d). Since the two newly excited EPWs go in opposite directions in the x and y direction, we see an asymmetry in the positive and negative directions for the trapping structures of the two EPWs in figures 4(c) and (d), which means figure 4 is well corresponding to figure 3(a).
5. Conclusion
We investigate the TPD instability of the scattered light of BSRS with the help of 1D and 2D PIC simulations. The 1D PIC simulation is performed for two reasons, one is to give an estimation of the total simulation time of the 2D PIC simulation, because we need to know how long it takes for the SRS to be excited. The other is to prove that the TPD instability of the scattered light could be a saturation scheme of BSRS and electrons heated only by BSRS cannot possess the energy exceeds 100 KeV. By comparing the simulation results of the 1D PIC simulation and results of the 2D PIC simulation, we find that it is possible for the backscattered light of BSRS to be excited by TPD instability. BSRS is suppressed compared to the 1D PIC simulation because of the TPD instability, even the BAMs caused by the electron trapping effects are also suppressed. Theoretically, when TPD of the scattered light occurs, the intensity of the scattered light will be decreased, which in turn decreases the intensity of the EPW. Thus, it is reasonable to conclude that the TPD instability of the scattered light could be a saturation scheme of BSRS. It is also shown that, after TPD occurs, the electrons will experience a two-stage or even three-stage acceleration and their energy is gradually close to or even over 100 KeV, which implies that the Langmuir waves of excited TPDs could be the source of super-hot electrons whose energy exceeds 100 KeV. Further, this mechanism could be seen in both indirect-drive ICF and shock ignition.
Acknowledgment
This research was supported by Science Challenge Project (Grant No. TZ2016005), China Postdoctoral Science Foundation (Grant No. 2017M620430), National Natural Science Foundation of China (Grant Nos. 11435011, 11575035, 11705180) and the National Basic Research Program of China (Grant No. 2013CB834101).






