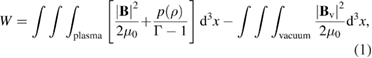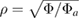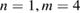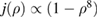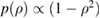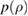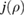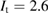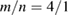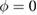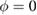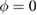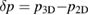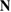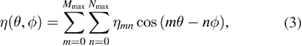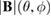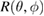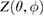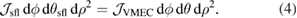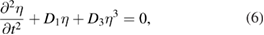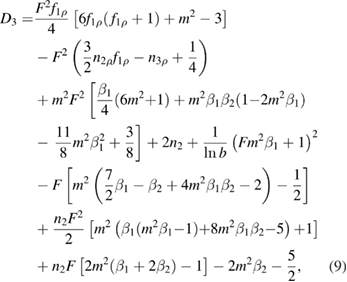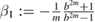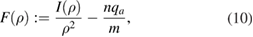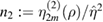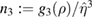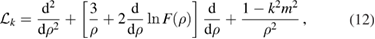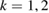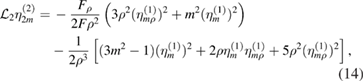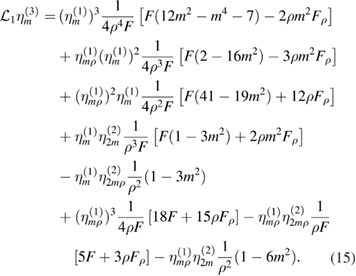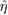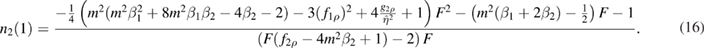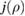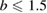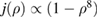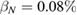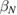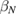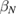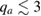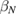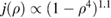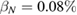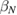Abstract
It is shown that free boundary 3D equilibrium calculations in tokamak geometry are capable of capturing the physics of non-linearly saturated external kink modes for monotonic current and q profiles typical of standard (baseline) plasma scenarios. The VMEC ideal MHD equilibrium model exhibits strong flux surface corrugations of the plasma vacuum boundary, driven by the core current profile. A method is presented which conveniently extracts the amplitude of the corrugation in terms of Fourier components in straight field line coordinates. The Fourier spectrum, and condition for non-linear corrugation agrees well with linear simulations, and the saturated amplitude agrees well with non-linear analytic calculations.

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
External kink modes are known [1, 2] to be of concern for the development of plasma scenarios. They set operational limits and define inaccessible windows for the edge safety factor and the peaking of the current profile. External kink modes tend to be linearly unstable for large current gradients, especially when these gradients are close to the plasma edge. After an initial linear growth in the non-linear phase, a mode usually saturates (non-linear stability) [3, 4], though in practice, the corrugation can be so large as to touch the vacuum vessel or plasma-facing components, thus causing disruptions [1].
The investigation of non-linear instabilities is typically carried out [5] with initial value codes (e.g. XTOR-2F [6]). Such simulations are computationally expensive due to the resolution and number of time steps necessary and require a certain level of parallelisation [7]. Since a saturated state without equilibrium flows is characterised by being time-independent, an equilibrium code can in theory obtain a saturated state, satisfying the force balance equation . Indeed, this was already shown for non-resonant internal kink modes with q > 1, where initial value (XTOR-2F) saturated states and VMEC fixed-boundary calculations showed similar m = n = 1 displacement amplitudes [5].
The goal of this paper is to investigate the degree to which 3D free-boundary equilibrium codes can model conventional external kink modes, driven by current gradients associated with standard tokamak operation (baseline scenario) with monotonic (standard (Wesson-like [2])) q profiles. The work differs from recent [8–10] deployment of VMEC for modelling edge harmonic oscillations in plasmas with low magnetic shear at the edge. Those oscillations are driven predominantly by pressure gradients, rather than current gradients. The 3D converged equilibria in this manuscript will be compared with the spectral properties of linear numerical stability analysis, and further verified by analytic non-linear calculations [4]. Lack of a converged equilibrium will be taken to mean that an unstable external kink mode forms, but non-linear saturation has not been achieved. The advantages of the equilibrium approach to external kink mode problems are numerous. First, the computations are fast and accurate, and second they provide convenient Fourier decomposed magnetic geometry for advanced studies such as fast particle [11] and impurity transport [12] in non-axisymmetric plasmas. Such studies require long and highly accurate particle simulations. To obtain the required accuracy, the VENUS-LEVIS guiding center code [13] for example exploits the Fourier decomposition of the magnetic field for orbit calculations.
In this letter we present ideal MHD free-boundary computations of JET-like plasmas carried out with the VMEC code [14]. First, the characteristics of the observed 3D equilibria and the choice of the coordinate system for mode spectrum analysis are discussed. This is followed by the VMEC calculation of the non-linear saturated displacement amplitude for varying edge q value, and two choices of current density profiles. The results are then compared with the helical external kink amplitude calculated from an analytical model based on a non-linear large aspect ratio expansion.
2. Non-axisymmetric VMEC equilibria
The computation of 3D ideal MHD equilibria is performed using the free-boundary VMEC code [14, 15], which arrives at an equilibrium state by minimising the energy functional
where is the magnetic field inside the plasma, is the vacuum magnetic field, is the pressure as a function of the radial variable . The toroidal flux is denoted by Φ, and subscript 'a' indicates that a quantity is evaluated at the plasma boundary. The poloidal and toroidal magnetic field coils are modeled as discretised filaments with specified coil currents. In this proof-of-principle study we employ an accurate model of the up-down symmetric toroidal and poloidal JET coils [10], but we do not include the effects of other coil systems (e.g. divertor coils), the vacuum vessel conductor nor iron core. The vacuum magnetic field is calculated from the coil currents according to the Biot–Savart law [16]. During the iterations that minimise the energy functional with respect to an artificial time variable, the plasma boundary is free to move. We impose stellarator symmetry on the 3D equilibrium and choose 289 flux surfaces with a mode spectrum of poloidal and toroidal modes. In order to converge towards the 3D equilibrium quickly, we provide a small perturbation to the magnetic axis initial guess.
The linear growth rate and the non-linear saturated amplitude of external kink modes depend on the distance to a conducting wall surrounding the plasma. The VMEC model does not include such a wall. Instead, the plasma is enclosed inside a structure of magnetic field coils at a finite distance from the plasma. We hence cannot investigate the influence of the wall distance on the VMEC edge corrugations. For comparison with VMEC, the conducting wall distance must be set to infinity (very large) for models that have the effect of a conducting wall. These models (linear and non-linear) well investigate the sensitivity of wall distance, and thus the likely correction to VMEC due to the vacuum vessel.
We start by examining dominant external modes with edge safety factor . Following the philosophy of previous studies of non-linear external kink modes [4] we choose a current density profile , which is similar to those used by Wesson [2], however with a steeper gradient to make the non-linear structure in VMEC simulations larger, and hence easier to resolve numerically. For all simulations the pressure is chosen to be . In order to investigate the effect of finite pressure on the resulting edge corrugations, is multiplied by a scalar to achieve different values of , where a is the minor radius, the toroidal magnetic field and Ip the plasma current. The value of qa (edge safety factor) is crucial for both linear and non-linear external kink stability. We vary Ip in the VMEC simulations in order to study the dependency of the saturated edge displacement η on qa with the given forms of and varying pressure. The q profiles resulting from these equilibrium configurations are monotonic where .
First, we simulate a plasma with a total toroidal current of MA such that the resulting edge safety factor of qa = 3.752 is below the rational value . The resulting VMEC equilibrium is non-axisymmetric with a strong edge corrugation in the toroidal and poloidal directions. This is illustrated in figure 1, where the plasma boundary and the magnetic axis are shown at different toroidal angles ϕ. From figure 2(a), which shows a poloidal cross section of the flux surfaces for the case of figure 1, it is evident that the perturbation is strongest at the plasma boundary and decreases towards the magnetic axis where it vanishes (hence only one cross observed in figure 1). This behaviour as expected is characteristic of external kink modes. By retaining only n = 0 modes, we can find a neighbouring axisymmetric state to the obtained 3D equilibrium. A comparison of 3D VMEC states with their neighbouring axisymmetric equilibria was previously used to determine toroidal field ripple [17]. Defining as being the difference of p in the 3D state compared to the axisymmetric state, we can identify the periodicity and the location of the perturbation. It is noted in passing that the 3D displacement ξ of the magnetic surfaces can be approximately determined via . Figure 2(b) shows for the case of figure 1. It can be seen that the perturbation is located at the plasma edge and the m = 4 character is evident.
Figure 1. Plasma boundary and magnetic axis (indicated by a cross) of a free-boundary VMEC equilibrium with qa = 3.752 and are shown at different toroidal angles ϕ. The non-axisymmetric edge corrugation is clearly visible.
Download figure:
Standard image High-resolution imageFigure 2. Visualisation of the resulting 3D equilibrium with qa = 3.752 shown for the case of figure 1. (a) Shape and position of the magnetic flux surfaces. The perturbation is strongest at the plasma edge and vanishes towards the magnetic axis. (b) Perturbation arising from the comparison of the pressure in the 3D equilibrium with the neighbouring state.
Download figure:
Standard image High-resolution imageTo determine the non-linear amplitude, emphasis has to be placed on the coordinate system underlying the spectral analysis of the displacement. From VMEC, the axisymmetric flux surface as well as 3D flux surface are known in VMEC flux coordinates [14]. For a given point lying on with normal vector , a convenient definition of the corrugation displacement at the edge is
The Fourier series representing η is of the same form as that of the magnetic field strength, i.e.
due to the imposed stellarator symmetry. We can calculate the mode spectrum separately for , as well as and at the edge. The spectrum of each of these quantities is rich and exhibits a variety of strong poloidal modes for n = 1. For the case shown in figure 2, the 4/1 VMEC coordinate coefficients of R, Z, and η are not dominant. This is in contradiction with the visual observations from the magnetic topology, which has a clear 4/1 structure. To allow a direct comparison with η obtained in straight field line (sfl) coordinates, the mode amplitudes for in VMEC coordinates can be seen in figure 3(a).
Figure 3. Mode spectrum of the edge displacement obtained in two different coordinate systems. (a) In VMEC coordinates. (b) In straight field line coordinates (dominant m = 4/n = 1 mode).
Download figure:
Standard image High-resolution imageMode spectra are expected to be most narrow for a straight field line coordinate system. Dominant poloidal modes can thus be identified for comparison with those seen in figures 1 and 2 (simply by inspection), and for suitable comparison with the non-linear analytic treatment described later. For this we need to transform the poloidal angle of the VMEC coordinate system to a straight field line angle by equating the volume elements in VMEC coordinates and straight field line coordinates
Since the toroidal angle ϕ and the radial variable ρ are identical in both coordinate systems, the only variables remaining are and θ. Integration of equation (4) yields
where was used and and R are computed by VMEC from the axisymmetric equilibrium. Now with equation (2) we are able to calculate the coefficients for the Fourier series of . In this sfl coordinate system the mode spectrum cleanly and clearly identifies a standard external kink mode. As shown in figure 3(b) the 4/1 mode is dominant as expected from the visual observations of figure 2 as well as from external kink mode theory. With all other modes being fairly weak compared to the dominant one, poloidal and toroidal coupling thus appears to have a weak effect. Toroidicity and beta can be expected to have only a mild effect on mode structure, and hence we can compare the mode amplitudes to an analytical model that assumes cylindrical geometry [4].
To obtain non-linearly saturated external kink modes, the system is initially required to be linearly unstable. This condition is verified from numerical computations with the linear eigenvalue code KINX [18]. The effects of small aspect ratio, shaping and finite beta are retained in these computations and in figures 4(a) and (b) the distance to the perfectly conducting wall surrounding the plasma is set to , i.e. sufficiently large to consider no effects due to the wall. The linear growth rate of the 4/1 mode is calculated as a function of qa. This is presented in figure 4(a), where γ is normalised by the Alfvén frequency . The 4/1 external kink mode is linearly unstable in a wide range of qa, where saturated non-linear states can possibly arise. The linear radial eigenfunctions of the sfl harmonics in KINX resemble the mode spectrum calculated in sfl coordinates in figure 3(b) (for the non-linear equilibrium calculations). For an edge safety factor below qa < 4, the eigenfunction (radial displacement) of the 4/1 mode is dominant at the plasma boundary. This is shown in figure 4(b) for the case with an edge safety factor of qa = 3.752. The similarity of these linear eigenfunctions and the non-linear saturated VMEC displacement as a function of the radial variable, shown in figure 4(c), is remarkable.
Figure 4. (a) Linear external kink growth rate γ of the 4/1 mode calculated with KINX. (b) Linear n = 1 (KINX) radial displacement functions for various poloidal mode numbers (sfl coordinates). (c) Non-linear n = 1 saturated (VMEC) radial displacement functions η for various poloidal mode numbers (sfl coordinates).
Download figure:
Standard image High-resolution image3. Comparison with saturated external kink mode amplitude
After demonstrating the external kink spectral properties of the VMEC 3D equilibria, we now compare the non-linear saturated amplitude of the displacement in VMEC with analytical predictions. In the following we provide a concise and self-contained summary of an analytical model [4] for the non-linear saturated external kink amplitude. In this context, we correct equation (34) of [4], where one term was found to be missing. The model assumes cylindrical geometry, circular cross section and no pressure effects. For non-resonant modes the non-linear evolution [19, 20] of the helical displacement η is given by the solution of
where the parameters D1 and D3 are defined below. For the saturated and hence time-independent state the solution to the amplitude η is
For linear instability D1 is negative. It is proportional to the square of the linear growth rate and thus D1 = 0 defines the marginal points. Non-linear stability is determined by the coefficient D3. The system is non-linearly stable, i.e. the mode can saturate if D3 > 0. We do not explicitly explore conditions of non-linear instability where D3 < 0. The coefficients D1 and D3 are obtained from physical constraints on the plasma surface [4] and read
and
where . The coefficients D1 and D3 in equations (8) and (9) differ from D1 and D3 in equation (6) by a constant but common factor that cancels out in the calculation of η in equation (7). The wall distance b is normalised by the minor radius, i.e. for b = 1 the wall is located at the plasma boundary and we define and . The function F is defined as
where is the total current enclosed by a flux surface with radius ρ and normalised such that . To obtain the functions f1, n2 and n3, the helical amplitude η is expanded up to third order and a coupled system of differential equations arising from the ideal MHD model is solved numerically providing a solution for η to each order. These solutions can be written as sums of homogeneous and particular solutions and are denoted to first, to second and to third order. They satisfy the boundary conditions
Using a normalisation constant , we further define the normalised solutions to second and third order and respectively. In equations (8) and (9), and are evaluated at . Defining the operator
with we obtain the solutions for η to each order from the following system of ODEs [4]:
The normalisation constant can be eliminated by exploiting pressure balance across the plasma surface [4], resulting in the expression
We stress the fact that in this model, η depends only on single helical mode numbers m and n (as expected for cylindrical geometry), current density profile , wall distance b and edge safety factor qa. In order to study the degree of relevance of the equilibrium free-boundary approach without a conducting wall, it is important to investigate the sensitivity of the effect of the conducting wall distance from the plasma on the non-linear saturated state. This is achieved with the analytical model. Figure 5 shows how η depends on qa for different values of the wall distance b. As the wall distance increases, not only does the mode amplitude grow, but also the unstable domain widens. The variation is strong for , but weak for b > 1.5. Thus we can approximately treat a wall distance of as if no wall was present. In the VMEC computations presented here, the field coils have a minimum distance of to the plasma surface.
Figure 5. Dependence of the saturated 4/1 external kink amplitude on the wall distance b as calculated from the non-linear analytical model.
Download figure:
Standard image High-resolution imageWe find that the behaviour of η calculated from VMEC agrees well with the expected characteristics of external kink modes. In particular, the window of qa over which η is non-zero, and also the shape of η with respect to qa is roughly mirrored by the shape of γ with respect to qa in figure 4(a). Figure 6 shows the amplitude of η for each m (with n = 1), with η calculated according to equation (2). For an edge safety factor larger than the upper marginal point—given by the rational value qa = m/n—the plasma remains (nearly) axisymmetric. Lowering qa below m/n results in 3D equilibria that have edge corrugations with external kink like properties as described previously. The amplitude of the saturated non-linear edge displacement is finite and dominated by a 4/1 component throughout the linearly unstable domain, as expected for the spectral properties of figure 3(b). As qa decreases below the lower marginal point, i.e. the value at which the linear external kink mode is stable, the displacement vanishes. For a small range of values of qa slightly higher than the upper marginal point, or slightly lower than the lower marginal point we see small perturbations to η. We do not yet know the origin of these weak 3D saturated states.
Figure 6. Lowest m components with n = 1 of the edge displacement obtained from free-boundary VMEC simulations with current profile and . is the dominant mode throughout the range of qa, where the external kink mode is expected to be linearly unstable and non-linearly stable. The two black lines indicate the position of the marginal points computed with KINX.
Download figure:
Standard image High-resolution imageA weak scaling of η with is observed as shown in figure 7, where calculated from VMEC at different values of is compared with the analytically predicted non-linear saturated external kink amplitude η. The mode is present already at very low , strongly indicating that the 3D states are dominantly current-driven, as expected for external kink modes. For the largest value of the lower marginal point is shifted towards lower qa, whereas it remains approximately constant for lower values. Since finite beta effects are neglected in the analytical model, the most relevant comparison between VMEC and the non-linear analytic model is for small in figure 7. Considering the shaped plasma and edge aspect ratio of the VMEC JET-like simulations, the comparison with the cylindrical analytic model in figure 7 is very good.
Figure 7. Amplitude of the saturated edge displacement of the 4/1 mode computed from VMEC simulations at various values of and comparison to the analytical model for current profile .
Download figure:
Standard image High-resolution imageNow that agreement between the VMEC displacement amplitude and the non-linear analytical external kink mode amplitude has been demonstrated, we further verify the results for a case with , for which a external mode is dominant. For this, in order to prevent the amplitude of the mode from becoming too large, we choose a less steep current profile . As seen in figure 8, the 3/1 component (evaluated in sfl coordinates) is dominant in the edge mode spectrum of the resulting VMEC 3D equilibria as expected for a current-driven external kink mode. Figure 9 shows the flux surfaces and the 3D pressure perturbation, which are both non-axisymmetric and consistent with the mode spectrum. In figure 10 the analytically predicted saturated external kink amplitude is compared with the 3/1 component of the VMEC edge displacement at different values of . Again a weak scaling of η with the pressure is observed. The upper marginal point agrees well with the analytical value, whereas the lower one differs slightly. The saturated external kink amplitude peaks at a value of qa closer to the lower marginal point, whereas the peak in the VMEC computations is somewhat shifted towards larger values. The reason for this is not currently certain, but it could be a result of finite aspect ratio and cross section shaping effects which are not taken into account in the analytic model.
Figure 8. Mode spectrum (straight field line coordinates) of the VMEC edge displacement obtained in a simulation with and qa = 2.913 at low pressure (). The m = 3/n = 1 mode is dominant.
Download figure:
Standard image High-resolution imageFigure 9. Visualisation of the 3D equilibrium with current profile , qa = 2.913 and shown at . (a) Flux surfaces. (b) Perturbation arising from the comparison of the pressure in the 3D equilibrium with the neighbouring state.
Download figure:
Standard image High-resolution imageFigure 10. Non-linear amplitude of the 3/1 mode obtained from VMEC with current profile and qa around 3 at two values of and comparison with the analytical prediction.
Download figure:
Standard image High-resolution image4. Conclusions
Employing 3D, free-boundary equilibrium computations, is shown to provide a novel way of obtaining saturated current-driven external kink modes. In principle, such saturated external states are time-independent and thus satisfy the force balance equation solved by an equilibrium code. For the first time, current-driven external kink modes are observed with an equilibrium code in free-boundary plasma configurations with standard monotonic current and q profiles typical of standard (baseline) tokamak plasma scenarios. Windows of the edge safety factor where external kink modes would be linearly unstable have been identified. In VMEC simulations with current profiles that result in an edge q value lying inside these regions, non-axisymmetric edge corrugations are observed. Analytical calculations of non-linear external kink modes reveal linear instability but non-linear stability, i.e. saturated mode amplitudes for the studied plasma configurations. To compare the analytic external kink amplitudes with VMEC, and thus verify that VMEC corrugations are those of standard non-linear saturated external kinks, the spectra of the VMEC fluctuations are converted to spectra of a straight field line coordinate system. The Fourier spectrum calculated in this coordinate system shows one dominant mode, thus indicating consistency between 3D VMEC equilibria and analytical external kink models. Even though the mode amplitude scales weakly with , the external perturbations seen in VMEC are of considerable size already at low , indicating a current driven mode. Finite pressure is shown to have a weakly destabilising effect. The edge displacement in VMEC is found to be comparable to the analytically calculated saturated external kink mode amplitude. Small differences are observed in the value of qa where the amplitude reaches a maximum. Due to the lack of the stabilizing effect of a conducting wall the 3D equilibrium simulations overestimate the saturated amplitude of a real tokamak by about 25% (for a wall distance b = 1.2a), the difference having been quantified via the analytic approach. We conclude that VMEC free-boundary calculations capture the salient features of saturated external kink modes, thus enabling efficient prediction of non-linear instability amplitudes, and e.g. fast ion and impurity transport studies.
Acknowledgments
This work has been carried out within the framework of the EUROfusion Consortium and has received funding from the Euratom research and training programme 2014–2018 under grant agreement number 633053. The views and opinions expressed herein do not necessarily reflect those of the European Commission. This work was supported in part by the Swiss National Science Foundation. The authors thank Dr. S.P. Hirshman for providing us with the VMEC equilibrium code. We furthermore thank H Eriksson for providing us with a corrected form of equation (16).