Abstract
The notion of a maximally entangled state depends on the measure used to give rise to a rich envision of multipartite state. Recently, Che et al presented a recurrence relation of multi-qubit states. According to this inspiration, we present an expanded recurrence relation of the maximally multipartite state. Using this expanded recurrence relation and Bell state, some new forms of the maximally four-, six-, eight-qubits states are presented. The construct of the maximally multipartite state through recurrence relationships is of great potential.
Export citation and abstract BibTeX RIS
1. Introduction
Quantum entanglement is a valuable resource for the implementation of quantum computation, and quantum communication protocols, like quantum teleportation [1], quantum secure direct communication [2], remote state preparation [3] and so on. The exploration of quantum entanglement in maximally multipartite quantum systems in a composite system is of great significance to the study of quantum entanglement and maximally multi-qubit entangled states [4, 5]. Due to its great relevance, from both the theoretical and practical points of view, it is imperative to explore and characterize all aspects of the quantum entanglement of maximally multipartite quantum systems [4, 6]. A considerable amount of research has been devoted to the study of multi-qubit entanglement measures defined as the sum of bipartite entanglement measures over all the possible bi-partitions of the full system [7–11]. The multipartite entanglement of system of qubits can be characterized in terms of distribution function of bipartite over all possible bipartitions of the qubits [6, 9, 10]. This led us to formulate the notion of maximally multipartite entangled states (MMES). In 2013, Zha et al presented to identified and generalized criterion for maximally entangled states of 2, 3, 4, 5, 6 and 8 qubits and gave some new maximally multipartite entangled state [11, 12]. In 2019, MMES via recurrence relation was introduced. Later, the five qutrits and seven ququarts MMES have been established using recurrence relation [13, 14]. Therefore, the construct of maximally multipartite state through recurrence relationship bears a great potential.
Recently, Che et al [15] presented a recurrence relation of multi-qubit states. According to this inspiration, we present an expanded recurrence relation of maximally entangled states between the maximally n-qubit entangled state and maximally n + 2-qubit entangled state. Furthermore, some new maximally four-, six-, eight-qubits states are also presented.
2. The expand recurrence relation of maximally entangled states
Recently, Che et al [15] gave a recurrence relation of multi-qubit states. According to this inspiration, we present an expand recurrence relation of maximally multi-qubit entangled states.
Let 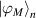 repress a maximally n-qubit entangled state, then maximally n + 2-qubit entangled state can be written as
repress a maximally n-qubit entangled state, then maximally n + 2-qubit entangled state can be written as
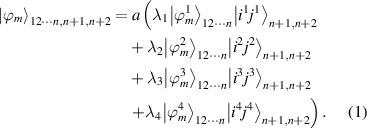
Where 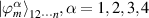 are all maximally n-qubit entangled state and satisfy
are all maximally n-qubit entangled state and satisfy
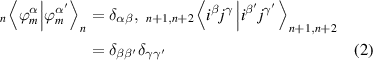
 ;
;  is coefficients satisfy the normalization condition.
is coefficients satisfy the normalization condition.
3. Constructing maximally four qubit via expanded recurrence relation
Without any loss of generality, we first consider maximally two-qubit state.
It is well know that Bell state  ,
,  are maximally two-qubit entangled state,
are maximally two-qubit entangled state,
Now let us construct a maximally four-qubit state. Using expand recurrence relation equation (1)
Let  ;
; 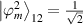
 ;
;
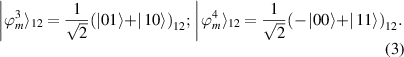
Then, we have
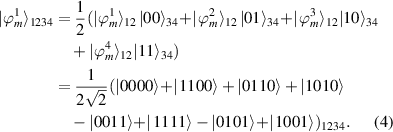
This state was presented by Yeo and Chua [16].
Also, let
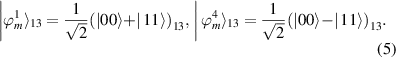
Then, we have
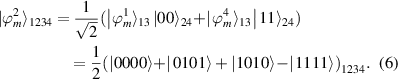
This state was just the cluster state given in [17–19]
Let
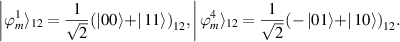
Then, we have
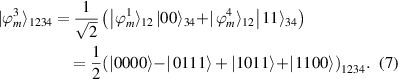
By careful calculation, we can obtain
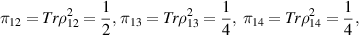
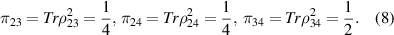
Therefore, we have [11]
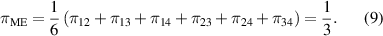
According to [11], this state is a maximally entangled four-qubit states.
Let
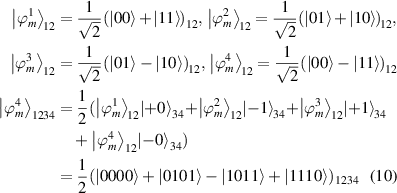
where 
Using equation (10), we can obtain
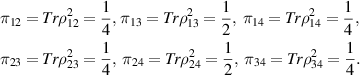
Then, we have
This state is also a maximally entangled four-qubit states.
4. Constructing maximally six qubit via expanded recurrence relation
Using equation (7), let

According to expand recurrence relation equation (1), we have
Using equation (13), we can obtain
Therefore, according to [14], this state is a maximally entangled six-qubit state.
Using equation (10), let
According to expand recurrence relation equation (1), we have
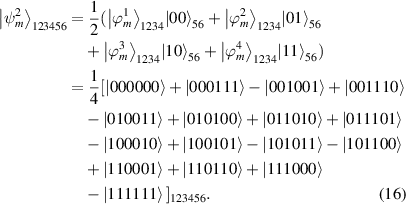
Similarly, we can show
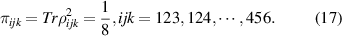
This six-qubit state have discovered by Borras et al [20]
5. Construct maximally eight qubit via expand recurrence relation
Using equation (16), let
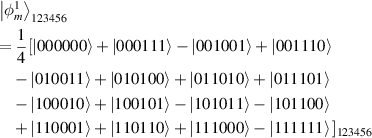
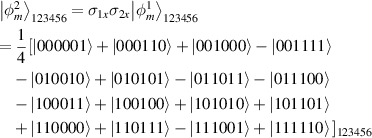
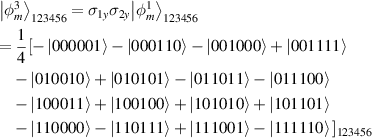
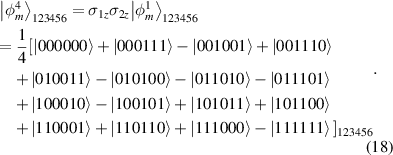
According to expand recurrence relation equation (1), we have
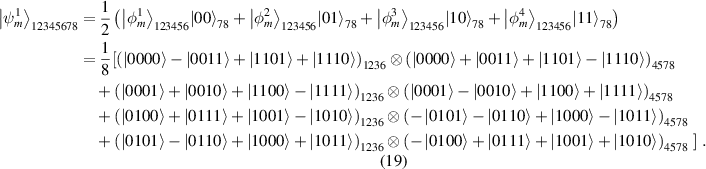
By careful calculation, we can obtain,
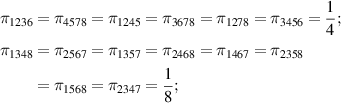
others
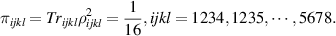
That is say, there are 56 of 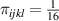 . 8 of
. 8 of 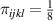 . 6 of
. 6 of 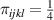 .
.
Therefore, we have
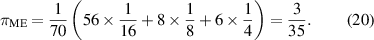
According to the criterion for a maximally entangled eight-qubits [11], this state is a maximally entangled states.
6. Conclusion
In summary, we have presented a expand recurrence relationship between the maximally n-qubit entangled state and maximally n + 2-qubit entangled state. Furthermore, some new maximally four-, six-, eight-qubits states are given. We believe this method can play an important role in constructed maximally entangled states.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (61705182), National Science Foundation of Shannxi Province (2017JQ6024).


