Allometry of Escherichia coli surface area with volume: effect of size variability, filamentation and division dynamics

E. coli cells are modeled as spherocylinders or 'capsule' shaped, consistent with morphological observations. Spherocylinders have two characteristic dimensions—the diameter of the rod (i.e. width) and the length. An increase in size can result from increase in one or both parameters. The growth of such a 'capsule' shaped cell will result in an increase in the SA and volume (V). How the two variables will change is expressed by the scaling expression:

$$\begin{equation} \mathrm{SA} = a \cdot \mathrm{V}^\gamma \end{equation} \tag{ 1 }$$

where γ is the scaling exponent and a is the pre-factor. The size and shape of a cell determines the scaling exponent γ. For simple rod-shaped ('capsule' shaped) cells a proportionate increase in length and width will result in $\gamma \sim$ 2/3 ≈ 0.66, as expected when the aspect ratio (A_R ), i.e. the ratio of length to width, is kept constant (figure 1(A)). However, if the cell length increases, while the width remains constant, for example due intracellular cytoskeletal factors like MreB, or the mechanics of the cell wall, then the scaling exponent is expected to be γ = 0.96 (figure 1(A)).

Zoom In Zoom Out Reset image size

In a population, cell size variability in terms of different lengths, and the presence of filamentous (i.e. elongated) cells arises from multiple factors or their combination such as single cell gene expression stochasticity (Elowitz et al 2002), variability of molecular partitioning at division (Rosenfeld et al 2005), replication stochasticity and coupling to division (Gangan and Athale 2017) or DNA damage response (Raghunathan et al 2020) as summarized in figure 1(B). At the same time the variability of widths has been variously reported to be constant (Taheri-Araghi et al 2015).

It remains unclear whether this variation in widths and lengths could affects the estimation of the scaling exponent. In order to examine this, we first examined SA-V scaling in filamentous E. coli.

Cell division in E. coli requires the assembly of a multi-protein complex. FtsI (PBP3) is one of the components, whose inhibition was shown to result in filamentous cells that continued to grow without septum formation (Spratt 1977, Botta and Park 1981). Cephalexin is a β-lactam antibiotic that acts to prevent septation by acylating FtsI (PBP3), resulting in cell lysis at high concentrations and filamentous cells at low concentrations (Eberhardt et al 2003). The effect of divisome inhibition is most prominent in rapidly dividing cells (Chung et al 2009). We therefore grew E. coli MG1655 cells in presence of 10 µg ml⁻¹ cephalexin and imaged them in phase contrast (label-free) microscopy. Treated cells were filamentous, while untreated cells divided normally and were shorter (figure 1(C)). An image analysis pipeline was used to automatically estimate cell lengths and widths from such label-free images (section 4). By using the cell midline contour as a measure of cell length, we avoid artifacts of errors in estimating cell lengths due to cell bending. Additionally cell width is estimated as the median of the line orthogonal to the cell midline, that intersects the cell boundaries (diameter). Cell lengths of E. coli treated with 10 µg ml⁻¹ cephalexin have a greater mean and spread as compared to untreated (figure 1(D)). Cell widths in both conditions however, have the same mean values around which the data is symmetrically distributed (figure 1(E)). The resulting distributions of the aspect ratio (length:width) follows the same trend as the length distributions, since the width distribution is effectively unchanged (figure 1(F)). The width is poorly correlated with the length as measured by the linear correlation coefficient (figure 1(F) (inset)). The SA (equation (2)) and volume, V (equation (3)) of individual cells were calculated from the lengths and widths as described in section 4. The plot of SA with V was fit to equation (1) to estimate γ, the scaling exponent (figures 1(G) and (H)) resulting in γ of 0.66 for untreated cells and 0.82 for filamentous cells. The goodness of fit, R², ranges between 0.96 and 0.98 for most fits. We also find that most of the data lies within the 95% confidence interval (CI) of the fit line (figures 1(G) and (H)). Binned averages based of the data also lie within the 95% CI range.

We can therefore show a deviation from the ideal geometric scaling of E. coli SA with V for filamentous E. coli. In order to test whether intermediate distributions of cell lengths also show this effect, we modulated nutrient availability, since it has been shown to change cell length distributions of populations.

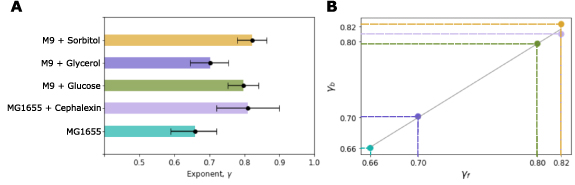
We tested the effect of modulating growth rates on cell sizes by growing them in minimal medium (M9 salts) supplemented with carbon sources—either 4% sorbitol, glycerol or glucose (section 4). While qualitatively the cells appear similar in size (figure 2(A)), the population distribution of cell lengths demonstrates highest modal lengths in M9 + Glucose, while the tail of the distribution in M9 + Glycerol was longer than M9 + Sorbitol, but their modes were comparable (figure 2(B)). Cell width distributions in all three conditions were comparable. The aspect ratio distribution shows qualitative differences between growth conditions (figure 2(C)), contrary to the constant aspect ratio hypothesis proposed in previous studies. This difference arises due to the fact that while the length distribution varies, the widths are mostly constant. The width as a function of length for individual cells from the three growth media has a low ρ, i.e. correlation coefficient suggesting the absence of a strong linear correlation (figure 2(C) (inset)). The scaling exponents of SA with V in all three media range between 0.7 and 0.8 (figures 2(D)–(F)). We find the resulting γ exponents increase with the growth rate (figure 2(G)).

Zoom In Zoom Out Reset image size

Taken together the growth rate appears to influence the aspect ratio of the population, that in turn alters the SA-V scaling exponent.

In order to test the robustness of the calculated exponents (γ) for different growth conditions, we bootstrapped the data. Specifically, we conducted 10³ bootstraps by sampling 1/5th of the data in each iteration. Each of the bootstrapped data-sets were fit to the power law (equation (1)) and their statistics estimated by using the 2.5% lower and the 97.5% higher quantile measures as measure of the 95% CI around the means (figure 3(A)). The values of γ range between 0.65 and 0.8. We use these estimates to compare to the fits in the previous figures and can show that these are strongly correlated (correlation coefficient ρ of 0.99) (figure 3(B)). The difference between the mean (m) and the two bounds, the upper (B $_\mathrm{u}$) and lower (B $_\mathrm{l}$), are averaged ($\langle$(m-B $_\mathrm{u}$), (m-B $_\mathrm{l}$)$\rangle$) to represent the error in estimating γ (figures 1(G), (H) and 2(D)–(F)). We also observe that the spread of the quantile ranges is wider in cephalexin treated cells as compared to untreated, correlating with the observed increase in length variability in treated cells.

Zoom In Zoom Out Reset image size

Experimentally measured differences in cell length obtained by modulating the growth rate alter both the mean and the spread of the distribution, as seen for example in the case of cephalexin treatment. In order to distinguish which of these influences the change in the SA-V scaling exponent, we used statistical simulations, since we were unable to separate the two effects experimentally.

Controlling cell length mean and standard deviations independently in experiments is technically challenging, therefore we use statistical simulations to address whether variability or means of lengths affect the scaling exponent. With these simulations we aim to find the statistical relations between cell lengths and widths that will give rise to the scaling observed. For simplicity, they do not include any mechanism or relation between cells over successive divisions. To this end we have modeled two scenarios:

Model 1: Increasing mean length with constant variability (s.d.): Motivated by Schaechter's law and our own experiments, where increasing growth rate results in increased mean cell lengths, we examined mean cell lengths ranging from 1 to 12 µm. In order to test the effect of increasing the mean and a proportionate standard deviation, we simulated cell lengths by sampling a lognormal distribution with increasing means from 0.1 to 2.5 µm and constant standard deviations (table 1). The resulting output arithmetic mean length and width distributions are comparable to experimentally measured cell lengths (figure S1(A)). The widths were simulated by sampling from normal distributions with their means increasing proportionately, based on a constant aspect ratio, A_R of 4.5 (figure S1(B)). As a result, for longer cells, the width is effectively constant, since the spread of cell lengths is much greater than that of the corresponding widths. As discussed in the earlier sections, constant width results in high scaling exponent values ($\gamma \sim 0.8$–0.9). Therefore, as expected, we find that the γ value of short cells (mean length 1.13 µm) is ∼0.65, while for long cells (mean length 12.44 µm) it increases up to ∼0.93 (figure S1(C)), with output means and standard deviations described in table 1. Averaging of SA and V, that eliminates population variability, results in the recovery of the geometric scaling exponent of γ = 0.67 (figure S1(C) inset). This demonstrates that even though the mean length and width increased proportionately (constant aspect ratio), the population variability governs the scaling relation. Thus averaging, that eliminates the variability, and the SA-V scaling exponent reverts to 2/3. When we maintain the distribution data, the increasing mean also corresponds to an increase in the exponent (figure S1(D)).

Table 1. Parameters used in the statistical simulations. Simulations of cell size lengths used INPUT lognormal mean (LM) length ($\mu_\mathrm{in}$) and standard deviations (LS) ($\sigma_\mathrm{in}$) resulting in OUTPUT values that are arithmetic mean (AM) $\mu_\mathrm{out}$ and s.d. (AS) $\sigma_\mathrm{out}$. The values correspond to data plotted in figures 4 and S1. The range of values used in the simulations correspond to the two models tested: (i) increasing values of length for constant s.d. and (ii) a range of s.d. for a constant mean. The models are described in detail in section 4.

INPUT		OUTPUT
$\mu_\mathrm{in}$	$\sigma_\mathrm{in}$	$\mu_\mathrm{out}$	$\sigma_\mathrm{out}$
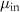
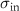
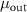
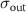
(i) Model of increasing means, constant s.d.
0.1	0.2	1.13	0.23
0.5	0.2	1.68	0.34
1	0.2	2.77	0.56
1.5	0.2	4.57	0.93
2.5	0.2	12.44	2.53
(ii) Model of constant mean, increasing s.d. (Simulation 0)
1	0.1	2.73	0.27
1	0.2	2.77	0.56
1	0.3	2.84	0.87
1	0.4	2.94	1.22
1	0.5	3.08	1.64

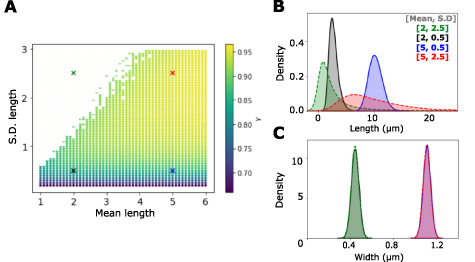
Model 2: Increasing variability (standard deviation) for constant mean length: In order to address whether the increase in γ seen in the earlier simulations can be attributed to spread alone, we simulated distributions with mean cell lengths between 2.73 and 3.05 µm and increasing standard deviation 0.27–1.64 µm, based on an input lognormal mean of 1 µm and lognormal s.d between 0.1 and 0.5 µm (figure 4(A)). While the distribution has a constant lognormal mean, the output arithmetic mean increases slightly from 2.73 to 3.08 µm, as a result of an increased s.d., a feature of the distribution. These changes are very small compared to those in Model 1. The corresponding mean widths calculated from the arithmetic mean length and constant aspect ratio (A_R = 4.5), therefore also show a slight increase 0.61–0.68 µm. (figure 4(B)). We find the SA scales with V with the exponent increasing from γ of 0.72 to 0.89 (figure 4(C)). Once more averaging the SA and V data from the population to get just one average value of SA and V for each distribution, resulted in the geometric scaling exponent of 0.67 (figure 4(D)). When the mean changes very little and the s.d. is increasing, the coefficient of variation of length (CV_L ), i.e. s.d./mean, is expected to increase. We find that this specific combination of the fixed mean and increasing s.d. results in an increase in the scaling exponent γ with CV_L , that is qualitatively similar to experiment (figure 4(E)). We refer to this as Simulation 0. In order to match experimental data, we simulated the simultaneously varying the mean and standard deviation, that we refer to as Simulations 1, 2 and 3 (table S1 and figure 4(E)).

Zoom In Zoom Out Reset image size

This led to a more general question of how changing the mean and standard deviation of a lognormal distribution of lengths could affect γ. In order to address this, we simulated a range of cell length distributions with their means and s.d. systematically varied, while widths were calculated as before to maintain a constant aspect ratio of 4.5. The fit of the resulting SA-V to the power-law (equation (1)) showed that estimated values of γ are more sensitive to the s.d. as compared to the mean (figure 5(A)). Representative distributions of four samples from this phase-like diagram are used to demonstrate the differences (figures 5(B) and (C)).

Zoom In Zoom Out Reset image size

Based on the results from experiment and simulation, variability appears to play an important role in estimating the exponent of SA-V scaling. Since experimental data was sampled from an unsynchronized population, we proceeded to test whether the statistics would still hold true for single cell data.

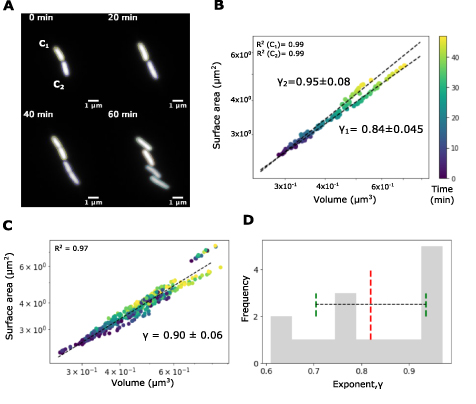
We grew E. coli MG1655 expressing GFP on nutrient agar pads and imaged them in fluorescence (section 4). Cells were visualized by expressing the fluorescent protein GFP from a plasmid. We used a MATLAB based image-analysis pipeline to track representative cells from image time series (figure 6(A) and supplementary videos SV1(A)–(C)) to obtain length and width dynamics. Representative scatter plots of SA with V for each individual cell as a function of cell division progression, with time encoded in color, were fit by the scaling relation (equation (1)) and resulted in an exponent γ between 0.8 and 0.9 (figure 6(B)). Pooling multiple cells (n = 12) with the time course data obtained from tracking resulted in a fit exponent value of γ of 0.9 (figure 6(C)). When each individual cell time course of SA-V was fit, it resulted in a distribution of γ with a mean of 8.2 (figure 6(D)).

Zoom In Zoom Out Reset image size

Thus we demonstrate that the scaling exponent of SA-V obtained from time-course dynamics population sampled exponents both exceed the 2/3 value expected from the geometric law.

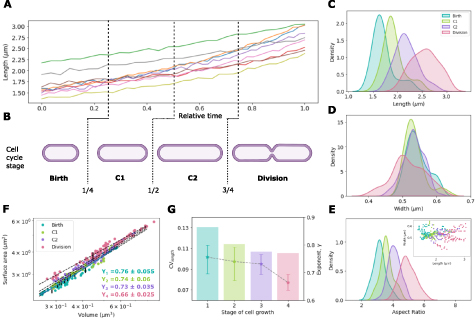
In order examine whether the SA-V scaling exponent has any relation with cell division stages, we 'virtually synchronized' the single cell time-series data. The frame in which cells are born were noted as time zero and every frame number in the time series, f_i (i $\mathrm{th}$ frame), is normalized by the doubling time resulting in a relative frame number $f_r = (f_i - f_b)/(f_d - f_b)$, where f_b and f_d are the frames corresponding to cell birth and division respectively. We divide this relative frame number series into four equal parts that we refer to as B [0–0.25], C1 (0.25–0.5], C2 (0.5–075] and D (0.75–1], with the values indicating boundaries (figures 7(A) and (B)). This allows us to analyze the cell size distributions from length (figure 7(A)) and width dynamics as a function of stages. We estimate SA-V scaling from the single cell time-series of each stage. As expected, the mean of the cell length increases with 'stage' of cell division (figure 7(C)), while the width appears to have a constant mean but slight increase in spread (figure 7(D)). The resulting aspect ratio increases as the cell cycle progresses, a trend similar to that observed for the length (figure 7(E)). The length-width scatter shows poor correlation (figure 7(E) (inset)). SA-V scaling analysis for cell cycle stages results in exponents that change within the lifetime of cells (figure 7(F)). Surprisingly, we find the exponent γ and variability of lengths (CV_L ) are the highest in B, and successively decrease in C1 and C2, and at division (D) $\gamma \sim0.66$, the geometric exponent (figure 7(G)). This suggests that cell size variability changes during the process of growth and division and is consistent with population statistics.

Zoom In Zoom Out Reset image size

Analysis of populations of cells sampled from mid-log involved growing E. coli MG1655 in multiple liquid media. Cells were grown in either (a) LB with and without 10 µg ml⁻¹ cephalexin for filamentation or (b) M9-salts supplemented with different carbon sources to modulate the growth rate, with either (i) glucose (4% w/v), (ii) sorbitol (4% w/v) or (iii) glycerol (4% v/v) (Fisher Scientific, Mumbai). Growth rates were measured by monitoring optical density at 600 nm (OD600) every 10 min in a multiwell plate reader (Varioskan Flash2, Thermo Fisher Scientific, Waltham, MA, USA) and fitting the data to a logistic function, as described previously (Gangan and Athale 2017). At mid log-phase, cells were sampled, washed three times with 1% sterile phosphate-buffered saline (PBS) and mounted on slides coated with 10 µl of 1% (w/v) low-melt agarose (HiMedia, Mumbai, India) and observed in microscopy.

Single-cell growth dynamics was performed using E. coli MG1655 transformed using the Hanahan's method of CaCl₂ chemical competence and heat shock (Sambrook and Russell 2001) with a GFP expression plasmid based on a pET15b backbone with a P$_\mathrm{lac-ara}$ hybrid promoter (AND-gate). Cells were grown overnight in LB at 37 ^∘C, of which 10 µl spread on an $2\times2$ cm² agarose pad made on a slide using 1.5% Agarose in LB supplemented with 100 µM IPTG and 0.7% (w/v) arabinose. A coverslip with the agarose pad was placed on a custom-built 3D printed holder for time-lapse microscopy.

Single time point microscopy of populations: Cells grown in growth media were washed in PBS and a 5 µl droplet was placed on an agarose-pad and imaged in 100× (N.A. 1.45) phase contrast mode using an Olympus upright microscope with Olympus cellSense Dimension 3.1 software for image acquisition (Olympus Corp., Japan) and a CCD camera Hamamatsu ORCA-flash4.0 (Hamamatsu Photonics, Japan).

Time-lapse microscopy of single cells: Cells were mounted between two coverslips and imaged using a 100× N.A. 1.4 objective in fluorescence (excitation/emission 488/510 nm) for GFP mounted on a Nikon TiE inverted epifluorescence microscope illuminated with a 130W Intensilight Optic Illumination with control software NIS Elements ver.4.30.01 (Nikon Corp., Japan). Images were acquired on a CCD camera Andor Clara 2 (Andor, NI, U.K). Images were acquired at 1 min intervals for 60 min.

All low level image intensity adjustment, selection of regions of interest and adding scale-bars was performed using Fiji (Schindelin et al 2012).

In order to detect cell outlines, we developed an analysis pipeline in MATLAB (Mathworks Inc. Natick, MA, USA) using functions provided through the Image Processing Toolbox. The workflow was as follows: (a) cell outlines were identified by a combination of edge-detection by the Canny method (Canny 1986), gaps filling, and regions bridging. (b) Cells were filtered based on a minimum solidity criterion between 0.3 and 1 to remove small and irregular objects, with cell boundaries were optimized using an edge-based active contour method (Kass et al 1988), with a smoothing factor 1 and a contraction bias of −0.1. (c) Optimized contour boundaries were overlaid on the original input image and artifacts were interactively deselected to avoid cell debris and out-of-focus cells. (d) The remaining cells with contours were analyzed for length and width by first detecting the midline, and widths taken from averaging the 3rd and 4th quartiles of the minimal distance between the midlines and the contour boundaries. By taking only the top 50% values we exclude narrow widths at the ends of the cell from the analysis.

The code is available as OpenSource and can be downloaded from https://github.com/CyCelsLab/bacterialsizeScaling. The mean, standard deviation and the CV of the obtained lengths and widths is reported in table 2.

This approach was used for both single time-point images in phase contrast as well as fluorescence images of E. coli expressing GFP with small changes in parameters for detection.

Bacterial growth rates in different media were estimated by fitting mean data obtained from triplicate measurements of optical density at 600 nm every 10 min for 3 h to a logistic model. Comparable to previous work, we assume the cell geometry to be a spherocylinder. This allows us to use the cell length and width to calculate the SA as:

$$\begin{equation} \mathrm{SA} = \pi \cdot L \cdot w \end{equation} \tag{ 2 }$$

while the volume (V) is given by:

$$\begin{equation} \mathrm{V}= \frac{\pi}{4}\cdot w^2 \cdot L - \frac{\pi}{12} \cdot w^3 \end{equation} \tag{ 3 }$$

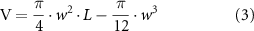
where L is the pole-to-pole length and w the cell width. The scaling relation between SA and volume (V) was obtained by fitting the data to the scaling relation in equation (1). To test the validity of the fit obtained by linear regression in log–log space, we estimated the bounds of the 95% CI using function regplot (Seaborn, Python) with the bootstrapping parameter n = 1000. The shaded area around the data represents the CI. The aspect ratio (A_R ) was calculated as $A_R = L/w$ for each data point. In-house developed Python scripts were used to perform the calculations (Python3) using Pandas, NumPy, SciPy packages and Matplotlib (v3.4.2), with polyfit used for curve-fitting (Harris et al 2020).

The CV was calculated as standard deviation/mean for the simulated distributions and length distributions from experiments.