Abstract
How cells build and maintain dynamic structures of defined size is currently an important unsolved problem in quantitative cell biology. The flagella of the unicellular green alga Chlamydomonas provide a highly tractable model system to investigate this general question, but while the powerful genetics of this organism have revealed numerous genes required for proper flagellar length, in most cases we do not understand their mechanistic role in length control. Flagellar length can be viewed as the steady state solution of a dynamical system involving assembly and disassembly of axonemal microtubules, with assembly depending on an active transport process known as intraflagellar transport (IFT). The inherent length dependence of IFT gives rise to a family of simple models for length regulation that can account for many previously described phenomena such as the ability of flagella to maintain equal lengths. But these models requires that the cell has a way to measure flagellar length in order to adjust IFT rates accordingly. Several models for length sensing have been modeled theoretically and evaluated experimentally, allowing them to be ruled out. Current data support a model in which the diffusive return of the kinesin motor driving IFT provides a length dependence that ultimately is the basis for length regulation. By combining models of length sensing with a more detailed representation of cargo transport and availability, it is now becoming possible to formulate concrete hypotheses to explain length altering mutants.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Flagellar length as a paradigm for understanding organelle size
Cells are complex structured physical systems, with different cell types showing reproducibly different geometries and arrangements of their components. Eukaryotic cells are partitioned into numerous organelles—sub-structures, often membrane bound, that contain specific biochemical pathways and serve different physiological functions. Different organelles differ in terms of not only function and composition, but also size and shape, and it is generally believed that the geometry of organelles is linked to their functions. Although molecular biology has been highly successful in discovering the molecular components from which cells and organelles are constructed, far less is known about how those components are assembled together to form organelles of specific sizes and shapes. In particular, the fundamental question of how organelle size is controlled remains largely unanswered (Levy and Heald 2012, Marshall 2016). Measuring organelle size can often be difficult due to the complex three-dimensional structure of many organelles, and it is not always clear which numbers are the most appropriate to represent the concept of size. For example, do we care most about surface area, volume, or diameter? One approach to this type of problem is to identify a simplified model system in which the geometry of the organelle makes measurement and modeling easier.
In the early 1960s, when the physicist Sir John Randall turned his attention to the question of organelle size control, he chose to use the flagella of the green alga Chlamydomonas reinhardtii (figure 1(A)) as a model system (Randall et al 1964, 1969). Chlamydomonas is a unicellular green alga that has two motile flagella per cell. These structures consist of nine doublet microtubules that support a protrusion of the plasma membrane. They are virtually identical to the cilia and flagella of other eukaryotic cells including humans. We note however that eukaryotic flagella are completely distinct from bacterial flagella, which are based on different proteins and are not membrane enclosed. Flagellar assembly and maintenance is a highly dynamic process and requires active transport mediated by motor proteins moving on the microtubule doublets (figures 1(B) and (C)).
Figure 1. Chlamydomonas flagella. (A) Chlamydomonas cell with two flagella. Inset shows a cross section illustrating the nine outer doublet microtubules. (B) Longitudinal view of one flagellum showing intraflagellar transport taking place along the outer doublets, only one of which is shown in this illustration. IFT particles (green) assemble into linear arrays known as trains, which move to the tip carrying cargo proteins like tubulin, and then return back to the base. The anterograde motion to the tip is powered by kinesin-II, while the retrograde motion back to the base is powered by cytoplasmic dynein. (C) The IFT system is based on two large protein complexes, known as the IFT A and IFT B complexes, which associate with a heterotrimeric kinesin-II and cytoplasmic dynein 2. During anterograde IFT, linear arrays of IFT complexes (IFT trains) are moved to the flagellar tip by kinesin-II. At the tip, kinesin-II dissociates from the IFT particles, which remodel into retrograde trains, which then move back to the flagellar base driven by cytoplasmic dynein 2. The outer doublet microtubules of the flagellum are depicted in blue.
Download figure:
Standard image High-resolution imageAs a physicist seeking to investigate biology, Randall sought out the simplest and most convenient system in which to combine quantitative measurements with genetic perturbations. Flagella have a major advantage for studying organelle size, because their diameters are constant, and the only variable is length. Thus, by studying the mechanisms controlling flagellar length, we can reduce the problem of organelle size to a single dimension. Chlamydomonas was chosen as a model organism because it is a unicellular alga that is easy to grow, has powerful genetics, and has flagella that are not only easy to visualize, but can be induced to detach and regrow, allowing the kinetics of flagellar growth to be analyzed. Randall's vision was to combine quantitative measurements with genetic analysis to uncover the physical principles by which the Chlamydomonas cell controlled the length of its flagella, with the goal of using this system as a paradigm to understand the more general question of organelle size control. In moving from physics to the biology of Chlamydomonas flagella, Randall joined a growing group of genetics and cell biology researchers who had already begun to tackle flagellar assembly in Chlamydomonas (Lewin 1953, Rosenbaum 1969) in a research program that continues to this day.
The advantages of Chlamydomonas flagella continue to be apparent (Wemmer and Marshall 2007)—easy cell growth, convenient live cell imaging, powerful yeast-like forward genetics, rapid purification of the organelle, and the ability to induce flagellar regeneration at a time of our choosing. A wealth of highly detailed molecular, genetic, and ultrastructural knowledge that has been gained about flagellar assembly in the past decades, yet the apparently simple question of what determines the length of the flagellum remains unanswered. In this review, we will start with an overview of what is presently known about flagellar length from cell biological and genetic experiments. We then discuss possible models for how a critical molecular transport process required for flagellar assembly is regulated as a function of length, and conclude with a discussion of existing physical models for the flagellar length control system.
1.1. Evidence for a control system
What do we mean when we talk about a flagellar length control system? What does it mean to say that length is 'controlled'? The implication is that length is more tightly regulated than what one would expect if each flagellum was assembled via a molecular self-assembly pathway in which length measurement was absent. Flagella in a population of Chlamydomonas cells vary in length by approximately 10%–20% (Bauer et al 2021). It is not obvious, however, how much variability one might expect in the absence of a control system. Why then do we talk of 'length control'?
Two phenomena have historically suggested the presence of a length control system. First, when flagella regenerate after removal (figure 2(A)), they grow back with decelerating kinetics, gradually approaching their final length (Randall et al 1969, Rosenbaum et al 1969). The decelerating kinetics suggest a control system at work, that senses the approach to final length, and slows down assembly accordingly. The fact that the length to which flagella regenerate is correlated with their length prior to detachment (Bauer et al 2021) is further evidence that the flagella are growing to some defined length.
Figure 2. Flagellar length dynamics in Chlamydomonas. (A) regeneration kinetics when both flagella are removed. Initially, cells have just tiny stumps where the flagella used to be. Over time, the flagella grow back to their normal length with decelerating kinetics. (B) Long-zero phenomenon, seen when a single flagellum is detached. As that flagellum regenerates, the other one shortens, as indicated by the red curve on the plot. When the two flagella reach equal lengths, they grow back out together to their final length.
Download figure:
Standard image High-resolution imageSecond, and more convincing, is the so called 'long-zero' phenomenon, which is observed when only one of the two flagella on a Chlamydomonas cell is detached (figure 2(B)). The detachment of one flagellum can be accomplished using mechanical pressure (Coyne and Rosenbaum 1970) but can also be achieved using laser ablation to target a single flagellum (Ludington et al 2012). After detachment, while the detached flagellum regenerates, the other flagellum, which presumably was not affected by the procedure, begins to shorten. The long flagellum continues to shorten as the short flagellum grows, until the two reach the same length, at which point they grow out together. Quantitative studies showed that the shortening of the long flagellum provided precursor protein that could be used by the short flagellum (Coyne and Rosenbaum 1970). The ability to equalize lengths in these long zero experiments suggests that processes inside one flagellum are able to induce length changes in response to the length of the other, revealing the presence of some sort of length control system involving information flow between flagella.
More recently, a third piece of evidence for length control has been obtained by measurement of flagellar length fluctuations in living cells (Bauer et al 2021). Flagellar assembly, like all molecular processes, is subject to thermal and other fluctuations. In the absence of a control system for length, the length fluctuations should drive a random walk in length. This is true at short time scales, but at longer time scales, the random walk is constrained, indicating some process that limits the accumulation of fluctuations away from some set point (Bauer et al 2021).
1.2. Genetics of flagellar length
The existence of mutations that affect flagellar length is also sometimes taken to indicate the presence of a control system, on the grounds that such genes must encode components of that system. Length mutants of Chlamydomonas fall into two main classes, long-flagella (lf) mutants (Barsel et al 1988; Berman et al 2003, Tam et al 2003, 2007, 2013), and short flagella (shf) mutants (McVittie 1972, Kuchka and Jarvik 1987, Perlaza et al 2022a), which increase and decrease, respectively, the average flagellar length. The mutants are sometimes interpreted as affecting molecular pathways that control length, and thus their existence is taken as evidence for a length control system. By itself this is not very convincing evidence, since one can easily imagine mutations that affect a molecular self-assembly processes, for example by changing the dissociation constant of a protein-protein interaction involved in building some multi-protein structure, and these would hardly be considered a length control system. The main value of length mutants is not as evidence for length control pe se, but as a means by which components of the length control mechanism, if there is one, can be identified. Thus a major question for the whole field is, how do these mutants lead to their effects on length?
1.3. Intraflagellar transport (IFT) and flagellar length
A major breakthrough in understanding both flagellar assembly and flagellar length regulation came from the discovery of an active transport process operating within flagella. This process, known as IFT, (figure 1(C), was first observed by differential interference contrast (DIC) microscopy in living Chlamydomonas cells, in which objects could be seen to move processively from the base of the flagellum out to the tip and from the tip back to the base (Kozminski et al 1993). The FLA10 gene was found to be required for this movement (Kozminski et al 1995) and, by comparing proteins in the flagella of wild-type versus fla10 mutants, it was possible to identify a set of proteins, known as IFT proteins, that compose the moving objects initially seen by DIC (Cole et al 1988). Subsequent studies have revealed IFT to be a highly complex and structured process (Rosenbaum and Witman 2002, Ishikawa and Marshall 2011, Bhogaraju et al 2013a), in which a heterotrimeric kinesin-II, of which the FLA10 gene encodes one of the motor subunits, interacts with a multi-protein complex known as an IFT particle. The IFT particle proteins contain binding sites for tubulin and other cargo proteins (Bhogaraju et al 2013b, Kubo et al 2016, Taschner et al 2016). These particles accumulate at the base of the flagellum (Deane et al 2001), apparently arriving via a diffusion-to-capture mechanism (Hibbard et al 2021), and self-assemble into linear arrays known as IFT trains (Pigino et al 2009, Vannuccini et al 2016, van den Hoek et al 2022), which enter the flagellum in a process known as IFT injection, and then move processively to the tip, powered by the kinesin-II motor. At the tip, the cargo is released and the IFT proteins remodel into retrograde trains (Chien et al 2017) that are then moved back to the base of the flagellum by a cytoplasmic dynein motor. If IFT trains are prevented from reaching the tip, they are still able to remodel into retrograde trains and return, arguing that remodeling is not triggered by a special environment at the tip but rather by the cessation of forward motion (Nievergelt et al 2022). IFT thus involves a continual back and forth motion of linear arrays of IFT particles (Iomini et al 2001), some moving anterograde (to the tip) and others moving retrograde (back to the cell body) as illustrated in figure 1(B).
Anterograde IFT is required for flagellar assembly as well as for flagellar maintenance (Kozminski et al 1995). Retrograde IFT is less critical—when it is blocked with mutants or chemical inhibitors, flagella are retained for many hours but begin to inflate with protein including many of the IFT proteins (Engel et al 2012). When temperature sensitive fla10 mutants are grown at intermediate temperatures between permissive and restrictive, cells grow flagella of intermediate lengths (Marshall et al 2005). Mutants with increased IFT compared to wild-type cells have increased flagellar lengths (Ludington et al 2013, Wemmer et al 2020). This link between IFT and length is a conserved feature of cilia and flagella in different organisms. In vertebrate cells, prostaglandin (PGE2) signaling promotes IFT and leads to increased ciliary length, while impairment of PGE2 signaling, which reduces IFT, leads to shorter cilia (Jin et al 2014).
Quantitative measurements of IFT trains moving from the base to the tip (anterograde trains) demonstrate that the size, frequency, and speed of the trains is a function of length, with longer flagella having smaller trains (in the sense of fewer IFT particles per train), arriving at the tip at a higher frequency, and with only a very slight dependence of speed on length (Engel et al 2009). The decrease in IFT particle number per train in longer flagella was confirmed by stepwise photobleaching (Engel et al 2009). The total transport rate of the IFT system is the product of the size of the trains and the frequency with which they arrive at the tip, and this product was found to be proportional to 1/L (Engel et al 2009, Ludington et al 2013). The same studies found that IFT particles, once having entered the flagellum, move processively to the tip, thus the rate of transport from the cell body to the tip depends only on the rate of IFT particles entering the flagellum, i.e. on 1/L, and not on their speed.
The 1/L dependence of IFT injection is only relevant for flagellar length dynamics because IFT transports precursor proteins, in particular tubulin (Hao et al 2011, Qin et al 2004, Craft et al 2015, Kubo et al 2016, Taschner et al 2016). It is only by bringing tubulin to the flagellar tip that IFT drives assembly, which means that assembly depends not only on IFT but also on precursor availability. As flagella grow, precursor proteins are gradually depleted from the cytoplasm, leading to slower assembly (Rosenbaum et al 1969). Many proteins contribute to flagellar assembly, but tubulin is apparently the most important for length maintenance, as judged by the fact that when both tubulin binding sites on the IFT particle are mutated so that they can no longer bind tubulin, the result is shf (Kubo et al 2016). The fact that the flagella are not zero length suggests that other mechanisms may exist to move tubulin, including other binding sites on IFT particles (Perlaza et al 2022a) or diffusive motion (Craft van de Weghe et al 2020), which will be discussed below in section 3.
From a physics perspective, IFT has many interesting features. Time-series analysis of IFT has shown hallmarks of avalanche-like behavior, including a power-law tailed distribution of train sizes and a correlation between injection event size and time between events (Ludington et al 2013). The same study also found that IFT shows long-memory behavior based on the Hurst exponent, and quasiperiodicity. Other studies have shown that IFT is able to avoid tug-of-war behavior between the kinesin and dynein motors, suggesting some level of coordination (Mijalkovic et al 2017).
1.4. Flagellar length as a steady state
IFT is required to maintain flagellar length because flagellar microtubules undergo continuous turnover, with new tubulin constantly being added to the tip. Length remains constant because tubulin is also constantly being removed from the tip (Marshall and Rosenbaum 2001). Flagella are thus steady-state structures, such that any control system that maintains length needs to ensure that the rates of assembly and disassembly are equal only at the correct length. When flagella are too short, the assembly rate must exceed the disassembly rate so that the flagellum can grow to the right length. If flagella become too long due to random fluctuations, disassembly must exceed assembly so that the flagellum can shorten back to the correct length.
When IFT is blocked using conditional mutations, such that no assembly can take place, flagella shorten at a constant rate (Kozminski et al 1995, Marshall and Rosenbaum 2001, Marshall et al 2005), which indicates that disassembly is length-independent. This allows us to define a parameter D that is the rate at which flagellar microtubules undergo disassembly. Because disassembly is length-independent, the control system, whatever it is, must act by regulating assembly.
We are now in a position to formulate a maximally simple model for flagellar length dynamics. We start with the observation that IFT particles enter the flagellum at a rate proportional to 1/L, and assume that the quantity of tubulin bound to each IFT particle is proportional to the quantity available in the cell. Representing the total quantity of tubulin as P, expressed in units of equivalent flagellar length, the rate at which the flagellum grows becomes A(P-2 l)/L where A is a coefficient that incorporates the affinity of tubulin binding and the rate of elongation as a function of cargo quantity. 2 l is subtracted from P to express the fact that each Chlamydomonas cell has two flagella, and the tubulin in each of the two flagella is no longer available for further assembly. With these three considerations (length-independent disassembly, IFT entry proportional to 1/L, and precursor availability dependent on how much precursor has already been incorporated), the dynamics of flagellar length can be expressed as
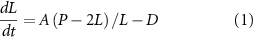
The two terms of equation are plotted in figure 3. The assembly curve represents the first term of equation (1) and is an hyperbola with a limiting value of −2 A and a scale factor of AP. In figure 3 we extend the plot to include larger values of L for which the first term becomes negative, although in reality the assembly rate would become zero once no more cargo is available. We do this to emphasize the hyperbolic shape of the first term. The disassembly curve is a horizontal line of value D.
Figure 3. Flagellar length as a steady state created by a balance of assembly and disassembly. (Green) assembly versus length, depicting the first term in equation (1). (Red) disassembly versus length, depicting the second term in equation (1). A steady state is reached when the two rates equal each other. Note that for the sake of completeness we extend the assembly curve to the point that the assembly curve drops below zero, but in reality this condition would never be reached since once all available tubulin was incorporated, the length could not be increased further.
Download figure:
Standard image High-resolution imageSince the assembly curve is a decreasing function of length, it can only intersect the disassembly curve at a single value, leading to a unique steady state solution. The solution is clearly stable, because for lengths greater than the intersection point, disassembly becomes greater than assembly, while for lengths less than the intersection point, assembly is greater than disassembly.
The steady state solution of this equation is easily found to be

This simple model can explain a number of previous observations. First, the 1/L dependence in the growth term explains the decelerating kinetics of flagellar regeneration. In fact, careful measurements of flagellar regeneration have shown that except at very short lengths, the rate of growth is proportional to 1/L (Marshall et al 2005).
Second, the model can explain the ability of flagellar lengths to equalize after one is severed, the so-called long-zero phenomenon (figure 2(B)). When the two flagella are at their steady state lengths, assembly and disassembly are balanced, so that the tubulin pool in the cytoplasm remains constant. If, however, one flagellum is severed and starts to regrow, it shifts from the steady state operating point to a new condition in which, because of the 1/L dependence on length, it is now a net consumer of tubulin from the cytoplasm. As tubulin is depleted, the other flagellum can no longer support the assembly rate needed to balance the disassembly rate D, and so it starts to shorten. Once the two flagella reach equal length, neither has an advantage over the other and so they both grow out together, with this growth requiring synthesis of new precursor protein (Coyne and Rosenbaum 1970). Simulations of the steady state model employing a 1/L dependence of IFT on length confirm this conceptual view (Marshall and Rosenbaum 2001, Ludington et al 2012, Banerjee and Banerjee 2022) and show that the long-zero phenomenon, which might appear to involve some complex process of length measurement and information exchange between flagella, actually can be explained just on the basis of competition for a common pool of tubulin.
Third, the model makes a clear prediction that the steady state flagellar length should change if the number of flagella per cell is altered. If, instead of having two flagella, a cell had n flagella, the steady state length would become
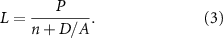
Testing this prediction is possible in Chlamydomonas using mutants known as vfl that cause cells to have variable numbers of flagella instead of the normal two flagella per cell. In a study using such mutants, it was claimed that length was independent of flagellar number (Kuchka and Jarvik 1982), which would not be consistent with the model. Careful measurements on several different vfl mutant strains, using different fixation conditions, found that in fact the variation of L with n was exactly consistent with equation (3) (Marshall et al 2005). Interestingly, the actual data in the Kuchka and Jarvik (1982) paper showed that in cells with more flagella, the length was in fact decreased. The reason for their conclusion was that they had been expecting to see a geometric dependence of length on number, and this was not the case.
Finally, the model predicts that growth rate during regeneration is dependent on length rather than time after the initiation of regeneration. This prediction contradicts a previously published result (Jarvik et al 1984), in which it was reported that when shf mutant cells with half-length flagella were fused to WT cells, so that the mutation was rescued, the half-length flagella started to elongate at the same rapid rate as normal flagella do at the start of regeneration. However, repetition of this experiment found that in fact that previously published result was incorrect due a mistake in the growth measurements of WT control cells, and that when the experiment was repeated, the initial growth rate of the half-length flagella exactly matched the growth rate of normal flagella when they have also reached half length (Marshall et al 2005).
The model of equations (1) and (2) is characterized by three parameters, only one of which is directly measurable. D, the rate of disassembly, has been measured using conditional mutants that stop IFT, leading to flagellar shortening. Under these conditions, flagella shorten by 10 μms in 15 min (Kozminski et al 1995, Marshall and Rosenbaum 2001, Marshall et al 2005) leading to a value for D of 0.011 μm s−1. Parameter P, which describes the total flagellar precursor protein content in units of equivalent length, has not been directly measured, but can be inferred from experiments. When flagella regenerate in the absence of protein synthesis, they regrow to half the normal length (Rosenbaum et al 1969). In such experiments, 2 l worth of protein is removed during deflagellation, such that the total precursor quantity is now P-2 l. Replacing this value into the numerator of equation (2) and then setting the steady state length equal to half the normal length leads to the result that P = 4 l. Since flagella are roughly 10 μms long, we obtain P = 40 μm. With these estimates for D and P, it is now possible to solve for A given that L is 10 μm. We obtain A = 0.0055. Unlike D and P, A is a lumped parameter that combines many individual molecular variables such as the affinity of IFT particles for precursor protein and the efficiency of precursor incorporation at the tip. This parameter also includes any gain or scaling factor relating 1/L to the actual rate of IFT injection, which will depend on the specific model for length sensing (see below).
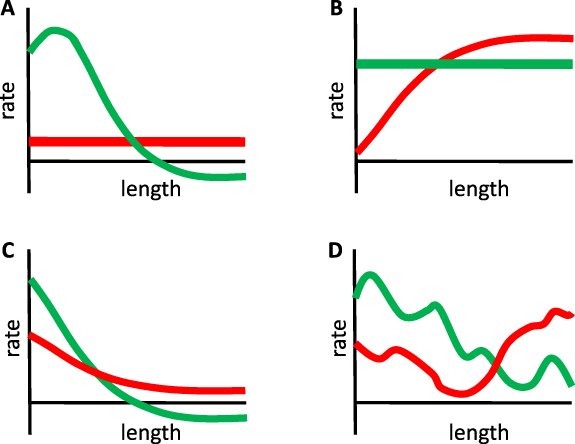
One final point worth noting about this model is that it actually represents a whole class of models, in which the size of a structure is the resultant of two processes, an assembly process and a disassembly process. As long as one process or the other (or both) is size-dependent, there is the potential to have a unique, stable steady state solution. The necessary condition to have a unique steady state solution is that the assembly and disassembly curves must intersect at a single value of length. The necessary condition for this solution to be stable is that for lengths less than the steady state value, the assembly rate must be greater than the disassembly rate, while for lengths greater than the steady state value, the disassembly rate must be greater than the assembly rate. Figure 4 shows several examples of purely hypothetical assembly and disassembly curves that would all yield stable, unique steady state sizes.
Figure 4. A unique, stable, steady state solution can be achieved by a variety of different assembly and disassembly curves. (A) Small variations in the shape of either curve have little effect on the steady state length, although they will affect the growth kinetics. (B) Either the assembly rate or the disassembly rate needs to be length-dependent, but either can produce a unique stable solution provided that the curves only intersect at one length and that assembly exceeds disassembly for lengths shorter than the intersection, and vice versa for lengths longer than the intersection. (C) Both assembly and disassembly can vary as a function of length provided the intersection conditions discussed in panel B still hold. (D) Assembly and disassembly curves do not need to be monotonic functions of length. As long as assembly exceeds disassembly for any length less than the steady state solution, the flagella will grow out to that length. As long as disassembly exceeds assembly for any length greater than the steady state solution, length fluctuations taking the flagella past that point will be corrected.
Download figure:
Standard image High-resolution image1.5. But do we understand how length control works?
Although this steady state model just presented can account for the previously published phenomenological and genetic data on flagellar length control in Chlamydomonas, the entire model hinges on the fact that the rate of IFT injection is proportional to 1/L. We know this is true from experimental measurements, but how does the cell measure flagellar length in order to gate entry of IFT particles accordingly? IFT particles assemble at the flagellar base (Wingfield et al 2017, van den Hoek et al 2022) and then must enter the flagellar compartment through the 'transition zone', a specialized region at the base of the flagellum that serves as a selectivity pore (Takao and Verhey 2016). Evidently, either the recruitment and assembly of IFT trains, or their passage through the transition zone, or both, are regulated as a function of flagellar length. There is evidence that IFT entry might be gated by a nuclear-pore like mechanism (Dishinger et al 2010), and that actin also influences IFT recruitment to the base of flagella (Avasthi et al 2014), but how either of these gating mechanisms might be regulated as a function of flagellar length is unknown. One key question is thus, how is IFT regulated as a function of length to create the 1/L dependence that underlies the steady state length control model. Without being able to answer this question, we cannot claim to know how length control works.
A second key question is how exactly the length-dependence of IFT fits with the rest of flagellar dynamics to create a length control system. The model shown above invokes a number of simplifying assumptions, including the assumption that the disassembly rate is constant and that the quantity of precursor protein carried by each IFT particle is a simple linear function of precursor quantity inside the cell. These assumptions are unlikely to be accurate, and as more quantitative data is acquired, we must determine whether the model breaks down or not. We also expect that understanding how length-altering mutants produce their phenotypes will require us to understand which model parameters are affected in a given mutant, which requires a model with enough detail to represent the activities of key molecular players.
We believe that how IFT is regulated and how IFT fits into an overall model of length control are distinct questions, with the answer to the first informing the possible answers to the second. The rest of this article is based around these two questions, exploring various proposals and their theoretical consequences while also considering how recent experimental results do or do not fit with the various models that result.
2. Models for IFT regulation
A number of models have been proposed for how the cell may sense flagellar length and regulate IFT so as to produce the 1/L dependence of IFT injection on length (Ludington et al 2015). Here we will consider four models which have been analyzed in some detail.
2.1. Initial bolus model
The simplest model for the 1/L dependence is one in which IFT particles do not actually enter or leave the flagellum, but simply circulate back and forth from the base to the tip (figure 5(A)), like subway cars moving back and forth on a track. In this model, the flagellar precursor proteins such as tubulin play the role of passengers, entering and leaving the flagellar compartment, and the apparent injection of IFT trains into the flagellum is actually just the departure of trains from the base as they move back out to the tip. This model was originally suggested by quantification of IFT inside flagella either by Western blotting, or by measurements of fluorescent intensity of IFT trains in flagella of fixed cells, both of which suggested that the total number of IFT particles inside the flagellum was independent of flagellar length (Marshall and Rosenbaum 2001, Marshall et al 2005).
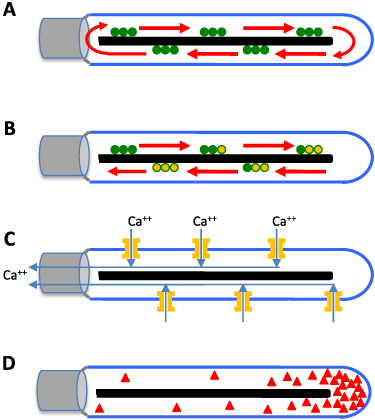
Figure 5. Hypothetical models for flagellar length sensing for IFT regulation. (A) Initial bolus model, in which a fixed pool of IFT particles (green) are loaded into the flagellum when it first forms, after which they cycle back and forth between base and tip, neither entering nor exiting the flagellar compartment. (B) Time of flight model in which a molecular timer attached to the IFT particle, such as a G protein or a phosphorylation site, is initialized to one state (for example GTP bound to a G protein, shown in green) and then gradually undergoes a switch to a second state (guanosine triphosphate (GTP) hydrolyzed to guanosine diphosphate (GDP), shown in orange). The fraction of timers that have switched state when the particles return is a proxy for flagellar length. (C) Calcium ion-current model in which calcium channels are present at a constant density in the flagellar membrane. As length increases, the constant density implies that the number of channels is greater. These channels thus admit increasing quantities of calcium as flagellar length increases. This calcium moves to the base and inhibits entry of IFT particles. (D) Diffusion model, in which a diffusible molecule, depicted by red triangles, is produced at the tip and diffuses to the base. Entry of IFT is promoted by adsorption of this molecule at the base.
Download figure:
Standard image High-resolution imageIf the IFT particles are trapped, their total number will be independent of any changes in length that may occur after they have become trapped inside. If we now consider the transport cycle executed by each IFT particle, it is evident that the round-trip transit time of the particle as it moves from the base to the tip, delivers its cargo, and then returns to the base, will be proportional to the length of the flagellum. If the length is L and the particle travels at an anterograde speed va and a retrograde speed vb, the round-trip transit time is the sum of the time required for the anterograde and retrograde legs of the journal, L/va + L/vb which can also be expressed as 2 l/veff where veff is the harmonic mean of the anterograde and retrograde velocities. The departure frequency from the base, as well as the arrival frequency at the tip, is the reciprocal of the transit time, such that if there are M particles inside the flagellum, the total frequency with which some particle arrives at the tip will be 2Mveff/L, thereby explaining the observed 1/L dependence. We refer to this model as the 'initial bolus' model because it depends on the injection of a bolus of IFT particles into the flagellum when it initially forms. The initial bolus model provides an explanation for equation (1), and therefore it can explain all of the phenomena that equation (1) does, such as the ability of flagella to equalize their lengths after one is severed.
This model avoids the need for any molecular mechanism to measure length—the length dependence arises from simple physics, as a consequence of the fact that it takes longer for a processive motor to travel a longer distance. Unfortunately this simple and elegant idea was disproven by fluorescence recovery after photobleaching experiments (Ludington et al 2015), which showed that when IFT proteins were tagged with fluorescent protein and then photobleached in the flagellum, they were rapidly replaced by new fluorescent trains, and the overall rate of fluorescence recovery matched that predicted if each train that entered the flagellum moved to the tip and back, and then exited the flagellum, to be replaced by new trains. Others have observed exit of IFT trains from flagella in other model systems (Buisson et al 2013).
But if IFT particles are free to move in and out of the flagellum, how can we explain the constancy of IFT particle numbers inside flagella? The 1/L dependence of injection rates provides a simple explanation. We start by noting that the 'dwell time' in the flagellum, i.e. the time it takes a newly injected particle to move to the tip, deliver cargo, and return, is proportional to L given some constant velocity. Previous measurements have found that IFT velocity is only weakly dependent on length (Engel et al 2009). The steady state number of particles, which is equal to the product of injection frequency and dwell time, thus becomes length independent.
The fact that the initial bolus model cannot hold, means that some mechanism must exist to regulate entry of IFT particles as a function of length.
2.2. Time of flight model
One mechanism proposed for length sensing is a 'time of flight' mechanism (Sloboda and Rosenbaum 2007, Patra et al 2020), based on the observation, mentioned above, that the round-trip transit time for an IFT particle after injection is 2 l/veff where veff is the harmonic mean of the anterograde and retrograde velocities. If a molecular timer existed that could read out the time the particle had spent inside the flagellum (figure 5(B)), this could be used to regulate IFT entry. There are many possible ways to implement a molecular timer. One possibility would be a small GTPase, which starts out loaded with GTP and then undergoes hydrolysis at some constant rate while inside the flagellum. Indeed, two IFT proteins, IFT22 and IFT27, are small GTPases (Qin et al 2007, 2012). Alternative ways to implement such a timer might include a phosphorylation site that becomes phosphorylated by a kinase localized inside the flagellum, (Cao et al 2013) or a protein that undergoes a conformational change.
All of these hypothetical timers are effectively the same in that they all invoke a molecule that switches from one state to another a constant rate, which implies that the distribution of switching times for a given molecule is exponentially distributed. If an ensemble of such molecular switches started out all in the initial state, and then was sent into the flagellum via IFT, the fraction that would still be in the initial state after a round-trip would be given by

where k is the rate constant for the switching. If we assume that the injection rate is proportional to the fraction of returning particles in the initial state, this produces an injection rate that is a decreasing function of L. In this case, injection would be an exponential function of length rather than varying as 1/L, but existing data is sufficiently imprecise that this could in face be the case. We can roughly estimate the time constant that a timer would need to have to function in this context: given the velocity of IFT particles in the range 1–3 μm s−1, and a flagellar length of 10 μm, the time constant of the timer would need to be on the order of 10 s, which is readily achievable by many different molecular processes.
One way to test such a model is to identify the timer and then make mutations to modify its rate of switching, and see how that affects IFT entry. However, as noted above, there are numerous ways to implement such a timer, so it is not obvious which molecule to modify. An alternative strategy was taken to test this class of models, by noting that a decrease in veff would cause the 'time of flight' inside the flagellum to become larger, which should be interpreted by the IFT injection system as an increase in length. Thus, if veff could be reduced, IFT injection rates should decrease. This proposal was tested using mutants that affect the speed of the dynein motor powering retrograde IFT, and it was found that the injection rate did not decrease (Ishikawa and Marshall 2017). This experiment was thus able to rule out the whole class of time of flight models, without needing to guess the molecular identity of a putative timer.
2.3. Ion current model
Another proposed way that the cell could measure the length of flagella is via a calcium current through the flagellar membrane (Rosenbaum 2003). This model is based on the observation that calcium channels have a constant density in the membrane, independent of flagellar length (Beck and Uhl 1994), which predicts that longer flagella could have larger calcium currents. It has been shown that a calcium dependent protein kinase (CDPK) phosphorylates the kinesin-II motor that drives IFT, preventing the motor from entering the flagellum (Liang et al 2014, 2018). The ion current model combines these observations and proposes that as the flagellum becomes longer, more calcium enters through flagellar membrane calcium channels, triggering an increase in CDPK activity, leading to decreased IFT injection (figure 5(C)). The prediction of this model is that decreasing calcium in the flagella, either by mutating the calcium channels or by depleting calcium from the media, should alleviate the inhibition by CDPK mediated phosphorylation, leading to increased IFT injection and an increase in flagellar length. However, recent experimental observations have shown that while total flagellar calcium is indeed length dependent as the model predicts, reducing calcium entry using channel mutants or calcium chelators did not have the predicted effect of increasing IFT injection or flagellar length (Ishikawa and Marshall 2017, Ishikawa et al 2023).
2.4. Diffusion model
A very general model for sensing the length of linear structures is to have a diffusible substance, produced at one end of the structure, that diffuses to the other end where there is a sink (figure 5(D)). In such a system, the concentration gradient, as well as diffusional flux, provide information about length (Levy 1974). This proposal was originally made without reference to any specific molecule as the signal. More recently, a clear candidate for the diffusible molecule has emerged. Using an ingenious photobleaching system to render individual kinesin molecules detectable inside the flagellum, Chien et al (2017) were able to show that while the IFT particles are brought back from the tip to the cell body by processive action of cytoplasmic dynein, the kinesin-II motor itself does not return processively, but via diffusion. As part of the IFT train remodeling process at the flagellar tip, the kinesin detaches from the rest of the train (figure 1(C)), and then has to diffuse back. This idea is supported by the fact that when retrograde transport is disrupted in dynein mutants, IFT proteins accumulate inside the flagellum, but kinesin-II does not (Engel et al 2012). It is also known that while most IFT proteins tagged with green fluorescent protein (GFP) show clear anterograde and retrograde traces in kymographs, kinesin-II only shows anterograde traces (Engel et al 2009, Ludington et al 2013), consistent with diffusive return.
A diffusion model based on kinesin-II postulates that IFT trains are recruited and assemble at the base of the flagellum at a rate that depends on the availability of kinesin-II as it returns from the tip of the flagellum. When enough kinesin has built up, a new train is injected. Stochastic simulations, as well as analytical solutions of this model, show that diffusion of kinesin-II can indeed account for a stable, unique steady state length, and can recapitulate regeneration with decelerating kinetics as well as the ability of flagellar lengths to equalize after one is severed (Hendel et al 2018, Ma et al 2020).
Taking into account the active processive motion of kinesin from the base to the tip, diffusive return of kinesin from the tip to the base, and the dwell time spent while the kinesins re-attach to the IFT trains at the base and detach from the trains during remodeling at the tip, we obtain (Ma et al 2020) an equation for flagellar growth:
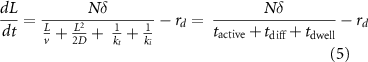
where v is the motor velocity, D is the diffusion constant (not to be confused with our use elsewhere of D as the disassembly rate—we use this alternative notation here to be consistent with standard usage for diffusion constants), rd is the disassembly rate, N is the number of IFT particles in the system, δ is the increment in length resulting from delivery of cargo by one IFT particle,  is the time for anterograde trains to move from the base to the tip,
is the time for anterograde trains to move from the base to the tip,  is the average time for kinesin-II to diffuse back to the base from the tip, and
is the average time for kinesin-II to diffuse back to the base from the tip, and  represents the combined motor dwell times during remodeling at the base and at the tip.
represents the combined motor dwell times during remodeling at the base and at the tip.
Experimental measurements (Chien et al 2017) obtained values for the diffusion coefficient of D∼2 μm2 s−1, for the motor velocity ν of roughly 2 μm s−1, and for the transition rate of remodeling at the tip (kt) of 0.5 s−1. The remodeling rate at the base is approximated by the injection rate of new IFT trains, which is 0.1 s−1 (Ma et al 2020).
At very short lengths,  dominates over the other two time scales, so the flagellar growth rate is independent of length. In fact, measurements have shown that for lengths shorter than approximately 1–2 μms, growth rate is length-independent (Marshall et al
2005). As L increases, the diffusive timescale
dominates over the other two time scales, so the flagellar growth rate is independent of length. In fact, measurements have shown that for lengths shorter than approximately 1–2 μms, growth rate is length-independent (Marshall et al
2005). As L increases, the diffusive timescale  dominates if
dominates if  is small, or the transportation timescale
is small, or the transportation timescale  dominates if
dominates if  is large. At intermediate values of
is large. At intermediate values of  , growth occurs in three phases, in which the dominant time scales are
, growth occurs in three phases, in which the dominant time scales are  ,
,  and
and 
This model predicts that the dependence of growth rate on L is more complicated than simply 1/L, suggesting that more precise measurements of growth rate would be useful in distinguishing this model from others.
At steady sate,
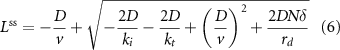
An important feature of this model is that depending on the motor speed and diffusion coefficient, either quantity can be limiting such that variations in the other have little effect on steady state length. Given that L is approximately 10 μm, v is approximately 2 μm s−1, and D has been measured as 2 μm2 s−1 inside flagella (Chien et al 2017), we can estimate that tactive ∼5 s and tdiff ∼25 s. Thus, we expect that under normal conditions, diffusion is limiting, and hence that changes in velocity would have minimal effect on steady state length. In an elegant experiment using a chimeric kinesin-II motor with reduced speed, Li et al (2020) found that the effect on steady state length was small, consistent with a model in which the diffusion timescale is limiting.
Kinesin-II is a heterotrimeric motor, with two motor domains and one non-motor domain. The function of the non-motor domain is unclear, but it is larger than either of the motor subunits. In the case that the diffusion constant determines steady state length, it is interesting to consider whether one function of the non-motor subunit might be to tune the diffusion constant in order to achieve a target length.
3. Towards a more realistic model for flagellar length control
In section 1 we presented a simple model for flagellar length control in which negative feedback arises from the 1/L dependence of IFT injection (equation (1)). Section 2 addressed some potential mechanisms by which the 1/L dependence of IFT injection rate on length may arise. A host of other questions remain about how precisely to represent the function of IFT in the overall process of length maintenance. Here we consider three potentially complicating factors, namely, the facts that (a) disassembly may not be length independent, (b) binding of tubulin and other flagellar precursors to IFT particles is saturable, and (c) the availability of precursors in the cytoplasm is itself a complex dynamical process.
3.1. What if disassembly is also length-dependent?
We have previously estimated the disassembly rate, D, based on the shortening rate of flagella in mutants that block assembly by stopping IFT (Kozminski et al 1995, Marshall and Rosenbaum 2001, Marshall et al 2005). Under such conditions, flagella shorten at a rate of 0.01 μm min−1. However, during the 'long zero' phenomenon discussed above, while the short flagellum is growing, the long flagellum shortens by a rate of 0.5 μm min−1 (Ludington et al 2012). Why is the shortening so much faster in this case? We hypothesize that the reason might be that IFT, which is still functional in long-zero cells, could be helping to accelerate disassembly, either by removing disassembled tubulin from the flagella (Qin et al 2004) or by helping depolymerizing factors, such as the microtubule depolymerizer kinesin-13 (Piao 2009), reach the tip. The latter type of model has been shown to be able to produce stable length control in microtubules (Kuan and Betterton 2013). Retrograde IFT particles contain acetylated tubulin, which, because acetylation takes place after incorporation into the flagellum, indicates that they are transporting disassembled tubulin out of the flagellum (Qin et al 2004). Thus, IFT may not only help assembly, but also disassembly, of the flagellar microtubules. In this case, the disassembly term for the equation governing flagellar length change must also be a function of 1/L, since it will depend on the frequency of IFT particles returning from the tip back to the cell body, which, since IFT particles do not accumulate in the flagellum, must equal the frequency of IFT particles entering the flagellum.
In order to incorporate IFT-dependent disassembly into the model, we note that when IFT is completely absent, disassembly still occurs, and so we need to retain the constant disassembly term D and add a second disassembly term that depends on 1/L We therefore modify equation (1) as follows:
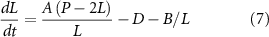
We can plot these curves, analogously to what was done for equation (1) in figure 3. In this case (figure 4(C)), the disassembly curve is no longer a flat line, but an hyperbola, just like the assembly curve. The two hyperbolas still intersect because they reach different limit at infinite length.
Because the curves intersect at a single point, and because the assembly rate is greater than the disassembly rate for L larger than this point, we can see immediately that the equation has a unique, stable, steady state solution. This steady state length can be solved as:

We conclude that even if disassembly is dependent on IFT, and therefore not length-independent, the model still results in a unique steady state length. At the most extreme, it is possible to construct a length control mechanism based entirely on length-dependent disassembly (Fai et al 2019). This type of mechanism is thought to be the basis of the ability of a single cell to have different flagella of different length, as seen in the protist parasite Giardia, which has eight flagella of different lengths and in which the length negatively correlates with the turnover rate inferred based on the quantity of kinesin-13 at the tip (McInally et al 2019). In the general case, distinguishing length control models based on length-dependent disassembly from models based on length-dependent assembly will require methods to measure microtubule assembly and disassembly rates at steady state in the presence of normal IFT activity.
3.2. Saturable binding of tubulin to IFT particles
Although much of the modeling and experimental work on length control has focused on IFT, the IFT particles contribute to length dynamics by carrying tubulin, and so any length control model needs to account for the binding and transport of tubulin or other cargos. When tubulin was imaged in Chlamydomonas flagella (Craft et al 2015), it was found that as flagella become longer, a decreasing fraction of IFT trains contained tubulin. The quantity of tubulin per IFT particle was not measured, just the fraction of trains with zero tubulin. The fact that more trains appeared 'empty' as L increased, in the sense that they lacked detectable tubulin, was taken as evidence that tubulin binding by IFT particles is length dependent. This argument ignores the fact that as L increases, the number of IFT particles per train decreases (Engel et al 2009). If we assume that the binding affinity of IFT particles for tubulin is length-independent, then we can say that even if cytoplasmic tubulin is held constant (which it probably is not), we would still see an increase in empty trains as length increases. Given a constant probability of an individual IFT particle having bound tubulin Pbound, the probability of a train being empty as a function of the number of particles in the train is:
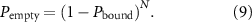
As L increases, the number of particles N per train decreases (Engel et al 2009, Ludington et al 2013), hence, Pempty should increase as L increases, even if Pbound is constant and not a function of length. In fact, the published measurements of Pempty as a function of length (Craft et al 2015) match this prediction exactly (Wemmer et al 2020). We conclude that while tubulin binding to IFT particles may be length-dependent, this is not established by existing data.
But even if the binding constant for tubulin to the IFT particle is not regulated as a function of length, it is clear that the simple assumption in equation (1), that the quantity of tubulin carried is proportional to the quantity available, is not biochemically plausible. Any binding interaction will be saturable, so that at some point, increasing the quantity of precursor available will not lead to an increase in occupancy. If the cell were operating in a condition of saturated binding, then equation (1) would reduce to the simpler form
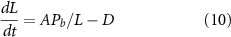
where Pb represents the maximum bound precursor quantity. This modified equation has a unique, stable, steady state solution

So, fully saturated binding would produce a length control system. However, saturated binding would not be able to account for the 'long zero' phenomenon, because now the two flagella would not be in competition for a pool of precursor. Likewise, fully saturated binding would not be able to account for the dependence of L on flagellar number, which is also a competition phenomenon. In any case, the fact that protein synthesis is required for flagella to grow at full speed or reach full length (Rosenbaum et al 1969) strongly implies that growth rates depend on precursor availability, arguing that tubulin binding sites are not normally fully saturated.
In between the two extremes of binding proportional to available tubulin (equation (1)) and saturated binding (equation (10)), the more reasonable assumption is that of binding to a saturable binding site with a finite dissociation constant.
If we modify equation (1) to include saturable binding of tubulin to the IFT particle with a dissociation constant Kd , we obtain:
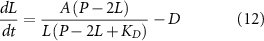
Setting dL/dt to zero leads to a quadratic equation for the steady state length, which has two solutions:
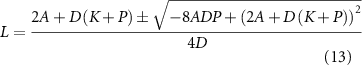
Both solutions give a positive value for L, but only one is stable:
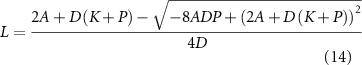
The other solution, which leads to a larger value for L, is half-stable in that any values greater than this solution will decay to it, but any perturbation to a smaller value will lead to the system switching to the lower solution. Given that flagella grow starting from short stubs, the initial conditions would never allow the upper solution to be reached, and even if it were to be reached, length fluctuations (Bauer et al 2021) would not permit it to be maintained. Thus, saturable binding of tubulin or other precursors still allows a unique stable steady-state length. We have shown using numerical simulations that the introduction of saturable tubulin binding into the model yields stable length control with regeneration curves similar to those seen in experiments, and with the ability to account, at least qualitatively, for the regeneration behavior of mutants in an IFT associated protein, Crescerin, that is predicted to contain tubulin binding sites (Perlaza et al 2022a).
We note that in equation (12), the parameter A reflects, among other molecular parameters, the number of tubulin binding sites on the IFT particle. Mutants that eliminate some of the tubulin binding sites would reduce A. When either of the two previously characterized tubulin binding sites, on IFT74 and IFT81 respectively, were mutated, the effect on flagellar length was slight, although the kinetics of growth were visibly reduced (Kubo et al 2016). However, when both binding sites were mutated, flagellar length became extremely short (Kubo et al 2016). Flagella were still present, possibly representing either additional tubulin binding sites (Perlaza et al 2022a) or an IFT independent component of tubulin transport. The latter was supported by the ability of mutant tubulins, altered to make them unable to bind to IFT proteins, to enter the flagellum and incorporate into the axoneme (Craft van de Weghe et al 2020).
3.3. Availability of flagellar precursors in the cytoplasm
While on the subject of precursor loading, what about the production of precursor in the first place? When flagella regenerate, genes encoding essentially all flagellar proteins are transcriptionally upregulated to produce a pulse of expression, with transcript levels rising during the early stages of regeneration, and dropping back down again as the flagella reach their steady state lengths (Schloss et al 1984, Stolc et al 2005, Perlaza 2022b). How does the cell know to trigger the transcription of these genes when the flagellum is regenerating? This remains an open question, but one recent proposal is that a transcriptional repressor is made in the cytoplasm and then sequestered inside the growing flagellum by IFT (Perlaza et al 2022b). According to this model, when flagella start to regenerate, the 1/L dependence of IFT injection on length means that the repressor is sequestered at a high rate, leading to a rapid increase in gene expression. As the flagellum elongates, IFT injection rates decrease, and the repressor is no longer sequestered effectively, allowing it to shut gene expression back of. This induction of gene expression in response to active growth of flagella is reminiscent of other examples of 'just in time' gene expression driven by metabolic needs related to cell growth (Zaslaver et al 2004, Teng et al 2013).
In the specific case of tubulin there is an additional complication, which is that the same tubulin used to build the flagellum is also used to build cytoplasmic microtubules. Inside the Chlamydomonas cell, there are four highly stable 'rootlet' microtubule bundles, but in addition, there are multiple dynamic cytoplasmic microtubules that run from the base of the flagella down the sides of the cell (Schibler and Huang 1991, Horst et al 1999, Wang et al 2013). There are approximately ten of these microtubules, each approximately 8 μms long (Schibler and Huang 1991). Comparing this to the two 10 μm long flagella, each of which contains nine doublets, the quantity of tubulin contained in the cytoplasmic microtubules is on the order of a third of the total. The Chlamydomonas genome encodes two identical alpha tubulins, and two identical beta tubulins, so that there cannot be distinct tubulins in the two types of microtubules. Instead, the flagellar and cytoplasmic microtubules must compete for a common pool of tubulin. When flagella regenerate, the cytoplasmic microtubules undergo a transient disassembly (Wang et al 2013), suggesting that flagellar assembly can successfully compete with cytoplasmic microtubules during the rapid growth phase of flagella.
That the converse is also true is suggested by mutations in proteins that destabilize cytoplasmic microtubules. The kinesin-13 family of microtubule motors catalyze disassembly of microtubules. In Chlamydomonas, knockdown of cytoplasmic kinesin-13 using RNAi caused a shf phenotype and a loss of cytoplasmic microtubule depolymerization during flagellar assembly, suggesting that when cytoplasmic microtubules cannot be disassembled, flagella are unable to make use of the tubulin that they contain, and this leads to less flagellar assembly. This conclusion was reinforced by the fact that when Chlamydomonas cells were treated with taxol, a microtubule stabilizing chemical, just prior to deflagellation, the rate of flagellar assembly was greatly decreased, and flagellar elongation became completely dependent on new protein synthesis (Wang et al 2013).
Consistent with these observations, mutations in the microtubule severing protein katanin, which is localized in the cell body, also lead to a shf phenotype characterized by slower flagellar growth (Kannegaard et al 2014). Given the complexity of microtubule dynamic instability, it is not trivial to incorporate cytoplasmic microtubule turnover into an analytical model of flagellar growth. By adding stochastic simulations of microtubule dynamics (Gregoretti et al 2006) to the steady state model for flagellar length dynamics (equation (1)), it has been shown that reduction in microtubule severing can be sufficient to produce the flagellar growth alterations seen in katanin mutants (Kannegaard et al 2014).
3.4. IFT-independent tubulin transport
A careful quantitative study found that when beta tubulin was mutated to make it unable to bind to IFT particles, the mutant tubulin is still imported into flagella and incorporated into the axoneme (Craft van de Weghe et al 2020). Because these mutations impaired tubulin function required for cell division, the mutant tubulin had to be expressed on a background of normal tubulin, and so these experiments could not directly address the role of IFT-mediated tubulin transport in length control, but they clearly suggest an IFT independent mechanism for tubulin entry into flagella.
On the other hand, the fact that double mutants affecting both IFT protein tubulin binding sites results in short steady state flagellar length (Kubo et al 2016) argues that the diffusive entry of tubulin may be less effective than IFT. One way to reconcile these results is that IFT may not be required for tubulin to enter the flagellum but may play a role in concentrating tubulin near the tip, where assembly and disassembly occur, by releasing it there. Photobleaching studies showed that even in wild-type flagella, there is a pool of soluble tubulin throughout the flagellum that undergoes diffusion (Craft et al 2015). Taken together, the evidence suggests that IFT-mediated transport is taking place on the background of a slower but non-negligible diffusive transport process, which may have an effect at very short lengths but is too slow to maintain a normal steady state flagellar length. Clearly, a fully comprehensive model of flagellar length control will need to take into account tubulin diffusion and the possibility of spatial concentration gradients within the flagellar compartment.
4. Can we explain length-altering mutants in Chlamydomonas
Chlamydomonas flagellar length has been a classical genetic problem, with many mutants identified over the years that affect length. Although a number of the genes involved in these mutations have been cloned, in most cases the identities of these genes have not suggested a mechanistic explanation for how the mutations change length. We believe that a theoretical understanding of length control can provide the missing conceptual basis for understanding the phenotypes of lf and shf mutants.
The modeling framework for flagellar length indicates that all length-altering mutants work in essentially the same way—by shifting the equilibrium value at which the assembly and disassembly rates balance each other, to a new length shorter or longer than wild type. In the models discussed above, alteration of any model parameter has the potential to alter the steady state length. If it were possible to determine which cellular processes or parameters are affected in a given mutation, it would then be possible to test potential length control models by asking whether the length phenotype is consistent with the predicted alteration in length caused by that particular parameter change. This, in turn, would provide an explanation for the length altering mutants.
Figure 6 gives four examples of length-altering perturbations to the simple model of equation (1). Increasing the assembly rate versus length curve, for example by increasing either the efficacy of IFT A or availability of precursor P, would increase the length at which the two curves intersect, leading to a long flagella phenotype (figure 6(A)). Decreasing the disassembly rate D, while leaving IFT and precursor parameters unchanged, would also lead to a steady state solution at a longer length (figure 6(B)). On the other hand, reducing IFT or precursor availability (figure 6(C)) would cause a shf phenotype, as would increasing the disassembly rate (figure 6(D)). There are thus at least four possible ways to make a length-altering mutation. Can all length altering mutants be accounted for by such parameter changes in IFT, precursor availability, or disassembly rates?
Figure 6. Simple models for length-altering mutants in Chlamydomonas based on steady-state length control. In each panel, dashed lines represent the wild-type assembly vs length and disassembly vs length curves, solid lines represent curves in mutant cells. Red depicts disassembly curve, green depicts assembly curve. Solid and dashed arrows indicate steady state solution for mutant and wild-type cells. (A) Long flagella mutant phenotype resulting from increased assembly, due to enhanced IFT or tubulin availability. (B) Long flagella mutant phenotype resulting from decreased disassembly. (C) Short flagella mutant phenotype resulting from decreased assembly, such as due to impaired IFT or reduced availability of tubulin. (D) Short flagella mutant phenotype resulting from increased disassembly.
Download figure:
Standard image High-resolution image4.1. LF mutants
Five LF (long flagella) genes have been identified, in which recessive mutations lead to increased flagellar length, and the genes affected by each mutation have been identified (Berman et al 2003, Nguyen et al 2005, Tam et al 2007, 2013). The LF2, LF4, and LF5 genes encode kinases, but their targets are not in general known, nor is it known what upstream signals, if any, may regulate their activity. When discussing length-altering mutants, it is tempting to assume that because a length-altering mutant affects a kinase, which typically play information transmitting roles in the cell, it must be part of a feedback loop that controls the length. By being part of a loop we mean that the kinase transmits information about length. If this were the case, then deletion of the protein would stop the flow of information, and so the system would no longer be aware of the length. This would make it impossible have stable length control.
The original lf4 mutant is a null mutant that does not make any functional protein (Berman et al 2003) and thus cannot transmit any information. If LF4 kinase was truly part of a feedback system, loss of the protein would eliminate the 1/L dependence of IFT and lead to deregulation of length. But this is not at all the case. First, length in these mutants is not random or unregulated—lf4 mutants stably achieve a quite reproducible length that is about twice that of wild-type cells. Second, if the flagella of lf4 mutant cells are detached, new flagella will grow back to the abnormal length (Asleson and Lefebvre 1998). Finally, the IFT injection rate still scales as 1/L in the lf4 null mutant (Ludington et al 2013). Thus, it is fairly clear that LF4 does not encode an essential information-transmitting component of a length feedback loop.
But as discussed above, there are many ways that a mutation could affect length, many of which do not require the protein to transmit information. For example, one could easily imagine that a mutation affecting the length-independent component of flagellar disassembly would lead to an alteration in length. So would increased production of precursor proteins like tubulin which, again, need not be dependent on length. Quantitative measurement of IFT in lf mutant cells have shown that lf1, lf2, and lf4 cells all show increased injection of IFT particles at any given length (Ludington et al 2013, Wemmer et al 2020). In the case of LF4, it has been shown that the loss of the protein leads to decreased phosphorylation of the FLA8 subunit of the IFT kinesin-II (Wang et al 2019). Phosphorylation of FLA8 is thought to impede IFT injection (Liang et al 2018), so loss of phosphorylation in an lf4 mutant could explain the increase in IFT, and therefore the increase in length. In the context of the diffusion model for length sensing, we speculate that phosphorylation of kinesin-II by LF4 kinase might alter the assembly kinetics of trains for a given rate of diffusive return of kinesin. It is not yet known how lf1 and lf2 mutants affect IFT injection.
Given that lf mutants affect IFT, the important question is whether the effect on IFT is the cause of the increased length. Wemmer et al (2020) showed that the average length seen in the lf mutants is indeed consistent with the increase in IFT caused by the mutants, arguing that other effects are not needed to account for the increase in length. This study illustrates that length-altering mutants can provide a way to test length control models, by determining which parameters are altered in a given mutant, and then asking if the model makes a correct prediction about the resulting length.
The two types of lf mutants depicted in figures 6(A) and (B) both share the feature that the assembly and disassembly curves intersect at a shallower angle, which means that fluctuations in length away from the steady state value will take longer to be corrected. Linear noise analysis shows that given a constant noise source in the assembly process, any parameter change in equation (1) that leads to an increased average length will lead to an increase in length variation accompanied by a longer correlation time in the fluctuations (Bauer et al 2021). Analysis of length variance as well as time-series analysis of length fluctuations in lf mutants compared to wt cells has confirmed both predictions (Bauer et al 2021).
4.2. Short-flagella mutants
The long flagella mutants have received the lion's share of attention from Chlamydomonas geneticists, but from the point of view of understanding the biological mechanism of length control, shf mutants are equally informative. The first short flagella mutant mapped, shf1 (Kuchka and Jarvik 1987) was recently found to represent a mutation in a flagella-localized homolog of the TOG-domain family protein Crescerin (Perlaza et al 2022a). Tumor overexpressed gene (TOG) domains can function both to bind tubulin dimers, and also to promote their polymerization onto growing microtubules (Slep 2009). Crescerin has previously been found to play a role in ciliary length maintenance in C. elegans (Das et al 2015). In light of the models above, loss of a protein that functions to either transport or assemble tubulin would be predicted to lead to a decreased steady state length, and indeed modeling studies incorporating tubulin binding affinity for the IFT particle were able to recapitulate the shf1 phenotype in terms of both steady state length and regeneration kinetics (Perlaza et al 2022a).
Another shf mutant that was identified in a forward genetic screen turned out to encode a mutation of the p80 subunit of katanin (Kannegaard et al 2014). This mutation has already been discussed above in section 3. It is perhaps informative that both of the known shf mutants affect proteins involved in microtubule dynamics. In this sense the shf mutants have proven more mechanistically informative than the lf mutants, for which a specific cellular function has been difficult to pin down.
4.3. Human diseases that affect ciliary length
Almost all cells in the human body contain cilia, which are closely related to the flagella of Chlamydomonas—both contain the same nine doublet microtubules, use IFT to assemble, and in general share an extremely high degree of molecular conservation. In humans, cilia not only perform motile functions like moving mucus in the airway, they also perform sensory functions for a number of signaling pathways (Singla and Reiter 2006). Consequently, mutations that affect ciliary assembly in humans lead to a wide range of different disease symptoms, collectively known as ciliopathies (Reiter and Leroux 2017). Treatments for ciliary defects do not currently exist, such that the only way to help ciliopathy patients is currently to try to mitigate the symptoms.
Interestingly, many ciliopathies appear to arise from alterations in the length of cilia. Mutations in many IFT proteins, which cause flagella to be short or missing in Chlamydomonas, also cause cilia to be short or missing in mouse or human cells and lead to polycystic kidney disease. It is thought that because cilia are too short in such patients, they are unable to perform their normal signaling function.
Abnormally long cilia have been reported in loss of function mutations in a number of gene involved in human ciliopathies, including mutations in MKS1 and MKS3 causing Meckel syndrome (Tammachote et al 2009); BBS4 causing Bardet-Biedl Syndrome (Mokrzan et al 2007); CEP290 or KIAA0556 both of which cause Joubert's syndrome (Sanders et al 2015, Ramsbottom et al 2018); NEK8 causing juvenile autosomal recessive polycystic kidney disease (Smith et al 2006); MAK causing retinitis pigmentosa (Ozgül et al 2011); and Kif7 (He et al 2014) which is involved in a variety of diseases including Joubert's syndrome and acrocallosal syndrome (Barakeh et al 2015).
The Joubert's syndrome gene KIAA0556 is particularly interesting, because it encodes a microtubule binding protein that stabilizes microtubules (Sanders et al 2015). We hypothesize that this protein may normally act in the cell body to stabilize cytoplasmic microtubules, thus reducing the pool of tubulin available for ciliary assembly, such that when the protein is lost, cilia can elongate because more tubulin is available. This would be the converse of the shf phenotype observed in Chlamydomonas shf mutants involving microtubule destabilizing proteins such as katanin or kinesin-13.
We also note that the MAK kinase involved in retinitis pigmentosa (Ozgül et al 2011) is closely related to the LF4 kinase in Chlamydomonas, and mutations in both cause increase in the length of cilia/flagella. Other related kinases in mammal, MOK and ICK, can affect ciliary length as well (Broekhuis et al 2014). In this latter study, it was shown that mutations affecting length did not strongly affect the velocity of IFT. However, as we have noted above, since IFT is processive, what matters is not how fast the trains travel from the base to the tip, but only how often the trains enter the flagellum or cilium. This is one example of how theoretical models of length control can help to clarify the effects one should expect for mutations affecting a given process, and indeed this is an important role for mathematical modeling in biology in general.
Given that such a wide range of genes and mutations can give rise to ciliary length alterations, and thereby cause ciliopathies, it might seem an impossible task to develop pharmacological treatments for each of them. However, because length is a steady state resulting from a balance between assembly and disassembly, it should be possible to shift this balance back to a more normal length by targeting any component of the length control system, even if it is not the component actually affected in a given disease. For example, any ciliopathy involving overly long flagella could potentially be reversed by slightly decreasing IFT. Whether this strategy would actually work in practice remains to be seen. Several small molecule screens (Besschetnova et al 2010; Engel et al 2011, Avasthi et al 2012, Firestone et al 2012, Khan et al 2016) as well as systematic genetic screens (Kim et al 2010) have identified modulators of ciliary length that point the way to such a therapeutic strategy.
5. Future directions
5.1. Towards an integrated model
In section 2, we considered several different models for IFT dependence on L, some of which predict exact 1/L dependence, and others slightly different dependencies. In section 3, we considered a series of modifications of the overall steady state balance model (equation (1)) so as to make the model more realistic. But we considered each of these alterations separately. An important research goal, that is beyond the scope of this review article, is to ask what happens when we combine all of these modifications into a single integrated model. Do we still obtain stable length control, or is stability now restricted to a limited region of parameter space? Do new types of dynamics arise that might be detectable in experiments?
The effort to integrate various models may highlight potential incompatibilities among them. As currently formulated, the model variants in section 3 do not seem to be mutually exclusive—there is no reason a priori why saturable tubulin binding, length-dependent disassembly, etc, could not all be taking place at the same time. The question is whether the combination of these process might break the stability of the system.
5.2. Measuring parameters
Thus far, models for length control have been simplified to the point that a meaningful quantitative comparison with data and with known parameter values has not been possible. It was sufficient to ask qualitative questions, such as, does increased IFT lead to increase steady state length. In a few cases, noted above, model parameters can be directly measured, while in other cases the parameters need to be inferred indirectly by fitting model predictions to data. This is inevitable given the abstract nature of the models. As the models become more realistic, it will become increasingly possible to relate model parameters to actual molecular processes that can, in principle, be directly monitored. As just one example, we discussed above how current parameter estimates for the disassembly rate D are based on flagellar shortening when IFT is shut off. However, using photoswitchable tubulin constructs or other means, it should be possible to measure tubulin disassembly in intact flagella while IFT is normally operating. If theoretical models for length regulation can motivate new experimental measurements, they will have proven their utility, even if the measurements end up invalidating the models.
The converse of using direct measurements of parameters to test models, is to use models as a tool to infer the value of parameters that might be difficult to measure directly. Again, as models become more realistic, parameter inference becomes more plausible. One important motivation to estimate parameters from models combined with observations, is as a way to map genetic phenotypes onto model parameters. If it turns out that the growth dynamics of some particular mutant can be explained by alteration of one particular parameter, it would provide evidence that the gene affected might play a role in whatever process that parameter determines.
5.3. Fluctuations and stochastic models of flagellar length
The discussion above focused on models to account for the average steady state flagellar length. For any such model, it is also interesting to ask what predictions it makes about the fluctuations around that length. Such fluctuation analysis is potentially useful as a way to discriminate models from one another. Moreover, by analyzing the magnitude and timescale of fluctuations, it may be possible to draw inferences about the microscopic events that underly the phenomenological parameters in the steady state models. In particular, there is an urgent need to find out more about events at the base and the tip of the flagellum. When we say that tubulin assembles or disassembles at the tip, does this mean addition or removal of individual tubulin dimers, or events involving larger assemblies of tubulin? Likewise, when IFT particles with their cargo assemble at the base and enter the flagellum, do individual proteins assemble onto the growing particles in some defined order? Do the trains assemble after the particles are complete? Structural studies using cryo-electron microscopy (cryo-EM) have made huge inroads into these questions, especially in shedding light on the assembly of IFT proteins at the base of the flagellum (Wingfield et al 2017, van den Hoek et al 2022), but such studies use static images. In other areas of biophysics, fluctuation analysis has a long track record of complementing structural studies by providing a window into microscale events that cannot be directly resolved, and we suggest that this approach may be of use here.
When length fluctuations were measured in living Chlamydomonas cells, the mean-squared change in length showed a linear dependence on time lag, suggesting a random-walk process, but eventually reached a plateau, indicating a constraint on the random walk (Bauer et al 2021). The slope of the linear portion of the curve was 0.0014 μm2 s−1. What does this value tell us?
One key question concerning the dynamics of flagellar assembly is the degree to which tubulin addition or removal is coupled to the arrival of IFT trains. At one extreme, which we term the directly coupled model of flagellar growth, trains arrive with tubulin which is then immediately incorporated, such that the statistics of train arrive dictate the length fluctuations. Given that IFT trains arrive at a rate of roughly 1.25 trains per second (Engel et al 2009), the directly coupled model predicts length fluctuations will occur with random steps of size δ taking separated by an average time of τ = 0.8 s. The slope of the means squared change in length versus time lag is then given by δ2/τ. To account for the measured slope, the step size associated with IFT train arrivals must then be 0.033 μm. Given 233 protofilaments per cross section of flagellum, the tubulin dimer length of 8 nm, each IFT train would need to carry approximately 960 tubulin dimers to account for this step size. IFT trains in Chlamydomonas flagella at steady state contain approximately 16 IFT particles (Pigino et al 2009, Vannuccini et al 2016). Thus, each IFT particle would need to carry on the order of 60 tubulins. In contrast, biochemical studies indicate that each IFT particle can only carry approximately four tubulin dimers (Bhogaraju et al 2013b).
If the directly coupled model does not hold, the alternative is that IFT delivers tubulin to a pool at the tip, which then exchanges with the microtubules of the outer doublets. But what is the nature of the exchange? In particular, a basic mechanistic question is whether tubulin is added or removed one dimer at a time. This is the assumption made in a number of recently formulated stochastic models for flagellar length (Datta et al 2020, Patra et al 2020, Banerjee and Banerjee 2022). These three studies analyzed distinct length control schemes, ranging from the 1/L dependent IFT assumed based on empirical data (Banerjee and Banerjee 2022), a time of flight model (Patra et al 2020), and a length-dependent disassembly model (Datta et al 2020). The range of fluctuation magnitudes predicted by these models based on dimer exchange are far less than what was actually measured (Bauer et al 2021), suggesting that tubulin dimers are being added or removed in larger groups. A constrained random walk model taking into account a 1/L restoring term, when fit to the observed length fluctuations, predicts that the individual steps of the random walk may involve thousands of tubulin timers at once, possibly via an alternation between processive periods of assembly and disassembly much like the dynamic instability of conventional microtubules, which switch between phases of growth and shrinkage, punctuated by catastrophe and rescue events. (Bauer et al 2021). These inferences suggest a need for better techniques to directly observe individual fluctuation events in real time.
Such burst-like changes in organelles size have also been inferred from quantitative analysis of other organelles (Amiri et al 2019). Fluctuation analysis has been used to study the effects of proteins like kinesin-8 on microtubule length dynamics (Kuan and Betterton 2013), and we believe that many parallels will emerge between fluctuation analysis of length control in flagellar axonemes and free microtubules.
Much of the work on stochastic modeling of flagellar length control has focused on the random process of subunit addition and removal at the tip. The contribution of randomness in IFT motility itself has been analyzed by Bressloff (2006). The injection of IFT, while on average proportional to 1/L, also shows random variation with a long tailed distribution (Ludington et al 2013). The development of an integrated model that incorporates the different features of length regulation (see above) will hopefully permit the relative contributions of fluctuations in the various contributing processes to be evaluated.
5.4. Beyond flagella
Flagella are just one type of organelle, and the question of size control applies to all the other organelles in the cell. In the cases where it has been investigated, it seems that a conceptually similar steady state framework, with assembly balanced by disassembly, will also apply. For example, in the vacuole of budding yeast, the surface area represents the balance of vesicle trafficking to and from the organelle, and mutations that alter trafficking rates lead to concomitant changes in steady state surface area (Chan and Marshall 2014, Chan et al 2016). As with flagella, measurements of organelle growth rate versus size, size versus number, and variation within and between cells, provide ways to probe potential size control mechanisms (Mukherji and O'Shea 2014, Amiri et al 2019).
Acknowledgments
The author gratefully acknowledges an uncountable number of interesting and useful discussions with Joel Rosenbaum of the past twenty five years. He also thanks Junmin Pan, Karl Lechtreck, William Dentler, Hongmin Qin, Ahmet Yildiz, Rui Ma, Jane Kondev, and past and present members of the Rosenbaum and Marshall labs, and the Chlamydomonas flagella community, for helpful suggestions and challenging feedback about modeling flagellar length control. This work was supported by NIH Grant R35 GM130327.
Data availability statement
No new data were created or analysed in this study.