Abstract
Eukaryotic cells face the challenging task of transporting a variety of particles through the complex intracellular milieu in order to deliver, distribute, and mix the many components that support cell function. In this review, we explore the biological objectives and physical mechanisms of intracellular transport. Our focus is on cytoplasmic and intra-organelle transport at the whole-cell scale. We outline several key biological functions that depend on physically transporting components across the cell, including the delivery of secreted proteins, support of cell growth and repair, propagation of intracellular signals, establishment of organelle contacts, and spatial organization of metabolic gradients. We then review the three primary physical modes of transport in eukaryotic cells: diffusive motion, motor-driven transport, and advection by cytoplasmic flow. For each mechanism, we identify the main factors that determine speed and directionality. We also highlight the efficiency of each transport mode in fulfilling various key objectives of transport, such as particle mixing, directed delivery, and rapid target search. Taken together, the interplay of diffusion, molecular motors, and flows supports the intracellular transport needs that underlie a broad variety of biological phenomena.
Export citation and abstract BibTeX RIS
1. Introduction
The movement of intracellular components, ranging from ions and small metabolites to proteins and micron-scale organelles, underlies the vast majority of cellular functions. Cellular transport needs vary from the nanoscale mixing that supports biomolecular reaction kinetics, to delivery and sorting of cargos across whole-cell scales that can reach up to a meter in length. Newly synthesized proteins or messenger RNA (mRNA) molecules must be transported from their site of synthesis in perinuclear regions to distant peripheral locations for secretion or insertion into the plasma membrane. Cellular growth and injury response, in particular, require a robust flux of components toward the newly synthesized regions of the cell. Conversely, external signals received at the cell membrane often require the transport of activated protein molecules toward the nucleus in order to initiate a transcriptional response. Cellular metabolism necessitates the efficient distribution of ATP and metabolites to all subcellular regions. In large cells such as neurons, the spatial organization of metabolism is key to supporting the energetic needs of localized regions with high metabolic demand. In addition, key functional roles are attributed to physical contacts between multiple organelles, and the formation of these contacts, as well as delivery of macromolecules to the contact zones, requires the regulated transport of cellular components.
In order to accomplish this diverse array of transport tasks, eukaryotic cells utilize several distinct physical mechanisms of transport (figure 1). For short distances and small (nanoscale) components, stochastic 'Brownian' motion allows for mixing and rapid particle encounters. For longer distances and larger particles, the cell harnesses the directed motion of molecular motors along cytoskeletal filaments to deliver vesicular organelles and RNA–protein complexes. The active transport machinery is controlled by a broad variety of regulatory factors that allow for controlled sorting and distribution of cellular components. In addition, many cell types utilize advective flows of cytosolic fluids to rapidly drive particles through the cytoplasm. Each of these transport modes is embedded in a highly complex, crowded, and actively fluctuating intracellular environment. Consequently, understanding the movement of cellular components requires expanding the classic models of physical transport processes to incorporate the unique milieu inside a living cell. In this sense, cell biology can serve as a source of inspiration for new fundamental questions in fields such as soft matter, non-equilibrium statistical mechanics and stochastic processes.
Figure 1. Overview of common physical mechanisms for intracellular transport. (a) Diffusive motion. Bottom: diffusion of membrane protein (Sec61) in peripheral tubular network of the ER, in COS7 cell (data from [1]) (b) motor-driven transport along cytoskeletal highways. Bottom: lysosome trajectory (red) and microtubules (green) in monkey kidney cell (image from [2]). (c) Advection in a flowing cytoplasm. Bottom: trajectories of acidified organelles in migrating HL60 cell (data from [3]).
Download figure:
Standard image High-resolution imageA number of studies have explored the connection between defects in intracellular transport and human pathologies (reviewed in [4, 5]). Owing to their spatially extended structure, human neurons are especially susceptible to diseases linked with transport defects. Neurodegenerative disorders such as multiple sclerosis, amyotrophic lateral sclerosis, Parkinson's disease, and Alzheimer's, among others, are attributed to disruption of axonal transport by mutations or other abnormalities [6–9]. Primary cilia in mammalian cells [10] provide a non-neuronal example of cellular structures that rely on functional transport processes for their formation. Defects in motor proteins result in abnormal ciliary structures which are linked to developmental defects, lung disease, and hearing loss [11]. A number of pathogenic viruses are also known to hijack the intracellular transport machinery to deliver them to different cellular regions and aid in uncoating, replication, and packaging [12–14]. For example, calciviruses rely on acidification within the endocytic pathway for their replication, a process dependent on vesicular transport [15]. The Ebola virus and some coronaviruses have also been shown to depend upon intracellular trafficking to late endosomes and lysosomal vesicles prior to release into the cytoplasm [16, 17]. A quantitative understanding of the limitations and consequences of intracellular transport is thus critical to unraveling the mechanistic basis for a variety of human pathologies.
In this review, we explore the biological objectives and physical mechanisms of intracellular transport. There are several existing reviews in the literature on the molecular components and biochemical regulation of motor-driven transport [18–20]. Our focus here is on the quantitative exploration of transport at the whole-cell scale, including diffusive, motor-driven, and advective motion. Given the broad diversity of tranport systems in different cell types, we focus on animal cells where possible, touching upon other eukaryotic cell systems when needed to illustrate specific physical effects. Furthermore, we restrict the discussion primarily to transport in the cytoplasm and within cytoplasmic organelles. The movement of particles across semipermeable membranes and within the nucleus is not considered.
We begin with a brief overview of the general properties of transport, in section 2. We then address the broad biological question: why do cells require transport? In section 3 we summarize several key functional roles played by transport processes in the cell, noting the relevant length and time scales. In section 4 we proceed to discuss the fundamental mechanisms of intracellular transport: diffusion, motors, and advection. In each case, we outline key physical parameters that govern transport efficiency and organization, as well as identifying the cellular mechanisms that modulate those parameters. In section 5 we highlight some outstanding physical questions regarding intracellular transport. The overarching aim of this review is to provide a broad overview of the physics of transport in animal cells, highlighting those aspects that support biological function.
2. Fundamentals of transport
Physical mass transport (as distinct from heat or information transfer), is defined by the movement of particles between different spatial regions. Transport behavior is generally characterized by the relationship between the length scale explored by the particles and the transport time. The nature of this relationship is itself determined by the transport mechanism (the forces that drive particle motion), as well as the properties of the environment in which transport occurs.
Intracellular transport, in particular, takes place within a dense aqueous medium where the motion of any particle necessitates flow or rearrangement of the surrounding fluid. Consequently, the response of a particle to applied force is determined in part by the hydrodynamic properties of the cytoplasmic medium. The importance of viscous versus inertial forces in a fluid is governed by the Reynolds number:
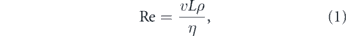
where v is the flow speed, L the characteristic linear size scale of the object in motion, ρ the fluid density, and η the fluid viscosity [21, 22]. Within a typical animal cell, the relevant length scale is generally L < 100 μm and transport velocities are v < 100 μm s−1. Even assuming a density and viscosity of pure water, the intracellular world has Re < 0.01, and is thus well in the regime of low Reynold's number hydrodynamics. Consequently, inertial forces inside a cell are negligible relative to viscous forces, and the instantaneous velocity rather than the acceleration of a particle is determined by the applied force. For example, if we consider a vesicle of size 1 μm moving at speed 1 μm s−1 in water, when the force pushing that organelle is removed it will coast a distance of less than 10−4 nm before coming to a stop [22, 23].
The relationship between length scale covered and transport time can often be expressed as a power-law L ∼ tγ. In the intracellular world, given the dominance of viscous versus inertial forces, the scaling exponent is generally in the range of 0 < γ ⩽ 1. For directed motion, driven by a constant force, we have γ = 1 and the particle moves at a constant velocity (L = vt). This type of motion is seen for the transport of cellular particles attached to active molecular motors (section 4.2) or for those driven by large-scale flows of the intracellular fluid (section 4.3). The velocity v, of course, can be both position- and time-dependent. However, so long as it has a finite average value, the long-time transport will obey this scaling behavior.
By contrast, a different scaling of length versus time [L ∼ (Dt)0.5] is expected for particles whose transport behavior resembles a random walk. This includes diffusive particles (with diffusivity D) in a viscous fluid, whose steps are uncorrelated over all time-scales. It also includes the long-time behavior of particles that switch the direction of transport many times, without retaining a memory of their previous motion [24]. Many cellular components engage in multiple forms of transport, switching between diffusive and motor-driven states [19, 25, 26], or undergoing diffusion superimposed on an underlying cytoplasmic flow [27–29].
The relative contribution of directed versus effectively diffusive transport is characterized by the dimensionless Péclet number [30–32]:
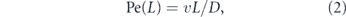
This number gives the ratio of time required to traverse a region of length L by diffusion (t ∼ L2/D) and by directed motion (t ∼ L/v). High values (Pe ≫ 1) indicate that processive transport is dominant. Because diffusivity increases inversely with particle size [23, 24, 33] while motor-driven and flow-driven transport tend to be size-independent [34], the Péclet number is particularly high for large particles transported over long distances.
Even slower scaling of distance explored versus time (γ < 0.5) arises when particles undergo so-called subdiffusive motion [35]. This form of transport (discussed further in section 4.1.2) is characterized by negative correlations in particle velocities during consecutive time-steps [36]. Such an effect can arise, for example, for particles that must push through a viscoelastic medium such as a polymer gel [33, 37, 38]. The cytoplasmic transport of large protein complexes and organelle-sized particles is generally observed to exhibit subdiffusive behavior [39–41].
The relevant lengths and times for intracellular transport vary broadly depending on the cell size, the particle type, and the functional role of the transport process. The need to transport material between the cell surface and the bulk has been suggested as a fundamental physical limitation on cell shape and size [32, 42–45]. At one extreme is the transport of small metabolites (∼1 nm in size, D ≈ 200 μm2 s−1 [46, 47]) between the cell periphery and metabolic organelles in globular cells such as fibroblasts, over length scales on the order of ∼2 μm. Diffusive transport is sufficient in this case to allow delivery in about 20 ms. At the other extreme is the transport of vesicles (∼100 nm in size, D ≈ 0.01 μm2 s−1 [26, 27, 34]) over the meter-long length of neuronal axons in the human peripheral nervous system. For this purpose, diffusive transport would require over a million years and is clearly impractical. Even motor-driven transport (at a typical rate of 1 μm s−1 [48]) requires about 10 days to deliver particles from the cell body to the tips of these long cellular projections. Time-scales that may be considered physiologically relevant for a given transport process also vary by many orders of magnitude. A turnover time of a week to deliver new mitochondria to distal regions of an axon seems to be sufficient to maintain a homeostatic population of these energy-producing organelles [48]. On the other hand, the most rapid intracellular enzymes can catalyze reactions with microsecond turnover [49], necessitating the delivery of reactants over these very rapid time-scales.
The many functional roles of intracellular transport (section 3) span across the broad range of relevant length and time scales. In addition, each comes with its own limitations in terms of the amount of material that must be transported and the necessity for precise control over where, when, and which intracellular components are transported. Cells thus rely on several complementary physical transport mechanisms (section 4) to address their functional transport needs.
3. Functional roles for transport
A fundamental question underlies, explicitly or indirectly, all studies of intracellular transport—what are the functional objectives or consequences of any given transport system? In this section, we outline several key categories of biological functions that rely on intracellular transport processes. The broad diversity of these functions suggests a variety of metrics for the utility of a transport process. While some transport systems need to be optimized for rapid delivery of components to a specific target within the cell, others require efficient mixing and uniform distribution of particles throughout a cellular region. In some cases a stable transport infrastructure is sufficient to meet cellular needs over long time periods, whereas other systems require the ability to respond quickly to variations in the desired flux or target location of delivered particles.
3.1. Delivery of secreted and plasma membrane proteins
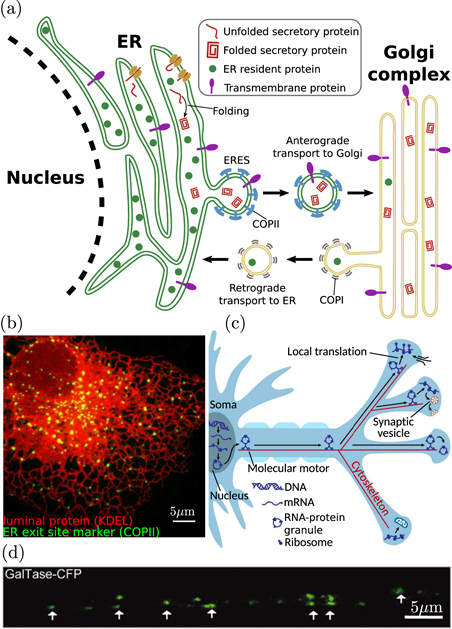
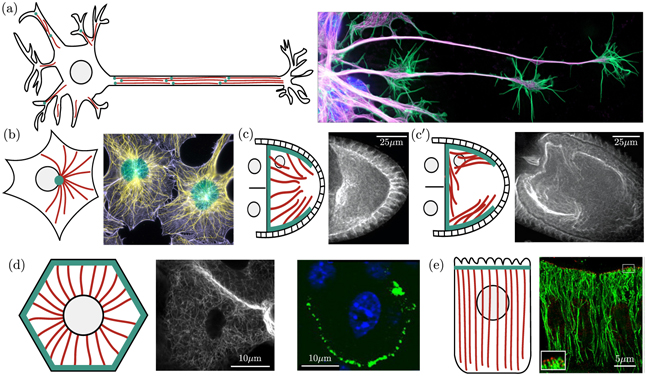
One major functional role for intracellular transport is to drive the secretory pathway (figure 2). Proteins destined for extracellular secretion or insertion into the plasma membrane are manufactured by ribosomes attached to the rough endoplasmic reticulum (ER), generally located adjacent to the cell nucleus [53, 54]. Such proteins are inserted co-translationally into the ER lumen or membrane, wherein they are folded and processed before moving into an ER exit site (ERES) [55, 56], as illustrated in figure 2(a). While transport within the ER is generally assumed to be diffusive in nature [57, 58], recent evidence from single particle tracking studies implies the existence of short-range processive movements that push proteins rapidly from node to node within the tubular ER network [59]. Exit sites appear as distinct long-lived puncta [60] scattered throughout both the perinuclear and peripheral ER network (figure 2(b)). There are on the order of 200 ERES [56, 61] in a typical-sized mammalian cell (40 μm in diameter), implying that proteins must explore over a spatial distance of roughly 3 μm to encounter a site for ER exit.
Figure 2. Transport processes in the early secretory pathway. (a) Newly-synthesized proteins are inserted into the ER lumen or membrane. After folding, these proteins are trafficked to the Golgi in vesicular bodies that form with the aid of COPII coat proteins. Retrograde trafficking of COPI-coated vesicles from the Golgi to the ER allows for homeostasis of ER-resident proteins. (b) Proteins must find punctate ERES to leave the ER and proceed along the secretory pathway. Green signal shows COPII proteins at ERES, while red signal shows ER structure via an ER-resident luminal marker protein [50]. (c) Schematic of mRNA transport and local translation in neuronal axons, involving motor-driven transport from the soma along the cytoskeleton to provide mRNA for translation at axonal terminals (adapted from [51]). (d) Dendritic Golgi outposts in rat hippocampal neuron indicate sites of local secretory processing (from [52], Copyright 2013, Society for Neuroscience).
Download figure:
Standard image High-resolution imageAt the ERES, proteins are packaged into vesicles coated with coat protein II (COPII) [62], which bud from the ER, shed their coats, and fuse into vesicular-tubular clusters termed the 'ER-Golgi intermediate compartments' (ERGICs) [63]. In mammalian cells, the ERGIC are thought to mediate transit to the Golgi by generating membrane-bound compartments of varying size that are transported along microtubule highways [64–67]. Microtubules in mammalian cells tend to be polarized with their minus ends anchored at a microtubule organizing center (MTOC) proximal to the Golgi, enabling rapid delivery of cargo-carrying compartments to the Golgi by minus-end directed dynein/dynactin motor complexes [65]. Mobile structures, generated from the ERGIC and carrying ER-derived proteins, have been observed to move processively on curvilinear trajectories toward the centrally located Golgi, over distances of 6–20 μm [65, 67].
During the early secretory pathway, transport of membrane-bound vesicular organelles serves not only to physically move proteins between compartments located in different areas of the cell, but also to mediate quality control and protein sorting [55, 63, 68, 69]. Packaging of proteins for ER exit relies on a combination of factors, including specific binding of secretion tags to ERES scaffolding proteins [70–72], bulk transport of small proteins captured within nascent vesicles [62, 73], and clustering of membrane proteins with similar transmembrane domain lengths that are poorly matched to the thickness of the ER membrane [74, 75]. Together, these factors combine to prevent many misfolded proteins or ER-resident proteins from being transported out of the ER. Once at the Golgi, a recycling pathway relies on the motor-driven transport of vesicles coated with coat protein I (COPI) to shuttle transport receptors and leaked ER-resident proteins back into the ER, maintaining proteostasis within the organelles [76].
In the Golgi, proteins are further processed and decorated with post-translational modifications, while passing from the perinuclear cis-Golgi region to the trans-Golgi side. The mechanism of transport within Golgi compartments remains under debate [77] and may include vesicular transport [78], progression and maturation of transient cisternae [79], or rapid partitioning between phase-separated lipid domains [80]. Recent theoretical work indicates that multiple mechanisms can be encompassed by a kinetic model that relies on tuning of vesicle fusion and budding rates to achieve optimal sorting [81]. From the trans-Golgi cisternae, secretory proteins are sorted into a network of membranous tubules that are extruded by the action of kinesin motors pulling along microtubule tracks [82]. The tubes are then cleaved to create pleiomorphic membranous carriers that are transported to the plasma membrane for secretion [83]. After fission from the trans-Golgi network, carriers are transported by kinesin motors across distances on the order of 10 μm in a typical mammalian cell [84].
Measurements of secretory pathway kinetics, via a retention and synchronized release system [85], indicate that newly released proteins are exported from the ER within 2–3 min, reach the Golgi within 10 min, and are secreted at the plasma membrane within 20 min. Given a directed transport rate for motor-driven exocytic vesicles of approximately 1 μm s−1, and a typical distance of 10 μm from the nucleus to the cell periphery, the transport of proteins across the cell does not appear to be rate-limiting in the secretory pathway, at least in globular animal cells. Notably, however, diffusion coefficients of vesicular organelles in cytoplasm tend to be in the range of 0.002–0.08 μm2 s−1 [27, 34, 86], implying a time-scale of several hours to traverse the cell by diffusion alone. Thus, motor-driven transport is a fundamental necessity for maintaining the complex secretion processes of eukaryotic cells. Vesicular packaging of proteins provides a functional benefit in allowing regulated protein sorting between different compartments, and processive transport of vesicles is then required to enable sufficiently rapid delivery to the cell periphery.
Highly extended cell types such as neurons face a particularly challenging transport problem to deliver components manufactured near the nucleus to distant secretion regions that can be up to a meter away. Neuronal axons are capable of rapidly releasing large quantities of secreted neurotransmitter proteins at the presynaptic terminals located on their distal tips. Rapid variation in the complement of neurotransmitter receptors expressed on the dendritic post-synaptic membrane plays an important role in synaptic plasticity and adaptation [87]. The critical need to control secreted and membrane protein availability at the distant tips of axons and dendrites raises the question of how the proteins themselves or the components needed for their manufacture are transported across such long distances from the cell nucleus. Many synaptic proteins are manufactured at the cell body via the canonical secretory pathway [88]. They are then sorted into post-Golgi vesicles bound toward either axonal or dendritic compartments and delivered to their eventual destinations by long-range motor-driven transport along microtubule highways [87, 89]. Even with rapid unidirectional motor-driven motion, a delivery time on the order of 10 days is required to transport somatically synthesized proteins to the end of a meter-long axon.
More efficient response to changing protein requirements at axonal and dendritic terminals can be achieved by local protein translation (figure 2(c)). The existence of rough ER, ERGIC, and Golgi outposts at distal dendritic regions (figure 2(d)) allows secretory protein synthesis and modification to proceed without the need for delivery to and from the cell body [90]. Emerging evidence indicates that local translation at axonal terminals is prevalent, particularly in the context of development, regeneration, and repair [51, 91–93]. Local translation bypasses the problem of long-range protein delivery but does require transport of mRNA, which is usually bound by RNA-binding proteins that couple directly to molecular motors [94]. This transport system allows for a constant, relatively slow, turnover of mRNA molecules at distal translation outposts, while enabling rapid variation in protein manufacture and secretion in response to local signals.
3.2. Distribution of components for growth, injury repair, and cell division
Growing and regenerating cells require the delivery of a broad array of structural components to supply the necessary material for growth and repair in specific regions. In addition, cell division and the separation of a syncytium into distinct cellular regions (as in fungal hyphae and animal embryonic development [98, 99]) necessitates the maintenance of a controlled distribution of proteins and organelles to ensure appropriate partitioning into the newly formed cells. All of these processes require intracellular transport of components, often along substantial cellular distances.
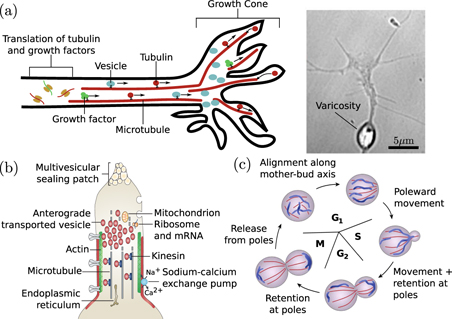
Neurons again present an important example where long-range transport is required for growth. Axonal growth during development and regeneration is mediated by a distal growth cone structure that contains both the cytoskeletal components that drive growth and an abundance of regulatory factors that determine growth rate and direction [100]. Axon protrusion is dependent on the delivery of microtubule components to the tip of the growth cone [101, 102] (figure 3(a)) where their incorporation into the axonal shaft both directly drives extension and contributes to mechanical forces that stretch the axonal axis [103]. Tubulin monomers are translated in the cell body and delivered to the growth cone via the so-called 'slow component' of axonal transport, which consists of sporadic bidirectional motion with average rates on the order of 0.05 μm s−1 [104]. The origin of this transport mechanism remains under debate [105], but it has been suggested to arise from transient interactions with molecular motors [106] or entrainment in cytoplasm dragged by passing motor-driven organelles [107].
Figure 3. Transport processes in cell growth, division, and healing. (a) Delivery to axonal growth cone. Left: motor-driven transport of tubulin, growth factors, and vesicles supports and directs growth cone protrusion. Right: varicosity in an advancing growth cone due to accumulation of vesicles (image from [95]). (b) Role of cytoplasmic transport in axonal injury response. The membrane at the injured end of an axon is sealed by accumulation of anterograde-moving motor-driven vesicles. Image adapted from [96]. (c) Schematic of mitochondrial rearrangement during cell division in budding yeast. Image adapted from [97].
Download figure:
Standard image High-resolution imageMotor-driven transport of tubulin also plays an important role in the extension of cellular projections such as flagella and primary cilia [108, 109]. The dynamics of the intraflagellar transport (IFT) trains responsible for tubulin delivery are crucial to regulating the length distribution of these organelles [110, 111].
In addition to cytoskeletal components, an axonal growth cone also requires the continuous incorporation of new proteins and lipids. While a number of proteins are locally translated at the growth cone [112], many others are delivered by Golgi-derived vesicles that also serve as a source of membrane upon eventual fusion with the growth cone tip [96]. Such vesicles have been shown to accumulate at the plus ends of microtubules in newly formed growth cones of regenerating axons [113]. In a growing axonal tip, the accumulation of these vesicles can out-pace their incorporation into the growth cone, leaving behind organelle-filled varicosities (figure 3(a), right) that then serve as nascent pre-synaptic structures [95]. The transport of protein-filled vesicles from the soma to the axonal tip, balanced against the rate of delivery and incorporation of structural growth cone components, thus plays an important role in both axon growth and the placement of pre-synaptic terminals.
In several cell types, rapid vesicle transport has the additional function of plugging holes in the plasma membrane generated by cellular injury. A severed axon seals its plasma membrane, over a time-scale of minutes to hours, with the aid of multi-vesicular structures derived from endocytosis along the axon membrane followed by transport of the resulting vesicles to the cut end [96, 114] (figure 3(b)). Certain fungi form extensive multi-cellular hyphae, where individual cells are separated by perforated septa that allow for free passage of cytoplasmic contents. In case of injury, peroxisome-derived organelles called Woronin bodies are rapidly delivered, primarily through bulk cytoplasmic flow, to plug up septal pores and prevent large scale loss of cytoplasm [115].
A further critical role for organelle transport in growth and development is to maintain a spatially well-mixed distribution of organelles, allowing for equitable partitioning during cell division or cellularization. In mammalian cells, motor-driven transport of mitochondria is required for maintaining their distribution throughout the soma [116], and in yeast cells an active transport mechanism is used to partition and sort mitochondria between the mother cell and the bud [97] (figure 3(c)). Furthermore, motor-driven transport enhances the fission and fusion of mitochondria [117], which can switch between globular and extensively networked structures to facilitate homogenization of mitochondrial contents [118, 119]. Other membrane-bound organelles such as peroxisomes also rely on microtubule-based transport mechanisms for controlling segregation between dividing cells. In mammalian cells, peroxisomes congregate at spindle poles to ensure equitable partitioning, in yeast they are delivered directly to the nascent bud, and in fungal hyphae they hitchhike on other motile organelles to allow rapid equilibration throughout the growing hypha [120]. An efficient transport process to either deliver the organelles to specific cellular regions or to maintain a uniform distribution of organelles throughout the cell is thus necessary for homeostasis of organelle content in growing and dividing cells.
3.3. Intracellular signal propagation
Given the complex spatial organization of eukaryotic cells, signals from the extracellular environment received at the cell periphery must be propagated over substantial distances to reach the nucleus or other distant cellular regions. In certain specific cases, such as the action potential in neurons or mitotic signaling in oocytes, these signals can propagate very rapidly by a 'trigger wave' mechanism, that involves local diffusion of activating factors that trigger a switch-like self-propagating response [121–123]. Many signaling pathways, however, rely on the physical transport of specific proteins from the cell periphery to the nucleus, where they can activate a response through transcriptional regulation.
A simple approach to transporting a signal across relatively small cellular distances relies on the diffusion of an activated protein to the nucleus (figure 4(a)). A well-known example is the JAK/STAT pathway, where an activated transmembrane receptor JAK (Janus kinase) phosphorylates latent transcription factors STATs (signal transducer and activator of transcription proteins) that reside in the cytoplasm [124]. These factors diffuse throughout the cell until they encounter the nucleus, where their phosphorylated nuclear localization sequence enables nuclear import, triggering subsequent cellular response through the regulation of gene expression.
Figure 4. Common pathways of signal propagation through physical transport of molecular components. (a) Signals activate cytoplasmic transcription factors which diffuse toward the nucleus. Schematic of the JAK/STAT signaling pathway is shown. (b) Signals result in translocation of receptor to another organelle and/or cleavage of activated region which diffuses to the nucleus and serves as a transcription factor. The ATF6 branch of the unfolded protein response pathway uses both mechanisms. (c) Activated receptors are encapsulated in vesicles and carried via motor-driven transport toward the nucleus or to contact other organelles which trigger deactivation, degradation, or recycling. The EGFR pathway is an example of this propagation mechanism. (d) IFT machinery controls receptor localization and turnover in primary cilia. Motor-driven motion along a central microtubule bundle allows for anterograde transport of inactive receptors to cilia tips and retrograde transport of activated receptors to the cell body.
Download figure:
Standard image High-resolution imageA related approach is exemplified by several receptor tyrosine kinase signaling pathways, including Notch and insulin signaling, where receptor activation at the plasma membrane triggers cleavage of a soluble intracellular domain that binds to a cytoplasmic transcription factor and escorts it diffusively toward nuclear import sites [125]. A similar strategy is employed by a branch of the unfolded protein response pathway, in which accumulation of misfolded proteins in the ER triggers the transport of the ATF6 (activating transcription factor 6) transmembrane protein from the ER to the Golgi. In the Golgi, ATF6 is cleaved to release a cytoplasmic domain that diffuses to the nucleus and serves as a transcription factor to upregulate the expression of chaperones promoting protein folding [126] (figure 4(b)).
The speed and efficiency of signal propagation to the nucleus using these diffusive mechanisms is limited by both the mobility of proteins in the cytoplasm and the timescale of deactivation and turnover of the signaling proteins. The typical diffusivity of globular proteins in mammalian cytoplasm is in the range of 3–30 μm2 s−1 [127–129], so that a signal from the plasma membrane would take on the order of 10 s to reach the nucleus in a modestly-sized cell of radius 15 μm. Given that dephosphorylation times for activated proteins tend to be on the order of 1 s, such signals would be attenuated to non-detectable levels before they ever reached the nucleus [130]. In small cells, the signal can be propagated over sufficient distances by cascades of sequential phosphorylation of multiple cytoplasmic proteins, as occurs in the mitogen-activated protein kinase (MAPK) pathway [131]. For larger animal cells, however, diffusive transport of activated proteins is too slow to be of practical use in signaling. For example, an activated peripheral protein would require several hours to diffuse to the nucleus in a 1 mm frog egg, and several months to diffuse from the distal tip of a centimeter-long axon to the cell body.
Many signaling pathways intertwine with the endocytic pathway, leveraging vesicular encapsulation and motor-driven transport to deliver activated components to regions near the nucleus. A canonical example of signaling via retrograde transport is the neurotrophic signaling pathway that regulates neuronal survival, axon and dendrite growth, and synapse formation [132]. Neurotrophin growth factors bind to receptors on the distal tips of axonal projections, which are packaged into endosomes and carried to the cell body by dynein motors walking along microtubule highways [133, 134]. For a meter-long axon, this process takes approximately 10 days, putting a substantial limit on the ability of the neuron to respond to distal growth signals.
In general, a broad variety of signaling cascades is known to involve packaging and activation of components within endosomes [135] (figure 4(c)). Motor-driven transport of the endosomes can rapidly deliver activated signals to the nucleus, as in the case of Smad proteins activated in the transforming growth factor beta signaling pathway [136]. Alternatively, early endosome-encapsulated receptors can be trafficked to a recycling compartment for return to the cell membrane or to multivesicular bodies and late endosomes [135]. Fusion of these organelles with lysosomes carrying proteolytic enzymes eventually results in cargo degradation, leading to attenuation of the signal. Other pathways, such as EGFR (epidermal growth factor receptor) signaling, rely on phosphatases localized to the perinuclear ER to dephosphorylate and shut off active receptors [137, 138]. Thus, the transport processes that shuttle endosomes to different cellular regions and facilitate organelle interactions play an important role in regulating the duration and time-course of signaling events [139, 140].
An additional transport process crucial to intracellular signaling is the IFT that moves proteins within primary cilia (figure 4(d)). Primary cilia are narrow cellular projections, roughly 5–10 μm long and 0.3 μm in width that serve as a signaling nexus in many mammalian cell types and play an important role in development, vision, and olfaction [10, 141]. Signaling receptors are concentrated on the ciliary membrane in a highly regulated manner that relies on their transport into, out of, and throughout the cilium by coupling to trains of molecular motors that move them along the central bundle of microtubules [142, 143]. A particularly well-characterized example is hedgehog signaling, which plays a key role in tissue development and homeostasis. The hedgehog ligand receptor, patched, accumulates in primary cilia in the absence of signaling, and is exported from the cilium upon activation, thereby allowing the ciliary entry and accumulation of other receptors such as Smo and Gli proteins [144]. The latter, in turn, are activated within the cilium, transported to the ciliary base, and from there relocate to the nucleus where they act as a transcription factor regulating gene expression [145, 146]. Mutations in adaptor proteins that form the complex connecting signaling receptors to IFT motors result in failure of signaling receptors to localize to cilia and/or abnormal accumulation of activated receptors within the cilium [147, 148]. IFT is thus critical for regulating the spatial organization of ciliary receptors as well as downstream signal propagation.
3.4. Organelle interaction and exchange
Membrane-bound organelles are topologically distinct compartments within eukaryotic cells that serve to spatially organize a broad array of intracellular reactions. Recent measurements have highlighted the plethora of direct physical interactions between different organelle structures [149], and the biological role of these inter-organelle contacts is increasingly appreciated [150–152]. Lipid droplets (LDs), mitochondria, peroxisomes, lysosomes, endosomes, the ER, and the Golgi complex all form an extensive dynamic network of interacting organelles that coordinate and colocalize with each other (figure 5). The establishment and turnover of contact sites relies on intracellular transport to place regions of different organelles in spatial proximity.
Figure 5. Interactions between various organelles. (a) Matrix representation of absolute number of contacts between lysosomes (Lyso), the Golgi body, the ER, mitochondria (Mito), peroxisomes (Perox), and lipid droplets (LDs) within a single cell. Color denotes number of contacts between each pair of organelles. (b) Network representation of interaction frequency. The length of an edge represents the inverse number of contacts between organelles at each end. Figures adapted from [149].
Download figure:
Standard image High-resolution imageOne well-established role for organelle contacts is lipid homeostasis and metabolism. Lipids are synthesized in the ER, stored and transported in lipid droplets, metabolized in mitochondria and peroxisomes, and recycled in lysosomes [153–157]. Colocalization of lipid droplets with mitochondria and lysosomes, in particular, is essential for fatty acid metabolism and starvation response [157, 158]. The organelles involved in lipid turnover are generally distributed throughout the cell, allowing for frequent transient contacts that permit signaling and delivery of components [159]. Maintaining the relatively uniform distribution of peroxisomes, lipid droplets, and ER tubules requires bidirectional motor-driven transport along microtubule highways [25, 26, 160–162]. The vesicular nature of lipid droplets, in particular, makes them well-suited for targeted transport of lipids to specific cellular regions with distinct metabolic requirements [163, 164]. Mitochondria and lysosomes also move in a regulated fashion along microtubules to enable the spatial organization of metabolism and lipid recycling [165, 166].
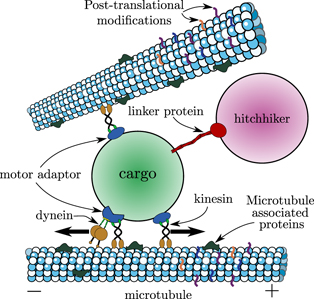
In addition to lipid transfer and signal propagation (discussed in the previous section), inter-organelle contacts can themselves facilitate the transport and morphological dynamics of the participating organelles. For example, peroxisomes and lipid droplets have both been shown to hitchhike on early endosomes [167, 168], allowing them to move rapidly through the cell by attaching to mobile carrier organelles. Contacts between ER tubules and mitochondria are known to be required for fission of mitochondrial networks into globular structures, which can be redistributed by transport processes throughout the cell [169]. Furthermore, motor-driven transport along the cytoskeleton allows for the formation of mitochondrial networks through fusion, allowing for the mixing of mitochondrial contents on a cellular scale [170].
Experimental evidence suggests that disrupting the cytoskeleton affects many features of the organelle interactome [149]. Transport processes thus play an important role in modulating organelle interactions that are crucial for cellular function.
3.5. Control of nutrient and metabolite gradients
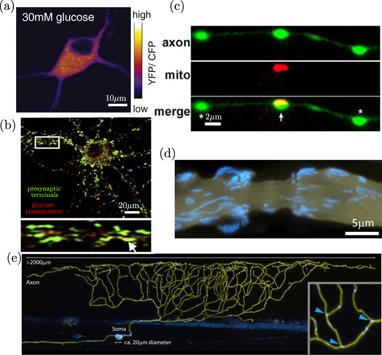
Several studies have pointed toward the existence of substantial intracellular gradients in nutrients, metabolites, and ATP [174–176], prompting increased interest in unraveling the spatial heterogeneity of metabolism [177, 178]. Although small metabolites diffuse rapidly through the cytoplasm (with diffusivity of around 200 μm2 s−1 for glucose and ATP [46, 47]) such gradients can arise as a result of locally enhanced metabolism in the vicinity of mitochondria or rapid ATP consumption in localized cellular regions. An additional source of metabolite gradients is extracellular spatial heterogeneity in nutrient levels [171], or spatial variation in the density of transporter proteins allowing nutrient import into the cell [172, 179] (figures 6(a) and (b)). Intracellular transport and positioning of mitochondria, glucose transporters, and a variety of metabolic enzymes thus have a key role to play in maintaining the spatial organization of metabolism, particularly in large cells such as oocytes, neurons, and plant cells. The mitigation and control of metabolite gradients in plant cells has long been proposed to rely on convective transport in a flowing cytoplasm [180], while motor-driven towing of mitochondria is thought to contribute to metabolic organization in neurons [165].
Figure 6. Spatially heterogeneous distribution of metabolic components in neurons. (a) Glucose sensor distribution in rat hippocampal neuron, from [171]. (b) Colocalization of presynaptic marker synaptophysin (green) and punctae of glucose transporter GLUT3 (red), from [172]. (c) Localized mitochondrion (red) and ATP sensor (green) at presynaptic boutons in rat hippocampal neuron, from [173]. (d) Mitochondria (blue) localized in region surrounding a node of Ranvier (membrane in yellow), from [48]. (e) Mitochondria (blue) in a zebrafish sensory neuron (membrane in yellow), from [48].
Download figure:
Standard image High-resolution imageNeuronal cells tend to exhibit a high degree of spatial and temporal heterogeneity in metabolic activity. Rapid ATP turnover is required for vesicle release in presynaptic boutons [181], with metabolic needs peaking during neuronal firing and activity [172, 179]. In myelinated neurons of the peripheral nervous system, saltatory signal conduction relies on ion channels localized near narrow nodes of Ranvier, which can be separated by hundreds of micrometers. The energetic demands of ion pumping to restore resting potential are then spatially peaked in the vicinity of these nodes [182, 183]. Neurons are known to regulate mitochondrial localization (figures 6(c)–(e)), concentrating them specifically in regions of high demand (including presynpatic boutons and areas near the nodes of Ranvier in electrically active neurons) to enable rapid local generation of ATP [165]. Such mitochondrial positioning is governed by a number of mechanisms for halting motor-driven transport in response to high calcium concentrations [183, 184] or high glucose [171]. These transport-regulation mechanisms enable mitochondria to accumulate in regions with both high activity levels and high fuel supply. It should be noted that mitochondria also act as calcium buffers for the cytoplasm, and their controlled localization helps to regulate calcium gradients crucial to neuronal signaling as well as gradients in ATP.
The task of mitochondrial localization poses a number of challenges to the intracellular transport machinery. It must be able to robustly control mitochondrial position in response to shallow gradients in long cellular projections [185]. Efficient redistribution of mitochondria must be achieved in response to growth, injury, or changing activity patterns [186–188]. In addition, because mitochondrial biogenesis and the synthesis of many mitochondrial proteins is believed to occur largely (though not entirely) in the soma [189], maintenance of localized mitochondrial health requires either periodic replacement by younger mitochondria or transient fusion and protein exchange with a motile mitochondrial population [48].
In very large cell types, active transport of small nutrient molecules themselves may be of functional benefit to the cell. An extreme example is the long-distance delivery of resources within the mycelial networks of filamentous fungi, which can stretch to many meters in extent, and whose multinucleated and septated structures blur the line between cells and tissues [98]. Given the enormous size of these syncytia in the uncontrolled environment of the forest floor, the extracellular nutrient levels can vary widely, necessitating long-range transport of resources through a combination of vesicle movement and flow of the cytoplasmic fluid [190, 191]. Several studies have shown that the slime-mold Physarum polycephalum reconfigures its own filamentous network morphology to connect multiple food sources in a manner reminiscent of man-made transportation networks [192, 193], optimizing the transport of nutrients and signaling molecules through peristaltic 'shuttle-streaming' flows [28, 194, 195]. In large algal cells, which can grow up to a millimeter in width and several centimeters long, cytoplasmic streaming flows are responsible for the long-distance delivery of nutrients from regions of uptake to sites of active growth [29, 196]. In each of these cases, with their broadly different cell types and morphologies, the necessity for nutrient dispersion over long length-scales requires the introduction of flow-based active transport mechanisms that vastly outpace diffusion.
4. Physical mechanisms of transport
In order to fulfill the varied functional objectives of intracellular transport, eukaryotic cells rely on transport mechanisms that can be categorized into three classes: (1) diffusion-like random motion of small particles down their concentration gradient, driven by broadly distributed fluctuations in the intracellular medium; (2) processive movements associated with the ATP hydrolysis-driven stepping of motor proteins along cytoskeletal highways; and (3) advective motion arising from fluid flows in the cytoplasmic medium.
Each of these mechanisms has its advantages and disadvantages for different cellular tasks. For instance, diffusion through the cytoplasm requires no additional energy input beyond the ongoing active processes that drive cytoplasmic fluctuations. This mechanism can be very efficient at spreading small molecules over relatively short distances (e.g.: proteins require only a few seconds to diffuse across a typical 20 μm animal cell).
Motor-driven transport, with its typical processive rates of ∼1 μm s−1, requires burning ATP for every step taken by a motor, but can allow much more rapid delivery of cargo over long distances. This form of active transport also has the advantage of enabling the cell to control which cargo gets delivered to which cellular region through selective packaging into vesicles, regulation of the motor complement attached to each organelle, and modification of the cytoskeletal tracks.
Advective flow can enable faster motions still (up to 1 mm s−1 in the shuttle flows of Physarum [197]), driving broad populations of intracellular particles, but with less control over the precise delivery of specific components. Below, we review the main physical factors that underlie each of these transport mechanisms, their inherent limitations, and their coupling and control in cellular systems.
4.1. Diffusive transport
The canonical diffusion of particles in a fluid arises from Brownian motion—spatially and temporally uncorrelated movements due to thermally driven fluctuations in the medium. Diffusing particles in a viscous medium execute random walks whose mean squared displacement (MSD) in each dimension scales linearly with time according to
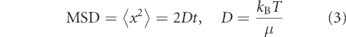
where μ is the friction coefficient of the particle, kB is Boltzmann's constant, and T is the temperature of the medium. The friction coefficient μ depends on the size and shape of the particle [198, 199], as well as the viscosity of the medium [200]. For a sphere, μ = 6πηa, where η is the medium viscosity and a the radius of the particle [23, 33].
The simple Stokes–Einstein relation (equation (3)) rests on several major assumptions: the particle must be embedded in a continuous, purely viscous, three-dimensional (3D) fluid of infinite extent, with no external sources of energy. Below we discuss how the breakdown of each of these assumptions affects intracellular particle diffusion.
4.1.1. Lateral diffusion on membranes
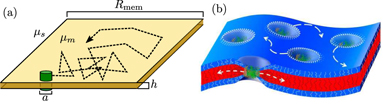
Many biologically important proteins are embedded in cellular lipid membranes, including both the plasma membrane surrounding the cell itself and the much more extensive membranes of eukaryotic organelles [202]. Lateral diffusivities of membrane proteins have ranges of 6–10 μm2 s−1 in plasma membranes [203] and 0.2–0.5 μm2 s−1 in the ER membrane [204]. Confinement of a particle to a two-dimensional fluid membrane fundamentally alters its diffusivity in a manner dependent on the thickness and curvature of the membrane. A critical feature of a purely two-dimensional fluid is that hydrodynamic correlations do not decay but rather extend over the entire domain, leading to the famous Stokes paradox [205]. As a consequence, the size of the domain can be an important length-scale for determining the diffusivity even of very small particles far from the boundary. The classic Saffman–Delbrück model [206] derives the lateral diffusivity of a particle of radius a in a thin membrane of thickness h and viscosity μm, embedded within a bulk fluid with lower viscosity μs, as

where γ ≃ 0.6 is the Euler constant and Rcorr gives an effective length-scale limiting planar hydrodynamic correlations. In contrast to free diffusion in a 3D solvent, this expression implies that lateral diffusivity on a membrane is only weakly dependent on particle size and is inversely proportional to the membrane thickness. The Saffman–Delbrück model is supported by in vitro experimental measurements [207], but requires significant alterations when the membrane is near a solid substrate [208], or when the protein radius is comparable to the membrane thickness [209]. The latter case, in particular, is relevant in the intracellular world, where typical membrane thicknesses (∼4 nm [210]) are comparable to protein dimensions.
The correlation length scale Rcorr is defined by an interplay of several physical effects. In the case of a very large flat membrane domain, it is given by the Saffman–Delbruck screening length [206]: LSD = hμm/μs, beyond which planar hydrodynamics are screened out by flows in the bulk fluid [208]. Alternately, it can be given by the overall extent of the membrane domain itself (Rmem; figure 7(a)), when this is smaller than the screening length [211]. The domain size Rmem is not well-defined for many biological systems. It may correspond to the size of membrane compartments with fixed boundaries defined by interaction with cytoskeletal filaments [212, 213]. In the specific case of particles diffusing laterally along a tubule-shaped membrane, it can be approximated as the radius of the tubule [214]. As a consequence, the lateral diffusivity of particles is expected to decrease with decreasing tubule radius, accounting for the experimentally observed slowing of diffusive spread on narrow reconstituted tubules [211].
Figure 7. Lateral diffusion of transmembrane proteins. (a) Schematic showing a membrane protein (green) diffusing in the plane of the membrane, with relevant parameters determining its diffusivity (equation (4)) labeled. (b) A thickness mismatch between a protein's transmembrane region and the membrane itself results in local membrane deformation that can bias diffusion and lead to interactions between neighboring proteins. (Image from [201]).
Download figure:
Standard image High-resolution imageMechanical properties of the membrane can also have an important impact on the lateral diffusivity of embedded proteins. For example, important physical effects arise when there is a mismatch between the preferred curvature of the embedded protein and the surrounding membrane curvature [215]. Alternately, many proteins show a mismatch between the length of the transmembrane region and the preferred thickness of the membrane [216] (figure 7(b)). In both cases, the mismatch engenders an elastic deformation field in the surrounding membrane [217, 218]. When multiple proteins come sufficiently close together for the deformation fields to overlap, they can experience attractive or repulsive forces mediated by the membrane elasticity [219]. Such interactions have a range of 1–2 nm for thickness deformations and 5–500 nm for curvature deformations [218].
As a result of these effects, membrane proteins diffuse across an effective potential energy landscape that can guide and modulate their motion. On a thermally fluctuating membrane, protein curvature preference has been postulated to enhance lateral diffusion by up to a factor of two, due to the attraction of the protein toward transient regions of matching curvature [220]. Both curvature and thickness preference can also attract proteins toward specific cellular regions. In particular, an energetic preference for membrane thickness has been implicated as a protein sorting mechanism in the secretory pathway [216, 221, 222], including capture at ERESs [55] and partitioning to secretion-bound lipid rafts in the Golgi [223, 224]. Similarly, curvature preference is believed to facilitate protein sorting into membrane tubules [225], the necks of budding vesicles [226], and the curved regions of dividing bacterial cells [227].
4.1.2. Medium rheology
For particles diffusing within the bulk of the cell, a key assumption of the Stokes–Einstein relation (equation (3)) is that the cytoplasmic environment behaves as a purely viscous medium. This assumption has been challenged by a variety of studies that actively probe the rheological properties of the cytoplasm [232, 233], or else leverage 'passive microrheology'—visualizing and tracking the apparently passive trajectories of individual particles in live cells [36, 39, 228, 231, 234]. These studies are summarized in several excellent reviews on intracellular rheology [200, 235].
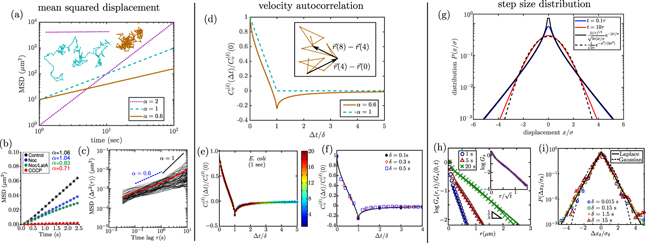
Passive particle-tracking microrheology enables explicit calculation of the MSD as a function of time (figures 8(a)–(c)), for comparison with the expected diffusive behavior described by equation (3). In some cases, injected beads or endogenous vesicles exhibit linear scaling of the MSD with time, as would be expected for a diffusing particle [26, 234, 236, 237]. More commonly, however, particle motion in cytoplasm is characterized as subdiffusive, with a sublinear scaling MSD ∼ tα, where α < 1 [39–41].
Figure 8. Characterizing diffusive transport by analysis of single particle trajectories. (a)–(c) MSD. (a) Expected behavior is shown for processive motion with speed 1 μm s−1 (dotted, purple), diffusion with D = 5 μm2 s−1 (dashed, cyan), and subdiffusion with α = 0.6 (solid, orange). Inset shows example trajectories for each type of motion. (b) MSD for peroxisomes in COS-7 cells, with black showing linear scaling for untreated cells, red showing subdiffusive scaling for ATP-depleted cells, from [26]. Blue and green curves are for cells treated with nocodazole (Noc) and latrunculin A (LatA) to hinder polymerizaton of microtubules and actin filaments, respectively. (c) Subdiffusive MSD for 100 nm nanoparticles in cytoplasm of 3T3 fibroblasts, adapted from [228]. Red line shows ensemble average. (d)–(f) Rescaled VACFs. (d) Expected VACF for a diffusing particle (dashed) and particle undergoing fractional Brownian motion with α = 0.6 (solid). Inset shows local displacements on a sample trajectory used to calculate the VACF at Δt = δ = 4. (e) VACF for RNA–protein particles in Escherichia coli cytoplasm, from [229]. (f) VACF for quantum dots in HeLa cells, adapted from [230]. (g)–(i) Distribution of step sizes. (g) Predictions for a diffusing-diffusivity model, with correlation time τ, showing transition from exponential scaling at short times (blue) to Gaussian scaling a long times (red). Solid and dashed black lines show the t ≪ τ and t ≫ τ limits, respectively. (h) Displacement distribution for colloidal beads in F-actin suspensions, over different time intervals, with inset showing universal behavior when distance is rescaled by  , from [231]. (i) Displacement distributions for RNA–protein particles in yeast cytoplasm, using rescaled distance, from [229].
, from [231]. (i) Displacement distributions for RNA–protein particles in yeast cytoplasm, using rescaled distance, from [229].
Download figure:
Standard image High-resolution imageSubdiffusive scaling is expected when motion is driven by thermal fluctuations in a power-law fluid—a material with complex rheology, whose viscous and elastic moduli vary as a characteristic power law of the probing frequency [235]. For example, subdiffusive motion with α ≈ 0.75 is both theoretically expected and observed for particles embedded in gels of semielastic polymer filaments, such as F-actin [39, 238].
The usual physical model for passive particle movement in a viscoelastic fluid is termed 'fractional Brownian motion' [37, 200, 239]. This model derives from an overdamped generalized Langevin equation [240] featuring a power-law memory kernel K(t) which is convolved with the past time-course of particle velocities to give the drag force:
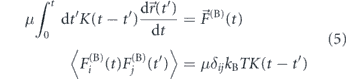
where F(B) is a Brownian force satisfying the fluctuation–dissipation relation and hence exhibiting the medium-dependent time correlations indicated above [241–244]. When the memory kernel is replaced by a delta-function, corresponding to an instantaneous relation between force and velocity as in a purely viscous fluid, the model reduces to classical Brownian motion. In a power-law fluid, the memory kernel is K(t) ∼ t−α, effectively replacing the medium viscosity η with a frequency-dependent viscosity η(ω) ∼ ωα−1 [200, 245]. Fractional Brownian motion gives rise to a sublinear MSD of passive particles [37]:
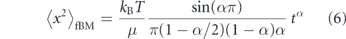
This model has been used to explain the observed subdiffusion of a variety of intracellular particles, including genomic loci [246, 247], mRNA molecules [248], and RNA–protein complexes [229, 247].
However, the MSD by itself cannot distinguish between several different models for subdiffusive motion [249]. For example, localization error [250] in tracking particle positions, crowding [251], confinement [252], or binding events with broadly distributed interaction timescales [253] can all give rise to MSDs with sublinear scaling. Other metrics have thus been developed to quantify the behavior of particles undergoing subdiffusive motion. One common metric is the velocity autocorrelation function (VACF), which tracks how velocities (defined by steps over different timescales δ) are correlated across a time-lag Δt. Namely, the velocity autocorrelation is given by
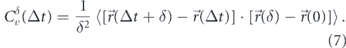
Unlike classical diffusion, where velocities are fully uncorrelated for all Δt > δ, fractional Brownian motion gives rise to negative velocity correlations that are self-similar across time-scales (figure 8(d)). Because several microrheology studies have shown similar behavior for the velocity autocorrelation of intracellular particles (figures 8(e) and (f)) [36, 229, 230, 246], the cytoplasm is often treated as a power-law fluid whose viscoelastic properties lead to fractional Brownian motion of passive components.
4.1.3. Active diffusion
Brownian or fractional Brownian motion in a passive medium is driven by equilibrium thermal fluctuations. Thermally generated fluctuating forces must have a specific time-dependent correlation function determined by the rheology of the medium (equation (5)). The interior of a living cell, however, is an environment that is manifestly outside the equilibrium regime, with fluctuations driven by a wide array of active energy-consuming processes with different underlying temporal correlations.
A plethora of recent experimental evidence has shown that even apparently diffusive particle dynamics rely on active cellular processes and are not driven primarily by thermal fluctuations [254]. Active microrheology measurements can be used to probe the force-response dynamics of the cytoplasm by directly controlling the forces applied to beads caught in optical and magnetic traps. Such measurements tend to indicate that the cytoplasm responds to force as a largely elastic material, in direct contrast with the apparently diffusive motion of passive particles [232, 255]. Attenuation of active cellular processes (e.g.: by ATP depletion) results in severe reduction in the mobility of cytoplasmic particles [26, 232, 256]. Furthermore, the temperature dependence of apparent particle diffusivity inside the cell is non-linear, in contrast to expected behavior for generalized diffusive motion (equation (5)). Instead, the temperature dependence is Arrhenius-like, with mobility scaling according to D ∼ exp(−Ea/kBT) as expected for reaction rates of activated processes [257].
A number of different active processes are believed to play a role in the apparent particle diffusivity inside the cell. Myosin motor activity been shown to contribute substantially to overall particle mobility in mammalian cytoplasm [232, 256, 258, 259]. Inhibition of directed motor-driven transport is also known to reduce active diffusivity of apparently passive organelles [26]. Recent evidence indicates the diffusivity of individual active enzyme molecules can be significantly enhanced in the presence of their substrates, through mechanisms that are currently unclear [260–262].
The behavior of particles driven by active fluctuations is determined by the spatiotemporal correlations of forces acting on the particles ![$\left[{ \overrightarrow {F}}^{\left(a\right)}\right]$](https://content.cld.iop.org/journals/1478-3975/17/6/061003/revision2/pbaba5e5ieqn2.gif) and the memory kernel (K) describing medium response. If the active forces have correlation
and the memory kernel (K) describing medium response. If the active forces have correlation  and the memory kernel scales as K(t − t') ∼ |t − t'|−α, then the MSD of the particle is given by [263]
and the memory kernel scales as K(t − t') ∼ |t − t'|−α, then the MSD of the particle is given by [263]
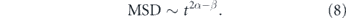
For a particle pushed by a purely processive force β = 0, while forces with delta-function correlations correspond to the limit β → 1. Linear scaling of the MSD arises for particles undergoing thermal diffusion in a purely viscous medium (α = β = 1). Alternately, it can also arise for particles in a purely elastic medium (α = 0) pushed by random processive forces that themselves accumulate as a random walk over time (β = −1). The latter model has been proposed for movement driven by an accumulation of actomyosin contraction events, over timescales shorter than the processivity time of an individual myosin motor [232]. In the interest of brevity, regardless of the underlying physical cause, we will refer to stochastic particle movements with negligible processivity as apparently diffusive in the remainder of this manuscript.
4.1.4. Crowding and heterogeneity
An assumption of the Stokes–Einstein relationship for diffusing particles (equation (3)) is that the particles are embedded in a continuous medium. The interior of a eukaryotic cell is inherently very crowded, with proteins constituting over 20% by mass of mammalian cell cytoplasm [264]. In addition, organelle structures ranging from vesicles to reticulated tubules and cytoskeletal networks are interspersed throughout the cell, occupying 40%–50% of cell volume [210]. In most models of particle motion within the cytoplasm, these crowding agents are averaged out to yield an effective viscous or viscoelastic medium. However, this approximation can lead to inaccurate predictions for transport behavior in the cytoplasm. For instance, the dependence of the diffusion coefficient on particle size (D ∼ R in a continuum fluid) is highly non-linear, with nanoscale proteins typically experiencing an effective viscosity that is orders of magnitude lower than that measured with micron-sized beads or vesicles [265]. Furthermore, protein complexes sized in the tens of nanometers tend to exhibit purely diffusive motion [266], rather than the subdiffusive behavior observed with vesicle-sized probes that are an order of magnitude larger [40, 41, 228]. This strong dependence of medium properties on probe size is generally found in gels, where particles much smaller than the pore size move freely through the gel while larger particles rely on rare jump events or large-scale rearrangements to move between pores [267, 268]. For proteins embedded in the plasma membrane, the actin cortex has also been shown to form a meshwork of obstacles that reduces effective diffusivity, particularly for larger probes [269].
In addition to individual crowders of all shapes and sizes, broadly-distributed spatial heterogeneity has been shown to play an important role in governing Brownian motion of cytoplasmic components. Quantification of individual step size distributions for RNA–protein particles [229], colloidal tracers [249, 270], and membrane-bound receptors [271] indicates that they do not follow a Gaussian distribution as would be expected for thermally diffusing particles in a uniform viscous or a viscoelastic medium (figures 8(g)–(i)). Instead, the step sizes have a Laplace distribution, with probability density P(Δx) ∼ exp[−Δx/λ(t)]. This scaling is indicative of a breakdown of spatiotemporal homogeneity in the particle motion, which would imply by the central limit theorem that each time-step should involve the sum of many uncorrelated displacements and should thus follow a Gaussian distribution. Similar long-tailed distributions of step-sizes are observed for the dynamics of tracers in a suspension of active swimmers [272], in glassy systems [273], and in polymer solutions (figure 8(h)) [231, 274].
The origin of such distributions has been attributed to broadly distributed diffusivities of individual particles caught in different regions of a heterogeneous environment [229, 275, 276], with exponential distributions of the diffusion constant giving rise to the observed Laplace distribution in stepping times. Indeed, diffusion coefficients extracted from individual trajectories of intracellular particles generally exhibit very broad distributions that are not strongly peaked around a preferred value [27, 247, 277]. In some cases, this observation has been attributed directly to local variations in the density of obstacles formed by organelle structures such as the ER [278].
More sophisticated models of 'diffusing-diffusivity' incorporate time correlations as the particle moves through the heterogeneous environment, with D(t) itself treated as a time-dependent random variable [276, 279, 280]. Beyond a characteristic correlation time, such a particle samples over many diffusivities and its step-size distribution again begins to look Gaussian (figure 8(g)), as has been observed in some experimental measurements [231, 280].
Overall, the broad non-Gaussian distributions of step sizes over commonly measured time-scales highlight the heterogeneity of the intracellular medium and the difficulty of making general conclusions based on 'typical' particle diffusivities.
4.1.5. Confinement and geometry
In addition to macromolecular crowding, the diffusion of many intracellular particles is limited by confinement in subcellular regions of complex geometry. Subcellular morphology is diverse, including shapes resembling spheres, tubes, sheets, labyrinths, beads on a string, and networks. Tubes and sheets are particularly common, and effectively confine diffusion to one or two dimensions, respectively. Here we outline the effect of these morphologies on the diffusive spreading of proteins confined within organelles.
The ER and mitochondria are ubiquitous intracellular structures that exemplify several of these morphologies. Both of these organelles can form extensive tubular networks (figures 9(a) and (b), left) [288–290] or dynamically break up into globular structures [291, 292] (restricted to certain stress or perturbative conditions in the case of the ER [293, 294]). The ER also forms stacks of flat membranous sheets in the perinuclear region (figure 9(a), bottom right). The morphology of these organelles is altered in different cell types [54, 295], growth conditions [296, 297], cell cycle stages [298, 299], or states of stress [300, 301]. The complex geometries of both ER and mitochondria are believed to be linked to their functional roles in the cell [290, 302].
Figure 9. Diffusive transport is modulated by confinement in intracellular structures of complex morphology. (a) Structure of the mammalian ER. Left: peripheral ER network in COS7 cell, from [281]. Right, top: cross-section of individual ER tubules, from [282]. Right, bottom: 3D reconstruction of helicoidal ramps connecting ER sheets in mouse salivary gland cell, from [283]. (b) Structure of mitochondrial network (left) in pancreatic β-cells, and the inner membrane cristae that form occlusions within a mitochondrion (right), from [284]. (c) Schematic of murine rod photoreceptor cell (left) and 3D reconstruction of membranous discs in the rod cell outer segment, adapted from [285]. (d) Dendritic spines that serve as diffusive traps in mouse pyramidal neurons, from [286]. (e) Confinement to curved surfaces results in reduced apparent diffusivity when measured with 2D or 3D Euclidean distance metrics (from [287]). Employing a geodesic distance over the surface corrects this effect. (f) Confinement within planar networks. Blue curve shows MSD of simulated particles on a fully connected (complete) honeycomb network, with effective diffusivity reduced by a factor of 2 compared to a free particle (black solid line). Red curve is for simulated particles on a honeycomb network with 29% of edges removed while maintaining a single connected component (decimated network). Both networks are confined in a circle of radius 20 μm, and particle diffusivity is set to D = 5 μm2 s−1, to give relevant units for proteins diffusing in an animal cell.
Download figure:
Standard image High-resolution imageConfinement within stable tubular geometries is found in mitochondrial [303], ER [290], and peroxisome [304, 305] networks, as well as bead-on-a-string structures formed by nuclei in certain cell types such as human leukocytes [306]. Transient tubules are also observed during vesicle budding and organelle fission [307], ER-to-Golgi transport [63], and peroxisome division [308, 309]. Tubule radii can range from ∼10 nm for dynamin-constricted regions [310] to ∼300 nm for mitochondrial network tubules [303]. For membrane proteins, models of diffusion on curved surfaces have shown that confinement to increasingly narrow tubules leads to slower spreading over the surface even when the diffusion constant and membrane surface area are kept constant [311]. This purely geometric effect is thought to arise from the local curvature and global topology of tubular membranes. Crowding of proteins on tubular membranes can lead to additional effects, including effectively anisotropic diffusion in the lateral versus circumferential directions [312].
For proteins in the lumen of a tubule, variation in tube radius can give rise to an entropic effect wherein locally narrower regions serve as effective diffusion barriers [313]. The local axial diffusivity in a tubule of heterogeneous radius R(x) is given by the Fick–Jacobs equation:
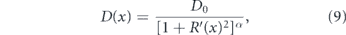
where D0 is the diffusivity in free space, α = 1/3 for two dimensions and α = 1/2 for three dimensions [313, 314]. An extreme case of entropic traps can be seen in geometries with narrow-necked regions branching away from a main tubule, as in dendritic spines (figure 9(d)). These traps serve as effective obstacles to diffusive motion along the tubule, resulting in a reduced diffusivity at long times (when many traps have been sampled) and anomalous diffusion at intermediate times [243, 315].
Confinement within complex organelle geometries gives rise to a discrepancy between the actual domain explored by a particle and its apparent motion in the 3D space where the organelle is embedded. For instance, particles on a curved membrane surface generally traverse longer lengths than the Euclidean distance between a start and end point (figure 9(e)), leading to underestimation of diffusivity when 3D spreading is analyzed [287]. Particles confined to a reticulated network of tubules are restricted to move along one dimension between each neighboring node. This effect decreases long-range diffusivity by a factor of 2 or 3 for a fully connected regular planar or 3D lattice, respectively (figure 9(f)). Comparison of fluorescence recovery after photobleaching experiments with simulations on extracted ER structures suggests that diffusive recovery times in the ER are 1.8–4.2× longer than would be expected from local diffusivity measurements [316]. Furthermore, the convoluted geometry of this organelle seems to have a greater effect on membrane than on luminal proteins. Simulations on realistic tubular ER geometries indicate that membrane proteins explore ER regions up to 4× slower than luminal ones, even when the diffusion coefficient is identical for both [317].
The effect of complex confining geometry or occluding barriers on long-range particle diffusion has been extensively explored in the context of transport through porous media and over spatial networks [318]. These effects are often described via an emergent quantity called 'tortuosity'—which is conceptually defined as the ratio between the typical length traversed by a diffusing particle and the Euclidean distance between its start and end points (figure 9(e)) [319]. A common simplifying model for environments with high tortuosity is that of percolation on a lattice [320]. The medium is represented as a lattice network with randomly removed edges. Such systems exhibit a phase transition when the fraction of remaining edges reaches a critical value pc, below which the network becomes disconnected and particles can no longer penetrate throughout the domain. Percolation systems exhibit a number of universal scaling behaviors, including a slow-down in effective diffusivity according to
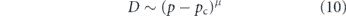
as the fraction of remaining edges approaches the critical value [321]. The scaling exponent is μ = 1.3 for two-dimensional and μ = 2.0 for 3D lattices [322].
Within cellular organelles, the connectivity of the space available for diffusion is determined by the overall organelle geometry, as well as the presence of intra-organelle substructures that serve as obstacles for mobility. The perinuclear ER presents an example of sheet geometry in the form of stacks of flat parallel cisternae bounded by membrane sheets [290]. The cisternae are interconnected with ramp-like spiral dislocations reminiscent of a parking garage [283] (figure 9(a), bottom right). The morphology of this structure is thought to directly modulate diffusion, with the ramps substantially enhancing diffusive transport between stacked cisternae when compared to individual holes in the membrane [323]. In particular, the unique connection geometry allows diffusing particles to transition between sheets by spiraling around dislocations rather than searching for small holes serving as localized connections between flat sheets. Even in the presence of these spiral structures, the limited connectivity of stacked ER sheets results in an effective perpendicular diffusion that is roughly 10-fold slower than local diffusivity [323].
An example of labyrinthine structures that limit connectivity within organelle compartments are the mitochondrial cristae—convoluted folds of inner mitochondrial membrane that occlude much of the mitochondrial matrix space (figure 9(b), right) [324]. There are about 6–8 cristae per μm of mitochondrial length, each of which serves as an impenetrable barrier to the diffusion of molecular species [325]. Early studies indicated that these protrusions must stretch across nearly the entire mitochondrial cross-section in order to have a substantial impact on diffusivity [326]. Simulations of diffusive spreading in the presence of multiple such overlapping barriers show that cristae are expected to slow long-range axial diffusion of matrix proteins by a factor of 5–6 [325]. Effective axial diffusion of proteins embedded in the inner mitochondrial membrane may also be slowed by up to an order of magnitude by the convoluted morphology of these structures [327].
In the outer segment of mammalian photoreceptor cells, flat lammellar disc membranes form similar occlusions, leading to a high tortuosity for axial transport (figure 9(c)) [328, 329]. Axial diffusivity in this compartment has been measured as roughly 50-fold slower than the nearby inner segment compartment, with a factor of 20–40× accounted for by the increased tortuosity due to membrane occlusions [329].
4.1.6. Diffusive target search
In the preceding discussion we addressed the impact of various physical factors on diffusive particle motion. Here, we consider the interplay of diffusion and morphology in limiting the kinetics of intracellular encounters and reactions. For freely diffusing particles in a 3D continuum, maximal reaction rates are proportional to particle concentrations. The steady-state current of particles to a perfectly absorbing spherical target of radius a is given by
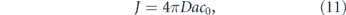
where D is the particle diffusivity, c0 the bulk particle concentration [333], and J represents the rate of particles arriving at the target. However, this linear relationship between concentration and reaction rate does not necessarily hold when particles are confined to complex geometries or embedded in domains of reduced dimensionality [318, 334].
Target search processes involving randomly moving particles fall into two broad categories: compact and non-compact [318, 335, 336] (see figure 10(a)). In a compact search process, a particle will cover most of the sites within each subregion it visits. Such particles generally find the target after comprehensively exploring a finite subsection of their domain, and their target search times strongly depend on their starting position [337]. By contrast, a non-compact search sparsely samples subregions of the domain, will generally reach the domain boundary before finding the target, and has search times largely independent of starting position.
Figure 10. Diffusive target search processes. (a) Illustration of non-compact (top) versus compact (bottom) search processes. Left: effect of medium dimensionality, with simulated diffusion trajectory in 3D (top) and on a network of 1D edges (bottom); color progression represents time. Right: transition from non-compact to compact search with increased compartmentalization of the domain (figure from [330]). (b) Dependence of search rate (inverse of mean first-passage time) on density of targets in a network structure extracted from fluorescent images of peripheral ER in COS7 cell, showing transition from an effectively 2D to effectively 1D search process. Yellow region indicates physiologically relevant concentrations. (c) Sample geometries for intracellular narrow escape processes: (i) transition from ER sheets to adjacent tubules (figure from [331]), (ii) protein accumulation at ERESs, (iii) transport of cytoplasmic transcription factors into nucleus and mRNA out of nucleus through nuclear pores [332], (iv) diffusion of ions and proteins into narrow-necked dendritic spines (figure from [286]).
Download figure:
Standard image High-resolution imageFor random walks on self-similar (i.e. fractal) geometries, the behavior of the search process is determined by two key dimensions. The dimensionality of the random walk itself (dw) can be defined by the scaling of MSD with respect to time (in the absence of confinement):  [318]. Equivalently, dw describes the scaling between the time to exit a sphere and the sphere size R:
[318]. Equivalently, dw describes the scaling between the time to exit a sphere and the sphere size R:  [338]. The fractal dimension (df) describes the dimensionality of the medium within which the walk is embedded, relating the number of sites (N) with the spatial extent of a region (R) according to
[338]. The fractal dimension (df) describes the dimensionality of the medium within which the walk is embedded, relating the number of sites (N) with the spatial extent of a region (R) according to  [318]. Compact search corresponds to the regime where dw > df, such as canonical diffusion (dw = 2) on a one-dimensional line (df = 1). The opposite regime (dw < df) is termed non-compact search and includes canonical diffusion in three dimensions (df = 3).
[318]. Compact search corresponds to the regime where dw > df, such as canonical diffusion (dw = 2) on a one-dimensional line (df = 1). The opposite regime (dw < df) is termed non-compact search and includes canonical diffusion in three dimensions (df = 3).
The mean time ⟨T⟩ for a randomly moving particle to find a target site in the fractal medium is then given by the following scaling laws with respect to the domain volume N and initial distance from the target r [338]:
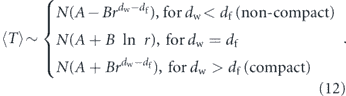
In the case of non-compact search, the dependence on starting position disappears for sufficiently large r, and the search time is simply proportional to the system volume, as expected for classical 3D kinetics (equation (11)). The distribution of search times in this case exhibits an exponential drop-off with a single characteristic time-scale corresponding to the average search time [335]. By contrast, the compact case results in 'geometry-controlled' kinetics, with a search time that depends strongly on starting position, even for initially distant particles. In this situation, the distribution of search times exhibits decay over a range of different time-scales whose breadth depends on the dimensions df and dw [335]. The mean search time, averaged over all starting positions, scales as  , indicating that the slowing of kinetics with increased volume is super-linear [335]. It should be noted, however, that the broadly distributed reaction times in compact systems are not well-described by this single mean first-passage time [339]. For particles undergoing unhindered canonical diffusion (dw = 2), the overall reaction rate for a particle to find any stationary target (defined by
, indicating that the slowing of kinetics with increased volume is super-linear [335]. It should be noted, however, that the broadly distributed reaction times in compact systems are not well-described by this single mean first-passage time [339]. For particles undergoing unhindered canonical diffusion (dw = 2), the overall reaction rate for a particle to find any stationary target (defined by  ) is expected to scale as follows depending on the dimensionality of the confining domain [337, 340]:
) is expected to scale as follows depending on the dimensionality of the confining domain [337, 340]:
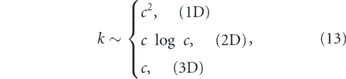
where c is the target concentration (or the inverse of the volume per target).
The impact of confinement geometry on target search is particularly relevant for molecules that must find sparsely scattered binding partners within an organelle. This includes, for example, newly-translated secretory proteins searching for an exit site within the ER network [341], or mitochondrial matrix proteins searching for nucleoids [342]. While realistic cellular structures are not true fractals, similar considerations of compact versus non-compact search processes can be applied to understand the effect of organelle morphology on kinetics. For example, calculation of diffusive first-passage times to find one of many point-like targets on planar ER networks extracted from mammalian cell images indicate that the search domain transitions from effectively 2D to effective 1D with increasing concentrations of the target sites (figure 10(b)). Due to the compact nature of this process, the rate at which proteins find punctate exit sites in the ER is expected to scale super-linearly with exit site density.
One important class of target-search processes, known as 'narrow escape' problems, consists of particles that must find their way to a very small region on the boundary of their confining domain. This class of problems encompasses molecules that need to exit specific cellular regions, such as ER proteins moving from cisternae to peripheral tubules [290] or reaching an exit site for export [55], signaling factors leaving dendritic spines [286], or mRNA encountering nuclear pores [343] (see figure 10(c)). It also includes reactions with a fixed target on the membrane of an organelle within which the searcher is confined. The mean first-passage time for a diffuser to reach a narrow target whose area covers a small fraction ( ) of the boundary can be approximated as:
) of the boundary can be approximated as:
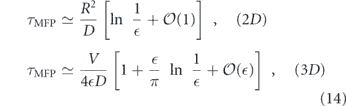
for a circular or a spherical domain, respectively [344–346]. The case of a particle trapped in a short cylinder lies intermediate between the two regimes, transitioning from two- to three-dimensional as the height of the cylinder increases [347]. This geometry can be particularly relevant for target search by particles trapped between flat sheets, as in the ER cisternae or lamellar discs of photoreceptor cells.
A common model for diffusion in the presence of obstacles or in reticulated or porous structures is to treat the process as a series of hops between compartments that are themselves rapidly equilibrated [330, 348]. Such geometries can result in a substantial reduction in long-range diffusivity without a concomitant decrease in the reaction rate [330]. Interestingly, the connectivity of compartments can be tuned in such a way that diffusive particles propagate in a wave-like manner, with transient concentration peaks appearing in different containers [348].
The nature of a target-search process in compartment networks is determined by the dimensionless parameter x = DL/D0a, where D0 is the diffusivity within a compartment, D the long-range effective diffusivity, L the compartment size, and a the particle reaction radius. The reaction rate exhibits one of two possible behaviors [330]:
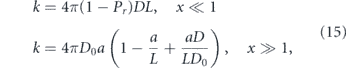
where Pr is the probability of returning to an already-sampled compartment. When x < 1, the process is compact and each compartment is fully explored as the particle moves through the medium (figure 10(a)). By contrast, for x > 1, the search process is sparse and the particle typically encounters the target only after multiple visits to the compartment containing the target. In this regime, when the target size is much smaller than the compartment, the long-range diffusivity may be greatly reduced (D ≪ D0) without significantly changing kinetic rates. For enzyme diffusion in the cytoplasm, estimated pore sizes are roughly 10 times bigger than the protein size [264, 349], implying that the sparse search regime is relevant for cytoplasmic kinetics.
The effect of macromolecular crowding on reaction rates can be approximated in an analogous manner by treating reactants as moving between crowder-free cavities [350]. It should be noted that non-specific binding to reactants, and finite local reaction rate upon encounter can further slow the overall reactive flux in the presence of crowding [350]. Once interacting molecules are coincident in space, they must also find the correct relative rotational orientation for binding or activity [351]. Molecules coming together will typically experience many 'microcollisions', allowing time for reorientation through random chance or intermolecular interactions that favor alignment [351]. Effective confinement from crowding cavities provides further opportunity for sites to align and a reaction or binding event to occur.
For particles diffusing on a network, the connectivity of compartments (or nodes) plays an important role in regulating target search times, as well as large-scale diffusivity [352]. For reticulated structures similar to those of the peripheral ER or mitochondrial networks, target search times were recently shown to be determined largely by the total network edge length and the loop (or cyclomatic) number [281, 289]. Loop number is a global metric of connectivity, defined by Γ = Ne − Nn + 1 where Ne is the number of edges and Nn is the number of nodes. The parameter corresponds to the number of independent cycles in the network structure [353]. Increasing loop number decreases search times, while increasing edge length increases them, with a scaling relationship that can be derived from the slowed diffusivity on a percolation lattice (equation (10)) [281]. A recent study on yeast mitochondrial networks demonstrated that network connectivity can be altered by mutations in specific proteins responsible for mitochondrial fusion and fission [289]. Simulations of diffusive search over these network structures indicate that the reduced connectivity in mutant networks is expected to slow encounter times by almost two-fold for particles at low concentrations [289].
Diffusive transport inside cells is modulated by the mechanics of intracellular media, by active non-thermal fluctuations, and by the presence of obstacles and complex subcellular geometries. These physical factors control both the overall dispersion and the rates of encounter between particles. Diffusive transport thus provides a physical link between the morphology and dynamics of cellular structures and the kinetics of biomolecular reactions that underlie cell function.
4.2. Motor-driven transport
For transport tasks where diffusive motion is too poorly controlled or too slow, eukaryotic cells have evolved an extensive system of motor-driven transport. This system relies on the attachment of cellular cargo to motor proteins, which employ ATP hydrolysis as an energy source to walk in a directed manner along cytoskeletal highways [354]. A variety of cargos including vesicles [355–357], mitochondria [165], ribonucleoprotein particles [358], protein complexes [359], and ER tubules [160], among others, navigate the cytoplasm using motor-based transport.
A key advantage of this transport mechanism is its ability to move cargo processively over very long length scales (up to a meter in neuronal axons). The relative efficiency of motor-driven versus diffusive transport over a given length scale can be quantified by the dimensionless Péclet number (equation (2)).
Typical velocities for motor-driven cargos in animal cells fall in the range of 0.3–2 μm s−1 [2, 48, 167, 355], with individual vesicle velocities reported up to 10 μm s−1 [355, 357]. Speeds of motor-driven cargo tend to be independent of particle size [34], allowing this transport mechanism to vastly outpace diffusion for long lengths and large cargos. For RNA–protein complexes and vesicular organelles, with typical cytoplasmic diffusivities of D ≈ 0.01–0.1 μm2 s−1 [26, 27, 34, 360], motor-driven motion tends to dominate (i.e.: Pe > 1) on length scales above a few microns.
An additional advantage to motor-driven motion is the ability to regulate and control transport behavior. The mechanochemical properties of individual motors can be tuned to optimize their speed or processivity under varying loads [361, 362]. Selective recruitment of different motor proteins and biochemical modification of key molecular components in the transport machinery can also tune cargo distribution and dynamics [20, 363]. Furthermore, the cellular-scale organization of cytoskeletal transport highways enables sorting of cargo to different destinations in the cell [364]. The plethora of molecular components involved in motor-driven transport thus allows for a broad variety of control mechanisms to regulate cargo delivery.
4.2.1. Components of the motor transport machinery
The basic components of motor-driven transport include the cargo itself, the motor proteins, a variety of adaptor proteins and linkers that attach motors to the cargo, and the cytoskeletal filaments that serve as a substrate for walking motors (figure 11). Both actin filaments and microtubules can serve as highways for motor-driven transport. Both are polarized, with distinct '+' and '−' ends, governing the direction of motor movement. In plant cells, the motion of a variety of myosin motors along polarized actin filaments is responsible for long-range cargo delivery, as well as the establishment of persistent cytoplasmic flows [365]. In animal cells, the myosin-V motor has been shown to contribute to local organelle positioning in actin-dense cortical regions [366–368]. However, long-distance transport in animal cells primarily occurs along microtubule highways.
Figure 11. Schematic of components involved in motor-driven transport on microtubules. Kinesin and dynein motors attach the cargo (in green) to the microtubule (blue and white) via motor adaptors (dark blue). A hitchhiking cargo (pink) can attach to a motor-driven carrier via a linker protein (red). Microtubule associated proteins (MAPs) and post-translational modifications to the microtubule help regulate motor-driven transport. Figure is not to scale [332].
Download figure:
Standard image High-resolution imageMicrotubules (MTs) form long hollow tubes, consisting of 13 parallel protofilaments, with motor proteins attaching to the outside of the tube. Interestingly, diffusive transport in the hollow interior of a microtubule has also been shown to play an important role in the spread of several microtubule-modifying proteins [369, 370]. Microtubules are quite stiff, with effective in vivo persistence lengths on the order of 30 μm, enabling them to fluctuate around relatively straight configurations on typical cellular scales [371]. In many animal cell types, they are organized with their minus ends anchored near the nucleus and their plus ends extending toward the cell periphery. Microtubules are highly dynamic, undergoing cycles of growth and depolymerization that allow for rapid remodeling of the transport highway network [372], as well as bending and sliding events that contribute to cargo motion [373].
Two families of motor proteins execute transport along microtubules. The kinesin superfamily [374] is generally responsible for anterograde transport: movement toward microtubule plus ends, which often corresponds to the direction away from the nucleus. Dynein motors drive retrograde motion toward microtubule minus ends [375, 376]. Both types of motors form protein complexes with two ATP-burning motor domains that bind to the microtubule, linked to a long tail that attaches to cargo, often via an adaptor complex [18]. The motors walk in a hand-over-hand fashion, with some (e.g.: kinesin-1) following individual protofilaments while others (including kinesin-2 and dynein) undergo frequent side-stepping to neighboring protofilaments [377, 378]. The mechanochemical behavior of individual molecular motors has been extensively explored at the single-molecule level in vitro [379, 380]. In a living cell, many motors can attach to each cargo, and their cooperative behavior determines the speed, processivity, and direction of cargo motion [19, 381–383].
Specialized adaptor proteins control the complement of motor molecules recruited to a particular cargo [20, 375]. These adaptors make it possible for a wide range of cargos to be transported by a limited variety of motor proteins, as well as controlling the direction and processivity of motion [376, 384–386]. In general, adaptor proteins are bound directly by receptors on the cargo surface, by both kinesin and dynein motor complexes, and by a variety of signaling proteins that serve to activate or repress transport [20].
As an alternative to the direct recruitment of motors via an adaptor protein, some cargos have been found to engage transiently with other motile organelles, moving by a non-canonical form of motor-driven transport termed 'hitchhiking' [9, 26, 167, 387–392]. In place of an adaptor protein, a linker protein attaches the hitchhiking cargo to a carrier organelle, which connects through an adaptor protein to the motor. Specific linker proteins have been identified for several hitchhiking cargos [9, 168, 392], and the density, length, and stiffness of these linker proteins can serve to modulate the efficiency of the hitchhiking interaction [393]. Both linker proteins and adaptors share the common feature of enabling specific control of transport for a particular cargo, without affecting the movement of other cellular components.
4.2.2. Direction and processivity along a microtubule
The direction and processivity of transport along a single microtubule can vary widely for different cellular systems. Some cargos, such as post-Golgi synaptic precursor vesicles in proximal regions of neuronal axons, move primarily in the anterograde direction toward the cell periphery [397–399]. Others, such as endocytic vesicles carrying growth factor signals [400] and neuronal autophagosomes [166], move primarily in the retrograde direction, toward the cell nucleus. Many cargos are bidirectional, exhibiting both types of motion with varying run-lengths prior to switching directions [19, 165, 401, 402]. At one extreme of highly processive bidirectional motion lie mitochondria in neuronal axons, which move for many tens of microns in either anterograde or retrograde directions, undergoing pauses of varying duration, but rarely reversing their direction after pausing (figure 12(a)) [394]. By way of contrast, lipid droplets in Drosophila embryos [403], lysosomes in neurons (figure 12(b)) [382], as well as endosomes and hitchhiking peroxisomes in fungal hyphae (figures 12(c) and (d)) [26, 392] all switch directions frequently, with typical run-lengths of about 0.3–10 μm. Cytosolic proteins engaged in slow axonal transport have been observed to exhibit even shorter processive runs of about 0.1 μm, thought to arise from transient interactions with passing cargos [106].
Figure 12. Bidirectional processive motion of cargo with varying run-lengths. (a) Long-range transport of mitochondria in the anterograde (top) and retrograde (bottom) direction (adapted from [394]). (b) Kymograph showing directional reversal of LysoTracker-labeled vesicles in primary neurons (image from [382]). (c) Kymograph showing bidirectional motility of early endosomes (green) in Ustilago maydis fungal hypha (image from [395]). (d) Kymograph of bidirectional processive transport for a peroxisome in Aspergillus nidulans fungal hypha (from [396]).
Download figure:
Standard image High-resolution imageThe direction and run-length for a motor-driven cargo moving along a single microtubule is thought to be determined by the complement of associated motors, as well as regulatory modifications to motors, adaptor proteins, and the microtubules themselves (figure 13). Cargos that exhibit bidirectional motion are generally attached to both kinesin and dynein motors simultaneously [382, 404–406]. Even axonal mitochondria and autophagosomes, with their very long processive run-lengths, have been shown to carry both kinesin and dynein motors regardless of whether they are stationary or moving in the anterograde or retrograde direction [166, 407, 408]. The question of how multiple motors coordinate to determine the direction, speed, and processivity of cargo has been the topic of much theoretical and experimental work over the past two decades.
Figure 13. Postulated mechanisms for pauses and reversals in microtubule-based transport. (a) 'Tug-of-war' between opposing motors. Pauses are resolved when force by engaged motors in one direction dominates. (b) Biochemical regulation of motors and adaptors. External signals can trigger pausing by dissociation of motors or cargo, or by tethering to the cytoskeleton. (c) Roadblocks in the form of microtubule-associated proteins and post-translational tubulin modifications can result in motor dissociation. (d) Cytoplasmic obstacles and intersections lead to pausing or directional changes. (e) Traffic jams of free motors reduce speed and processivity.
Download figure:
Standard image High-resolution imageThe classic model for opposing motor interactions is a 'tug-of-war' between multiple motors that come on and off the microtubule stochastically and pull in their characteristic direction when engaged (figure 13(a)), with the overall direction of movement dictated by the net generated force [381, 409]. When coupled with experimental measurements of the number of motors on a cargo and the force-response parameters of individual motors, the tug-of-war model can quantitatively recapitulate aspects of in vivo bidirectional motion for vesicles in mammalian neurons [382] and endosomes in Dictyostelium slime molds [410], as well as multi-motor assemblies in vitro [411].
However, this simple model fails to account for a number of puzzling observations indicating cooperative rather than competitive behavior between kinesin and dynein motors on the same cargo [19, 383]. Qualitatively, the presence of both kinesin and dynein motors has been found to be necessary to activate motion in both anterograde and retrograde directions [412–414], raising the so-called 'paradox of co-dependence' [19]. Quantitatively, a thorough parameter scan for the tug-of-war model has shown that no variant of the model can simultaneously reproduce the in vivo distribution of run-lengths and pausing behavior of bidirectionally motile lipid droplets [415, 416].
A number of mechanisms for positive cooperativity between opposing motors have been proposed as an alternative to the antagonistic tug-of-war model [19]. One possibility is the existence of direct biochemical and mechanical interactions wherein one motor type serves to activate the other or to push it out of an auto-inhibited state [406, 414, 417]. An alternate mechanism relies on inactive motors entering a weakly-bound diffusive state wherein they function as tethers that prevent cargo dissociation from the microtubule and hence increase processive run-lengths driven by the dominant active motor [19]. Such an effect may account for the increased processivity of kinesin-carried cargos along microtubules in the presence of myosin-V motors, and the reciprocal increase in myosin-V processivity on actin filaments in the presence of kinesin [418, 419].
Cooperation between multiple motors pulling in the same direction has also been proposed to enhance the speed and processivity of transport. In vitro measurements on reconstituted systems show that the presence of multiple kinesin motors allows for longer run lengths and larger stall forces [420, 421], with similar cooperative effects observed for multiple dyneins [422]. Furthermore, coupling of many kinesins bound to a fluid lipid membrane has been shown to increase cargo transport velocity without altering the behavior of individual motors [423]. Theoretical studies of load-sharing between motors help clarify the importance of key mechanical parameters in determining motor cooperativity, as well as highlighting the limitations of purely mechanical models and the need to incorporate biochemical coupling effects [383, 424–426].
In addition to interactions between the complement of motors attached to a cargo, processive motion along a microtubule can also be regulated by external signals targeting motors and adaptor proteins [427] (figure 13(b)). These signals often take the form of a biochemical modification through a signaling pathway that responds to the local intracellular environment or the state of the cargo itself. For example, calcium ion binding to the mitochondrial adaptor complex consisting of Miro and Milton proteins results in transient halting by dissociation of kinesin motors from the microtubule [165, 407]. Similarly, a byproduct of glucose metabolism serves as a substrate for modifying the Milton adaptor protein, inhibiting mitochondrial motility [171]. By coupling transport behavior to the local biochemical environment, these pathways can result in targeted localization of mitochondria to regions with high metabolic demand [48, 184, 428] or high glucose supply [171, 185] within extended neuronal projections.
A permanent cessation of mitochondrial transport can also be triggered through the PINK1/Parkin pathway, which is activated when the mitochondrial membrane potential (a marker for mitochondrial health) drops too low and results in the degradation of the Miro adaptor protein [165]. A cell can thus precisely control the positioning of its mitochondria in response to local cytoplasmic conditions and mitochondrial health. Another example of organelle state modulating transport behavior can be seen in neuronal autophagosomes, whose biochemical maturation is coupled to their transition from bidirectional motion near sites of synthesis at distal axonal tips to robust retrograde motility toward the cell body [166].
Microtubules themselves can serve as a substrate for post-translational modifications and other signals that regulate transport processivity [427, 429, 430] (figure 13(c)). MAPs bind to the external surface of microtubules and differentially regulate motor protein behavior. For example, tau proteins tend to cause kinesin detachment at low concentrations with little effect on dynein [431]. Gradients of tau proteins (which have been observed in neuronal axons [432]), can thus be used to tune the anterograde or retrograde bias, as well as processivity, of cargo transport [421, 433–435]. Other MAPs differentiate the microtubule-binding affinity of separate types of kinesin motors, allowing kinesin-3-bearing cargos to be sorted into dendritic projections while those carrying kinesin-1 are relegated to the axons [436].
Even in the case where a cargo follows a single microtubule or polarized bundle, its direction and run-length are thus a complicated function of the complement of attached motors, the decoration of the microtubule track, and the spatial profile of signaling molecules that inhibit transport.
4.2.3. Obstacles and traffic jams
The processive motion of a motor-driven cargo along a microtubule is inherently limited by the crowded environment within a living cell. Crowding by filamentous macromolecules gives rise to a viscoelastic rheology of the cytoplasm (section 4.1.2) which results in size-dependent and time-dependent drag forces experienced by the moving cargo. As a consequence, in vivo movements of cargo tend to be 'bursty', with speed fluctuations consistent with a slow build-up and rapid release of mechanical stresses [437, 438]. Models of motor-driven motion which incorporate complex fluid rheology predict the emergence of an anomalous transport regime with superdiffusive yet sub-ballistic scaling of the mean-squared displacement (MSD ∼ tα with 1 < α < 2) [439, 440]. In reconstituted in vitro systems with a viscoelastic medium, increased densities of filamentous crowders have been shown to drastically reduce the transport velocity of cargos carried by teams of kinesin motors [441].
In addition to altering the rheology of the cytoplasmic medium, crowded conditions within the cell imply the ubiquitous presence of obstacles, both directly bound to the microtubule track and in the cytoplasm at large [442]. Individual molecular motors vary in their ability to bypass MAPs that serve as roadblocks along the transport highway (figure 13(c)). Single kinesin-1 motors generally dissociate when encountering a road-block, though teams of such motors can effectively bypass the obstacle [377]. Individual dynein motors, on the other hand, are much more capable of side-stepping to neighboring protofilaments, allowing them to successfully bypass microtubule-bound obstacles [377, 443]. The increased ability to maneuver around obstacles afforded by the presence of different motor types has been proposed as a key evolutionary advantage to bidirectional motion [444].
When encountering large obstacles, such as other vesicles attached to the same track or intersecting microtubules (figure 13(d)), 3D motion of the cargo around its track is required for maneuvering around the obstacle [445]. In vivo tracking of anisotropic particles indicates that 3D rotation of the cargo occurs during long pauses that result in directional reversals on the same microtubule or a nearby parallel track [446]. These pauses were postulated to arise from obstacle encounters, with release and engagement of alternate motors allowing the cargo to bypass the obstacle. When encountering a microtubule intersection, cargo can also switch to the intersecting microtubule, reverse, or pass by it, in a manner dependent on the geometry of the intersection [447] and the complement of attached motors [356, 448]. The extent to which bypassing of an intersection in vivo involves side-stepping of individual motors versus switching or tug-of-war behavior between multiple motors remains largely unknown [445].
An additional source of transport obstacles comes from traffic jams formed by individual molecular motors bound to and moving along microtubules (figure 13(e)). These traffic jams can be described by the classic physical model of a 'totally asymmetric simple exclusion process' [449], which consists of non-intersecting particles moving along a line and predicts the onset of jamming as a phase transition [450–452]. Such models are quantitatively consistent with in vitro observations of the steep drop in both velocity and run-length when the density of kinesin-1 motors on a microtubule reaches a critical value [453]. Because traffic jams depend both on total motor density and accumulation at microtubule ends, the moderate processivity and high end detachment rates of kinesin have been hypothesized to be advantageous for overall cellular transport [454]. Interestingly, for cargo that can bind motors reversibly, increased free motor density can actually give rise to longer run-lengths [455], possibly due to the cargo's ability to associate with more motors to bypass localized traffic jams or effectively surf along densely packed neighboring motors [442].
The motion of a motor-driven cargo along a single microtubule is determined by a complex interaction between the complement and regulation of motors attached to the cargo, the distribution of roadblocks and traffic jams along the microtubule, and the presence of cytoplasmic obstacles encountered by the cargo. We next proceed to consider how cargo distribution on a cellular scale is governed by a combination of limited-processivity runs interspersed with passive periods.
4.2.4. Run and pause: intermittent transport
Cellular cargos engaged in long-range transport often undergo periods of processive runs interspersed with pauses of varying duration [19, 26, 382, 393–395]. The pauses can be very long, as is the case for axonal mitochondria that have been observed to switch from a motile to a long-lived stationary state [165]. They can also be transient, associated with maneuvering around an obstacle [2, 446], tug-of-war between opposing molecular motors [382, 456], or dissociation from the microtubule or hitchhiking carrier [26, 457]. During such pauses the cargo can remain stationary, tethered to the microtubule itself or to nearby filaments of the actin cytoskeleton [165, 458, 459]. Alternatively, the cargo can be free to diffuse within the cytoplasm until the next run of processive motion [26, 457].
A simple mathematical model for transport consisting of interspersed periods of diffusive and processive motion is the one-dimensional 'halting creeper' (figure 14, inset) [25]. This model comprises one-dimensional particle motion, switching at fixed rate kstop from processive motion with velocity ±v to pauses with diffusivity D and vice versa with rate kstart. Such a particle has a run length ℓ = vkstop and is processive a fraction f = kstart/(kstart + kstop) of its time. The 1D model is particularly relevant for particles within cellular regions that form highly extended tubules, such as fungal hyphae and neuronal axons.
Figure 14. Dispersion of particles via multimodal transport. Inset: schematic of the halting creeper model for a particle switching between ballistic and diffusive motion. Plot shows range explored by a halting creeper versus time. Two transitions in behavior are evident: at t*, x* processive motion begins to dominate; at t∗∗, x∗∗ a sufficient number of reversals have occurred that particle motion begins to look effectively diffusive. Parameters used apply to peroxisome transport in fungal hyphae (D = 0.015 μm2 s−1, v = 2 μm s−1, ℓ = 6 μm, f = 0.05). Adapted from [25], copyrighted by the American Physical Society.
Download figure:
Standard image High-resolution imageThe transport range (length of domain explored) for a halting creeper particle transitions from a diffusion-dominated regime at short times, to a ballistic intermediate motion above a characteristic length scale x* which can be estimated by setting fPe(x*) > 1 [25]. At much longer length and time scales, when the particle has had the opportunity to sample repeatedly between the different modes, it again exhibits effectively diffusive transport (figure 14). Similar transitions, albeit on different time-scales, are also observed for the MSD of a particle engaged in multi-modal transport [409, 460].
The relative importance of diffusive versus processive motion thus depends on both the length scale of interest and the overall objective of transport. For instance, the uniform dispersion of an initially concentrated bolus of particles is optimized at intermediate values of the run length ℓ and of the active fraction f [25]. For particles that are only able to carry out their function in the passive state (e.g.: proteins that must be released from a vesicle), reaction kinetics are fastest at intermediate fractions of time in active motion [461]. Even for constantly active particles, when the domain is sufficiently long and f is sufficiently high, the search time for a single particle to hit a target is also optimized at intermediate run lengths, which preclude very long excursions in the wrong direction [462].
When the transport objective comprises efficient encounter of a target by the first in a uniform population of particles, the relevant length scale becomes the inverse of the particle spatial density, which tends to be on the order of 0.1–10 μm. For densities higher than 1/x*, target search is dominated by diffusive transport, whereas for lower densities motor-driven motion predominates. Interestingly, many organelles capable of motor-driven transport have been found to spend only a small fraction of time actually engaged in processive motion [26, 382, 392, 457]. These particles can have sufficiently high values of x* such that both diffusion and active transport contribute substantially to target search processes [25].
While the velocity v of processive motion is fairly constant (of order 1 μm s−1), cells can regulate both the typical run length ℓ and the pause time tpause = 1/kstart for transported particles. The pause time, in particular, can be reduced by tethering the particle to the microtubule track and thereby increasing the rate at which it can re-engage with the machinery for motor-driven transport. Such tethering is particularly effective when the microtubules themselves are sparsely distributed and diffusion toward a microtubule becomes rate-limiting for initiating transport [25, 393]. Recent mechanical modeling of hitchhiking transport for fungal peroxisomes indicates that tethering to microtubules could enhance the rate of starting a hitchhiking run by up to an order of magnitude [393]. For directly motor-driven cargo, tethering and preventing dissociation from the microtubule has been proposed as a cooperativity mechanism for motors with opposing polarity [19]. In terms of transport efficiency, the enhanced starting rate for active motion due to tethering is balanced by reduced diffusive exploration during the paused state. For organelles that spend a small fraction of time engaged in processive motion, tethering is beneficial for transport only on length scales beyond  , where â is the ratio between the capture radius around a microtubule and the characteristic separation between parallel microtubules [25].
, where â is the ratio between the capture radius around a microtubule and the characteristic separation between parallel microtubules [25].
By tuning pause rates and durations, as well as the mobility state of a particle while paused, cells can thus regulate overall particle dispersion through an interplay of passive and processively moving transport modes.
4.2.5. Organization of cytoskeletal tracks
The intracellular distribution of cargos and their efficiency at reaching cellular regions can be controlled at several levels. As discussed in section 4.2.2, biochemical modification or binding of signaling molecules to motor-proteins, adaptors, linkers, and cytoskeletal tracks can regulate the processivity and directional bias of cargo moving along a single microtubule. However, models of transport that rely on uniform constant-rate processes at the single-cargo level tend to be insufficient to reproduce the complex behavior of motor-driven cargos in vivo [19, 415, 416]. Some of this complexity may be due to spatially or temporally heterogeneous regulation, with gradients in signaling molecules responsible for modulating transport parameters in different regions of the cell [185, 188, 435]. However, an additional key source of spatial heterogeneity is the organization of the cytoskeletal highways themselves. This organization both determines and is set by cell shape and polarity, allowing for a close coupling between cellular function, morphology, and transport logistics [364]. In some systems, incorporating the explicit distribution of cytoskeletal filaments has been shown to be sufficient to explain observed transport behavior while maintainining spatially uniform cargo unbinding rates [469–471].
The two types of cytoskeletal filaments serving as transport highways exhibit very different organizations within the cell. Actin filaments tend to form branched networks of varying densities. In mammalian cells, dense actin networks are usually restricted to a cortical layer (∼100 nm thick) beneath the cell membrane [472]. Away from the leading edge of migrating cells, these cortical actin filaments tend to be isotropic, without a defined polarity [473]. Consequently, transport within the actin network tends to appear characteristically diffusive, even when driven by motor proteins [366, 461]. The effective diffusivity of particles moving within the actin network is thought to be regulated in different cellular states by altering the switching probability at each filament intersection, thereby controlling the processive run-length of the cargo [366].
By contrast, the microtubule cytoskeleton can form a variety of structures with different degrees of polarity and spatial organization. Microtubules nucleate at discrete sites termed MTOCs, which anchor their minus ends while allowing plus ends to grow outward. The best-studied MTOC in animal cells is the centrosome, which is located near the nucleus, and nucleates an aster-like structure of microtubules extending their plus ends toward the cell periphery [463] (figure 15(b)). At the periphery, microtubules can penetrate the cortical actin network, allowing cargos to switch from long-range transport on microtubules to short range motion on actin filaments [474], in a manner dependent on the complement of attached motors [475]. A number of non-centrosomal microtubule-organizing structures have also been identified, allowing for anchoring of minus ends in many different cellular regions, and giving rise to microtubule networks with varying polarity and orientational alignment [463] (figure 15). Some MTOCs are associated with the Golgi body and its outposts, allowing for direct delivery of dynein-driven vesicles carrying secretory cargo from the ER to the Golgi [476].
Figure 15. Patterns of cytoskeletal organization in animal cells. Sketches of microtubule organization show nuclei in gray, microtubules in red, minus ends in cyan (adapted from [463]). (a) Polarized microtubules in a neuronal axon organize in bundles. Right: confocal migrograph of growing neurons show microtubules in purple, actin in green, and nuclei in blue (from [464]) (b) radially polarized microtubules in mouse fibroblast cell. Right: fluorescent image of actin (purple) and microtubules (yellow) (from [465]). (c) and (c') Microtubule organization in Drosophila oocytes changes depending on the stage of development. Microtubules are visualized via immunofluoresence in early (c) and late (c') stages of embryo development (micrographs from [466]). (d) A reverse polarized organization is seen in mouse keratinocytes. Middle: apical confocal slice of fixed primary cultured keratinocytes with fluorescently labeled microtubule binding protein (esconsin). Right: for the same cell type, nucleus labeled in blue and microtubule-anchoring protein ninein shown in green. Micrographs from [467]. (e) Unidirectionally polarized microtubules in intestinal epithelial cells. Right: Super-resolution image showing minus-end binding protein CAMSAP3 (red, inset) and microtubules (green). Micrograph from [468].
Download figure:
Standard image High-resolution imageIn certain cell types, including Drosophila [477] and Xenopus [478] oocytes as well as epithelial cells [479], microtubule nucleation is localized at the cell cortex (figures 15(c)–(e)). While fully polarized epithelial cells can establish unidirectional microtubule structures (figure 15(e)), oocytes tend to exhibit largely disordered cytoskeletal organization [477]. Nevertheless, a statistical bias in microtubule orientation can be sufficient to enable robust localization of cellular components [358, 470, 471, 480]. For Drosophila oocytes in particular, a gradient of microtubule nucleation densities at the cell periphery was shown to be sufficient to establish a structured velocity field for motor-driven motion throughout the ooplasm, when averaged over many realizations of a cytoskeleton that turns over on minute time-scales [470]. The resulting orientational bias allows kinesin-driven mRNA molecules to accumulate at the posterior pole despite executing many rapid runs in all directions [481]. Simulation studies incorporating the biased orientation field accurately reproduce both this posterior localization and the more complex splitting behavior of dynein-driven mRNAs, whose ultimate localization depends on the point of injection [470, 482].
Elongated cellular regions, such as neuronal projections or fungal hyphae, generally exhibit arrays of parallel microtubules, arranged into polarized bundles [483]. Microtubules in neuronal axons are uniformly oriented, with their plus ends pointing to the distal end of the projection [484]. In dendrites, the orientation can be uniform with minus end outwards (in Drosophila and Caenorhabditis elegans neurons) [484] or mixed with plus ends in both directions (in vertebrate neurons) [485]. The ability of cargos to be transported selectively to dendrites or axons is thought to rely on varying recruitment of motor subtypes [486] together with post-translational modifications of the microtubule tracks [483].
The parallel architecture of microtubules in these cellular projections is conducive to modeling studies that treat the system as essentially one-dimensional, representing the density of microtubules, cargos, and motors as mean-field distributions along the axis of the projection. For example, a model of dynein-driven dendritic transport showed that microtubule arrays of mixed polarity resulted in slower delivery of cargo to the dendrite tip but more efficient establishment of a uniform distribution of cargos within the dendrites [486]. Modeling of early endosome transport in fungal hyphae demonstrated that spatially uniform rates of motor switching and microtubule nucleation are sufficient to reproduce experimentally observed accumulation of endosomes in different hyphal regions in response to dynein and kinesin-3 motor mutations [469].
Additional effects beyond a purely one-dimensional system arise when considering the radial spacing of microtubules within a cylindrical cellular projection. Because motor-driven organelle transport can only be initiated when the organelle passes close to a microtubule track, the cross-sectional movement of organelles can play an important role in their dispersion. Modeling of 3D particle dynamics has shown, for instance, that tethering of hitchhiking peroxisomes to microtubule tracks is expected to greatly increase their overall rate of transport, particularly when there are very few parallel microtubules in the cellular region [393]. Cylindrical models with explicit microtubule arrangements form a natural transition from one-dimensional models to local regions of fully 3D systems that are lacking in microtubule intersections. For example, the asymmetric densities of parallel microtubules observed in Drosophila cell spindles can be incorporated into a 1D transport model that explains the uneven distribution of endosomes between daughter cells [487]. Other modeling efforts have shown that random spacing of locally parallel microtubules leads to a higher long-range effective diffusivity of motor-driven particles than does purely uniform spacing [471].
In many animal cell types, microtubules form 3D networks with frequent intersections between individual filaments [2, 356]. These intersections serve as both obstacles for cargo moving along a microtubule (section 4.2.3) and as an opportunity to alter the direction of motion. The probability of switching tracks at a microtubule intersection is dependent on the 3D spacing and orientation of the intersecting microtubules [2, 447], as well as the cargo size [445] and complement of attached motors [448]. Live-cell tracking studies indicate that most cargos tend to preserve the anterograde or retrograde polarity of their motion upon passing microtubule intersections [2], an effect which may arise from the radially polarized organization of the microtubule network.
As with one-dimensional models, the motion of motor-driven particles over cytoskeletal networks is generally assumed to consist of stochastic switching between processive runs along filaments and slow passive phases [461]. While the passive phases are generally treated as diffusive, they may also involve tethering to stationary structures [19, 458, 459]. Recent work in which the passive mode is treated as a continuous-time random walk with broadly distributed step times indicates that such intermittent motion would give rise to a characteristic distribution of first passage times to the cell periphery [488]. Namely, a peak of particles arriving at short times is expected, followed by a sustained long tail of sporadic particle arrivals—a biphasic pattern which has been observed for the exocytic release of insulin granules [489].
The density, spatial distribution, and polarity of cytoskeletal filaments in a 2D or 3D cellular region plays an important role in determining the overall transport of cargo. Denser networks of filaments allow cargos to spend more time in the actively moving phase. However, more dense networks also imply more frequent filament intersections and thus shorter processive runs. Simulations on randomly oriented 2D networks indicate that the mean first-passage time from a central nucleus to the cell periphery is largely determined by the total mass of cytoskeletal tracks, with faster transport at higher total filament content [490]. For the same total network densities, structures with a few long filaments tended to exhibit much greater variation in transit times than those with many short filaments, an effect arising from the presence of 'traps' where processively moving cargo is directed into a localized region of the network [490, 491]. The polarity of randomly scattered filaments plays an important role in determining transition times across the network, and reversing the polarity of a single filament can alter the first-passage times several-fold [491].
Spatially inhomogeneous network structures can also help optimize transport of intermittently motor-driven cargos. Regions of randomly oriented short filaments serve to locally enhance the effective particle diffusivity. Continuum models show that when such a region is placed closer to the center of a circular domain, the mean first-passage time of particles from the center to the domain boundary can be significantly decreased [490]. By contrast, when the goal of a transport system involves locating a specific narrow target on the periphery, then optimal search rates can be obtained by an ordered radial arrangement of polarized filaments in the cell bulk, coupled with a thin shell of random filaments near the periphery [474, 492]. In this case, cargo is delivered in a directed fashion to the peripheral layer, followed by effectively diffusive exploration of the boundary. Such a morphology is indeed observed in many cell types which maintain a radially polarized microtubule cytoskeleton originating at the centrosome near the nucleus and a thin largely disordered cortex of actin filaments that may contribute to localized cargo transport in peripheral or distal regions [368].
Motor-driven transport is a ubiquitous feature of eukaryotic cells. Its unique advantage lies in its ability to deliver and disperse cargo in an efficient and regulated manner that can be modified via a plethora of control parameters tuned for different cargos, cell types, and cellular states. The factors subject to cellular control include cytoskeletal organization, motor recruitment, processivity of individual motors, and cooperative interactions between motor teams. However, motor transport is limited in its maximum speed, has a high metabolic cost in ATP consumption, and requires additional complexity in the packaging of molecular components into vesicles or motor-driven complexes. An alternate mode of directed intracellular transport, the movement of particles by cytoplasmic flow, offers cells the opportunity to circumvent some of these challenges.
4.3. Advective transport: intracellular flows
In addition to directed motor-driven motion along cytoskeletal highways, active transport in the cell can be achieved through advection, with particles carried along by the flow of intracellular fluids. This phenomenon was first discovered in plant cells [493, 494], but has since been observed in a variety of protist [194, 495, 496], fungal [26, 497], and animal [3, 466, 498] cell types. In plant cells, particularly, cytoplasmic flow has long been thought to play a crucial role in distributing molecular components throughout the cell: replenishing depleted regions, controlling delivery rates of metabolic reactants, and (with the aid of diffusion) smoothing intracellular gradients [180, 499].
The processivity, speed, and spatial correlations for transport by fluid flow can vary widely among different cellular systems. At one extreme are highly coordinated and extensive flows in macroscopic cells, such as cytoplasmic streaming in the internodal cells of characean algae (persistent spiral flows over centimeter scales at speeds of 100 μm s−1) [29, 32] or peristaltic shuttle flows in the hyphae of the giant slime mold P. polycephalum (reaching speeds up to 1 mm s−1) [194, 197]. At the other extreme are short-range perturbations due to hydrodynamic entrainment by passing motor-driven cargo, which have been hypothesized to contribute to 'active diffusion' of axonal vesicles [107] and fungal peroxisomes [26].
For simplicity, many studies of intracellular fluid flow represent the cytoplasm as a linearly viscous (i.e.: Newtonian) fluid, subject to various boundary conditions and perturbed by stresses that can be generated both at the cellular boundary and within the bulk [3, 28, 29, 107, 500, 501]. More complex mechanical models have also been developed, treating the cytoplasm as a poroelastic material consisting of a fluid phase intercalated with and rubbing against an elastic solid phase [502, 503]. Such poroelastic models can more accurately reproduce the flow patterns arising in response to specific cellular forces involved in blebbing, motility, and indentation [349, 496, 504], as well as propagating waves that arise from mechanochemical coupling between cytoplasmic activators and cytoskeletal contractions [505]. Here, we focus primarily on the role of flow patterns in particle transport, and we restrict our discussion to models of the cytoplasm as a simple fluid.
4.3.1. Fundamentals of advective transport
As discussed in section 2, flows of intracellular fluids generally lie in the regime of very low Reynold's numbers, where viscous forces dominate over inertia. In this 'Stokes flow' regime, fluid flows are laminar, particle velocities are proportional to applied forces, and flow patterns are established nearly instantaneously throughout the domain for any given pattern of applied stresses [21]. Such systems are subject to an effect which has been whimsically referred to as the 'scallop theorem', where time-reversing flows result in no net movement of the advective particles [22]. In essence, particles that are mixed by stirring in a low Reynold's number fluid can be un-mixed by repeating the same stirring motions in reverse [499, 510, 511]. As a result, simple oscillatory back-and-forth flows cannot, in and of themselves, result in particle transport. However, long-range transport can be achieved by the establishment of steady, persistent flow patterns (as for cytoplasmic streaming in plant cells [32, 512]) or by coordinated oscillations that propel material via peristalsis (as in the shuttle flows of slime molds [194, 197]).
The spatiotemporal distribution c(x, t) of particles subject to both diffusive motion and flow is described by the advection-diffusion-reaction equation [513]:
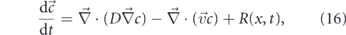
where D is the diffusivity,  the fluid flow field (which can vary over space and time), and R is a reaction term that describes sources or sinks that may arise from chemical reactions. This general equation can be leveraged to describe pattern formation and signal propagation in a variety of cellular systems with cytoplasmic flow [28, 506]. The importance of flow versus diffusion over a length scale L is characterized by the Péclet number Pe(L) [32], which is defined generally for directed transport processes (equation (2)).
the fluid flow field (which can vary over space and time), and R is a reaction term that describes sources or sinks that may arise from chemical reactions. This general equation can be leveraged to describe pattern formation and signal propagation in a variety of cellular systems with cytoplasmic flow [28, 506]. The importance of flow versus diffusion over a length scale L is characterized by the Péclet number Pe(L) [32], which is defined generally for directed transport processes (equation (2)).
A large Péclet number (Pe ≫ 1) indicates advection-dominated transport. For non-stationary flows, the length scale can be replaced by L = vτ, where τ is the persistence time of the flow pattern. Cellular transport systems where advection is believed to play an important biological role have Péclet numbers in the range Pe ≈ 2–1000, as summarized in table 1.
Table 1. Péclet numbers for example cellular systems where flows have been shown to play a role in cytoplasmic transport.
| Particle | Cell type | Péclet number | References |
|---|---|---|---|
| PAR proteins | C. elegans zygote | 3 | [506] |
| Acidified vesicles | Human neutrophil-like (HL-60) | 11 | [3] |
| mRNA | Drosophila oocytes | 10–100 | [507] |
| Bicoid morphogens | Drosophila embryos | 80 | [508, 509] |
| Small molecules | Characean algae internodal cells | 100–1000 | [500] |
4.3.2. Generating cytoplasmic flow patterns
Several distinct mechanisms are capable of generating intracellular flows. The first mechanism relies on the contraction of actin filament networks by myosin motors. Large-scale flow patterns have been observed in reconstituted in vitro active gel systems with actin turnover and myosin activity [517, 518]. Waves of actomyosin contraction are responsible for the peristaltic shuttle flows in slime mold hyphae [197, 519], as well as flows that drive spindle positioning in mammalian oocytes [520] and nuclei dispersion in Drosophila embryos [508]. Myosin-driven contraction at the cell rear also drives flow toward the leading edge in migrating keratocytes [521] and neutrophil cells [522]. These flows can be regulated by gradients in the distribution of myosin motors or of signaling molecules that trigger myosin activation. When the molecules regulating contraction are driven by the flow itself, precise patterning of flows and molecular distributions can be established across the entire cell [28, 508, 523, 524]. Example flow patterns generated by actomyosin contraction are shown in figures 16(a)–(c).
Figure 16. Spatial patterns of cytoplasmic flow. (a) Peristaltic shuttle flow in P. polycephalum plasmodium fragment (from [514]). (b) Elongational flow and unidirectional flow in contracting starfish oocytes (from [498]). (c) Bidirectional fountain flow in Drosophila embryo, at cell cycle 6. Red arrows show cytoplasmic flow and blue arrows show nuclear trajectories (adapted from [508]). (d) Flow in migrating neutrophil-like HL60 cell associated with deformation of cell boundary (pink arrows). Red arrows show velocity of acidified organelles, green arrows show the computed flow pattern based on boundary deformation (adapted from [3]). (e) Eddies formed near pore constriction for hyphal flow in Neurospora crassa fungi (adapted from [515]). (f) Reverse fountain flow in lily pollen tube, with organelle velocities shown (from [516]). (g) Spiral streaming in characean algae, with indifference zone marking boundary between axial flow directions (from [32]). (h) Disordered yet spatially correlated flows in stage 9 Drosophila oocyte (from [507]). (i) Circulating flow in stage 11 Drosophila oocyte (from [466]).
Download figure:
Standard image High-resolution imageLarge-scale contraction of the actomyosin network is often associated with deformation of the cell shape during migration [496, 522, 525], division [526, 527], and development [498, 528]. In many cases, however, cell shape dynamics are driven primarily by leading edge extension through directed polymerization of the actin cytoskeleton [529–531], as in the migrating neutrophil-like cell in figure 16(d). Growing cells, such as fungal hyphae, may also harness gradients in osmotic or turgor pressure to drive flow toward extending tips [497, 532] (figure 16(e)). Regardless of its origin, deformation of the cell boundary gives rise to cytoplasmic flows that can contribute to intracellular mixing [3] or overall translation of the cytoplasm [514].
An additional major source of flow is hydrodynamic entrainment by motor-driven cargo. Long-range, persistent flows are particularly prominent in plant cells (figures 16(f) and (g)), where myosin motors carry a variety of organelles along bundled actin filaments organized around the cell periphery [29, 499, 533, 534]. The motion of these organelles entrains a thick layer of cytoplasmic fluid, resulting in streaming flows that can reach 100 μm s−1 [534]. In animal cells, entrainment-driven flows tend to be slower and more spatially heterogeneous. In Drosophila oocytes, for instance, kinesin-bound cargos are responsible for slow, apparently random flows (25 nm s−1) and rapid, coordinated streaming (300 nm s−1) during different stages of oogenesis [466] (figures 16(h) and (i)). Seemingly random flow patterns in the early oocyte tend to be spatially correlated on the few-micron scale (figure 16(h)), likely due to the underlying organization of the microtubule cytoskeleton [86, 507, 538] (see figures 15(c) and (c')).
In other systems, where cellular-scale flows are not directly evident, the bidirectional motion of motor-driven cargos may nevertheless give rise to very short-range entrainment events for nearby tracer particles [107]. When the cargo motion is slightly biased toward one direction, an overall slow flow of passive cytoplasmic contents will arise. For example, a bias toward anterograde cargo motion in growing fungal tips has been suggested to give rise to a very slow directed polar drift (0.5 nm s−1) that leads to organelle accumulation when other active transport mechanisms are removed [26].
The variety of spatiotemporal flow patterns generated by different cellular mechanisms contributes to the distribution and dispersion of intracellular particles ranging from small nutrient molecules to proteins and organelles. Unlike diffusion, flows can drive the motion of even very large particles. Unlike motor-driven active transport, they affect all particles passing a particular region, without the level of regulation derived from specific adaptors coupling motors to cargos. We proceed to consider the functional consequences of various flow patterns on both directed localization of cellular components and overall mixing of cell contents.
4.3.3. Directed transport and localization by flow
Stable, persistent cytoplasmic flow provides a mechanism for directed transport of cellular components, allowing the establishment of intracellular gradients and the localized positioning of organelles. In mammalian oocytes, cytoplasmic flow drives the placement of the meiotic spindle near the cortical cap [520]. In C. elegans zygotes, flows with Pe ≈ 3 contribute to the anterior accumulation of PAR proteins [506, 535]. Directional advective transport also contributes to delivering cytoplasmic contents that drive cellular growth in a variety of systems, including the developing axon [536], slime mold plasmodium [194], fungal hypha [497], and elongated plant and algal cells [32, 512].
The simplest model for localization and gradient-formation by advection consists of a one-dimensional domain of length L with reflecting boundary conditions and a steady unidirectional flow of velocity v. The steady-state distribution of a particle with diffusivity D is then given by solution of equation (16) as
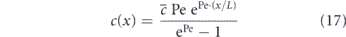
where  is the average density and Pe is the Péclet number over the domain. High Péclet numbers lead to sharp accumulation of density at the domain boundary, while lower values result in a more uniform distribution (figure 17). Because diffusivity generally scales with particle size, larger particles develop sharper gradients under a given flow—an effect that has been used to estimate flow velocities in the leading edge of crawling keratocytes [521].
is the average density and Pe is the Péclet number over the domain. High Péclet numbers lead to sharp accumulation of density at the domain boundary, while lower values result in a more uniform distribution (figure 17). Because diffusivity generally scales with particle size, larger particles develop sharper gradients under a given flow—an effect that has been used to estimate flow velocities in the leading edge of crawling keratocytes [521].
Figure 17. Particle localization through the interplay of advection, diffusion, and binding. Solid lines show steady-state profile of particles at average concentration  in a 1D domain under the influence of flow and diffusion (equation (17)). Color corresponds to different Péclet numbers. Dashed lines show the distribution profiles in the presence of binding sites at concentration
in a 1D domain under the influence of flow and diffusion (equation (17)). Color corresponds to different Péclet numbers. Dashed lines show the distribution profiles in the presence of binding sites at concentration  and dissociation constant
and dissociation constant  , located within the last 10% of the domain (green region). Inset illustrates example particle distributions corresponding to these profiles.
, located within the last 10% of the domain (green region). Inset illustrates example particle distributions corresponding to these profiles.
Download figure:
Standard image High-resolution imageGradients can be further enhanced by a polarized distribution of molecules capable of binding the particle of interest (figure 17). Weak binding, along with directed flow, can combine to segregate a molecule into a specific cellular region, while allowing for rapid equilibration within that region. An analogous mechanism has recently been shown to underlie the accumulation of proteins in the outer segment of mammalian photoreceptor cells [537]. It should be noted that the distributions described by equation (17) and its generalizations do not require that v represent fluid flow specifically. Any kind of directed transport process that moves all relevant particles passing a particular point in space with the same velocity can supply the advective drift v. This could include, for instance, the IFT trains that transport proteins into primary cilia [142, 143]. By interacting only with certain specific proteins, such forms of directed transport allow for more precise control over the patterning and accumulation of intracellular particles.
Conservation of mass implies that when advective flow delivers cytoplasmic contents to specific cellular regions, the fluid itself must either recirculate or deform the cell contour. In growing or migrating cells, expansion of protrusions provides a reservoir for newly arriving cytoplasm (figures 16(a) and (d)). Other transport systems rely on fountain flow patterns (figures 16(c) and (f)) that cycle the incoming fluid with peripheral flow in the reverse direction from flow along the central axis. In these flow patterns, local binding or rapid removal via metabolism or exocytosis is needed to prevent newly delivered molecules from being flushed back by the recirculating flow [516]. Yet another pattern of advective delivery is seen in some fungal hyphae, where flows pass between cellular regions separated by septa with a narrow central pore (figure 16(e)). The focusing of flow through the pore leads to the formation of circular eddies on the upstream side of the septum, which can serve as a subcellular compartment. These compartments locally entrap nuclei that proceed to differentiate to a transcriptional program which differs from other nuclei in the same cytoplasm [515]. Furthermore, the flow-driven accumulation of vesicles at the septa has been hypothesized to contribute to hyphal branch formation [191].
The entrainment of cytoplasm by motor-driven cargo also raises the problem of fluid cycling when the cargo approaches the end of a cellular region. Modeling studies indicate that the recirculatory flow engendered by this entrainment may counteract directed transport, washing unbound cargo and other passive particles out of the target zone [538]. The resultant coupling between motor-driven motion and advective flow implies that disordered, weakly directional cytoskeletal networks may in fact lead to more optimal local accumulation of particles [538].
Many cellular advective transport systems rely on relatively stationary flow patterns that persist over sufficient time periods to enable particle delivery across the cell. However, important counterexamples exist, where large-scale directed movement of cytoplasmic contents is achieved through coordinated time-varying flows. A particularly well-studied example is the peristaltic shuttle flow observed in slime molds, both in their migrating ameboid [496] and their hyphal network [194] state. These flows are generated by directionally propagating contraction fronts that are thought to be self-organizing via a signaling molecule that both amplifies contractions and is advected by the flow itself [28]. In general, peristaltic flows require an organized spatial gradient of contraction phases, allowing for overall directed transport of fluid contents [539]. In tubular network structures, advective transport is optimized when the wavelength of the peristaltic wave is comparable to the network size, consistent with the observed phase correlation patterns in P. polycephalum hyphae [194]. An alternate example of cytoplasmic transport by oscillatory flows has recently been observed in multinucleate Drosophila embryos, where vortex-like flow patterns (figure 16(c)) oscillate in coordination with the cell cycle. These flows are able to drive the separation of nuclei originally clustered near the embryo center to well-spaced positions along the anterior–posterior axis [508].
4.3.4. Enhancing mixing through flow
In addition to targeted delivery and patterning, cytoplasmic flows can also drive more efficient mixing of cellular components. Mixing in the world of low Reynold's number fluids relies on two distinct physical effects: Taylor dispersion (the smearing out of concentration gradients by diffusion) [541, 542] and Lagrangian stirring (the chaotic motion of particles driven by a spatially heterogeneous, unsteady, non-reversing flow) [543, 544]. Taylor dispersion arises from spatially varying rates of flow, which give rise to gradients in particle densities, resulting in an effectively higher diffusivity of particles across the streamlines (figure 18(a)). For steady Poiseuille flow in a tube [545], the effective diffusivity along the cross-section of the tube is given by
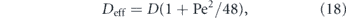
where Pe refers to the Péclet number (equation (2)) computed for the average velocity in the tube over the length-scale of the tube radius. For the rapid contractile flows in P. polycephalum (velocity ≈ 0.1 mm s−1, radius ≈ 50 μm, Pe ≈ 50), the effective dispersion of small molecules (defined as  ) is increased by up to 7-fold [195].
) is increased by up to 7-fold [195].
Figure 18. Enhancement of mixing by cytoplasmic flow. (a) Taylor dispersion of simulated particles in a Poiseuille flow (red arrows). Initial bolus of particles is shown spreading by flow only (Pe = inf), diffusion only (Pe = 0), and both processes (Pe = 100). (b) Computed distribution of material in the cross-section of a cylindrical algal cell undergoing spiral streaming. Flow generates steep asymmetric gradients, increasing flux of diffusive material into cell (from [29]). (c)–(e) Lagrangian stirring by unsteady flows. (c) Stretching and folding of initial particle distribution due to flows in a 2D circular domain with boundary dynamics representing deformation of migrating HL60 cell (adapted from [3]). (d) Simulated spreading of initially clustered nuclei along the cell axis, based on measured fluid flows in Drosophila embryos during cell cycles 4–7 (from [508]). (e) Computed trajectories of a tracer sphere entrained in the flow field generated by an active sphere moving processively along the central axis of a no-slip cylinder. Spheres represent organelles of radius 100 nm; cylinder represents a hypha of radius 1 μm. Each trajectory corresponds to a different starting position. Inset shows entrained sphere velocity at each position. Flow field computed as described in [540].
Download figure:
Standard image High-resolution imageSeveral cellular systems with more complicated flow patterns have also been hypothesized to enhance diffusive transport through the flow-induced formation of steep gradients. In late-stage Drosophila oocytes, streaming flows exhibit faster velocities toward the cortex (figure 16(i)), leading to cytoplasmic shear gradients that may contribute to mixing [466]. In the long cylindrical cells of characean algae, high shear rates result from rapid spiral cytoplasmic streaming [29, 32, 500]. These flows are expected to give rise to radial concentration gradients that augment diffusive entry of nutrients into the cell (figure 18(b)). Interestingly, the geometry of flow patterns can be used to tune the gradient steepness and hence the rate of mixing or diffusive uptake. Internodal cells of the algae Nitella axillaris alter the wavelength of their spiral flows as the cell grows, with a maximum in both diffusive uptake and growth rate arising at a specific cell length [29]. Foraging P. polycephalum slime molds prune their network structure to increase flow speeds in a few large central tubules, increasing particle dispersion [195].
In addition to Taylor dispersion, Lagrangian stirring resulting from unsteady fluid flow patterns also contributes to mixing in cellular systems, even for particles whose diffusion is negligible. Stirring is often described by quantifying the extent to which a given region of fluid stretches and folds under the flow (figure 18(c)), increasing the length of its boundary with the surrounding fluid [544]. These boundaries mark regions of high gradients, which can then be smoothed by diffusion. Stirring thus acts together with Taylor dispersion to mix the system across different length scales. Lagrangian stirring arises from the fact that even a relatively simple laminar flow pattern for a low Reynold's number fluid can nevertheless lead to highly complex (chaotic) trajectories of individual particles or fluid elements [543, 546, 547]. Chaotic trajectories are characterized by positive Lyapunov exponents [544], which quantify the exponential divergence of paths for two initially close particles carried by the fluid. Although a steady flow field can yield such diverging trajectories in three dimensions, time-varying flow patterns are needed to generate chaotic stirring in 2D fluids [544, 547]. An example of diverging particle trajectories due to unsteady flow is seen in the spreading of nuclei along the anterior–posterior axis of Drosophila embryos (figure 18(d)) [508].
In practice, extensive and efficient stirring can be achieved by unsteady flows that are not time-reversing. In such systems, the Péclet number associated with instantaneous flow velocities does not adequately describe the overall stirring behavior, since partial flow reversals tend to drive particles back toward their starting points. Instead, one can characterize the effect of flow on mixing by defining an 'effective Péclet number' on any given time-scale, as the overall displacement of a tracer particle driven by flow alone versus the diffusive displacement over the same time period [3]. Starfish oocytes serve an example of a cellular system with rapid back and forth flows (figure 16(b)) but no significant overall displacement of large cytoplasmic particles [498]. More complex dynamically evolving flow patterns are observed in the cytoplasm of crawling cells executing amoeboid-like deformations [3, 496, 548]. Numerical simulations indicate that the flows arising from deformation of neutrophil-like migrating cells (figure 16(d)) are sufficient to substantially enhance the mixing of lysosome-like organelles in the cytoplasm (Peeff ≈ 11 over 30 s timescales) [3]. In late-stage Drosophila oocytes, dynamic buckling of microtubule tracks due to drag forces on motor-driven cargo is thought to give rise to local time-variation in the overall flow pattern [466, 549]. The resulting unsteady flows (figures 16(h) and (i)) have been shown to homogenize the distribution of initially concentrated yolk granules within the cytoplasm [466, 550].
Locally oscillating flows can efficiently drive dispersion when the particles are confined in a domain of complex geometry and the overall spatial pattern of flows is stochastic. A biologically relevant example is the luminal flow generated by random contractions in a tubular network, as in slime-mold hyphae [195]. In order for such flows to contribute substantially to mixing, they must be rapid enough and persistent enough to enable individual particles to transition between nodes before the contraction re-opens, reversing the flow. Once a particle reaches a network junction, flow splitting and small time delays in flow reversal at adjacent edges ensure that the particle does not get restored to its initial position, thereby promoting mixing through Lagrangian stirring [551].
On a smaller scale, flows arising from uncoordinated tubular contractions have recently been hypothesized to drive node-to-node transport of proteins in the mammalian ER network [59]. Processive particle velocities on the order of 20 μm s−1, over time scales of 30 ms, have been measured for individual proteins tracked in ER tubules, which exhibit a luminal diffusivity in the nodes of about 0.5 μm2 s−1 [59]. These estimates yield a Péclet number of Pe ≈ 20 and allow for individual processive trajectories to cover a distance comparable to the typical edge length in an ER network (∼1.5 μm).
An additional role for stochastic intracellular flows in driving cytoplasmic mixing is through uncoordinated entrainment by motor-driven cargos. Such entrainment events result in short-range runs, leading to an enhanced 'active diffusion' driven by bidirectionally moving cargos. Localized entrainment has been hypothesized to account for the 'slow component' of axonal transport [107] and the kinesin-dependent 'active diffusion' of peroxisomes in fungal hyphae [26], although direct evidence of their importance in cellular transport is still lacking. In a tubular system, each entrainment event from the passage of a single organelle should yield a finite short displacement (ℓ) of a tracer particle of length comparable to the organelle size [107] (figure 18(e)). If organelles pass near the tracer at a frequency kpass, the effective diffusion coefficient for the tracer is then given by
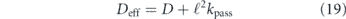
where D is the tracer diffusivity in the absence of active motion. In fungal hyphae, knocking out an endosomal motor adaptor results in a decrease in the diffusivity of passive peroxisome organelles by ΔD ≈ 0.01 μm2 [26]. This effect is comparable to the predicted contribution due to entrainment by passing endosomes, at a frequency of kpass ≈ 1/s [392], in accordance with equation (19).
Flow of cytoplasmic fluids thus constitutes a versatile mechanism for transport across a broad range of length scales. Coordinated patterns of flow can result in the directed delivery of bulk cytoplasmic contents at speeds far higher than those reached by motor-driven transport. Furthermore, flows contribute to mixing of cytoplasmic contents through the formation of gradients smoothed by Taylor dispersion, through Lagrangian stirring, and potentially through the generation of effectively diffusive active motion via stochastic local entrainment events.
5. Perspectives
Over the past decades, many of the molecular components driving transport within eukaryotic cells have been characterized in great detail. Studies of in vitro systems have allowed for a quantitative understanding of the mechanochemical behavior of molecular motors, both individually [379, 380] and in cooperating or competing groups [19, 383, 403, 423]. More recently a plethora of adaptors and regulatory factors modifying either the motor-cargo complex or the cytoskeletal tracks have been identified [20, 427, 430]. In the context of non-directed transport, the effects of crowding [265], filamentous networks [267, 268], and actively contracting gels [517, 518] on particle motion have also been extensively explored in reconstituted systems. However, the behavior of this formidable array of molecular players in the complex and dynamic intracellular environment remains in many ways mysterious. We summarize below some of the main outstanding questions associated with each of the physical transport modes employed by eukaryotic cells.
Perhaps one of the largest outstanding questions pertaining to the stochastic 'Brownian' motion of intracellular particles is the nature of the non-thermal active forces that drive their movements. How much of the apparently diffusive particle motion can be attributed to active contraction of cytoskeletal networks [232, 259], to localized hydrodynamic entrainment [26, 107], or to non-specific microscopic agitation of the medium associated with conformational changes of ATP-burning enzymes [260, 262]? To what extent can decreased mobilities associated with ATP depletion or myosin inhibition be treated as a rigidification of the medium [552, 553] or a reduction in the 'effective temperature' [554] within the cell? Recent studies have begun to tease apart the nature of these delocalized driving forces, separating them out from the continuum rheological properties of the intracellular medium [232, 255]. However, the consequences of this breakdown in the fluctuation–dissipation relationship on the overall cellular-scale transport of molecules and organelles remain unclear.
With regards to motor-driven transport, our understanding of what controls processive run-lengths, pausing, directionality, and track selection in vivo remains incomplete. One of the key unanswered questions is the extent to which cargo sorting and distribution by motor-driven transport is locally self-organized [469] versus guided by external signals such as pre-existing spatial heterogeneity in, e.g., adaptor-binding signaling factors or microtubule-associated proteins [188, 435]. Recent live-cell measurements have begun to identify the role of microtubule intersections in pauses, reversals, and directional switches of moving cargos [2, 445]. However, the contribution of other factors in regulating processivity in vivo remains unclear. Furthermore, the factors that control the particular set of motors recruited to a given cargo, the interaction of those motors under in vivo conditions, and the consequences of motor interactions on cellular-scale cargo delivery remain topics of ongoing research.
The role of fluid flows in driving intracellular transport and mixing is beginning to be appreciated in a widening variety of cell types. While rapid, extensive flows in plant cells, fungi, and slime molds have been the target of extensive study, the contribution of more modest flows in animal cells is now beginning to be unraveled. Cytoplasmic flows help drive the segregation of subcellular components in development [508], generate gradients that establish cell polarity [506], and may enhance the mixing and dispersion of molecules and vesicular organelles [3, 107]. A potential role for flow in driving mixing within reticulated organelles has also been recently proposed [59]. Primary outstanding questions include the extent to which cells can control flow patterns to regulate advective transport and the importance of flow relative to other mechanisms for specific transport systems.
An overarching question of key biological importance is how to draw a quantitative connection between our understanding of transport (i.e.: speed, directional bias, processivity of particle movement) and the kinetics of reactions between cellular components. The roles of confinement in complex morphologies, as well as crowding and medium viscoelasticity, in modulating diffusion-limited reaction rates have been explored theoretically [330, 335, 338, 350]. However the importance of these effects in specific intracellular reaction systems remains unclear. Similarly, the interplay of motor transport, flow, and diffusion [474, 492, 538], as well as the role of cytoskeletal track arrangements [30, 31] in particle delivery and sorting is still an area of active exploration. The contribution of transport limitations to the behavior of complex biochemical reaction networks in eukaryotic cells remains poorly understood, although theoretical studies hint at their qualitative as well as quantitative importance [555, 556].
Ultimately, unraveling the biological consequences of transport, its defects, and its regulation, will require synthesizing our understanding of multiple physical transport mechanisms with newly emerging data on patterns of motion within living cells.
Acknowledgments
We thank Matthias Weiss, Laura Westrate, Christopher Obara, and Jenna Christensen for sharing data prior to publication. This work was supported in part by funding from the NSF CAREER grant PHY-1848057, the Hellman Fellows Fund, and the Alfred P Sloan Foundation, as well as a predoctoral fellowship to SSM from the Visible Molecular Cell Consortium / Center for Trans-scale Structural Biology and Biophysics.