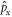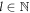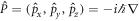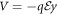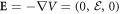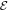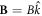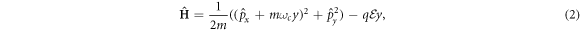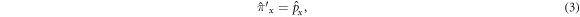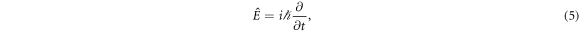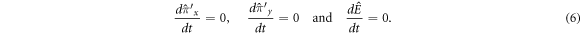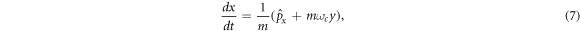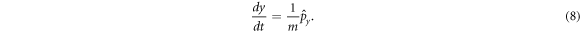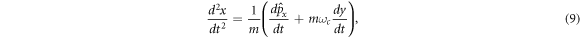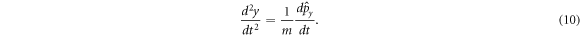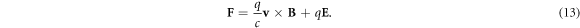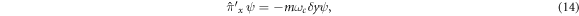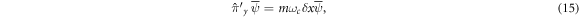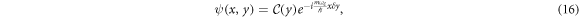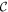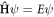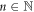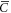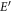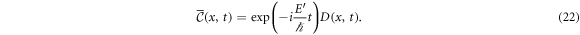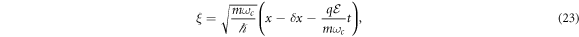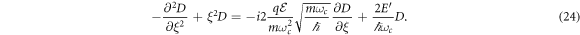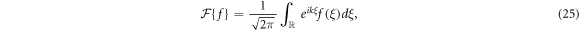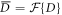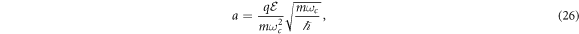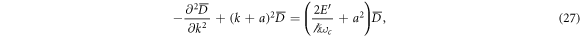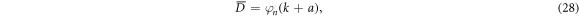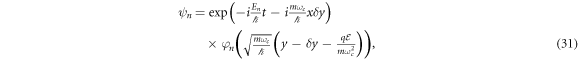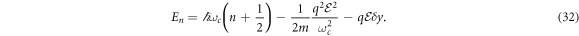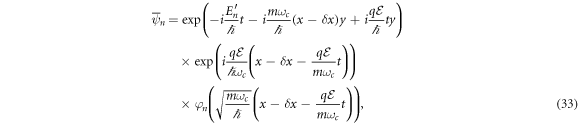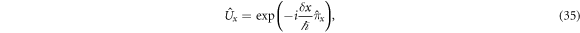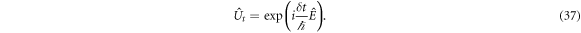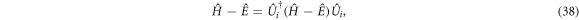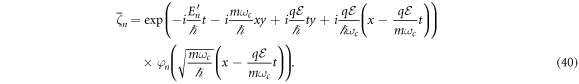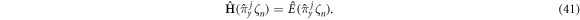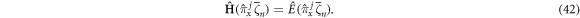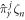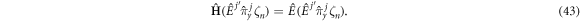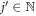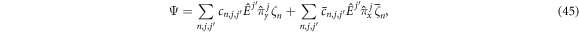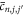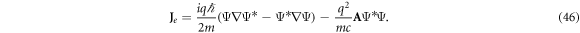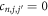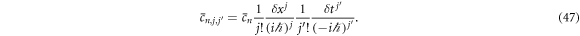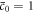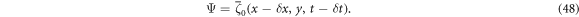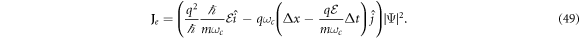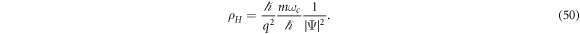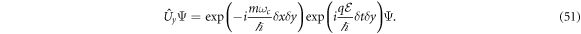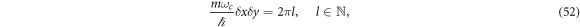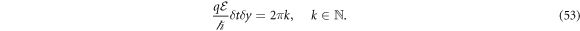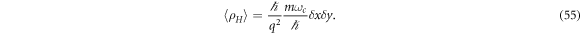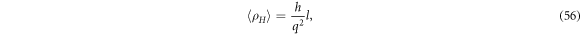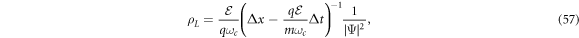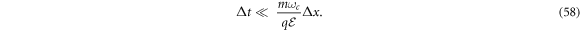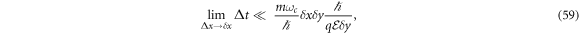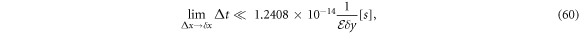Quantization of resistivity as consequence of symmetry invariance

Wave functions for the Schrödinger equation involving a constant electromagnetic field have been obtained using different methods such as perturbation theory [1, 2]. The most common way to solve this equation analytically is by using Landau's ansatz, which is based on the search for conserved operators for the specific choice of gauge and electric potential, leading to a separable variable solution of plane waves along the x-axis (or y-axis) when the magnetic field is described using Landau's gauge, and plane waves along the angular coordinate when the symmetric gauge is used [3–5]. This work focus on the latter case.

The Schrödinger equation for a spinless electron under a constant electromagnetic field is solved, where the magnetic field is described using Landau's gauge and the electric field is perpendicular to it. This configuration conserves the momentum ${\hat{p}}_{x}$ allowing the use of Landau's ansatz. However, to accurately describe the force acting on the particle via Lorentz's law a second conserved operator is necessary. This operator has the characteristic of being time-dependent, leading to an interesting scenario where the wave function cannot be separated into a product of a coordinate-dependent function and a time-dependent function. The conserved operators serve as generators of solutions and determine the system's degeneracy. Furthermore, they define a set of unitary operators that characterize the system's symmetries and facilitate the construction of the general solution, simplifying the identification of the time-dependent ground state. This ground state exhibits quantized resistivity when it remains invariant under a unitary transformation given by the operator equation (36), reminiscent of the experimental findings by Störmer [6]. It is noteworthy that the existence of this ground state, arising from the system's degeneracy, aligns with Tao and Wu's analysis, which accurately quantizes conductance to rational values [7]. It should be pointed out that one can find theoretical hypothesis trying to explain the resistivity quantization of the form ρ = hl/q², where h/q² = 25 812.807 45[Ω] is the Klitzing's constant [8] and $l\in {\mathbb{N}}$ [9–11]. However, these hypotheses primarily aim to determine a ground state wave function for a many-body system, which sometimes is constrained to odd values of l [10]. This constraint poses a challenge when attempting to explain resistivity quantization with even values of l which has been reported experimentally [12–15]. Key contributions of this work are: (1) the demonstration that a single-particle ground state wave function can exhibit quantized resistivity as integer multiples of Klitzing's constant, and (2) the finding that this quantization is not constrained by the parity (odd or even nature) of the index l.

This work is organized as follows: in section 2, the conserved quantities of the Hamiltonian are analyzed, and it is shown that Lorentz's Force for a constant electromagnetic field is recovered when two conserved quantities are considered. Section 3 demonstrates how to obtain solutions for the system using the conserved operators, including Landau's solution and a non-separable variable solution. Section 4 utilizes the conserved operators to analyze the degeneracy of the system and construct the general solution for this problem. Finally, in section 5, a ground state is constructed such that it exhibits a quantized resistivity proportional to integer multiples of the von Klitzing's constant [16].

The Hamiltonian we are interested in is written in CGS units as:

$$\begin{eqnarray}&&\hat{H}=\displaystyle \frac{1}{2m}{\left(\hat{{\bf{P}}}-\displaystyle \frac{q}{c}{\bf{A}}\right)}^{2}+V,\end{eqnarray} \tag{ 1 }$$

where m is the mass of the particle, q is the charge of the particle, c is the speed of light, $\hat{P}=({\hat{p}}_{x},{\hat{p}}_{y},{\hat{p}}_{z})=-i{\hslash }{\rm{\nabla }}$ is the momentum operator, A = (A_x , A_y , A_z ) is the vector potential (or gauge) such that the magnetic field is given by it curl, that is B = ∇ × A and $V=-q{ \mathcal E }y$ is the electric potential such that ${\bf{E}}=-{\rm{\nabla }}V=(0,{ \mathcal E },0)$ where ${ \mathcal E }$ is the electric field intensity. We set our magnetic field such that is parallel to the z axis, ${\bf{B}}=B\hat{k}$, where B is constant and described by the Landau's gauge A = B(–y, 0, 0). From now on we are only interested in the dynamics of the particle in the x − y plane, therefore we set p_z = 0 and A_z = 0. Hence, the Hamiltonian can be written as:

$$\begin{eqnarray}&&\hat{{\bf{H}}}=\displaystyle \frac{1}{2m}\left({\left({\hat{p}}_{x}+m{\omega }_{c}y\right)}^{2}+{\hat{p}}_{y}^{2}\right)-q{ \mathcal E }y,\end{eqnarray} \tag{ 2 }$$

where the cyclotron frequency is defined as ω_c = qB/mc. Then the following operators can be defined

$$\begin{eqnarray}&&\hat{\pi }{{\prime} }_{x}={\hat{p}}_{x},\end{eqnarray} \tag{ 3 }$$

$$\begin{eqnarray}&&\hat{\pi }{{\prime} }_{y}={\hat{p}}_{y}+m{\omega }_{c}x-q{ \mathcal E }t,\end{eqnarray} \tag{ 4 }$$

and

$$\begin{eqnarray}&&\hat{E}=i{\hslash }\displaystyle \frac{\partial }{\partial t},\end{eqnarray} \tag{ 5 }$$

such that all of them are conserved, that is

$$\begin{eqnarray}&&\displaystyle \frac{d\hat{\pi }{{\prime} }_{x}}{{dt}}=0,\quad \displaystyle \frac{d\hat{\pi }{{\prime} }_{y}}{{dt}}=0\quad \mathrm{and}\quad \displaystyle \frac{d\hat{E}}{{dt}}=0.\end{eqnarray} \tag{ 6 }$$

The operator (3) is commonly considered when searching for the basis of the system, as discussed in [4] and related works. However, the operator (4) is also necessary for a full description of the system. This assertion can be demonstrated as follows. The commutation of the positions x and y with the Hamiltonian equation (2) can be calculated and used to determine the first total variation of the coordinates,

$$\begin{eqnarray}&&\displaystyle \frac{{dx}}{{dt}}=\displaystyle \frac{1}{m}\left({\hat{p}}_{x}+m{\omega }_{c}y\right),\end{eqnarray} \tag{ 7 }$$

and

$$\begin{eqnarray}&&\displaystyle \frac{{dy}}{{dt}}=\displaystyle \frac{1}{m}{\hat{p}}_{y}.\end{eqnarray} \tag{ 8 }$$

Then, taking the second total variation of both of the above expressions, one can write

$$\begin{eqnarray}&&\displaystyle \frac{{d}^{2}x}{{{dt}}^{2}}=\displaystyle \frac{1}{m}\left(\displaystyle \frac{d{\hat{p}}_{x}}{{dt}}+m{\omega }_{c}\displaystyle \frac{{dy}}{{dt}}\right),\end{eqnarray} \tag{ 9 }$$

and

$$\begin{eqnarray}&&\displaystyle \frac{{d}^{2}y}{{{dt}}^{2}}=\displaystyle \frac{1}{m}\displaystyle \frac{d{\hat{p}}_{y}}{{dt}}.\end{eqnarray} \tag{ 10 }$$

Substituting the first and second conserved equality of equation (6) in equation (9) and equation (10) respectively,

$$\begin{eqnarray}&&m\displaystyle \frac{{d}^{2}x}{{{dt}}^{2}}=m{\omega }_{c}\displaystyle \frac{{dy}}{{dt}},\end{eqnarray} \tag{ 11 }$$

$$\begin{eqnarray}&&m\displaystyle \frac{{d}^{2}y}{{{dt}}^{2}}=-m{\omega }_{c}\displaystyle \frac{{dx}}{{dt}}+q{ \mathcal E }.\end{eqnarray} \tag{ 12 }$$

These last two equations can be combined into a vectorial form as Newton's second law

$$\begin{eqnarray}&&{\bf{F}}=\displaystyle \frac{q}{c}{\bf{v}}\times {\bf{B}}+q{\bf{E}}.\end{eqnarray} \tag{ 13 }$$

And Lorentz's force is obtained. Hence, both conserved operators (3) and (4) are equally important to fully describe the system.

Once the conserved operators are known, it can be used to define a set of eigenvalue equations that facilitate the determination of the system's basis. For simplicity, we express these equations as:

$$\begin{eqnarray}&&\hat{\pi }{{\prime} }_{x}\psi =-m{\omega }_{c}\delta y\psi ,\end{eqnarray} \tag{ 14 }$$

$$\begin{eqnarray}&&\hat{\pi }{{\prime} }_{y}\overline{\psi }=m{\omega }_{c}\delta x\overline{\psi },\end{eqnarray} \tag{ 15 }$$

where δ x and δ y are real constants. Solving equation (14), one find that

$$\begin{eqnarray}&&\psi (x,y)={ \mathcal C }(y){e}^{-i\tfrac{m{\omega }_{c}}{{\hslash }}x\delta y},\end{eqnarray} \tag{ 16 }$$

where the function ${ \mathcal C }$ can be determined by substituting it in the eigenvalue equation $\hat{{\bf{H}}}\psi =E\psi$ where the Hamiltonian (2) is used. The resulting equation that satisfies this function is the displaced harmonic oscillator as is already known [4]. Therefore, defining the function

$$\begin{eqnarray}&&{\varphi }_{n}(\xi )=\displaystyle \frac{1}{\sqrt{{2}^{n}n!}}{\left(\displaystyle \frac{m\omega }{\pi {\hslash }}\right)}^{1/4}\exp \left(-\displaystyle \frac{{\xi }^{2}}{2}\right){H}_{n}(\xi ),\end{eqnarray} \tag{ 17 }$$

where $n\in {\mathbb{N}}$ and H_n are the Hermite polynomials, the function ${ \mathcal C }$ is

$$\begin{eqnarray}&&{ \mathcal C }(y)={\varphi }_{n}\left(\sqrt{\displaystyle \frac{m{\omega }_{c}}{{\hslash }}}\left(y-\delta y-\displaystyle \frac{q{ \mathcal E }}{m{\omega }_{c}^{2}}\right)\right),\end{eqnarray} \tag{ 18 }$$

being the eigenvalues

$$\begin{eqnarray}&&{E}_{n}={\hslash }{\omega }_{c}\left(n+\displaystyle \frac{1}{2}\right)-\displaystyle \frac{1}{2m}\displaystyle \frac{{q}^{2}{{ \mathcal E }}^{2}}{{\omega }_{c}^{2}}-q{ \mathcal E }\delta y.\end{eqnarray} \tag{ 19 }$$

On the other hand, solving equation (15) gives

$$\begin{eqnarray}&&\overline{\psi }(x,y,t)=\overline{{ \mathcal C }}(x,t)\exp \left(-i\displaystyle \frac{m{\omega }_{c}}{{\hslash }}(x-\delta x)y+i\displaystyle \frac{q{ \mathcal E }}{{\hslash }}{ty}\right),\end{eqnarray} \tag{ 20 }$$

note that in this case, the wavefunction is time-dependent and so is the function $\overline{{ \mathcal C }}$. Therefore, to determine this function, it is necessary to substitute the above wavefunction into the complete Schrödinger equation, $\hat{{\bf{H}}}\overline{\psi }=\hat{E}\overline{\psi }$, instead of the stationary one. By doing so, the following equation is obtained:

$$\begin{eqnarray}&&\displaystyle \frac{1}{2m}\left({\hat{p}}_{x}^{2}\overline{{ \mathcal C }}+{(m{\omega }_{c}(x-\delta x)-q{ \mathcal E }t)}^{2}\overline{{ \mathcal C }}\right)=\hat{E}\overline{{ \mathcal C }}.\end{eqnarray} \tag{ 21 }$$

Even though in the above equation the variables x and t are not longer separable, the function $\overline{C}$ still has the information of the energies of the system (denoted by $E^{\prime}$). Hence, is helpful to rewrite the function as

$$\begin{eqnarray}&&\overline{{ \mathcal C }}(x,t)=\exp \left(-i\displaystyle \frac{E^{\prime} }{{\hslash }}t\right)D(x,t).\end{eqnarray} \tag{ 22 }$$

Substituting this expression in equation (21) and defining the variable

$$\begin{eqnarray}&&\xi =\sqrt{\displaystyle \frac{m{\omega }_{c}}{{\hslash }}}\left(x-\delta x-\displaystyle \frac{q{ \mathcal E }}{m{\omega }_{c}}t\right),\end{eqnarray} \tag{ 23 }$$

an equations for D is obtained

$$\begin{eqnarray}&&-\displaystyle \frac{{\partial }^{2}D}{\partial {\xi }^{2}}+{\xi }^{2}D=-i2\displaystyle \frac{q{ \mathcal E }}{m{\omega }_{c}^{2}}\sqrt{\displaystyle \frac{m{\omega }_{c}}{{\hslash }}}\displaystyle \frac{\partial D}{\partial \xi }+\displaystyle \frac{2E^{\prime} }{{\hslash }{\omega }_{c}}D.\end{eqnarray} \tag{ 24 }$$

Applying Fourier transform, defined as

$$\begin{eqnarray}&&{ \mathcal F }\{f\}=\displaystyle \frac{1}{\sqrt{2\pi }}{\int }_{{\mathbb{R}}}{e}^{{ik}\xi }f(\xi )d\xi ,\end{eqnarray} \tag{ 25 }$$

to this equation, defining $\overline{D}={ \mathcal F }\{D\}$ and the constant

$$\begin{eqnarray}&&a=\displaystyle \frac{q{ \mathcal E }}{m{\omega }_{c}^{2}}\sqrt{\displaystyle \frac{m{\omega }_{c}}{{\hslash }}},\end{eqnarray} \tag{ 26 }$$

one can write down the displaced harmonic oscillator equation in Fourier space

$$\begin{eqnarray}&&-\displaystyle \frac{{\partial }^{2}\overline{D}}{\partial {k}^{2}}+{(k+a)}^{2}\overline{D}=\left(\displaystyle \frac{2E^{\prime} }{{\hslash }{\omega }_{c}}+{a}^{2}\right)\overline{D},\end{eqnarray} \tag{ 27 }$$

whose solutions are again given by equation (17)

$$\begin{eqnarray}&&\overline{D}={\varphi }_{n}(k+a),\end{eqnarray} \tag{ 28 }$$

having the eigenvalues

$$\begin{eqnarray}&&{E}_{n}^{{\prime} }={\hslash }{\omega }_{c}\left(n+\displaystyle \frac{1}{2}\right)-\displaystyle \frac{1}{2m}\displaystyle \frac{{q}^{2}{{ \mathcal E }}^{2}}{{\omega }_{c}^{2}}.\end{eqnarray} \tag{ 29 }$$

The first term on the right-hand side of the above expression represents the usual Landau levels [4], while the second term accounts for the contribution of the nonlinear Stark effect induced by the electric field [17], p. 257–272. It is important to note that the eigenvalues shown in equation (19) include an additional term associated with the linear Stark effect [18]. This term can be interpreted as a consequence of the system's continuous degeneracy due to the parameter δ y. In the next section, it will be demonstrated that this term also arises from a unitary transformation of the wave function, which can be eliminated by performing the transformation with the adjoint operator. However, one more necessary step remains to find the solution in the original variables. This step involves performing the inverse Fourier transform of equation (28). Given that the inverse Fourier transform of a harmonic oscillator is another harmonic oscillator, we can write:

$$\begin{eqnarray}&&D={e}^{{ia}\xi }{\varphi }_{n}(\xi ).\end{eqnarray} \tag{ 30 }$$

Once the process of obtaining the solutions for this system from its conserved properties has been illustrated, it is helpful to compile the results for comparison. From the conserved operator equation (3), one can derive the following wave functions

$$\begin{eqnarray}\begin{array}{rcl}{\psi }_{n} & = & \exp \left(-i\frac{{E}_{n}}{{\hslash }}t-i\frac{m{\omega }_{c}}{{\hslash }}x\delta y\right)\\ & & \times {\varphi }_{n}\left(\sqrt{\frac{m{\omega }_{c}}{{\hslash }}}\left(y-\delta y-\frac{q{ \mathcal E }}{m{\omega }_{c}^{2}}\right)\right),\end{array}\end{eqnarray} \tag{ 31 }$$

having the energies defined as

$$\begin{eqnarray}&&{E}_{n}={\hslash }{\omega }_{c}\left(n+\displaystyle \frac{1}{2}\right)-\displaystyle \frac{1}{2m}\displaystyle \frac{{q}^{2}{{ \mathcal E }}^{2}}{{\omega }_{c}^{2}}-q{ \mathcal E }\delta y.\end{eqnarray} \tag{ 32 }$$

On the other hand, from the conserved operator equation (4), one obtains the following wave functions:

$$\begin{eqnarray}\begin{array}{rcl}{\overline{\psi }}_{n} & = & \exp \left(-i\displaystyle \frac{{E}_{n}^{{\prime} }}{{\hslash }}t-i\displaystyle \frac{m{\omega }_{c}}{{\hslash }}(x-\delta x)y+i\displaystyle \frac{q{ \mathcal E }}{{\hslash }}{ty}\right)\\ & & \times \exp \left(i\displaystyle \frac{q{ \mathcal E }}{{\hslash }{\omega }_{c}}\left(x-\delta x-\displaystyle \frac{q{ \mathcal E }}{m{\omega }_{c}}t\right)\right)\\ & & \times {\varphi }_{n}\left(\sqrt{\displaystyle \frac{m{\omega }_{c}}{{\hslash }}}\left(x-\delta x-\displaystyle \frac{q{ \mathcal E }}{m{\omega }_{c}}t\right)\right),\end{array}\end{eqnarray} \tag{ 33 }$$

where the energies are defined as

$$\begin{eqnarray}&&{E}_{n}^{{\prime} }={\hslash }{\omega }_{c}\left(n+\displaystyle \frac{1}{2}\right)-\displaystyle \frac{1}{2m}\displaystyle \frac{{q}^{2}{{ \mathcal E }}^{2}}{{\omega }_{c}^{2}}.\end{eqnarray} \tag{ 34 }$$

The first difference to note is that equations (31) and (33) involve oscillations along the x-axis and y-axis, respectively. This corresponds with the classical idea that the particle describes a drifted circle. Hence, each wave function can be seen as a projection of this motion along its respective axis. However, there is another notable difference: the system's energies are not exactly the same. Comparing the expressions in equations (32) and (34), one can observe that ${E}_{n}^{{\prime} }-{E}_{n}=q{ \mathcal E }\delta y$. This suggests that there must be an even more fundamental form of the solutions. The conserved operators in equations (3), (4), and (5) can be used to define a set of unitary operators

$$\begin{eqnarray}&&{\hat{U}}_{x}=\exp \left(-i\displaystyle \frac{\delta x}{{\hslash }}{\hat{\pi }}_{x}\right),\end{eqnarray} \tag{ 35 }$$

$$\begin{eqnarray}&&{\hat{U}}_{y}=\exp \left(-i\displaystyle \frac{\delta y}{{\hslash }}{\hat{\pi }}_{y}\right),\end{eqnarray} \tag{ 36 }$$

and

$$\begin{eqnarray}&&{\hat{U}}_{t}=\exp \left(i\displaystyle \frac{\delta t}{{\hslash }}\hat{E}\right).\end{eqnarray} \tag{ 37 }$$

All of the above unitary operators define the symmetries of the system in the Heisenberg picture, meaning that the Schrödinger equation remains invariant under a transformation of the form:

$$\begin{eqnarray}&&\hat{H}-\hat{E}={\hat{U}}_{i}^{\dagger }(\hat{H}-\hat{E}){\hat{U}}_{i},\end{eqnarray} \tag{ 38 }$$

such that i = x, y, t. However, in Schrödinger picture, where the unitary operators are applied to the wave function, one can define ${\zeta }_{n}={\hat{U}}_{y}^{\dagger }{\psi }_{n}$ being

$$\begin{eqnarray}&&{\zeta }_{n}=\exp \left(-i\displaystyle \frac{{E}_{n}^{{\prime} }}{{\hslash }}t\right){\varphi }_{n}\left(\sqrt{\displaystyle \frac{m{\omega }_{c}}{{\hslash }}}\left(y-\displaystyle \frac{q{ \mathcal E }}{m{\omega }_{c}^{2}}\right)\right).\end{eqnarray} \tag{ 39 }$$

Similarly, we can define ${\overline{\zeta }}_{n}={\hat{U}}_{x}^{\dagger }{\overline{\psi }}_{n}$ and write down the function

$$\begin{eqnarray}\begin{array}{rcl}{\overline{\zeta }}_{n} & = & \exp \left(-i\displaystyle \frac{{E}_{n}^{{\prime} }}{{\hslash }}t-i\displaystyle \frac{m{\omega }_{c}}{{\hslash }}{xy}+i\displaystyle \frac{q{ \mathcal E }}{{\hslash }}{ty}+i\displaystyle \frac{q{ \mathcal E }}{{\hslash }{\omega }_{c}}\left(x-\displaystyle \frac{q{ \mathcal E }}{m{\omega }_{c}}t\right)\right)\\ & & \times {\varphi }_{n}\left(\sqrt{\displaystyle \frac{m{\omega }_{c}}{{\hslash }}}\left(x-\displaystyle \frac{q{ \mathcal E }}{m{\omega }_{c}}t\right)\right).\end{array}\end{eqnarray} \tag{ 40 }$$

Both wave functions in equations (39) and (40) are the fundamental solutions of the Schrödinger equation, defined by the Hamiltonian in equation (2), and they have the same energies given by equation (34). This situation arises from the fact that the parameter δ y causes the states to be continuously degenerated. However, there is another discrete degeneracy in this system, which we will now analyze. When it comes to time-independent operators, like equation (3), they are conserved for one of two reasons: (1) because they share a basis with the Hamiltonian, or (2) because they act as eigenfunction generators. On the other hand, the situation with time-dependent conserved operators is analogous, except instead of acting as eigenfunction generators, they generate solutions of the time-dependent Schrödinger equation. This characteristic arises from the fact that a wave function cannot simultaneously share a basis with all operators.

For the wave function equation (39), the generator of solutions is the operator equation (4), i.e. $\hat{{\bf{H}}}({\hat{\pi }}_{y}{\zeta }_{n})=\hat{E}({\hat{\pi }}_{y}{\zeta }_{n})$. This can be easily generalized to any $j\in {\mathbb{N}}$ applications of the operator, that is

$$\begin{eqnarray}&&\hat{{\bf{H}}}({\hat{\pi }}_{y}^{j}{\zeta }_{n})=\hat{E}({\hat{\pi }}_{y}^{j}{\zeta }_{n}).\end{eqnarray} \tag{ 41 }$$

On the other hand, for the wave equation equation (40) the generator of solutions is the operator equation (3) that is

$$\begin{eqnarray}&&\hat{{\bf{H}}}({\hat{\pi }}_{x}^{j}{\overline{\zeta }}_{n})=\hat{E}({\hat{\pi }}_{x}^{j}{\overline{\zeta }}_{n}).\end{eqnarray} \tag{ 42 }$$

The same situation happens with the operator equation (5), when we apply it to a time-dependent wave function. While the application of equation (5) to the wave function equation (39) is elementary, it is not when it is applied to the wave function ${\hat{\pi }}_{y}^{j}{\zeta }_{n}$, since the result is not proportional to the original function. Hence, another set of solutions of the Schrödinger equation is given by applying the conserved operator equation (5) as follows

$$\begin{eqnarray}&&\hat{{\bf{H}}}({\hat{E}}^{j^{\prime} }{\hat{\pi }}_{y}^{j}{\zeta }_{n})=\hat{E}({\hat{E}}^{j^{\prime} }{\hat{\pi }}_{y}^{j}{\zeta }_{n}).\end{eqnarray} \tag{ 43 }$$

such that $j^{\prime} \in {\mathbb{N}}$. Similarly, applying equation (5) to the functions ${\hat{\pi }}_{y}^{j}{\overline{\zeta }}_{n}$, due to the conservation of the operator, one have that

$$\begin{eqnarray}&&\hat{{\bf{H}}}({\hat{E}}^{j^{\prime} }{\hat{\pi }}_{y}^{j}{\overline{\zeta }}_{n})=\hat{E}({\hat{E}}^{j^{\prime} }{\hat{\pi }}_{y}^{j}{\overline{\zeta }}_{n}).\end{eqnarray} \tag{ 44 }$$

Finally, the general solution for this system can be written as

$$\begin{eqnarray}&&{\rm{\Psi }}=\displaystyle \sum _{n,j,j^{\prime} }{c}_{n,j,j^{\prime} }{\hat{E}}^{j^{\prime} }{\hat{\pi }}_{y}^{j}{\zeta }_{n}+\displaystyle \sum _{n,j,j^{\prime} }{\overline{c}}_{n,j,j^{\prime} }{\hat{E}}^{j^{\prime} }{\hat{\pi }}_{x}^{j}{\overline{\zeta }}_{n},\end{eqnarray} \tag{ 45 }$$

where ${c}_{n,j,j^{\prime} }$ and ${\overline{c}}_{n,j,j^{\prime} }$ are constants.

Once we have our general solution, equation (45), it can be used to calculate the electric current produced by it, defined as

$$\begin{eqnarray}&&{{\bf{J}}}_{e}=\displaystyle \frac{{iq}{\hslash }}{2m}\left({\rm{\Psi }}{\rm{\nabla }}{{\rm{\Psi }}}^{* }-{{\rm{\Psi }}}^{* }{\rm{\nabla }}{\rm{\Psi }}\right)-\displaystyle \frac{{q}^{2}}{{mc}}{\bf{A}}{{\rm{\Psi }}}^{* }{\rm{\Psi }}.\end{eqnarray} \tag{ 46 }$$

However, due to the degeneracy of the system, working with the general solution is a challenging task. Nevertheless, we can make two considerations that simplify this situation. One consideration pertains to the structure of the constants involved in equation (45), while the other is based on the assumption that we are interested in the system's properties when it is in its ground state. Considering that when the quantization of the resistivity is observed, the longitudinal resistivity vanishes [6, 12, 16, 19–22], it implies that the particle's motion along the y-axis ceases. This condition implies that ${c}_{n,j,j^{\prime} }=0$. On the other hand, the remaining constants can be chosen such that the unitary operators equations (35) and (37) are recovered, i.e.

$$\begin{eqnarray}&&{\overline{c}}_{n,j,j^{\prime} }={\overline{c}}_{n}\displaystyle \frac{1}{j!}\displaystyle \frac{\delta {x}^{j}}{{(i{\hslash })}^{j}}\displaystyle \frac{1}{j^{\prime} !}\displaystyle \frac{\delta {t}^{j^{\prime} }}{{(-i{\hslash })}^{j^{\prime} }}.\end{eqnarray} \tag{ 47 }$$

Then, since the system is expected to be in its ground state, i.e., ${\overline{c}}_{n}=0$ for all n ≠ 0 and ${\overline{c}}_{0}=1$, the general solution can be written as

$$\begin{eqnarray}&&{\rm{\Psi }}={\overline{\zeta }}_{0}(x-\delta x,y,t-\delta t).\end{eqnarray} \tag{ 48 }$$

Defining Δx = x − δ x, Δt = t − δ t and using equation (46) to calculate the electric current produced by this ground state, one can write down

$$\begin{eqnarray}&&{{\bf{J}}}_{e}=\left(\displaystyle \frac{{q}^{2}}{{\hslash }}\displaystyle \frac{{\hslash }}{m{\omega }_{c}}{ \mathcal E }\hat{i}-q{\omega }_{c}\left({\rm{\Delta }}x-\displaystyle \frac{q{ \mathcal E }}{m{\omega }_{c}}{\rm{\Delta }}t\right)\hat{j}\right)| {\rm{\Psi }}{| }^{2}.\end{eqnarray} \tag{ 49 }$$

By definition, the current per unit of electric field, ${{\bf{J}}}_{e}/{ \mathcal E }$, is equal to the conductivity. It is also noted that, by the way the system was set up, the coordinate along the x-axis represents the Hall conductivity, and the coordinate along the y-axis represents the longitudinal conductivity. Therefore, the Hall resistivity produced by this ground state is

$$\begin{eqnarray}&&{\rho }_{H}=\displaystyle \frac{{\hslash }}{{q}^{2}}\displaystyle \frac{m{\omega }_{c}}{{\hslash }}\displaystyle \frac{1}{| {\rm{\Psi }}{| }^{2}}.\end{eqnarray} \tag{ 50 }$$

As we mention in the previous section, in Heisenberg picture the Schrödinger equation is invariant under the unitary transform given by the operator equation (36). However, in Schrödinger picture, the same transformation acting on the ground state equation (48) leads to

$$\begin{eqnarray}&&{\hat{U}}_{y}{\rm{\Psi }}=\exp \left(-i\displaystyle \frac{m{\omega }_{c}}{{\hslash }}\delta x\delta y\right)\exp \left(i\displaystyle \frac{q{ \mathcal E }}{{\hslash }}\delta t\delta y\right){\rm{\Psi }}.\end{eqnarray} \tag{ 51 }$$

Hence, the ground state is invariant under this unitary transformation only if the following conditions are satisfied

$$\begin{eqnarray}&&\displaystyle \frac{m{\omega }_{c}}{{\hslash }}\delta x\delta y=2\pi l,\quad l\in {\mathbb{N}},\end{eqnarray} \tag{ 52 }$$

and

$$\begin{eqnarray}&&\displaystyle \frac{q{ \mathcal E }}{{\hslash }}\delta t\delta y=2\pi k,\quad k\in {\mathbb{N}}.\end{eqnarray} \tag{ 53 }$$

Equation (52) represents the already known magnetic flux quantization [23], since, substituting the value of the cyclotron frequency and rearranging, it could be rewritten as

$$\begin{eqnarray}&&B\delta x\delta y=\displaystyle \frac{{hc}}{q}l,\quad {\rm{(CGS}}\,{\rm{units)}}\end{eqnarray} \tag{ 54 }$$

where h = 2π ℏ and B δ x δ y is the flux going through an area A = δ x δ y. Hence, calculating the expected value of the resistivity, equation (50), inside this same area leads to the following result

$$\begin{eqnarray}&&\langle {\rho }_{H}\rangle =\displaystyle \frac{{\hslash }}{{q}^{2}}\displaystyle \frac{m{\omega }_{c}}{{\hslash }}\delta x\delta y.\end{eqnarray} \tag{ 55 }$$

Therefore, when this invariant condition is met, the Hall resistivity, equation (55), is quantized in integer multiples of the von Klitzing's constant

$$\begin{eqnarray}&&\langle {\rho }_{H}\rangle =\displaystyle \frac{h}{{q}^{2}}l,\end{eqnarray} \tag{ 56 }$$

On the other hand, whenever the Hall resistivity is quantized it is expected that the longitudinal resistivity, given by the expression

$$\begin{eqnarray}&&{\rho }_{L}=\displaystyle \frac{{ \mathcal E }}{q{\omega }_{c}}{\left({\rm{\Delta }}x-\displaystyle \frac{q{ \mathcal E }}{m{\omega }_{c}}{\rm{\Delta }}t\right)}^{-1}\displaystyle \frac{1}{| {\rm{\Psi }}{| }^{2}},\end{eqnarray} \tag{ 57 }$$

will vanish [6, 16, 20, 22]. From the above expression, one can note that this will happen when the time interval is such that

$$\begin{eqnarray}&&{\rm{\Delta }}t\ll \,\displaystyle \frac{m{\omega }_{c}}{q{ \mathcal E }}{\rm{\Delta }}x.\end{eqnarray} \tag{ 58 }$$

The idea that the longitudinal resistivity vanishes after a given time interval can already be found in the literature as the relaxation time condition [24], p. 498. However, there is a difference with this last expression, and that is that the time interval is bounded.

As an example of the expression equation (56), see [6], when the resistivity is quantized to h/q² it implies that l = 1. Hence, from expression equation (54) the only possible parameter to be determined is the area A = hc/qB. The magnetic field intensity selected is the one at the middle point of the plateau when l = 1, which matches with the linear behaviour of the resistivity, leading to a value of B₀ = 50(kG) and an area of A ≈ 8.27 × 10⁻⁴ μ m². Once the area is calculated it can be used to estimate the middle point of the plateau when 〈ρ_H 〉 = 3h/q², that is for l = 3, using equation (54) one can write B = 3B₀ = 150(kG) which matches with the reported value. At the same time, the condition for the longitudinal resistivity to vanish, equation (58), in the limit when Δx → δ x, can be written as follows

$$\begin{eqnarray}&&\mathop{\mathrm{lim}}\limits_{{\rm{\Delta }}x\to \delta x}{\rm{\Delta }}t\ll \,\displaystyle \frac{m{\omega }_{c}}{{\hslash }}\delta x\delta y\displaystyle \frac{{\hslash }}{q{ \mathcal E }\delta y},\end{eqnarray} \tag{ 59 }$$

or, in the presented example, when l = 3 and h/q = 4.136 × 10⁻¹⁵[J · s/C]

$$\begin{eqnarray}&&\mathop{\mathrm{lim}}\limits_{{\rm{\Delta }}x\to \delta x}{\rm{\Delta }}t\ll \,1.2408\times {10}^{-14}\displaystyle \frac{1}{{ \mathcal E }\delta y}[s],\end{eqnarray} \tag{ 60 }$$

the quantity ${ \mathcal E }\delta y$ (having units of voltage and therefore the time interval is measured in seconds) represents the voltage along the y axis. Even though, this voltage was not reported in [6], it gives an estimated of how small it could be. For instance, a voltage of the order of 10⁻¹⁴[V] it will take ∼1.2[s] to vanish.

The conserved operators of the non-relativistic Hamiltonian with a constant electromagnetic field were analyzed, demonstrating their necessity for a comprehensive description of the system; without them, the Lorentz force for this system cannot be recovered. Utilizing the conserved operators equation (3) and equation (4) solutions to the Schrödinger equation were derived, yielding two fundamental wave functions: one describing oscillations along the y-axis (which corresponds to Landau's solution) and the second oscillating along the x-axis. These two oscillations can be interpreted as projections of the classical drifted circular movement of the particle. Further analysis revealed that these conserved operators establish a discrete degeneracy of the system, which was subsequently utilized to formulate the general solution as a linear combination of all solutions. Finally, a ground state of the single particle was deduced. This state exhibits quantized Hall resistivity as integer multiples of the von Klitzing's constant if it remains invariant under the unitary transform of the operator defined in equation (36). Additionally, it was shown that the longitudinal resistivity vanishes when the time interval condition in equation (58) is satisfied.

This work was supported by the DGAPA-UNAM Postdoctoral Program (POSDOC).

All data that support the findings of this study are included within the article (and any supplementary files).