Abstract
The collapse of man-made and natural structures is a complex phenomenon that has been studied for centuries. Existing models often focus on a 'critical point' where failure becomes imminent. This work presents a radically different perspective: large earthquakes may not arise from critical states, but instead develop dynamically from the subcritical regime as rare, extreme events. Our approach hinges on an extension of Onsager's reciprocal theorem, allowing us to delve into this subcritical realm. We demonstrate that within such a regime, excitable systems, like those underlying earthquakes, are dynamically renormalised towards a nonlocal equilibrium. For these systems, the maximum entropy production of at least two interacting phases is used to replace the local equilibrium assumption for the subcritical state. Typically, dissipative processes at larger scales arrest these self-amplifying feedbacks. However, in rare instances, they can morph into intricate tensor networks of instabilities that ripple from microscopic scales to the entire system, culminating in an extreme event like a catastrophic earthquake. This novel framework offers a potentially deeper understanding of earthquake precursors and paves the way for exploring earthquake prediction based on the statistics of subcritical dynamics.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The analysis of catastrophic instabilities in man-made and natural systems has long occupied a central role in various scientific disciplines. While the traditional focus has emphasized critical points as the attractors of collapse [1], a gap remains in our understanding of instabilities that erupt from the subcritical regime [2], in the form of short-lived extreme events [3]. In this contribution we investigate the possible dynamics emerging out of the subcritical regime where the material is in a state below the critical point, which from the perspective of criticality is simplified as a stable deformation mode. While the scale-free characteristics of the Gutenberg Richter relationship suggests self-organized criticality, more refined statistical analyses of worldwide earthquakes [2] emphasised the role of subcritical behaviour, suggesting that fault networks mainly evolve far from a critical point, which has major implications for the prediction of large events. In the self-organized critical scenario, each event is no different from all others, making prediction impossible. However, if the fault network remains far from criticality, more sporadic singularities may appear, potentially allowing for the prediction of upcoming catastrophic events. This implies that, in addition to the well established concept of self-organized criticality, a different statistical behaviour of abnormal phenomena may exist, which could be analysed as precursors to large earthquakes [4].
The new concept of dynamic events out of subcritical behaviour postulates that the dynamics of fault networks are most of the time not in a critical state [2], with renewed opportunities for potential forecasting of large earthquakes. If fault networks are not in a critical state, then it may be possible to predict large earthquakes by looking for sporadic singularities. This finding motivated our research focusing on precursor instabilities that may occur in the subcritical regime, before the main earthquake event. We hence follow the recent call for analysing pre-earthquake processes, which requires a multidisciplinary approach to earthquake prediction studies [5].
This work presents a novel framework for studying such events, investigating the subcritical regime as the potential root cause of catastrophic instabilities. The framework provides a semi-analytical approach for the investigation of the transition from subcritical, dissipative processes spinning out into a cascade of events across multiple physics and multiple scales for which we propose a tensor network architecture. This was so far only accessible to numerical studies with billions of degrees of freedom or statistical analyses [6]. Such studies of the subcritical regime were carried out, for instance, in aqueous sediment gravity flows, driven by the density difference between the heavy fluid and the clear water above [7]. Turbulence operating initially at grain-scale level can intermittently cascade to hundreds of kilometers, and the flow instability can last for several days [7]. We propose here to generalize a generic framework for reaction-cross-diffusion (RXD) processes [8], which have been shown to capture the interplay between spatial transfer, kinetics, and multiphysics coupling, in order to understand and model the emergence of extreme events out of the subcritical regime. The RXD versatility and adaptability of explicitly connecting space and time make them an essential tool for understanding the underlying mechanisms governing complex systems across various scientific disciplines. Specifically, an extended RXD framework is proposed for understanding multiscale coupling across multiphysics fields. These fields each have their own self-diffusion length scale, and coupling between at least two internal processes is proposed to be characterized by their own cross-diffusion length scale. The concise mathematical form of the RXD framework leverages the proven ability of reaction-diffusion formulations to capture the spatial dynamics, emergent behaviour, cross-field coupling, and adaptability that are essential for understanding the complexities of nonlinear systems.
The special significance of the RXD formulation is that it allows investigation of the microscopic processes in the subcritical regime. Conventional critical point models often assume stable states. However, if we admit the possibility that earthquakes originate in the subcritical regime, where fluctuations exist and stability is not guaranteed, different outcomes are expected. The nonlocal equilibrium concept of the RXD formulation acknowledges this by maximizing entropy production within interacting phases, capturing a more realistic subcritical state. Specifically, earthquakes are thought to involve interactions between various phases (e.g., solid rock, fluids). The nonlocal equilibrium framework inherently considers these interactions, unlike traditional critical point models that often focus on single-phase systems or multi-phase systems characterised by the local equilibrium assumption.
Here, we propose to extend the RXD framework to account for the distinct properties and interactions between multiple physical processes. The extension is considering a hierarchical structure which enables handling of complex geometries and multiscale interactions. These interactions refer to problems involving coupled physical phenomena like heat transfer, mass transfer, and chemical reactions. Choosing a hierarchical structure allows for efficient representation of the system at different scales, from microscopic to macroscopic. Tensor trees offer compact mathematical tools used to represent and manipulate multidimensional data, including stress and strain tensors, crucial for capturing the feedback processes between different physical processes. They are also suitable for capturing the anisotropic behaviour of materials. In the present manuscript we remain, however, in the isotropic space for simplicity.
Recently [9–11] demonstrated the emergence of instability networks in controlled systems analogous to earthquakes (e.g., granular media, high porosity solids). These experiments exhibit features similar to the tensor networks proposed in this study, such as multiscale propagation and amplification of fluctuations. These dynamic systems are prone to non-reciprocal phase transitions where in addition to the classical self-organisation out of equilibrium, synchronisation, flocking and pattern formation are encountered in a wide range of systems such as networks of neurons, social groups, directional interface growth phenomena and metamaterials [12].
Our findings offer a fresh perspective on the genesis and predictability of catastrophic instabilities. By shifting the focus from critical points to the subcritical regime, we pave the way for the development of novel early warning systems and mitigation strategies. The mathematical framework presented here provides a potent tool for analyzing diverse systems vulnerable to extreme events, ranging from engineered structures and power grids to geological processes, ecosystems, biological, social, and even financial networks.
Without restricting the proposed framework to a particular use case, we illustrate the novel concept and discuss a prime example of multiphysics and multiscale interactions. We investigate the phenomenon of seismicity as a fast instability that is part of extremely slow background deformation processes in the Earth. These are driven by plate velocities of the order of cm/year. Earthquakes are rare events thought to involve multiple microscopic Thermo-HydroMechanical-Chemical (THMC) processes such as rock-fluid interactions [13], chemical reactions or mineral breakdown [14] and thermally-activated friction [15]. The intricate interactions of micro- and macro-scale processes in multiphase materials like geomaterials make them a formidable challenge for study. Deciphering how these forces interact across scales remains a hurdle, even casting doubt on the possibility of physics-based earthquake forecasting [1].
While earthquake prediction may still reside on the horizon, examining such multiscale instabilities can serve as a powerful thought experiment. It allows us to delve into the underlying physics of these materials, where internal structures can trigger cascading instabilities across all scales. This paper takes geomaterials as an example, which are often two-phase systems (i.e., a porous rock with voids filled with fluid) undergoing complex dynamic processes under natural or engineered stresses. The processes envelop a spectrum of scales: system size, inherent fractures, microscopic features, and even the characteristic length scales of internal couplings within the material itself. Our aim is to establish a systematic approach that seamlessly links coarse-grained, larger-scale dynamics with explicit micro-scale feedback mechanisms. Traditionally, computational mechanics has spearheaded the effort to understand these intricate systems. Techniques like multiscale homogenization methods [16] and multiphysics phase field simulations [17] have provided valuable insights. However, the quest for a comprehensive framework that fully captures the intricate interplay between scales remains ongoing.
Leveraging on a novel RXD formulation for poromechanics [9, 18–21], we propose a fresh perspective for multiscale interactions. This framework provides insights into dynamic meso-scale processes through a thermodynamic Ansatz, akin to the phase field approach [17], but assigns a physical meaning to the internal length scale. Unlike a typical assumed value, this scale emerges from meso-scale interactions within the multiphase system. Importantly, the nonlocality of the cross-diffusion formalism enables semi-analytical bridging between micro-mechanical interactions and large-scale behaviour. We proceed by summarizing our proposed nonlocal extension of the Onsager-Casimir theorem, followed by introducing cross-diffusion waves as subcritical bifurcations and, finally, the proposition of earthquake events as spectral collapses of these cross-diffusion waves.
2. The non-local Onsager's reciprocal theorem and parity-time processes
In an earlier contribution [9], we investigated multiphysics feedback processes for which the Onsager reciprocal theory provides a phenomenological approach of coupling several dissipative processes. Onsager conceived a linear relationship between the generalised flux Ji and the gradient of a generalised thermodynamic force Xj . The dot product of the transpose flux matrix JT i and the force vector Xj defines the local irreversible entropy production. The thermodynamic force is the thermodynamic potential difference e.g., Thermal, Hydro, Mechanical, or Chemical (THMC) resulting in generalised thermodynamic flux described through e.g., Fourier (T)-, Darcy (H)-, Fick (C)- and solid matrix pressure (M)- diffusion laws where the diffusion coefficients Lij are denoted by the coupled processes.
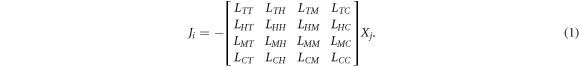
The time-symmetric state of the irreversible entropy production is described by Onsager-Casimir thermodynamic reciprocal probability statement [22, 23] of the relaxed system (non-equilibrium steady state):
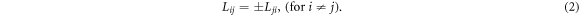
Onsager's reciprocal theorem [22] has been used in a variety of fields such as chemistry, solid mechanics, biology, and geophysical fluid dynamics. The principle delivers phenomenological constitutive laws describing quasi-steady states of the dissipative process based on Rayleigh's 'principle of the least dissipation of energy'.
The force-flux relationship in solid-like materials is, however, often nonlinear and in addition, it is necessary to use Ziegler's orthogonality principle to constrain the constitutive relationship between forces and fluxes [24] defined by the Maximum Entropy Production of the product of forces and fluxes, formulating the basics of so-called 'Thermomechanics'. Ziegler's orthogonality principle is in turn, a special case of a Hermitian Hamiltonian system. Hermiticity requires that the system eigenvalues must be real; its eigenstates are orthogonal with each other and the set of all its eigenfunctions is complete. Ziegler's Thermomechanics theory is restricted to thermostatic conditions. The thermostatic assumption can be relaxed by defining a thermal reference state in local equilibrium [25]. The Hermitian assumption leads to a dissipative steady state defined by the diagonalization of the diffusion matrix, where all cross-diffusion coefficients are zero in the canonical form [26]. This implies that a linearly coupled THMC system can simply be written and solved as a set of independent equations if a local equilibrium exists and the system can be described by a Hermitian Onsager Matrix. When considering, however, the discrete dissipation process at micro-mechanical level the Hermitian matrices disguise the nonlocal entropy production by using an adiabatic elimination of the cross-coupling coefficients.
A closer inspection shows that in some regions of the parameter space, adiabatic elimination is possible and the eigenvalues are real; however, in some other regions, cross-couplings are important and the eigenvalues are complex conjugate. As highlighted in [8] in this region an oscillatory relaxation of any small perturbation to the equilibrium state is expected, even in the absence of a reaction. If the cross-diffusion process is coupled with a reaction, this oscillatory response leads to the formation of an 'active zone' in which the microphysics reactions can form propagating network structures well-known from 'active matter' [9].
In order to analyse the reaction-diffusion cross-couplings from a micro-mechanical perspective, we performed coarse-graining of the Langevin equation between two tightly coupled microprocesses and found it necessary to relax the local equilibrium assumption of Onsager's reciprocal theorem [9]. Onsager's concept is restricted to the ideal assumption of complete isolation of the local system from its surrounding environment. However, in many THMC systems, the feedback between multiphysics processes inevitably requires the exchange of energy with their environment. A local microreversible system can thus at best be described as an extreme end-member of a more general non-local microreversible system. An example of such a non-local system might be fluid flow in a porous matrix in interaction with the compaction of the solid matrix. Using the concept of dynamic renormalization of active zones [27] we showed that there exists a diffusion-regularized optimal solid-fluid transport phenomenon described by a skew-symmetric Onsager constitutive operator. The skew symmetry captures the opposite directions of mass transfer between two coupled feedback processes (e.g. compaction of the solid matrix driving fluids in the opposite direction). If both processes reach a quasi-steady state over a common non-local diffusive length scale, the process itself becomes independent of time. Associated with this time symmetry there is a mirrored space symmetry, i.e. a parity operation in space where the spatial coordinates of the two interacting species have a flip in sign of the spatial coordinates.
This is also known as a Parity-Time PT symmetry [28]. PT systems have the interesting property that there exists a point in the parameter space where the real valued eigenvalues and eigenvectors of the Hamiltonian coalesce and they can become complex conjugate at which point the Hermitian system becomes a non-Hermitian system. This branching from a Hermitian operator to a non-Hermitian one occurs at the Exceptional Point (EP) [29] which acts as a threshold for the transition from a PT-symmetric phase (with real eigenvalues) to a PT-broken phase (with complex eigenvalues). The branching phenomenon at the exceptional point in PT systems may be seen as a solution to the problem of macroscopic irreversibility stemming from microscopic reversibility, also known as Loschmidt's paradox [30] as the system can feature two different realities: (local reversible) Hermitian or (local irreversible) non-Hermetian realities depending on the value of a bifurcation variable. The role of EP's lays the foundation for generalizing the theory of critical phenomena [31] to non-Hermitian systems [12]. In this generalization exceptional points are understood as spontaneously breaking the PT symmetry to dynamically restore self-organization into three archetypal out of equilibrium structures: synchronization, flocking, and pattern formation [12].
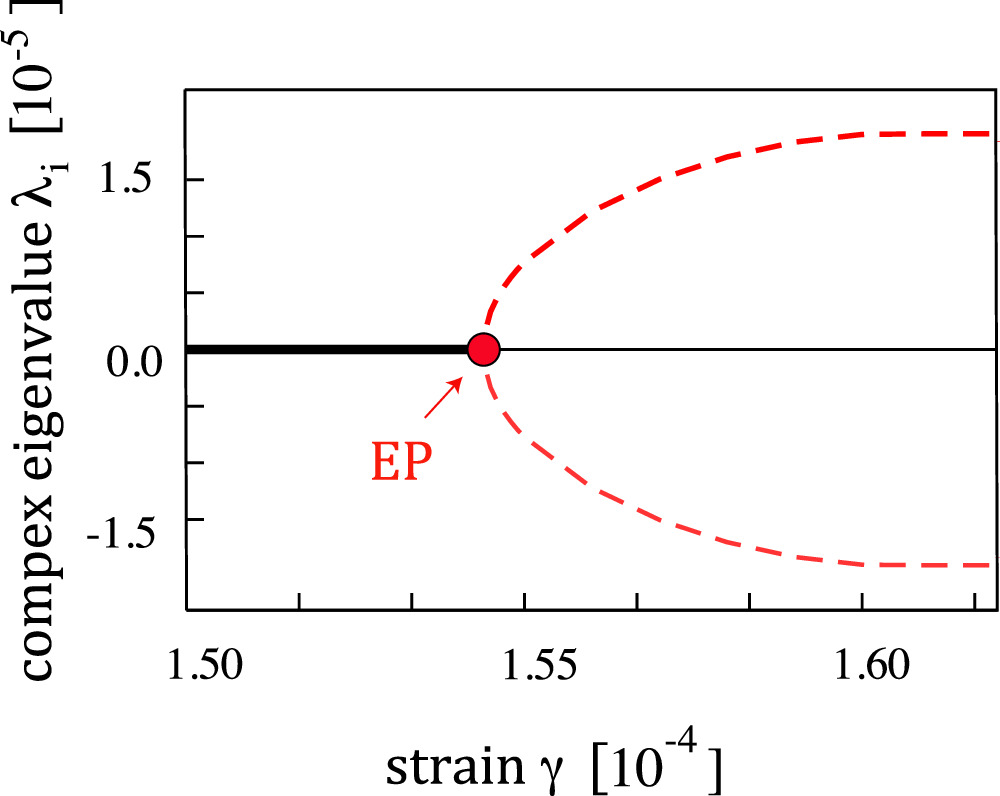
The physics of the EP is most actively studied in quantum systems for laser optics, electromagnetism, atomic and molecular physics, quantum phase transitions, quantum chaos and more [33]. In classical system the phenomenon of the nucleation of complex eigenvalues was perhaps first described in 1986 [34] to explain the physics of thermal Rossby wave in oceans which can nucleate in rotating fluids with significant horizontal temperature gradients. These waves propagate along the direction of the temperature gradient, typically eastward in the Earth's oceans. Another well-known fluid dynamic instability is the fingering instability which can travel at a constant speed when the system reaches complex conjugate eigenvalues [35]. In solid mechanics the nucleation of complex conjugate eigenvalues has been attributed to flutter instabilities preceding macroscopic failure [36]. Recently, numerical experiments based on Molecular Dynamics Simulation (LAMMPS) with frictional materials revealed the exceptional point phenomenon in a solid mechanical system [32]. The frictional material has real valued eigenvalues at low strain and behaves like a Hermetian system. However, at the EP, defined by a critical strain, the frictional grains exhibit an exchange of energy with their environment, and the system responds by an oscillatory exponential growth of perturbations at granular level. This non-Hermitian deformation mode is characterized by the nucleation of complex eigenvalues at the EP (figure 1).
Figure 1. Frictional granular matter, when driven past a critical strain γ, experiences a transition past the exceptional point [EP] where granular oscillatory excitations are characterized by conjugate complex eigenmodes. Modified after [32].
Download figure:
Standard image High-resolution imageSince the solution can be written as ![$\exp \left(-i{\lambda }_{n}t\right)=\exp \left[-i\mathrm{Re}\left({\lambda }_{n}\right)t\right]\exp \left[\mathrm{Im}\left({\lambda }_{n}\right)t\right]$](https://content.cld.iop.org/journals/1402-4896/99/5/055019/revision2/psad36f2ieqn1.gif) the granular medium shows an oscillatory motion with an exponential growth wavelength λn
for any deviation from a state of mechanical equilibrium, and the second pair is an exponentially decaying wavelength. The pitchfork bifurcation in figure 1 is a classic example of a transition from Hermitian to a non-Hermitian system at a critical control parameter (here the strain). The transition is marked by a stable solution with a real eigenvalue to an oscillatory solution with complex eigenvalues at the EP.
the granular medium shows an oscillatory motion with an exponential growth wavelength λn
for any deviation from a state of mechanical equilibrium, and the second pair is an exponentially decaying wavelength. The pitchfork bifurcation in figure 1 is a classic example of a transition from Hermitian to a non-Hermitian system at a critical control parameter (here the strain). The transition is marked by a stable solution with a real eigenvalue to an oscillatory solution with complex eigenvalues at the EP.
3. The exceptional point in THMC systems
In the context of the above example, the conditions for the exceptional points are spectral degeneracy and the breakdown of the diagonalizability of the Onsager operator. The possibility of the nucleation of an oscillatory instability in frictional materials at the exceptional point was proposed to be relevant to the physics of earthquakes [32]. The authors of the experiment shown in figure 1 argue that the self-amplification of small perturbations at the exceptional point might be the micromechanical reason for the phenomenon of dynamic weakening through acoustic fluidisation, observed in geophysical experiments [37]. However, they stipulate that the study of the behaviour of frictional disks does not include the rich multiphysis of the Earth and its faults. In this contribution, we put forward a proposition that can overcome this limitation.
We suggest that it is possible to couple the multiphysics THMC matrix through reduction to multiple degeneracy of exceptional points where the complex eigenvalues of paired microprocesses coalesce. The concatenation of bipartite couplings is an essential feature of the physics of exceptional points, which are connected through N(N − 1) square-root exceptional branch points in the complex plane [33]. A minimum of N = 2 processes is required with complex eigenvalues Em and En , where each of these can be connected to the next nearest singularity through further conjugate pairs of N eigenvalues.
The far from equilibrium dynamic state for the nucleation of earthquake instabilities is exemplified by the THMC coupled processes, seen as a multi-scale and multiphysics array defined by the contraction of multiple coupled processes forming a tensor network. This Riemann sheet structure of a bilinear general vector space describes the reference frame of the multiple interacting microprocesses with a symplectic basis. A system-scale extreme event is triggered for the multiscale, THMC symplectic reference case where the excitation phenomena can synchronise across scale.
4. Network reduction of the multiscale THMC tensor network
In a recent contribution, we have presented the criterion for nucleation of non-Hermitian complex eigenmodes for a candidate earthquake trigger in subduction zones, based on a micro-mechanism capable of pumping fluids into the fault zone [9]. Coarse graining of the micromechanism resulted in an Onsager matrix with non-local cross-couplings. The cross-coupling coefficients were found to be functions of the dynamic interactions between the THMC processes. The exact way in which the different microprocesses may interact in a multiscale scenario was not discussed.
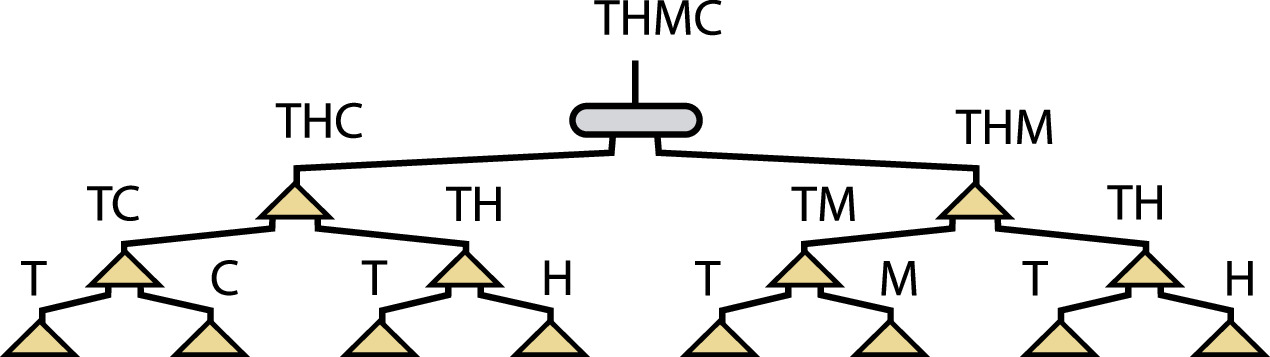
Here, we propose to extend the theory by a multiscale tensor network [38] in order to allow hierarchical connections of individual Riemann sheet structures of the multiphysics processes. The lowest level of the tensor network is defined by the uncoupled individual thermodynamic T, H, M and C reaction-self-diffusion equations. The next level up considers bipartite coupling by introducing cross-diffusion coefficients in the RXD equation. For the binary couplings of cross-reactions, we propose a particular hierarchy. However, we note that each problem may have its own hierarchy of processes supported by variant tensor network structures, including possible disentangler operations between branches at each scale [38]. This depends on the specific configuration, the proximity of their complex-valued energy eigenstates, and the growth or decay nature of their eigenstates at the exceptional point. For earthquake physics, it may also be useful to include electrical processes, as electro-chemical reactions may be important. As an example of a candidate earthquake mechanism, we assume the feedback of chemical (serpentinite breakdown) and a mechanical reaction (Griffith microcracking) as the resulting largest-scale feedback process of the hierarchical tree.
Choosing Fourier's law as the basis, we start by coupling individual HMC- processes with a T-reaction diffusion equation, thus defining the dissipative ground state of the multiphysics-coupled problem. This implies that other possible direct couplings like CM or HM request the participation of temperature as a degree of freedom and are thereby implicit in the second level. Therefore, the first level of paired couplings leads to reaction-cross-diffusion equations represented by 2 × 2 skew symmetric tensors TC, TH, TM which form the lowest level of binary non-local couplings. It is assumed here that one or more of these binary coupled states is in a state where a small perturbation can trigger a spectral collapse phenomenon, in which a group of interacting cross-diffusion waves condense their energy into a localized, singular point within the spectrum.
Multiple mechanisms for such a dramatic energy concentration are known for interacting nonlinear dispersive waves. In optics, fluid dynamics and plasma physics, spectral collapse can be caused by either a modulation instability, dispersive wave breaking, Brillouin backscattering, resonant interaction, or nonlinear wave collisions, leading to merging and focusing of the energy of nonlinear dispersive waves into a solitary standing wave [39]. The analytically tractable solution for the simple case of the Nonlinear Schrödinger equation is a typical solution and will be discussed later. The important point for the network reduction is the assumption that spectral collapse allows wave energy from binary coupled processes at small scale to be pumped up to a larger scale, such that the perturbations out of the subcritical regime are amplified and focused in space and time.
The second-level nodes labeled THC and THM may receive these large deviations and result in the 3 × 3 matrices in equations (3) and (4). This example defines the candidate coupled microprocesses that may lead for a critical state (here, a critical strain) to an exceptional point phenomenon for the nucleation of multiscale complex eigenstates of the THMC problem. A cascade of oscillatory, excited material states is proposed to exist that is capable of synchronizing and communicating the amplification of small perturbations across scales, increasing their energy level as they climb through the hierarchical network. The delicate interplay between subcritical fluctuations, nonlocal equilibrium, and the explosive cascade of instabilities that defines a true catastrophic event is defined by spectral collapse for all or at least a single space-time coupled THMC cascade of candidate microphysics processes discussed in figure 2. The THMC coupled system is described at the highest level as a THC and THM coupled system with coupling between following skew-orthogonal Onsager matrices having cross-coupled, nonlocal, bipartite processes LTH = − LHT and LTM = − LMT thus using identities of the skew coefficients the 3 × 3 matrices are:
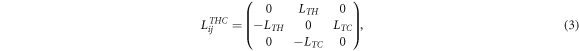
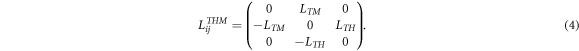
Figure 2. Illustration of a multiscale hierarchical Tucker tensor network. These networks retain multiscale information in coarse graining networks in physics and are here applied for coupling THMC reaction-diffusion transport processes. [38] proposes an inverse application to for adaptive learning of multiscale features from data. We have adapted figure 2 of [38] to the forward problem of a THMC network and propose a coupled forward-inverse data assimilation approach allowing the identification of multiscale dynamic coefficients of the RXD equations. The coupled nodes represent tensors, and the lines represent the binary connection forming the higher-level tensor nodes. Each of the legs connects the individual branches of a Riemann sheet structure [33].
Download figure:
Standard image High-resolution imageWe can reduce the network structure further by considering only the highest-level binary coupling between THC and THM processes (figure 2), assuming that lower-level couplings have reached their excited state and have synchronized spectral collapse so that they can supply energy to the two highest-level in a highly focused event in space and time.
While this defines the candidate internal processes, an additional assumption is the consideration of the large-scale boundary condition. For this, we consider only slow slip of low magnitude and do not consider TM coupling that can contribute to significant heating on the fault plane during rupture [40]. If we are interested in the precursor phenomena to the catastrophic failure, we may assume a steady state for the temperature implying that Onsager's local thermal equilibrium assumption holds for the thermal state, justifying a Thermomechanics approach where a reference temperature is chosen to simplify the equations [25]. This allows the elimination of the temperature from the THC and THM binary couple. We end up with a reduced HC and HM binary coupled matrix. If we further on assume that the cross-diffusion processes involving chemical reactions have reached their activation threshold and can be coarse-grained into a fluid reaction term, we may simplify the problem to a hydromechanically coupled 2 × 2 (HM) Onsager matrix where the self- and cross-diffusion coefficients are now effective coefficients incorporating the physics of lower-level couplings.
5. Hydromechanics (HM) binary-coupling and large scale instabilities
Hydromechanical coupling is often encountered in civil engineering applications (foundation analysis), geodynamic processes triggered by mineral dehydration reactions, hydro-poro-mechanics research for energy resource extraction (geothermal, oil & gas), CO2-sequestration and groundwater flow. It considers the intertwined response of a fluid and the solid porous medium it interacts with. This interaction arises from the mutual influence of fluid pressure and mechanical deformation on each other. Increased fluid pressure within the pores of the solid medium can lead to expansion and deformation of the medium. This can induce changes in volume, shape, and stress distribution within the solid. The relationship between fluid pressure and mechanical deformation is often nonlinear and can include nonlocal gradients of solid and fluid mass exchange, particularly at high-frequency responses. However, at low frequencies, nonlinear interactions can also appear when the solid phase is stressed past the plastic limit and responds through a nonlinear viscous slow creeping flow mechanism known as the Perzyna overstress plasticity [41].
While, due to the slow deformation of the matrix, inertial terms can often be neglected the creeping flow assumption makes it impossible to use the local equilibrium assumption of Biot's poromechanics. Biot's poromechanics assumption makes the solutions more tractable for analysis by collapsing the two partial differential equations (pde's) for pore fluid and solid matrix pressure into a single equation by using just one pressure field variable. This is achieved by using Biot's poro-elastic coefficient, that characterizes the stress transferred to the solid skeleton in a fully saturated medium and is equivalent to the Terzaghi effective stress formulation.
The creeping flow assumption is often used in geodynamic applications [42] to simplify the analysis of the deformation of the solid matrix, which is interpreted as a highly viscous fluid. However, the low frequency interactions encountered in the competition between the two governing pde's representing the skeleton as a nonlinear high viscosity fluid, and the linear low viscosity pore fluid are poorly explored. The specific consideration of the nonlinear interaction between the two phases opens the possibility for a wide range of instabilities such as porosity waves, cnoidal wave instabilities, ductile fracture, damage mechanics, cavitation, fluid channelling instabilities and other two-phase phenomena [18, 43–48] not covered by the classical geomechanics theories.
By extending Onsager's approach to such nonlocal interactions we have combined meso-scale biphasic models that include cross-reactions and cross-diffusion with a macro-scale continuum described by the familiar self-diffusion and reaction processes. We therefore separate out two interacting pressures: the overstress 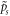 in the solid skeleton and the fluid stress
in the solid skeleton and the fluid stress  respectively, in the RXD framework. We assume a nonlinear power series expansion for the reaction term of the solid high viscosity matrix including a cross-reaction term for the fluid phase
respectively, in the RXD framework. We assume a nonlinear power series expansion for the reaction term of the solid high viscosity matrix including a cross-reaction term for the fluid phase 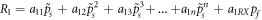 . Empirical creep laws of rocks often can be truncated at third order expansion but exponential creep laws may also require consideration of higher orders [49]. For the pore filling fluid phase we assume, similar to the reaction-diffusion equations in chemical systems [8], a linear reaction term
. Empirical creep laws of rocks often can be truncated at third order expansion but exponential creep laws may also require consideration of higher orders [49]. For the pore filling fluid phase we assume, similar to the reaction-diffusion equations in chemical systems [8], a linear reaction term 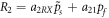 , where a2RX
is a linear cross-reaction source term stemming from the fluid release of the solid phase and a21 is the linear fluid pressure source term.
, where a2RX
is a linear cross-reaction source term stemming from the fluid release of the solid phase and a21 is the linear fluid pressure source term.
We nondimensionalise the system of equations by introducing following parameters: 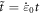 ,
, 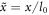 ,
, 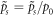 ,
,  , where
, where 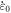 , l0, p0 are the reference strain rate, reference length, and reference stress, respectively. The RXD expanded to third order now reads:
, l0, p0 are the reference strain rate, reference length, and reference stress, respectively. The RXD expanded to third order now reads:
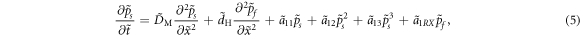
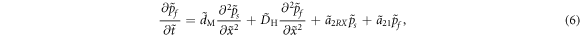
The normalized self- and cross- diffusion coefficients are expressed as: ![${\tilde{D}}_{{\rm{M}}}={D}_{{\rm{M}}}/[{{l}_{0}}^{2}{\dot{\varepsilon }}_{0}]$](https://content.cld.iop.org/journals/1402-4896/99/5/055019/revision2/psad36f2ieqn11.gif) ,
, ![${\tilde{D}}_{{\rm{H}}}={D}_{{\rm{H}}}/[{{l}_{0}}^{2}{\dot{\varepsilon }}_{0}]$](https://content.cld.iop.org/journals/1402-4896/99/5/055019/revision2/psad36f2ieqn12.gif) ,
, ![${\tilde{d}}_{{\rm{H}}}={d}_{{\rm{H}}}/[{{l}_{0}}^{2}{\dot{\varepsilon }}_{0}]$](https://content.cld.iop.org/journals/1402-4896/99/5/055019/revision2/psad36f2ieqn13.gif) ,
, ![${\tilde{d}}_{{\rm{M}}}={d}_{{\rm{M}}}/[{{l}_{0}}^{2}{\dot{\varepsilon }}_{0}]$](https://content.cld.iop.org/journals/1402-4896/99/5/055019/revision2/psad36f2ieqn14.gif) , and the normalized reaction coefficients are
, and the normalized reaction coefficients are 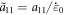 ,
, 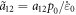 ,
,  ,
,  ,
,  ,
,  .
.
5.1. Linear stability analysis
The proposed system of the RXD (equations (5) and (6)), describing the porous material behaviour in the creeping flow regime, are high-order nonlinear partial differential equations, for which no exact analytical solutions can be obtained. We therefore perform a linear stability analysis by applying a small perturbation (noted with *) around the steady state, denoted as ( ,
, 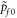 )=(0, 0):
)=(0, 0):
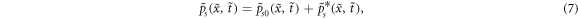
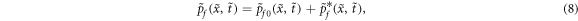
The perturbation (in solid and fluid pressures) satisfies the linearized version of the above-described cross-diffusion equations:

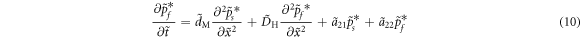
where 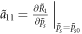 ,
, 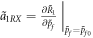 ,
,  ,
,  are the first order derivatives of the normalized reaction terms.
are the first order derivatives of the normalized reaction terms.
By applying a space Fourier transformation, the perturbation can be written as:

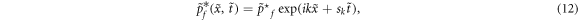
where k denotes the wavenumber in space, sk denoting the growth rate of the perturbation. Substituting equation (11) and equation (12) into equation (9) and equation (10), we have
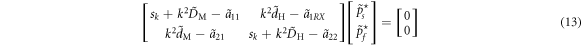
which leads to the condition
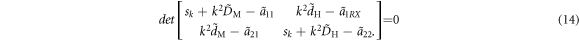
From equation (14), the characteristic equation of the growth rate sk is derived as
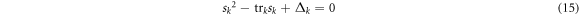
where 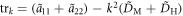 and
and  . The solution of equation (14) is expressed as:
. The solution of equation (14) is expressed as:
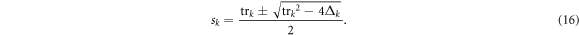
The linear stability analysis identifies three different types of instabilities of the Jacobian matrix for small changes in the state of a system: (1) supercritical Hopf bifurcations, (2) Turing bifurcations and (3) cross-diffusion waves.
The supercritical Hopf bifurcation belongs to the group of bifurcations that develop as a pitchfork at the EP as illustrated in figure 1. When crossing the EP a stable state turns into a periodic orbit characterized by complex conjugate eigenmodes, where the imaginary part of the complex conjugate eigenvalues determines the frequency of the oscillations in the periodic orbit. The Hopf bifurcation has a maximum real valued amplification 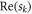 of the complex valued perturbation at zero wavenumber k, i.e. it is controlled by the system size. If the real value is positive a stable orbit is obtained and an autonomous oscillator can be identified.
of the complex valued perturbation at zero wavenumber k, i.e. it is controlled by the system size. If the real value is positive a stable orbit is obtained and an autonomous oscillator can be identified.
This type of instability has therefore been used to model the characteristic periodic oscillatory signal recorded by GPS stations on subduction zones, which are known as Episodic Tremor and Slip (ETS) instabilities [21]. Fitting of the time-series observation has successfully been used to invert reaction rates (fluid-release reactions from minerals) on the slipping interface [21]. We would like to emphasize at this point that this class of instability has the property of focusing wave energy in time and not in space.
Turing bifurcations are also controlled by the system size but do not display oscillatory behaviour in time as their imaginary parts remain zero. They develop a standing wave pattern, turning a stable homogeneous state into a stable patterned state by focusing wave energy into the pattern. Because of their stable nature in time, they are the most widely recognized structures in nature that are attributed to reaction-diffusion processes. In porous geological media, these features are known as 'deformation bands' and in pure compression, as 'compaction bands'. Compaction bands have been described through the elimination of the cross-diffusion terms as the cnoidal wave solution of the Korteweg-de-Vries (KdV) equation [50]. This type of instability can focus wave energy in space and not in time.
Cross-diffusion wave instabilities, also known as quasi-solitons [51], are a special class as they mostly have complex conjugate eigenmodes, but some quasi-solitons can also have purely real eigenmodes. They are best studied in quantum and plasma physics [52] where true soliton behaviour is understood to represent idealized models of stable localized structures. Quasi-solitons, on the other hand, feature the richness and complexity of real-world systems. What makes them different is their dispersive nature, expanding and contracting as they propagate, and their unusual response to collisions, where they can interact with each other like quasi-particles, leading to mergers, collisions, and fluctuations in their shape and energy. They can combine both features for energy focusing from Turing and Hopf bifurcation. Their capability to focus wave energy in both space and time makes them an attractive proposition for explaining the nucleation of extreme events [53].
6. Extreme events controlled by cross-diffusion
The dynamic system in equations (5) and (6) transforms for specific dynamic Onsager coefficients into the nonlinear-Schrödinger equations [19]. These conditions are, for instance, met when fluids are captured in solid phases and heated, leading to a propensity to escape from the heated dense solid matrix. Tight binary coupling between solid and fluid pressure  and
and  is required to enable dewatering. This is a plausible situation in a subduction environment where surface fluids are absorbed into the downgoing slab and form the solid serpentinite group minerals of a dense (no-porosity) matrix. If the slab enters the thermal regime where the mineral becomes metastable, the fluid can only be released through tight coupling between mechanical dilatancy and fluid flow, first observed by Osborne Reynolds who called the phenomenon 'dilatancy pumping' [54, 55].
is required to enable dewatering. This is a plausible situation in a subduction environment where surface fluids are absorbed into the downgoing slab and form the solid serpentinite group minerals of a dense (no-porosity) matrix. If the slab enters the thermal regime where the mineral becomes metastable, the fluid can only be released through tight coupling between mechanical dilatancy and fluid flow, first observed by Osborne Reynolds who called the phenomenon 'dilatancy pumping' [54, 55].
Assuming a hydro-elastic process for opening the void space for fluids we imply that the self-diffusion coefficients Lii
= 0 of the matrix are not contributing to the process. The matrix is impermeable (LHH
= 0, no Darcy diffusivity) and the viscous deformation of the matrix is not important (LMM
= 0), as we are considering a perfectly elastic micromechanism for dilatancy. A special situation arises, when the cross-diffusion coefficients are maximised and set to opposite sign 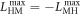 which is what is required to draw the maximum available power out of the exothermic system of serpentinite breakdown reactions. This results in the following equations for the evolution of solid and fluid pressures:
which is what is required to draw the maximum available power out of the exothermic system of serpentinite breakdown reactions. This results in the following equations for the evolution of solid and fluid pressures:
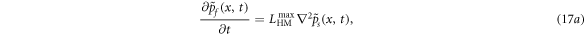
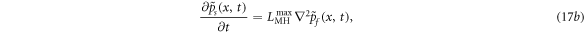
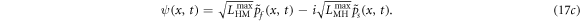
where ψ(x, t) denotes the wave function of solid and fluid pressures. As the self-diffusion coefficients are neglected the nonlinear-Schrödinger (NLS) equation becomes an extreme form of the cross-diffusion equation. This phenomenon is well known in photonics, where it can explain optical rogue waves [56], however, its analytical self-focusing 1-D solution in the x-direction was first given by [57] who applied it to weakly nonlinear water waves. The soliton solution is:
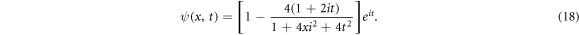
The self-focusing wave appears from low background oscillations over a very long wavelength. The rogue-wave phenomenon develops out of these localised pulses converting them into a plane wave soliton with spatial and temporal compression of wave energy by sampling energy from the far field. An illustration of such a self-focusing wave of serpentinite breakdown for a low-amplitude long-wavelength perturbation is shown in figure 3.
Figure 3. Applying a small perturbation (e.g., the largest Earth tidal signal M2) onto a maximally cross-coupled metastable serpentinite system defined by equation (17). The resulting Peregrine soliton amplifies the power of the wave through extreme self-focusing of wave energy in space and time. The Peregrine soliton solution [57] has provided a robust explanation for rogue wave observations in various materials. For the application to the subduction problem in Cascadia we propose to continue monitoring and inversion of evolving dynamic parameters of the RXD equation. In a preliminary study [21] the characteristic periodic oscillatory signal recorded by GPS stations has been shown to allow derivation of the reaction rates and cross-diffusion coefficients. If in the future the cross-diffusion coefficients evolve towards maximum values the M2 tidal [58] forcing (blue curve) may be sufficient to trigger the Peregrine soliton as a self-focusing wave in space and time of fluids creating a large earthquake.
Download figure:
Standard image High-resolution image7. Discussion
This paper presents the first application of non-local micromechanical coupling to explain earthquake mechanisms. We focus on the highest-level feedback loops within the dilatancy pumping mechanism, acknowledging potential complexities like additional exceptional point phenomena influencing fluid injections (tremor events). These sustained, very low-frequency tremors often accompany low-frequency earthquakes and aseismic fast episodic slip events detected by GPS [59]. Interestingly, the time series of these GPS-recorded episodic slow slip events resemble the behaviour of autonomous supercritical Hopf oscillators.
The RXD equations (5)and (6)) predict supercritical Hopf-oscillators across the entire parameter space of positive reactive source terms, suggesting their prevalence in earthquake dynamics. We extracted cross-diffusion parameters by fitting Cascadian GPS data, capturing a supercritical Hopf bifurcation with a 13.4-month repeat period [21]. This observation, coupled with evidence for tidally-triggered low-frequency earthquakes (LFEs) in Cascadia, leads to a novel explanation for Cascadian mega-earthquakes. If LFEs represent smaller energy release earthquakes for the same underlying mechanism as larger ones, we can propose an extreme event scenario involving networks of synchronized LFEs.
This scenario envisions a slab-wide dehydration event triggered by tidal forces. This event would generate a pulsed fluid surge towards the Peregrine wave crest, effectively lubricating the entire plate interface and potentially triggering a Cascadian mega-earthquake. Such an event, with a repeat time ranging from centuries to millennia [60], would explain the otherwise aseismic nature of the Cascadia margin outside these catastrophic occurrences. The youngest buried soil, preserved in tidal marsh deposits near the estuary mouth of the Coquille river in southwestern Oregon, records that the last big event struck in A.D. 1700 [60].
High-resolution geophysical data opens doors to exploring finer-grained space-time scales for earthquake dynamics. Future work should focus on analyzing the multiscale energy eigenstates within the entire THMC tensor network in figure 2. Expanding the network to incorporate electrical reaction-diffusion processes (THMCE) could further refine our understanding. This candidate tensor network (or variants thereof) can be viewed as a hypergraph for potential earthquake source physics, suitable for hypothesis testing and data assimilation techniques. Such techniques could reveal how energy released from LFEs cascades across scales, ultimately triggering large earthquakes.
Synchronization of exceptional points with positive exponential growth is crucial for extreme events. Conversely, close proximity between complex conjugate pairs, which can cancel each other, should be avoided to prevent disengagement of branches in figure 2. For earthquake mechanisms, the connection between multiscale energy levels and their potential to release work and trigger global elastic energy release on the future fault plane is of particular interest. Positive multilevel coupling can achieve ultra-high peak amplitudes [61] of the multilevel NLS soliton solution shown in figure 3. Such amplification may be expected if positive coupling is achieved in the earthquake mechanism hypergraph (figure 2).
The theory is based on minimising the rate function of probabilities for the relative entropy, also known as Sanov's theorem. It reveals that spontaneous noise-induced stochastic events are possible where the Onsager cross-diffusion coefficients can for extremely short-lived extreme events, become the driving mechanism of the instability from the subcritical regime. The success of such an approach relies on accurately estimating the rate function which requires detailed knowledge of the underlying system dynamics for which this paper has proposed a candidate mechanism. To take this further, we need advanced geophysical sensors like fiber optics or electrical sensors if THMCE feedback is considered useful for forecasting. These could detect early warning signals for large events potentially nucleating from the unpredictable subcritical regime as revealed by recent statistical analyses of large earthquakes [2].
Experimental evidence for the newly identified dynamic response in the subcritical regime of driven disordered systems is difficult to obtain for earthquake systems. We have, however, already proceeded to test the predictions in controlled laboratory experiments with compaction experiment on granular media (snow) and high porosity solids (carbonates) to test theoretical predictions of the new theory [9].
Thermodynamic-based upscaling of the feedback between the reacting constituents in such systems identified the role of an entropic velocity that regularises the propagation of deformation bands and successfully solves problems in matching experimental data of compaction of high porosity carbonates with the existing modified Cam-Clay plasticity models [10]. The theoretical work also predicted a new form of dissipative waves which were identified in experiments with compacting snow [11].
While the earthquake example is a simplified illustration, the RXD framework is broadly applicable across diverse fields like geomechanics, materials science, and even biology. For practical applications, the 1-D model can be extended to higher dimensions and even incorporate higher-order pde's, offering a richer mathematical playground for exploring theoretical concepts and complex wave phenomena in nonlinear, dissipative media. This special volume provides valuable tools and novel ideas to delve deeper into such analyses.
For instance, investigating the slow evolution of amplitude and phase in dispersive waves might necessitate higher-order pde's. The second-order NLS equation serves as an envelope equation for the integrable third-order KdV-Benjamin-Bona-Mahony equation. This equation is useful for analyzing long waves with small amplitudes in plasma physics, fluids, and other weakly dispersive media [62]. Similarly, the reduced Jimbo-Miwa equation, another third-order pde, is used to study long waves in shallow water, internal fluids, and weakly nonlinear elastic media [63]. For analyzing nonlinear waves in higher spatial dimensions, like multi-rogue waves, the 2 + 1 dimensional Fokas equation offers a powerful tool [64]. This equation can be reduced to the NLS in one dimension.
8. Summary and conclusions
This paper proposes a novel theory for earthquake mechanisms, drawing on non-local micromechanical coupling and reaction-diffusion equations (RXD). It offers an alternative explanation for phenomena previously attributed to self-organized criticality, including supercritical Hopf oscillations and low-frequency earthquakes (LFEs). Specifically, the theory suggests that reaction-cross-diffusion processes drive these behaviours.
While recognizing the model's mathematical simplicity as a strength, the authors acknowledge potential limitations. Simplifying assumptions might overlook crucial complexities of real earthquakes. Gathering experimental evidence for the proposed subcritical dynamics in Earth systems presents a significant challenge. However, initial tests in controlled laboratory experiments with analogous materials have shown promise. Further research is necessary to address dynamic changes in material properties and validate the theory using higher-dimensional models. Additionally, the proposed prediction method based on the statistics of excitable systems in the subcritical regime requires detailed knowledge of the underlying earthquake dynamics, which may not always be readily available. The study serves as a pilot demonstration of the RXD formalism's potential to identify precursor events leading to catastrophic failures. The bipartite coupled RXD equations bridge the gap between microscopic feedback processes and macroscopic material response. They reveal how cross-diffusion feedback loops trigger subcritical cross-diffusion (quasi-soliton) waves that propagate through the material, potentially paving the way for failure. As the dissipation in the subcritical regime is expected to modify the material properties the dynamic coefficients of the RXD could also change for continued deformation. Monitoring and inverting these coefficients to detect conditions favourable for the Peregrine wave may serve as a first step towards earthquake forecasting (see figure 3).
While future work is proposed to address the dynamic changes in material properties, this study establishes a general framework for identifying multiphysics feedback processes that can cascade into subcritical instabilities across scales. The introduced tensor networks serve as useful tools for mapping potential pathways for these global instabilities. Furthermore, the study demonstrates how cross-diffusion coefficients dictate the dynamics of these instabilities within multiphase systems and, under specific conditions, can ultimately lead to catastrophic failure.
Acknowledgments
We acknowledge the support of the Research Grant Council of Hong Kong (ECS 27 203 720 and GRF 17 206 521) and the Australian Research Council (ARC DP170104550, DP170104557, DP200102517, LP170100233). We would also like to thank Qinpei Sun for calculations shown in figure 3.
Data availability statement
No new data were created or analysed in this study.