Abstract
A mapping from the triaxial rotor Hamiltonian to that of the O(6) limit in the interacting boson model (IBM) is established, which is achieved by introducing the symmetry-conserving high-order interactional terms The validity of the proposed mapping scheme is further examined for the cases with γ = 0 and γ = π/6, respectively. It is shown that the rotor model results can be well reproduced in its O(6) image especially for the low-spin states. It thus provides an alternative way to understand the triaxiality in the finite-N systems and additional insight into the O(6) IBM theory.
Export citation and abstract BibTeX RIS
1. Introduction
The quantum rotor model plays an important role in elucidating rotational excitations in quantum many-body systems [1–4]. How to understand the rotor dynamics in finite nuclei has attracted considerable attentions since the seminal works of Elliott opened the door to a microscopic explanation of rotational spectra in light systems [5, 6]. Based on the similarity in algebraic relations [7], it was shown that dynamics of the quantum rotor can be well realized from the SU(3) image of the shell model [8–10]. Similarly, algebraic realization of the rotor dynamics was also achieved in the SU(3) limit of the interacting boson model (IBM) [11] and an exact mapping scheme for the IBM realization has been established [12] by analogy with that in the SU(3) shell model [8]. Recently, the mapping scheme was further applied to explain the anomalous E2 transitions in neutron-deficient nuclei [13]. All these demonstrate new understanding of the rotor dynamics in a system of interacting fermions (nucleons) or bosons (nucleon pairs) from the SU(3) symmetry [14].
Intrinsic deformation (axial or triaxial) is thought to be a precondition of generating rotational spectrum, which is in turn considered as the quantum mechanics manifestation of intrinsic deformation of a many-body system [15]. In the IBM [16], different intrinsic deformations will be generated by different interactional terms, which are all constructed in terms of two kinds of boson operators, namely the s boson with Lπ = 0+ and the d boson with Lπ = 2+. For example, the angular momentum operator and quadrupole operator in the IBM can be constructed by
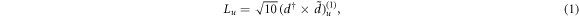
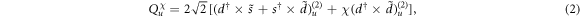
where χ is a control parameter with  and χ = 0 indicating the definition given in the SU(3) and O(6) limit, respectively. Then, axially symmetric deformation with γ = 0° or γ = 60° can be well recognized at the mean-field level from the two-body Q · Q interaction in the SU(3) limit. In contrast, triaxial deformation with 0° < γ < 60° cannot be generated by any IBM Hamiltonian up to two-body interaction. A valid way of generating triaxiality in the IBM is to include high-order interactions [17]. Specifically, the potential energy surface with a stable, triaxial minimum at γ = 30° can be produced by the cubic term
and χ = 0 indicating the definition given in the SU(3) and O(6) limit, respectively. Then, axially symmetric deformation with γ = 0° or γ = 60° can be well recognized at the mean-field level from the two-body Q · Q interaction in the SU(3) limit. In contrast, triaxial deformation with 0° < γ < 60° cannot be generated by any IBM Hamiltonian up to two-body interaction. A valid way of generating triaxiality in the IBM is to include high-order interactions [17]. Specifically, the potential energy surface with a stable, triaxial minimum at γ = 30° can be produced by the cubic term  [17]. The influence of this term on the IBM spectra have been studied in detailed [18–20]. It has been also revealed [21] that a parameter region of triaxiality with 0° < γ < 60° would be allowed if the cubic combination of Q operators,
[17]. The influence of this term on the IBM spectra have been studied in detailed [18–20]. It has been also revealed [21] that a parameter region of triaxiality with 0° < γ < 60° would be allowed if the cubic combination of Q operators, ![${[{Q}^{\chi }\times {Q}^{\chi }\times {Q}^{\chi }]}^{(0)}$](https://content.cld.iop.org/journals/1402-4896/99/1/015305/revision2/psad16b3ieqn3.gif) , is added to the well-known consistent-Q Hamiltonian [22]. Note that this extended consistent-Q Hamiltonian can not only be applied to generate triaxial deformation at given parameters but also hold a very rich shape (deformation) phase structure, which provides a new angle to see triaxiality from the point of shape phase transition [21]. Along this way, there would be more chances to generate triaxial deformations in the IBM if higher-order terms are allowed. However, triaxial deformation at mean-field level may be not a sufficient condition for producing triaxial rotor dynamics. It has been shown [11, 12] that realizing a triaxial rotor in the SU(3) limit of the IBM may need terms like (L × Q × L)(0), which contributes nothing to intrinsic deformation in the large-N limit [12, 13]. Since algebraic realization of the rotor dynamics has been established in the SU(3) limit of the IBM, whether a similar construction can be achieved in the other IBM systems such as the O(6) limit would be an interesting question. Traditionally, understanding of the O(6) limit is often limited to two-body terms [23], which may generate the spectra corresponding to the γ-unstable model of Wilets and Jean [24] rather than the rigid rotor model of Dovydov and Filippov [4]. In fact, it has been justified [25, 26] that the cubic term (Q × Q × Q)(0) in the O(6) limit can produce a new type of axially rotational spectrum different from those in the SU(3) limit [16], while the analysis in [27] indicates that the
, is added to the well-known consistent-Q Hamiltonian [22]. Note that this extended consistent-Q Hamiltonian can not only be applied to generate triaxial deformation at given parameters but also hold a very rich shape (deformation) phase structure, which provides a new angle to see triaxiality from the point of shape phase transition [21]. Along this way, there would be more chances to generate triaxial deformations in the IBM if higher-order terms are allowed. However, triaxial deformation at mean-field level may be not a sufficient condition for producing triaxial rotor dynamics. It has been shown [11, 12] that realizing a triaxial rotor in the SU(3) limit of the IBM may need terms like (L × Q × L)(0), which contributes nothing to intrinsic deformation in the large-N limit [12, 13]. Since algebraic realization of the rotor dynamics has been established in the SU(3) limit of the IBM, whether a similar construction can be achieved in the other IBM systems such as the O(6) limit would be an interesting question. Traditionally, understanding of the O(6) limit is often limited to two-body terms [23], which may generate the spectra corresponding to the γ-unstable model of Wilets and Jean [24] rather than the rigid rotor model of Dovydov and Filippov [4]. In fact, it has been justified [25, 26] that the cubic term (Q × Q × Q)(0) in the O(6) limit can produce a new type of axially rotational spectrum different from those in the SU(3) limit [16], while the analysis in [27] indicates that the  term can generate a γ = 30° triaxial rotor spectrum. It is thus expected that an algebraic realization of the quantum rotor model may be alternatively achieved in the O(6) limit of the IBM.
term can generate a γ = 30° triaxial rotor spectrum. It is thus expected that an algebraic realization of the quantum rotor model may be alternatively achieved in the O(6) limit of the IBM.
In this work, we will construct an O(6) IBM image of the triaxial rotor Hamiltonian. The resulting mapping scheme is supposed to work for any quadrupole systems.
2. Algebraic image of the quantum rotor
The symmetry group of the quantum rotor for the quadrupole system [7] is the semidirect product, T5⨂sSO(3), where T5 is an Abelian group generated by the mass quadrupole moment operator  and SO(3) is the rotational group generated by the angular momentum operator Lu
. Here, the superscript 'c' is appended to denote collective model operator [8]. The Lie algebra are accordingly denoted by t5⊕sso(3). The relevant operators are defined as
and SO(3) is the rotational group generated by the angular momentum operator Lu
. Here, the superscript 'c' is appended to denote collective model operator [8]. The Lie algebra are accordingly denoted by t5⊕sso(3). The relevant operators are defined as
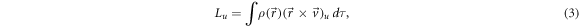
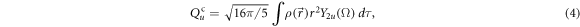
where  represents nuclear mass density and the integration is over the whole nuclear volume. It can be proven that these operators satisfy the commutation relations [7]
represents nuclear mass density and the integration is over the whole nuclear volume. It can be proven that these operators satisfy the commutation relations [7]
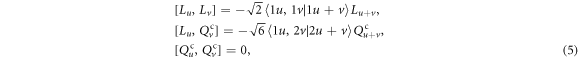
which define the algebraic structure of t5⊕sso(3).
The irreducible representations (IRREPs) of a given group are often characterized by the eigenvalues of the Casimir operators, which are defined as the independent functions of the group generators that commute with all the generators. For T5⨂sSO(3), the Casimir operators are [9]
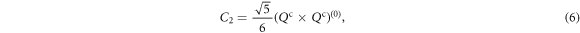
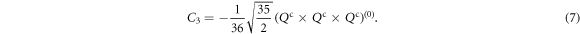
In the body-fixed, principal-axes system, the eigenvalues are given by
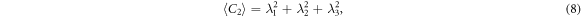
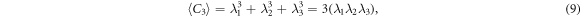
where λα
with α = 1, 2, 3 (or x, y, z) are the expectation values of the quadrupole matrix in the principal-axes system with  . Here, Qc is a traceless matrix with λ1 + λ2 + λ3 = 0, by which one can prove the last equation shown in (9). λα
are related to intrinsic deformation of a given system with their values solved from the cubic equation [28]
. Here, Qc is a traceless matrix with λ1 + λ2 + λ3 = 0, by which one can prove the last equation shown in (9). λα
are related to intrinsic deformation of a given system with their values solved from the cubic equation [28]

The real solutions can be expressed in a unified form [9] with
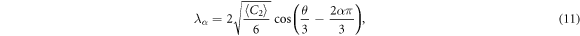
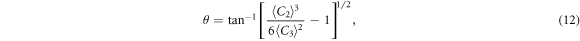
where 〈C2〉3 ≥ 6〈C3〉2 is required to guarantee the real solutions. Clearly, if one can find a way to determine 〈C2〉 and 〈C3〉, λα can be directly read from (11).
The Hamiltonian of rigid quantum rotor can be generally written by [4]
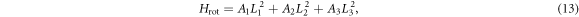
where Lα
is the projection of the angular momentum onto the α-th body-fixed principal axis and Aα
is the corresponding inertia parameter. If Aα
≠ Aβ
for α ≠ β, the Hamiltonian (13) describes an asymmetric top, while symmetric top corresponds to a case with two of Aα
(α = 1, 2, 3) being equal. The rotor Hamiltonian is invariant under the rotations by 180° about the three principal axes. These rotations denoted by  together with the identity operator E generate the dihedral group (D2). The invariance means [Hrot, Tα
] = 0 [8, 9]. Wavefunctions that carry the IRREPs of the D2 group can be constructed by a combination of Wigner D-functions with the four IRREPS denoted by A, B1, B2 and B3, respectively. For even–even nuclei, only the A-type representation is allowed [8]. Then, the eigenfunction of Hrot can be solved from diagonalizing the Hamiltonian in the A-type basis [29]
together with the identity operator E generate the dihedral group (D2). The invariance means [Hrot, Tα
] = 0 [8, 9]. Wavefunctions that carry the IRREPs of the D2 group can be constructed by a combination of Wigner D-functions with the four IRREPS denoted by A, B1, B2 and B3, respectively. For even–even nuclei, only the A-type representation is allowed [8]. Then, the eigenfunction of Hrot can be solved from diagonalizing the Hamiltonian in the A-type basis [29]
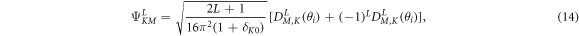
in which  are the Wigner D-functions of Euler angles θi
with i = 1, 2, 3. In addition, the rotor model has been also treated in other ways [30–33] and extended to describe the spectral properties of odd-A nuclei [34–36] especially those of high-spin states.
are the Wigner D-functions of Euler angles θi
with i = 1, 2, 3. In addition, the rotor model has been also treated in other ways [30–33] and extended to describe the spectral properties of odd-A nuclei [34–36] especially those of high-spin states.
On the other hand, one can construct three frame-independent scalars [8–10]
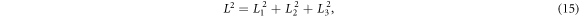
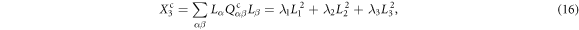
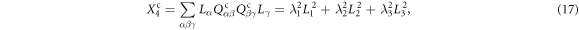
where Lα
and  are the cartesian form of Lu
and
are the cartesian form of Lu
and  introduced in (3) and (4). The last expression in each equation is obtained from the body-fixed, principal axes system. With the spherical tensor formulas,
introduced in (3) and (4). The last expression in each equation is obtained from the body-fixed, principal axes system. With the spherical tensor formulas,
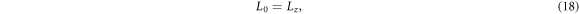
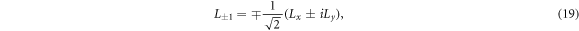
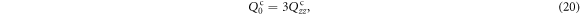
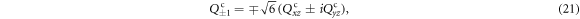
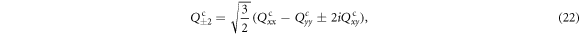
the three scalars can be further expressed as
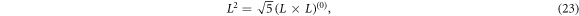
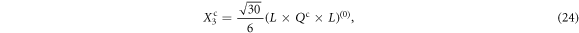
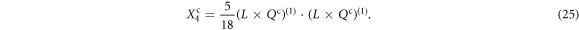
Based on equations (15)–(17), one can derive that
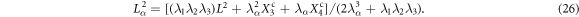
Accordingly, the rotor Hamiltonian (13) can be rewritten as
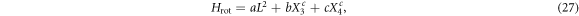
in which the parameters a, b, and c will be determined from the inertia parameters Aα and the eigenvalues of Qc via
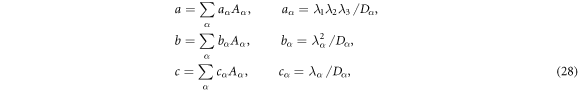
and

In short, the rotor model Hamiltonian has been exactly expressed as a frame-independent form as shown in (27), which contains only the scalar function of L and Qc. This is just the so-called algebraic realization of the triaxial rotor, which suggests an alternative way to understand the rotor dynamics in a finite system.
3. New mapping scheme for the rotor model
An SU(3) algebraic realization of the triaxial rotor was achieved by replacing L and Qc with the SU(3) group generators, L and Q [8–10]. The su(3) algebraic relation is given as
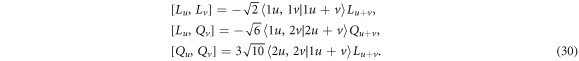
If rescaling Q with Q/〈C2[SU(3)]〉, the su(3) algebraic relation given in (30) will contract to that of the t5⊕sso(3) shown in (5) for λ, μ ≫ L. Here, C2[SU(3)] is the second-order Casimir operator of the SU(3) group with (λ, μ) used to label the SU(3) IRREPs. Specifically, the Casimir operators are defined as [11]
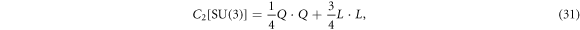
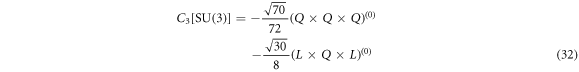
with their eigenvalues given by
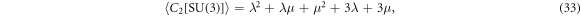
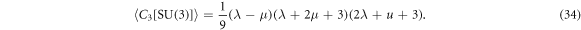
A relation between (λ, μ) and λα was derived [9] by invoking a linear mapping between the invariants {〈C2〉, 〈C3〉} for T5⨂sSO(3) and {〈C2[SU(3)〉, 〈C3[SU(3)〉} for SU(3). It is given by
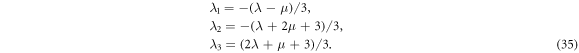
Then, the SU(3) image of the rotor Hamiltonian have the same functional form as in (27) but with {L, Qc} replaced by the SU(3) group generators, {L, Q}. In addition, a simple relation between the SU(3) IRREP and the triaxial deformation parameter was also established [9] and given by
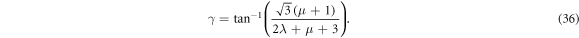
Although an SU(3) realization of the rotor dynamics can be abstracted from (27) through the replacement {L, Qc} → {L, Q}, the resulting Hamiltonian does not contain any information of nuclear deformation, which has to be additionally input by either adding an intrinsic part to the Hamiltonian or directly modeling the inertia parameter Aα based on the assumptions of nuclear flow. This has been achieved in the shell model realization of a rotor by considering the mean-field contribution of nucleons [8–10], which generates the so-called leading SU(3) IRREP (λ0, μ0) to describe the ground-state configuration of a given nucleus. The similar procedure was also realized in the SU(3) limit of the IBM [12]. Specifically, the angular momentum and quadrupole operators in the SU(3) limit are defined by
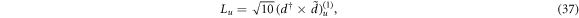
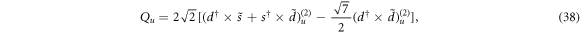
where Q is actually the same as that given in (2) but choosing  . One can prove that these operators satisfy the su(3) algebraic relation shown in (30). Differently from the shell model, intrinsic deformations in the SU(3) limit of the IBM are dynamically realized [11, 12] by adding C2[SU(3)], C2[SU(3)]2 and C3[SU(3)] to the Hamiltonian. This mapping scheme was recently applied to explain the anomalous E2 transitions in some neutron-deficient nuclei [13].
. One can prove that these operators satisfy the su(3) algebraic relation shown in (30). Differently from the shell model, intrinsic deformations in the SU(3) limit of the IBM are dynamically realized [11, 12] by adding C2[SU(3)], C2[SU(3)]2 and C3[SU(3)] to the Hamiltonian. This mapping scheme was recently applied to explain the anomalous E2 transitions in some neutron-deficient nuclei [13].
In view of the SU(3) algebraic realization of the rotor mode, one may ask whether or not the similar procedure can be applied to the O(6) limit. The O(6) group generators in the IBM [16] are constructed by
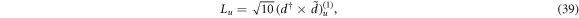
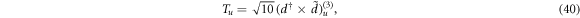

in which the quadrupole operator Qu is just that defined in (2) but choosing χ = 0. The 2nd-order Casimir operator of O(6) is accordingly written as
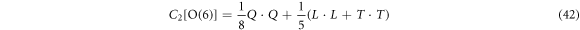
with the expectation value given by

where σ is a quantum number used to label the O(6) IRREPs. Similarly to the SU(3) system, if the quarupole operator in O(6) is rescaled with qu = Qu /〈C2[O(6)]〉, one can prove that Lu and qu in the σ ≫ L limit may satisfy the commutation relation [37–39]
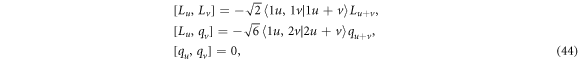
which is exactly as same as that given in (5). By further considering the fact that SO(5) generated by Lu and Tu is a subgroup of both O(6) and E(5), the o(6) algebra reduction in the large σ limit can be expressed by [39]
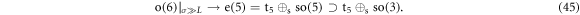
This algebraic contraction implies that the rotor dynamics may be realized in the O(6) limit via a procedure similar to the SU(3) realization. The left question is how to generate stable γ deformation in an O(6) system. Since two-body terms in the O(6) limit like Q · Q can only yield a γ-unstable mean-field picture, one has to introduce high-order terms to produce γ-stable deformations as shown below.
The Hamiltonian for the O(6) algebraic realization of the rotor model is designed to be divided into two parts,
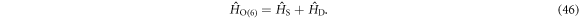
The dynamic part is given by
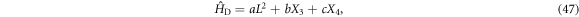
in which the terms X3 and X4 take the same form as that of  and
and  shown in (24)–(25) except for adopting Lu
and Qu
defined in O(6). The static part is constructed as a polynomial in Q and given by
shown in (24)–(25) except for adopting Lu
and Qu
defined in O(6). The static part is constructed as a polynomial in Q and given by
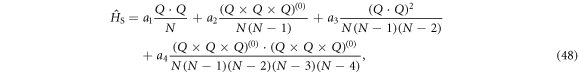
where ai with (i = 1, 2, 3, 4) are real parameters. Note that if adopting the Q operator defined in the SU(3) limit as given in (38), the first three terms in (48) are enough to generate stable γ deformation (axial or triaxial) and therefore employed in the previous SU(3) realization of the rotor model [11–13]. But if adopting the Q operator defined in the O(6) limit as given in (41), the first three terms can only produce axial deformation or γ-unstable deformation. So, the higher-order term like the fourth term in (48) is needed in order to generate triaxial deformation at the mean-field level. This point can be understood by examining the the potential function of the O(6) system. To illustrate that, the classical limit of HS is worked out by adopting the IBM coherent state [16]
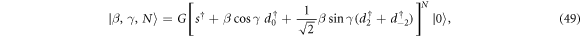
where  is the normalization constant. The classical potential corresponding to the Hamiltonian is then derived as
is the normalization constant. The classical potential corresponding to the Hamiltonian is then derived as
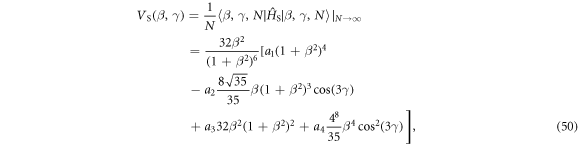
by which the ground-state energy per boson is obtained by minimizing the potential with respect to β and γ, namely  . The potential form given in (50) is similar to the one discussed in [40], where a semi-classical treatment of the coherent-state model was provided. It should be noted that VS(β, γ) is supposed to describe the classical limit of the ground state generated by
. The potential form given in (50) is similar to the one discussed in [40], where a semi-classical treatment of the coherent-state model was provided. It should be noted that VS(β, γ) is supposed to describe the classical limit of the ground state generated by  as the dynamical part 〈HD
〉/N is supposed to contribute nothing in the large N limit, which may be realized by adding an additional 1/N factor to HD [13]. This point can be also understood from the fact that the real ground state of
as the dynamical part 〈HD
〉/N is supposed to contribute nothing in the large N limit, which may be realized by adding an additional 1/N factor to HD [13]. This point can be also understood from the fact that the real ground state of  may correspond to L = 0, which makes the matrix elements of any terms containing L like those in HD be zero at quantal level. Based on the classical potential (50), one can deduce that the terms Q · Q and (Q · Q)2 can only produce a γ-independent mean-field structure, while (Q × Q × Q)(0) in the classical limit describes axial deformation, which corresponds to γ = 0 or γ = π/3 depending on the sign of a3. In contrast, the term
may correspond to L = 0, which makes the matrix elements of any terms containing L like those in HD be zero at quantal level. Based on the classical potential (50), one can deduce that the terms Q · Q and (Q · Q)2 can only produce a γ-independent mean-field structure, while (Q × Q × Q)(0) in the classical limit describes axial deformation, which corresponds to γ = 0 or γ = π/3 depending on the sign of a3. In contrast, the term  has
has  involved in its γ-dependence, thus pointing to a stable triaxial deformation at γ = π/6. In principle, a term like
involved in its γ-dependence, thus pointing to a stable triaxial deformation at γ = π/6. In principle, a term like  can be also added to the Hamiltonian but it will not induce extra γ deformation. Anyway, the classical potential VS(β, γ) can cover different types of quadrupole deformation through adjusting the parameters ai
in (48).
can be also added to the Hamiltonian but it will not induce extra γ deformation. Anyway, the classical potential VS(β, γ) can cover different types of quadrupole deformation through adjusting the parameters ai
in (48).
In addition, one needs to find a way to determine 〈C2〉 and 〈C3〉 in order to further fix the parameters in (47). In the O(6) system, this can be achieved via the following two steps: (I) based on the algebra contraction between o(6) and t5⊕sso(3), the invariants C2 and C3 defined in (6)–(7) are first mapped into the O(6) system through replacing the involved Qc operator by that defined in (41); (II) 〈C2〉 and 〈C3〉 are then evaluated at the mean-field level using the optimal values (β0, γ0), with which the ground-state energy  is simultaneously obtained. After the two steps, one can solve the λi
values from equation (10) and the parameters a, b, c in HD will be further read from equation (28). Clearly, this mapping scheme can be extended to any other quadrupole systems because the only assumption adopted here is the dynamic equivalence between different quadrupole operators. In fact, if applying the present scheme to the SU(3) limit of the IBM, the solved λi
values for large N cases would be rather close to those obtained from equation (35).
is simultaneously obtained. After the two steps, one can solve the λi
values from equation (10) and the parameters a, b, c in HD will be further read from equation (28). Clearly, this mapping scheme can be extended to any other quadrupole systems because the only assumption adopted here is the dynamic equivalence between different quadrupole operators. In fact, if applying the present scheme to the SU(3) limit of the IBM, the solved λi
values for large N cases would be rather close to those obtained from equation (35).
4. Numerical examination of the O(6) image
To check the validity of the mapping scheme, we select two cases in the rotor model, which are described by the axially symmetric top with A1: A2: A3 = 0.5: 0.5: 2.5 and the axially asymmetric top with A1: A2: A3 = 1.0: 0.33: 1.33, respectively. The algebraic images of the two types of rotor are assumed to be produced from the O(6) systems with the intrinsic deformation γ0 = 0 and γ0 = π/6, respectively. Note that no assumption is made regarding a relationship between γ and the inertia parameter Ai [8]. To generate the corresponding γ deformations in the O(6) system, the parameters in HS are set by choosing (a2 = 0.0442, a1 = a3 = a4 = 0) and (a1 = − 0.0125, a4 = 0.00195, a2 = a3 = 0), respectively. The resulting potential surfaces VS(β, γ) are shown in figure 1. It can be found that the potential shown in figure 1(a) indeed has its minimum located at γ0 = 0, which indicates axial deformation, while the potential shown in figure 1(b) presents a minimal point near γ0 = π/6, which thus suggests a stable triaxial deformation. With these intrinsic deformations, we further evaluate the invariants 〈C2〉 and 〈C3〉 at the mean-field level to get the parameters a, b, c according to the mapping scheme. Specifically, it is given by a: b: c = 0.7: 0.0935: 0.00115 for the axially-deformed case and a: b: c = 1.0: 0.0589: − 0.00278 for the triaxially-deformed case. With these parameter values, we diagonalize the algebraic Hamiltonian (46) with the total boson number set by N = 10. The solved level patterns are shown in figure 2 to compare with those directly solved from the rotor model Hamiltonian (13). In the calculation for B(E2), the E2 operator in the O(6) image is simply chosen as the quadrupole operator Q defined in (41), while the one for the rotor model is adopted as
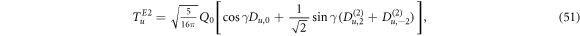
where Q0 denotes the intrinsic charge quadrupole moment and the deformation parameter γ is taken as γ = γ0.
Figure 1. (a) The potential surface obtained from (50) with a2 = 0.0442 and a1 = a3 = a4 = 0. (b) The potential surface obtained from (50) with a1 = − 0.0125, a4 = 0.00195 and a2 = a3 = 0.
Download figure:
Standard image High-resolution imageFigure 2. (A) The level pattern solved from the axial-symmetric rotor with A1: A2: A3 = 0.5: 0.5: 2.5 are shown to compare with that obtained from the O(6) Hamiltonian with the parameters determined by the proposed mapping scheme (see text). (B) The same as in (a) but for the triaxial case with A1: A2: A3 = 1.0: 0.33: 1.33. All the level energies have been normalized to E(2g ) = 1.0 with the typical ratios defined as R42 = E(4g )/E(2g ), R22 = E(2γ )/E(2g ), B42 = B(E2; 4g → 2g )/ = B(E2; 2g → 0g ) and B22 = B(E2; 2γ → 2g )/ = B(E2; 2g → 0g ).
Download figure:
Standard image High-resolution imageAs seen from figure 2(A), the dynamical structures of both the ground-state band and γ band generated from the axial rotor are very similar to the ones solved from the O(6) image. The similarities can be partially observed from the typical energy and B(E2) ratios. For example, R4/2 = 3.33 indicating the L(L + 1) law is well reproduced in the O(6) image, which is dominated by cubic term QQQ in its Hamiltonian. The results thus confirm the previous analysis [25, 26] that this term may generate an axial rotor spectrum in the O(6) limit that is different from those in the SU(3) limit. However, the previous calculations [25] meanwhile predicted much weaker but nonzero values for the interband B(E2) transition in contrast to B22 = 0 predicted by the present calculations. This can be be explained by that the mapping Hamiltonian (47) has included some terms like LQL that were not considered previously [25]. If the additional terms are removed, the exactly same results would be obtained under the same parameters. As further seen from figure 2(B), the triaxial rotor spectrum can be also reproduced very well in its O(6) image. Apart from the typical ratios, the consistencies are alternatively reflected by the odd–even staggering shown for the γ bands. Specifically, the staggering feature with the near degenerated partners (2γ , 3γ ), (4γ , 5γ ), ⋯ are clearly exhibited in the spectrum solved from the O(6) image. It should be mentioned that the two-body O(6) Hamiltonian can also yield an odd–even staggering feature but with the sign of staggering being completely inverse to that shown in figure 2(b). Such a difference is actually thought to be a key feature to distinguish the γ-rigid rotor from the γ-unstable rotor [41] in contrast to the similar B(E2) properties of the two modes [42]. In addition, one may find from figure 2(B) that the energies of high-spin levels like E(81) cannot be well reproduced in the O(6) image. This point actually reflects that the algebra contraction will only occur for the σ ≫ L limit as described above. In other words, the mapping scheme may work better for the low-spin states. Besides, the triaxial potential well for a certain set of given parameters is shown to be more shallow thus less bound [43] than the axial potential as seen from figure 1. This may, in part, explain why E(81) in the triaxial case is reproduced slightly less well than in the axial case as shown in figure 2. Anyway, the above two examples confirm that an algebraic realization of the quantum rotor model can be indeed achieved in the O(6) limit of the IBM.
As mentioned above, the SU(3) algebraic realizations of the quantum rotor model has been applied [13] to explain the B(E2) anomaly in some neutron deficient nuclei which are supposed to be more or less triaxially deformed. A key factor of generating B(E2) anomaly characterized by B42 < 1.0 in the SU(3) limit is to introduce symmetry-conserving high-order terms [12, 44]. In contrast, the recent analysis given in [45] indicates that the O(6) Hamiltonian similar to that used in the SU(3) scheme [44] cannot bring B(E2) anomaly in yrast states. In fact, this point can be better understood from the above discussions. It has been pointed out above that triaxial deformation cannot be produced in the O(6) limit up to the fourth-order interactions as adopted in [45]. Meanwhile, it is also shown here that adding the higher-order terms like  in the O(6) limit could generate triaxial deformation as well as triaxial rotor-like dynamics. It means that there is a possibility of producing B(E2) anomaly in the O(6) limit by introducing the symmetry-conserving interactional terms up to sixth order. More detailed analysis of this point may be presented elsewhere as the main purpose of this work is just give an O(6) algebraic realization of the rotor model.
in the O(6) limit could generate triaxial deformation as well as triaxial rotor-like dynamics. It means that there is a possibility of producing B(E2) anomaly in the O(6) limit by introducing the symmetry-conserving interactional terms up to sixth order. More detailed analysis of this point may be presented elsewhere as the main purpose of this work is just give an O(6) algebraic realization of the rotor model.
5. Summary
In summary, a new IBM mapping scheme of the quantum rotor has been proposed by introducing the symmetry-conserving high-order terms in the O(6) limit. A detailed description of the mapping procedure has been given with two concrete examples being provided to illustrate the validity of the scheme. The results indicate that the dynamics of both the axial and triaxial rotors can be well reproduced in the corresponding O(6) images, which thus suggests an alternative angle to see the rotor dynamics in finite-N systems after the previous SU(3) realization [9]. The present mapping scheme can be extended to any other quadrupole systems satisfying the following conditions: (A) the algebraic relation for Lu and Qu in the large-N limit will contract to that for t5⊕sso(3); (B) the system can achieve an intrinsic γ deformations at the mean-field level. The first condition is generally satisfied by the IBM systems even for cases deviating from the SU(3) and O(6) limits [16]. Nonetheless, triaxial deformation in the IBM can only be achieved through a designed Hamiltonian form which usually involves high-order terms An example worth of special attention is the extended consistent-Q Hamiltonian [21] since it suggests a natural extension of the widely used two-body IBM Hamiltonian and meanwhile allows triaxial deformation at the mean-field level. It would be interesting to see whether or not the mapping scheme can work for this Hamiltonian or the other cases deviating from the O(6) and SU(3) limits. Related work is in progress.
Acknowledgments
Support from the Natural Science Foundation of China (12375113,11875158) is acknowledged.
Data availability statement
No new data were created or analysed in this study.




