Abstract
We have calculated the differential cross sections for the elastic, excitation to H(n = 2), and electron-transfer processes in He+ + H collision using a semiclassical atomic-orbital close-coupling method within two-electron treatment. The calculations have been implemented with four different basis sets to see the effects of electron-exchange, electron-transfer channels, and continuum channels. The results are compared with those of experiments and other calculations.
Export citation and abstract BibTeX RIS
1. Introduction
The He+(1s)+H(1s) collision is the simplest system, where two electrons are involved and the projectile has a structure. The integrated cross sections (ICSs) for the excitation to H(n = 2) states have been measured by Young et al [1], Mckee et al [2], Geddes et al [3], and Aldag et al [4, 5]. The ICSs for electron transfer, He+(1s) + H(1s) → He + H+, have been measured by Lockwood et al [6], Olson et al [7], and Hvelplund et al [8]. Hsu et al [9] have reported the ICS data for the ionization of H atom. Within the one-electron approximation where He+(1s) is treated as a core or the electron in He+(1s) is frozen, the ICSs were calculated for the H(n = 2) excitation [10–14], ionization of H [11, 15], and electron transfer [11–13, 15]. The calculations based on the molecular orbital close-coupling (MOCC) method have been used to calculate the ICSs for the excitation of H and electron transfer [13, 16, 17]. While, the atomic-orbital close-coupling (AOCC) method with considering two electrons have been also reported [11, 18, 19] for the ICSs of H(n = 2) excitation and electron transfer.
Present work is concerned with the differential cross sections (DCSs) with respect to the projectile scattering angle for the He+(1s)+H(1s) collision. Fayeton et al [20] have measured the DCSs for the elastic scattering, H(n = 2) excitation, and electron capture into He(1s2p) with the incident energy (E) of He+ ion for 0.1875 ≤ E ≤ 0.625 keVu−1. Full quantal calculations based on a molecular treatment [20–22] were applied to analyze the experimental data of Fayeton et al [20]. Bordnave-Montesqiue et al [23] measured the DCSs for elastic scattering and H(n = 2) excitation at large scattering angles for 0.375 ≤ E ≤ 6.25 keVu−1. While, the DCSs for H(n = 2) excitation at small angles were measured by Aldag et al [5] for 3.75 ≤ E ≤ 25 keVu−1. Within the frozen He+(1s) model, Flannery et al [10] calculated the DCSs for the elastic scattering and excitation to H(n = 2) states with close-coupling (CC) calculations, where the channels of He+(1s) + H(n ≤ 2) were coupled. The DCSs for the H(n = 2) excitation were also calculated within the frozen He+(1s) model by Maidagan et al [24] using the two-state CC method and by Ramírez et al [14] using the symmetric eikonal (SE) approximation. Franco used Glauber approximation for the excitation [25], but a further approximation was adopted to make the calculation tractable. In these calculations [10, 14, 24, 25], the electron-exhange effect is neglected. Errea et al [26] have used MOCC method to analyze the experimental data of Fayeton et al [20], Bordnave-Montesqiue et al [23], and Aldag et al [5]. Errea et al [26] also presented the DCSs for the electron-transfer below 6.25 keVu−1. For the electron transfer, there exists no experimental work above 1 keVu−1 and no theoretical work above 6.25 keVu−1. The experimental data of DCSs for H(n = 2) excitation are limited below 25 keVu−1, and the same is true for the calculations except for reference [10]. Thus, the DCSs of He+(1s) + H(1s) collision have not been explored adequately.
Recently, we have calculated the ICSs for elastic scattering, H(n = 2) excitation, and electron transfer using a two-electron version of the AOCC method with considering both the electron-transfer and ionization channels [27]. The atomic basis are prepared using Gaussian-type orbitals which allow analytic evaluation of matrix elements. Similar AOCC calculations have been applied to ion-atom and ion-molecule collisions involving multi-electrons at intermediate enegy region [28–33]. In this work, the calculation [27] is applied to calculate the DCSs for 2.5 ≤ E ≤ 200 keVu−1.
Atomic units are used throughout this paper except when otherwise stated.
2. Theory
We extend the previous work [27] for the ICSs in He+(1s)–H(1s) collision to the calculation of the DCSs. The calculation is based on the impact parameter method, and the position vector of He2+ nucleus from H+ is classically described by R = (b, Z = vt) = b + v t, where b is the impact parameter vector and v (⊥b) the incident velocity of He+ ion. The z-axis is taken parallel to v.
The electronic wavefunction Ψ(S) for spin state S(= 0 or 1) at an impact parameter b is expanded as
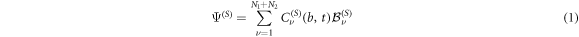
where  are the channel functions for He+ + H arrangement (ν = 1–N1) and He + H+ arrangement (ν = N1+1–N1+N2), respectively (see equations (7) and (8) of [27]).
are the channel functions for He+ + H arrangement (ν = 1–N1) and He + H+ arrangement (ν = N1+1–N1+N2), respectively (see equations (7) and (8) of [27]).
The expansion coefficients  satisfy
satisfy
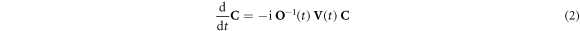
with  and
and  , where H is the electronic Hamiltonian of the system.
, where H is the electronic Hamiltonian of the system.
The off-diagonal couplings become negligible for large ∣t∣ ≥ t1(> 0). The coupled equations in (2) are solved from t = − t1 to t = t1 under the initial condition  , where ν0 denotes the initial channel, He+(1s) + H(1s). Considering the internuclear interaction, VNN
= ZP
ZT
/R = 2/R (ZP
and ZT
are the nuclear charges of projectile and target, respectively), the transition amplitude is written as
, where ν0 denotes the initial channel, He+(1s) + H(1s). Considering the internuclear interaction, VNN
= ZP
ZT
/R = 2/R (ZP
and ZT
are the nuclear charges of projectile and target, respectively), the transition amplitude is written as
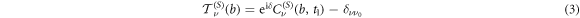
with ![$\delta =-{\int }_{-{t}_{1}}^{+{t}_{1}}{V}_{N}(t){dt}=\eta (\mathrm{log}b-\mathrm{log}[R({t}_{1})+{{vt}}_{1}])$](https://content.cld.iop.org/journals/1402-4896/99/1/015404/revision2/psad131dieqn6.gif) with η = 2ZP
ZT
/v. The ICS for the transition to channel ν for spin state S is calculated by
with η = 2ZP
ZT
/v. The ICS for the transition to channel ν for spin state S is calculated by
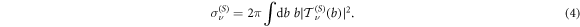
The DCS for the projectile scattering angle is given by
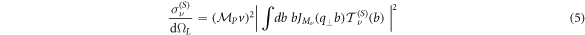
with  , where
, where  is the mass of projectile nucleus (4He2+) and θL
is the projectile scattering angle in the laboratory system. In equation (5), Mν
(≥ 0) is the magnitude of the z-component of the angular momentum of two electrons for channel ν, and JM
is the Bessel function of the first kind. For large q⊥, the main contribution in the integral in equation (5) comes from small b due to the rapidly oscillating function biη
in eiδ
, and the DCS may be approximated by
is the mass of projectile nucleus (4He2+) and θL
is the projectile scattering angle in the laboratory system. In equation (5), Mν
(≥ 0) is the magnitude of the z-component of the angular momentum of two electrons for channel ν, and JM
is the Bessel function of the first kind. For large q⊥, the main contribution in the integral in equation (5) comes from small b due to the rapidly oscillating function biη
in eiδ
, and the DCS may be approximated by
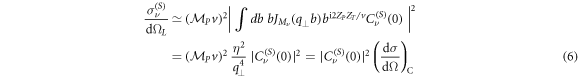
with  =
= and
and  . The notation
. The notation  corresponds to the DCS for the Coulomb scattering of He2+ by H+.
corresponds to the DCS for the Coulomb scattering of He2+ by H+.
3. Results
The atomic basis used in equations (1) are the sames as the previous work [27], and the numbers of channels become 70 and 69 for the spin states S = 0 and S = 1, respectively. The calculations are called CC-full. The results in this work are averaged over spin states with weight 1/4 for S = 0 and 3/4 for S = 1, unless otherwise stated.
We have calculated the DCSs in four types of CC methods; CC4-wo (four-channel calculation [He+(1s) + H(1s, 2s, 2p0,1)] without the electron-exchange effect), CC4 (four-channel calculation [He+(1s) + H(1s, 2s, 2p0,1)]), CC8 (eight-channel calculation [He+(1s) + H(1s,2s,2p0,1), H(1s2, 1s2s, 1s2p0,1) + H+]), and CC-full.  is replaced as
is replaced as  +
+  →
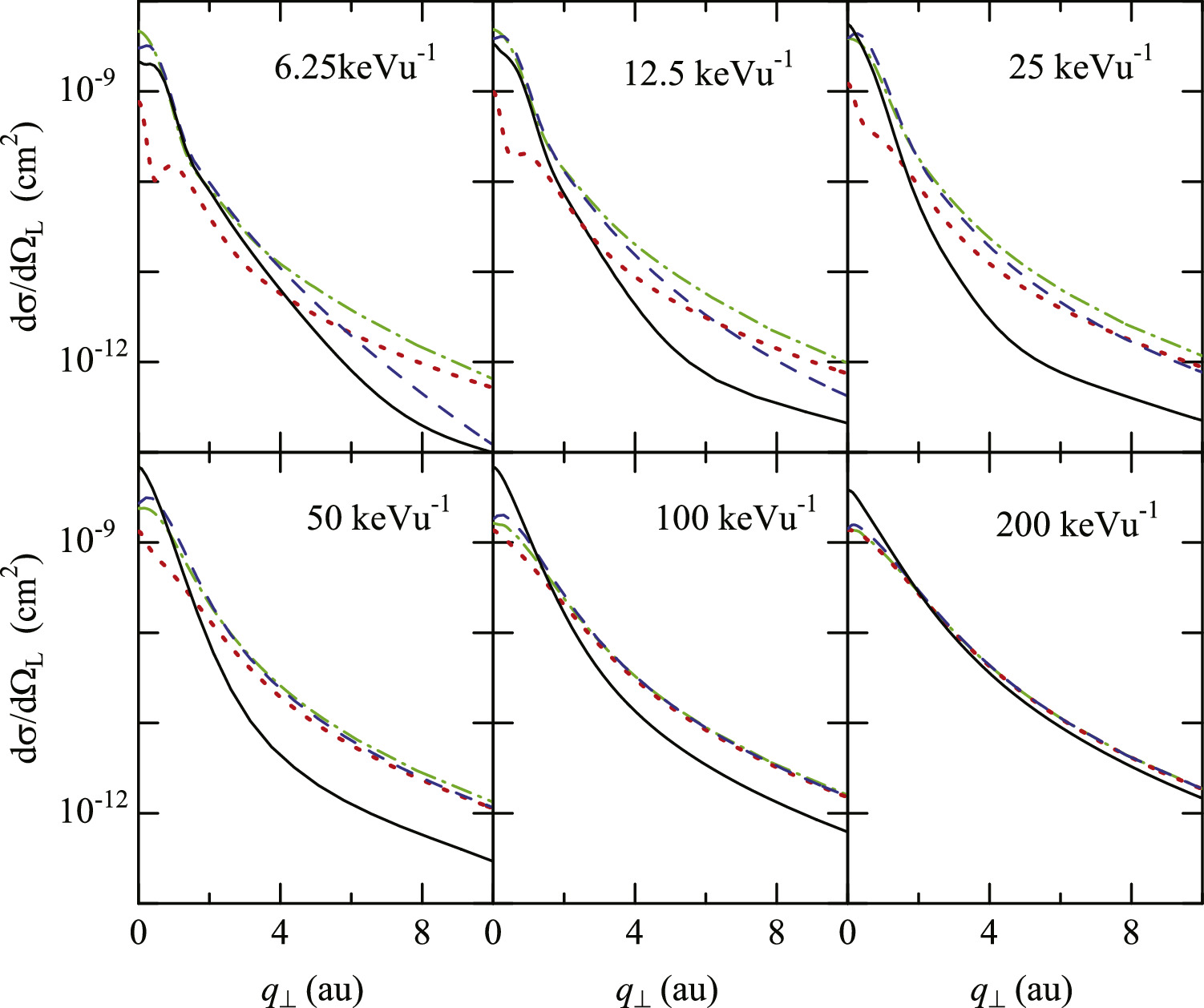
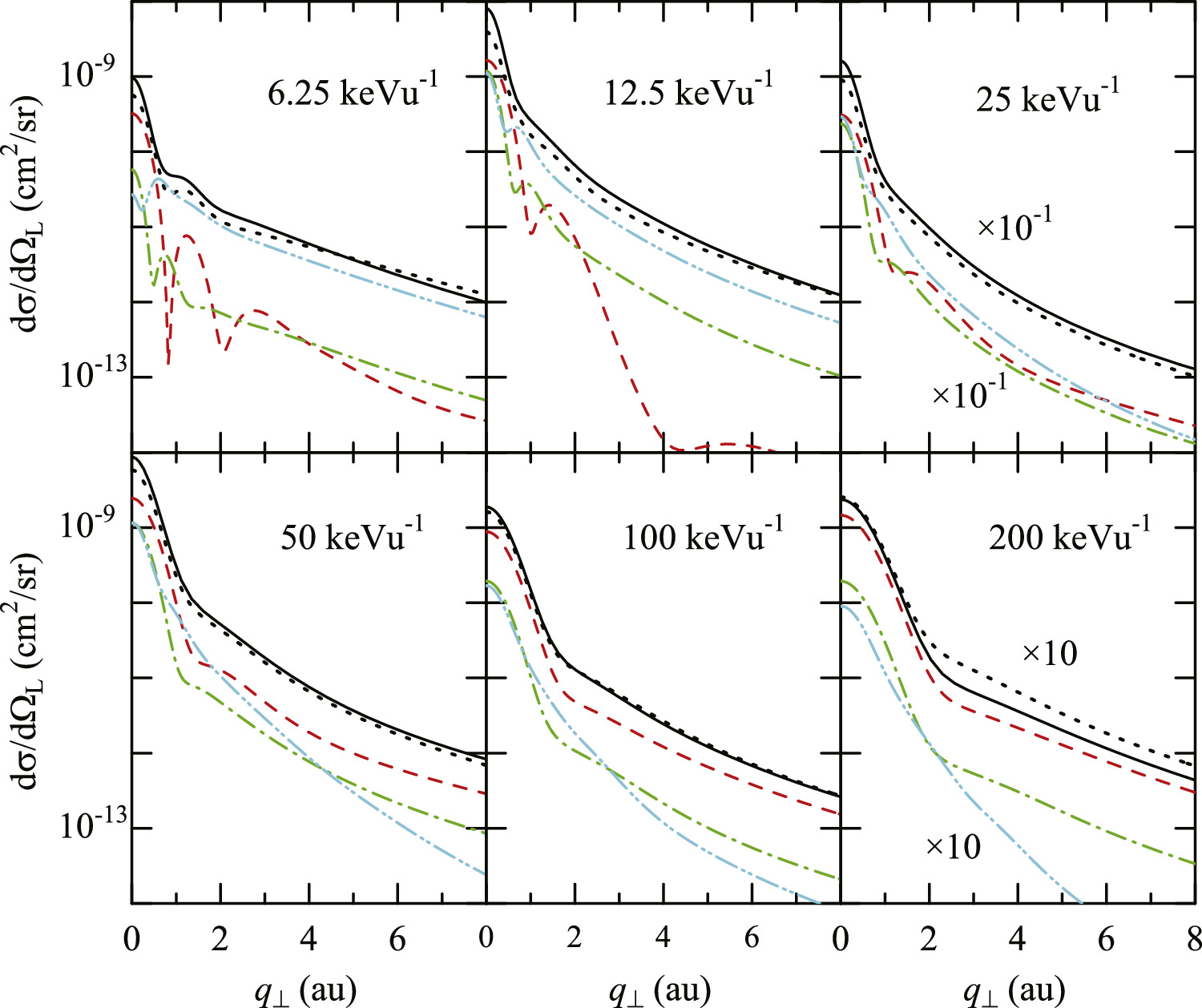
→ in CC4-wo (see equation (7) of [27]), and the electron-exchange effect is neglected in the He+ + H channels. The electron transfer channels are considered in CC8, but not in CC4-wo and CC4. CC-full includes the continuum channels, but not in the other three calculations. Figure 1 compares the elastic DCSs in the four CC calculations. For E = 6.25–50 keVu−1, the DCSs in CC4-wo are smaller than those in the other calculations at small q⊥ owing to the lack of electron-exchange effect. Above 25 keVu−1, CC-full gives larger (smaller) DCSs at small q⊥ (large q⊥) due to the effect of continuum channels. All the DCSs come to agree for higher energies.
in CC4-wo (see equation (7) of [27]), and the electron-exchange effect is neglected in the He+ + H channels. The electron transfer channels are considered in CC8, but not in CC4-wo and CC4. CC-full includes the continuum channels, but not in the other three calculations. Figure 1 compares the elastic DCSs in the four CC calculations. For E = 6.25–50 keVu−1, the DCSs in CC4-wo are smaller than those in the other calculations at small q⊥ owing to the lack of electron-exchange effect. Above 25 keVu−1, CC-full gives larger (smaller) DCSs at small q⊥ (large q⊥) due to the effect of continuum channels. All the DCSs come to agree for higher energies.
Figure 1. DCSs for He+(1s) + H(1s) elastic collision with the four calculations in this work. CC-full (solid line), CC8 (dashed line), CC4 (dot-dashed line), CC4-wo (dotted line).
Download figure:
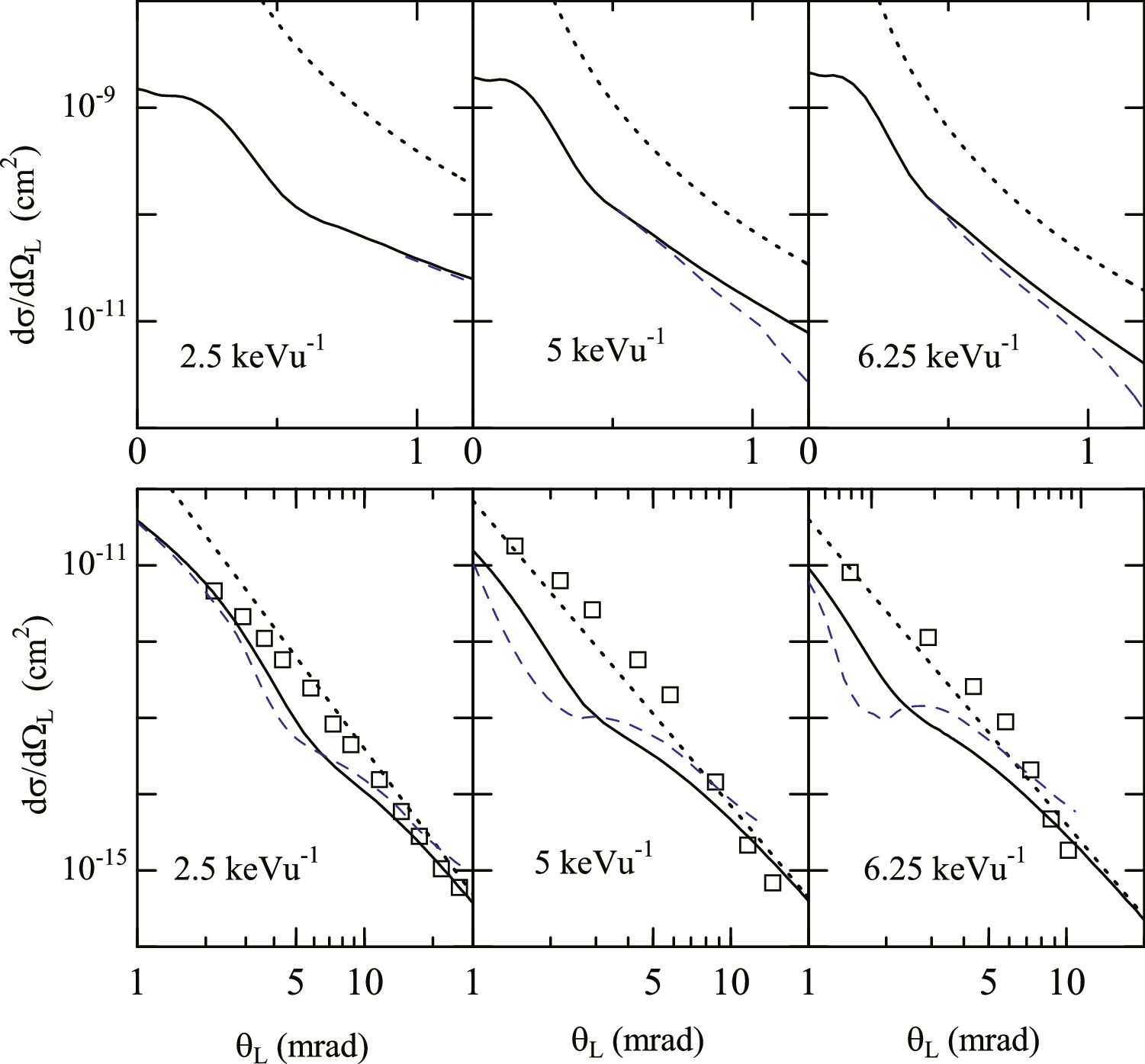
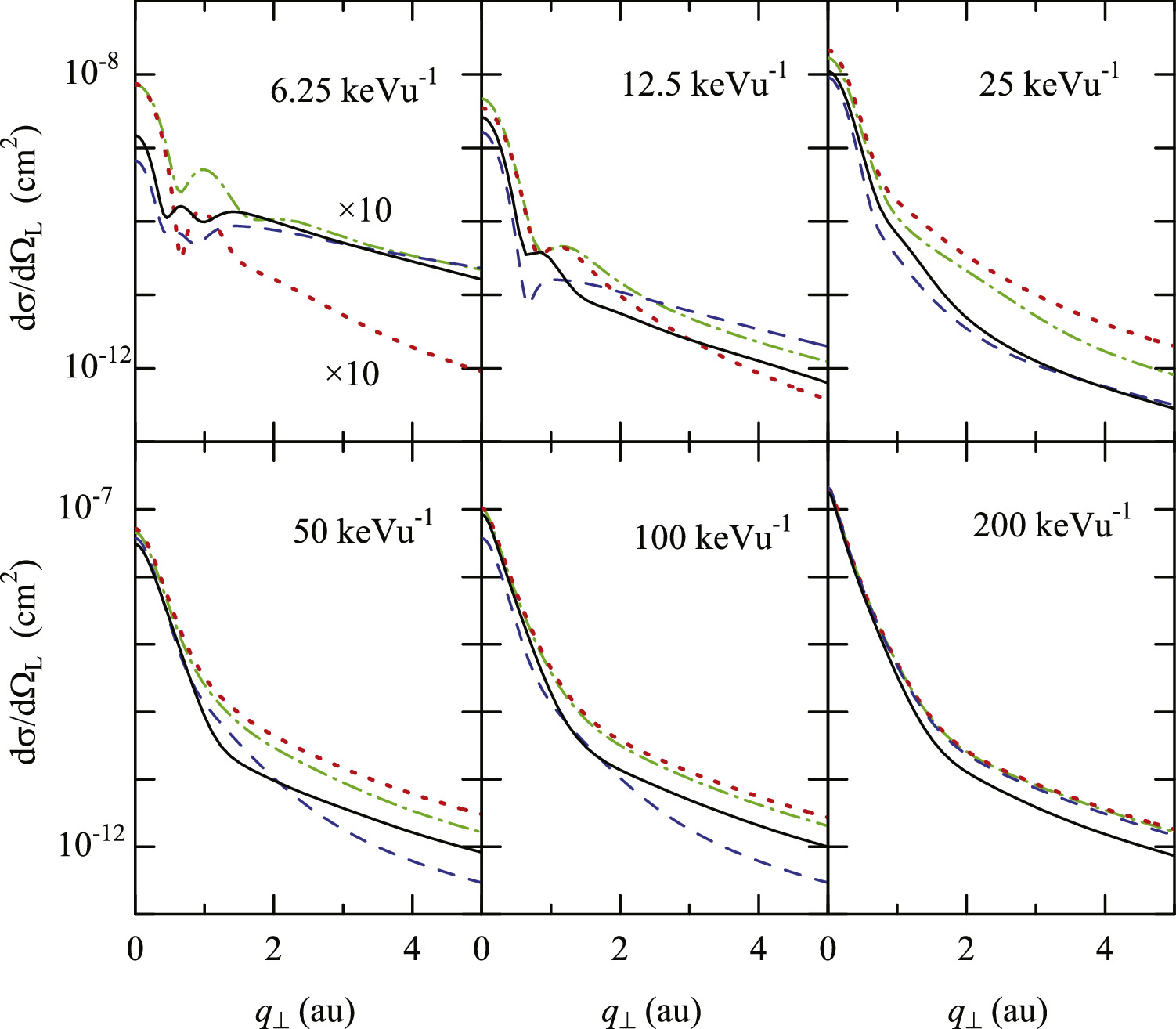
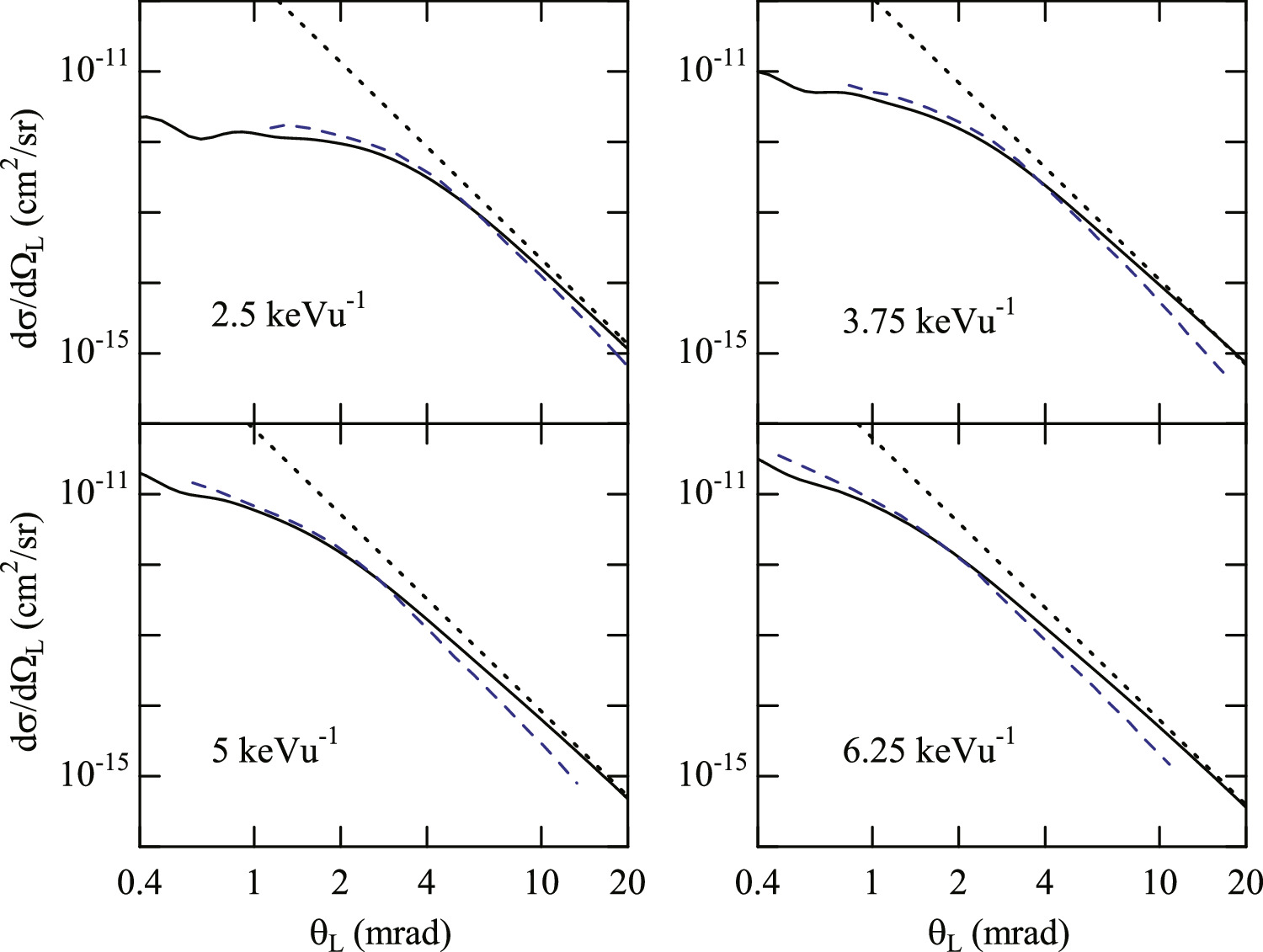
Standard image High-resolution imageBordnave-Montesqiue et al [23] have reported the DCSs of elastic scattering and H(n = 2) excitation for E = 0.425–6.25 keVu−1 and θL > 1 mrad. In figure 2, the experimental data for elastic scattering at E = 2.5, 5, and 6.25 keVu−1 are compared with the DCSs in CC-full and MOCC of Errea et al [26], and the Rutherford-type DCSs in equation (6) within CC-full (R-CC-full). The DCSs in R-CC-full are much larger than those in CC-full at small θL , but they are in better agreement with the experimental data than those in CC-full and MOCC for θL > 1 mrad. At 2.5 keVu−1, the DCSs of Errea et al and CC-full are fairly close and they show a kink near θL = 5 mrad. At 5 and 6.25 keVu−1, the DCSs in CC-full and MOCC are close at θL = 0.5 mrad, but the kink structures of MOCC are stronger than those of CC-full for 1 ≤ θL ≤ 5 mrad. The experimental data do not show any kink. Figure 3 shows the DCSs of H(n = 2) excitation calculated with the four CC calculation. The DCSs in CC4-wo and CC4 differ considerably for q⊥ > 0.5 at 6.25 keVu−1 owing to the electron-exchange effect, and they become similar for E > 25 keVu−1. The differences between CC4 and CC8 are seen below 100 keVu−1, where the electron-transfer channels affect the excitation DCSs. At 200 keV, the DCS in CC-full shows a slight deviation from the others due to the contribution from the continuum channels. Flannery et al [10] used the CC method corresponding to CC4-wo to calculate the DCSs for the elastic scattering and the H(2s) and H(2p) excitation at E = 6.25, 25, 100, and 225 keVu−1. Their DCSs are generally in good agreement with those in the present CC4-wo at the overlapping energies (E = 6.25, 25, and 100 keVu−1, not shown in the figures 1 and 3), but one exception is seen for the elastic DCS at E = 25 keVu−1 (v = 1) [10]: their DCS shows a deep dip near θL = 0.04 mrad (not shown).
Figure 2. Elastic DCSs for He+(1s) + H(1s) collision. Upper (lower) panels are for small (large) angle region at E = 2.5, 5, and 6.25 keVu−1. Calculations: CC-full (solid line), R–CC-full (dotted line), MOCC of Errea et al [26] (dashed line). Experiment: Bordenave-Montesquieu et al [23] (open square).
Download figure:
Standard image High-resolution imageFigure 3. Excitation DCSs for He+(1s) + H(1s) → He+(1s) + H(n = 2) with the four calculations in this work. CC-full (solid line), CC8 (dashed line), CC4 (dot-dashed line), CC4-wo (dotted line). The DCSs at 6.25 keVu−1 are multiplied by 10.
Download figure:
Standard image High-resolution imageThe experimental data of Bordnave-Montesqiue et al [23] for H(n = 2) excitation are compared in figure 4 with the DCSs in CC-full and MOCC of Errea et al [26]. The DCSs in MOCC are in fairly good agreement with those in CC-full. The experimental data are generally in accord with the DCSs in CC-full and MOCC. The DCS of R-CC-full converges to that of CC-full at large angles. The DCSs for H(2s) and H(2p) excitations are shown in figure 4, where the DCSs of H(2p) are larger than those of H(2s).
Figure 4. DCSs for excitaion He+(1s) + H(1s) →He+(1s) + H(n = 2). Calculations: CC-full (solid line), R-CC-full (dotted line), MOCC of Errea et al [26] (dashed line). Experiment: Bordenave-Montesquieu et al [23] (open square). Partial excitation cross sections in CC-full: H(2s) (dot-dashed line), H(2p) (dot-dot-dashed line).
Download figure:
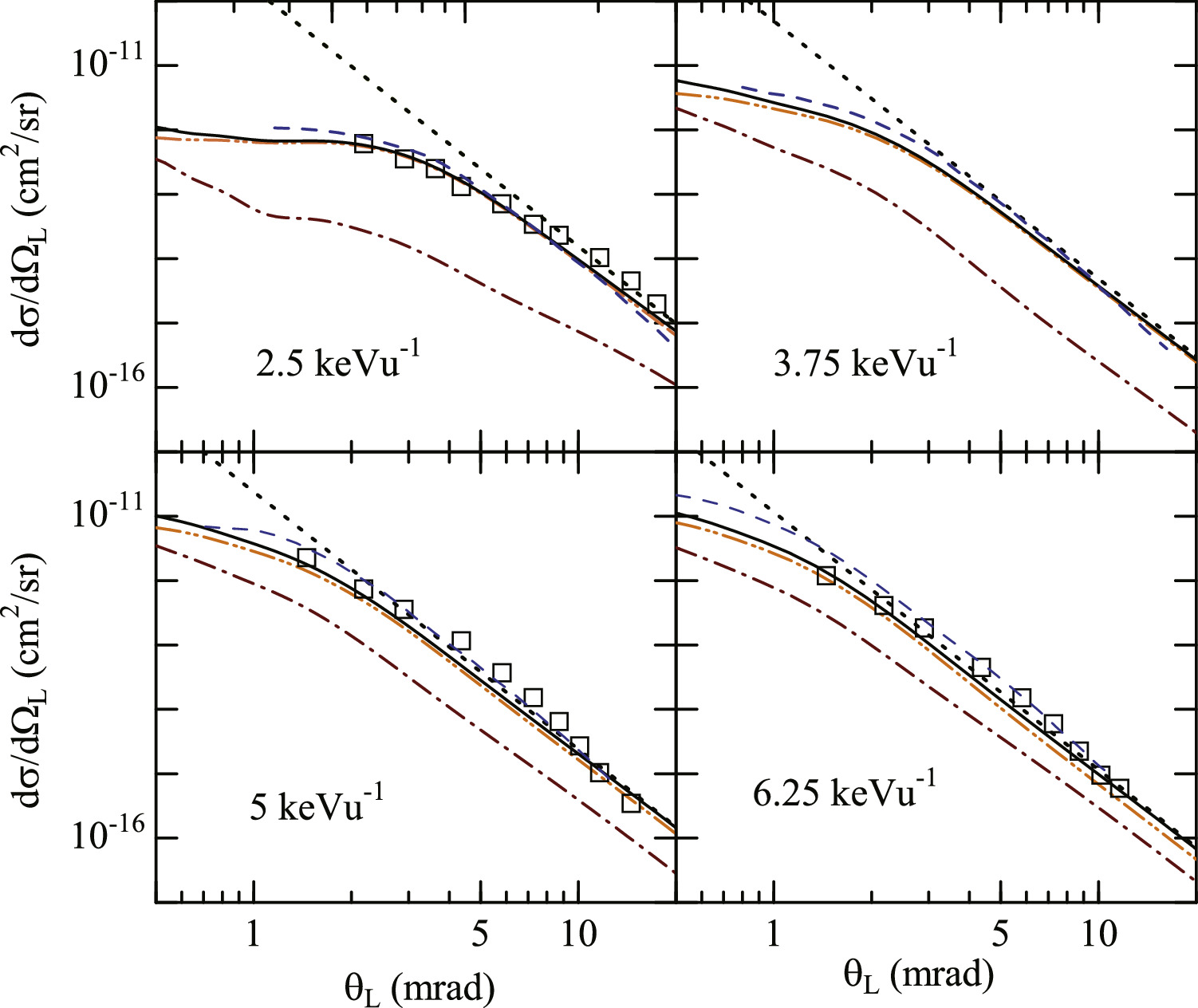
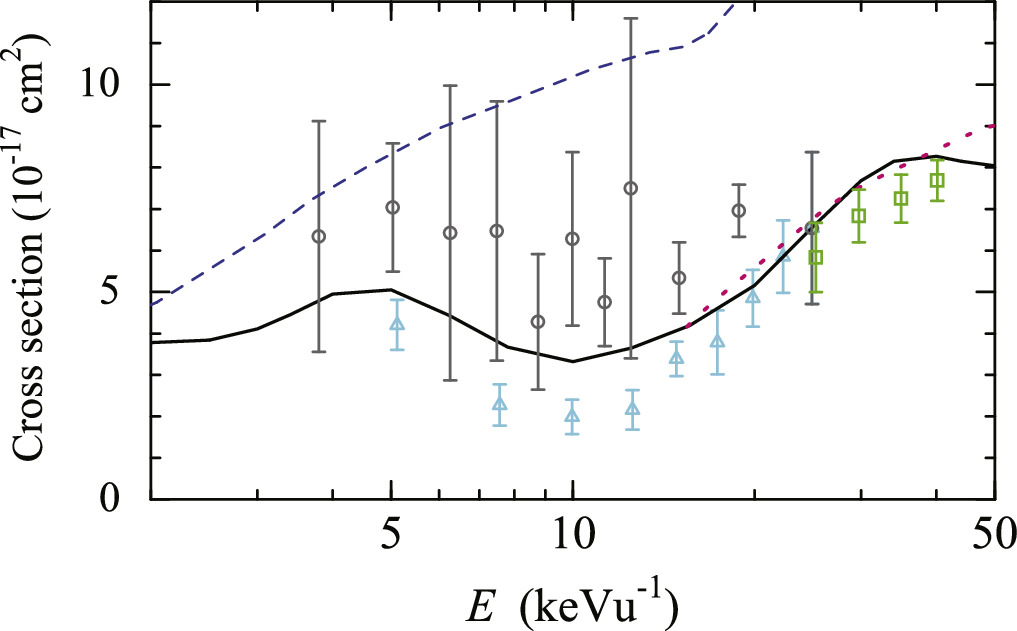
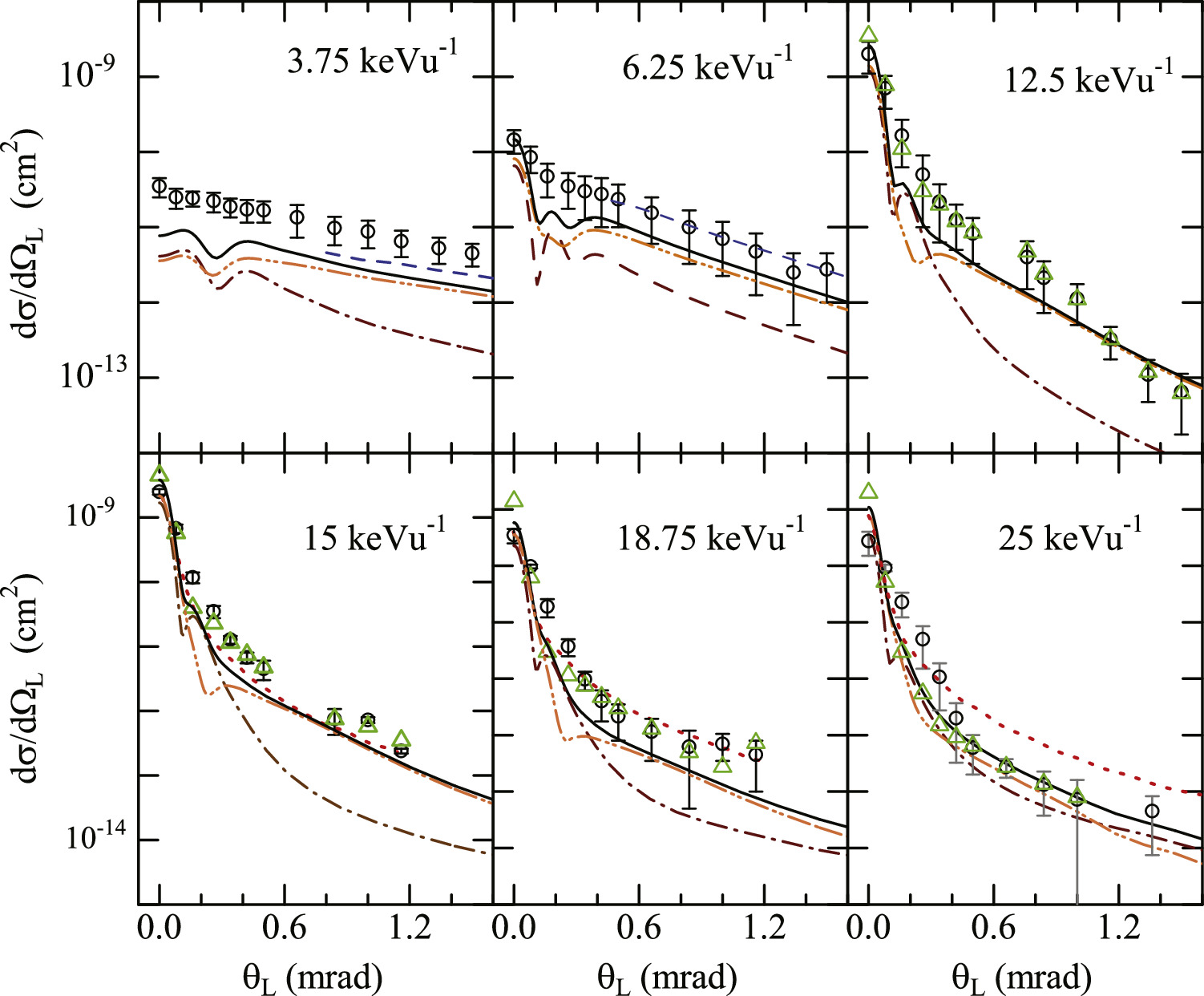
Standard image High-resolution imageAldag et al [5] measured the DCSs for the H(n = 2) excitation and obtained the ICSs of H(n = 2) excitation for E = 3.75–25 keVu−1. Before comparing the DCS data with theoretical results, we revisit the ICSs for H(n = 2) excitation (see figure 5, and also figure 4 in reference [27]). The experimental data of Aldag et al have large uncertainties and considerably larger than the results in CC-full, which are in better agreement with the data measured by Geddes et al [3]. The results of Errea et al [17] are much larger than those of CC-full for E > 5 keVu−1. Figure 6 shows the experimental data of Aldag et al [5] and the theoretical DCSs in CC-full, MOCC of Errea et al [26] (3.75 and 6.25 keVu−1), and SE approximation of Ramírez et al [14] (15, 18.75, and 25 keVu−1). The DCSs in CC-full are overall smaller than the experimental data as expected from the comparison of the ICSs, but the angular distributions are similar. The DCSs in CC-full show structures for θL < 0.5 mrad and E ≤ 12.5 keVu−1, where the experimental data are rather smooth. The DCSs in MOCC of Errea et al [26] are in accordance with the experimental data at 3.75 and 6.25 keVu−1 (the DCSs at small angles are not shown in reference [26]). Aldag et al [5] derived the DCSs with numerical extraction method (E = 3.75–25 keVu−1) , and forward modeling approach to consider the angular width of incident beam (E = 12.5–25 keVu−1). The DCSs derived with the forward modeling approach are closer to the DCSs in CC-full for E = 15–25 keVu−1. The result of Ramírez et al is close to that in CC-full at 15 keVu−1, but they are larger than those in CC-full at large angles at 18.75 and 25 keVu−1. For the energy region in figure 6 (E < 25 keVu−1), the DCSs of H(2s) and H(2p) are comparable near the forward direction, and the DCS of H(2p) dominates at large angles. For higher energy, the DCS of H(2p) (H(2s)) becomes dominant at small (large) angles.
Figure 5. ICSs for excitation He+(1s)+ H(1s) → He+(1s) + H(n = 2). Calculations: CC-full (solid line), MOCC of Errea et al [17] (dashed line), SE approximation of Ramírez et al [14] (dotted line). Experiments: Aldag et al [5] (open circle), Aldag et al [4] (open square), Geddes et al [3] (open triangle).
Download figure:
Standard image High-resolution imageFigure 6. DCSs for excitation He+(1s)+ H(1s) →He+(1s) + H(n = 2). CC-full (solid line), MOCC of Errea et al [26] (dashed line at E=3.75 and 6.25 keVu−1), SE approximation of Ramírez et al [14] (dotted lines at E = 15, 18.75, and 25 keVu−1). Experiment of Aldag et al [5]: numerical extraction method (open circle) and forward modeling approach (open triangle). Partial excitation cross sections in CC-full: H(2s) (dot-dashed line), H(2p) (dot-dot-dashed line).
Download figure:
Standard image High-resolution imageFigure 7 show the DCSs for electron transfer in CC8 and CC-full, and partial DCSs to He(1s2,1s2s,1s2p) in CC-full. Note that the electron transfer to He(1s2) is not allowed for the triplet spin state. The DCSs in CC8 and CC-full are generally close, indicating that the continuum channels do not affect the electron transfer so much. For the partial contributions at 6.25 and 12.5 keVu−1, the electron transfer to He(1s2) is largest near the forward angle, and that to He(1s2p) is dominant overall. With increasing energies, the electron transfer to He(1s2) becomes dominant at all angles.
Figure 7. DCSs for electron transfer He+(1s) + H(1s) → He + H+ with the four calculations in this work. CC-full (solid line), CC8 (dotted line). Partial transfer cross sections in CC-full: He(1s2) (dashed line), He(1s2s) (dot-dashed line), and He(1s2p) (dot-dot-dashed line). The DCSs of 25 keVu−1 and 200 keVu−1 are multiplied by 10−1 and 10, respectively.
Download figure:
Standard image High-resolution imageThe experimental DCSs have not been reported for the electron transfer process above 1 keVu−1. The theoretical DCSs for electron transfer is reported by Errea et al for E ≤ 6.25 keVu−1 [26]. We compare the DCSs in CC-full with those in MOCC of Errea et al at E = 2.5, 3.75, and 6.25 keVu−1 in figure 8. The DCSs in CC-full and MOCC are in good agreement at these low collision energies. The DCSs in R-CC-full converge to those in CC-full at large angles.
Figure 8. DCSs for electron transfer He+(1s) + H(1s) → He + H+. CC-full (solid line), R-CC-full (dotted line), MOCC of Errea et al [26] (dashed line).
Download figure:
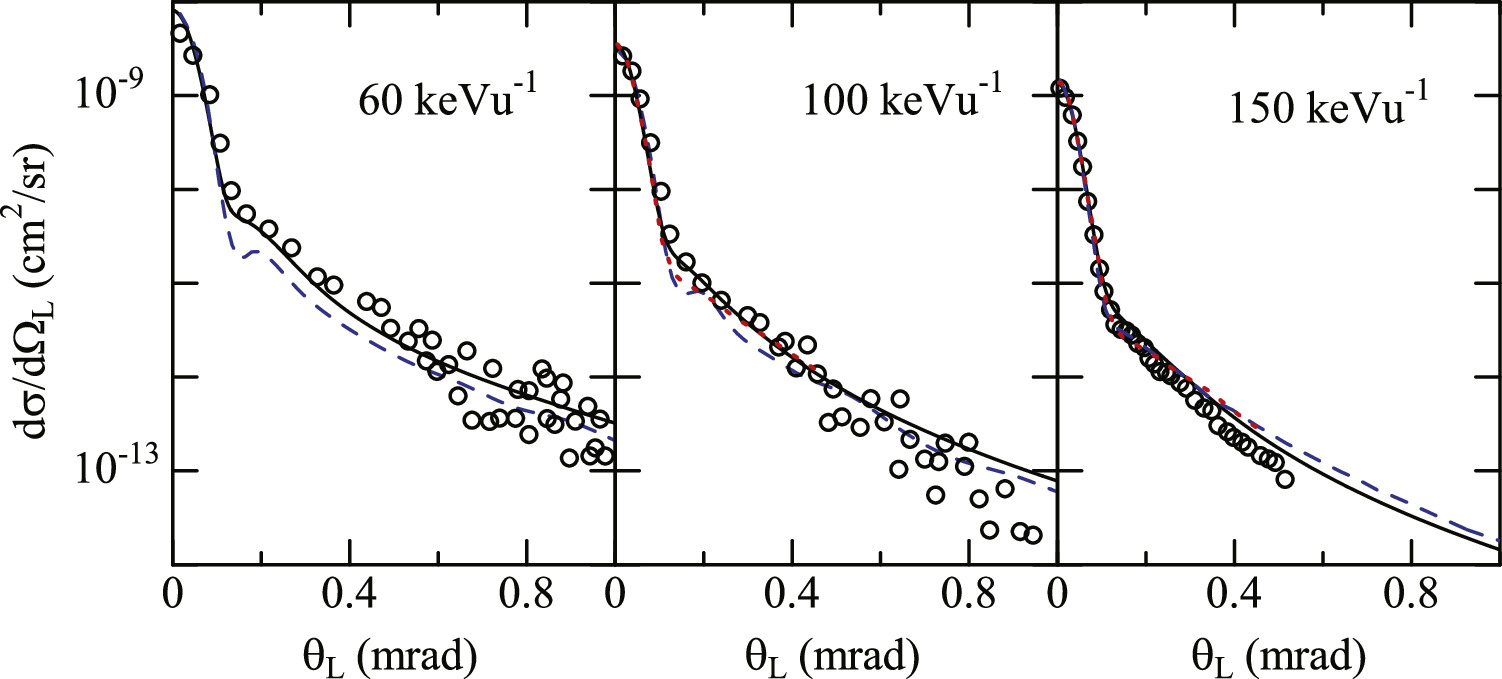
Standard image High-resolution imageWe show the DCSs of electron-transfer He+(1s) + H(1s) → He(1s2) + H+ for singlet spin state at E = 60, 100, and 150 keVu−1 in figure 9. The DCSs for the time reversal have been measured by Schöffler et al [34], and calculated by Zapukhlyak et al [35] with the two-center extension of the basis generator method (TC-BGM) and by Spicer et al [36] using the wave-packet convergent close-coupling (WP-CCC) approach. After conversion, they are in good agreement with the DCSs in CC-full in figure 9.
Figure 9. DCSs of electron transfer He+(1s) + H(1s) →He(1s2) + H+ for singlet spin state. CC-full (solid line), TC-BGM [35] (dashed line), WP-CCC [36] (dotted line), and experimental data of Schöffler et al [34] (open circles). The DCSs except for CC-full are converted from those of time reversal process H+ + He(11S) →H(1s) + He+(1s)
Download figure:
Standard image High-resolution image4. Summary
In the present work, we have applied the AOCC method to calculate the DCSs for the elastic, H(n = 2) excitation, and electron-transfer in He+ + H collision for E = 2.5–200 keVu−1.
For the elastic scattering (figure1), the electron-exchange effect is important for small angle scattering below 50 keVu−1, and the continuum channels affect the DCS up to 200 keVu−1. The elastic DCSs in CC-full (figure 2) are similar to those in MOCC by Errea et al [26], but the experimental DCS of Bordnave-Montesqiue et al [23] are closer to R-CC-full than those in CC-full and MOCC.
For the H(n = 2) excitation, the electron-exchange effect is seen at large angles for E ≤ 6/25 keVu−1, the electron-transfer channels affect the excitation DCSs below 100 keVu−1, and the continuum channels are important for E = 12.5-200 keVu−1 (figure 3). The DCSs for H(n = 2) excitation in CC-full and MOCC are generally in accord with the experimental data of Bordnave-Montesqiue et al [23] for θL > 1 mrad and E < 6.25 keVu−1 (figure 4). The DCSs in CC-full are overall smaller than the experimental data of Aldag et al [5] for E = 3.75–25 keVu−1 (figure 6), but the angular distributions are similar.
For the DCSs of electron transfer, the continuum channels do not affect the electron transfer so much (figure 7). The DCSs in CC-full and MOCC of Errea et al are in good agreement for E = 2.5–6.25 keV (figure 8). The DCSs in CC-full for the electron transfer to the ground state of helium are in good agreement with the results converted from the reported works for the time reversal process [34–36] (figure 9).
Acknowledgments
This work is performed with the support and under the auspices of the NIFS Collaboration Research Program (NIFS23KIPF006). The computation was performed using Research Center for Computational Science, Okazaki, Japan (Project: 23-IMS-C179).
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).