Abstract
We evaluate a one-way, bidirectional, and cyclic quantum controlled teleportation with two controllers. We show that the controllers' agreement mimics the OR logic gate, i.e., the teleportation succeeds with only one of the controllers' cooperation, and it does not matter which one. This result is generalized to multi-way quantum controlled teleportation with N controllers. The proposed protocols are evaluated by considering a noisy environment in the form of phase-damping noise and amplitude-damping noise and the dependence of fidelity only on the decoherence rate and the initial state's amplitude parameter were established. It is interesting to note that for the phase-damping noise case, there are states with perfect fidelity (and the entropy equal to zero) even in a noisy environment. We discuss the novelty of the proposed protocols and highlight that they can be useful if the information to be teleported needs an OR-logic-gate-like controllers' agreement combination, which cannot be done with other existing protocols.
Export citation and abstract BibTeX RIS
1. Introduction
Quantum teleportation is a branch of quantum information theory that has seen rapid development. First introduced by Bennett et al [1], the teleportation can send an unknown arbitrary one-qubit state via an Einstein-Podolsky-Rosen state assisted with two classical bits. The teleportation protocol has been tested in many experiments [2–7], which further opened the possibility of its future implementation.
Many protocol extensions were proposed. For example, in 1998, Karlsson et al [8] added a controller to the protocol. They used the GHZ state as the quantum channel and showed that the receiver needs the controller's cooperation to rebuild the sender's initial state. In 2013, Zha et al [9] proposed an alternative protocol in which the teleportation is done in two ways, i.e., from a sender to a receiver and vice versa. The protocol is called bidirectional quantum teleportation protocol. They used a five-qubit cluster state as the quantum channel, with one qubit of the channel qubits belonging to a controller. Another teleportation scheme was proposed by Sang et al [10] in 2018, in which the teleportation is done by three parties cyclically. They used a seven-qubit entangled state as the quantum channel with one qubit is for a controller. Many different variations of these protocols were reported in [11–27].
It is also of interest to consider quantum teleportation protocol under a noisy environment. Zhou et al [28] evaluated a bidirectional quantum teleportation of a two-qubit state via a seven-qubit entangle state. They also considered a noisy environment of the form of amplitude-damping noise and phase-damping noise. They showed that the teleportation fidelity value depends on the amplitude parameter of the initial state and the decoherence rate. In another study, Kaur et al [29] proposed an asymmetric quantum controlled teleportation via an eight-qubit entangled state in a noisy environment and arrived at the same conclusion on fidelity value dependence on the amplitude parameter of the initial state and the decoherence rate. Seida et al [30] evaluated bidirectional teleportation via an amplitude-damping channel and showed that the fidelities of the teleported state can be improved by applying weak and reversal measurements (WRM) on the initial quantum channel between the parties. In another work, Seida et al [31] investigated bidirectional quantum teleportation of single-qubit state under typical correlated noisy channels such as bit-flip, phase-flip, depolarizing, and amplitude-damping channels. They showed that the effect of the noise on entanglement, averaged fidelities of teleportation, and quantum Fisher information could be noticeably reduced due to the noise channel correlations. The noise evaluation has also been investigated in a multipartite teleportation [32], in which each party has the unknown state of being teleported, a trigger state, and two storage states. It was shown that the maximization/minimization of the fidelity of the teleported state depends on the teleported information, the trigger's states of the receiver, and the mediator. Another noise evaluation has also been investigated in [33], showing that the bidirectional teleportation fidelities and the quantum Fisher information depend on the survival amount of entanglement in the quantum channel, on the decoherence factor, and the correlation degree of the decoherence channel. Further studies on quantum teleportation in noisy environment can be found in [34–38].
In this work, we propose a one-way, bidirectional, cyclic quantum controlled teleportation with two controllers. We will show that teleportation can succeed with only one of the two controllers' cooperation (and it does not matter which one), which mimics the OR logic gate. We also generalize the protocol to a multi-way quantum controlled teleportation protocol with N controllers. Furthermore, we evaluate the protocols by considering a noisy environment in the form of phase-damping and amplitude-damping noise. We evaluate the protocol's fidelity value and the output density operator entropy and discuss the result. Lastly, we compare the proposed protocol with the previous works and discuss the differences.
This article is composed of five sections. The first section discusses the introduction, followed by an investigation of the one-way, bidirectional, and cyclic quantum controlled teleportation with two controllers as well as its generalization to multi-way quantum controlled teleportation with N controllers in section two. The third section discusses the effect of the phase-damping noise and amplitude-damping noise on the teleportation fidelity value and the output density operator entropy. We end with discussion and conclusion.
2. Quantum controlled teleportation with OR-logic-gate-Like controllers' agreement
In this section, we evaluate one-way, bidirectional, and cyclic quantum controlled teleportation with two controllers and generalize the result to the multi-way quantum controlled teleportation with N controllers, as described in the following subsections.
2.1. One-way quantum controlled teleportation with two controllers
Suppose there are four parties: Alice as a sender, Bob as a receiver, Charlie as the first controller, and David as the second controller. To do the teleportation, they should pre-share a four-qubit entangled channel state before doing the teleportation process. We build the channel state by preparing four ∣0〉 states as ∣0000〉1234. Index 1 to 4 represent the 1st to 4th channel's qubit.
We build the four-qubit entanglement by applying Hadamard gates on qubit 1 and 2, followed by a CNOT gate on qubit 4 with qubit 1 as the control qubit, then other CNOT gates on qubit 3 and 4 with qubit 2 as the control qubit. The final channel state is
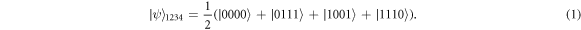
The rank of the reduced density matrix of the state [39] is greater than one, showing that the state is completely entangled. The state also has high persistency of entanglement [40], i.e., we need to perform at least two measurements in order to make the state completely unentangled. If we measure qubit 1 or 4 with computational bases, the remaining qubit collapse into a GHZ state [41], while for qubit 2 and 3, two of the three remaining qubits collapse into a Bell state.
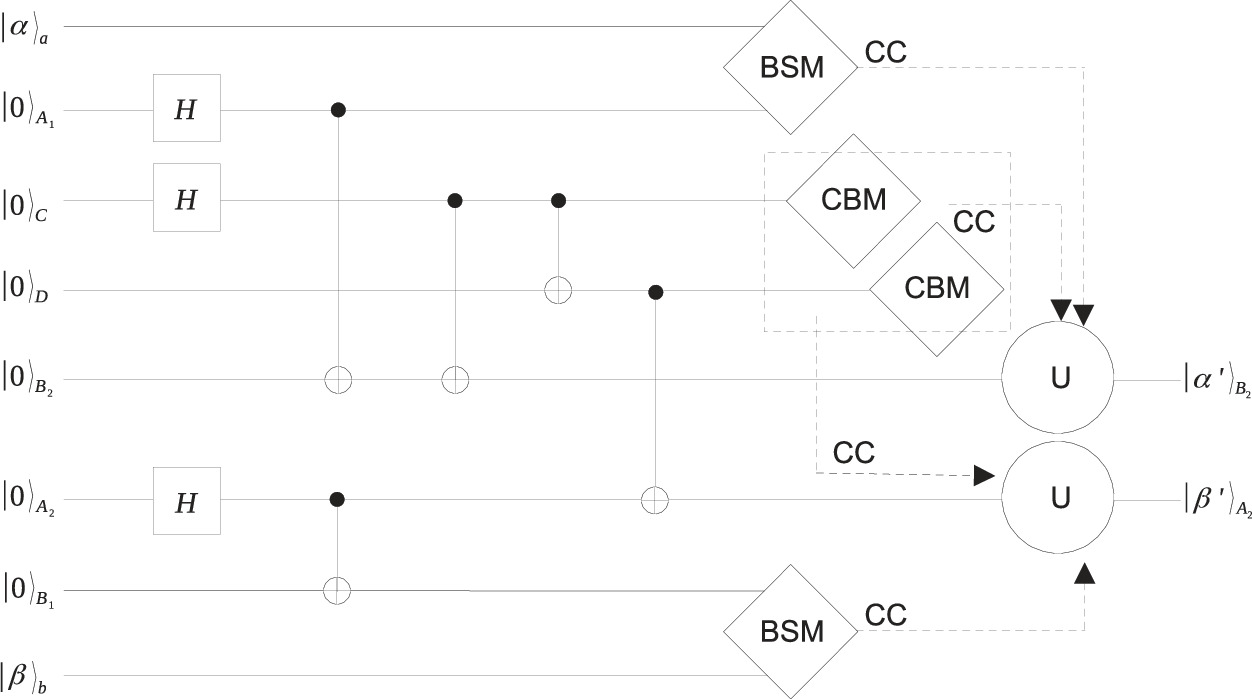
Before the teleportation process, the qubits are distributed to the four parties as ∣ψ〉ACDB = ∣ψ〉1234. Indexes A, C, D, and B indicate that the corresponding qubit belongs to Alice, Charlie, David, and Bob, respectively. We use the state as the channel because Charlie and David's qubits, i.e., qubits 2 and 3, always have the same state, which means if they were measured in computational bases independently, they would always show the same result. The behavior will generate the OR-logic-gate-like controllers' combination in the teleportation process, described as follows.
Alice, as the sender, has an arbitrary qubit
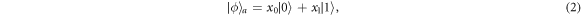
with x0 and x1 are complex numbers satisfying normalization condition 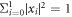 . The teleportation circuit scheme is shown in figure 1. Alice wants to teleport her state to Bob with Charlie and David's cooperation. She mixes her state with the channel state as ∣Ψ〉aACDB
= ∣ϕ〉a
⨂ ∣ψ〉ACDB
, then performs a Bell State Measurement [1] on her two qubits, i.e., a projection measurement on qubits aA in Bell Bases
. The teleportation circuit scheme is shown in figure 1. Alice wants to teleport her state to Bob with Charlie and David's cooperation. She mixes her state with the channel state as ∣Ψ〉aACDB
= ∣ϕ〉a
⨂ ∣ψ〉ACDB
, then performs a Bell State Measurement [1] on her two qubits, i.e., a projection measurement on qubits aA in Bell Bases  and
and 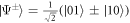 . Suppose the measurement result is ∣Φ+〉, the remaining qubits collapse to
. Suppose the measurement result is ∣Φ+〉, the remaining qubits collapse to
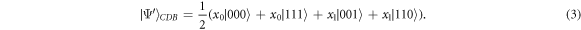
Charlie and David perform computational bases measurement independently. If Charlie's measurement result is ∣0〉, the remaining qubits collapse to ∣Ψ''〉DB
= x0∣00〉 + x1∣01〉 = ∣0〉 ⨂ (x0∣0〉 + x1∣1〉), indicating that David's result is also ∣0〉. If Charlie's measurement result is ∣1〉, the remaining qubits collapse to 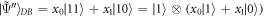 , indicating that David's result is also ∣1〉. The states show that David's result is always the same as Charlie's. All possible measurement results and the corresponding receiver's unitary operators are shown in table 1, showing that the controllers' results are correlated with the receiver's operator. However, the controllers always have the same result, which makes the receiver only need one of the controllers' cooperation, and it does not matter which one. Hence, the controllers' behaviour has the properties of the OR logic gate, one of the fundamental gates in communication science. The teleportation is useful if the information to be teleported requires the cooperation of one of two other parties (controllers), and it does not matter which one.
, indicating that David's result is also ∣1〉. The states show that David's result is always the same as Charlie's. All possible measurement results and the corresponding receiver's unitary operators are shown in table 1, showing that the controllers' results are correlated with the receiver's operator. However, the controllers always have the same result, which makes the receiver only need one of the controllers' cooperation, and it does not matter which one. Hence, the controllers' behaviour has the properties of the OR logic gate, one of the fundamental gates in communication science. The teleportation is useful if the information to be teleported requires the cooperation of one of two other parties (controllers), and it does not matter which one.
Figure 1. One-way quantum controlled teleportation with two controllers circuit scheme. BSM, CBM, U, and CC, refers to Bell State Measurement, computational bases measurement, Unitary Operation, and Classical Channel, respectively.
Download figure:
Standard image High-resolution imageTable 1. List of Alice, Charlie, and David's measurement results, Bob's qubit state, and Bob's unitary operator.
| MA a | MC b | MD c | Bob's 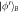 state state | UB d |
|---|---|---|---|---|
| ∣Φ+〉 | ∣0〉 | ∣0〉 | x0∣0〉 + x1∣1〉 | I |
| ∣Φ+〉 | ∣1〉 | ∣1〉 | x0∣1〉 + x1∣0〉 | σx |
| ∣Φ−〉 | ∣0〉 | ∣0〉 | x0∣0〉 − x1∣1〉 | σz |
| ∣Φ−〉 | ∣1〉 | ∣1〉 | x0∣1〉 − x1∣0〉 | σz σx |
| ∣Ψ+〉 | ∣0〉 | ∣0〉 | x0∣1〉 + x1∣0〉 | σx |
| ∣Ψ+〉 | ∣1〉 | ∣1〉 | x0∣0〉 + x1∣1〉 | I |
| ∣Ψ−〉 | ∣0〉 | ∣0〉 | x0∣1〉 − x1∣0〉 | σz σx |
| ∣Ψ−〉 | ∣1〉 | ∣1〉 | x0∣0〉 − x1∣1〉 | σz |
a Alice's measurement result. b Charlie's measurement result. c David's measurement result. d Bob's Unitary operator.
This subsection's protocol agrees with the previous work by Wang et al [42] who proposed a Hierarchical Quantum Information Splitting which also can be used as a Quantum Controlled Teleportation with Two Controllers, but with different channel state. The advantage of our channel state is that it only requires Hadamard and CNOT gates to build it. Moreover, it can be applied to build a bidirectional protocol as described in the following subsection.
2.2. Bidirectional quatum controlled teleportation with two controllers
In this subsection, four characters are introduced, Alice and Bob as the senders as well as the receivers, Charlie and David as the first and second controller, respectively. Before the teleportation process, they pre-share a six-qubit entangled state to be used as the teleportation channel. By using the controllers' OR-logic-gate-like behaviour in the previous subsection, we build the state by using equation(1) and preparing another two ∣0〉 qubit states as ∣ψ〉1234 ⨂ ∣00〉56. The additional qubits will be used for the transmission from Bob to Alice in the bidirectional teleportation. We apply a Hadamard gate on qubit 5 and a CNOT gate on qubit 6 with qubit 5 as the control qubit, followed by another CNOT gate on qubit 5 with qubit 3 as the control qubit. The final result is
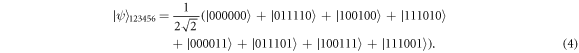
All of the reduced density matrix rank of the state is greater than one, indicating that the state is completely entangled [39].
We distribute the channel qubit to the four parties as 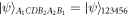 . Qubit A1 and A2 belong to Alice, B1 and B2 belong to Bob, C and D belongs to Charlie and David, respectively. Alice and Bob has an arbitrary one-qubit state as
. Qubit A1 and A2 belong to Alice, B1 and B2 belong to Bob, C and D belongs to Charlie and David, respectively. Alice and Bob has an arbitrary one-qubit state as
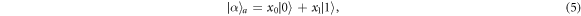
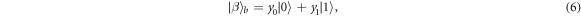
respectively, with x0, x1, y0 and y1 are complex numbers satisfying normalization condition 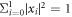 and
and  .
.
The teleportation circuit scheme is shown in figure 2. Alice and Bob start the teleportation process by mixing their state into the channel state as  . Alice and Bob perform Bell State measurement [1] independently on qubit aA1 and bB1, respectively. Suppose their measurement results are both ∣Φ+〉, the remaining qubits collapse to
. Alice and Bob perform Bell State measurement [1] independently on qubit aA1 and bB1, respectively. Suppose their measurement results are both ∣Φ+〉, the remaining qubits collapse to
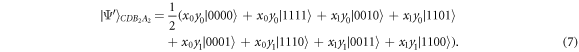
Charlie and David perform a computational bases measurement independently. Similarly as in Section 2.1, the remaining qubits collapse to
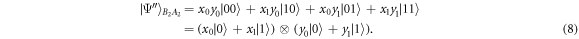
For this case, Alice and Bob perform nothing on their qubit. The teleportation is complete.
Figure 2. Bidirectional quantum controlled teleportation with two controllers circuit scheme. BSM, CBM, U, and CC, refers to Bell State Measurement, computational bases measurement, Unitary Operation, and Classical Channel, respectively.
Download figure:
Standard image High-resolution imageAll of the possible measurement result is presented in table 2. The table shows that both receivers cannot rebuild their corresponding initial state without the help of at least one of the controllers. As in the previous subsection, the two controllers' agreement combination mimics the OR logic gate. This result is applied to the cyclic teleportation scheme as described in the next subsection.
Table 2. List of Alice, Bob, and Charlie/David's measurement results, Alice and Bob's qubit state, Alice and Bob's unitary operator.
| MA a | MB b | MC c | MD d |
 state state | UA e | UB f |
|---|---|---|---|---|---|---|
| ∣Φ+〉 | ∣Φ+〉 | ∣0〉 | ∣0〉 | (x0∣0〉 + x1∣1〉) ⨂ (y0∣0〉 + y1∣1〉) | I | I |
| ∣Φ+〉 | ∣Φ+〉 | ∣1〉 | ∣1〉 | (x0∣1〉 + x1∣0〉) ⨂ (y0∣1〉 + y1∣0〉) | σx | σx |
| ∣Φ+〉 | ∣Φ−〉 | ∣0〉 | ∣0〉 | (x0∣0〉 + x1∣1〉) ⨂ (y0∣0〉 − y1∣1〉) | I | σz |
| ∣Φ+〉 | ∣Φ−〉 | ∣1〉 | ∣1〉 | (x0∣1〉 + x1∣0〉) ⨂ (y0∣1〉 − y1∣0〉) | σx | σz σx |
| ∣Φ+〉 | ∣Ψ+〉 | ∣0〉 | ∣0〉 | (x0∣0〉 + x1∣1〉) ⨂ (y0∣1〉 + y1∣0〉) | I | σx |
| ∣Φ+〉 | ∣Ψ+〉 | ∣1〉 | ∣1〉 | (x0∣1〉 + x1∣0〉) ⨂ (y0∣0〉 + y1∣1〉) | σx | I |
| ∣Φ+〉 | ∣Ψ−〉 | ∣0〉 | ∣0〉 | (x0∣0〉 + x1∣1〉) ⨂ (y0∣1〉 − y1∣0〉) | I | σz σx |
| ∣Φ+〉 | ∣Ψ−〉 | ∣1〉 | ∣1〉 | (x0∣1〉 + x1∣0〉) ⨂ (y0∣0〉 − y1∣1〉) | σx | σz |
| ∣Φ−〉 | ∣Φ+〉 | ∣0〉 | ∣0〉 | (x0∣0〉 − x1∣1〉) ⨂ (y0∣0〉 + y1∣1〉) | σz | I |
| ∣Φ−〉 | ∣Φ+〉 | ∣1〉 | ∣1〉 | (x0∣1〉 − x1∣0〉) ⨂ (y0∣1〉 + y1∣0〉) | σz σx | σx |
| ∣Φ−〉 | ∣Φ−〉 | ∣0〉 | ∣0〉 | (x0∣0〉 − x1∣1〉) ⨂ (y0∣0〉 − y1∣1〉) | σz | σz |
| ∣Φ−〉 | ∣Φ−〉 | ∣1〉 | ∣1〉 | (x0∣1〉 − x1∣0〉) ⨂ (y0∣1〉 − y1∣0〉) | σz σx | σz σx |
| ∣Φ−〉 | ∣Ψ+〉 | ∣0〉 | ∣0〉 | (x0∣0〉 − x1∣1〉) ⨂ (y0∣1〉 + y1∣0〉) | σz | σx |
| ∣Φ−〉 | ∣Ψ+〉 | ∣1〉 | ∣1〉 | (x0∣1〉 − x1∣0〉) ⨂ (y0∣0〉 + y1∣1〉) | σz σx | I |
| ∣Φ−〉 | ∣Ψ−〉 | ∣0〉 | ∣0〉 | (x0∣0〉 − x1∣1〉) ⨂ (y0∣1〉 − y1∣0〉) | σz | σz σx |
| ∣Φ−〉 | ∣Ψ−〉 | ∣1〉 | ∣1〉 | (x0∣1〉 − x1∣0〉) ⨂ (y0∣0〉 − y1∣1〉) | σz σx | σz |
| ∣Ψ+〉 | ∣Φ+〉 | ∣0〉 | ∣0〉 | (x0∣1〉 + x1∣0〉) ⨂ (y0∣0〉 + y1∣1〉) | σx | I |
| ∣Ψ+〉 | ∣Φ+〉 | ∣1〉 | ∣1〉 | (x0∣0〉 + x1∣1〉) ⨂ (y0∣1〉 + y1∣0〉) | I | σx |
| ∣Ψ+〉 | ∣Φ−〉 | ∣0〉 | ∣0〉 | (x0∣1〉 + x1∣0〉) ⨂ (y0∣0〉 − y1∣1〉) | σx | σz |
| ∣Ψ+〉 | ∣Φ−〉 | ∣1〉 | ∣1〉 | (x0∣0〉 + x1∣1〉) ⨂ (y0∣1〉 − y1∣0〉) | I | σz σx |
| ∣Ψ+〉 | ∣Ψ+〉 | ∣0〉 | ∣0〉 | (x0∣1〉 + x1∣0〉) ⨂ (y0∣1〉 + y1∣0〉) | σx | σx |
| ∣Ψ+〉 | ∣Ψ+〉 | ∣1〉 | ∣1〉 | (x0∣0〉 + x1∣1〉) ⨂ (y0∣0〉 + y1∣1〉) | I | I |
| ∣Ψ+〉 | ∣Ψ−〉 | ∣0〉 | ∣0〉 | (x0∣1〉 + x1∣0〉) ⨂ (y0∣1〉 − y1∣0〉) | σx | σz σx |
| ∣Ψ+〉 | ∣Ψ−〉 | ∣1〉 | ∣1〉 | (x0∣0〉 + x1∣1〉) ⨂ (y0∣0〉 − y1∣1〉) | I | σz |
| ∣Ψ−〉 | ∣Φ+〉 | ∣0〉 | ∣0〉 | (x0∣1〉 − x1∣0〉) ⨂ (y0∣0〉 + y1∣1〉) | σz σx | I |
| ∣Ψ−〉 | ∣Φ+〉 | ∣1〉 | ∣1〉 | (x0∣0〉 − x1∣1〉) ⨂ (y0∣1〉 + y1∣0〉) | σz | σx |
| ∣Ψ−〉 | ∣Φ−〉 | ∣0〉 | ∣0〉 | (x0∣1〉 − x1∣0〉) ⨂ (y0∣0〉 − y1∣1〉) | σz σx | σz |
| ∣Ψ−〉 | ∣Φ−〉 | ∣1〉 | ∣1〉 | (x0∣0〉 − x1∣1〉) ⨂ (y0∣1〉 − y1∣0〉) | σz | σz σx |
| ∣Ψ−〉 | ∣Ψ+〉 | ∣0〉 | ∣0〉 | (x0∣1〉 − x1∣0〉) ⨂ (y0∣1〉 + y1∣0〉) | σz σx | σx |
| ∣Ψ−〉 | ∣Ψ+〉 | ∣1〉 | ∣1〉 | (x0∣0〉 − x1∣1〉) ⨂ (y0∣0〉 + y1∣1〉) | σz | I |
| ∣Ψ−〉 | ∣Ψ−〉 | ∣0〉 | ∣0〉 | (x0∣1〉 − x1∣0〉) ⨂ (y0∣1〉 − y1∣0〉) | σz σx | σz σx |
| ∣Ψ−〉 | ∣Ψ−〉 | ∣1〉 | ∣1〉 | (x0∣0〉 − x1∣1〉) ⨂ (y0∣0〉 − y1∣1〉) | σz | σz |
a Alice's measurement result. b Bob's measurement result. c Charlie's measurement result. d David's measurement result. e Alice's Unitary operator. f Bob's Unitary operator.
2.3. Cyclic quantum controlled teleportation with two controllers.
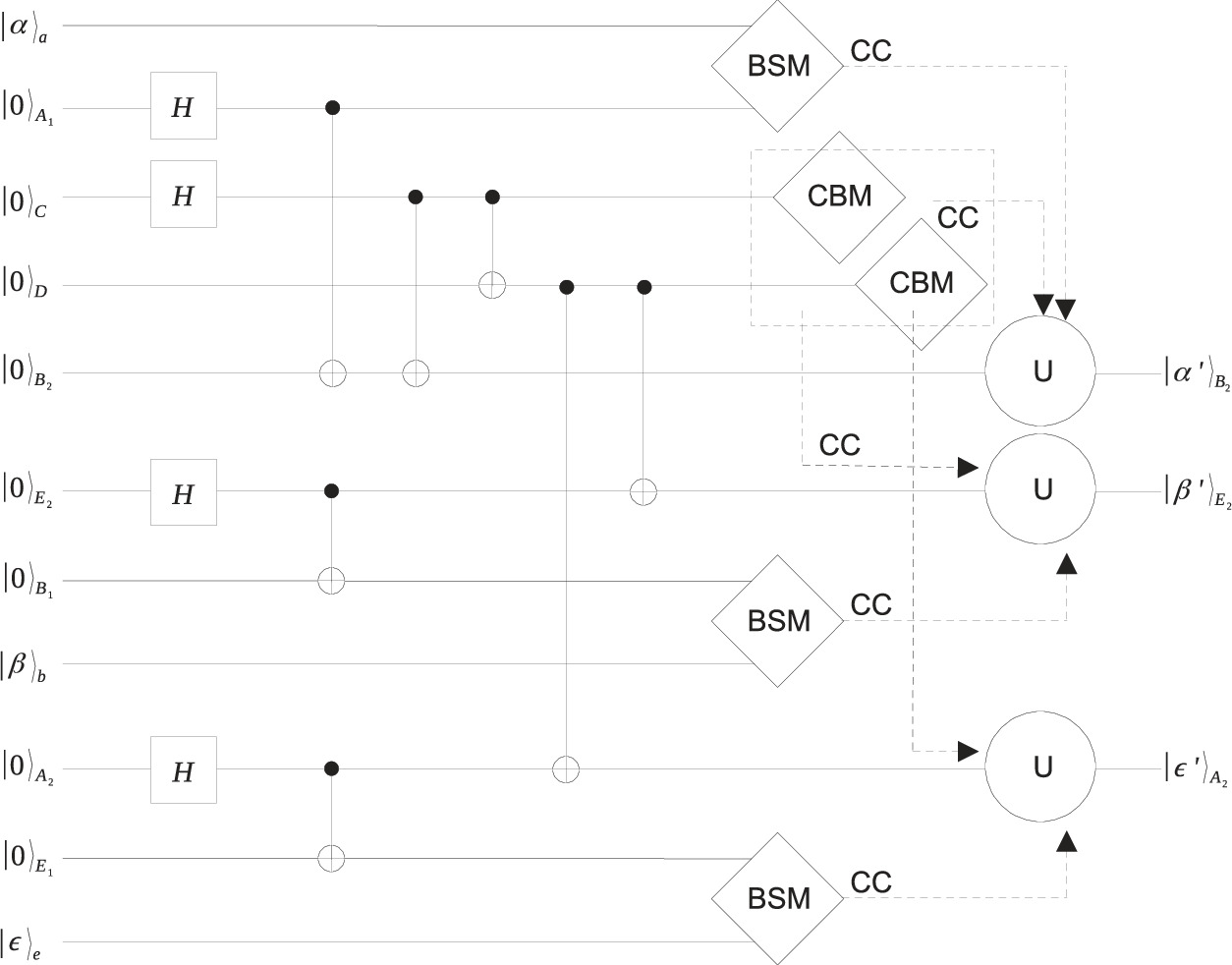
In this subsection, five characters are introduced. Alice as the first senders (also as the third receiver), Bob as the second senders (also as the first receiver), Evelyn as the third sender (also as the second receiver), Charlie as the first controller, and David as the second controller. Taking the controllers' OR-logic-gate-like behaviour in the previous subsection, we built the channel state by using equation(4) and preparing other two ∣0〉 qubit states as ∣ψ〉123456 ⨂ ∣00〉78. Qubits 7 and 8 will be used as the third transmission channel in the cyclic scheme. We perfrom a Hadamard gate on qubit 7 followed by a CNOT gate on qubit 8 with qubit 7 as the control qubit. After that, we apply another CNOT gate on qubit 7 with qubit 3 as the control qubit. This resulting a state
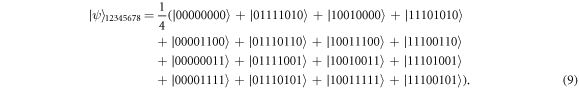
The channel qubit is distributed to the five parties as 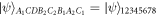 . Qubit A1 and A2 belong to Alice, B1 and B2 belong to Bob, C belongs to Charlie, D belongs to David, E1 and E2 belong to Evelyn.
. Qubit A1 and A2 belong to Alice, B1 and B2 belong to Bob, C belongs to Charlie, D belongs to David, E1 and E2 belong to Evelyn.
Alice, Bob, and Evelyn, have an arbitrary state
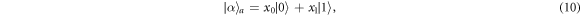
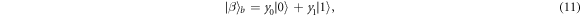

respectively, with x0, x1, y0, y1, z0 and z1 are complex numbers satisfying normalization condition  ,
,  , and
, and 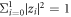 . Alice wants to teleport her state to Bob, Bob to Evelyn, and Evelyn to Alice. They start the teleportation process by mixing their initial state with the channel state as
. Alice wants to teleport her state to Bob, Bob to Evelyn, and Evelyn to Alice. They start the teleportation process by mixing their initial state with the channel state as 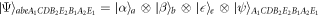 . The teleportation circuit scheme is shown in figure 3.
. The teleportation circuit scheme is shown in figure 3.
Figure 3. Cyclic quantum controlled teleportation with two controllers circuit scheme. BSM, CBM, U, and CC, refers to Bell State Measurement, computational bases measurement, Unitary Operation, and Classical Channel, respectively.
Download figure:
Standard image High-resolution imageAlice, Bob, and Evelyn perform a Bell State Measurement independently on qubit aA1, bB1, and eE1, respectively. Suppose their measurement results are all ∣Φ+〉, the remaining qubits collapse to
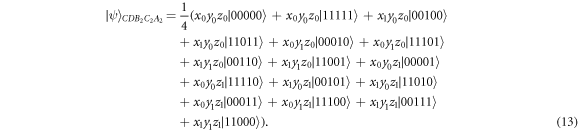
Similarly, as in the previous subsections, Charlie and David, as the controllers, perform a computational bases measurement independently. Suppose their measurement results are ∣0〉, the remaining qubits can be written as

Alice informs her measurement result to Bob, Bob to Evelyn, and Evelyn to Alice. Charlie and David broadcast their measurement result to the other three parties. Using the information received, for this case, Alice, Bob, and Evelyn perform nothing on their qubit. Equation (14) shows that Alice already receives Evelyn's initial state, as well as Bob and Evelyn receive Alice and Bob's initial state, respectively. The other possible measurement results are evaluated similarly. As in the previous two subsections, each receiver cannot rebuilt their state without the help of at least one of the two controllers, which again, micics the OR logic gate.
The work in [43] proposed a tridirectional quantum teleportation via a twenty-one-qubit state as the quantum channel, with each seven-qubit state facilitating the transmission in each direction. The work shows that any one of the three parties can send their arbitrarily entangled states to the other two simultaneously. This subsection protocol can also be used in another tridirectional scheme, i.e., asymmetric tridirectional controlled teleportation, in which one of the parties can send a single qubit state and a two-qubit state into another two with OR-logic-gate-like controllers via a twenty-four qubit channel state, which each eight-qubit state responsible for the transmission between each two parties. The channel used in each transmission is  , where ∣ψ〉12345678 is from equation (9), in which a single qubit state is transmitted from A1 to B1, and a two-qubit state is transmitted from B2
B3 to A2
A3 with one of C and D's cooperations. The whole tridirectional channel state is
, where ∣ψ〉12345678 is from equation (9), in which a single qubit state is transmitted from A1 to B1, and a two-qubit state is transmitted from B2
B3 to A2
A3 with one of C and D's cooperations. The whole tridirectional channel state is 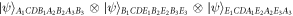 . This channel still uses this subsection's channel state in equation (9), indicating that the OR-logic-gate-like controllers properties are still applied, i.e., the tridirectional transmission can succeed with one of the two controllers' cooperation, and it does not matter which one.
. This channel still uses this subsection's channel state in equation (9), indicating that the OR-logic-gate-like controllers properties are still applied, i.e., the tridirectional transmission can succeed with one of the two controllers' cooperation, and it does not matter which one.
2.4. Generalization to multi-way quantum controlled teleportation with N controllers
In this subsection, we generalize the previous subsections' result to build a Multi-Way Quantum Controlled Teleportation with N controllers. All of the protocols, i.e., the one-way, bidirectional, and cyclic, has the similar two controllers combination, that is mimicing the OR logic gate. These properties come from the nature of how the channel state is entangled. If we observe the channel used in the three protocols, equations (1), (4) and (9), the controllers' qubit (qubit 2 and 3) always has the same state in each term, which is if we measure one of them in computational bases, the remaining controller's qubit will be in an untangled state (resulting the OR logic gate properties). Then, we can build the one-way protocol with N controllers using a channel state
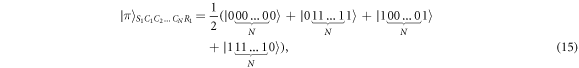
with S1, R1, and Ck for k = {1, 2,...,N} is the sender, the receiver, and the kth controller, respectively. The channel state makes the one-way teleportation will success with only one of the controllers agreement, and it does not matter which one.
We observe the senders and receivers qubit on equations (4) and (9). In the last two subsections, we added the additional sender and receiver by preparing two ∣0〉 states and transform it into a Bell State, i.e., by performing a Hadamard followed by a CNOT gate, then entangling it with the channel state by performing another CNOT gate on one of the qubit in the Bell state with qubit 3 as the control qubit, see sub 2.2 and 2.3. We can use the idea to build a channel state that can be used by multi-senders and multi-receivers. The channel building operation is shown in equation (16).
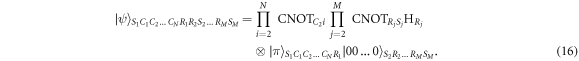
The CNOT and
and 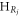 gates are entangling the qubit Rj
and Sj
, the CNOT
gates are entangling the qubit Rj
and Sj
, the CNOT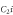 is entangling the qubit Rj
Sj
with Qubit S1
C1
C2...CN
R1. The CNOT
is entangling the qubit Rj
Sj
with Qubit S1
C1
C2...CN
R1. The CNOT and
and  gates must be applied first before the CNOT
gates must be applied first before the CNOT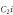 gate. The resulting state can be used as the channel to teleport a single state form sender Sk
to receiver Rk
with the cooperation of one of the controlles C1 to CN
, with k = {1, 2, 3,...,M}.
gate. The resulting state can be used as the channel to teleport a single state form sender Sk
to receiver Rk
with the cooperation of one of the controlles C1 to CN
, with k = {1, 2, 3,...,M}.
The protocol detail is similar with the previous proposed protocols. Suppose each sender Sk
has an arbitrary qubit 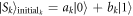 with ak
and bk
are complex numbers satisfying normalization conditions
with ak
and bk
are complex numbers satisfying normalization conditions  , for k = {1, 2, 3,...,M}. Each sender mixes their qubit into the corresponding channel qubit and performs a Bell State Measurement, i.e., on qubit initialk
and Sk
. After that, the controllers perform computational bases measurement. Each sender and the controllers (who agreed to cooperate) send their measurement results to the corresponding receiver, i.e., Sk
to Rk
and the controllers broadcast to all of the receivers. Each receiver performs an appropriate unitary operation and the teleportaion is finish. The explanation implies that the Multi-Way Quantum Controlled Teleportation with N Controller protocol can be achieved by using a channel state in equation (16), Bell State measurement by the senders, computational bases measurement by the controllers, assisted with classical communication followed by unitary operations. The receivers need only one of the controllers' agreement (and it does not matter which one) to rebuild the corresponding senders' initial state.
, for k = {1, 2, 3,...,M}. Each sender mixes their qubit into the corresponding channel qubit and performs a Bell State Measurement, i.e., on qubit initialk
and Sk
. After that, the controllers perform computational bases measurement. Each sender and the controllers (who agreed to cooperate) send their measurement results to the corresponding receiver, i.e., Sk
to Rk
and the controllers broadcast to all of the receivers. Each receiver performs an appropriate unitary operation and the teleportaion is finish. The explanation implies that the Multi-Way Quantum Controlled Teleportation with N Controller protocol can be achieved by using a channel state in equation (16), Bell State measurement by the senders, computational bases measurement by the controllers, assisted with classical communication followed by unitary operations. The receivers need only one of the controllers' agreement (and it does not matter which one) to rebuild the corresponding senders' initial state.
As a comparison, the work in [44] evaluates a controlled quantum broadcast protocol in which a receiver can send 2N qubit states into 2N receivers. This subsection protocol can also be modified into the broadcast one. It can be done by setting the ownership of all Sk qubits in equation(16) into only one sender. It modifies the protocol into the broadcast one in which a sender can send M single qubit states into M receivers with the cooperation of N controllers. The modification does not change the controllers' qubits; hence, the OR-logic-gate-like controllers' combination properties remain. Then, even though there are N controllers, the resulting broadcast teleportation only needs one of the controllers' cooperation, and it does not matter which one.
3. Effect of the phase-damping and amplitude-damping noise
Noise is an inevitable phenomenon. So looking at the protocol's performance in a noisy environment becomes important. In this section, we evaluate the effect of a noisy environment on the teleportation process. We choose the noisy environment in the form of phase-damping noise (PDN) and amplitude-damping noise (ADN) represented by the Kraus Operators [45] as
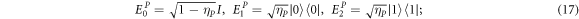
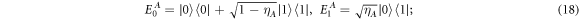
where ηP (0 ≤ ηP ≤ 1) and ηA (0 ≤ ηA ≤ 1) are decoherence rate of the PDN and ADN noise, respectively. The parameter describes the possibility of occurring error in the quantum state due to travel qubit [34].
The evaluation started by taking account to the general case, i.e., multi-way quantum controlled teleportation with N controllers. Before the teleportation prosess, we asume the controllers prepare the channel state as in equation (16), then distribute it to the senders and the receivers. The effect of the noisy channel can be written in Kraus Operators acting on the density operator of the channel state, i.e.,  , as
, as
with r ∈ {P, A}, {m1, m2,...,m2M } = {0, 1, 2} for r = P, and {m1, m2,...,m2M } = {0, 1} for r = A. The subscript Ri and Sj for {i, j} = {1, 2,...,M} indicates which qubits are performed by the Kraus Operator. In equation (19), we assume that each senders and receivers' channel qubits have the same decoherence rate parameter value.
In the teleportation process, each sender mixes their initial state with the channel state, and the teleportation is done as described in subsection 2.4. After the teleportation process, the density matrix of the output state becomes
with U is the unitary operation to describe the teleportation process, i.e.,  , with
, with 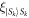 is BSM on qubit ∣Sk
〉 and Sk
by Sender Sk
,
is BSM on qubit ∣Sk
〉 and Sk
by Sender Sk
, 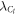 is single qubit measurement by Controller Cl
, and
is single qubit measurement by Controller Cl
, and 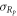 is unitary operation by Receiver Rp
, for {k, p} = {1, 2,...,M} and l = {1, 2,...,N}.
is unitary operation by Receiver Rp
, for {k, p} = {1, 2,...,M} and l = {1, 2,...,N}.
We consider the effect of the noise environment to the fidelity value. It can be calculated by
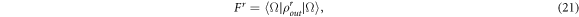
with ∣Ω〉 is the actual output state, i.e., the output state if we take noisless case. We evaluate the effect of the noises in the following subsections.
3.1. Phase-damping noise
We evaluate the phase-damping noise case first. We choose M = 1 for simplicity. The protocol reduces to one-way scheme as in section 2.1. Equation (19) reduces to 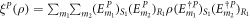 , with
, with 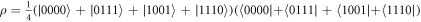 , see equation (1). The equation can be written as
, see equation (1). The equation can be written as
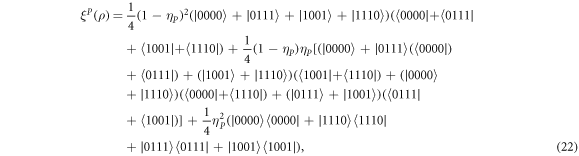
The trace of equation (22) is always equal to one (we mention it for the discussion in the next section). By using equation (20), after detailed calculations, the output density operator is
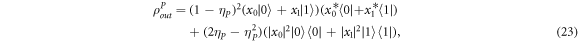
for any sender and controllers' measurement result. From equation (21) the fidelity value is
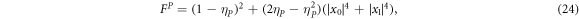
which depends on the decoherence rate and initial state's amplitude parameters only. To illustrate it, we plot the fidelity for vaious ηP and ∣x0∣2 value as shown in figure 4(a). Suppose we take the acceptable fidelity value to be equal to 0.8. Then, we add a contour line to divide the greater or lower area than the value. The region outside the contour represents the greater-than case. The figure shows that the protocol works well (the fidelity is always greater than the acceptable value for any initial state) for a relatively low decoherence rate of about 0.2 or less. Besides that, the protocol only has an acceptable fidelity for some particular initial states. However, if ∣x0∣2 = {0, 1}, the fidelity always equals one, even in a noisy environment.
Figure 4. (a) Effect of the phase-damping noise on the teleportation fidelity value for various ηP
and ∣x0∣2 value for the proposed one-way teleportation. The black curve indicates the contour line of the acceptable fidelity value (0.8). (b) Entropy (S) and fidelity (F) value of the output density operator affected by phase-damping noise for 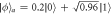 , (c)
, (c) 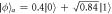 , and (d)
, and (d) 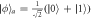 .
.
Download figure:
Standard image High-resolution imageAs an alternative method in the noise evaluation, we also calculate the entropy of the output density operator. Using the Von Neumann entropy formula, 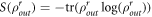 , we plot the entropy (S) of some initial states and the corresponding fidelity (F) value as shown in figures 4(b)–(d). The plots show that the entropy analysis agreed with the fidelity value, i.e., the lower the F, the higher the S. The higher S means higher information loss, implying lower F, indicating that the teleported state is less similar to the initial state. For some particular cases that satisfy ∣x0∣2 = {0, 1}, the output density operator in equation (23) reduces to a pure state, which has a zero-value entropy, meaning there is no information loss. This also agrees with the fidelity value that is always equal to one.
, we plot the entropy (S) of some initial states and the corresponding fidelity (F) value as shown in figures 4(b)–(d). The plots show that the entropy analysis agreed with the fidelity value, i.e., the lower the F, the higher the S. The higher S means higher information loss, implying lower F, indicating that the teleported state is less similar to the initial state. For some particular cases that satisfy ∣x0∣2 = {0, 1}, the output density operator in equation (23) reduces to a pure state, which has a zero-value entropy, meaning there is no information loss. This also agrees with the fidelity value that is always equal to one.
For the bidirectional, cyclic, or the other M values schemes, the analysis can be done similarly. We evaluate the amplitude-damping noise in the following subsection.
3.2. Amplitude-damping noise
Similarly as in the previous subsections, we choose M = 1. Equation (19) reduces to  , or can be written as
, or can be written as
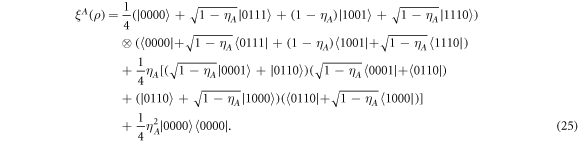
Its trace is always equal to one (again, we mention it for the discussion in the next section). Using equation (20), one can show that the output density operator depends on the sender and controllers' measurement results. Then, we present the operator as a statistical mixture  with ρi
is the possible output density operator, and Pi
is its corresponding probability. After detailed calculations, it can be written as
with ρi
is the possible output density operator, and Pi
is its corresponding probability. After detailed calculations, it can be written as
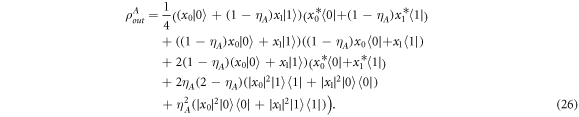
Using equation (21), the mixture produces an average fidelity value equation, i.e.,
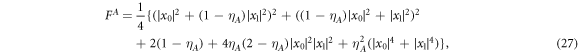
which only depends on the decoherence rate and the initial state amplitude parameters only. We illustrate the fidelity by plotting it with respect to the parameters as shown in figure 5(a). We also added a contour line to represent acceptable fidelity value (0.8). The area above the contour line has a greater than 0.8 value. We also interested in the entropy evaluation of equation (26). We plot the graph for some initial state to illustrate it, as shown in figures 5(b) and (c), showing that the entropy analysis also agreed with the fidelity analysis, similarly as in the PDN case.
Figure 5. (a) Effect of the amplitude-damping noise on the average teleportation fidelity value for various ηP
and ∣x0∣2 value for the proposed one-way teleportation. The black curve indicates the contour line of the acceptable fidelity value (0.8). (b) Entropy (S) and fidelity (F) value of the output density operator affected by amplitude-damping noise for 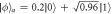 and (c)
and (c)  .
.
Download figure:
Standard image High-resolution imageWe compare the fidelity of the ADN and the PDN case by plotting it with respect to the decoherence rate parameter for various initial qubit state amplitude parameter, as shown in figures 6(a)–(c). The comparison shows that the teleportation performs better under the PDN for relatively small (and large) ∣x0∣2 parameter value, i.e., values close to zero or one. However, for ∣x0∣2 = 0.5, it performs better under the ADN for all of the decoherence rate parameter.
Figure 6. Comparison of fidelity affected by the amplitude-damping noise (ADN) and phase-damping noise (PDN) for (a) ∣x0∣2 = 0.1 (a similar graph also produced for ∣x0∣2 = 0.9), (b) ∣x0∣2 = 0.3 (a similar graph also produced for ∣x0∣2 = 0.7), and (c) ∣x0∣2 = 0.5.
Download figure:
Standard image High-resolution imageOur noise analysis assumption (the last sentence of the second paragraph of this section) is different from other previous works [29, 34, 35, 38], which will be discussed in the next section.
4. Discussion
In this section, we compare our proposed protocols with other similar studies. We compute the efficiency by using [46]
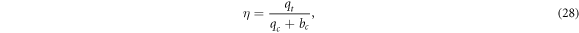
with qt , qc , and bc is number of teleported qubit, number of channel qubit, and number of classical bit required, respectively, and compare with other protocols as shown in table 3. It shows that the efficiencies of the proposed one-way, bidirectional, and cyclic protocols are not among the highest. However, the main novelty of the proposed protocols is that they can be used to teleport information that requires an OR-like controller's combination agreement, which can not be done with other existing protocols.
Table 3. Comparison between the proposed quantum teleportation protocol with previous studies. QCT, BQCT, CQCT, MQCT refer to one-way, bidirectional, cyclic, and multi-way quantum controlled teleportation. BQT refers to bidirectional quantum teleportation.
| Scheme | ToP a | NoQT b | ToQC c | Controller | Efficiency |
|---|---|---|---|---|---|
| [47] | QCT | 1 | GHZ-like | Yes | 16.6% |
| [34] | BQCT | 4 | 7-qubit | Yes | 26.6% |
| [48] | BQCT | 2 | 6-qubit | Yes | 25% |
| [35] | BQCT | 4 | 8-qubit | Yes | 25% |
| [49] | BQCT | 3 | 7-qubit | Yes | 21% |
| [50] | BQCT | 4 | 9-qubit | Yes | 22.2% |
| [51] | BQT | 3 | 5-qubit cluster | No | 33% |
| [11] | QCT | 1 | GHZ-like | Yes | 16.6% |
| [36] | BQCT | 5 | 8-qubit cluster | Yes | 38% |
| [28] | BQCT | 4 | 9-qubit | Yes | 22.2% |
| [37] | BQT | 2N | 2N Bell states | No | 28% |
| [29] | BQCT | 4 | 8-qubit | Yes | 26.6% |
| [52] | CQCT | 6 | 10-qubit | Yes | 31.5% |
| Section 2.1 | QCT | 1 | 4-qubit | Yes | 14.3% |
| Section 2.2 | BQCT | 2 | 6-qubit | Yes | 16.7% |
| Section 2.3 | CQCT | 3 | 8-qubit | Yes | 17.6% |
| Section 2.4 | MQCT | M | (2M+N)-qubit | Yes | up to 20% |
a Type of protocol. b Number of qubit transmitted. c Type of quantum channel.
Specifically, for the multi-way protocol (see subsection 2.4), qt , qc , and bc are equal to M, 2M + N, and 2M(from BSM in each sender)+M(from controllers) respectively. The bc parameter value does not depend on the number of controllers N because the teleportation only needs one of the controllers' cooperation, so it only needs one classical bit. However, the controller needs to broadcast his measurement result to every receiver; hence it needs M classical bits. Then, the efficiency can be written as
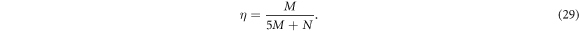
The upper bound of the efficiency value is achieved by taking the limit of M into infinity with a finite value of N, which makes the efficiency equal to up to 20%.
In the proposed protocols, we used the traditional teleportation procedures, i.e., the teleportation is done via an entangled channel state, and projections measurements assisted with classical communication without introducing any additional operations or ancillary qubits. Hence, the four-qubit, six-qubit, and eight-qubit channel states are the minimum number of qubits required to do a one-way, bidirectional, and cyclic teleportation with two controllers, respectively [1, 8]. As a comparison, Ahmadkhaniha et al [53] proposed an alternative teleportation method, i.e., an enable-based bidirectional quantum teleportation protocol, leveraging distributed quantum gates with minimal resource requirements. They showed that by using their proposed method, the entangled state required as the quantum channel can be reduced to a more efficient number. However, the application of that method in this work's protocols is not part of this article and is left for future work.
In the previous section, we evaluated the effect of phase-damping noise and amplitude-damping noise on the proposed protocols' fidelity value. As an alternative method, we also evaluated its entropy value and showed that for the PDN case, there are some particular initial qubit states that can make the fidelity reaches a unit value (and the entropy is zero, indicating no information loss), which is similar to the previous works' result [29, 34, 35, 38]. However, it does not happen in the ADN case. Despite reaching the similar results with other studies, we used a different assumption: the senders and receivers' channel qubits have the same decoherence rate parameter value but independent Kraus Operators' indexes as in equation (19). In contrast, the other studies used dependent (the same) Kraus operators' indexes. The channel density operators affected by the PDN may have a non-unit trace value. For example, if we take the decoherence rate equal to one, the work in [29, 34, 35, 38] will have a phase-damping noise density operator as 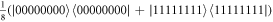 ,
,  ,
,  , and
, and  〈000000000∣ + ∣111111111〉〈111111111∣), respectively. A similiar result also happen for the ADN case. All of the density operators have an interpretation difficulty and a non-unit trace value, one of the density operator properties for pure or mixed state. As a comparison, our assumption always keeps the trace value equal to one for any decoherence rate value, thus avoiding the difficulties of previous studies.
〈000000000∣ + ∣111111111〉〈111111111∣), respectively. A similiar result also happen for the ADN case. All of the density operators have an interpretation difficulty and a non-unit trace value, one of the density operator properties for pure or mixed state. As a comparison, our assumption always keeps the trace value equal to one for any decoherence rate value, thus avoiding the difficulties of previous studies.
5. Conclusion
We successfully realized a one-way, bidirectional, and cyclic quantum controlled teleportation protocol with two controllers. We showed that the teleportation only requires one of the controllers' cooperation, and it does not matter which one, resulting in an OR-logic-gate-like controllers' combination agreement. We also generalized the result to build a multi-way quantum controlled teleportation with N controllers, which has the same controllers' combination properties. The proposed protocols are useful when the information to be teleported needs a special controllers' agreement combination, i.e., OR-logic-gate-like. We also discussed the proposed protocol fidelity value in the presence of phase-damping noise and amplitude-damping noise, and demonstrated the effect of these noises on one-way scheme. We also calculated the entropy of the output density operator as an alternative noise evaluation method. The evaluation showed that the fidelity and entropy analysis agreed with each other. It also showed that the fidelity value depends only on the decoherence rate and the initial state's amplitude parameter. We also compared the result between the two noises and showed that the teleportation works better under the phase-damping noise for a relatively small (and large) ∣x0∣2 parameter value, i.e., values close to zero or one. However, if ∣x0∣2 equals one-half, it performs better under the amplitude-damping noise for all decoherence rate parameters. Interestingly, for the case of phase-damping noise, there are some particular initial states that make the fidelity always equal to one (and the entropy equal to zero) for any decoherence rate parameter.
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).