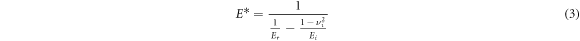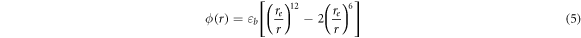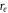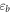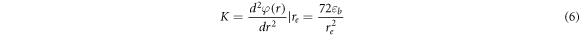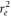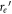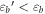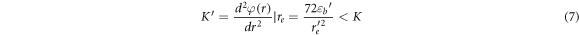Abstract
Determination of the intrinsic Young's modulus (E) is essential for material design and applications. However, the commonly used micro/nano-indentation method does not give accurate intrinsic Young's modulus, since the measured modulus comes from the damaged zone under the indent tip. In this study, we analyze the intrinsic Young's modulus or that without local damage caused by indentation, and determine that the intrinsic Young's modulus can be determined by extrapolation of the E ∼ load curve as the indentation load approaches zero. To support this finding, indentation behaviors of five ceramic materials (Al2O3, Si3N4, ZrO2, glass and cemented WC/Co) were analyzed and compared with those determined using an acoustic method. The intrinsic Young's modulus measured, e.g., using the acoustic method, are appropriate for material ranking, while Young's moduli of different materials measured by indentation under the same load could give misleading information because of different degrees of local damage to the materials under the indenter. Underlying mechanisms for the observed phenomena shown in this novel and unique study are elucidated based on the interatomic bonding. Hardness versus load curves show trends similar to those of Young's modulus. However, unlike the Young's modulus, the hardness values measured under the same load can be directly used to rank materials; the reason behind is also discussed.

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Young's modulus is one of the fundamental mechanical properties of materials, which reflects their atomic bond strength and resistance to elastic deformation. Young's modulus is usually measured using tensile test, bending test or non-destructive resonance frequency measurement [1, 2]. However, these methods are not suitable for determining Young's modulus of coatings or thin films on substrates, e.g., ceramic coatings or films on steel tools for resisting wear and corrosion [3–5]. For coatings and thin films, the nano/micro-indentation method is a routine method, which is also commonly used for in situ evaluation of local hardness and Young's moduli of bulk materials. Thus, it is of importance to analyze and ensure the accuracy of intrinsic Young's modulus of materials using the indentation method.
The indentation method has also been utilized to evaluate other mechanical properties, such as creep, stiffness, fracture toughness, etc [6–9]. Developing hardness and elastic modulus models for improved accuracy has never been stopped [10–15]. It is well known that the indentation load affects the hardness measurement; the indentation hardness increases with decreasing the indentation depth [16–18]. The situation is similar to the Young's modulus measurement [19]. Such phenomena are related to plastic deformations or dislocation generation in alloys during indentation [20–23]. Similar phenomena are observed for ceramic materials, which are suggested to be ascribed to the plasticity of ceramics as well [16, 24–27]. However, ceramic materials are generally brittle with little or rather limited plasticity, so that the influence of cracking or fracture on the results of indentation measurement is not unexpected [28]. For Young's modulus, the reason for the decreased value with increasing the indentation load is not very clear [19, 29, 30]. The change in Young's modulus may not be obvious for ductile or less brittle materials [31–33]. However, for hard and brittle ceramic materials, the decreasing trend with the indentation load is commonly observed [34–36].
For hardness, its value varies with the indentation load. Ranking hardness values of different materials can be achieved by performing indentation tests on the materials under the same indentation load, since hardness is the resistance of a material to plastic deformation or damage. However, the measured Young's moduli of the different materials may not be suitable for directly ranking their Young's modulus, since the Young's modulus is derived from the slope of the unloading curve [10]. Or in other words, the measured is not the intrinsic Young's modulus of the material but that of the damaged or plastically deformed zone under the indenter tip [37–39]. The degrees of damage or deformations of different materials under the same load are different, so the measured Young's moduli should not be directly used to rank Young's moduli of different materials.
Extensive studies on indentation methods for ceramic materials and associated cracking phenomena are more focused on fracture toughness analysis based on the crack length [6, 18, 28], which is a commonly used to the fracture toughness of ceramic materials [6, 40–42]. The accuracy of Young's modulus measurement via the indentation method receives less attention, although some relevant studies can be found in the literature. E Case and Zimmerman showed influences of crack density on Young's modulus, Poisson's ratio and Shear modulus, respectively [43, 44]. Although the influence of microcracks introduced by indentation on Young's modulus of ceramic materials was recognized, determining Young's modulus based on the microcrack-elasticity theories is complicated and not feasible due to the complex microcracking process during indentation. Efforts were made to generally relate the crack density and geometry with Young's modulus [45, 46], showing that a higher crack density generally corresponds to a lower Young's modulus. However, regardless of the accuracy in determining Young's modulus of a specific material when crack density, geometry, material, and parameter fitting are considered, ranking Young's moduli of different materials is less reliable since the generation of micro-cracks and their configurations are different in different materials under the same indentation condition. To address the above-mentioned issues, we conducted this study with the following objectives:
- (1)Understand the influence of the indentation load on Young's modulus and hardness measurements using the indentation method, under the influence of defects and cracking which are generated during indentation.
- (2)Finding a feasible approach to determine intrinsic Young's modulus of materials for effective property evaluation and ranking purposes.
- (3)Elucidate the underlying mechanisms for in-depth material analysis and accurate property evaluation.
2. Materials and methods
In this work, five materials, cemented WC-6%Co (50.0 × 7.2 × 7.6 mm3), Al2O3 (114.5 × 114.5 × 1.5 mm3), Si3N4 plate (50.0 × 50.0 × 4.0 mm3), ZrO2 (50.0 × 50.0 × 4.0 mm3) and standard quartz (fused glass) (Φ25.0 mm × 5.0 mm), were used to study their responses to indentation. The WC-Co and Al2O3 for the study were purchased from McMaster-Carr Supply Company. Samples of the materials, except the standard fused glass sample (with smooth surface), were ground with grit 80 and 180 sandpapers, followed by polished successively using 20 μm, 15 μm, 8 μm, and 3 μm diamond pastes. The polished samples were tested using an impulse excitation method on an IMCE instrument and analyzed with the RFDA software (IMCE NV, Genk, Belgium), which is a non-destructive technique for intrinsic Young's modulus measurement. At least five tests were performed for each material to obtain an average value of its Young's modulus. The same samples were tested using an Anton Paar NHT3 indention tester equipped with a Berkovich diamond tip for Nano/micro-indentation measurement. Eight loads from 10 mN to 500 mN were used for the indentation tests. The obtained results were analyzed with Oliver and Pharr's approach [10]. Macro-indentation was also performed for the materials using a Zwick/Roell ZHR type indenter with a Vickers tip to examine the crack development at the indentation site. A scanning electron microscope (SEM) with a Hitachi S-4800 FESEM was used to observe micro-cracks at the nano-indentation sites.
The nano/micro-indentation hardness and Young's modulus were calculated with Oliver and Pharr method [10]. The equation for the hardness measurement is expressed as
where P is the normal load, and AP is the projected area under the indenter. Young's modulus was calculated with the initial slope of the unloading curve, as pure elastic deformation occurs when unloading starts [10]. The reduced modulus Er is given as:
where S is the contact stiffness with slope fitting 98% to 40% of the max load of the unloading curve. Ap (hc ) is the projected area as a function of contact when maximum load is applied. β is a geometric factor equal to 1.034 for the Berkovich tip. The plane strain modulus E* is then calculated after Er is determined [10, 47]:
where Ei and νi are the elastic modulus and Poisson's ratio of the indenter, which is the diamond. The indentation modulus EIT then can be calibrated with a proposed sample Poisson's ratio, [10]:
These equations are derived from indentation-caused geometric changes and contact mechanics without considering defects or cracks generated by indentation. Figure 1 displays a flow diagram showing the arrangement of sample preparation and testing.
Figure 1. (A) flow chart of sample preparation and testing, including the impulse excitation and nanoindentation methods for determining Young's modulus and hardness for comparison.
Download figure:
Standard image High-resolution image3. Results and discussion
Figure 2 illustrates the measured Young's moduli and hardness of the five materials under different maximum indentation loads. As seen, Young's moduli decrease with increasing the indentation load. When the indentation load is larger than 200 ∼ 300 mN, Young's moduli tend to be independent of the load. For comparison, their Young's moduli were also measured using the non-destructive method (acoustic) and average values are illustrated in figure 2(a). The Young's moduli determined by the non-destructive measurement are 670 GPa for WC/Co, 430 GPa for Al2O3, 73 GPa for fused glass, 357 GPa for for Si3N4, and 276 GPa for ZrO2. The values obtained from the non-destructive measurement should represent their intrinsic Young's moduli, which are consistent with or close to those reported in the literature (in the range of 636–645 GPa for WC/Co, 384–436 GPa for Al2O3, 68–73 for fused glass, 270–330 GPa for Si3N4, and 200–215 GPa for ZrO2 and) [48–58]. As illustrated in figure 2(a), as the indentation load decreases, Young's moduli of the materials gradually approach the moduli measured using the non-destructive method. This phenomenon indicates that (1) the intrinsic Young's modulus could be determined by extrapolation of the E ∼ indention load curve as the indentation load approaches zero; (2) ranking Young's moduli of different materials using the modulus values obtained under a specific load is not appropriate; this can be clearly seen when looking at the ratio of measured Young's moduli of the different materials. The ratio of intrinsic Young's modulus of the five materials, measured with the non-destructive acoustic method, is 9.2:5.9:4.9:3.8:1.0. However, Young's moduli ratio measured using the indentation method varies with the indentation load. Under the load of 500 mN, the ratio becomes 6.4:4.7:3.6:3.6:1.0 (see values in table 1). Such a change makes Young's modulus ranking apart away from its intrinsic values, generating misleading information on the elastic moduli of the materials. The ratio determined using the extrapolated modulus values at P = 0 is close to the intrinsic one determined using the acoustic method.
Figure 2. (a) Young's modulus and (b) hardness of the five materials under study with respect to the indentation load. Young's moduli measured using the non-destructive acoustic method are given as the dashed lines illustrate.
Download figure:
Standard image High-resolution imageTable 1. Young's moduli of the five materials measured with the acoustic and indentation methods under different loads, respectively, and their ratios (relative to that of the fused glass).
| E Material | Intrinsic E (acoustic), GPa | Ratio | E, indentation P = 0 mN, GPa | Ratio | E, indentation P = 50 mN, GPa | Ratio | E, indentation P = 300 mN, GPa | Ratio | E, indentation P = 500 mN, GPa | Ratio |
|---|---|---|---|---|---|---|---|---|---|---|
| WC/Co | 670 | 9.2 | 630 | 8.6 | 575 | 7.9 | 470 | 6.7 | 430 | 6.4 |
| Al2O3 | 430 | 5.9 | 460 | 6.3 | 400 | 5.5 | 350 | 5 | 315 | 4.7 |
| Si3N4 | 357 | 4.9 | 300 | 4.1 | 283 | 3.9 | 265 | 3.8 | 243 | 3.6 |
| ZrO2 | 276 | 3.8 | 270 | 3.7 | 265 | 3.7 | 250 | 3.6 | 243 | 3.6 |
| Fused glass | 73 | 1 | 73.5 | 1 | 72.5 | 1 | 70 | 1 | 67.5 | 1 |
The variations in Young modulus with the indentation load come from the material damage in the vicinity of the indentation head, as schematically illustrated in figure 3. Young's modulus is measured based on the slope of the unloading curve, as illustrated in figure 3(b), which reflects the response of the material to elastic deformation. However, such measured Young's modulus is the modulus of the damaged zone under the indenter rather than the intrinsic Young's modulus. The larger the indentation load, the more damage to the material under the indenter [17]. Such an influence of the indentation damage on Young's modulus measurement appears saturated when the indentation load reaches a certain level.
Figure 3. Schematic illustration of cracking in the vicinity of indenter head, and load ∼ depth curves of the five materials under different maximum indentation loads.
Download figure:
Standard image High-resolution imageOn the other hand, as the indentation load decreases, the damage becomes less severe and eventually disappears as the load decreases toward zero. Figure 4 illustrates the cracking of WC-Co sample under different indentation conditions. As shown, cracks are generated at the edge and corners of the indenter and extend during the indentation process. At lower loads, cracking becomes much more minor and irregular. It is suggested that as the load decreases, the densification, which is an inelastic deformation accompanied by a change in volume, reduces residual stress around the indentation, thus increasing the barrier to crack initiation [24, 39]. When the indentation load is very small, there could be a threshold for cracking [6, 59], e.g., the threshold for cracking can be smaller than 5 mN for brittle materials [59]. These may minimize cracking and render cracking irregular with disordered minor cracks. Nevertheless, without the effect of cracking on Young's modulus, the value of Young's moduli of the materials measured under the near-zero load or at the extrapolating point of the E ∼ load curve at zero load approaches the intrinsic Young' moduli measured, e.g., using the acoustic method, as shown in figure 2(a).
Figure 4. Indentation tests on WC-Co sample using Berkovich (upper row) and Vickers (lower row) heads under loads of 100 mN, 300 mN, 500 mN, 15 N, 30 N, and 60 N, respectively. When the indentation test is made under low loads, cracking becomes less severe or not visible as the indentation load continuously decreases.
Download figure:
Standard image High-resolution imageThe mechanism for the lowered Young's modulus measured by indentation can be seen from the influence of cracking on atomic bonding or energy based on the interatomic potential. We may use Lennard-Jones potential for a straightforward illustration. Although L-J potential is the simplest form proposed to describe the interatomic interaction, it reflects the general behavior or the trend of variations in atomic interaction with respect to the atomic spacing for both physical and chemical interactions. Lennard-Jones potential has been widely used for simulating and analyzing material cracking phenomena and Young's modulus [60–63]. The change in Young's modulus can be interpreted by comparing the atomic bond energy with or without local micro-cracking. Figure 5 illustrates interatomic potential between two adjacent atoms, simply illustrated using the Lennard-Jones potential [64, 65],
where is the atomic spacing in equilibrium and is the bond energy. Considering the atomic bond as a spring, based on Hooke's law, the spring constant is equal to [65]
Figure 5. Interatomic potential of a pair of atoms in equilibrium; the bond energy () becomes smaller () as the atomic spacing increases from to when the crystal lattice contains nano/micro-cracks.
Download figure:
Standard image High-resolution imageYoung's modulus of a solid also depends on the atomic bonding and crystal structure, which is proportional to the bond energy and inversely proportional to the atomic spacing square (). When a solid has micro-cracks, some atomic bonds are broken, leading to a decrease in Young's modulus. Or one may consider that the density of the solid decreases, as figure 5 schematically illustrates. Equivalently, the solid would have a larger average atomic spacing (), corresponding to a lowered bond energy (). As a result, the equivalent spring constant decreases to
As a result, the measured Young's modulus decreases accordingly. In this simplified model, the change in modulus is obvious with a slight distance change. In a bulk sample, the cracks are associated with broken atomic bonds in the local region. The broken bonds lead to increased atomic spacing with lowered bond energy. A looser crystal structure would have a lower Young's modulus. For instance, Young's modulus of crystalline Si3N4 is higher than that of its amorphous counterpart, which has a lower packing density [66]. Consequently, the more cracks generated under a larger indentation load, the lower the measured Young's modulus. Since the indentation-induced damage or cracking depends on the indentation load, indenter size and the material, ranking Young's moduli of materials measured under the same maximum load could lead to misleading information, as indicated earlier. Instead, the intrinsic Young's moduli should be used for the ranking purpose. According to the E ∼ load curves and the dashed line corresponding to the Young's modulus determined using the acoustic method (figure 2), one should measure E under different loads and determine the intrinsic Young's modulus, which is the value on the extrapolated E ∼ load curve at the indentation load equal to zero.
The above-described method for measuring intrinsic Young's modulus and ranking Young's moduli of different materials using the indentation technique also applies to other types of material, such as metallic materials. For metals, the measured Young's modulus is influenced by plastic deformation rather than cracking or fracture [67]. Plastic deformation also lowers Young's modulus due to decreased density and lowered electron work function [68], so the measured Young's modulus is not the intrinsic Young's modulus but that of plastically deformed material. The above-described approach of Young's modulus measurement by indentation method could also be used to estimate and rank intrinsic Young's moduli of metallic materials.
It should be pointed out that, as commonly observed [7, 27, 36], the hardness measured using the indentation method decreases when the load is increased, as illustrated in figure 2(b). This happens because the induced cracks make further penetration of the indenter head easier. The increase in hardness at lowered indentation loads was explained by the Indentation Size Effect [67], which stated that as the indentation load decreased or the indent became smaller, geometrically necessary dislocation density rose, resulting in a higher hardness [20, 31]. For ceramic material with little or limited slip systems, the situation underneath the indenter is however complicated. Localized damage and densification [39, 69] all could be involved. Once a crack initiates, crack propagation becomes easier according to Griffth's criterion [70]. Or in other words, at the beginning of indentation test, when the indentation load is very low, an undamaged ceramic solid should show a higher resistance to indentation than a damaged one. Such an argument is also consistent with the increase in Young's modulus as the indentation load is decreased, since an undamaged ceramic solid without broken atomic bonds should exhibit the intrinsic Young's modulus that is higher than that measured under a larger indentation load which damages or fractures the region under the indenter. The consistency between the Young's moduli measured respectively using the acoustic method and indentation method as illustrated in figure 2 provides a support to the above viewpoint.
According to studies reported in the literature, densification under the indenter may locally harden ceramic materials [69, 71–74]. This process of volumetric shrinkage in the rigid state may help resist indentation. However, once atomic bonds are broken, their contributions to Young's modulus should be decreased, although the densification may help reduce the stress build-up or residual stress and enhance the resistance to indentation (hardness). The consistency between Young's moduli measured using the acoustic method and the extrapolated Young's modulus at zero indentation load also favours the above argument.
Regarding hardness ranking, unlike Young's modulus, which represents the resistance to elastic deformation without damage, hardness represents the direct resistance of a material to irreversible deformation involving damage/fracture (ceramic) or plastic deformation (metallic). Thus, the hardness of different materials can be ranked using their hardness values measured under the same maximum indentation load or the same indentation condition.
4. Conclusions
Based on the results of this study, the following conclusions can be drawn:
- 1.Using Young's moduli of materials measured via indentation tests under the same maximum load for ranking purposes is inadequate or inaccurate, since Young's modulus measured by indentation is not the intrinsic Young's modulus but the one under the influence of lattice damage in the region under the indenter head.
- 2.To determine the intrinsic Young's modulus and rank Young's moduli of different materials, a 'zero-load' method could be used by determining the Young's modulus at zero load via extrapolation of the E ∼ load curve as the indentation load approaches zero, where the curve is obtained by measuring Young's modulus (E) of a material under different loads.
- 3.Ranking hardness of materials can be achieved via indentation tests under the same maximum load, since hardness is the resistance of a material to irreversible deformation involving fracture for ceramic materials or plastic deformation for metals.
Acknowledgments
The authors gratefully for the support from the Natural Science and Engineering Research Council of Canada, Trimay and Mitacs.
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).
Conflict of interest
The authors declare here that there is no conflict of interest for this work.