Abstract
The high internal quantum efficiency observed in higher plants remains an outstanding problem in understanding photosynthesis. Several approaches such as quantum entanglement and quantum coherence have been explored. However, none has yet drawn an analogy between superlattices and the geometrical structure of granal thylakoids in leaves. In this paper, we calculate the transmission coefficients and perform numerical simulations using the parameters relevant to a stack of thylakoid discs. We then show that quantum resonant tunneling can occur at low effective mass of particles for 680 nm and 700 nm incident wavelengths corresponding to energies at which photosynthesis occurs.
Export citation and abstract BibTeX RIS
1. Introduction
Photosynthesis allows organisms such as algae, plants and certain bacteria, to convert solar energy into chemical energy. The process can be divided into two reactions, light-dependent and light-independent reactions. The chemistry of the photosynthetic process seems well accepted [1, 2], however, for the physics of the light-dependent process many questions remain unresolved. In particular, the internal quantum efficiency or photon-energy-charge conversion efficiency of photosynthesis is known to be high and under certain conditions, may reach 100% [3, 4]. This amazing feat of nature is looked up to as an inspiration for the design, development, and upscaling of cost-effective technologies such as solar cells that would efficiently capture and store solar energy [5]. In contrast, for instance, Shockley and Quisser determined theoretically that a single-junction solar cell has the maximum energy conversion efficiency of only 33% [1, 3, 6]. More recently, Asahi, Kita, and their colleagues reported a structure capable of theoretically achieving up to 63% energy conversion [7]. Hitherto, the conversion efficiency in photosynthesis is not yet fully explained thus posing a major impediment for utilizing the mechanism as a viable pathway for high-efficiency solar cells [5].
The physics of photosynthesis has been previously approached as a problem of quantum entanglement and quantum coherence [3, 8, 9]. This is not surprising since quantum entanglement was observed in the light-harvesting complexes involving proteins found in photosynthetic organisms [9]. However, calculated efficiencies still do not match nature's standards. In this paper, we provide an alternative understanding of photosynthesis by focusing on the geometric structures of thylakoids which are starkly reminiscent of semiconductor superlattices. The fact that both thylakoids and superlattices have dimensions in the order of 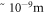 further compels us to draw an analogy between the two. By applying the same physics of the semiconductor nanostructure on this biological structure, we explore the behaviour and investigate the possibility of resonant tunneling as a contributing factor to the quantum efficiency of photosynthesis. Resonant tunnelling was shown by Tsu and Esaki in the early 1970's for a system with several periodic potential barriers [10], and this phenomenon has been studied and observed in different quantum systems with similar structures [11–15]. Here, we adopt the resonant tunneling approach of Yamamoto et al in their 1989 paper [16]. In section 2, we discuss the parameters and typical dimensions of stacked thylakoids. This is followed in section 3 by the mathematical framework for resonant tunneling. The Results and Discussion are in section 4, and section 5 gives the Conclusion.
further compels us to draw an analogy between the two. By applying the same physics of the semiconductor nanostructure on this biological structure, we explore the behaviour and investigate the possibility of resonant tunneling as a contributing factor to the quantum efficiency of photosynthesis. Resonant tunnelling was shown by Tsu and Esaki in the early 1970's for a system with several periodic potential barriers [10], and this phenomenon has been studied and observed in different quantum systems with similar structures [11–15]. Here, we adopt the resonant tunneling approach of Yamamoto et al in their 1989 paper [16]. In section 2, we discuss the parameters and typical dimensions of stacked thylakoids. This is followed in section 3 by the mathematical framework for resonant tunneling. The Results and Discussion are in section 4, and section 5 gives the Conclusion.
2. Experimental parameters in photosynthesis
As measured through electron tomography, nanostructures inside the chloroplast are observed to have grana stacks composed of 5 to 20 thylakoids made up mostly of photosystem II (PSII) and light-harvesting complex II (LHCII) [2, 17–19]. Photosynthesis occurs at the membrane of each thylakoid where a supply of energized electrons is needed for the light-independent part of the process. The supplier of electrons is water oxidized in the thylakoid membrane through photolysis in the oxygen-evolving complex (OEC) embedded in PSII. Light is needed in PSII (P680 or pigment absorbing light at 680 nm) where chlorophyll stores light energy not only to energize electrons, but also to replenish electrons by oxidizing water. Excited electrons from PSII are carried to photosystem I (PSI), called P700, via an electron transport chain within each thylakoid membrane. The electrons in PSI are further energized through a pigment absorbing light at 700 nm. Hence, both photosystems PSI and PSII would need light to excite electrons [2].
In a stacked granum of, for example, 20 thylakoids [19], it is quite possible that some thylakoid membranes are not directly accessed by light. For thylakoid membranes not accessed by light, one would wonder where the required excited electrons could be obtained within each membrane. Traditional understanding says excited electrons cannot be produced in the absence of light as may happen in a thylakoid buried deep in a stacked thylakoid granum. The need for excited electrons, however, can be addressed if photons from the uppermost thylakoid accessed by light tunnels through the 20 or so stacked thylakoid disks without losing energy. This way, resonant tunneling in stacked thylakoids could shed light on the internal quantum efficiency problem.
To investigate resonant tunnelling in a stacked thylakoid granum, we note that the thickness of grana disks is typically 8.5 nm and stromal gap is 7.2 nm (see, Fig. 1). The lumenal space is about 4.5 nm thick, the stromal space is 3.2 nm and the membrane is 4.0 nm [17–19]. We take the energy to be that of the incident photon, 680 nm and 700 nm [1, 2], and the membranes are assumed to act like a dielectric with capacitance from which we can calculate the barrier potential.
Figure 1. Three adjacent membranes, each of thickness 4.0 nm, from two thylakoids separated by a 3.2 nm stromal space with distances of the intervening spaces.
Download figure:
Standard image High-resolution image3. Mathematical framework
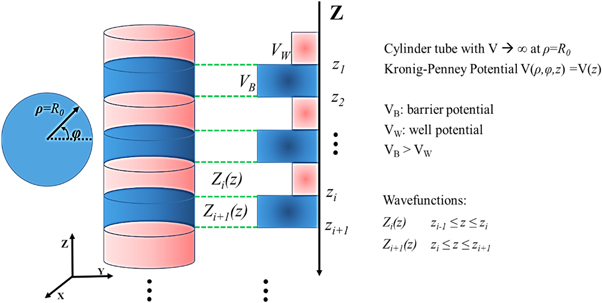
We treat the thylakoids stacked in the chloroplast as a cylindrical quantum system with periodic barrier potential along the cylindrical axis (see, Fig. 2) which may be described by the Krönig-Penney model [20, 21]. In modeling the stacked thylakoids, we proceed by setting up the Schrödinger equation in circular cylindrical coordinates with n-barrier potentials and then resolve the radial, azimuthal and axial parts. Since we are interested in resonant tunneling, we focus on calculating the transmission coefficient for the system up to n-barrier potentials. Application of the boundary conditions to the axial part, allows the transmission coefficient to be calculated from the resulting transfer matrix equations following the work of Yamamoto, et al [16].
Figure 2. Quantum system with periodic barrier potential in cylindrical coordinates.
Download figure:
Standard image High-resolution imageWe write the time-independent Schrödinger equation, 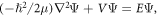 in circular cylindrical coordinates where,
in circular cylindrical coordinates where,  with,
with,  and
and  as the radial, azimuthal and axial components, respectively. Here, the potential of the system is taken as,
as the radial, azimuthal and axial components, respectively. Here, the potential of the system is taken as, 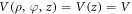 which depends only on the axial part. By separation of variables, we have the wave function,
which depends only on the axial part. By separation of variables, we have the wave function, 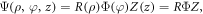 where,
where,
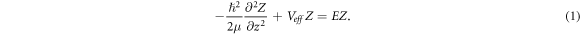
In equation (1), we define the effective potential  with the constant q absorbing both radial and azimuthal parts. The solution of equation (1) is of the form,
with the constant q absorbing both radial and azimuthal parts. The solution of equation (1) is of the form, 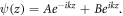
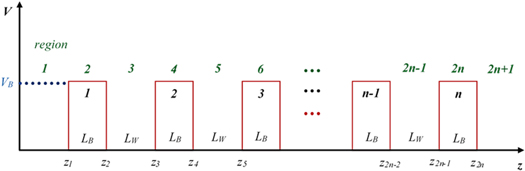
Figure 3 shows the same superlattice as Fig. 2 containing n number of identical rectangular barrier potentials with thickness LB
and potential height VB
and n−1 wells of thickness LW
arranged periodically in 2n + 1 regions. From equation (1), the wave function at the j-th region is 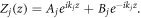 By applying the following boundary conditions: (a)
By applying the following boundary conditions: (a) 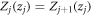 and, (b)
and, (b) 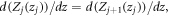 we obtain the following transfer matrix equation
we obtain the following transfer matrix equation
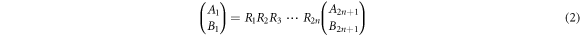
where 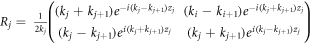 and j = 1, 2, 3, ..., 2n. By taking the following characteristic values,
and j = 1, 2, 3, ..., 2n. By taking the following characteristic values,
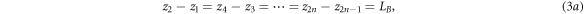
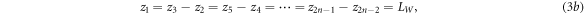
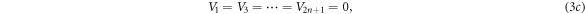
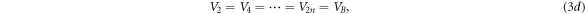
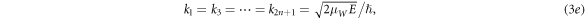
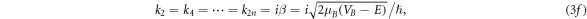
we obtain the expression for transmission coefficient Tn [16] for n-barriers with 0 < E < VB ,
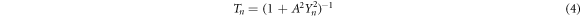
where ![$A={V}_{B}\,\sinh \,\beta {L}_{B}/2{\left[E\left({V}_{B}-E\right)\right]}^{1/2},$](https://content.cld.iop.org/journals/1402-4896/96/12/125038/revision2/psac3c58ieqn14.gif) with,
with, 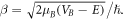 The Yn
is expressed as
The Yn
is expressed as
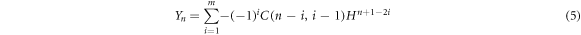
where ![$H=2\,\cosh \left(\beta {L}_{B}\right)\cos \left(k{L}_{W}\right)-\left(2E-{V}_{B}\right)\sinh \left(\beta {L}_{B}\right)\sin \left(k{L}_{W}\right)/\sqrt{\left[E\left({V}_{B}-E\right)\right]},$](https://content.cld.iop.org/journals/1402-4896/96/12/125038/revision2/psac3c58ieqn16.gif)
 for index m, when n is even, m = n/2 but when n is odd, m = (n+1)/2. Therefore, resonance (Tn
= 1) occurs when Yn
= 0. For any system of n barriers, we can compute the expression of Yn
assuming effective masses
for index m, when n is even, m = n/2 but when n is odd, m = (n+1)/2. Therefore, resonance (Tn
= 1) occurs when Yn
= 0. For any system of n barriers, we can compute the expression of Yn
assuming effective masses 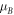 and
and 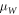 are both equal. Note that, in equation (3c), the well potential is set at
are both equal. Note that, in equation (3c), the well potential is set at  as a reference point to facilitate the calculation. Putting a nonzero constant value,
as a reference point to facilitate the calculation. Putting a nonzero constant value, 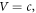 for the well potential would simply shift the barrier potential, equation (3d), to
for the well potential would simply shift the barrier potential, equation (3d), to  Choosing
Choosing 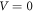 translates the whole quantum system down to where the potential wells are equated to zero without affecting the potential differences between the barriers and the wells.
translates the whole quantum system down to where the potential wells are equated to zero without affecting the potential differences between the barriers and the wells.
Figure 3. Superlattice with n-fold barrier potential where the horizontal axis is the axial part of the system.
Download figure:
Standard image High-resolution imageFrom equation (4), the transmission coefficient Tn
is dependent on the dynamics of A2
Yn
2
. If this term is zero, obviously, we have a transmission equal to unity, Tn
=1, meaning full or resonant transmission. Since the expression of Yn
changes for a different number of barriers, we need to look at this term and check conditions at which Yn
= 0. From equation (5), we can see that Yn
= Y(H). Note that H, and ultimately Yn
, is dependent on six parameters, namely, energy E, potential VB
, effective masses 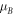 and
and 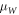 for barriers and wells, respectively, and barrier thickness LB
and well thickness LW
. Here, we vary the energy E in the parameter
for barriers and wells, respectively, and barrier thickness LB
and well thickness LW
. Here, we vary the energy E in the parameter 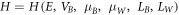 and use the membrane and stromal space thickness from the study of Daum et al [19] as the barrier thickness or length LB
and well thickness or length
and use the membrane and stromal space thickness from the study of Daum et al [19] as the barrier thickness or length LB
and well thickness or length 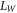 or vice versa whichever has the higher potential.
or vice versa whichever has the higher potential.
4. Results and discussion
The thylakoid membrane is viewed in analogy to a dielectric material in a capacitor so that the potential VB is just the energy stored in a capacitor. If we consider the membrane to be the cylindrical disk having a diameter between 0.3 μm to 0.6 μm [22] with a membrane capacitance of 1 μF cm−2 [2], at 11 mV, the potential would be between 0.26 eV to 1.06 eV. This is the basal potential of the membrane, i.e., the resting potential of the membrane when there is no light [2]. Since wavelengths 680 nm and 700 nm carry energy at 1.82 eV and 1.77 eV, respectively, then during transition from darkness to illumination, the incident photon passes through the membranes easily.
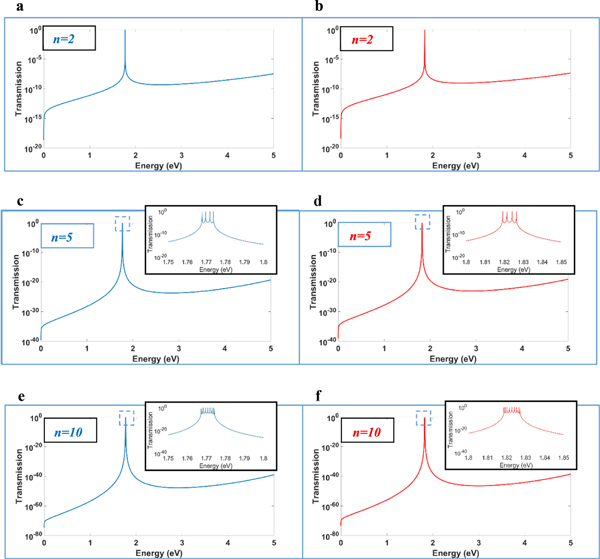
Light-induced electric potential difference can peak to at least 100 mV depending on ionic concentrations and conditions, among others [2]. In our numerical simulation, the barrier potential was set at 10 eV. The 10 eV is chosen based on the potential difference across the thylakoid membrane from Lyu and Lazar [2], and within the bounds of the potential difference measured by Vredenberg [23]. By modeling the thylakoid membrane as a capacitor dielectric, 10 eV gives a potential difference between 33.8 mV to 67.6 mV depending on the diameter of the thylakoid disc. From the results of Daum et al [19], the length of the barrier potential, LB , is 4.0 nm while the length of the well potential, LW , is 3.2 nm (see, Fig. 4). Moreover, we take the two lengths to be fixed in our simulations circumventing the possibility that the grana stacks can vary vertically based on light conditions, i.e., expands at low-light conditions and contracts at high-light conditions in several studies reported in Daum et al [19]. It was also observed that plants at low-light conditions might contain up to 100 grana in a stack compared to plants at high-light conditions, with fewer, about 5 to 15 grana [17]. The transmission coefficients corresponding to the energy of the incident photon were calculated using these parameters and for n = 2, which is simply the basic composition of the structure, for n = 5 and n = 10 based on the number of stacked thylakoids according to existing studies [17, 19, 22]. Figure 5 shows the simulation results. Blue graphs on the left side are spectra for when the peak is at 1.77 eV or 700 nm while the red graphs on the right side are spectra for when the peak is at 1.82 eV or 680 nm. The peaks are the incident energy whose transmission coefficient equals one. This is the condition at which resonant tunneling can occur. Increasing the number of barriers only increases the number of peaks to n−1 and peaking around values that are the same for n = 2. Photosynthetic organisms at low-light conditions may then compensate for their energy requirement by having a relatively greater number of stacked thylakoids where resonant tunneling can still occur. Note that there are several energies that spike up for a system with more than two barriers.
Figure 4. The cylindrical disk model of the thylakoid membranes: m—membrane, s—stromal gap. Photon tunnels through the membranes. The red line on the right panel indicates an electron tunneling. The yellow line indicates a photon tunneling.
Download figure:
Standard image High-resolution imageFigure 5. Transmission coefficient versus the energy of incident photon. The particle tunnels through several barriers n = 2, 5, 10 with 10 eV barrier potential. (a), (c) and (e) are graphs (blue) that peak at around 1.77 eV or 700-nm wavelength. (b), (d) and (f) are graphs (red) that peak at around 1.82 eV or 680 nm.s.
Download figure:
Standard image High-resolution imageFor n = 2, 5, 10, when the energy is at 1.77 eV, the effective masses are, 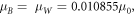 and when the energy is at 1.82 eV, the effective masses are,
and when the energy is at 1.82 eV, the effective masses are, 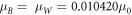 where
where 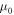 is the free electron rest mass. Throughout the simulation, the effective masses are held constant except for variation only at different energies. Moreover, it is observed that the translational movement of peaks along the energy axis is very sensitive to minute changes in effective mass and the barrier potential. This may suggest that there are many combinations that would allow resonant tunneling to occur. Interestingly, a low effective mass may suggest two possibilities, electron tunneling and photon tunneling, or perhaps, both occurrences may take place. In the right panel of Fig. 4, the red line shows an electron tunneling through the system after getting knocked off by incident light while the yellow line is the incident light tunneling through system. A more recent study has shown theoretically that extreme anisotropy of effective mass and low intrinsic resistance to movement, even having a zero effective mass, may be exhibited by semiconductor superlattices in a direction of electron motion [24]. It is also suggested that electron flow can super-collimate when effective mass is low. The consequences are quite profound: higher conductivity and ultra-fast and extremely strong electron response for faster electronics and functional materials [24]. In the case of photon tunneling, different sets of parameters such as refractive index, angular frequency and angle of incidence have to be considered aside from incident energy, effective mass and potential barrier in describing a system [15]. Fortuitously, recent studies have shown the relation between angular frequency and refractive index to the effective mass of photons within a medium [25–27]. Although not an ideal comparison, the effective masses determined earlier have similar orders of magnitude [25]. Hence, having low and largely different values for effective mass is not at all impossible.
is the free electron rest mass. Throughout the simulation, the effective masses are held constant except for variation only at different energies. Moreover, it is observed that the translational movement of peaks along the energy axis is very sensitive to minute changes in effective mass and the barrier potential. This may suggest that there are many combinations that would allow resonant tunneling to occur. Interestingly, a low effective mass may suggest two possibilities, electron tunneling and photon tunneling, or perhaps, both occurrences may take place. In the right panel of Fig. 4, the red line shows an electron tunneling through the system after getting knocked off by incident light while the yellow line is the incident light tunneling through system. A more recent study has shown theoretically that extreme anisotropy of effective mass and low intrinsic resistance to movement, even having a zero effective mass, may be exhibited by semiconductor superlattices in a direction of electron motion [24]. It is also suggested that electron flow can super-collimate when effective mass is low. The consequences are quite profound: higher conductivity and ultra-fast and extremely strong electron response for faster electronics and functional materials [24]. In the case of photon tunneling, different sets of parameters such as refractive index, angular frequency and angle of incidence have to be considered aside from incident energy, effective mass and potential barrier in describing a system [15]. Fortuitously, recent studies have shown the relation between angular frequency and refractive index to the effective mass of photons within a medium [25–27]. Although not an ideal comparison, the effective masses determined earlier have similar orders of magnitude [25]. Hence, having low and largely different values for effective mass is not at all impossible.
5. Conclusion
For the first time, the resonant tunneling phenomenon, first theorized by Tsu and Esaki [10] and since then has been proven experimentally and widely applied in semiconductor systems, is applied in a natural photosynthetic system. We showed the possible occurrence of resonant tunneling by working with the geometrical dimensions and empirical measurements of the stacked structure of grana thylakoids and considering them as superlattices. This behavior originally observed in semiconductors may contribute to the internal quantum efficiency or photon-energy-charge energy conversion in photosynthesis because the energy gets transported across the whole grana stacks with minimal reduction. In all of our simulations, the transmission coefficients of the incident energies would peak, i.e., transmission coefficient 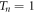 for n barriers, at energies widely known to be used by plants corresponding to wavelengths of 680 nm and 700 nm. This is the condition stipulated for resonant tunneling. Such analysis also addresses the problem of deep thylakoid membranes not readily accessed by light because of their location near or at the bottom of 20 or more stacked thylakoids. Indeed, the number of barriers does not even matter since their respective transmission spectra can peak at the said energies. We note that in our simulation, a choice is made to fix the lengths of the barrier and potential wells since different specimens may have differences in dimensions [19]. In addition, the light-induced potential difference across the membrane varies significantly depending on the conditions [2, 28]. However, our simulation reveals that a minor tweaking of parameters causes significant changes to transmission spectra. This allows for many configurations or conditions where resonant tunneling can occur.
for n barriers, at energies widely known to be used by plants corresponding to wavelengths of 680 nm and 700 nm. This is the condition stipulated for resonant tunneling. Such analysis also addresses the problem of deep thylakoid membranes not readily accessed by light because of their location near or at the bottom of 20 or more stacked thylakoids. Indeed, the number of barriers does not even matter since their respective transmission spectra can peak at the said energies. We note that in our simulation, a choice is made to fix the lengths of the barrier and potential wells since different specimens may have differences in dimensions [19]. In addition, the light-induced potential difference across the membrane varies significantly depending on the conditions [2, 28]. However, our simulation reveals that a minor tweaking of parameters causes significant changes to transmission spectra. This allows for many configurations or conditions where resonant tunneling can occur.
Another feature for resonance tunneling in photosynthetic systems is a very low effective mass. The low effective masses allow tunneling particles to interact readily and move easily across the membranes. Two types of particles could tunnel through grana thylakoids to achieve a supply of excited electrons even at the bottom of a grana stack hardly accessible to light for photosynthesis to occur at thylakoid membranes. The first type is an electron with low effective mass arising from interactions with the medium. For instance, a transport regime in a semiconductor superlattice with low effective mass for an electron has been discussed [24]. In fact, probing the low effective masses of tunneling electrons has been a continuing experimentally active area [29, 30]. On the other hand, a low but finite effective mass for the photon has also been crucial in the creation of a stable luminous quantum fluid of light when photons are spatially confined [25–26]. Further experimentation would be required to determine whether it is the photon or electron that tunnels, or both, which could account for the high internal quantum efficiency of photosynthesis. It is vital to explore this further as resonant tunneling in photosynthesis could have implications for designing more efficient solar cells.
Acknowledgments
K. M. G. gratefully acknowledges the support of the Department of Science and Technology-Science Education Institute through the Accelerated Science and Technology Human Resource Development Program—National Science Consortium (ASTHRDP-NSC).
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).
Declarations
The authors have no conflicts of interest to declare that are relevant to the content of this article.