Abstract
By virtue of the superoperator technique, we solve analytically the non-Markovian master equation that describes single-mode continuous variable system interacting with a structure reservoir. Our analytical solution allows us to investigate the non-Markovian effects on the dynamics of quantum coherence and non-classicality of Schrödinger cat states embedded in various types of structured reservoirs. We show that the dynamical behaviors of the fidelity, entanglement potentials, and higher-order antibunching of such states can be divided into two phases: they decay rapidly within a short time, but would either vanish completely or tend to a nonzero steady-state value in the long-time limit depending on the initial Schrödinger cat states and system parameters. We also show that by examining the Wigner function and higher-order sub-Poissonian statistics, the super-Ohmic environment can better help to protect the non-classicality, whereas the sub-Ohmic environment causes the disappearance of the non-classicality. Our approach is concise and can generalize to other open quantum system coupled to non-Markovian environment at finite-temperature or to linear non-Markovian Gaussian system.
Export citation and abstract BibTeX RIS
1. Introduction
The question to whether a given quantum state is classical or not has become an enigmatic topic from the beginning of quantum theory and then scientists have developed several different ways to test and quantify non-classicality of quantum state. The earliest study of non-classicality can date back to the Glauber-Sudarshan P-representation theory [1, 2], where a quantum state is nonclassical if its Glauber-Sudarshan P function fails to be interpreted as a probability density. Otherwise, it is referred to as classical. However, this quantity is often highly singular and its identification poses operational difficulties. So various suggestions have been made to study non-classical characters of quantum state using the negativity of the Wigner function [3], anti-bunching [4], sub-Poissonian photon statistics [5], photon number oscillations [6], and squeezing in one of the quadratures of the fields [7]. It is generally acknowledged that such criteria are a sufficient but not necessary condition for the non-classicality. For example, the Wigner function of squeezed state is positive everywhere and the even coherent state doesn't exist no antibunching, but such two states are known to be an important nonclassical ones [8]. On the other hand, there has been a considerable amount of research on quantifying the degree of non-classicality for quantum state, i.e. non-classicality measure. In 1991, Lee introduced a quantitative measure of non-classicality: nonclassical depth of quantum state [9]. This measure is bounded between 0 and 1. As expected, it is equal to zero for an arbitrary coherent state, but is always equal to 1 for all non-Gaussian pure state [10], not allowing us to implement a comparative study of the amount of non-classicality among non-Gaussian states. Very recently, Asboth et al suggested to use entanglement potentials (negativity potential and concurrence potential) as a measure of quantifying non-classicality for single-mode quantum state, which is combined with the vacuum at a beam splitter, then the two-mode entanglement is regarded as its value of non-classicality [11]. These entanglement potentials have been applied extensively to the assessment of the non-classicality amount of some quantum states such as superposition of N coherent states [11], sing-mode photon added coherent state [12], and single-qubit photon-number state [13]. Ryl et al formulated two ways to quantifying the degree of non-classicality based on the characteristic function [14]. One sees that the first way is limited only for states with a finite Fock-state expansion because the characteristic function is apolynomial characteristic function, while the second way is based on arbitrary characteristic functions, thus allowing us to estimate the degree of non-classicality for arbitrary state. However, we shall emphasize that the second way gives experiment-friendly criteria to ensure a certain amount of non-classicality.
The even and odd coherent states were introduced in [15] and called Schrödinger cat states [16], originating from the famous Schrödinger's thought experiment [17]. The single-mode even and odd Schrödinger cat states are superposition of two highly distinguishable coherent states and contain only even and odd photon numbers, respectively. Such states have some interesting properties. For instance, the even Schrödinger cat state (ESCS) exhibits squeezing but not sub-Poissonian statistics whereas the odd Schrödinger cat state (OSCS) has sub-Poissonian statistics but not squeezing [18, 19]. These quantum states have been successfully generated experimentally in various physical systems such as optic system [20, 21], superconducting quantum inference device [22], and trapped ion system [23, 24]. Simultaneously, they are important in many quantum information processing applications such as quantum teleportation [25, 26], quantum cryptography [27] and entanglement preparation [28, 29].
Towards practical quantum information processing, the environment-induced decoherence cannot be ignored since it is likely to limit the dynamical evolution of open quantum systems and more worsely, ruins completely quantum coherence of quantum states, leading to the failure of implementing quantum information processing tasks. According to whether or not the memory effect of the environment is negligible, the environments can be commonly grouped into the two principle categories: Markovian and non-Markovian ones [30–48]. The memoryless environment is recognized as Markovian; conversely, one is said to be non-Markovian. Many efforts have been made to investigate the dynamics of non-classicality for Schrödinger cat states in Markovian environment in the past decades [49–52]. It was found in [49, 52] that under the influence of a dissipative environment, such a quantum state decoheres and eventually evolves into a state that can be considered purely classical, namely a statistical mixture of the two coherent states, implying that the non-classical superposition states cannot be saved from Markovian case. Therefore, it is highly desirable to consider how the non-classicality of quantum state evolves in non-Markovian environment. Quite recently, Xiong et al investigated the non-Markovian dynamics of the complexity of quantum-to-classical transition for four scenarios: thermal state, thermal-like state, quantum steady state, or oscillating quantum nonstationary states [53]. It was found that in the latter two scenarios, the system can retain partial or full quantum coherence, and then the quantum-to-classical transition never occurs. To the best of our knowledge, the non-classicality behavior of Schrödinger cat states has not been studied systematically in a non-Markovian environment using different non-classicality measures.
As is mentioned above, the non-Markovian process is ubiquitous and can be observed in a variety of systems, such as ultracold neutral plasma [54], high-Q microwave cavities [55], optical fiber [56], and solid state system [57], etc. On the other hand, in recent decades, the experimental detection of nonclassical character of quantum state has received more attention using different criteria [58–60]. For example, Zavatta et al verified the non-classicality of single-photon-added thermal states using three tomographic approaches: the measured negativity of the Wigner function at the origin, the quadrature-based Richter-Vogel (RV) criterion, and the entanglement potential [58]. It has shown that they are in agreement with each other on testing non-classicality of such states. Kiesel et al performed an experimental scheme for testing non-classicality of phase-diffused squeezed states via different nonclassical criteria in 2009 [59]. It was found that the characteristic function of the P function function outperforms the other criteria of non-classicality such as higher-order squeezing. Inspired by their work, in this paper we will explore in more detail how the non-classicality of Schrödinger cat states evolves in a non-Markovian environment. More specifically, we will focus on a bosonic field mode traveling through a non-Markovian environment at zero-temperature and study the decoherence and evolution of the non-classicality of single-model Schrödinger cat states where the decoherence is quantified by the fidelity and the nonclassical feature is measured by various non-classicality measures above. We find that for a given amplitude of cat states, the larger the Ohmicity parameter s, the higher the asymptotic value of the fidelity. The sub-Ohmic environment can cause the negativity of Wigner function for even cat state to disappear, but not for odd cat state. The entanglement potentials of all cat states are very robust against the super-Ohmic environment. We also find that the higher-order antibunching for the odd cat states does not disappear in a non-Markovian environment, while their higher-order sub-Poissonian photon statistics is very fragile against the sub-Ohmic environment.
This paper is structured as follows. In section 2 we provide a description of single-mode bosonic field coupled to a non-Markovian environment at zero-temperature and give its solution of the master equation by the superoperator method. We also present an analytic expression for the decay factor of the environment conditioned on its spectral density. In section 3, we investigate the decoherence and the dynamics of non-classicality of single-mode even and odd Schrödinger cat states in non-Markovian environment,respectively. Finally, section 4 includes the summary of our results and some outlook on future research.
2. Non-Markovian master equation and its solution
We consider a physical model of a quantum harmonic oscillation with frequency ω0 coupled to a zero temperature relaxation environment described by a collection of bosonic oscillators with the frequency ωk. The total Hamiltonian for this model is given by (ℏ = 1)
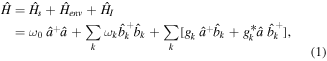
where 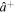 and
and  are the usual creation and annihilation operators of quantum harmonic oscillation,
are the usual creation and annihilation operators of quantum harmonic oscillation, 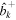 and
and 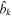 are the creation and annihilation operators of the field mode of the environment, and gk is the coupling constant between the oscillator and each environmental mode. In the continuum limit
are the creation and annihilation operators of the field mode of the environment, and gk is the coupling constant between the oscillator and each environmental mode. In the continuum limit 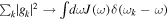 , where J(ω) is the reservoir spectral density. Typical examples of such a model include the light mode propagating in a structured bosonic reservoir [61] and a microcavity interacting with the reservoir being photonic crystal [62].
, where J(ω) is the reservoir spectral density. Typical examples of such a model include the light mode propagating in a structured bosonic reservoir [61] and a microcavity interacting with the reservoir being photonic crystal [62].
Using the influence-functional method of Feynman and Vernon [63], the non-Markovian master equation in the interaction picture for harmonic oscillation reduced density matrix ρ(t) is given by [61, 62, 64]
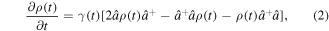
where γ(t) is a time-dependent damping rate and its functional form depends on the spectral structure of the environment in which the system is embedded. In the weak-coupling case and for times larger than the type reservoir correlation time scale τR, equation (2) recovers the well known Markovian master equation for a damped quantum harmonic oscillator at a zero-temperature environment.
In what follows, we seek to find the solution of equation (2) for an harmonic oscillator in the coherent-state representation. To do so, we introduce the superoperators as 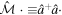 ,
, 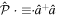 , and
, and 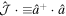 in such a way that they act on an operator ρ given by
in such a way that they act on an operator ρ given by 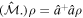 ,
,  , and
, and 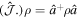 , respectively. According to the fundamental relation
, respectively. According to the fundamental relation ![$[\hat{a},{\hat{a}}^{+}]=1$](https://content.cld.iop.org/journals/1402-4896/95/7/075102/revision2/psab8c67ieqn12.gif) , we can obtain the commutation relations between these superoperators:
, we can obtain the commutation relations between these superoperators:

Defining  , we can write the non-Markovian master equation in the compact form
, we can write the non-Markovian master equation in the compact form
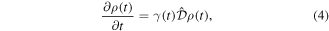
whose formal solution is given by the expression
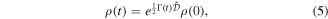
where we have defined 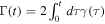 .
.
Using the commutation relations (3) and the following identify

with two operators 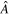 and
and 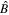 satisfying the commutator
satisfying the commutator ![$[\hat{A},\hat{B}]=-\hat{A}$](https://content.cld.iop.org/journals/1402-4896/95/7/075102/revision2/psab8c67ieqn17.gif) , we further write equation (5) after some straightforward calculations as
, we further write equation (5) after some straightforward calculations as
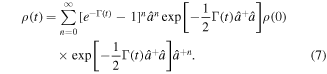
Thus, for an arbitrary initial element 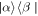 , it evolves as
, it evolves as
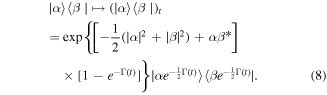
Now we examine in detail the decoherence factor Γ(t). For a zero temperature environment [65], it can be expressed as
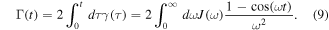
We consider a general spectral density of a bosonic environment of the form
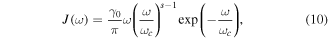
where ω is the frequency of the environment, ωc is the high-frequency cutoff, γ0 is a parameter characterizing the strength of the dissipation, and s is the Ohmicity parameter. By changing the s parameter, one can classify the environment as Ohmic (s = 1), sub-Ohmic (0 < s < 1), and super-Ohmic (s > 1) reservoirs, respectively. Different spectral densities manifest different non-Markovian decoherence dynamics.
We can obtain a closed analytic expression for the time-dependent rate in the zero-T limit [66]

where ![$\tilde{{\rm{\Gamma }}}[s]$](https://content.cld.iop.org/journals/1402-4896/95/7/075102/revision2/psab8c67ieqn19.gif) is the Eurler gamma function.
is the Eurler gamma function.
Finally, the decoherence function Γ(t) can be obtained as

3. Non-classicality dynamics
In this section we describe Schrödinger cat states, present the solution in a non-Markovian environment, and investigate the dynamics of decoherence by using the fidelity and of non-classical features of such states using various non-classicality measures.
3.1. Decoherence of Schrödinger cat states
Let us consider a quantum harmonic oscillator initially in Schrödinger cat state, which is represented by a coherent superposition of two coherent states 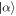 and
and 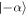 , as follows [67]
, as follows [67]
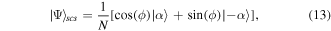
where 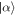 denotes a coherent state with amplitude α, ϕ is the relative phase, and
denotes a coherent state with amplitude α, ϕ is the relative phase, and 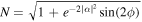 is a normalization factor. In this paper, we take
is a normalization factor. In this paper, we take 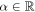 for simplicity. Obviously, if ϕ = π/4, equation (13) is equal to the even coherent state; when ϕ = − π/4, then equation (13) describes the odd coherent state; and for
for simplicity. Obviously, if ϕ = π/4, equation (13) is equal to the even coherent state; when ϕ = − π/4, then equation (13) describes the odd coherent state; and for 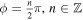 , the state (13) is equal to the Yurke-Stoler coherent state. In the Fock-state representation, the even and odd coherent states can be written as [18, 19]
, the state (13) is equal to the Yurke-Stoler coherent state. In the Fock-state representation, the even and odd coherent states can be written as [18, 19]
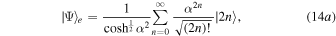
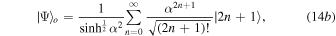
where the subscripts e and o denote the even and odd Schrödinger cat states, respectively.
Under the influence of non-Markovian environment (2), Schrödinger cat state evolves as
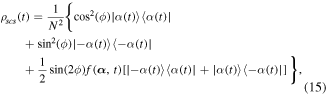
where we have assumed 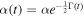 and the decay factor
and the decay factor ![$f({\boldsymbol{\alpha }},t)=\exp \left\{-2[1-{e}^{-{\rm{\Gamma }}(t)}]{\alpha }^{2}\right\}$](https://content.cld.iop.org/journals/1402-4896/95/7/075102/revision2/psab8c67ieqn27.gif) .
.
It is well-known that the fidelity is meant to measure the degree of similarity between two quantum states. As such, it is a natural tool of quantifying the loss of coherence of a quantum state under a noisy quantum channel. The fidelity can be defined as
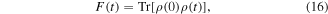
where ρ(0) is the density matrix at initial time and ρ(t) is the density matrix at later time. In ideal case, one would like to have F(t) = 1, corresponding to perfect, noiseless memory.
On substituting equations (13) and (15) into equation (16), we obtain for the fidelity of even and odd coherent states the following expression

where the plus (minus) sign denotes the even (odd) coherent state and  . Obviously, one sees from equation (17) that
. Obviously, one sees from equation (17) that 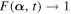 at initial time t = 0. One also sees that the dynamical behavior of decoherence given by (17) for Schrödinger cat states will be determined by the fastest time scale of the environment
at initial time t = 0. One also sees that the dynamical behavior of decoherence given by (17) for Schrödinger cat states will be determined by the fastest time scale of the environment 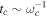 and the spectral function J(ω). Next, we will analyze this behavior in the sub-Ohmic, Ohmic, and super-Ohmic environments by means of the numerical simulation, respectively.
and the spectral function J(ω). Next, we will analyze this behavior in the sub-Ohmic, Ohmic, and super-Ohmic environments by means of the numerical simulation, respectively.
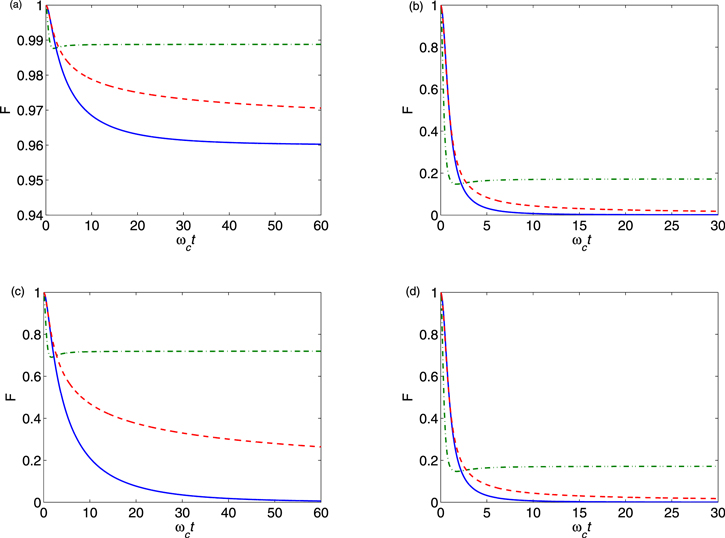
In figure 1, the dynamics of the fidelity F(α, t) of even and odd Schrödinger cat states in a zero-temperature non-Markovian environment is shown as a function of scaled time ωct for different values of α and s with γ0 = 0.5. It was observed that the fidelity has two different dynamical regimes. For times t < ω−1, it quickly damps with increasing of scaled time, irrespective of s, but it reaches asymptotically a steady-state value at times t > ω−1. This steady-state value is determined by both α and s. It is interesting to see that if the amplitude α of the field mode is fixed, the larger the Ohmicity parameter s, the higher the steady-state value of fidelity. It shows that the super-Ohmic environment can help to protect quantum coherence of Schrödinger cat states compared with another two types of environment. On the other hand, the decoherence dynamics of Schrödinger cat states is significantly influenced by its amplitude. It is found that if the Ohmicity parameter s is fixed, the Schrödinger cat states with smaller amplitudes α can obtain a very high fidelity even in the long-time limit. For example, for a case of even coherent state with α = 0.2, we can obtain the steady-state fidelities as 0.9603 for s = 0.5, 0.9706 for s = 1, and 0.9888 for s = 3, respectively. This is completely different from the Markovian decoherence model. We can explain as follows. In the Markovian environment, we have 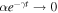 in the long-time limit [49], so the Schrödinger cat state is completely degraded, while for non-Markovian case, we have the decoherence function
in the long-time limit [49], so the Schrödinger cat state is completely degraded, while for non-Markovian case, we have the decoherence function 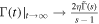 from equation (12) and then
from equation (12) and then 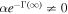 , implying that the Schrödinger cat state is partly degraded. For Schrödinger cat state with larger amplitude, the fidelity quickly reduces and tends to a relatively small value(even almost to zero) in the long-time limit. Therefore. in the following cases, we will restrict ourselves to the case of the reservoirs with sub- and super-Ohmic spectral functions and mainly choose Schrödinger cat states with larger amplitude (i.e., α = 2) as initial state. That is because for some realistic quantum information processing, the fidelity with cat states at least as large as α > 1.22 needs to be remained at near-unit fidelity [68, 69].
, implying that the Schrödinger cat state is partly degraded. For Schrödinger cat state with larger amplitude, the fidelity quickly reduces and tends to a relatively small value(even almost to zero) in the long-time limit. Therefore. in the following cases, we will restrict ourselves to the case of the reservoirs with sub- and super-Ohmic spectral functions and mainly choose Schrödinger cat states with larger amplitude (i.e., α = 2) as initial state. That is because for some realistic quantum information processing, the fidelity with cat states at least as large as α > 1.22 needs to be remained at near-unit fidelity [68, 69].
Figure 1. Plots of fidelity 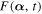 in equation (17) for even (Top) and odd (Bottom) Schrödinger cat states in non-Markovian environment versus scaled time
in equation (17) for even (Top) and odd (Bottom) Schrödinger cat states in non-Markovian environment versus scaled time 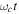 . In (a) and (c), α = 0.2, while in (b) and (d), α = 2. The solid line to s = 0.5, dashed line corresponds to s = 1, and dashed-dotted line to s = 3. The value of the other parameter is γ0 = 0.5.
. In (a) and (c), α = 0.2, while in (b) and (d), α = 2. The solid line to s = 0.5, dashed line corresponds to s = 1, and dashed-dotted line to s = 3. The value of the other parameter is γ0 = 0.5.
Download figure:
Standard image High-resolution image3.2. Non-Markovian dynamics of quantum interference and non-classicality
The Wigner function is one of the quasi-probability functions, which contains full information about the quantum system and can reconstruct via optical homodyne tomography [70]. The Wigner function of a quantum state ρ can be defined as
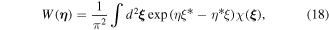
where ![$\chi ({\boldsymbol{\xi }})=\mathrm{Tr}[\rho \exp ({\hat{a}}^{+}\xi -\hat{a}{\xi }^{* })]$](https://content.cld.iop.org/journals/1402-4896/95/7/075102/revision2/psab8c67ieqn36.gif) is the symmetrically ordered characteristic function.
is the symmetrically ordered characteristic function.
The Wigner function associated with such an noisy state (15) is
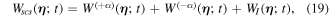
with
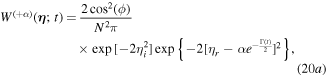

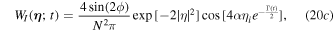
where 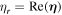 and
and 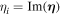 . As is known to all, the Wigner function for single-mode Schrödinger cat state consists of two Gaussian Bells corresponding to statistical mixture of individual composite states and interference fringes in between originating from the superposition between different components of the states, which vanishes for classical statistical mixture. So it can be viewed as a useful mark of the quantum to classical transition, which can be commonly quantified by the fringe visibility function [71]
. As is known to all, the Wigner function for single-mode Schrödinger cat state consists of two Gaussian Bells corresponding to statistical mixture of individual composite states and interference fringes in between originating from the superposition between different components of the states, which vanishes for classical statistical mixture. So it can be viewed as a useful mark of the quantum to classical transition, which can be commonly quantified by the fringe visibility function [71]
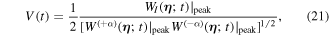
where 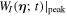 is the value of the Wigner function at η = (0,0) and
is the value of the Wigner function at η = (0,0) and 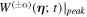 are the values of the Wigner function at η = ( ± α,0), respectively. This quantity is responsible for the effect of environment-induced decoherence of quantum state.
are the values of the Wigner function at η = ( ± α,0), respectively. This quantity is responsible for the effect of environment-induced decoherence of quantum state.
Considering equation (19), we can obtain the fringe visibility of ESCS and OSCS as
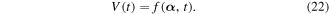
One sees from equation (22) that these interference terms are decaying by the factor ![$f({\boldsymbol{\alpha }},t)=\exp \left\{-2[1-{e}^{-{\rm{\Gamma }}(t)}]{\alpha }^{2}\right\}$](https://content.cld.iop.org/journals/1402-4896/95/7/075102/revision2/psab8c67ieqn41.gif) , which is closely related to the spectral structure of the environment. According to equation (12), one can see that for very short times
, which is closely related to the spectral structure of the environment. According to equation (12), one can see that for very short times 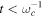 , the super-Ohmic environment induces the fastest decoherence, but in the long-time limit, we can obtain the asymptotic expression of the fringe visibility as
, the super-Ohmic environment induces the fastest decoherence, but in the long-time limit, we can obtain the asymptotic expression of the fringe visibility as ![$V(t)=\exp \left\{-2[1-{e}^{-{\rm{\Gamma }}(\infty )}]{\alpha }^{2}\right\}$](https://content.cld.iop.org/journals/1402-4896/95/7/075102/revision2/psab8c67ieqn43.gif) , It is easy to see that the asymptotic value has a very close connection with the type of the environment and is significantly larger for the super-Ohmic type than for other two types. As is well known, under the influence of Markovian environment, the two Gaussian peaks of the statistical mixture part of Schrödinger cat states move towards the origin and eventually merge into each other. A natural question arises: how does the wake-packet evolution of Wigner function for Schrödinger cat states in a non-Markovian environment?
, It is easy to see that the asymptotic value has a very close connection with the type of the environment and is significantly larger for the super-Ohmic type than for other two types. As is well known, under the influence of Markovian environment, the two Gaussian peaks of the statistical mixture part of Schrödinger cat states move towards the origin and eventually merge into each other. A natural question arises: how does the wake-packet evolution of Wigner function for Schrödinger cat states in a non-Markovian environment?
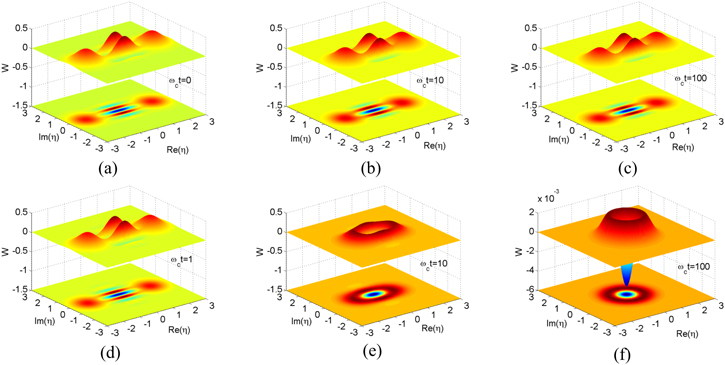
In figures 2 and 3, we plot the time evolution of Wigner function for even and odd Schrödinger cat states in a non-Markovian environment at zero temperature, respectively. One sees that when Schrödinger cat states are expected in presence of non-Markovian environment, the two Gaussian peaks go to the origin and the oscillation behavior becomes weaker and weaker. It is interesting to see that in super-Ohmic environment, this oscillation doesn't disappear completely in the long-time limit, irrespective of even or odd Schrödinger cat state. This is completely different from the result obtained in [49]. In addition, within the effects of the environmental noise, the negativity of the Wigner functions, a signature of nonclassical effect of quantum state [72], is progressively attenuated, even up to a complete deletion at certain conditions. For example, sub-Ohmic environmental noise causes the disappearance of the negativity of Wigner function for even Schrödinger cat state, whereas the Wigner function of odd Schrödinger cat state can always take the negative values during the evolution, regardless of s. Compared figure 2(f) with figure 3(f), we see that Wigner functions of Schrödinger cat states have eventually different shapes in the sub-Ohmic reservoirs. For an even Schrödinger cat state, it becomes more and more similar to Gaussian form of vacuum, while odd Schrödinger cat state is close to the Wigner function of single-photon state. These can be clearly checked from equations (14b) and (15) with a special case of 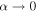 .
.
Figure 2. The Wigner functions for even Schrödinger cat states are depicted for different values of decay time ωct: (b)–(c) correspond to s = 3;(d)–(f) to s = 0.5. The other parameters are α = 2 and γ0 = 0.5.
Download figure:
Standard image High-resolution imageFigure 3. The Wigner functions for odd Schrödinger cat states are depicted for different values of decay time ωct. The parameters and captions are the same as figure 2.
Download figure:
Standard image High-resolution imageOn the other hand, we further investigate the non-classicality dynamics for single-mode Schrödinger cat states in non-Markovian environment by means of Wootters' concurrence [73]. When the evolving quantum state (15) is mixed with vacuum state at a 50:50 beam splitter, the resulting two-mode state becomes
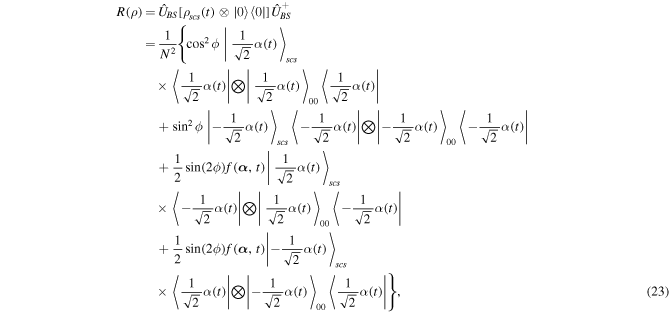
where we have used the following relation

where ![${\hat{U}}_{{BS}}=\exp \left[\tfrac{\pi }{2}({\hat{a}}^{+}\hat{b}-\hat{a}{\hat{b}}^{+})\right]$](https://content.cld.iop.org/journals/1402-4896/95/7/075102/revision2/psab8c67ieqn45.gif) corresponds to a 50:50 beam splitter.
corresponds to a 50:50 beam splitter.
In order to calculate the degree of entanglement of quantum state (23), we will need transform a two-mode quantum state into a two-qubit state and thus define the zero and one qubit states, respectively, as
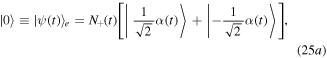

where the normalization factor ![${N}_{\pm }{(t)}^{-1}=\sqrt{1\pm \exp [-2{\alpha }^{2}{e}^{-{\rm{\Gamma }}(t)}]}$](https://content.cld.iop.org/journals/1402-4896/95/7/075102/revision2/psab8c67ieqn46.gif) . The two logical qubit states are orthogonal to each other even in the limit of
. The two logical qubit states are orthogonal to each other even in the limit of 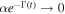 . Then the density operator equation (23) for
. Then the density operator equation (23) for 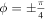 can be written, in the standard basis
can be written, in the standard basis 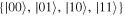 , as
, as
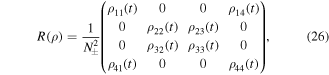
with
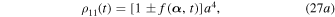


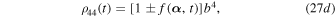
where 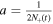 and
and 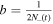 .
.
The entanglement of the two qubits could be quantified by concurrence, which is defined as [73]

where the λj are the square roots of the eigenvalues of the matrix 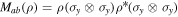 , in decreasing order, and σy the Pauli matrix. As usual for entanglement measures, concurrence ranges from zero (no entanglement) to one (maximally entanglement).
, in decreasing order, and σy the Pauli matrix. As usual for entanglement measures, concurrence ranges from zero (no entanglement) to one (maximally entanglement).
For a X-shape state (26), its concurrence can be simplified to
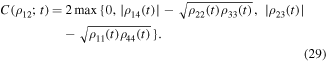
Figure 4 shows the entanglement potential dynamics for single-mode even and odd Schrödinger cat states in a non-Markovian environment. One sees that for these states, their entanglement shows the same behaviors as that of their decoherence during the evolution. That is, at shorter times 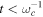 , the entanglement deteriorates rapidly and ultimately tends to zero or does stay a steady-state value conditioned on the Ohmicity parameter s. In particular, it is shown that the entanglement is hardly decayed in super-Ohmic environment at longer times, clearly showing that there is some residual entanglement left in the steady state of light field modes, revealing that the non-classicality of these input Schrödinger cat states is very robust against super-Ohmic environmental noise. We want to point out that the phenomena of sudden death, revivals and oscillations of two-mode entanglement aren't observed at all in our non-Markovian noisy model, which can be explained with the fact that at the zero-temperature non-Markovian environment, the decay rate Γ(t) is always positive and the monotonic increasing functions of ωct. So this positivity ensures the monotonic decrease of C(t), but not oscillations.
, the entanglement deteriorates rapidly and ultimately tends to zero or does stay a steady-state value conditioned on the Ohmicity parameter s. In particular, it is shown that the entanglement is hardly decayed in super-Ohmic environment at longer times, clearly showing that there is some residual entanglement left in the steady state of light field modes, revealing that the non-classicality of these input Schrödinger cat states is very robust against super-Ohmic environmental noise. We want to point out that the phenomena of sudden death, revivals and oscillations of two-mode entanglement aren't observed at all in our non-Markovian noisy model, which can be explained with the fact that at the zero-temperature non-Markovian environment, the decay rate Γ(t) is always positive and the monotonic increasing functions of ωct. So this positivity ensures the monotonic decrease of C(t), but not oscillations.
Figure 4. Dynamics of concurrence in equation (29) for even (a) and odd (b) Schrödinger cat states in a non-Markovian environment. The blue solid line to s = 3, and red dashed line corresponds to s = 0.5. The other parameters are α = 2 and γ0 = 0.5.
Download figure:
Standard image High-resolution image3.3. Non-Markovian dynamics of higher order antibunching and sub-Poissonian photon statistics
Finally, we study the dynamic of another two nonclassical properties, higher order antibunching (HOA) and sub-Poissonian photon statistics, of odd Schrödinger cat state in non-Markovian environment since no antibunching and sub-Poissonian photon statistics can exist for even Schrödinger cat state.
The phenomena of antibunching is an important aspect of quantum mechanical states, closely related to the photon statistics. Its concept was introduced by Lee in 1990 using the theory of majorization [74, 75]. Subsequently, Ba An [76] and Pathak and Garcia [77] modified Lee's criterion for HOA and presented a simplified counterpart for HOA. According to Pathak-Garcia criterion [77], a quantum state is said to be the lth order antibunching if it obeys the following inequality

otherwise, it does not exist higher-order antibunching. For l = 1, it recovers a usual antibunching criterion and for l ≥ 2, it corresponds to higher-order antibunching criterion.
Using the following identity
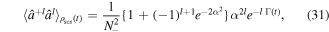
we can obtain the higher-order antibunching of odd Schrödinger cat state in a non-Markovian environment as
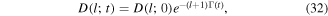
where 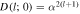
![$\left\{\tfrac{1}{{N}^{2}}{\left[1-{\left(-1\right)}^{l}{e}^{-2{\alpha }^{2}}]-\tfrac{1}{{N}^{2(l+1)}}[1+{e}^{-2{\alpha }^{2}}\right]}^{l+1}\right\}$](https://content.cld.iop.org/journals/1402-4896/95/7/075102/revision2/psab8c67ieqn55.gif) is the higher-order antibunching of odd coherent state at the initial time. It shows clearly that the odd coherent state satisfies always the inequality equation (29) since
is the higher-order antibunching of odd coherent state at the initial time. It shows clearly that the odd coherent state satisfies always the inequality equation (29) since 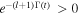 and
and 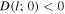 , and hence odd coherent state may exhibit the higher-order antibunching in non-Markovian environment. But the depth of higher-order antibunching has the same dynamical behavior as the decoherence obtained in section 3.1.
, and hence odd coherent state may exhibit the higher-order antibunching in non-Markovian environment. But the depth of higher-order antibunching has the same dynamical behavior as the decoherence obtained in section 3.1.
The indication of the non-classicality and statistics properties of the radiation field can also be revealed by the photon sub-Poissonian statistics, which does not have any classical counterparts. In quantum optics, a quantity that characterizes the departure from Poissonian photon statistics is given by the well-known Mandel's Q parameter defined as [78]
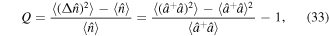
where 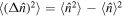 . A state is defined to be sub-Poissonian when its photon number variance
. A state is defined to be sub-Poissonian when its photon number variance 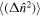 is smaller than its average photon number
is smaller than its average photon number 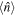 . For Poissonian statistics, Q = 0. If Q < 0, the field mode is said to be sub-Poissonian; otherwise, it is super-Poissonian. However, we do not discuss it separately, as it can be obtained as a special case of higher order nonclassical criteria. In 2002, Kim et al has generalized the notion of sub-Poissonian statistics to higher-order sub-Poissonian photon one in terms of factorial moment [79]. They defined the higher-order Qm-parameter as
. For Poissonian statistics, Q = 0. If Q < 0, the field mode is said to be sub-Poissonian; otherwise, it is super-Poissonian. However, we do not discuss it separately, as it can be obtained as a special case of higher order nonclassical criteria. In 2002, Kim et al has generalized the notion of sub-Poissonian statistics to higher-order sub-Poissonian photon one in terms of factorial moment [79]. They defined the higher-order Qm-parameter as
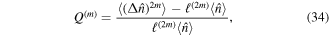
where  denotes the higher-order moment. Thus, the photon statistics is called mth-order sub-Poissonian if
denotes the higher-order moment. Thus, the photon statistics is called mth-order sub-Poissonian if 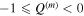 . For later calculations, we write the first four expressions for
. For later calculations, we write the first four expressions for 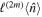 as
as
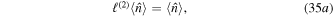
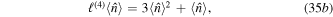

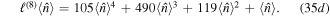
Using the following identity

and the relationship between 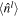 and
and 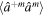

we can easily investigate the dynamics of higher-order sub-Poissonian photon statistics of odd Schrödinger cat state in a non-Markovian environment using equations (33)–(37).
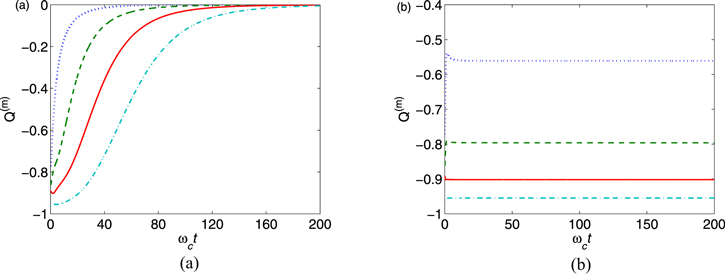
Figure 5 shows the time evolution of higher-order Qm-parameter for odd coherent state in a non-Markovian environment. It is clear that at the initial time, the value of  increases with the increase of the order m, indicating that the higher-order sub-Poissonian character is more pronounced than the usual sub-Poissonian behavior. However, one sees that for given amplitude
increases with the increase of the order m, indicating that the higher-order sub-Poissonian character is more pronounced than the usual sub-Poissonian behavior. However, one sees that for given amplitude 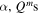 tend rapidly to zero under the influence of sub-Ohmic non-Markovian environment. That is, the higher-order sub-Poissonian of the initial Schrödinger cat state is very fragile against sub-Ohmic non-Markovian environmental noise. For super-Ohmic case, it is more favorable for non-classicality Qm preservation. In particular, we can see from figure 5(b) that the higher-order sub-Poissonian photon statistics shows more depth of non-classicality than corresponding lower-order counterparts. Therefore, we conclude that the higher order sub-Poissonian photon statistics may be useful in detecting weak non-classicality.
tend rapidly to zero under the influence of sub-Ohmic non-Markovian environment. That is, the higher-order sub-Poissonian of the initial Schrödinger cat state is very fragile against sub-Ohmic non-Markovian environmental noise. For super-Ohmic case, it is more favorable for non-classicality Qm preservation. In particular, we can see from figure 5(b) that the higher-order sub-Poissonian photon statistics shows more depth of non-classicality than corresponding lower-order counterparts. Therefore, we conclude that the higher order sub-Poissonian photon statistics may be useful in detecting weak non-classicality.
Figure 5. Dynamics of higher-order Qm-parameter for odd coherent state in a non-Markovian environment with s = 0.5 (a) and s = 3 (b). The dotted line corresponds to Q(1); dashed line to Q(2); solid line to Q(3), and dashed-dotted line to Q(4). The other parameters are α = 0.8 and γ0 = 0.5.
Download figure:
Standard image High-resolution image4. Summary and conclusions
In conclusion, we have investigated the non-Markovian dynamics of the decoherence and non-classicality of Schrödinger cat states evolving in a zero-temperature relaxation environment. We have obtained the analytical solution and decoherence factor of this decoherence model in the coherent-state representation with the help of the superoperator method. We have shown that under the influence of the non-Markovian environment, Schrödinger cat states exhibit two different dynamical behaviors. But unlike the Markovian case, these states would be partly degraded and save some residual non-classicality in the long-time limit. Although the negativity of Wigner function is strongly affected by the Ohmicity types of environment and becomes progressively attenuated, this negativity always remains unchanged in the super-Ohmic environment. We have also shown that the entanglement potential, higher-order antibunching, and higher-order Poissonian photon statistics of Schrödinger cat states are deteriorated seriously. But the super-Ohmic environment can better help to keep these non-classical properties.
The present study is of significance to the case of multi-mode GHZ- and W-coherent entangled states in an local non-Markovian environment. Such a generalization would be desirable since quantum information is distributed among many users. We also believe that our approach could be exploited to other open quantum systems coupled to non-Markovian environments at finite-temperature or to linear non-Markovian Gaussian systems, allowing us to further investigate quantum-to-classical transition as well as the intrinsic characteristics of non-Markovianity of quantum processes.
Acknowledgments
This work is supported by the Natural Science Foundation of Hunan Province, China under Grant No. 2017JJ2214, and the Key Project Foundation of Hunan Provincial Education Department, China under Grant No. 14A114.