Abstract
Linearized stochastic nanomechanical systems operating at nonzero temperatures and constant frequency and damping are restricted in their capacity to reduce noise in nonlinear combinations of the canonical variables. Nonlinear dynamics are then required in order to overcome these limits. Here we demonstrate how to make these limits explicit in the form of a threshold for nonlinear squeezing of the motional variables. Noise suppression below the threshold cannot be explained by linearized dynamics and is helpful in low-noise nonlinear devices at an ambient temperature. We predict that a state of the art levitating particle, exposed to cubic or quartic trapping potentials for a short interval will display nonlinear squeezing of stochastic motion that cannot be replicated by linear motion.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Noise reduction is an essential tool for the sensing and manipulation of stochastic nonlinear nanomechanical systems [1–6]. A thread of research in classical stochastic mechanics going back to the late twentieth century investigated the classical analogue of quantum squeezing called thermal squeezing [4, 7–10]. More recent investigations look into the properties of squeezed phonons in bulk solids [6, 11–13] or thermodynamic processes [14]. While a property associated with linear oscillators, squeezing can be used to estimate the strength of a nonlinear potential [15, 16].
Indeed mechanical systems in general are not linear oscillators and may be exposed to diverse nonlinear potentials in experimental settings such as electromechanics [5, 17–19], bulk resonators [20] and nanoparticle levitation [21], the last of which has ongoing theoretical efforts to detect nonlinear dynamics [22]. The inherent instability of many nonlinear potentials produces divergent mean and variance in finite time [23, 24]. Moreover, nonlinear responses to thermal noise can autonomously produce coherent motion with a signal-to-noise ratio that increases with the thermal noise [16, 24]. These unstable potentials and their effects are best understood in their short-time evolution, particularly to reduce the effects of damping and environment noise and avoid divergent behavior. Consequently parametric oscillations, while typical for squeezing experiments, are not appropriate for such unstable potentials.
Since conventional thermal squeezing of linear variables [4] can always be associated with a state of the system resulting from linear motion, it cannot distinguish these kinds of nonlinear motion. Instead we are lead to examine the squeezing of a nonlinear variable, which we denote nonlinear squeezing. Nonlinear squeezing has already been shown to be indispensable for optimal performance in quantum applications [25] and, as with thermal squeezing, this quantum-inspired approach suggests that analogous control over nonlinear squeezing in classical stochastic devices will be beneficial. In this article we propose and demonstrate a methodology to derive thresholds for nonlinear squeezing, based on short time behavior, that establish the limits of linear motion in modifying statistical properties of stochastic motion. We focus the discussion on short transient cubic and quartic (Duffing) dynamics in order to suggest a proof-of-principle experiment to obtain noise reduction that breaks the limits set by linear motion. Breaking such a threshold provides conclusive evidence that the nonlinear squeezing detected is incompatible with our general model of linear motion. Nonlinear squeezing can also function as a signpost for achieving even more visible nonlinearities, as greater nonlinear squeezing typically implies stronger nonlinear stiffness.
First, we develop the models of linear motion we wish to exclude via the thresholds for nonlinear squeezing. Second we develop the mathematics that allows us to derive such thresholds, using a statistical quantity motivated by cubic dynamics as an exemplar. Finally, we show how the derived threshold can be overcome by nonlinear motion.
2. Results and discussion
2.1. Nonlinear squeezing criteria for nonlinear motion
2.1.1. Linear stochastic motion
Stochastic mechanical systems, characterized by fixed mass m, are typically assumed to be immersed in a Markovian environment at constant temperature T > 0 with fixed linear damping Γ. Since, in the classical description, any noise can be eliminated trivially by cooling to zero temperature, useful theoretical thresholds will always require prior assumptions such as these.
The Markovian stochastic dynamics for a one-dimensional mechanical system in an arbitrary potential are described by the Langevin equation

where V(x) is a potential depending only on the mechanical position,  is the inverse temperature, with T the fixed temperature of the environment and
is the inverse temperature, with T the fixed temperature of the environment and  the Boltzmann constant,
the Boltzmann constant,  is the medium damping with Γ the drag coefficient of the medium (e.g. air at low pressure) and
is the medium damping with Γ the drag coefficient of the medium (e.g. air at low pressure) and  is the Langevin force of a thermal bath satisfying the Markov conditions
is the Langevin force of a thermal bath satisfying the Markov conditions  and
and  . Observe that both the damping and the Langevin force depend on γ, so that γ = 0 retrieves conservative motion.
. Observe that both the damping and the Langevin force depend on γ, so that γ = 0 retrieves conservative motion.
For any potential locally described by an up-to-quadratic potential  , with ω the frequency and F arising from a constant force, the system is defined to be linear. Many nonlinear oscillators operate in a regime close to the equilibrium position which can be well approximated by such a linear potential. Such oscillators are referred to as linearized and are included in the following derivation of the threshold. In deriving the threshold we will assume that ω and F are constant in time during a single experimental run and may only vary randomly between independent experimental runs, as opposed to parametrically driven systems, in which frequency may be a periodic function of time. For many experiments, the position statistics are accumulated over time and the momentum statistics are well-estimated from numerical differentiation of the measured position [16] and so in reality, even when m, β and γ remain constant during measurement the potential might vary. This introduces a statistical mixture over the potential parameters ω, F of equation (1). However the thresholds for nonlinear squeezing will turn out to be independent of such variation.
, with ω the frequency and F arising from a constant force, the system is defined to be linear. Many nonlinear oscillators operate in a regime close to the equilibrium position which can be well approximated by such a linear potential. Such oscillators are referred to as linearized and are included in the following derivation of the threshold. In deriving the threshold we will assume that ω and F are constant in time during a single experimental run and may only vary randomly between independent experimental runs, as opposed to parametrically driven systems, in which frequency may be a periodic function of time. For many experiments, the position statistics are accumulated over time and the momentum statistics are well-estimated from numerical differentiation of the measured position [16] and so in reality, even when m, β and γ remain constant during measurement the potential might vary. This introduces a statistical mixture over the potential parameters ω, F of equation (1). However the thresholds for nonlinear squeezing will turn out to be independent of such variation.
The simplest nonlinearity taking the system beyond the linear dynamics of  is the pure cubic potential
is the pure cubic potential  . This potential cannot be approximated by a harmonic potential in any limiting cases. Motivated by the short-term deterministic dynamics of a massive particle in a cubic potential [23, 24, 26] we examine the nonlinear variable
. This potential cannot be approximated by a harmonic potential in any limiting cases. Motivated by the short-term deterministic dynamics of a massive particle in a cubic potential [23, 24, 26] we examine the nonlinear variable  . This variable is chosen as an exemplar, however the principles applied to derive the threshold may be applied to other variables such as
. This variable is chosen as an exemplar, however the principles applied to derive the threshold may be applied to other variables such as  , providing a collection of thresholds for nonlinear motion. Here
, providing a collection of thresholds for nonlinear motion. Here  is a parameter characterizing the choice of nonlinear variable, analogous to varying the angle in phase space for linear variables [7].
is a parameter characterizing the choice of nonlinear variable, analogous to varying the angle in phase space for linear variables [7].
Nonlinear variables such as  involve higher order moments. For Gaussian distributions, the higher order moments are fixed by the first and second, and thus cannot vary arbitrarily. We will leverage this property into a noise threshold that captures when the measured statistics of a dynamical system cannot be explained by any model of the form of equation (1) under up-to-quadratic potentials.
involve higher order moments. For Gaussian distributions, the higher order moments are fixed by the first and second, and thus cannot vary arbitrarily. We will leverage this property into a noise threshold that captures when the measured statistics of a dynamical system cannot be explained by any model of the form of equation (1) under up-to-quadratic potentials.
2.1.2. Conservative non-Gaussian motion
In order to describe how to construct this threshold, we begin by observing some general properties of equation (1) under linear potentials. For an initially Gaussian phase space distribution the Gaussian form is preserved [27]. Thus, we may assume that at any time t, even in the limit  , the distribution ρ and its associated covariance matrix Σ take the following forms
, the distribution ρ and its associated covariance matrix Σ take the following forms
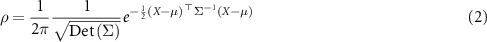

where  and
and  is the corresponding vector of mean values.
is the corresponding vector of mean values.
In this general form the variance  can be evaluated via a Gaussian integral to be
can be evaluated via a Gaussian integral to be
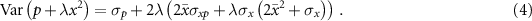
Observe the independence of this expression from  , which is important in applying the threshold to mixtures of Gaussian distributions. Also note that, since
, which is important in applying the threshold to mixtures of Gaussian distributions. Also note that, since  , we may replace the correlations σxp
with the determinant. Then it is straightforward to minimize the variance for Gaussian distributions. The result is the threshold
, we may replace the correlations σxp
with the determinant. Then it is straightforward to minimize the variance for Gaussian distributions. The result is the threshold

It is worthwhile to reflect on the meaning of this threshold. Formally, if the statistical quantity  of a pair of random variables x and p is below the threshold then a certain class of multivariate normal distributions (those with bounded
of a pair of random variables x and p is below the threshold then a certain class of multivariate normal distributions (those with bounded  ) are excluded as possible models for the multivariate probabilistic system.
) are excluded as possible models for the multivariate probabilistic system.
To connect this to the noisy damped linear dynamics of equation (1) we must associate a physical meaning with Σ. For conservative linear dynamics, γ = 0, the determinant of the covariance matrix is preserved and, via the decomposition of Williamson's theorem [28], always associated with a fixed thermal distribution of a fiducial harmonic oscillator, for which we have  . Nontrivial noise thresholds can only be derived when bounds are placed on temperature, and so we have assumed constant β. What remains is to set a fiducial, or reference, frequency ω0 associated with the fiducial harmonic oscillator. We then express the conservative threshold as
. Nontrivial noise thresholds can only be derived when bounds are placed on temperature, and so we have assumed constant β. What remains is to set a fiducial, or reference, frequency ω0 associated with the fiducial harmonic oscillator. We then express the conservative threshold as

Any nonlinear squeezing below the threshold, resulting from conservative dynamics and under the conditions specified, i.e. fixed mass and temperature and an associated reference frequency ω0 indicates conservative non-Gaussian motion.
A quantum mechanical treatment of this problem, replacing the fiducial states at frequency ω0 with the minimum uncertainty states, recovers the threshold for quantum non-Gaussianity reported in [29]. The threshold of equation (6) for the transient dynamics does not depend on mass m and holds even for stochastic mixtures of the distributions arising from conservative linear dynamics with random linear potentials (see SM for details).
2.1.3. Damped non-Gaussian motion
More generally, for γ > 0,  is not preserved. This can be easily seen by the fact that for
is not preserved. This can be easily seen by the fact that for  a new equilibrium distribution is achieved which may have arbitrary
a new equilibrium distribution is achieved which may have arbitrary  when the dynamical frequency ω is different from the fiducial frequency ω0. At first glance it appears that loosening the restriction on
when the dynamical frequency ω is different from the fiducial frequency ω0. At first glance it appears that loosening the restriction on  trivializes the threshold, but remarkably this is not the case. Consider that in the fully general case of noisy damped dynamics (equation (1)) the system relaxes from the state associated with the fiducial frequency ω0 to a new equilibrium state defined by the frequency ω and a linear force F. During the relaxation process the threshold equation (6) is indeed violated, indicating that the conservative motion threshold can be passed merely by the application of damped linear dynamics. However thorough numerical analysis reveals that such damped dynamics are also subject to limitations due to their linearity. Since the distribution remains Gaussian it is not possible to achieve arbitrarily low values of
trivializes the threshold, but remarkably this is not the case. Consider that in the fully general case of noisy damped dynamics (equation (1)) the system relaxes from the state associated with the fiducial frequency ω0 to a new equilibrium state defined by the frequency ω and a linear force F. During the relaxation process the threshold equation (6) is indeed violated, indicating that the conservative motion threshold can be passed merely by the application of damped linear dynamics. However thorough numerical analysis reveals that such damped dynamics are also subject to limitations due to their linearity. Since the distribution remains Gaussian it is not possible to achieve arbitrarily low values of  simply by changing the potential parameters, even if no simple geometric picture is possible.
simply by changing the potential parameters, even if no simple geometric picture is possible.
However the threshold must now be modified to accommodate any transient damping effects up to and including equilibration to the thermal bath. For the up-to-quadratic potential  , the equilibrium distributions are described by the Gaussian distributions
, the equilibrium distributions are described by the Gaussian distributions
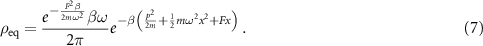
The noise in the nonlinear variable for these equilibrium distributions is given by
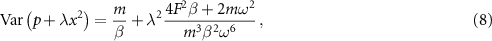
irrespective of γ. For such equilibria, if the dynamical frequency ω is allowed to vary such that  , then the nonlinear variance reduces to a constant noise floor given by
, then the nonlinear variance reduces to a constant noise floor given by  , representing an equilibrium threshold, independent of λ. No adjustment of the linear potential parameters F or ω can produce equilibrium distributions with
, representing an equilibrium threshold, independent of λ. No adjustment of the linear potential parameters F or ω can produce equilibrium distributions with  below this threshold.
below this threshold.
However, an appropriate selection of ω, F and transient time t will result in the equilibrium threshold being surpassed by transient conservative linear motion in the region  . Outside this region the noise floor can only be approached by the relaxation process induced by damping. Thus a candidate for the full threshold for noise in the nonlinear variable
. Outside this region the noise floor can only be approached by the relaxation process induced by damping. Thus a candidate for the full threshold for noise in the nonlinear variable  , for noisy damped linear dynamics, is a piecewise function of the noise floor
, for noisy damped linear dynamics, is a piecewise function of the noise floor  and the conservative motion threshold
and the conservative motion threshold  . In order to also accommodate the transient damping effects we must ensure that for no value of γ can the damped transient linear dynamics violate this candidate for the full threshold. Although
. In order to also accommodate the transient damping effects we must ensure that for no value of γ can the damped transient linear dynamics violate this candidate for the full threshold. Although  can be expressed analytically (methods detailed in SM) optimization over the parameters γ, F and ω must be performed numerically. Our numerical testing provides evidence that damped noisy linear dynamics cannot surpass these combined thresholds (see SM). The full threshold is therefore finally expressed as
can be expressed analytically (methods detailed in SM) optimization over the parameters γ, F and ω must be performed numerically. Our numerical testing provides evidence that damped noisy linear dynamics cannot surpass these combined thresholds (see SM). The full threshold is therefore finally expressed as
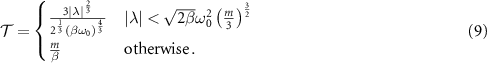
If, while mass m and temperature β are fixed, the statistics in the nonlinear variable  go below the threshold in equation (9), then they cannot be achieved by noisy damped up-to-quadratic dynamics following the Markovian model in equation (1), starting from a Gaussian distribution with fiducial frequency ω0. Additionally, given these fixed parameters, these statistics cannot be represented as a mixture of any Gaussian distributions dynamically available starting from the fiducial distributions and are non-Gaussian in this sense. This approaches refines definitions of classical non-Gaussian states for Markovian dynamics at a fixed temperature T. We observe that the threshold depends only on the mass m for the equilibrium noise threshold and this explains why it is required to be fixed (or at least lower bounded) whenever the transient frequency ω may be freely chosen. Alternatively, one may fix the transient frequency and allow mass to become a varying parameter (see SM). In this case the threshold is identical in form to the conservative threshold
go below the threshold in equation (9), then they cannot be achieved by noisy damped up-to-quadratic dynamics following the Markovian model in equation (1), starting from a Gaussian distribution with fiducial frequency ω0. Additionally, given these fixed parameters, these statistics cannot be represented as a mixture of any Gaussian distributions dynamically available starting from the fiducial distributions and are non-Gaussian in this sense. This approaches refines definitions of classical non-Gaussian states for Markovian dynamics at a fixed temperature T. We observe that the threshold depends only on the mass m for the equilibrium noise threshold and this explains why it is required to be fixed (or at least lower bounded) whenever the transient frequency ω may be freely chosen. Alternatively, one may fix the transient frequency and allow mass to become a varying parameter (see SM). In this case the threshold is identical in form to the conservative threshold  , where the fiducial frequency is replaced by
, where the fiducial frequency is replaced by  .
.
In fact, since the threshold  is monotonic in these variables, it is sufficient to bound the mass and temperature from below and the fiducial frequency from above. In order to surpass the threshold under these conditions nonlinear stochastic dynamics are required.
is monotonic in these variables, it is sufficient to bound the mass and temperature from below and the fiducial frequency from above. In order to surpass the threshold under these conditions nonlinear stochastic dynamics are required.
2.2. Exclusion of linear motion models
2.2.1. Nonlinear squeezing in cubic potentials
To nontrivially overcome the threshold in equation (9) we examine the transient effects of the cubic potential  on an initially Gaussian distribution. The cubic potential is softer then the inverted quadratic potential on one side and harder than quadratic on the other side and so the particle motion quickly diverges in finite time [23, 24] irrespective of the linear damping strength. Therefore we examine the motion in the short transient, starting from a zero-mean Gaussian distribution with
on an initially Gaussian distribution. The cubic potential is softer then the inverted quadratic potential on one side and harder than quadratic on the other side and so the particle motion quickly diverges in finite time [23, 24] irrespective of the linear damping strength. Therefore we examine the motion in the short transient, starting from a zero-mean Gaussian distribution with  ,
,  and
and  .
.
Such an initial distribution can be obtained by the linear dynamics of equation (1) from the values of  ,
,  and
and  corresponding to the fiducial equilibrium state. Here we distinguish an initial distribution, as a possibly engineered Gaussian distribution prepared for cubic dynamics, and the fiducial equilibrium state. The fiducial distribution is used to define the noise scale and contains our prior assumptions mentioned in the above introduction of linear stochastic motion. Any initial distribution, prepared by linear dynamics from the fiducial distribution, can be used to improve the generation of the nonlinear squeezing without exiting these conditions as it is guaranteed to begin from above the threshold and cannot surpass it through any further linear dynamics.
corresponding to the fiducial equilibrium state. Here we distinguish an initial distribution, as a possibly engineered Gaussian distribution prepared for cubic dynamics, and the fiducial equilibrium state. The fiducial distribution is used to define the noise scale and contains our prior assumptions mentioned in the above introduction of linear stochastic motion. Any initial distribution, prepared by linear dynamics from the fiducial distribution, can be used to improve the generation of the nonlinear squeezing without exiting these conditions as it is guaranteed to begin from above the threshold and cannot surpass it through any further linear dynamics.
One of the primary candidates for implementing cubic-like potentials for a free mechanical particle is modern systems of levitating nanoparticles [30] and in what follows we use the parameters  kHz,
kHz,  kg and T = 300 K derived from state of the art experiments [15, 16, 31]. In the high pressure regime the Langevin dynamics of equation (1) can be approximated by the overdamped equation
kg and T = 300 K derived from state of the art experiments [15, 16, 31]. In the high pressure regime the Langevin dynamics of equation (1) can be approximated by the overdamped equation

where  is the stiffness of the cubic potential normalized to the damping Γ. In this approximation the noise in the nonlinear variable
is the stiffness of the cubic potential normalized to the damping Γ. In this approximation the noise in the nonlinear variable  for the short transient, with vanishing mean position
for the short transient, with vanishing mean position  (see SM for the derivation), reads
(see SM for the derivation), reads
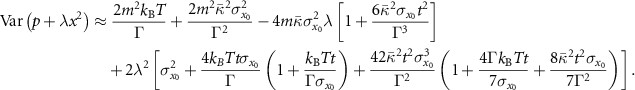
Note that in the limit of large damping Γ, the surviving term from equation (11) is  which indicates nonlinear squeezing is always below the threshold of linear dynamics (equation (9)). At realistic high pressures of the order of γ = 200 kHz ≈ 200 mbar [32, 33], and evolution in the cubic potential for
which indicates nonlinear squeezing is always below the threshold of linear dynamics (equation (9)). At realistic high pressures of the order of γ = 200 kHz ≈ 200 mbar [32, 33], and evolution in the cubic potential for  s (figure 1 panel (h), red dots), the short time approximation of equation (11) (red solid) accurately predicts a noise suppression below the threshold of linear dynamics (dashed blue). Note how the strong damping decreases the fluctuations of both x and p (panel (d)) compared to the initial thermal distribution (panel (a)). This noise reduction due to damping occurs before the noise begins to diverge due to the cubic dynamics, and aids the observation of nonlinear squeezing. In fact, if the Gaussian approximation to this non-Gaussian distribution is constructed from the covariance matrix it also shows nonlinear squeezing below the threshold, due to this initial noise reduction. In contrast, the overdamped regime with up-to-quadratic potentials does not pass the threshold and therefore, the nonlinear squeezing visible from this non-Gaussian distribution is more correctly attributed to the cubic dynamics rather than the large damping.
s (figure 1 panel (h), red dots), the short time approximation of equation (11) (red solid) accurately predicts a noise suppression below the threshold of linear dynamics (dashed blue). Note how the strong damping decreases the fluctuations of both x and p (panel (d)) compared to the initial thermal distribution (panel (a)). This noise reduction due to damping occurs before the noise begins to diverge due to the cubic dynamics, and aids the observation of nonlinear squeezing. In fact, if the Gaussian approximation to this non-Gaussian distribution is constructed from the covariance matrix it also shows nonlinear squeezing below the threshold, due to this initial noise reduction. In contrast, the overdamped regime with up-to-quadratic potentials does not pass the threshold and therefore, the nonlinear squeezing visible from this non-Gaussian distribution is more correctly attributed to the cubic dynamics rather than the large damping.
Figure 1. Nonlinear thermal squeezing during the short time dynamics from a cubic potential. Dots are molecular dynamics simulations of equation(1), using  , lines are analytical results. Top: (a), (b) An initial thermal equilibrium phase-space distribution at T = 300 K in a harmonic potential
, lines are analytical results. Top: (a), (b) An initial thermal equilibrium phase-space distribution at T = 300 K in a harmonic potential  of frequency
of frequency  kHz, and (c) an initial thermal distribution (see parameters in text) in a tilted harmonic potential
kHz, and (c) an initial thermal distribution (see parameters in text) in a tilted harmonic potential  of frequency
of frequency  and tilt
and tilt  . Below we plot output distributions obtained after the dynamics in cubic potential (d)–(g). Bottom: Nonlinear squeezing obtained after evolving these initial distributions in a cubic potential with stiffness
. Below we plot output distributions obtained after the dynamics in cubic potential (d)–(g). Bottom: Nonlinear squeezing obtained after evolving these initial distributions in a cubic potential with stiffness  . (h) The cubic dynamics in the overdamped regime suppresses the noise below the threshold given by equation (9) (blue) even for a short transient evolution
. (h) The cubic dynamics in the overdamped regime suppresses the noise below the threshold given by equation (9) (blue) even for a short transient evolution  s of an initial thermal distribution (red dots). Equation (11) (solid red) describes such noise suppression well. Longer dynamics (green) display divergent behavior, while still lying below the threshold. (i) In the underdamped regime, a short transient
s of an initial thermal distribution (red dots). Equation (11) (solid red) describes such noise suppression well. Longer dynamics (green) display divergent behavior, while still lying below the threshold. (i) In the underdamped regime, a short transient  s evolution of an initial thermal distribution (red dots), does not suppress the noise below the threshold (blue). Equation (12) (red solid) well describes the noise suppression at damping
s evolution of an initial thermal distribution (red dots), does not suppress the noise below the threshold (blue). Equation (12) (red solid) well describes the noise suppression at damping  . Evolving an engineered linear distribution for
. Evolving an engineered linear distribution for  s in the cubic potential (yellow dots), allows the suppression of the noise below the threshold. The statistics are generated from 1000 trajectories with a timestep of
s in the cubic potential (yellow dots), allows the suppression of the noise below the threshold. The statistics are generated from 1000 trajectories with a timestep of  s. Despite hardly observable deviation from the Gaussian distribution, the nonlinear squeezing threshold is able to detect the presence of such correlations and show that they cannot be replicated by linear dynamics.
s. Despite hardly observable deviation from the Gaussian distribution, the nonlinear squeezing threshold is able to detect the presence of such correlations and show that they cannot be replicated by linear dynamics.
Download figure:
Standard image High-resolution imageAs time increases (green dots, panel (h)), the nonlinear variance moves closer to the threshold, as the increasing noise in position (panel (e)) hinders the noise suppression. However, it is still below the threshold. This highlights the benefit of large damping as a tool to observe nonlinear squeezing for the first time below the threshold of linear dynamics for slower experiments with timeframes of up to t = 40 ms. Of course, it is more practically important to observe nonlinear squeezing with decreasing damping approaching conservative dynamics, therefore we focus on this case in what follows.
In the levitodynamics operational regime, with  Hz
Hz  kHz [15, 31, 34–37], the fiducial thermal distribution does not display nonlinear squeezing below the threshold when evolved for transient times in a cubic potential, as visible in figure 1 (panel (i), red dots). The approximate expression for the noise in the nonlinear variable
kHz [15, 31, 34–37], the fiducial thermal distribution does not display nonlinear squeezing below the threshold when evolved for transient times in a cubic potential, as visible in figure 1 (panel (i), red dots). The approximate expression for the noise in the nonlinear variable  for an arbitrary initial Gaussian distribution is too large to report here, however for vanishing means (
for an arbitrary initial Gaussian distribution is too large to report here, however for vanishing means ( ) it corresponds well in the short-time approximation to
) it corresponds well in the short-time approximation to
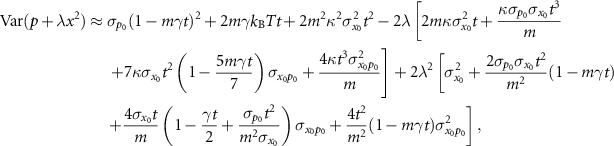
where  is the stiffness of the cubic potential k3 normalized to the mass of the particle. For initial thermal equilibrium distributions we have
is the stiffness of the cubic potential k3 normalized to the mass of the particle. For initial thermal equilibrium distributions we have  , and in the low pressure regime with γ < 200 kHz such distribution (red line) does not exhibit nonlinear squeezing in the short time approximation given by equation (12). Outside the short time evolution the system begins to exhibit divergent behavior and the noise in position and momentum increases rapidly, and nonlinear squeezing is not achievable.
, and in the low pressure regime with γ < 200 kHz such distribution (red line) does not exhibit nonlinear squeezing in the short time approximation given by equation (12). Outside the short time evolution the system begins to exhibit divergent behavior and the noise in position and momentum increases rapidly, and nonlinear squeezing is not achievable.
In order to observe nonlinear squeezing, a more suitable initial distribution can be prepared from the fiducial distribution, by allowing it to evolve it in a harmonic potential with fixed temperature and damping prior to the cubic dynamics. In general, out-of-equilibrium dynamics involving both a new frequency and a linear force F is required to create such a distribution. Merely displacing the fiducial state or the generation of nonzero correlations σxp appears to be insufficient (see SM).
One example of such a sensitive initial distribution can be created by evolving the fiducial equilibrium distribution in a tilted quadratic potential of frequency  and linear force
and linear force  (figure 1 panel (c)). This state, after transient cubic dynamics, shows nonlinear squeezing (figure 1, yellow dots, panel (i)) below the threshold. Here the full form of equation (12), including arbitrary initial Gaussian distributions, still accurately describes the noise suppression (solid yellow). Such behavior displays a high tolerance to damping (up to γ < 200 kHz) where the short-time approximation holds. The preparation of suitable initial distributions can also be accomplished via postselection of recorded trajectories [16].
(figure 1 panel (c)). This state, after transient cubic dynamics, shows nonlinear squeezing (figure 1, yellow dots, panel (i)) below the threshold. Here the full form of equation (12), including arbitrary initial Gaussian distributions, still accurately describes the noise suppression (solid yellow). Such behavior displays a high tolerance to damping (up to γ < 200 kHz) where the short-time approximation holds. The preparation of suitable initial distributions can also be accomplished via postselection of recorded trajectories [16].
2.2.2. Nonlinear squeezing in quartic potentials
Levitated platforms, as well as many NEMS experiments [38–46], more commonly experience nonlinearities in the form of a Duffing oscillator. A Duffing oscillator  (
( ) adds a softening character (
) adds a softening character ( ) to the harmonic oscillator. To best access the nonlinearity at transient times, a linear tilt
) to the harmonic oscillator. To best access the nonlinearity at transient times, a linear tilt  is added to the Duffing potential. Extensive numerical simulations in the underdamped regime
is added to the Duffing potential. Extensive numerical simulations in the underdamped regime  Hz, performed with
Hz, performed with  N [31],
N [31],  kHz, and
kHz, and  [16], reveal a nonlinear squeezing below the threshold of equation (9) only for engineered distributions initially squeezed and displaced to negative momentum and positive positions (see SM).
[16], reveal a nonlinear squeezing below the threshold of equation (9) only for engineered distributions initially squeezed and displaced to negative momentum and positive positions (see SM).
In the opposite regime of hardening character ( ), and strong (
), and strong ( ) quartic bound, the dynamics is dominantly characterized by the linear drift at short transients, where the nonlinear traits are encoded in the higher moments of position. To achieve noise suppression below the threshold equation (9) for such transients
) quartic bound, the dynamics is dominantly characterized by the linear drift at short transients, where the nonlinear traits are encoded in the higher moments of position. To achieve noise suppression below the threshold equation (9) for such transients  s, an initially squeezed distribution displaced to negative momentum and positive positions is required (see SM).
s, an initially squeezed distribution displaced to negative momentum and positive positions is required (see SM).
3. Conclusion
Current nonlinear stochastic mechanical systems are approaching low-damping and low-temperature regimes and can reshape the noise of the system in ways inaccessible to linear dynamics, even during short-time evolution. We have demonstrated an easily extendable methodology to derive sufficient conditions on statistical quantities which conclusively exclude linear dynamics, with an example motivated by the recently accessible cubic nonlinearity in one dimension [23, 24, 26]. These conditions come in the form of nonlinear mechanical squeezing of the thermal noise in phase-space variables, that cannot be explained by any mixture of linear dynamics. Furthermore, we have shown that such nonlinear squeezing may be visible with already established experiments, and will form the first venture into conclusive and operational identification of such nonlinear properties. Experimental verification of this methodology will open the path to investigating further, possibly more complex, nonlinearities and solidify our understanding of their behavior in the classical regime. Beyond classical physics, the threshold we have derived for conservative linear motion connects directly to that in the quantum regime [29] (also see SM). This opens the possibility to observe and distinguish nonlinear effects driven by classical stochastic uncertainty versus genuine quantum noise.
Acknowledgments
We acknowledge the grant 23-06224S of the Czech Science Foundation, project SPARQL from the MEYS of the Czech Republic (Grant Agreement 8C22001). Project SPARQL has received funding from the European Union's Horizon 2020 Research and Innovation Programme under Grant Agreement Nos. 731473 and 101017733 (QuantERA). Moreover, we have further been supported by the European Union's 2020 research and innovation programme (CSA—Coordination and support action, H2020-WIDESPREAD-2020-5) Under Grant Agreement No. 951737 (NONGAUSS).
Data availability statement
No new data were created or analyzed in this study.
Supplementary data (0.6 MB PDF)




