Abstract
We sketch a relation between two crucial, yet independent, fields in quantum information research, viz. quantum decoherence and quantum cryptography. We investigate here how the standard cryptographic assumption of shielded laboratory, stating that data generated by a secure quantum device remain private unless explicitly published, is disturbed by the einselection mechanism of quantum Darwinism explaining the measurement process by interaction with the external environment. We illustrate the idea with a paradigmatic example of a quantum random number generator compromised by a quantum analog of the Van Eck phreaking. In particular, we derive a trade-off relation between the eavesdropper's guessing probability 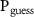 and the collective decoherence factor Γ of the simple form
and the collective decoherence factor Γ of the simple form 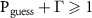 .
.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 license. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
Quantum cryptography [1, 2] is one of the most spectacular successes of quantum information theory. It provides new means of detection of eavesdropping by observing a disturbance of intercepted quantum states [3] not possible in classical cryptography, and even allows to certify security when using cryptographical systems from untrusted vendors [4]. Quantum devices can be used for such applications as secure key distribution [5] or generation of private random number [6] based on elementary physical phenomena.
Still, humans can deal only with classical data, and thus at some stage, any quantum cryptographic device has to generate classical output data. This process is known as quantum measurement [7]. Even though the measurement is one of the most basic processes in quantum mechanics, it remains to be one of the most mysterious phenomena since the very beginning of the theory [8–10]. This so-called measurement problem still lacks a definitive solution, with the decoherence theory being one of the most popular approaches [11].
The trailblazing works of Żurek [12, 13] elucidated the problem in which basis the quantum measurement is actually being performed, by the introduction of the concept of the pointer basis, i.e. the eigenbasis of observables commuting with the Hamiltonian determining the interaction of the measuring apparatus with the environment; the fact that the interaction with the environment is the factor that determines the measurement basis is called environment-induced superselection, or einselection [13, 14]. This result accentuated the role of the external world in the process of measurement and revealed that without this interaction, only the premeasurement, i.e. the correlation of the apparatus with the observed system, can occur.
The idea developed into the quantum Darwinism theory [15] explaining that information that is being successfully proliferated and distributed in many copies in multiple parts of the environment becomes classical. Such a framework directly relates classical outcomes of quantum devices with information leakage beyond the scope of the control. The process of information propagation can be viewed as eavesdropping of the information about the system being measured by the environment [16].
The role of the exterior world in the working of quantum devices seemingly contradicts the natural and necessary assumption, that the cryptographic devices are located inside a shielded laboratory protecting against the outflowing of the private data. Indeed, a crucial condition for the privacy of numbers, constituting e.g. a secure key, is that they remain secret unless intentionally revealed. This is particularly important for providing the information-theoretic level of security [17, 18].
On the other hand, quantum Darwinism [15] suggests that without this information propagation or leakage, the decoherence will not occur, leading, in principle to Wigner's friend paradox [19, 20]. To our knowledge, the problem of this prominent role of the environment has not been investigated in the context of cryptographical applications. The most related considerations concerned only the role of noise in cryptography [21, 22]. This paper aims to provide an example, of how the direct connection between the low-level description of the measurement process, and the high-level specification of application protocols can be done.
We emphasize the role of quantum Darwinism theory in the proposed cryptographical examination. This goes beyond the classical analysis of quantum cryptographical devices that would take into account only the bounds of the correlations between the eavesdropper and the device. The undertaken survey scrutinizes the information transfer not directly to the eavesdropper, but a more subtle and general scenario of leakage outside the safe room, and the imminence that this can be further exploited by the eavesdropper.
The information broadcast elucidated by quantum Darwinism, up to our knowledge, has not been investigated in the cryptographical context before this work. The community working on the decoherence theory, in particular with quantum Darwinism, has been widely investigating the fact that the information widespread is present and necessary for the quantum-to-classical transition, but it has never been examined whether this widespread has any relevance to cryptography. The leakage is inevitable and beyond any control by the very fact that a quantum-to-classical transition has taken place.
Since the topic of this paper is highly interdisciplinary, integrating results of decoherence theory and quantum Darwinism, with attacks characteristic to classical devices in the framework of quantum communication protocols with an application for secure randomness generation, we decided to provide a relatively expanded introduction with an overview of basic concepts of each of these fields. In particular, we propose a quantity investigated in cryptography, viz. the guessing probability, and the closely related min-entropy, as a new figure of merit of investigation of the quantum Darwinism theory, that was till now concerned mainly with the mutual information.
In section 1 we overview the decoherence theory, with particular attention to information imprinting in the environment as analyzed by quantum Darwinism. Then, in section 2.1 we describe a particular form of attacks on classical devices called Van Eck phreaking and efforts to protect against it called emission security. Next, in section 2.2 we overview a particularly relevant type of attack on quantum protocols called intercept-and-resend attacks. In section 2.3 we argue that the topic of providing privacy for random numbers has many important applications and point out that the aspect of their security analyzed in this work has till now been neglected. We describe the formalism and methodology used in our security analysis of randomness generation using quantum measurements in shielded laboratories in section 3, and in section 4 apply these methods to cases of incoherent attacks in section 4.1 and coherent attacks in section 4.2. We conclude and pose some new open problems in section 5.
1. Decoherence theory and quantum Darwinism
Decoherence is the process of losing the coherence between subsystems, where the coherence is a uniquely quantum type of correlation between separated objects, represented by off-diagonal terms of the density matrix. A perfectly isolated system remains coherent, whereas in open systems coherence is being gradually shared with the environment, ultimately leading to its decay. The notion of decoherence has first been used by Zeh in 1970 [23]. The review of the theory describing the decoherence process is given in [11, 24].
Suppose a quantum state is represented by a normalized positive semi-definite matrix ![$[\sigma_{i,j}]_{i,j}$](https://content.cld.iop.org/journals/1367-2630/24/11/113054/revision2/njpaca558ieqn3.gif) . One often measures decoherence using the collective decoherence factor [25]:
. One often measures decoherence using the collective decoherence factor [25]:

Obviously, this quantity depends on the choice of the basis in which the quantum state representation is given, but for any practical application one considers the unique (up to permutations) classically meaningful basis of macroscopically observed quantities, viz. the pointer basis. For a decohered quantum state, we have  .
.
The key element of decoherence is the following fact. Even though the evolution of every quantum system is given by unitary operators, and thus is reversible, when only one subsystem is considered and the rest is being ignored, or traced out, its evolution may not be unitary [26–28]. This allows for relieving the tension between the unitary character of quantum evolution and the irreversibility of quantum measurement. In particular, it can be shown that quantum randomness is a result of losing the coherence [29, 30]. The decoherence theory is used to model the collapse of the wave function, and transition to a mixed state in the eigenbasis of some local observable, while the quantum superposition of the state of the global wave function of the Universe undergoes the unitary evolution.
Important progress in the theory of decoherence was a series of works by Żurek in 1980s [12, 13] explaining that the basis in which the wave function collapse occurs, viz. the mentioned above pointer basis, is determined by the interaction with the exterior of the measured system and the measuring apparatus, i.e. with the environment, in the process called einselection. We elaborate on this idea more in section 3, when we adopt the formalism of these works. This approach allowed Żurek to compute the rate at which a pure state evolves into a mixed state via an interaction with the environment in a thermal equilibrium [31].
Another crucial progress made by Żurek was giving an even more important role in the quantum measurements to the environment. In [32] it was shown that the environment not only plays the passive role of a reservoir selectively destroying the coherence but also the environment selectively proliferates some part of the information about the system in multiple copies. It revealed that the pointer states are the ones that are able to leave a redundant and thus detectable imprint on the environment. In consequence, many observers by probing different parts of the environment can gain consistent information about the pointer basis, and this consent is the distinctive property of classical information that, in opposition to the quantum information [33], can be cloned [34].
The work [34] elucidated the nature of the existence of multiple copies of classical information by the introduction of the notion of the information plateau, as defined below. The whole considered Universe in this framework of quantum Darwinism consists of the system S and the environment E. The environment E is divided in arbitrary way into multiple subenvironments
 , in a sense
, in a sense 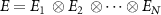 . A fragment, or macrofraction [25], is a grouping of several subenvironments, with notation
. A fragment, or macrofraction [25], is a grouping of several subenvironments, with notation  for
for 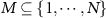 . Each observer is assumed to capture a random fragment of the environment.
. Each observer is assumed to capture a random fragment of the environment.
The maximum information that potentially can be accessed about the system S is its von Neumann entropy ![$H(S) = -\mathrm{Tr} \left[ S \log (S) \right]$](https://content.cld.iop.org/journals/1367-2630/24/11/113054/revision2/njpaca558ieqn9.gif) . Quantum Darwinism consider the information about S contained in a fragment EM
, i.e. the mutual information
. Quantum Darwinism consider the information about S contained in a fragment EM
, i.e. the mutual information  . If this information satisfies
. If this information satisfies 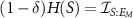 we say that δ is the information deficit of EM
. Define Nδ
as the number of disjoint fragments EM
satisfying
we say that δ is the information deficit of EM
. Define Nδ
as the number of disjoint fragments EM
satisfying  , and for
, and for 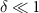 this number is closely related the so-called redundancy of the information, with large Nδ
being an indicator that indeed the information, called classical information, is present in multiple copies in different fragments of the environment; see section 2 of [34] for a detailed discussion.
this number is closely related the so-called redundancy of the information, with large Nδ
being an indicator that indeed the information, called classical information, is present in multiple copies in different fragments of the environment; see section 2 of [34] for a detailed discussion.
Note that the maximal value of 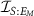 is
is  , not H(S), as it stems from a well-known fact that for pure ρSE
it holds that
, not H(S), as it stems from a well-known fact that for pure ρSE
it holds that 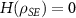 and
and  .
.
The average mutual information 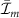 is the result of averaging over all fragments of size m. It was observed [34] that for relatively small values of m it holds
is the result of averaging over all fragments of size m. It was observed [34] that for relatively small values of m it holds

and that only for m close to N it holds that 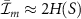 . The large region of values of m satisfying (2), that excludes only very small and very large m, is the information plateau; see [15] for a concise overview of the main properties of quantum Darwinism.
. The large region of values of m satisfying (2), that excludes only very small and very large m, is the information plateau; see [15] for a concise overview of the main properties of quantum Darwinism.
2. Classical and quantum cryptography overview
In this section, we provide a brief overview of selected topics and tasks from classical and quantum cryptography that are relevant to this work. In section 2.1 we describe a particular type of attack on classical devices with support of antennas, then in section 2.2 we discuss the intercept-and-resent type of attacks on quantum cryptography, being a quantum version of the classical man-in-the-middle attacks [35], and in section 2.3 we overview the problems of random number generation, classical and quantum, and its vital role for security.
2.1. Van Eck eavesdropping
All electronic devices necessarily radiate some electromagnetic signals that are correlated to their current state and working. If this radiation is not properly shielded, then an eavesdropper can collect with an antenna part of this signal and use it to regain some information regarding the devices. This kind of attack is sometimes called electromagnetic analysis attack [36].
National Security Agency provides so-called TEMPEST specifications referring to security against information leakage through unintentional radiation. The investigation covers both the ways to convey such attacks and protect against them; the latter is referred to as emission security (EMSEC), and covers not only electromagnetic radiations but also mechanical vibrations and sounds caused by the working of devices. We refer to [37, 38] for an overview.
Whereas this potentiality was obvious for most of the engineers and military, with the earliest mentions in the 19th Century [39], it was Van Eck [40] who first showed that such an attack is possible to be conducted using cheap equipment at a range of a hundred meters and that this way a substantial amount of information about real working devices can be obtained. In classical cryptography, this kind of attack with introducing additional side channels [41] gains a large interest and is considered a serious threat [42].
It has been shown that e.g. by monitoring power consumption signals one may breach smart-card security and vulnerability of the Data Encryption Standard (DES) [43–46] and Advanced Encryption Standard [47]. In [40, 48] eavesdropping risk from cathode-ray tube (CRT) monitors, and in [49] for LCDs, has been analyzed. The work [50] considers four types of emanation analysis attacks on wired and wireless keyboards, in [51] attacks using radiation of field programmable gate array are discussed, [52] consider similar attacks on RS-232 cables, [53] analyze an optical attack via LED indicators, [54] attacks on displays using reflections from other objects, [55] acoustic attacks on printers.
In [56] a way of software control over electromagnetic radiation has been proposed, both as a way to reduce the vulnerability to eavesdropping, and as a new possibility for a malevolent designer to increase its susceptibility. Also, hardware designers consider ways to prevent attacks based on radiation [36, 57]. Both power consumption and electromagnetic analysis attacks have simple and differential variants. One of the approaches is to employ a red-black architecture that separates carefully shielded plain-text data, called red, and encrypted information, called black, so that the shielding requirements may be lessened.
2.2. Intercept and resend attacks in quantum cryptography
The first cryptographical protocol with security arising from the use of quantum resources is the well-known BB84 protocol [3] for quantum key distribution (QKD), where one of the communicating parties, Alice, transmits to the other party, Bob, a qubit either in the computational basis 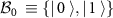 , or in the Hadamard (conjugate) basis
, or in the Hadamard (conjugate) basis 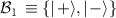 with
with ![$| \, + \rangle \equiv (1/\sqrt{2}) [| \, 0~\rangle + | \, 1~\rangle]$](https://content.cld.iop.org/journals/1367-2630/24/11/113054/revision2/njpaca558ieqn22.gif) and
and ![$| \, - \rangle \equiv (1/\sqrt{2}) [| \, 0~\rangle - | \, 1~\rangle]$](https://content.cld.iop.org/journals/1367-2630/24/11/113054/revision2/njpaca558ieqn23.gif) , and afterward Bob performs his measurement also in one of these bases. The procedure is repeated multiple times for subsequent quantum systems. Finally, both parties reveal part of their results, use them to evaluate the reliability of their communication, which covers potential eavesdropping, and eventually perform some post-processing for error correction and privacy amplification [58]. This is paradigmatic for further developed protocols, see [1] for an overview.
, and afterward Bob performs his measurement also in one of these bases. The procedure is repeated multiple times for subsequent quantum systems. Finally, both parties reveal part of their results, use them to evaluate the reliability of their communication, which covers potential eavesdropping, and eventually perform some post-processing for error correction and privacy amplification [58]. This is paradigmatic for further developed protocols, see [1] for an overview.
A possible attack on a wide class of protocols is for the eavesdropper, Eve, to intercept some of the transmitted states, perform some action on them, and in place pass (resend) some quantum states to Bob. The passed state can either be transformed [59, 60], or Eve can measure the intercepted state and prepare a new one [61], or use some implementation-dependent attacks [62–66].
The former approach uses the concept of nondemolition measurement [67]. The idea is the following [59]. We assume that Eve knows that the intercepted state will be one of the non-orthogonal states  , each occurring with probability pi
. This assumption is justified by the construction of the cryptographic scheme. Without measurement Eve's uncertainty regarding the transmitted subsystem is the ordinary Shannon entropy
, each occurring with probability pi
. This assumption is justified by the construction of the cryptographic scheme. Without measurement Eve's uncertainty regarding the transmitted subsystem is the ordinary Shannon entropy 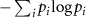 . The most general unitary transformation U possible to be performed by Eve on an intercepted qubit is [60]
. The most general unitary transformation U possible to be performed by Eve on an intercepted qubit is [60]
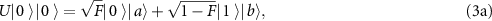
where  ,
,  ,
,  , and
, and 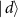 are states of Eve's subsystem after the interaction, and F is the fidelity of Bob's subsystem. In [59, 60] a trade-off between the gain of information by Eve, and the disturbance caused to Bob, was investigated.
are states of Eve's subsystem after the interaction, and F is the fidelity of Bob's subsystem. In [59, 60] a trade-off between the gain of information by Eve, and the disturbance caused to Bob, was investigated.
2.3. Private randomness generation
Randomness is a crucial resource for multiple tasks in information and communications technology (ICT). Random numbers have many uses in such fields of application as cryptography and authentication, system modeling and simulation e.g. using Monte Carlo methods, or in gambling. Most random number generators (RNGs) are based on purely algebraic manipulations on an initial seed. Because the series of numbers produced in such a generator is created in a deterministic way, those RNGs are called pseudo-RNGs (PRNGs).
There are also RNGs based on some chaotic classical physical processes such as electrical or atmospheric noise or by estimating the entropy of hardware state [68]. In order to validate that the source of the numbers is reliable, some statistical tests can be used [69]. Still, these tests are not able to guarantee that the numbers were indeed private, that is, cannot be predicted by an eavesdropper.
To see why privacy and unpredictability of the sequences of numbers are important, let us note the following places, where random numbers are crucial in establishing a secure classical cryptographical protocol. Out of 64 bits used for the DES key, 56 are randomized (Federal Information Processing Standards, FIPS 46, 1977); ANSI X9.8-1:2003 standard for PIN and FIPS 181-1993 for automatic password generation extensively use random numbers; the standard ANSI—X9.82-1 provides general requirements for (pseudo) random numbers to be used in all cases where security has to be ensured; see [70–77] for an overview of attacks on classical computing systems based on weaknesses of used PRNGs.
Thus, it is natural to try to use a property of quantum mechanics to generate completely random sequences of numbers. There exist methods exploiting such quantum processes as nuclear decay [78–80], or photons hitting a translucent mirror, e.g. id Quantique RNG [81]. Intrinsic indeterminacy of measurement results of quantum mechanics in a simple way enables the generation of numbers that are guaranteed to be unpredictable by the laws of Nature.
The most trivial case is the quantum measurement of a state prepared in a basis different from the one used in the measurement. For instance, a qubit prepared in the computational basis  , being thus either
, being thus either 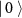 or
or 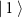 , when measured in the Hadamard basis
, when measured in the Hadamard basis 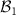 will result in outcomes + and − with equal probability 0.5, leading to perfectly random numbers, see the discussion in section 3 below.
will result in outcomes + and − with equal probability 0.5, leading to perfectly random numbers, see the discussion in section 3 below.
A great effort has been put into ensuring that the numbers generated by a quantum device are indeed random, with most of the current attention paid to validation that the devices work in a way declared by the constructor, who is considered to be untrusted [82, 83].
Below in this paper, we consider a caveat omitted by all these analyses, as we show that even if the constructor is trustworthy, the very nature of the quantum measurement forces the information about the random number to be insecure and publicly accessible. Similarly, the fact that every electric device is necessarily sending some radiation was well known much earlier than the work of Van Eck in the 1980s, as discussed in section 2.1. Nonetheless, before his work, it was not considered a real danger. The Van Eck innovation was in showing that radiation can substantially be used for wiretapping. We show that the information propagation recognized earlier by the quantum Darwinism research to be ineluctable is also actually cryptographically sound.
3. Methods
We concentrate on an elementary operation of a qubit measurement, as a basic operation for the majority of quantum devices. We follow [12] and call the observed qubit a system (S), the measuring device an apparatus (A); the third subsystem an environment (E).
We model the premeasurement upon rank-1 projectors 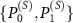 , with
, with 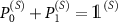 by a
by a  operation conditioned on them, i.e.
operation conditioned on them, i.e. 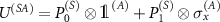 , where superscripts in parenthesis denote the subsystem. The interaction of the apparatus with the environment is given by the unitary transformation:
, where superscripts in parenthesis denote the subsystem. The interaction of the apparatus with the environment is given by the unitary transformation:
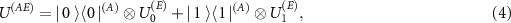
leading to the decoherence in the computational basis 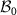 of (A).
of (A).
To illustrate a simple scenario of quantum randomness generation we consider the measurement of the state  in the computational basis, with projectors
in the computational basis, with projectors  ,
,  , and with subsystems (A) and (E) initially in 0th state leading to
, and with subsystems (A) and (E) initially in 0th state leading to ![$\rho^{(SA)}(T) \equiv \mathrm{Tr}_{E} \left[ | \, \phi \rangle \langle \phi \, |^{(SAE)} \right]$](https://content.cld.iop.org/journals/1367-2630/24/11/113054/revision2/njpaca558ieqn42.gif) , where
, where
and where T is the time after which all the interactions occur. We get that 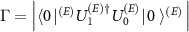 is the collective decoherence factor, see (1), of the joint state
is the collective decoherence factor, see (1), of the joint state 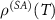 equal to
equal to
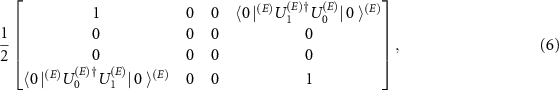
and the full orthogonalization of measurement results occur [25]. For the measurement to betide we need also the full decoherence, i.e. 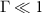 .
.
The above model refers to the simplest quantum randomness generation, where the measured state 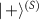 is prepared in a basis that is unbiased [84] to the basis
is prepared in a basis that is unbiased [84] to the basis 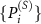 in which the premeasurement is performed, and the results are stored in the computational basis of the subsystem (A) that is initially preset to
in which the premeasurement is performed, and the results are stored in the computational basis of the subsystem (A) that is initially preset to 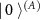 to maximize its information capacity [85]. The interaction part
to maximize its information capacity [85]. The interaction part 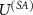 is designed by the user of the quantum device that calibrates the measuring device to measure in the selected basis, possibly taking into account the characteristics of his source of states; this part is also responsible for apparatus state orthogonalization.
is designed by the user of the quantum device that calibrates the measuring device to measure in the selected basis, possibly taking into account the characteristics of his source of states; this part is also responsible for apparatus state orthogonalization.
The actual measurement is finalized by the interaction 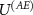 .
. 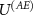 is partially engineered by the vendor of the measuring apparatus; the computational basis of (A) is actually the one that is being displayed to the user and the shape of
is partially engineered by the vendor of the measuring apparatus; the computational basis of (A) is actually the one that is being displayed to the user and the shape of  is determined by the device's case, like e.g. plastic housing of a USB stick, or metal frame of a rack-mounted multimeter together with the shielding of the laboratory, thus it also depends on the owner of the laboratory and should be considered as a part of the quantum device.
is determined by the device's case, like e.g. plastic housing of a USB stick, or metal frame of a rack-mounted multimeter together with the shielding of the laboratory, thus it also depends on the owner of the laboratory and should be considered as a part of the quantum device.
We consider a 4th subsystem, denoted (V) for Van Eck-type eavesdropper since our approach is a quantum analog of the Van Eck attack in classical cryptography, see section 2.1, where the electromagnetic radiation of classical devices is captured by antennas and used to intercept the private content.
In the attack, the eavesdropper intends to capture information regarding the measurement result stored in the apparatus. Since both the former and latter are classical data, we assume the result of wiretapping is stored in the computational basis. We consider a passive reception of the content of the environment, i.e. eavesdropper does not change it. This restricts his action to unitary operations conditioned on some projectors. Further in this text, we consider the particular case of the  operation conditioned on a pair of orthogonal projectors
operation conditioned on a pair of orthogonal projectors 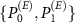 , with
, with 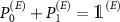 , i.e.
, i.e.

The eavesdropper's initial state is 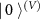 .
.
Direct calculations show the final state 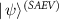 is
is
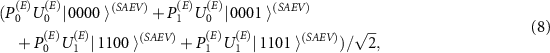
and thus the joint state of the user apparatus and the eavesdropper ![$\rho^{(AV)}(T) = \mathrm{Tr}_{SE} \left[ | \, \psi \rangle \langle \psi \, |^{(SAEV)} \right]$](https://content.cld.iop.org/journals/1367-2630/24/11/113054/revision2/njpaca558ieqn58.gif) is a state diagonal in the computational basis with coefficients:
is a state diagonal in the computational basis with coefficients: 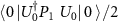 ,
, 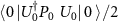 ,
, 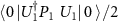 , and
, and 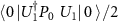 , where we omitted the superscript (E).
, where we omitted the superscript (E).
The figure of cryptographical merit we consider here is the probability that the eavesdropper correctly guesses the measurement result of the apparatus [86–89], denoted 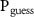 . This happens when both two-dimensional subsystems (A) and (V) indicate the same binary value, thus it is given by:
. This happens when both two-dimensional subsystems (A) and (V) indicate the same binary value, thus it is given by:
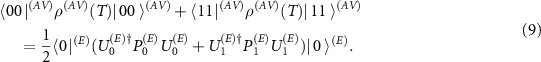
The environment (E) mediates between subsystems (A) and (V) and can be of a much larger dimension.
From (9) we see, that the guessing probability depends both on the ability of the environment to gather information regarding the apparatus, modeled by 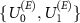 , and on the possibility of collecting the signal from the environment through the Van Eck-type antenna, modeled by
, and on the possibility of collecting the signal from the environment through the Van Eck-type antenna, modeled by 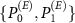 . The shielded laboratory assumption refers to the case with
. The shielded laboratory assumption refers to the case with 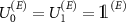 ; then the value of (9) is 0.5, so no information leaks outside the laboratory, and simultaneously
; then the value of (9) is 0.5, so no information leaks outside the laboratory, and simultaneously  , thus the measurement does not occur. Note that the guessing probability in (14) is the probability that the eavesdropper's subsystem (V) indicates the same state as the apparatus (A), and since we consider binary measurement, both subsystems are two-dimensional.
, thus the measurement does not occur. Note that the guessing probability in (14) is the probability that the eavesdropper's subsystem (V) indicates the same state as the apparatus (A), and since we consider binary measurement, both subsystems are two-dimensional.
The antenna determines the evolution 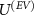 and is possessed by the wiretapper, and its capabilities are limited by his resources, reflecting his control over the information scattering. The rest of this paper aims to model the dependence of the guessing probability (9) on the power of the eavesdropper.
and is possessed by the wiretapper, and its capabilities are limited by his resources, reflecting his control over the information scattering. The rest of this paper aims to model the dependence of the guessing probability (9) on the power of the eavesdropper.
The scheme for information retrieval by an eavesdropper we propose here can be compared to the intercept-and-resend attack on QKD protocols discussed in section 2.2. Even though we deal with a single honest party, Alice, and there is no intentionally communicated second party, Bob, we still can view the protocol of a measurement process as a state preparation of the environment, that is formally close to the state submission to another party. From this point of view, the subsystem of the environment (E) plays a partially analogous role to the prepared and transmitted state; thus the first subsystem in (3) refers to (E) and the second subsystem to (V) using the notation of this section. Nonetheless, the differences between both schemes are fundamental, and should not be neglected. We summarize them as follows:
- (a)The essence of the security assured in QKD protocols against intercept-and-resend attack stem from the fact that the eavesdropper does not know the correct measurement basis. Thus, in the average case, the eavesdropper necessarily introduces some disturbance to the transferred quantum systems. Security is achieved as this disturbance can be further utilized by the users of the quantum protocol to detect the fact of wiretapping. In the attack proposed in this paper, any disturbance pertains to the environment external to the cryptographic system and has not been investigated as a potential diagnostic of aggression.
- (b)In QKD protocols, the prepared and transmitted quantum state is intended to be further measured after being received. After the measurement, the information can be copied perfectly and under control without any disturbance. In the introduced attack, the preparation of the state of the environment is unintentional, and the environment is beyond the control of the users of the QKD protocol. Nonetheless, the eavesdropper can perform a measurement on part of the environment, that, as shown in this work, can influence security.
- (c)In the proposed scheme the preparation of the state accessible to the eavesdropper is not intended to transmit information to other parts of the world; what is more, any information transfer is a kind of necessary evil needed for the local process of the measurement to betide, and the violated shielded laboratory assumption would demand this information be nullified if it were possible. On contrary, in ordinary quantum cryptographic protocols, the transmitted subsystem intentionally contains information, in fact as much information as it could accommodate.
- (d)In the proposed scheme the eavesdropper has much more control over the 'transferred' subsystem, viz. the environment after the measurement process containing information on the measurement result, that is intended to be kept secret. In QKD protocols the integrity of the transmitted states is checked at the stage when parties publish parts of their data and use it to evaluate some certificate of their security. This aspect has not been to date considered from the point of view of necessary information wide spreading during the measurement process, and thus in all currently existing protocols, Alice overlooked an eavesdropping antenna potentially standing very next to her laboratory.
In other words, there is no other way to use any quantum device and perform a quantum measurement than to make the measurement result publicly accessible to the environment outside the shielding. This is an intrinsic property of any possible quantum protocol, not only the simplified randomness generation in the considered example. If one uses a perfectly shielded laboratory, then she or he cannot perform a quantum measurement; if one performs a quantum measurement, then her or his laboratory cannot be perfectly shielded—if it can be shielded at all.
4. Results
In this section, we provide the results of applying the techniques of section 3 to two particular examples of the interaction of the measuring apparatus with the environment with the eavesdropper monitoring it with an antenna. In section 4.1 we provide an analytical study of a case with an environment consisting of multi two-level quantum system, and an eavesdropper accessing part of them in an incoherent way. In section 4.2 we present numerical results regarding a coherent attack on a part of a multi-level coherent environment.
4.1. Multi-qubit environment with incoherent eavesdropper
Now, let us use the above results to analyze a case of the environment consisting of N qubits. We follow the standard approach [16, 90] and model the 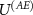 interaction as N independent imperfect
interaction as N independent imperfect 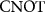 defined as
defined as
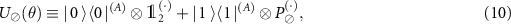
with 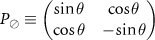 , and θ fixed for the setup, i.e.
, and θ fixed for the setup, i.e.
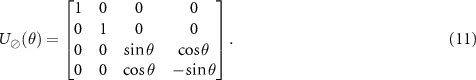
Thus, we have 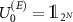 and
and 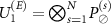 , where (s) denotes sth environmental qubit.
, where (s) denotes sth environmental qubit.
From this, it follows that the collective decoherence factor 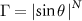 , or, that for a specific value of Γ an interaction with at least
, or, that for a specific value of Γ an interaction with at least 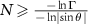 environmental qubits is required. The factor dependent on θ is an engineering parameter, and Γ is a quantumness parameter, thus we may assume that the number
environmental qubits is required. The factor dependent on θ is an engineering parameter, and Γ is a quantumness parameter, thus we may assume that the number  of qubits accessible to the eavesdropper is
of qubits accessible to the eavesdropper is  , for some function µ.
, for some function µ.
Let us consider the case when the eavesdropper is not able to perform a coherent measurement on multiple qubits and needs to perform the guess based on many separate single-qubit measurements. If he performs the Helstrom measurement [91], with one of the projectors given by  , on a specific environmental qubit, the success probability of correct distinguishing its state is
, on a specific environmental qubit, the success probability of correct distinguishing its state is 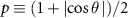 .
.
Suppose that the guess is given as the majority of n single-qubit guesses, i.e. it succeeds when at least 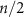 of these guesses is correct. Thus, the total success probability of the guess (9) is equal to
of these guesses is correct. Thus, the total success probability of the guess (9) is equal to 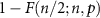 , where
, where 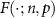 is the cumulative distribution function of the binomial distribution with n Bernoulli trials with success probability p. Now, we ask, for what range of Γ, θ, and µ do we have
is the cumulative distribution function of the binomial distribution with n Bernoulli trials with success probability p. Now, we ask, for what range of Γ, θ, and µ do we have 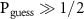 ?
?
It can be shown [92, 93] that for 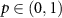 and a < p it holds
and a < p it holds 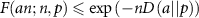 , where
, where 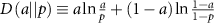 is the Kullback–Leibler divergence between Bernoulli random variables. Using the above formulae for n and p we directly get
is the Kullback–Leibler divergence between Bernoulli random variables. Using the above formulae for n and p we directly get
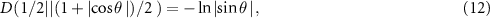
and thus

and the lower bound does not depend on θ. From these considerations it follows that taking any µ satisfying  and
and 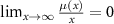 we have that in the classical limit an arbitrarily small fraction of all environmental qubits is enough to provide the eavesdropper full access to cryptographic data.
we have that in the classical limit an arbitrarily small fraction of all environmental qubits is enough to provide the eavesdropper full access to cryptographic data.
The fact expressed in (13), that the larger part of the environment is being observed, the more information about the system is gathered, complies with the information plateau observation of the quantum Darwinism [15, 34, 94], see section 1. We would like at this point to briefly discuss the relation between these two facts.
One of the central outcomes of quantum Darwinism is the result, that the mutual information between a measured (or observed) subsystem and a small fraction of the surrounding environment, is close to the von Neumann entropy of the former, H(S). In a sense, H(S) sets the limit on the classical information that the environment (E) can acquire about (S). It can also be observed, that when almost all the environment (E) is considered, it contains also the almost full quantum information about (S), as noted in section 1. It can be shown that the potential of acquisition of the quantum information is significantly diminished when any initial mixedness, or haziness, is present in the environment [94].
On the other hand, the quantity being paramount to our analysis is the guessing probability, directly related to min-entropy 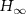 [88], viz. for a classical probability distribution we have
[88], viz. for a classical probability distribution we have  . The conditional quantum min-entropy is a single-shot [95] version of the conditional quantum entropy, in a sense that the latter may be considered as a limit of the former when an infinite number of copies of the states are available, as stated by the quantum asymptotic equipartition property (QAEP) [96].
. The conditional quantum min-entropy is a single-shot [95] version of the conditional quantum entropy, in a sense that the latter may be considered as a limit of the former when an infinite number of copies of the states are available, as stated by the quantum asymptotic equipartition property (QAEP) [96].
Thus, the approach to quantum Darwinism that we propose, employing the analysis of the guessing probability instead of the mutual information, supplies a related, but a new point of view on the concept of redundant imprinting of information in quantum Darwinism. Obviously, the larger the quantum mutual information the larger the classical guessing probability can be expected, and vice versa. However, a goal of quantum Darwinism, as a quantum-to-classical transition theory, is to elucidate the classical properties of quantum systems. Thus, a quantity that is classical in its nature, viz. the guessing probability, may be expected to provide new insight into the problem.
In quantum Darwinism, the fact that the classical information about (S) is present in the environment is expressed by the observation that multiple fragments of the environment (E) have large mutual information with (S). In contrast, in the view of QAEP, min-entropy and the guessing probability concern the situation when there exists at least one fragment of the environment with the classical information imprint. We leave a further investigation of the relation of these approaches to quantum Darwinism for future work.
We note that when the whole environment is accessible to the eavesdropper, even in an incoherent, semi-classical, manner, i.e. for 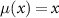 , the relation (13) takes a simple trade-off form
, the relation (13) takes a simple trade-off form

We see that the shielded laboratory assumption 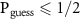 entails
entails 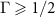 , viz. restricts the measurement to premeasurement. The trade-off (14) in particular states that the eavesdropper's ability to read out the information of the measurement limits the degree of decoherence.
, viz. restricts the measurement to premeasurement. The trade-off (14) in particular states that the eavesdropper's ability to read out the information of the measurement limits the degree of decoherence.
The above model is exceedingly simplistic, covering only a particular form of potential attacks of Van Eck's type, and may not be the most efficient one. Yet, this restricted and fairly simple and natural form of gathering information from the surroundings is enough to compromise the security of a device producing private numbers showing that the discussed sort of attack is a serious threat.
Let us summarize the assumptions we make in the derivation of the lower bound (13). We assume a particular form of the interaction  justified by the functioning of a measuring device. The decomposition of the measurement process into parts
justified by the functioning of a measuring device. The decomposition of the measurement process into parts 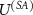 and
and 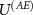 is justified by its logical order in the measurement, i.e. first occurs the premeasurement, and then occurs the decoherence. Thus, stating that the measuring device interacts with the environment via some interaction
is justified by its logical order in the measurement, i.e. first occurs the premeasurement, and then occurs the decoherence. Thus, stating that the measuring device interacts with the environment via some interaction 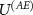 is not restrictive. Next, we perform the calculations using a particular form of
is not restrictive. Next, we perform the calculations using a particular form of 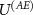 used in [16, 90]; we leave considerations with more general
used in [16, 90]; we leave considerations with more general 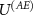 as an important new engineering task of designing cryptographical devices in a way more secure against Van Eck's attacks. The considered form of the interaction
as an important new engineering task of designing cryptographical devices in a way more secure against Van Eck's attacks. The considered form of the interaction  does not restrict the generality of our results, as it is sufficient for the trade-off relation to occur. We show that such interaction exists, possibly there exists another interaction
does not restrict the generality of our results, as it is sufficient for the trade-off relation to occur. We show that such interaction exists, possibly there exists another interaction 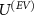 for which the trade-off relation is even stronger; we also leave this for a further study of the interplay between designing devices with more suitable
for which the trade-off relation is even stronger; we also leave this for a further study of the interplay between designing devices with more suitable 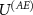 and attacks with more efficient
and attacks with more efficient 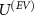 .
.
To see the consequences of the above analysis, we start with the simplest case with one environmental qubit interacting via a perfect CNOT, viz.
N = 1 and θ = 0. We have the full decoherence with 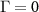 but, if the only environmental qubit is intercepted by the eavesdropper, we also have
but, if the only environmental qubit is intercepted by the eavesdropper, we also have 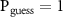 . For a toy model of decoherence with N = 20 and
. For a toy model of decoherence with N = 20 and 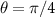 we have
we have 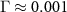 ; then for 1, 3, and 5 intercepted environmental qubits
; then for 1, 3, and 5 intercepted environmental qubits 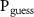 is 0.85, 0.94, and 0.98, respectively. For the more realistic case with
is 0.85, 0.94, and 0.98, respectively. For the more realistic case with 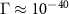 [97] if the van Eck's antenna observes
[97] if the van Eck's antenna observes 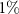 or
or 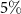 of the environment, then
of the environment, then 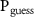 is 0.6 or 0.99, respectively.
is 0.6 or 0.99, respectively.
4.2. Coherent eavesdropping from moderate-size environment
To investigate how the privacy of quantum random numbers from the above model is compromised by a coherent Van Eck-type antenna we performed also numerical simulations. Let 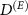 denote the dimension of the environment, and
denote the dimension of the environment, and 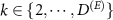 be the number of degrees of freedom of the environment the antenna can faithfully distinguish; the ratio
be the number of degrees of freedom of the environment the antenna can faithfully distinguish; the ratio 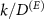 can be considered as the measure of how much of the environment is monitored, or controlled, by the eavesdropper.
can be considered as the measure of how much of the environment is monitored, or controlled, by the eavesdropper.
In the numerical calculations we consider Haar distributed [98] 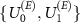 . To simulate the limitations of Van Eck's antenna we now consider
. To simulate the limitations of Van Eck's antenna we now consider 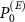 of the following form. We decompose the space of the environment
of the following form. We decompose the space of the environment 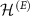 into two parts:
into two parts: 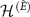 , and
, and 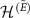 , with dimensions k and
, with dimensions k and 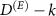 , respectively; so that
, respectively; so that 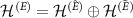 , where
, where 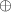 denotes the direct sum of spaces. We take
denotes the direct sum of spaces. We take 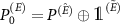 , where
, where 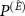 is an arbitrary projector on
is an arbitrary projector on  with the rank
with the rank 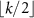 .
.
We executed the computation of (9) for 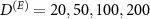 . To this end, for each instance, we parametrized the operator
. To this end, for each instance, we parametrized the operator 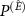 and performed a gradient search to maximize the value of the guessing probability. We averaged the results of several (15, 8, 11, and 4, respectively) instances with different
and performed a gradient search to maximize the value of the guessing probability. We averaged the results of several (15, 8, 11, and 4, respectively) instances with different 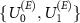 . The results are shown in figure 1.
. The results are shown in figure 1.
Figure 1. The dependence of the guessing probability of the indicator of the measuring apparatus by a Van Eck-type eavesdropper depending on the relative size of the part of the environment observed by the wiretapping antenna for different dimensions 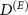 of the environment.
of the environment.
Download figure:
Standard image High-resolution imageIt can be observed that the guessing probability is more or less proportional to the observed part of the environment. We note that even when the eavesdropper possesses full access to the environment's information, she or he still may not be able to achieve the value 1 of guessing probability since not all information could have been propagated, especially when the value of  is small. This relates to the situation with
is small. This relates to the situation with 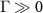 , so with no full measurement inside the laboratory.
, so with no full measurement inside the laboratory.
5. Conclusions
Despite this work being embedded in the framework of einselection and quantum Darwinism, we do not consider here the usual scenario of information widespread in multiple copies of independent parts of the environment. We concentrate on the observation of a single observer, so, this cannot be understood as a model of objectivity [99] (or inter-subjectivity [25, 100]) as investigated in the recent works [16]. Yet, it is obvious, that after a measurement is performed, then knowing what has been measured (i.e. the basis), should imply the ability to copy and disseminate the result [33, 101].
We have seen that the shielded laboratory assumption prevents the occurrence of measurement; and that by relaxing this assumption, we open a way for attacks similar to the Van Eck phreaking. We note that although figure 1 shows cases with relatively small sizes of the environment compared to macroscopic objects, it suggests that the greater the dimension, the lower part of the laboratory's surroundings has to be under control for the significant potential for eavesdropping. Indeed, the relation (13) we derived for incoherent qubits phreaking clearly indicates that any sort of cryptographic protocol is prone to the discussed type of attacks.
We would like to stress that our topic is not the analysis of the case when the device that processes quantum information happens not to be perfectly shielded due to imperfections. We also do not consider the case when the eavesdropper is vetting any classical information encoded microscopically in the cryptographical equipment after potentially gaining access to it. On contrary, we show that for any quantum measuring-based device to function properly it is necessary to drop the perfect shielding assumption by the design, and adjust to the fact delivered from quantum Darwinism, that after the quantum-to-classical transition the uncontrolled information leakage is ineluctable.
In this preliminary study, we investigated only the simplest case where the quantum randomness is obtained from the measurement on a different basis than the prepared state. Although simple, this scenario is ubiquitous as an ingredient of more involved and complex quantum protocols.
This work intends to show that the quantitative investigation of the relation between two important, yet till now disjoint, areas of quantum information, viz. theory (quantum Darwinism) and application (quantum cryptography) of measurements are possible. Quantum cryptography is a wide field and is currently the only quantum information research area with serious commercial deployments [102, 103]. Our main premise is to change one of the essential parts of the paradigm of quantum cryptography that was based on neglecting, or abstracting from, the way the quantum measurement is performed in cryptographic devices. We also suggest that the guessing probability together with the related concept of min-entropy may be a relevant quantity to be investigated in quantum Darwinism in a way similar to the mutual information.
We expect the presented result will encourage researchers working on decoherence theory to contribute to the development of the design of cryptographic devices, similarly as they contribute to the area of quantum computation [104–106]. We consider it an interesting and vital problem, how such analysis can be extended to more complicated scenarios, and cover such problems as quantum communication [3] or QKD [107], not only in a device-dependent scenario, like in this work, but possibly in device-independent [108], or semi-device-independent [109] frameworks.
We close this work with the practical open question of whether it is possible to protect against the introduced type of attacks. We predict the general answer, with the eavesdropper with sufficient control over the environment, to be negative. Still, it is plausible that under some reasonable assumptions regarding the technology of the eavesdropper, one can engineer the shielding in such a way that the measurement does occur while the wiretapping task becomes burdensome. Another possible way of defense could potentially be to adopt the ordinary quantum cryptographical methods [3, 60] to somehow detect the action of a Van Eck-type eavesdropper on the environment.
Acknowledgment
The work is supported by the Foundation for Polish Science (IRAP project, ICTQT, Contract No. 2018/MAB/5, co-financed by EU within Smart Growth Operational Programme), NCBiR QUANTERA/2/2020 (www.quantera.eu), an ERA-Net cofund in Quantum Technologies, under the project eDICT, and NCN grant SHENG (Contract No. 2018/30/Q/ST2/00625). The numerical calculations we conducted using OCTAVE 6.1 [110], and packages QETLAB 0.9 [111] and Quantinf 0.5.1 [112].
Data availability statement
The work does not involve any data not included in the text. The MATLAB source codes used to prepare figure 1 are available upon request from the author. All data that support the findings of this study are included within the article (and any supplementary files).
Conflicts of Interest
The author declare no conflict of interest.
Ethical statement
The work is purely theoretical. No ethical issues were noted by the author.




