Abstract
The concept of topological crystalline insulators (TCIs) protected by crystallographic symmetries has been proposed for over ten years. The diversity of spatial symmetries leads to various TCI phases, among which the mirror-protected TCI phase was firstly verified by experiments. The mirror-protected TCIs host robust spin and charge transports which are expected to have wide devices applications. In this work, through the first-principles calculations, we identify 67 mirror-protected TCIs. The corresponding topological surface states are also studied. Especially, among these TCIs, Bi3STe2 and Pt3Sn with space groups 164 and 221 are chosen as representatives to demonstrate further analyses of the bulk topology and mirror-protected surface states. The predicted mirror-protected TCIs are expected to provide a useful reference for experimentalists and promote realistic device applications.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Due to novel electronic properties, the topological materials have been a persistent hot-topic in condensed matter physics. In the early stage, protected by time-reversal symmetry (TRS), the 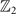 topological insulators (TIs) were proposed and realized [1–3]. Other than the internal symmetry, fruitful crystal spatial symmetries could bring topological crystalline insulators (TCIs) phases [4, 5]. Due to various crystallographic symmetries, different TCI phases were gradually proposed such as mirror-protected TCIs [6], glide symmetries protected hourglass insulators [7], rotation protected TCIs [8] and higher-order TIs [9–14] and so on. The topological classifications of insulating electronic states have been greatly developed after the introduction of TCIs.
topological insulators (TIs) were proposed and realized [1–3]. Other than the internal symmetry, fruitful crystal spatial symmetries could bring topological crystalline insulators (TCIs) phases [4, 5]. Due to various crystallographic symmetries, different TCI phases were gradually proposed such as mirror-protected TCIs [6], glide symmetries protected hourglass insulators [7], rotation protected TCIs [8] and higher-order TIs [9–14] and so on. The topological classifications of insulating electronic states have been greatly developed after the introduction of TCIs.
While the rotation symmetry protected TCI phase was proposed by toy models in the pioneering work for TCIs [4], the mirror-protected TCI phase was first predicted in real materials [6] and then verified by the angle-resolved photoemission spectra experiment [15]. The main feature of a mirror-protected TCI is that the Dirac cones protected by mirror symmetries would emerge on the surface Brillouin zone (BZ), and the number of them is equal to a topological invariant: mirror Chern number (MCN) [16]. To be specific, the MCN is defined on a mirror invariant plane in the bulk BZ, and this plane corresponds to a mirror invariant line in a surface BZ. Then surface Dirac cones (the number is equal to MCN) emerge on this line. According to the above description, the surface Dirac cones of mirror-protected TCIs possess a higher tunability than that of 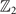 TIs where Dirac cones are only located at the time-reversal invariant momenta (TRIM) in surface BZ [17].
TIs where Dirac cones are only located at the time-reversal invariant momenta (TRIM) in surface BZ [17].
Since the mirror-protected TCI phase was revealed, up to now, several mirror-protected TCIs have been proposed [6, 15, 18–31]. For example, rocksalt materials which have the similar structure and topology with SnTe: Pb1−x Snx Te/Se, SnS, SnSe and PbPo [18–20, 24]; antiperovskite material family with the chemical formula A3BX where A = (Ca, Sr, La), B = (Pb, Sn) and X = (C, N, O) [21]; full-Heusler material family [25]; dual TIs including additional weak TI phase: Bi2TeI [22], BiTe [26], Pt2HgSe3 [31]. In addition, the mirror-protected TCI phase could coexist with other topological phases. For example, KHgX where X = (As, Sb, Bi) [7] and BiSe [9], proposed as candidates for hourglass insulators and higher-order TIs, respectively, both have nonvanishing MCNs. As a result, the mirror-protected TCI phases could be expected to be found in many materials with various crystal structures and chemical compositions. Furthermore, the mirror-protected TCI phase could bring some novel properties such as Dirac mass generation from ferroelectric distortion [32, 33] and flat band superconductivity induced by strain [34], which could be applied in new novel devices. In addition, the nonvanishing MCN of the mirror-protected TCI is also key to identify other TCI phases [35]. Therefore, a work to identify possible mirror-protected TCIs is meaningful and should be important for both fundamental research and device applications.
In recent years, along with the development of the method of symmetry indicators (SIs) [36] or topological quantum chemistry [37], three databases of topological materials including TCIs have been built [38–40]. In this work, we focus on the database built by Tang et al [40]. This database provides a series of TCIs with relatively clean Fermi surfaces. The mirror-protected topological boundary states are probably observed relatively clearly in these TCIs, which motivates us to further identify them by first-principles calculations. We firstly exclude TCIs belong to the space groups (SGs) which have no mirror symmetries. The number of these excluded materials is six, corresponding to cases of SGs 2, 14, 88, 148 in the table of TCIs (table 2 in the supplementary of reference [40]). Then for identifying the bulk topology and checking the nature of TCI phases for the rest of candidates, their SIs are calculated. Hereafter the MCNs of these materials are calculated to completely determine the mirror-protected phase. When accomplishing above two processes, if a material is checked as a TCI and has nonvanishing MCNs, we could identify this material as a mirror-protected TCI. We find 67 mirror-protected TCIs and list them in table 1, the SIs and MCNs of all materials are listed in supplemental material (SM) (https://stacks.iop.org/NJP/23/103032/mmedia) [41]. In the main text, Bi3STe2 and Pt3Sn crystallizing in SGs 164 and 221, respectively are chosen as representative materials to demonstrate calculations of SIs, MCNs and topologically nontrivial surface states. The results of identifications for other materials with nonvanishing MCNs are also shown in the rest part of main text. The corresponding details of calculations are left to SM [41].
Table 1. Materials with nonvanishing MCNs in this work. This table includes their SGs, corresponding SIs and MCNs (given in parentheses behind material names). The materials marked in black color are mirror-protected TCIs which could be identified from our first-principles calculations, and that in red are strong TIs.
| SG | SI | Materials |
|---|---|---|
| 11 | (1, 0, 0, 2) | Sb2Sr( ) [55] ) [55] |
| 12 | (0, 0, 1, 0) | Bi2ITe(2) [56] |
| 51 | (0, 1, 1, 0) | GaPt2( ) [57] ) [57] |
| 62 | (0, 0, 0, 2) | HgSr3(20) [58] |
| 63 | (1, 1, 0, 2) | AlGeLu(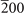 ) [59], BaGe(200) [60], BaPb(202) [61], BaSi(002) [62] ) [59], BaGe(200) [60], BaPb(202) [61], BaSi(002) [62] |
PbSr(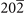 ) [63], SnSr( ) [63], SnSr(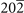 ) [64], BaSn(002) [60], Ba3Pb5( ) [64], BaSn(002) [60], Ba3Pb5( ) [65] ) [65] | ||
CaGe( ) [66], CaSn( ) [66], CaSn(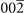 ) [67], Ba5Cd2FSb5(200) [68] ) [67], Ba5Cd2FSb5(200) [68] | ||
| 71 | (1, 1, 1, 2) | Ba3Bi4Li4(002) [69] |
| 123 | (0, 3, 6) | As3CsZn4(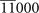 ) [70], As3RbZn4( ) [70], As3RbZn4(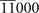 ) [70] ) [70] |
| (0, 2, 0) | Pd3Sn(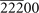 ) [71] ) [71] | |
| 129 | (0, 0, 1, 2) | GeHfTe(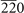 ) [72], GeNbSb(220) [73], SiTeZr( ) [72], GeNbSb(220) [73], SiTeZr( ) [74], SnTeZr( ) [74], SnTeZr(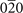 ) [74] ) [74] |
| 137 | (0, 0, 0, 2) | Ba2LiN(20) [75] |
| 139 | (1, 2) | AsBa2(200) [76], Ba2Bi(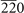 ) [77], Ba2Sb(200) [78] ) [77], Ba2Sb(200) [78] |
BiSr2( ) [78], Br2Ca3Si( ) [78], Br2Ca3Si(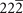 ) [79], SbSr2( ) [79], SbSr2(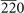 ) [80] ) [80] | ||
| (0, 4) | AsCa2(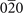 ) [81], Bi2F2OSr2Ti2( ) [81], Bi2F2OSr2Ti2( ) [82] ) [82] | |
| 140 | (1, 0) | Bi(44) [83] |
| (0, 4) | GePt3(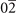 ) [84] ) [84] | |
| 164 | (0, 0, 1, 0) | BaSi2( ) [85], BiTe(2) [86], Bi2Pb2Te5(2) [87], Bi2Se2(2) [88], Bi3STe2(2) [52] ) [85], BiTe(2) [86], Bi2Pb2Te5(2) [87], Bi2Se2(2) [88], Bi3STe2(2) [52] |
| 166 | (1, 1, 1, 0) | Bi4Se3( ) [89], Bi8Se9( ) [89], Bi8Se9( ) [90] ) [90] |
| 187 | (1, 0) | CHf(110) [91], NY(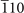 ) [92] ) [92] |
| 189 | (1, 0) | AgAsCa(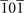 ) [93], AgCaP( ) [93], AgCaP(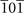 ) [94], AsLuPd( ) [94], AsLuPd(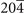 ) [95] ) [95] |
| 191 | (3, 8) | B2Zr(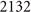 ) [96] ) [96] |
| 193 | 10 | Pb3SZr5(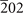 ) [97] ) [97] |
| 194 | 8 | AsHgK(020) [98], CdNa2Sn(020) [99], HgKSb(020) [98] |
| 221 | (2, 4) | CaPd(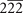 ) [100] ) [100] |
| (0, 2) | Ca3GeO(202) [101], Ca3OPb(202) [102] | |
Ca3OSn(202) [101], NY( ) [92], OPbSr3(202) [101] ) [92], OPbSr3(202) [101] | ||
| (1, 0) | NTi3Tl( ) [103] ) [103] | |
| (3, 6) | PbPt3( ) [104], Pt3Sn( ) [104], Pt3Sn( ) [105] ) [105] | |
| 225 | 2 | AsSc( ) [106], CPt( ) [106], CPt(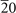 ) [107], SbSc( ) [107], SbSc(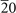 ) [108] ) [108] |
| 6 | Au2InSc(20) [109], Au2InY(20) [110] | |
| 4 | Ba(40) [111], BiI3(02) [112], Ca(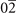 ) [113], SSn( ) [113], SSn(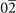 ) [114], SeSn( ) [114], SeSn(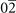 ) [115], SnTe( ) [115], SnTe(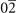 ) [116] ) [116] |
aThe integers in parentheses correspond to the SIs defined in reference [35] for different SGs. To be specific, (z2,1, z2,2, z2,3, z4) for SGs 11, 12, 51, 62, 63, 71, 129, 137, 164, 166; (z2,1, z4m,π
, z8) for SG 123; (z2,1, z8) for SGs 139, 140; (z3m,0, z3m,π
) for SGs 187, 189; (z6m,π
, z12) for SG 191; 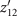 for SGs 193, 194; (z4m,π
, z8) for SG 221; z8 for SG 225. bFor the sake of clarity, the names of materials in this paper follow that in the database [40]. cEvery integer in parentheses behind materials names corresponds to MCNs for inequivalent mirror planes. Here for the compact representation, negative number −m is replaced by
for SGs 193, 194; (z4m,π
, z8) for SG 221; z8 for SG 225. bFor the sake of clarity, the names of materials in this paper follow that in the database [40]. cEvery integer in parentheses behind materials names corresponds to MCNs for inequivalent mirror planes. Here for the compact representation, negative number −m is replaced by 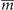 . The definitions and order of inequivalent mirror planes for every SG follow the mapping table between SIs and topological invariants [35].
. The definitions and order of inequivalent mirror planes for every SG follow the mapping table between SIs and topological invariants [35].
This work is organized as follows. The computational methods are described in section 2. In section 3, we analyze the bulk topology of the representative materials Bi3STe2 and Pt3Sn, which confirms the nature of mirror-protected TCI phases. The topological nontrivial surface states based on tight-binding (TB) models of Wannier functions are demonstrated in section 4. The identifications of other materials with nonvanishing MCNs are put into section 5. Lastly, we perform the conclusions and discussions in section 6.
2. Computational details
The first-principles calculations are based on the density functional theory (DFT) implemented by Vienna ab initio simulation package (VASP) [42, 43]. The Perdew–Burke–Ernzerhof functional of generalized gradient approximation is chosen as the exchange–correlation potential [44], and the projector augmented wave method is used to treat core–valence electron interactions [45, 46]. The TRS and spin–orbit coupling (SOC) are taken into account in all calculations. We use 1.5 times maximum cut-off energy recommended in pseudopotential files as the plane wave cut-off energy and do the convergence test for k point parameters of every structure. The experiment crystal structures are used. MCN calculations could be realized through Z2Pack interfaced to VASP [47, 48]. The high quality TB models under atom-centered Wannier functions have been constructed by Wannier90 package [49]. The calculations of surface states are completed by using iterative Green's function method in WannierTools package [50, 51] based on corresponding TB models.
3. Identifications of mirror-protected TCI phases in representative materials
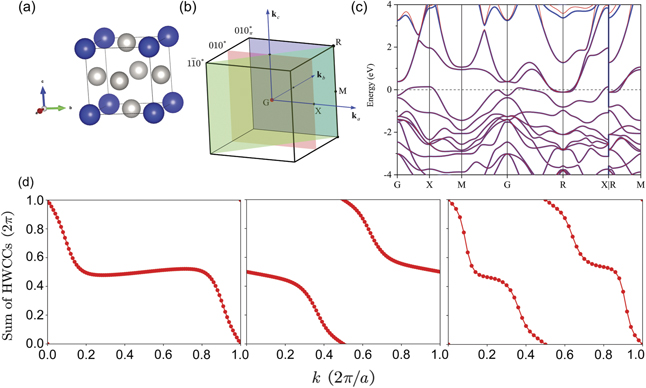
We mainly analyze the bulk topology of the representative materials in this section, after which their mirror-protected TCI phases are revealed. The material Bi3STe2 [52] crystallizing in SG 164, called sulphotsumoite, has two chemical formulae in the primitive unit cell (figure 1(a)). This unit cell forms by stacking two Bi2Te2S quintuple layers and a bismuth bilayer sandwiched by them along c axis. Therefore, the (001) surface states of Bi3STe2 are expected to be studied in experiments due to more easily cleaving layer structures along this direction. The point group of Bi3STe2 is D3d
. This point group includes 12 symmetry operators where inversion P, two fold rotation 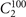 and three fold rotation
and three fold rotation 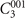 generators (100 and 001 represent the direction of rotation axes under the a, b, c in figure 1(a)). In this work with the theme of mirror-protected TCI phases, we naturally pay our attention to mirror symmetries. The mirror plane
generators (100 and 001 represent the direction of rotation axes under the a, b, c in figure 1(a)). In this work with the theme of mirror-protected TCI phases, we naturally pay our attention to mirror symmetries. The mirror plane  is perpendicular to the axis 100 and denoted as 100 mirror plane. On account of
is perpendicular to the axis 100 and denoted as 100 mirror plane. On account of 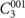 , Bi3STe2 has three equivalent mirror planes in total (represented by dash lines in figure 1(a)), and thus only one mirror plane needs to be considered in the following analysis.
, Bi3STe2 has three equivalent mirror planes in total (represented by dash lines in figure 1(a)), and thus only one mirror plane needs to be considered in the following analysis.
Figure 1. (a) (Left panel) The primitive unit cell of Bi3STe2, where the purple, gray, yellow balls denote Bi, Te, S atoms, respectively. (Right panel) The top view of the lattice. Dash lines represent three equivalent mirror planes related by 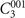 in SG 164. (b) The bulk BZ of Bi3STe2. High symmetry points G, M, K, A, L, H are shown. The MCN calculation is performed in the green rectangle zone, corresponding to 100* plane. (c) The electronic band structure of Bi3STe2 which shows continuous and finite direct gap around the Fermi level (set to 0 eV). The blue and red lines correspond to the band structures calculated by first-principles and Wannier TB model, respectively. (d) The evolution of the sum over occupied bands of HWCCs for subspace with mirror eigenvalue +i along ka
, where the horizontal axis is in the unit of ka
while the vertical axis is in the unit of 2π.
in SG 164. (b) The bulk BZ of Bi3STe2. High symmetry points G, M, K, A, L, H are shown. The MCN calculation is performed in the green rectangle zone, corresponding to 100* plane. (c) The electronic band structure of Bi3STe2 which shows continuous and finite direct gap around the Fermi level (set to 0 eV). The blue and red lines correspond to the band structures calculated by first-principles and Wannier TB model, respectively. (d) The evolution of the sum over occupied bands of HWCCs for subspace with mirror eigenvalue +i along ka
, where the horizontal axis is in the unit of ka
while the vertical axis is in the unit of 2π.
Download figure:
Standard image High-resolution imageThe electronic structure of Bi3STe2 is shown in figure 1(c). From energy bands along high symmetry lines in bulk BZ (figure 1(b)), we find a continuous direct gap and the relatively clean Fermi surface, which implies the probably well-defined MCNs and the observable surface states. The p type orbitals of all elements in Bi3STe2 dominate the energy range around Fermi level. To be specific, the 6p, 5p, 3p orbitals of Bi, Te, S, respectively dominate the conduction states in the energy range from 0 eV to 4.5 eV and the valence states from −6 eV to 0 eV. These orbitals have a large hybridization. Therefore, the electrons occupied on these atomic orbitals are valence electrons in Bi3STe2. There are 42 valence electrons in a primitive unit cell.
Then, by means of the SI theory, the bulk topology of Bi3STe2 is carefully analyzed. According to this theory, the topology of a system could be confirmed by calculating the irreducible representations (irreps) of occupied bands of high symmetry k points [36, 53]. In the case of Bi3STe2, the high symmetry points have been shown in figure 1(b), and the corresponding irreps of 42 occupied bands are listed below in the type of a vector:
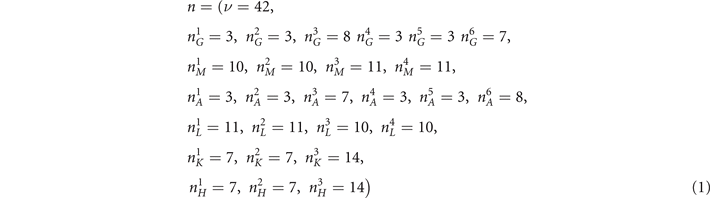
where ν is the number of occupied bands and 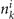 represents the number of appearance of ith irrep at the high symmetry point k for occupied bands. The order of irreps follows reference [54]. For the sake of getting SI, this vector needs to be expanded by atomic insulator basis (AIB). The AIB set of SG 164 could be found in reference [40], including 9 AIBs (denoted by ai
, i = 1, 2, ..., 9) in total and each of them has a common factor (denoted by Ci
, i = 1, 2, ..., 9). The result of expansion could be easily acquired:
represents the number of appearance of ith irrep at the high symmetry point k for occupied bands. The order of irreps follows reference [54]. For the sake of getting SI, this vector needs to be expanded by atomic insulator basis (AIB). The AIB set of SG 164 could be found in reference [40], including 9 AIBs (denoted by ai
, i = 1, 2, ..., 9) in total and each of them has a common factor (denoted by Ci
, i = 1, 2, ..., 9). The result of expansion could be easily acquired: 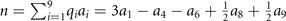 . SI is defined as the set qi
Ci
mod Ci
, Ci
> 1, in this case all common factors are equal to 1 except C8 = 2 and C9 = 4, thus the SI of Bi3STe2 is (1, 2) and the corresponding group is
. SI is defined as the set qi
Ci
mod Ci
, Ci
> 1, in this case all common factors are equal to 1 except C8 = 2 and C9 = 4, thus the SI of Bi3STe2 is (1, 2) and the corresponding group is 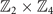 due to the common factors 2 and 4 [36, 53]. This result of SI means that Bi3STe2 is a TCI, which consistents with the identification in the database. In addition, a series of Fu–Kane-like formulae have been tabulated in reference [35], from which we could calculate the SIs of all 230 SGs easily. To be specific, in the case of SG 164, we could acquire the SI from calculating a set of indicators (z2,1, z2,2, z2,3, z4) where
due to the common factors 2 and 4 [36, 53]. This result of SI means that Bi3STe2 is a TCI, which consistents with the identification in the database. In addition, a series of Fu–Kane-like formulae have been tabulated in reference [35], from which we could calculate the SIs of all 230 SGs easily. To be specific, in the case of SG 164, we could acquire the SI from calculating a set of indicators (z2,1, z2,2, z2,3, z4) where 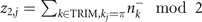 and
and  . Here TRIM is time-reversal invariant momenta,
. Here TRIM is time-reversal invariant momenta, 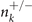 represents the number of occupied Kramers pairs with even or odd parity, respectively. As a matter of fact, for SG 164,
represents the number of occupied Kramers pairs with even or odd parity, respectively. As a matter of fact, for SG 164, 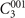 brings three equivalent L and three equivalent M points within eight TRIM (figure 3(a)). As a result, z2,1 and z2,2 are always trivial, and only z2,3 and z4 are meaningful. (z2,3, z4) actually represents the SI of SG 164 we defined above. According to the parity of occupied eigenstates at eight TRIM, we find that (z2,1, z2,2, z2,3, z4) = (0, 0, 1, 0), and therefore the SI is (1, 0). Although this result is different from (1, 2) we analyzed above, the same topology could also be given: z4 is the criterion of strong TI or TCI phases, here the result of z4 = 0 consists with the TCI phase of Bi3STe2. In addition, z2,j
is weak topological index, z2,3 = 1 reveals the weak TI phase in Bi3STe2 other than the TCI phase, and even number of Dirac cones are expected in the (100) and (010) surface BZs.
brings three equivalent L and three equivalent M points within eight TRIM (figure 3(a)). As a result, z2,1 and z2,2 are always trivial, and only z2,3 and z4 are meaningful. (z2,3, z4) actually represents the SI of SG 164 we defined above. According to the parity of occupied eigenstates at eight TRIM, we find that (z2,1, z2,2, z2,3, z4) = (0, 0, 1, 0), and therefore the SI is (1, 0). Although this result is different from (1, 2) we analyzed above, the same topology could also be given: z4 is the criterion of strong TI or TCI phases, here the result of z4 = 0 consists with the TCI phase of Bi3STe2. In addition, z2,j
is weak topological index, z2,3 = 1 reveals the weak TI phase in Bi3STe2 other than the TCI phase, and even number of Dirac cones are expected in the (100) and (010) surface BZs.
As we mentioned above, only the MCN of one mirror plane has to be acquired. Here we choose the 100 mirror plane for the MCN calculation. The corresponding high symmetry plane in the bulk BZ is denoted by 100* plane, and this plane is clearly demonstrated by the shaded rectangle zone in figure 1(b). To acquire MCN of this plane, we calculate the hybrid Wannier charge centers (HWCCs) of this shaded rectangle zone on the basis of details in SM [41]. The evolution of the sum of HWCCs for the subspace with mirror eigenvalue +i is shown in figure 1(d), from this we conclude that the MCN is equal to 2. This nonvanishing MCN verifies the mirror-protected TCI phase in Bi3STe2, and corresponding two Dirac cones emerge on the mirror invariant (001) surface BZ. Considering that there are other two equivalent mirror planes as shown in figure 1(a), six mirror-protected Dirac cones should emerge on this surface BZ in total.
Then we discuss the next representative material Pt3Sn crystallizing in SG 221. Pt3Sn has the simple face-centered cubic structure with a cubic primitive unit cell (figure 2(a)). The point group corresponding to this SG is Oh
which includes 48 operations in total, and five generators: P, 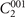 ,
, 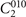 ,
,  ,
, 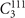 . Same as the case of Bi3STe2, after combining P and all C2 operations, there are nine mirror operations in total while the number of inequivalent mirror planes is only two. Here we pay attention to the inequivalent 010 and
. Same as the case of Bi3STe2, after combining P and all C2 operations, there are nine mirror operations in total while the number of inequivalent mirror planes is only two. Here we pay attention to the inequivalent 010 and 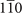 (here the negative number −1 is replaced by
(here the negative number −1 is replaced by 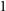 for the compact representation) mirror planes in the following analysis related to mirror symmetries such as MCNs.
for the compact representation) mirror planes in the following analysis related to mirror symmetries such as MCNs.
Figure 2. (a) The primitive unit cell of Pt3Sn, where the gray and blue balls denote Pt and Sn atoms, respectively. (b) The bulk BZ of Pt3Sn. High symmetry points G, X, M, R are shown. The MCN calculations are performed in the green, pink, blue rectangle zones, corresponding to 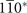 , 010*,
, 010*, 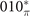 planes, respectively. (c) The electronic band structure of Pt3Sn which also shows continuous and finite direct gap around the Fermi level (set to 0 eV). (d) The evolution of the sum over occupied bands of HWCCs for subspace with mirror eigenvalue +i in different cases of mirror planes. From left to right, the results correspond to 010*,
planes, respectively. (c) The electronic band structure of Pt3Sn which also shows continuous and finite direct gap around the Fermi level (set to 0 eV). (d) The evolution of the sum over occupied bands of HWCCs for subspace with mirror eigenvalue +i in different cases of mirror planes. From left to right, the results correspond to 010*, 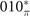 ,
, 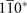 planes, respectively.
planes, respectively.
Download figure:
Standard image High-resolution imageSimilarly, we also demonstrate the results of electronic properties for Pt3Sn in figure 2(c). A continuous direct gap and the relatively clean Fermi surface could also be found from energy bands along high symmetry lines in bulk BZ (figure 2(b)). Here the energy range from −14 eV to 8 eV around the Fermi level is dominated by 5d, 6s, 6p orbitals of Pt and 5s, 5p orbitals of Sn. These orbitals are also hybridized together. According to the 5d96s1 and 5s25p2 electron configurations in fact for Pt and Sn, respectively, the number of occupied bands of Pt3Sn should be 34.
The topology of these 34 occupied bands is also studied by SI theory. In the case of SG 221, the irreps of these occupied bands of high symmetry points: Γ, X, M, R as shown in figure 2(b) need to be calculated, and the corresponding results are also written as a vector:
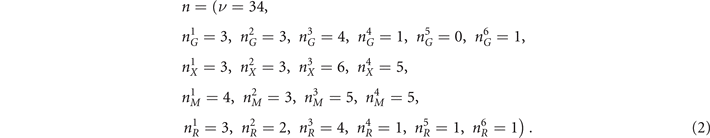
Then refer to the process before, this vector should be expanded by the AIBs of SG 221 for acquiring SI. There are 14 AIBs in the case of SG 221 (denoted by ai
, i = 1, 2, ..., 14) [40], and the corresponding result of expansion is 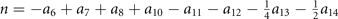 . Here the AIBs with common factors not equal to 1 are a13 and a14 whose common factors are 4 and 8, respectively. As a result, the SI of Pt3Sn is (3, 4) in the group
. Here the AIBs with common factors not equal to 1 are a13 and a14 whose common factors are 4 and 8, respectively. As a result, the SI of Pt3Sn is (3, 4) in the group 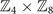 , which is also consistent with the class of TCI in the database. As we mentioned before in the case of Bi3STe2, we could use the Fu–Kane-like formula of SG 221 to calculate this SI directly, which also needs the
, which is also consistent with the class of TCI in the database. As we mentioned before in the case of Bi3STe2, we could use the Fu–Kane-like formula of SG 221 to calculate this SI directly, which also needs the 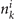 in equation (2). As a result, we directly calculate the SI: (z4m,π
, z8) = (3, 6), which also reveals the same topology: the indicator z8 is the criterion of strong TI or TCI phases, and a TCI phase could be concluded from the even number of z8 above. It is worth noting that despite the SI of SG 221 is different from that in SG 164, the indicator (z2,1, z2,2, z2,3, z4) in SG 164 could also be calculated in the case of SG 221 due to the existence of inversion symmetry. However, three z2,j
indices are strictly same on account of three equivalent X and three equivalent M points within eight TRIM (figure 4(a)), and thus the weak topological indices (z2,1, z2,2, z2,3) should be (0, 0, 0) or (1, 1, 1) in SG 221. We find that (z2,1, z2,2, z2,3) = (1, 1, 1) after calculating the parity of occupied eigenstates at inequivalent TRIM. Hence Pt3Sn also has the weak TI phase, the corresponding surface Dirac cones would emerge on three equivalent surface BZs: (100), (010), (001).
in equation (2). As a result, we directly calculate the SI: (z4m,π
, z8) = (3, 6), which also reveals the same topology: the indicator z8 is the criterion of strong TI or TCI phases, and a TCI phase could be concluded from the even number of z8 above. It is worth noting that despite the SI of SG 221 is different from that in SG 164, the indicator (z2,1, z2,2, z2,3, z4) in SG 164 could also be calculated in the case of SG 221 due to the existence of inversion symmetry. However, three z2,j
indices are strictly same on account of three equivalent X and three equivalent M points within eight TRIM (figure 4(a)), and thus the weak topological indices (z2,1, z2,2, z2,3) should be (0, 0, 0) or (1, 1, 1) in SG 221. We find that (z2,1, z2,2, z2,3) = (1, 1, 1) after calculating the parity of occupied eigenstates at inequivalent TRIM. Hence Pt3Sn also has the weak TI phase, the corresponding surface Dirac cones would emerge on three equivalent surface BZs: (100), (010), (001).
Then we also identify the mirror-protected TCI phase through calculating MCNs for Pt3Sn. To be specific, the MCNs of 010 and 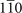 mirror planes need to be calculated as we mentioned before. These mirror planes are also demonstrated in bulk BZ (shaded rectangle zones in figure 2(b)). Especially, an important thing has to be noted: when the mirror plane in reciprocal space translates by half of a reciprocal lattice vector not in this plane, a mirror plane could also be acquired. For example, the mirror plane represented by the blue rectangle zone in figure 2(b), comes from translating 010* plane by kb/2 (denoted by
mirror planes need to be calculated as we mentioned before. These mirror planes are also demonstrated in bulk BZ (shaded rectangle zones in figure 2(b)). Especially, an important thing has to be noted: when the mirror plane in reciprocal space translates by half of a reciprocal lattice vector not in this plane, a mirror plane could also be acquired. For example, the mirror plane represented by the blue rectangle zone in figure 2(b), comes from translating 010* plane by kb/2 (denoted by 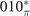 plane). In these new mirror planes, the eigenstates of energy could also be classified by mirror eigenvalues, and hence the MCNs could also be defined. In principle, MCNs of these mirror planes need to be calculated in the process of identification. However, according to the summary in reference [35], other than the
plane). In these new mirror planes, the eigenstates of energy could also be classified by mirror eigenvalues, and hence the MCNs could also be defined. In principle, MCNs of these mirror planes need to be calculated in the process of identification. However, according to the summary in reference [35], other than the 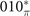 plane of Pt3Sn, the MCNs of
plane of Pt3Sn, the MCNs of 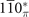 plane of Pt3Sn and
plane of Pt3Sn and 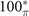 plane of Bi3STe2 are always zero. Therefore, we only calculate the MCNs of planes through Γ in these two cases (the green zones in figures 1(b) and 2(b)). As a result, according to the evolution of the sum of HWCCs as shown in figure 2(d), for Pt3Sn, the MCNs of 010 mirror plane are −1 for both original and translational planes, and the MCN of
plane of Bi3STe2 are always zero. Therefore, we only calculate the MCNs of planes through Γ in these two cases (the green zones in figures 1(b) and 2(b)). As a result, according to the evolution of the sum of HWCCs as shown in figure 2(d), for Pt3Sn, the MCNs of 010 mirror plane are −1 for both original and translational planes, and the MCN of 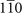 mirror plane is −2. Pt3Sn is a mirror-protected TCI with corresponding mirror-protected Dirac cones on (001) surface BZ which is symmetric under 010 and
mirror plane is −2. Pt3Sn is a mirror-protected TCI with corresponding mirror-protected Dirac cones on (001) surface BZ which is symmetric under 010 and 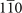 mirror operations.
mirror operations.
4. Topological surface states in representative materials
In this section, we demonstrate the surface states corresponding to all revealed nontrivial phases including mirror-protected TCI and weak TI through TB models based on Wannier functions. We have analyzed main orbital components around the Fermi level for representative materials before, which could help us to construct ideal Wannier functions. To be specific, using the following orbitals as the initial guess of Wannier functions could fit DFT energy bands well (figures 1(c) and 2(c)): for Bi3STe2, the p-like orbitals on every atom site; for Pt3Sn, the s, p, d-like orbitals on Pt sites and the s, p-like orbitals on Sn sites. Furthermore, after checking the transformation of Wannier functions under operations in SGs 164 and 221, we confirm that the TRS and spatial symmetries are guaranteed in these TB models, and the first-principles results of SIs and MCNs could be reproduced.
For Bi3STe2, this kind of surface states should emerge on the mirror invariant (001) surface of Bi3STe2. Hence we calculate the (001) surface energy spectra (figure 3(b)). A clear surface Dirac cone around 0.067 eV could be found in the general position of 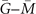 path. Then considering the TRS or inversion symmetry, another surface Dirac cone is expected to appear on
path. Then considering the TRS or inversion symmetry, another surface Dirac cone is expected to appear on 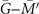 path. As a result, two Dirac cones emerging on
path. As a result, two Dirac cones emerging on 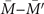 path consists with the absolute value of MCN (=2) for 100 mirror plane. There are other two mirror planes equivalent to 100 plane for Bi3STe2, which brings the same number of Dirac cones on corresponding projection lines, and there are six mirror-protected Dirac cones on (001) surface BZ in total. In addition, the spin texture of one of these six Dirac cones at 0.07 eV energy contour are shown in figure 3(c). The corresponding clockwise spin orientation implies a left-handed helicity. On account of the equivalence, other Dirac cones in (001) surface BZ have spin textures with the same helicity.
path consists with the absolute value of MCN (=2) for 100 mirror plane. There are other two mirror planes equivalent to 100 plane for Bi3STe2, which brings the same number of Dirac cones on corresponding projection lines, and there are six mirror-protected Dirac cones on (001) surface BZ in total. In addition, the spin texture of one of these six Dirac cones at 0.07 eV energy contour are shown in figure 3(c). The corresponding clockwise spin orientation implies a left-handed helicity. On account of the equivalence, other Dirac cones in (001) surface BZ have spin textures with the same helicity.
Figure 3. (a) (001) and (010) surface BZs with high symmetry points 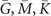 and
and 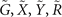 for Bi3STe2. Eight TRIM are also shown within the bulk BZ. (b) (001) surface energy spectra along
for Bi3STe2. Eight TRIM are also shown within the bulk BZ. (b) (001) surface energy spectra along 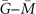 . (c) Spin texture of the Dirac cone located at a general position in
. (c) Spin texture of the Dirac cone located at a general position in 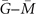 at 0.07 eV energy contour. (d) (010) surface energy spectra along
at 0.07 eV energy contour. (d) (010) surface energy spectra along 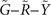 .
.
Download figure:
Standard image High-resolution imageAs we mentioned before, on the basis of SI, the weak TI phase is also revealed for Bi3STe2 and the corresponding Dirac cones are expected in (100) and (010) surface BZs. Considering the 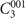 operation, these two surfaces are equivalent, and here we only take (010) surface into account. This surface BZ is shown in figure 3(a), and the energy spectra are shown in figure 3(d). We find a clear Dirac cone at
operation, these two surfaces are equivalent, and here we only take (010) surface into account. This surface BZ is shown in figure 3(a), and the energy spectra are shown in figure 3(d). We find a clear Dirac cone at 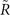 , around −0.025 eV. This cone originates from the weak TI phase and is located at the high symmetry point, which is different from the previous mirror-protected Dirac cone located at a general position. The weak TI Dirac cone could be further explained by calculating the time-reversal polarization (TRP) [17]. To be specific, in this case,
, around −0.025 eV. This cone originates from the weak TI phase and is located at the high symmetry point, which is different from the previous mirror-protected Dirac cone located at a general position. The weak TI Dirac cone could be further explained by calculating the time-reversal polarization (TRP) [17]. To be specific, in this case, 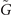 ,
, 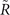 ,
, 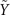 are both the bulk TRIM's projections on (010) surface BZ (figure 3(a)). Hence TRPs for these three points could be defined, and then calculated through: π(Λa
) = δ(Γi
)δ(Γj
). Γi
, Γj
represent bulk TRIM and their projection on (010) surface BZ is Λa
. For example,
are both the bulk TRIM's projections on (010) surface BZ (figure 3(a)). Hence TRPs for these three points could be defined, and then calculated through: π(Λa
) = δ(Γi
)δ(Γj
). Γi
, Γj
represent bulk TRIM and their projection on (010) surface BZ is Λa
. For example, 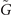 is the projection of two bulk TRIM: G and M3 (figure 3(a)). δ(Γi
) is the product of parity for occupied Kramers pairs at Γi
. According to the calculations of bulk states before, the number of occupied Kramers pairs is equal to 21, and δ(G), δ(Mi
), δ(A), δ(Li
) are equal to −1, 1, 1, −1, respectively. As a result,
is the projection of two bulk TRIM: G and M3 (figure 3(a)). δ(Γi
) is the product of parity for occupied Kramers pairs at Γi
. According to the calculations of bulk states before, the number of occupied Kramers pairs is equal to 21, and δ(G), δ(Mi
), δ(A), δ(Li
) are equal to −1, 1, 1, −1, respectively. As a result, 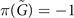 ,
,  ,
, 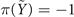 . This change of sign for TRPs supports the Dirac cone at
. This change of sign for TRPs supports the Dirac cone at 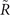 when the path traces
when the path traces 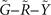 .
.
Then we demonstrate the nontrivial surface states for Pt3Sn. Similar to the case of Bi3STe2, mirror-protected TCI and weak TI phases also arise simultaneously. However, in Pt3Sn, the surface states corresponding to these phases would both emerge on (001) surface based on the previous analysis. According to the surface energy spectra demonstrated in figure 4(b), we find two Dirac cones both connecting the projections of valence and conduction bulk states. One of them is located at 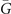 around 0.16 eV, and the other one around −0.7 eV appears at
around 0.16 eV, and the other one around −0.7 eV appears at 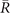 . After considering the C4 rotation symmetry of (001) surface, we could conclude that 2, 1, 1 Dirac cones emerge on
. After considering the C4 rotation symmetry of (001) surface, we could conclude that 2, 1, 1 Dirac cones emerge on 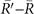 ,
, 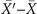 ,
, 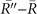 paths (figure 4(a)), respectively. One should note that the three paths above correspond to the projections of
paths (figure 4(a)), respectively. One should note that the three paths above correspond to the projections of 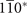 , 010*,
, 010*, 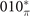 planes in the bulk BZ, respectively. As a result, the number of Dirac cones on (001) surface BZ we found consists with the absolute value of MCNs for corresponding mirror planes we calculated. These Dirac cones are protected by
planes in the bulk BZ, respectively. As a result, the number of Dirac cones on (001) surface BZ we found consists with the absolute value of MCNs for corresponding mirror planes we calculated. These Dirac cones are protected by 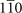 and 010 mirror planes. The spin textures of two Dirac cones in figure 4(b) are also revealed. As shown in figures 4(c) and (d), all energy contours are C4 symmetric loops. To be specific, the loop in figure 4(c) corresponds to the upper Dirac cone at
and 010 mirror planes. The spin textures of two Dirac cones in figure 4(b) are also revealed. As shown in figures 4(c) and (d), all energy contours are C4 symmetric loops. To be specific, the loop in figure 4(c) corresponds to the upper Dirac cone at 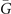 and exhibits an anticlockwise spin texture. Referring to the (001) surface energy spectra on
and exhibits an anticlockwise spin texture. Referring to the (001) surface energy spectra on 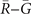 and
and 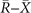 (figure 4(b)), the upper and lower parts of the Dirac cone at
(figure 4(b)), the upper and lower parts of the Dirac cone at  could emerge on −0.6 eV energy contour at the same time, corresponding to inner and outer loops in figure 4(d), respectively. We find that the upper and lower parts have the opposite helicity. It should be noted that the upper parts of Dirac cones at
could emerge on −0.6 eV energy contour at the same time, corresponding to inner and outer loops in figure 4(d), respectively. We find that the upper and lower parts have the opposite helicity. It should be noted that the upper parts of Dirac cones at 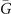 and
and 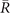 have the same helicity, which consists with the same sign of three MCNs we calculated for Pt3Sn.
have the same helicity, which consists with the same sign of three MCNs we calculated for Pt3Sn.
Figure 4. (a) (001) surface BZs with high symmetry points 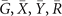 for Pt3Sn. Eight TRIM are also shown within the bulk BZ. (b) (001) surface energy spectra along
for Pt3Sn. Eight TRIM are also shown within the bulk BZ. (b) (001) surface energy spectra along 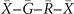 . (c) Spin texture of the Dirac cone located at
. (c) Spin texture of the Dirac cone located at 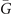 at 0.25 eV energy contour. (d) Spin texture of the Dirac cone located at
at 0.25 eV energy contour. (d) Spin texture of the Dirac cone located at 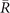 at −0.6 eV energy contour.
at −0.6 eV energy contour.
Download figure:
Standard image High-resolution imageThe mirror-protected Dirac cones are located at high symmetry points of (001) surface BZ for Pt3Sn, which is different from the case of a general position in Bi3STe2. This is because the weak TI phase also appears on (001) surface of Pt3Sn, and then makes mirror-protected Dirac cones pinning at high symmetry points. The results of TRPs could also be used to explain this change of Dirac cones' positions. In this case, the high symmetry points  ,
, 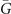 ,
, 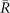 are projections of TRIM in bulk BZ as shown in figure 4(a). Similarly, from the calculation of bulk states, we find that the number of occupied Kramers pairs is equal to 17, and δ(G), δ(Xi
), δ(Mi
), δ(R) are equal to −1, 1, 1, −1, respectively. Then
are projections of TRIM in bulk BZ as shown in figure 4(a). Similarly, from the calculation of bulk states, we find that the number of occupied Kramers pairs is equal to 17, and δ(G), δ(Xi
), δ(Mi
), δ(R) are equal to −1, 1, 1, −1, respectively. Then  ,
, 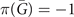 ,
, 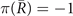 could be concluded, and the Dirac cones demonstrated in figure 4(b) could be explained as following. From
could be concluded, and the Dirac cones demonstrated in figure 4(b) could be explained as following. From  to
to  , the sign of TRP changes, which consists with the fact that the surface energy spectra intersect once a generic energy within the gap of bulk states in
, the sign of TRP changes, which consists with the fact that the surface energy spectra intersect once a generic energy within the gap of bulk states in  path. However, from
path. However, from 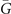 to
to 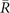 , there is no change of the sign, and hence even number of intersections are expected. In figure 4(b), we indeed expect two intersections in
, there is no change of the sign, and hence even number of intersections are expected. In figure 4(b), we indeed expect two intersections in 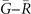 path. Finally, the sign of TRP changes from
path. Finally, the sign of TRP changes from 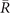 to
to 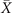 , and the number of intersections in this path is same as the case of
, and the number of intersections in this path is same as the case of 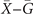 path. Therefore, the Dirac cones we found on (001) surface BZ of Pt3Sn are not only mirror-protected, but also originated from the weak TI phase.
path. Therefore, the Dirac cones we found on (001) surface BZ of Pt3Sn are not only mirror-protected, but also originated from the weak TI phase.
5. The rest of mirror-protected TCIs
In this section, we list the materials with nonvanishing MCNs in table 1, and all mirror-protected TCIs could be identified in this table. The detailed results of all materials we calculated are shown in SM [41]. The SGs in table 1 could be divided into two classes: the one with inversion symmetry and the other one without inversion symmetry. The former class includes all SGs other than SGs 187 and 189 in table 1. The SIs of these SGs have strong topological indicators. Therefore, we could conclude that the materials in table 1 belong to these SGs are TCIs through even strong SIs and nonvanishing weak SIs [35]. Then combining with their nonvanishing MCNs, all of these materials are identified as mirror-protected TCIs. One should note that for a TCI with nontrivial SI group, the possible MCNs are determined when its SI is given [35]. For example, considering the material Bi in SG 140. The SI is (z2,1, z8) = (1, 0), and there are four possible sets of MCNs for mirror plane 001 and 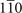 : (00), (02), (40), (42). Here our calculated set is (44). In view of there is a cutoff for every MCN in the mapping table in [35], our MCN results here should module 8 and 4, respectively. After this we get the result (40) which coincides with one possible set. We check the results of calculated SIs and MCNs for all identified mirror-protected TCIs and find that they are all satisfied with possible combinations in the mapping table in [35]. This fact means the rationality of our MCN results.
: (00), (02), (40), (42). Here our calculated set is (44). In view of there is a cutoff for every MCN in the mapping table in [35], our MCN results here should module 8 and 4, respectively. After this we get the result (40) which coincides with one possible set. We check the results of calculated SIs and MCNs for all identified mirror-protected TCIs and find that they are all satisfied with possible combinations in the mapping table in [35]. This fact means the rationality of our MCN results.
The latter class includes SGs 187 and 189 in table 1, and the SIs of these two SGs without inversion symmetry do not have strong topological indicators. Hence we cannot diagnose the TCI phase simply from the calculation of SI. At this stage, the MCN results could be used to define the strong topological indicator and help to solve this problem. According to reference [35], the strong topological indicator of SGs 187 and 189 could be defined as the parity of the difference between MCNs of 001* and 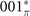 planes in the bulk BZ [6], which is found to be odd for every material marked in red color belongs to these SGs in table 1. Therefore, these materials marked in red color are identified as strong TIs in fact. Here only the material AsLuPd crystallizing in SG 189 has mirror-protected TCI phase. This identification could be easily performed on account of its
planes in the bulk BZ [6], which is found to be odd for every material marked in red color belongs to these SGs in table 1. Therefore, these materials marked in red color are identified as strong TIs in fact. Here only the material AsLuPd crystallizing in SG 189 has mirror-protected TCI phase. This identification could be easily performed on account of its 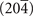 MCN set. Finally, in this work, we successfully identify 67 mirror-protected TCIs belong to 19 different SGs in total. They are marked in black color in table 1.
MCN set. Finally, in this work, we successfully identify 67 mirror-protected TCIs belong to 19 different SGs in total. They are marked in black color in table 1.
6. Conclusions and discussions
In this paper, by means of the first-principles calculations of SIs and MCNs, we perform a systematic identification of the TCIs from the database [40], and predict 67 mirror-protected TCIs in total. These materials are marked in black color in table 1. The identified mirror-protected TCIs Bi3STe2 and Pt3Sn crystallizing in SGs 164 and 221, respectively, are chosen as illustrative examples. We carefully analyze their bulk topology, and then uncover their mirror-protected TCI and weak TI phases. The corresponding topological surface states are also revealed. For Bi3STe2, the Dirac cones emergent on (001) and (010) surface BZ are originated from mirror-protected TCI and weak TI phases, respectively. Whereas for Pt3Sn, (001) surface Dirac cones are protected by mirror symmetry and weak topology simultaneously. In addition, the spin textures of helical surface Dirac states are also shown. We expect that our identified mirror-protected TCIs could be verified by experiments and provide a good platform for further theoretical studies.
Acknowledgments
We were supported by the National Key&D Program of China (Grant Nos. 2017YFA0303203 and No. 2018YFA0305704), the National Natural Science Foundation of China (NSFC Grants Nos. 11834006, 51721001, and 11790311) and the excellent program at Nanjing University. XW also acknowledges the support from the Tencent Foundation through the XPLORER PRIZE. FT was supported by the Fundamental Research Fund for the Central Universities (Nos. 14380144, 14380157). Supported by the program B for Outstanding PhD candidate of Nanjing University.
Data availability statement
All data that support the findings of this study are included within the article (and any supplementary files).