Abstract
The coherent manipulation of the electron wavefunction at the atomic spatial and temporal scales is the fundamental breakthrough underlying far-reaching ultrafast phenomena as high-order harmonic radiation and attosecond pulse generation. In this work, we present a next step in the coherent control of matter waves by translating the concept of Talbot interferometry to the subnanomenter–femtosecond realm. We study the high-harmonic emission from a periodic system irradiated by an intense mid-infrared laser beam at grazing incidence. Our calculations show that Bloch electrons, once ionized, follow a sequence of ultrafast (femtosecond) revivals associated with the temporal Talbot effect. We demonstrate that these revivals leave a distinct signature in the high-frequency harmonic spectrum, in the form of structures extending beyond the main spectral cutoff, toward the x-rays. The reinterpretation of the process of high-order harmonic generation as the temporal realization of a Talbot–Lau interferometer suggests high-harmonic spectroscopy as an appropriate scheme to develop subnanometer ultrafast Talbot interferometry.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Ultrashort laser sources, with femtosecond and attosecond durations, are extraordinary tools for the manipulation of elemental matter constituents in their natural scales. The design of proper interaction geometries leads to a fine control of the electron dynamics preserving the coherence of their wavefunction. A paradigmatic example of this control can be found in the process of high-order harmonic generation (HHG), where the high-frequency emission is produced by an oscillating dipole, resulting from the coherent superposition of the bound and the ionized electron wavefunctions. The ultrafast scenario, therefore, turns out as an attractive playground for the translation of conventional matter-wave coherent optics to the subnanometer and subfemtosecond scales which, to the best of our knowledge, has not been fully addressed yet.
Coherent optics—based on the manipulation of light preserving its phase—lies at the core of outstanding applications in different areas, such as metrology, imaging and information. Remarkably, holography and Talbot image formation represent two paradigmatic examples of relevant phenomena involved in many technical applications of coherent optics. In view of this, the exploration of the corresponding coherent counterparts in matter waves has been a main interest right after the first demonstration of atom optics. As such, Talbot self-imaging [1] represents an excellent case of practical application of the principles of coherent manipulation of waves. Talbot revivals are a consequence of near-field diffraction, consisting in the appearance of subsequent images of an initial periodic pattern. Since the invention of the laser, the optical Talbot effect has been used in a wide range of applications such as image processing, photolithography, optical metrology and testing, among others. The possibility of lens-less image formation has also technological applications in x-ray and electron optics and particle beams. While first described in light, Talbot phenomena have also their translation to matter waves. The sequence of matter revivals has been described, and experimentally observed, in electron diffraction by nanostructured gratings [2], atoms [3, 4] and Bose–Einstein condensates [5].
In its most frequent configuration, Talbot revivals follow from the elastic scattering of the wave by a periodic structure. As the energy of the scattered wave is unchanged, Talbot interferences result in image replicas at distance multiples of the Talbot length, DT = 2d2/λdB, for a 1D grating with spatial period d, λdB being the deBroglie's wavelength. For dispersive waves, the inelastic scattering with a transient periodic grating leads to a temporal Talbot effect [5] where the diffracted wave follows periodic time revivals, with a Talbot period of TT = 2md2/h, m being the mass and h the Plank's constant. The temporal Talbot effect has technological implications in communications [6, 7] and optical and quantum computing [8, 9].
In this paper we propose the translation of matter Talbot interferometry into the unprecedented spatial nanometer and temporal subfemtosecond scales. We show how HHG from periodic crystals can be both an scheme to induce the electron Talbot effect and a realization of an ultrafast nanometric Talbot–Lau interferometer. With our work, Talbot interferometry and high-harmonic spectroscopy converge to a new class of ultrafast technique, sensitive to the details of the coherent dynamics of the electronic wavefunction in its natural spatial and time scales. HHG is a robust technique to generate extreme-ultraviolet (EUV) and soft x-ray coherent radiation [10–14], emitted in the form of attosecond bursts. The process has been thoroughly studied in atomic and molecular gases [15, 16], where it is understood in terms of the so-called three-step model [17, 18]. According to this view, during the interaction of an intense laser field with an atom or molecule, tunnel ionization liberates electronic wave packets, that are subsequently accelerated by the electromagnetic field. Upon reversal of the field force, the electronic wave packets are redirected to rescatter with the parent ion, emitting radiation in the form of high-order harmonics of the driving laser frequency. In the atomic/molecular case, the HHG spectrum consists on several harmonics with similar intensities conforming a single plateau that extends up to an abrupt cut-off.
The emergence of HHG studies in crystalline solids in the last decade—either in bulk [19, 20] or in low dimensional configurations [21–23]—demonstrates unprecedented ultrafast control over electron dynamics in solids. High-harmonic spectroscopy from solid targets allows for unveiling details of the band structure [24], the interaction dynamics [25], and the electron wavepacket coherence [26]. In the case of low-dimensional solids, most of the studies consider the electric field polarization parallel to the target plane. However, efficient HHG can be also obtained using a grazing incidence geometry [27], i.e. for an electric field polarization perpendicular to the layer. In this later case, the physics behind the HHG emission can be understood in terms of a three-step mechanism similar to the one derived for atomic and molecular targets. The grazing incidence configuration generates tunnel-ionized wave-packets with a periodic structure, evolving free in the continuum, a scenario with clear parallelism with that of Talbot diffraction from gratings [28]. As the oscillating dipole follows from the interference between the ground state and the recolliding wavefunction, the harmonic spectrum contains interferometric information of Talbot revivals that can be retrieved using high-harmonic spectroscopy techniques.
In particular, our theoretical simulations show that the mechanism leading to HHG from low-dimensional periodic structures corresponds to a temporal realization of a sub-nanometric Talbot–Lau interferometer. Thus, we propose ultrafast Talbot spectroscopy (UTS) as a new technique for interfermetric measurements in the subfemtosecond subnanometric scale.
2. Physical concept
We consider the HHG geometry depicted in the upper left panel in figure 1(a), where a few cycle mid-infrared laser pulse interacts with a periodic structure at grazing incidence. The simulation of HHG in such grazing geometry, when the extremely well-resolved spatio-temporal grids are needed, requires modeling the problem in reduced dimensions, a well-known strategy to reduce computational load in strong-field calculations. In our case, the crystal layer is modeled as a periodic chain, with a period of d = 2.1 Å (4 a.u.), that has been chosen to reproduce the Talbot distance from the graphene hexagonal lattice, DT,hex = 3a2/2λ, with a = 2.46 Å being the graphene's lattice constant [29]. The other parameters of our model potential are chosen to obtain a work function of 5 eV, similar to that of graphene (see methods section). Note that, although both theoretical and experimental works have been carried out in low-dimensional systems like graphene, the usual scheme considers a perpendicularly incident laser, i.e. the electric field is polarized in the target plane, a geometry that does not allow for Talbot revivals.
Figure 1. Scheme of ultrafast matter-wave Talbot effect. (a) The upper left panel represents the schematic view of HHG from a low-dimensional solid under grazing incidence: a periodic wavefunction (green) created in a periodic potential (blue) is released in the continuum at t1, then accelerated (t2) and finally, driven back to the crystal (t3). The main panel shows this process as a function of time, where a periodic wavefunction (green) is ionized and driven back to to rescatter with the crystal after an excursion through the continuum, where Talbot revivals emerge. The Talbot revival signatures are encoded in the HHG spectrum as a sequence of high-energy plateau structures (upper right panel). (b) Electronic band structure of the periodic potential used in our calculations, where the workfunction | 0(0)| = IW
is 5 eV and Δ, accounting for the band bending due to the interaction with the periodic potential, is 0.9 eV at the band's edge. The purple-filled area represents the continuum states.
0(0)| = IW
is 5 eV and Δ, accounting for the band bending due to the interaction with the periodic potential, is 0.9 eV at the band's edge. The purple-filled area represents the continuum states.
Download figure:
Standard image High-resolution imageIn addition to the interaction geometry, the upper left panel in figure 1(a) schematizes the process of HHG at grazing incidence: a periodic wavefunction (green) is released into the continuum, then accelerated and driven back to the crystal upon reversal of the electromagnetic driving field. The main panel in this figure sketches this process as a function of time, emphasizing the temporal Talbot revivals and the parallelism of the HHG sequence with the configuration of a Talbot–Lau interferometer, in which the diffracted wave is tested using a replica of the diffraction mask, i.e. the crystal potential, at the moment of recombination of the electronic wave packets. As we will discuss below, upon rescattering, the ultrafast Talbot revivals leave a unique signal in the HHG spectrum: a series of frequencies well above the cut-off that depend on the spatial frequency content of the crystal state, as shown in the upper right panel in figure 1(a).
Figure 1(b) shows the band structure of our model potential (see methods for details). Incidentally, we note that it is similar to the electronic structure of carbyne [30], a consequence of the dimensional reduction in our model. We stress, however, that the geometrical details of the energy levels are a secondary aspect in ionization-mediated strong-field phenomena, where an accurate description of the ionization potential, work function, and electron continuum structure is more relevant.
3. Results
We plot in figure 2 the high-harmonic spectra extracted from the numerical solution of the time-dependent Schrödinger equation (TDSE), for a five-cycles 3 μm driving field, with a peak intensity of 1013 W cm−2 (see methods). The blue-filled plots in figure 2(a) (main and inset) correspond to the harmonic spectra radiated from an electron initially occupying a single Bloch state (k = 0.2g, where g = 2π/d). The purple-filled plots in figure 2(a) depict the HHG spectra corresponding to the total contribution of a set of initial Bloch states in the valence band, equally distributed along the Brillouin zone (BZ), kr = rΔk, where Δk = g/10, g = 2π/d and r is an integer in the interval (−5, 5]. The main panel plots the low-energy structure, while the complete spectrum is shown in the inset.
Figure 2. (a) High-harmonic spectrum from a 3 μm, 1 × 1013 W cm−2 driving. The blue line shows the contribution of a single Bloch state, at k = 0.2g, and the purple line shows the contribution of ten states, regularly spaced along the BZ. The blue dashed lines represent the Talbot frequencies given by equation (6) for k = 0.2g and different values of n. The numbers enclosed in parentheses correspond to the values of n and k/g for the Talbot frequencies present in the single Bloch state spectrum (blue) and in the ten states spectrum (purple). (b) High-harmonic spectra for the same parameters. The purple curve represents the contribution of the same ten states as in (a). The green line represents the contribution of five of those ten states, corresponding to a situation with the first band partially filled (Fermi level intersecting the first band).
Download figure:
Standard image High-resolution imageThe harmonic spectra extend toward 0.8 keV photon energies in the form of a succession of plateaus with decreasing efficiency. The structure of these higher-order plateaus is better resolved in the case of the emission from the single state (blue filled curve), where their nature as replicas of the first plateau becomes evident. Each plateau in the sequence is shifted toward higher energies by a discrete set of energy displacements  (n being an integer and
(n being an integer and  the reduced Bloch wavevector), highlighted as vertical dashed lines in figure 2(a), and defined later in equation (6). The extension of the first plateau (marked with a horizontal double arrow) corresponds approximately to the one expected from the atomic case if the ionization potential were set to the crystal's work function. A second relevant feature is the presence of prominent pairs of harmonic peaks at the left side of each of the plateau's replicas, which can be associated with the corresponding copies of the peak at the fundamental frequency (and its negative frequency counterpart), shifted by the same set of energy displacements,
the reduced Bloch wavevector), highlighted as vertical dashed lines in figure 2(a), and defined later in equation (6). The extension of the first plateau (marked with a horizontal double arrow) corresponds approximately to the one expected from the atomic case if the ionization potential were set to the crystal's work function. A second relevant feature is the presence of prominent pairs of harmonic peaks at the left side of each of the plateau's replicas, which can be associated with the corresponding copies of the peak at the fundamental frequency (and its negative frequency counterpart), shifted by the same set of energy displacements,  . Note that the width of these peaks corresponds approximately to the inverse of the driving field pulse duration, being similar to those obtained in atomic/molecular HHG. This reflects the fact that the Talbot oscillations appear in HHG during all the interaction with the driving field, since the HHG mechanism ionization–excursion–recollision) is repeated every half-period of the driving field. Finally, the purple-filled spectra, representing the total contribution of the set of Bloch states, can be understood in terms of the superposition of the individual emissions from each wavevector {kr
}, resulting in wider and less resolved high-order plateau structures, toward a supercontinuum, with peaks emerging at frequencies
. Note that the width of these peaks corresponds approximately to the inverse of the driving field pulse duration, being similar to those obtained in atomic/molecular HHG. This reflects the fact that the Talbot oscillations appear in HHG during all the interaction with the driving field, since the HHG mechanism ionization–excursion–recollision) is repeated every half-period of the driving field. Finally, the purple-filled spectra, representing the total contribution of the set of Bloch states, can be understood in terms of the superposition of the individual emissions from each wavevector {kr
}, resulting in wider and less resolved high-order plateau structures, toward a supercontinuum, with peaks emerging at frequencies  . It is worth mentioning that the relative intensity between the first plateau and the replicas drops drastically for shorter driving wavelengths, being several orders of magnitude for the case of near infrared driving fields (800 nm).
. It is worth mentioning that the relative intensity between the first plateau and the replicas drops drastically for shorter driving wavelengths, being several orders of magnitude for the case of near infrared driving fields (800 nm).
As we will show next, the rise of such complex spectra is the consequence of the mingling of the rescattering-induced dipole oscillations and the Talbot modulations in the probability density of the rescattering electron. Since the characteristic de Broglie's wavelength of the rescattering electron is  , Up being the ponderomotive energy, the scale of the Talbot distances corresponds to Å, and the temporal scale to hundreds of attoseconds. Therefore, high-order harmonic spectroscopy emerges as a pivotal technique for electron Talbot ultrafast interferometry from sub-nanometer periodic structures, that we refer as UTS. Figure 2(b) shows an example of UTS, demonstrating the spectral variations associated with the details of the band occupation. We compare the spectra corresponding to the Fermi level located in the first gap of the band structure (purple-filled)—where the ten valence states considered above are occupied and, therefore, contribute to the harmonic emission—, with the case in which the Fermi Level crosses the first band, EF = −3.7 eV (green-filled)—where only five valence states are occupied. In this later case, the harmonic spectra shows selective suppression at the spectral regions corresponding to the unoccupied crystal states.
, Up being the ponderomotive energy, the scale of the Talbot distances corresponds to Å, and the temporal scale to hundreds of attoseconds. Therefore, high-order harmonic spectroscopy emerges as a pivotal technique for electron Talbot ultrafast interferometry from sub-nanometer periodic structures, that we refer as UTS. Figure 2(b) shows an example of UTS, demonstrating the spectral variations associated with the details of the band occupation. We compare the spectra corresponding to the Fermi level located in the first gap of the band structure (purple-filled)—where the ten valence states considered above are occupied and, therefore, contribute to the harmonic emission—, with the case in which the Fermi Level crosses the first band, EF = −3.7 eV (green-filled)—where only five valence states are occupied. In this later case, the harmonic spectra shows selective suppression at the spectral regions corresponding to the unoccupied crystal states.
4. Discussion
A very successful approach to the quantum description of HHG [31] is based on the so-called strong-field approximation (SFA) [32–34] where, once ionized, the electron is assumed to evolve in the absence of the Coulomb interaction with the ion. Among other characteristics, SFA in atoms and molecules reproduces the plateau in the harmonic spectrum, extending up to a cut-off frequency, proportional to the intensity and wavelength of the driving field [31]. Following the analogy with light, the formal parallelism between the SFA description of HHG and Fresnel diffraction can be derived, allowing to translate the most fundamental diffraction phenomena in optics to the recolliding electron scenario [35].
In order to drive a fundamental understanding of UTS, we have developed an SFA description for the dynamics of the ionization wavepacket and HHG from the crystal. In this framework, the solution of the TDSE is written as
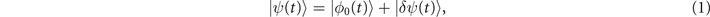
with |ϕ0(t)⟩ the field-free evolution of the eigenstate initially occupied by the electron, and |δψ(t)⟩ the ket describing the electron in the continuum. This later is defined as the superposition of the wavepackets ionized at all previous times ti
, and propagated to time t,  , where
, where

GF
(t; ti
) being the Green's propagator for a free electron in the presence of the oscillating electric field, i.e. in the absence of the crystal potential. This later dynamics is ruled by the Hamiltonian  , with
, with  . Note that according to our configuration (see figure 1(a)), HF
is separable, HF
= HF,x
+ HF,y
, with
. Note that according to our configuration (see figure 1(a)), HF
is separable, HF
= HF,x
+ HF,y
, with  and
and  . Therefore, we can factorize
. Therefore, we can factorize

We perform the partial projection of the field-free evolving initial state in equation (1) over x. In accordance with the periodical nature of the crystal, we describe it as a Bloch wave along the x dimension, with Fourier amplitudes |un ⟩y ,

where  0(k) is the energy of the state, and the subindex y refers to kets in the Hilbert space along the y dimension.
0(k) is the energy of the state, and the subindex y refers to kets in the Hilbert space along the y dimension.
The ionized wavefunction has the following form (see methods):

with

and where Δ(k) accounts for the band bending due to the interaction with the crystal potential (see figure 1(c) and methods),  .
.
The amplitude in equation (5) and the frequency in equation (6) are the corresponding generalizations of the formulae in [5], reporting the temporal matter-wave Talbot effect (in our case the matter wave has non-vanishing initial transverse momentum ℏk). The reinterpretation the present case in terms of [5] is straightforward: first, the Bloch electron corresponds to the matter wave upon difraction by the crystal potential. Second, after ionization, the electron is promoted to the continuum where it is dispersed, as each Fourier component of the Bloch state evolve as a planewave with its free electron energy. Conversely, in [5], the raising of a transient light standing wave creates a scattered Bose–Einstein condensate wavefunction of similar structure to the Bloch state, that is further dispersed as a free wave. In both cases, the resulting wavefunctions have analogous discrete momentum–energy distributions and, therefore, follow a dispersive behavior leading to the temporal Talbot effect.
Following our discussion, let us now consider the time evolution of the electron's probability density, integrated along the y dimension, associated to the wavepacket ionized at ti . Using equation (5) we can write,
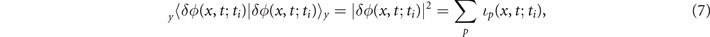
where
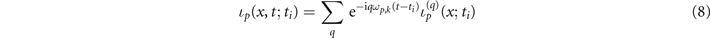
with

being the qth component of the Fourier transform (8)
In the optical analogy, the probability density in equation (7) corresponds to an intensity distribution at the image plane, built as a superposition of the sub-images ιp
. As a result of the discreteness of the superposition in equation (8), each of the sub-images ιp
(x; t, ti
) shows Talbot revivals with periods Tp,k
= 2π/ωp,k
. Note however that, as the Talbot frequency is different for each sub-image p, it is not possible to expect a complete revival of the total ionized probability (7), a phenomenon analogous to the so-called partial Talbot effect [36]. The scenario is simplified when considering the relative weights of the sub-image components  in equation (9). For the lowest band, the most relevant Bloch coefficients in equation (4) have index n = 0, therefore equation (9) shows that the Talbot image ιp
is dominated by the q = p term. In addition, the most prominent elements of this sub-set will be those with the smallest index p.
in equation (9). For the lowest band, the most relevant Bloch coefficients in equation (4) have index n = 0, therefore equation (9) shows that the Talbot image ιp
is dominated by the q = p term. In addition, the most prominent elements of this sub-set will be those with the smallest index p.
Figure 3(a) shows the illustration of this discussion by plotting the Talbot carpet corresponding to the ionized wavefunction from the exact solution of the TDSE, at a given instant of time. In order to allow for better legibility, we have considered for this picture a driving field of only one cycle with square envelope, and a hypothetical crystal structure with parameter d = 20 a.u. (10.6 Å), so that the Talbot frequencies are smaller and the carpet structure can be clearly depicted. For this figure, the initial state corresponds to an electron in the first band with k = 0. The electron in the crystal is tunnel-ionized into the continuum near the driving field peak, at ti ≃ 0.25 cycles, and access to the spatial region where the ionized population is computed, around 0.2 cycles later. The white solid line indicates the structure of the density probability of the initial state, as a reference. The carpet structure in figure 3(a) clearly shows the temporal sequence of Talbot images with period TT ≃ 0.3 cycles, in agreement with that expected for the crystal parameter employed in this calculation. The vertical white dashed lines indicate instants of perfect and inverse images, tP and tI. Additionally, figure 3(b) shows the Fourier transform of the temporal Talbot carpet for the one-cycle driving field and now using a crystal with parameter of 4 a.u. (2.1 Å), the one used in the TDSE computations shown in figure 2. The Fourier transform evidences the sequence of peaks associated with the Talbot frequencies qωp,0, found in our SFA discussion, as reflected in equations (6)–(9) with the main weight corresponding to the contribution p = q = 1.
Figure 3. (a) Temporal Talbot carpet depicting the density of probability (log10 scale, arb. units) of the ionized electrons in a crystal with d = 20 a.u. (10.6 Å) along x direction, during one cycle of a 3 μm laser field. The dashed lines represent two instants of time where we find an inverse image (tI) and a perfect image (tP). The white-solid line shows the initial electronic distribution in the crystal. (b) Fourier transform of the time-dependent ionized density of probability in a crystal d = 4 a.u. (2.1 Å) integrated along y. The dashed lines represent the frequencies corresponding to the q = pth Fourier component of the pth sub-image. The rest of frequencies are labeled with their corresponding (p, q) indices. (c) Classical trajectories of the ionized electron (blue) along y direction, during its interaction with the electric field (red). The dashed lines indicate the three instants of time shown in the following graphs. (d)–(f) Time evolution of the probability density (logarithmic scale, arbitrary units) in a linear crystal with a lattice parameter of 20 a.u. (10.6 Å) during the interaction with a 3 μm one-cycle laser pulse. The white-solid line shows the initial electronic distribution in the crystal.
Download figure:
Standard image High-resolution imageOnce we have demonstrated that the SFA leads to a description of ionization and Talbot revivals consistent with the exact TDSE results, we use the SFA framework to discuss the extended spectral structures in the harmonic spectra shown in figure 2. According to the SFA description, each of the ionized wavepackets contributes to the complex dipole acceleration as  , with
, with  , where |ϕ0(x, t)⟩ and |δϕ(x; t, ti
)⟩ are given by equations (4) and (14), respectively. Therefore the contribution to the HHG spectrum is described by the Fourier transform of
, where |ϕ0(x, t)⟩ and |δϕ(x; t, ti
)⟩ are given by equations (4) and (14), respectively. Therefore the contribution to the HHG spectrum is described by the Fourier transform of

with

Note that an
(t, ti
) has the same form of the dipole emitted by a one-dimensional atom, defined along the coordinate y, with ionization potential | 0(0) − Δ(k)|. Therefore, the HHG spectrum obtained from the dipole acceleration in equation (10), corresponds to the convolution of the atomic-like spectrum, a single plateau, with the Talbot oscillations. Thus, the superposition of atomic-like spectra shifted by frequencies nωn,k
, given by equation (6) and labeled with tuples (n, k/g) in figure 2, gives rise to the multiple plateaus in the TDSE HHG.
0(0) − Δ(k)|. Therefore, the HHG spectrum obtained from the dipole acceleration in equation (10), corresponds to the convolution of the atomic-like spectrum, a single plateau, with the Talbot oscillations. Thus, the superposition of atomic-like spectra shifted by frequencies nωn,k
, given by equation (6) and labeled with tuples (n, k/g) in figure 2, gives rise to the multiple plateaus in the TDSE HHG.
Figures 3(c)–(f) shows an illustration of the physical mechanism for which the Talbot frequencies emerge in the harmonic spectra. Panel (c) shows schematically the electron trajectories in the continuum according to the semiclassical picture mentioned in the introduction: electrons are ionized near a field maximal amplitude and evolve in the continuum following rescattering trajectories. Panels (d) to (f) illustrate the probability density of the electronic wave-packet from the TDSE calculation. To enhance visibility, we consider again the hypothetical crystal with parameter d = 20 a.u. (10.6 Å) interacting with a one-cycle square pulse. The panels correspond to three different rescattering times, labeled with vertical dashed lines in panel (c). The white curve in (d)–(f) represents the probability density distribution of the initial state. As the maximal efficiency of the dipole emission corresponds to times of maximal overlap of the ionized and initial wavefunction, the HHG is modulated by the Talbot shaping of the ionized wavefunction. In particular, in the case shown in panel (e) the Talbot image is formed at the moment of rescattering, maximizing the HHG efficiency. On the contrary, in panels (d) and (f) the initial wavefunction profile does not overlap optimally with the Talbot maxima of the rescattering wavefunction, thus diminishing the HHG efficiency. Note, however, that the translation of the Talbot images to the temporal oscillations of the harmonic spectrum is not one-to-one, as the dipole oscillations are calculated from the probability amplitude, equation (6), not from the probability density in equations (7)–(9). Both, nevertheless, contain the frequencies corresponding to the Talbot revivals (6).
Before concluding we should note that, since the HHG signal is more efficient when the recolliding electron wavepacket has a maximum overlap with the crystal potential, the HHG signal can be reinterpreted as the temporal correspondent of a Talbot–Lau interferometer. In this later, the Talbot image is probed by a replica of the diffraction mask located at some distance.
In conclusion, we have demonstrated that the HHG signal from a periodic low-dimensional target irradiated at grazing incidence contains the spectral signature of the Talbot revivals in the ionized electron's wavefunction. We also show that the process of HHG is the counterpart of Talbot–Lau interferometry in the unprecedented subfemtosecond temporal and nanometer spatial scales. High-order harmonic spectroscopy, therefore, emerges as a suitable tool for a new class of measurements, that we refer to as UTS. We have also show how this new technique can be used to reveal details of the crystal electron occupation.
5. Methods
5.1. The crystal potential
The crystal is modeled by a 2D Mathieu-type potential, periodic along the crystal axis and shaped by a soft-core Coulomb potential in the perpendicular direction [37],
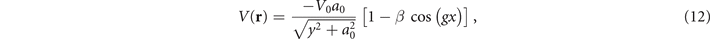
where V0 = 15.5 eV, a0 = 0.539 Å is the Bohr radius, and β = 0.11. g is the reciprocal lattice vector, 2π/d, where d = 2.1 Å (4 u.a.) is the crystal lattice constant.
5.2. Integration of the TDSE.
It is known that many-body interactions add an extraordinary complexity to the electron crystal dynamics, and collective effects are found essential to describe the lowest frequency part of the harmonic spectrum. For HHG from ionized electrons, however, the relative weights of the high-order spectral signals can be still properly described in the independent particle approximation [27]. Thus, we solve numerically the time-dependent Schrödinger equation (TDSE), for an electron of the linear chain interacting with a femtosecond laser pulse, linearly-polarized along the direction perpendicular to the crystal axis, with vector potential A(t),
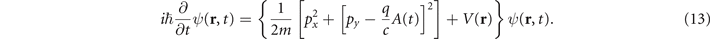
The time integration is carried on using a split operator scheme, where the evolution is computed using Fourier/Crank–Nicolson method, depending on the periodic/vanishing boundary condition in the x/y dimension. The harmonic spectrum is computed as the Fourier transformation of the mean value of the acceleration operator  . We model the driving laser pulse envelope as a sinus-squared function of 5 cycles of duration (18 fs FWHM) with peak intensity 1.03 × 1013 W cm−2, corresponding to the tunnel ionization regime (Keldysh parameter <1).
. We model the driving laser pulse envelope as a sinus-squared function of 5 cycles of duration (18 fs FWHM) with peak intensity 1.03 × 1013 W cm−2, corresponding to the tunnel ionization regime (Keldysh parameter <1).
5.3. Strong-field description of the ionized electron
Using equation (4), and introducing the identity operator I = ∫|xi ⟩⟨xi |dxi with the factorization in equation (3) in (2), the projection of the ionized wavepacket |δϕ(t; ti )⟩ on the x dimension reads as

with Fn (x, t; xi , ti ) is defined as

where GF,x (t; ti ) corresponds to the free electron propagator along the x dimension, from the ionization time ti to t. We have, therefore

Note that the analogy with coherent optics follows from the formal equivalence of equation (16) with the 1D Fresnel propagator,
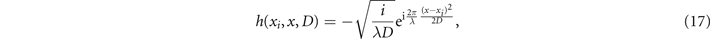
where xi and x are the coordinates at the aperture and the screen where the diffraction image is projected, respectively, and λ is the wavelength of the diffracted field. The equivalence of equations (17) and (16) follows upon the substitutions D → c(t − ti ) and k → mc/ℏ.
Using (15) and (16) and integrating over xi , we find the expression for the ionized wavefunction (14) as

with
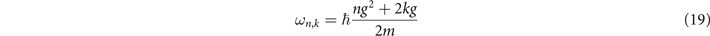
and where we have factorized the Bloch electron energy as  0(k) =
0(k) =  0(0) + ℏ2
k2/2m −Δ(k), where Δ(k) accounts for band bending due to the interaction with the periodic crystal potential (see figure 1(c)).
0(0) + ℏ2
k2/2m −Δ(k), where Δ(k) accounts for band bending due to the interaction with the periodic crystal potential (see figure 1(c)).
Acknowledgments
We acknowledge support Ministerio de Ciencia e Innovación (PID2019-106910GB-I00). This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (Grant Agreement No. 851201). We also acknowledge support from Junta de Castilla y León FEDER funds (Project No. SA287P18). AG-C acknowledges support from Ministerio de Educación, Cultura y Deporte (FPU18/03348). CH-G acknowledges Ministerio de Ciencia, Innovación, y Universidades for a Ramón y Cajal contract (RYC-2017-22745), co-funded by the European Social Fund.
Data availability statement
The data that support the findings of this study are available upon reasonable request from the authors.






