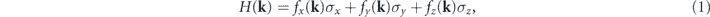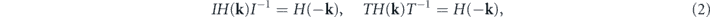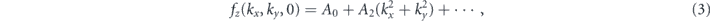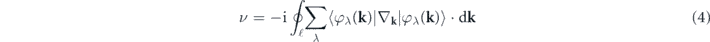Topological phase transition from T-carbon to bct-C₁₆

Carbon is a high-profile element due to its ability to form numerous allotropes with emergent properties. The most famous carbon allotropes are graphite and diamond. At ambient conditions, graphite is the thermodynamically most stable phase with layered honeycomb lattices. Based on graphite, many structural transformations can be occurred at high pressures and temperatures [1–4]. For instance, cubic and hexagonal diamond can be obtained from graphite at pressures above 15 GPa and temperatures above 1300 K [3, 4]. Besides, graphite can be converted into diamond-like cold-compressed phases at the room temperature [5–9]. Distinguished from semimetallic graphite that possesses an all sp² bonding state, the metastable carbon allotropes mentioned above host the sp³ hybridization and thus are insulators. Furthermore, graphite can also be exfoliated or wrapped to other structures with sp² bonding states, such as zero-dimensional (0D) fullerenes [10], one-dimensional (1D) nanotubes [11], and two-dimensional (2D) graphene [12]. Among these lower dimensional sp² carbon allotropes graphene is particularly important. As is well-known, topological semimetallic features in graphene have significantly impacted on the field of topological materials [13]. Motivated by great achievements in graphene, it is promising to investigate symmetry-protected topological fermions in three-dimensional (3D) carbon allotropes. In addition, the investigation of topological bosons, such as nontrivial phonons in carbon phases, are also addressed recently [14, 15]. In comparison with 2D graphene, 3D carbon allotropes have a higher thermodynamic stability, which facilitates the observation of topological fermions in experiments.

To design 3D carbon allotropes with semimetallic phases, we recall electron configurations of a carbon atom, which possesses 2s²2p² valence electrons. Thus, the conductivity requires that 3D carbon allotropes with nontrivial fermions must be in all sp² structures or sp²–sp³ hybridized network structures. With this guidance, a series of 3D conductive carbon allotropes with sp² bonding or sp²–sp³ hybridized structures have been intensively predicted [16–24]. As expected, most of them host topological semimetallic features, such as nodal line fermions in 3D graphene networks [16], body-centered orthorhombic C₁₆ [17], and body-centered tetragonal C₁₂ [18], C₁₆ [19], and C₄₀ [20], as well as beyond [21–24]. These advancements greatly inspire us to find more novel 3D carbon allotropes with nontrivial fermions. However, the topological fermions in 3D carbon allotropes have been not verified in experiments. We find that most of reported topological 3D carbon allotropes possess complicated crystal structures and many atoms in a unit cell. Therefore, the discovery of high-symmetric topological 3D carbon allotropes is highly desirable. Of equal importance is the realization that there are fewer atoms in a unit cell, which can intuitively exhibit the relation between topological orders and symmetries and even realize topological applications in carbon based-materials.

In this paper, by using first-principle calculations, it is found that an all-quasi-sp² bonding carbon allotrope named bct-C₁₆, which crystallizes in a body-centered tetragonal (bct) lattice, can be obtained from T-carbon phase [25]. bct-C₁₆ hosts the high symmetry (i.e., D_4h) and there are only eight carbon atoms in one unit cell. We show by a symmetry and effective model analysis that bct-C₁₆ belongs to the Dirac node-line semimetal phase, in which an ideal nodal ring exactly crosses the Fermi level and is protected by the coexistence of inversion and time reversal symmetries. Our work provides an avenue for obtaining the carbon phase bct-C₁₆ and exploring the nodal line fermions in this carbon phase.

First-principles calculations are performed using the Vienna ab inito simulation package with the projector augmented wave method [26]. A plane wave expansion with an energy cutoff of 600 eV is used in all calculations. The generalized gradient approximation with Perdew–Burke–Ernzerhof (PBE) functional is chosen to describe exchange–correlation energy [27, 28]. Ab initio molecular dynamic simulation (AIMD) is also implemented to investigate the temperature effect on T-carbon. An initial temperature of 100 K according to a Boltzmann distribution is assigned to the T-carbon in a 2 × 2 × 1 supercell with 128 carbon atoms. A series of temperatures from 100 K to 600 K with a temperature step of 50 K in an NVT ensemble are considered in 2 ps, and each equilibrium structure at a constant temperature maintains 20 ps with Nose thermostat. The timestep of this AIMD simulation is 1 fs. We also check the band inversion and topology in Heyd–Scuseria–Ernzerhof (HSE06) hybrid functional [29]. The ionic relaxation and electronic self-consistent iteration are converged to 0.01 eV Å⁻¹ and 10⁻⁶ eV with a Γ-centered k-mesh of 11 × 11 × 11. In order to reveal topological electronic features of bct-C₁₆, we construct a tight-binding (TB) Hamiltonian based on maximally localized Wannier functions projected from the bulk Bloch wave function in the WANNIER90 package [30]. The crystal orbital Hamilton populations (COHPs) [31–33] of T-carbon and bct-C₁₆ are implemented in the LOBSTER code [34].

As shown in figures 1(a) and (b), according to the ab initio molecular dynamic simulations (AIMD), it is found that the T-carbon phase undergoes a structural phase transition to bct-C₁₆ at the temperature of ∼500 K (figure 1(b)). In this process, the internal carbon-tetrahedron of T-carbon is destroyed to form a non-planar carbon-square, i.e., bct-C₁₆ is present, The dynamical process of this AIMD simulation is shown in a video (see the Video SM, which is available online at https://stacks.iop.org/NJP/22/073036/mmedia). To understand the intrinsic mechanism of the phase transition from T-carbon to bct-C₁₆, we calculated the COHP of T-carbon and bct-C₁₆, respectively. As shown in figure 2(b), the absolute integral values of COHP confirm that the bonding network of T-carbon will be translated to a more stable carbon phase bct-C₁₆ in thermal fluctuations. Moreover, the potential energy of this system is also shown in figure 2(a), which shows that there exists a dramatic reduction of potential energy in 500 K, also confirming the phase transition from T-carbon to bct-C₁₆. These results insure that the phase transition is properly exist during the heating process of T-carbon. Furthermore, figure 1(d) shows that the T-carbon phase are transformed to the bct-C₁₆ carbon phase by doping the transition elements (Cu, Fe), which might be experimentally realized by ion implantation, or being introduced in preparation. These results indicate that bct-C₁₆ is a fairly stable carbon phase and could be synthesized from T-carbon.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

As shown in figures 3(a) and (b), the carbon phase bct-C₁₆ is constructed to investigate the corresponding properties. The optimized lattice parameters of bct-C₁₆ are a = 6.588 Å, c = 3.378 Å. Each carbon atom is connected by three neighbors, forming non-planar geometries composed by four- and eight-membered rings. Different from the unique bond length ∼ 1.414 Å in graphite, there are two non-equivalent carbon-carbon bond lengths denoted as d₁ = 1.361 Å and d₂ = 1.483 Å in bct-C₁₆, which alternately arrange in an eight-membered ring. In figure 3(c), we plot the bulk bct BZ and the corresponding (001) surface BZ, in which high-symmetry points are highlighted as red-solid points. The dynamical and thermal stabilities of bct-C₁₆ is confirmed by phonon spectra (in the SM) and a 5 ps AIMD simulation. The AIMD simulation is performed in 500 K with a 3 × 3 × 3 supercell.

Zoom In Zoom Out Reset image size

Next, we focus on the electronic properties of bct-C₁₆. The electronic band structure along high-symmetry paths of the BZ is shown in figure 4(a). Comparing to the semiconductor T-carbon phase in which the band gap is 3.0 eV [25], the bands of bct-C₁₆ possess semimetallic features. The partial density of states depicted in figure 4(b) indicate that p_z orbital dominates the contributions near the Fermi level, confirming the quasi-sp² bonding features of bct-C₁₆. Remarkably, two bands exactly cross each other with linear dispersions at the Fermi level in the Γ–X and Γ–M directions (see figure 4(c)). The two crossing bands belong to opposite eigenvalues ±1 of mirror symmetry M_z. Considering this M_z symmetry, two crossing bands with an inversion gap of ∼1.75 eV at the Γ point form a continuous topological nodal ring in the k_z = 0 plane. Figure 4(d) shows a map of energy difference between the lowest conduction band and highest valence band, and the nodal ring is denoted as the white feature, indicating a zero gap in the k_z = 0 plane. Besides, we carry out HSE06 calculations with more accurate correlations than PBE functional to check band inversion in bct-C₁₆. The results show that HSE06 functional only slightly shift the band profile and confirm the same band topology (see figure 4(a)). Moreover, we also consider the spin–orbital coupling (SOC) effect on the band structures of bct-C₁₆. The results show that the global gap is present (see the SM). In this case, bct-C₁₆ is converted to a strong topological insulator with Z₂ index (1;001). However, the values of gap are very tiny (<1 meV) due to the weak SOC effect of the carbon element, so the nodal ring in bct-C₁₆ can be guaranteed to be nearly intact even though the SOC is present.

Zoom In Zoom Out Reset image size

To insightfully understand the band topology in bct-C₁₆, we perform a symmetry analysis and effective k ⋅ p model to demonstrate that the nodal ring exist in the k_z = 0 plane. The symmetry of bct-C₁₆ at the band inversion Γ point is D_4h = D₄ ⊗ C_i , including an inversion symmetry I, two-fold rotational symmetries C_2x and C_2y, a four-fold rotational symmetry C_4z, and a mirror symmetry M_z. Two crossing bands with a band inversion can be generally described by a 2 × 2 k ⋅ p Hamiltonian,

$$\begin{equation}H\left(\mathbf{k}\right)={f}_{x}\left(\mathbf{k}\right){\sigma }_{x}+{f}_{y}\left(\mathbf{k}\right){\sigma }_{y}+{f}_{z}\left(\mathbf{k}\right){\sigma }_{z},\end{equation} \tag{ 1 }$$

where H is referenced to the Fermi level, k is the momentum vector related to the Γ point, f_i(k) (i = x, y, z) are real functions, and σ_i are Pauli matrices. The two inverted bands have opposite mirror eigenvalues ±1, so we can represent the inversion symmetry as I = σ_z. Besides, the time-reversal symmetry T exists in a non-magnetic system of bct-C₁₆. As a result, the presence of I and T symmetries constrain the Hamiltonian as

$$\begin{equation}IH\left(\mathbf{k}\right){I}^{-1}=H\left(-\mathbf{k}\right),\quad TH\left(\mathbf{k}\right){T}^{-1}=H\left(-\mathbf{k}\right),\end{equation} \tag{ 2 }$$

which leads to that f_x(k) ≡ 0, f_y(k) is an odd function, and f_z(k) is an even function. The zero-energy solutions of two crossing bands [i.e., f_y(k) = 0 and f_z(k) = 0] induce codimension 1, signaling the presence of nodal lines in momentum space. Additionally, the four-fold rotational symmetry C_4z and mirror symmetry M_z constrain f_y(k) and f_z(k). These symmetries guarantee the nodal ring locating in the k_z = 0 plane with respect to four-fold rotational z axis. In this case, only f_z(k) is nonzero and it can be expanded in the low-energy as

$$\begin{equation}{f}_{z}\left({k}_{x},{k}_{y},0\right)={A}_{0}+{A}_{2}\left({k}_{x}^{2}+{k}_{y}^{2}\right)+\cdots ,\end{equation} \tag{ 3 }$$

When the parameters A₀ and A₂ satisfy A₀A₂ < 0, the closed nodal ring is present in the k_z = 0 plane.

The topological nodal ring in bct-C₁₆ connects to a quantized Berry phase ν,

$$\begin{equation}\nu =-{\text{i}\oint }_{\ell }\sum _{\lambda }\langle {\varphi }_{\lambda }\left(\mathbf{k}\right)\vert {\nabla }_{\mathbf{k}}\vert {\varphi }_{\lambda }\left(\mathbf{k}\right)\rangle \cdot \mathrm{d}\mathbf{k}\end{equation} \tag{ 4 }$$

which is related to wave functions φ_λ(k) of valence bands cumulated from a symmetric circle ℓ surrounding the nodal ring. The circle ℓ can be continuously deformed into 1D subsystem along the k_z directions with one inside the nodal ring and the other outside. As shown in figure 5(a), it is found that the Berry phase inside the nodal ring is nontrivial, i.e., ν = π mod 2π. From the bulk-boundary correspondence, the nontrivial Berry phase leads to topological-protected drumhead surface states lying inside the projection of the nodal ring on the surface BZ. To obtain the topological surface states, we employ the iterative Green's function method with a Wannier TB Hamiltonian [35, 36]. We plot the local density of states (LDOS) projected on the semiinfinte (001) surface of bct-C₁₆ in figure 5(b). As expected, we can see that occupied drumhead surface states cover the internal region of the projection of nodal ring on the (001) surface BZ. Panel (c) of figure 5 shows the evolution of the projected Fermi surface with respect to E − E_F. For the energy E = E_F − 0.3 eV (see figure 5(d)), a continuous Fermi arc is clearly visible on the projected Fermi surface.

Zoom In Zoom Out Reset image size

In summary, by using first-principle calculations, we find a phase transition from T-carbon to bct-C₁₆. Importantly, there exist two ways to realize this phase transition. The first way is to heat T-carbon to 500 K and the second way is to dope some transition elements (i.e., Cu, Fe) to break the carbon-tetrahedron. Furthermore, based on a symmetry and effective model analysis, we reveal that the Dirac node-line semimetal phase of bct-C₁₆ is protected by the coexistence of inversion and time reversal symmetries. The nodal ring in bct-C₁₆ can be guaranteed to be nearly intact even though the SOC is present since carbon element possesses extremely weak SOC effects. The calculated Berry phase and drumhead surfaces states further support nodal line semimetallic features. Our work provides an avenue for obtaining the carbon phase bct-C₁₆ and exploring the nodal line fermions in this carbon phase.

This work was supported by the National Natural Science Foundation of China (NSFC, Grants No. 11974062, No. 11947406, and No. 11505003), the Chongqing National Natural Science Foundation (Grants No. cstc2019jcyj-msxmX0563), The Open Project of State Key Laboratory of Environment-friendly Energy Materials under Grant No. 19kfhg03, and the Fundamental Research Funds for the Central Universities of China (Grants No. cqu2018CDHB1B01, and No. 2020CDJQY-A057)