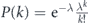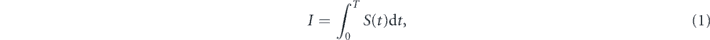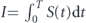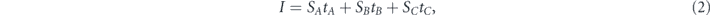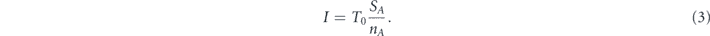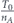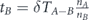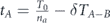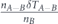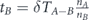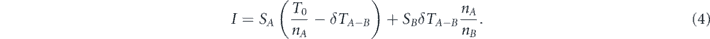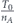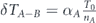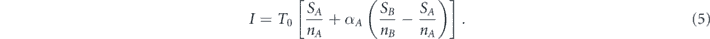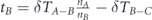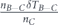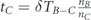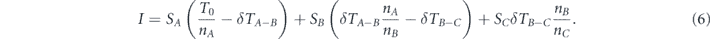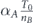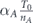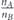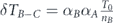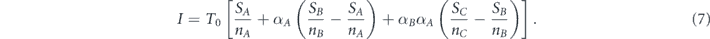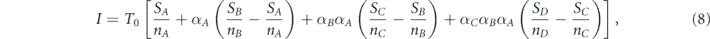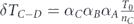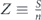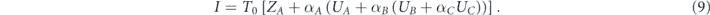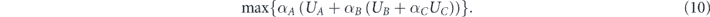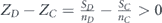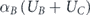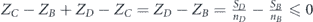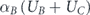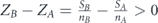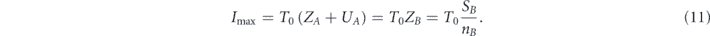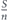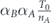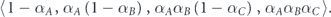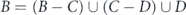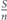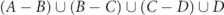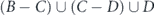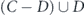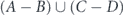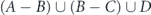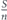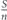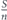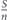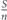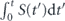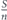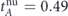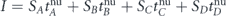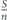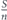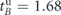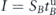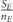Optimal resource allocation for network functionality

The robustness of a network, which is the capability of a network to keep its functionality even when some of its nodes (or links) are removed, is an issue that has been studied widely [1–23]. Traditionally, the measurement of network robustness has been performed in states of a removal of nodes due to an attack on the network. Research has mainly focused on two types of attacks: (i) random attack, where the choice of the network's nodes for removal is performed randomly, without preference of a node to be removed over any other node in the network, and (ii) targeted attack where, in contrast to random attack, the attack is targeted against the nodes with the central role of maintaining the connectivity of the network.

There have been many studies on network robustness, that are based on percolation theory [1–10]. According to this approach, there are two states in which a network can be found—the subcritical state where the network is fragmented to many small components each of them of fixed size, i.e. their size grows sublinearily with the network growth, and the supercritical state where there exists a relatively large component with the characteristic that its size grows linearly with the network size, i.e. scales as O(N), named the giant component, and aside from it there possibly exist small components. The transition between the supercritical state to the subcritical state, where the giant component is fragmented into small components, occurs when a critical combination of the network's nodes is removed. The fraction of the network's nodes that remain functional in order to guarantee the existence of the giant component, is named the percolation threshold of the network, denoted by p_c.

In [1–3], the percolation thresholds were calculated for two classes of random networks that have been studied widely: Erdős–Rényi (ER) networks [24, 25], where the nodes' degrees follow a Poisson distribution $P\left(k\right)={\mathrm{e}}^{-\lambda }\frac{{\lambda }^{k}}{k!}$, and scale-free (SF) networks, a topology that was found in many real networks [26–29], where the nodes' degrees follow a power-law distribution P(k) ∼ k^−γ, such that most of the nodes have very small degrees, while a small fraction of the nodes have very high degrees that are named hubs. It was found that ER networks are significantly more vulnerable to random attack than SF networks, such that for the latter, for γ ⩽ 3, p_c approaches 0. In contrast, for targeted attacks, SF networks are significantly more vulnerable than ER network, since removing only the very small group of the network's hubs, that have a critical role of maintaining the network connectivity, causes the network to be fragmented. There are also studies regarding percolation thresholds in other types of attacks on networks, such as localized attack, where just a certain region of the network is attacked [30], k-core percolation [31] and bootstrap percolation [32, 33].

In addition to the percolation threshold parameter, additional parameters have been defined for measuring network robustness, such as the change in the network diameter [13, 14, 19], the relative size of the giant component [15], the change in the betweenness centrality [16], connectivity loss [17], and f-robustness [18]. Efforts also have been made to find a topology for random network on which the robustness is optimized both for random and targeted attack, based on diameter change [19] or percolation threshold [6]. There are also some studies about real networks robustness like the North American power grid [17] and optical communication networks [20].

A later and innovative approach to network robustness has been proposed in [21, 22]. This approach considers the entire life span of a network in measuring its robustness, in different way from the traditional methods that are based on comparison of network's parameters after and before an attack on it took place, with no consideration to the network's functionality in the intermediate state during the attack. This approach measures network robustness by integrating the fraction of nodes in the giant component with respect to the number of nodes were removed from the network, during all the stages of the network attack.

This approach was further elaborated in [23], where the effect of node aging—the non effectiveness of a node after its survival time duration—its lifetime—is passed—has been added, as a factor that should be considered in measuring network robustness. Accordingly, a network survivability function, which is the integral of the giant component size with respect to time during the entire life span of the network T, has been defined

$$\begin{equation}I={\int }_{0}^{T}S\left(t\right)\mathrm{d}t,\end{equation} \tag{ 1 }$$

where S(t) is the giant component size at time t. The survivability function—equation (1)—is very similar in nature to the robustness integral in [21, 22] as was described above.

For maximizing the network robustness according to the later approach, the following problem has to be solved: in the network design stage, given a total budget of lifetime to be allocated between the network's nodes, what is the optimal way of allocation such that the survivability I in equation (1) is maximized? Indeed, in [23] it was shown numerically, that when a node's lifetime is taken from a distribution with an expectation equals k^α, where k is the node's degree, then dependent on a network topology, a critical value α_c exists, such that determining the distribution expectation to be ${k}^{{\alpha }_{\mathrm{c}}}$, produces the optimized lifetime allocation with it the network survivability is maximized.

However, all the previous solutions for the survivability function maximization [21–23], are network's parameters dependent, and are numerical solutions or based on simulations only. In this paper we present an analytical solution for this problem, which is a general network's parameter independent solution.We develop analytically a criterion for choosing the right set of nodes on which the total budget of lifetime should be allocated, and also we find analytically the optimal way of allocating the lifetime between the nodes of the chosen set, in such a way that the network survivability is maximized.

We address the following question: we are given the number of network's nodes and the degree distribution of the nodes p_k, but not the topology of the network and the links between the nodes. We are also given some budget, pronounced by a total lifetime that can be allocated between the nodes. The goal is to choose the right set of nodes to be allocated with the total lifetime, and the right way of allocating the total lifetime between the nodes of this set, such that the integral $I{=\int }_{0}^{T}S\left(t\right)\mathrm{d}t$ is maximized.

It is important to note that if the network's topology and the links between the nodes are known, the problem becomes trivial. Its solution then is an allocation of the entire lifetime budget to a connected component that is a subset of the network's giant component. However, the solution we present is, as mentioned, based on assuming of knowing only the nodes' degrees. This assumption is realistic, since an equipment manufacturer has some control on the degrees of the network's items (nodes) he manufactures (such as the maximum number of connections of a router), but has no control on the location of the sold equipment in the network topology, and on the nodes to which each of them would be connected.

3.1. Presentation of network survivability

We assume a budget of lifetime for allocating between network's nodes, denoted T₀. We begin by choosing a finite sequence of sets of the network's nodes A, B, C, D, E, F..., subject to the condition of being a decreasing sequence with inclusion relation between each set in the sequence to the set follows it, such that A ⊃ B ⊃ C ⊃ D ⊃ E ⊃ F.... Except this condition, the choice of the nodes that are belong to each of the sets, is completely arbitrary.

We first allocate T₀ uniformly between set A nodes. Obviously, the nodes of sets B, C, D, E, F... are also allocated in this stage, since, by definition, they are all subsets of set A.

Then comes a stage of transferring lifetime between subsets, as follows: (i) first transfer from set A − B to set B—we distinguish the set of nodes that are belong to set A but not belong to set B, denoted as set A − B. We subtract an equal part of lifetime units from each of the nodes of set A − B. Then we transfer the entire lifetime was subtracted from set A − B, to set B nodes. The lifetime allocation is performed uniformly between set B nodes. (ii) Second transfer from set B − C to set C—in similar way to the first transfer, we distinguish the set of nodes that are belong to set B but not belong to set C, denoted as set B − C. We subtract an equal part of lifetime units from each of the nodes of set B − C. Then we transfer the entire lifetime was subtracted from set B − C, to set C nodes. The lifetime allocation is performed uniformly between set C nodes. (iii) In similar way a lifetime transfer is performed from set C − D to set D, and then from set D − E to set E etc, until the last lifetime transfer to the smallest subset in the decreasing sequence of sets was chosen. Figures 1(a–c) is an illustration of this model for a sequence of three sets A ⊃ B ⊃ C.

Zoom In Zoom Out Reset image size

Figure 1(d) presents the network state after the end of the lifetime transfers. The lifetime of set A is represented by the height of the blue bars and denoted by t_A. It is terminated after the collapse of set A − B nodes. The lifetime of set B over its superset A is represented by the height of the red bars and denoted by t_B. It is terminated after the collapse of set B − C nodes. The lifetime of set C over its superset B is represented by the height of the green bars and denoted by t_C. It is terminated after the collapse of set C nodes. According to this, in this state with three sets only, the survivability of the network is

$$\begin{equation}I={S}_{A}{t}_{A}+{S}_{B}{t}_{B}+{S}_{C}{t}_{C},\end{equation} \tag{ 2 }$$

where S_A is the size of the giant component constructed from set A nodes, S_B is size of the giant component constructed from set B nodes and S_C is the size of the giant component constructed from set C nodes. In the general case with any finite number of sets, we would have to add to the summation in equation (2), the terms S_Dt_D, S_Et_E, and in similarly to all the sets.

3.2. Analysis of network survivability

We now analyze and calculate the network survivablity I in equation (2) in more details. We begin with the first stage of allocating the entire lifetime budget T₀ uniformly between set A nodes. The number of nodes in set A is denoted n_A. Therefore, at the end of this stage the lifetime of each of the nodes of set A is ${t}_{A}=\frac{{T}_{0}}{{n}_{A}}$, and the network survivability is

$$\begin{equation}I={T}_{0}\frac{{S}_{A}}{{n}_{A}}.\end{equation} \tag{ 3 }$$

Figure 2(a) illustrates this stage for network with 10 nodes.

Zoom In Zoom Out Reset image size

Then we perform the first lifetime transfer—we subtract an equal part of lifetime units from each of the nodes of set A − B, denoted by δT_A−B. The entire lifetime was subtracted from set A − B, which is n_A−BδT_A−B (n_A−B is the size of set A − B), is allocated uniformly between the nodes of set B. At the end of this stage t_A becomes less than its value at the end of the previous stage. Its current value is ${t}_{A}=\frac{{T}_{0}}{{n}_{a}}-\delta {T}_{A-B}$. The lifetime t_B of set B over its superset A, is combined of two parts—(i) the subtraction of δT_A−B from set A − B, causes automatically the lifetime of set B to be greater than its superset A by δT_A−B lifetime units. (ii) The allocation of the entire lifetime subtracted from set A − B to each of the nodes of set B, increases the lifetime of each of these nodes by $\frac{{n}_{A-B}\delta {T}_{A-B}}{{n}_{B}}$ lifetime units. The addition of these parts gives ${t}_{B}=\delta {T}_{A-B}\frac{{n}_{A}}{{n}_{B}}$. Figure 2(b) illustrates this stage.

Accordingly, the network survivability at the end of this stage is

$$\begin{equation}I={S}_{A}\left(\frac{{T}_{0}}{{n}_{A}}-\delta {T}_{A-B}\right)+{S}_{B}\delta {T}_{A-B}\frac{{n}_{A}}{{n}_{B}}.\end{equation} \tag{ 4 }$$

Since δT_A−B is not greater than the total lifetime of set A − B which is $\frac{{T}_{0}}{{n}_{A}}$, we define $\delta {T}_{A-B}={\alpha }_{A}\frac{{T}_{0}}{{n}_{A}}$, where 0 ⩽ α_A ⩽ 1. Substituting it into equation (4) and rearranging it, gives the following

$$\begin{equation}I={T}_{0}\left[\frac{{S}_{A}}{{n}_{A}}+{\alpha }_{A}\left(\frac{{S}_{B}}{{n}_{B}}-\frac{{S}_{A}}{{n}_{A}}\right)\right].\end{equation} \tag{ 5 }$$

In the next stage we perform the second lifetime transfer—we subtract an equal part of lifetime units from each of the nodes of set B − C, denoted by δT_B−C. The entire lifetime was subtracted from set B − C, which is n_B−CδT_B−C, is allocated uniformly between the nodes of set C. At the end of this stage t_Bbecomes less than its value at the end of the previous stage. Its current value is ${t}_{B}=\delta {T}_{A-B}\frac{{n}_{A}}{{n}_{B}}-\delta {T}_{B-C}$. The lifetime of set C over its superset B—t_C—is combined again of two parts—(i) the subtraction of δT_B−C from set B − C, causes automatically the lifetime of set C to be greater than its superset B by δT_B−C lifetime units. (ii) The allocation of the entire lifetime subtracted from set B − C to each of the nodes of set C, increases the lifetime of each of these nodes by $\frac{{n}_{B-C}\delta {T}_{B-C}}{{n}_{C}}$ lifetime units. The addition of these parts gives ${t}_{C}=\delta {T}_{B-C}\frac{{n}_{B}}{{n}_{C}}$. Figure 2(c) illustrates this stage. The network survivability at the end of this stage is

$$\begin{align}\hfill I& ={S}_{A}\left(\frac{{T}_{0}}{{n}_{A}}-\delta {T}_{A-B}\right)+{S}_{B}\left(\delta {T}_{A-B}\frac{{n}_{A}}{{n}_{B}}-\delta {T}_{B-C}\right)+{S}_{C}\delta {T}_{B-C}\frac{{n}_{B}}{{n}_{C}}.\hfill \end{align} \tag{ 6 }$$

As before, since δT_B−C is not greater than the total lifetime of set B − C which is ${\alpha }_{A}\frac{{T}_{0}}{{n}_{B}}$ (multiplication of ${\alpha }_{A}\frac{{T}_{0}}{{n}_{A}}$ by $\frac{{n}_{A}}{{n}_{B}}$), we shall define $\delta {T}_{B-C}={\alpha }_{B}{\alpha }_{A}\frac{{T}_{0}}{{n}_{B}}$, where 0 ⩽ α_B ⩽ 1. Substituting it into equation (6) and rearranging it, gives the following

$$\begin{equation}I={T}_{0}\left[\frac{{S}_{A}}{{n}_{A}}+{\alpha }_{A}\left(\frac{{S}_{B}}{{n}_{B}}-\frac{{S}_{A}}{{n}_{A}}\right)+{\alpha }_{B}{\alpha }_{A}\left(\frac{{S}_{C}}{{n}_{C}}-\frac{{S}_{B}}{{n}_{B}}\right)\right].\end{equation} \tag{ 7 }$$

In similar way, at the end of the next stage of transfering lifetime from set C − D to set D, the network survivablity is

$$\begin{equation}I={T}_{0}\left[\frac{{S}_{A}}{{n}_{A}}+{\alpha }_{A}\left(\frac{{S}_{B}}{{n}_{B}}-\frac{{S}_{A}}{{n}_{A}}\right)+{\alpha }_{B}{\alpha }_{A}\left(\frac{{S}_{C}}{{n}_{C}}-\frac{{S}_{B}}{{n}_{B}}\right)+{\alpha }_{C}{\alpha }_{B}{\alpha }_{A}\left(\frac{{S}_{D}}{{n}_{D}}-\frac{{S}_{C}}{{n}_{C}}\right)\right],\end{equation} \tag{ 8 }$$

where 0 ⩽ α_C ⩽ 1 and $\delta {T}_{C-D}={\alpha }_{C}{\alpha }_{B}{\alpha }_{A}\frac{{T}_{0}}{{n}_{C}}$.

In the same way, we should add terms to equation (8), for the next subsets of the sequence of descending sets was chosen.

For the sake of convenience, from now on we develop the theory for only four sets A ⊃ B ⊃ C ⊃ D, but the generalization to any number of sets is straightforward. For each set we define $Z\equiv \frac{S}{n}$, as the ratio between its giant component size and its size. We also define U_A ≡ Z_B − Z_A, U_B ≡ Z_C − Z_B and U_C ≡ Z_D − Z_C. Accordingly, equation (8) becomes

$$\begin{equation}I={T}_{0}\left[{Z}_{A}+{\alpha }_{A}\left({U}_{A}+{\alpha }_{B}\left({U}_{B}+{\alpha }_{C}{U}_{C}\right)\right)\right].\end{equation} \tag{ 9 }$$

3.3. Maximization of network survivability

Maximization of the network survivability presented in equation (9), is achieved by maximizing the following

$$\begin{equation}\mathrm{max}\left\{{\alpha }_{A}\left({U}_{A}+{\alpha }_{B}\left({U}_{B}+{\alpha }_{C}{U}_{C}\right)\right)\right\}.\end{equation} \tag{ 10 }$$

The maximization is implemented by determining the α's values from inside out, according to the rule: if the expression multiplied by α is greater than 0, then α = 1, and if it is less than or equal to 0, then α = 0.

We introduce a specific example: first, we have to maximize α_CU_C. Assume that U_C > 0 (which means ${Z}_{D}-{Z}_{C}=\frac{{S}_{D}}{{n}_{D}}-\frac{{S}_{C}}{{n}_{C}}{ >}0$), then α_C is determined to be 1, and α_CU_C becomes U_C. Accordingly, the next expression to be maximized is ${\alpha }_{B}\left({U}_{B}+{U}_{C}\right)$. Assume that U_B + U_C ⩽ 0 (which means ${Z}_{C}-{Z}_{B}+{Z}_{D}-{Z}_{C}={Z}_{D}-{Z}_{B}=\frac{{S}_{D}}{{n}_{D}}-\frac{{S}_{B}}{{n}_{B}}{\leqslant}0$), then α_B is determined to be 0, and ${\alpha }_{B}\left({U}_{B}+{U}_{C}\right)$ becomes 0. Accordingly, the last expression that has to be maximized is α_AU_A. Assume that U_A > 0 (which means ${Z}_{B}-{Z}_{A}=\frac{{S}_{B}}{{n}_{B}}-\frac{{S}_{A}}{{n}_{A}}{ >}0$), then α_A is determined to be 1, and α_AU_A becomes U_A. Therefore, according to equations (9) and (10) we get for the maximum of network survivability in this example

$$\begin{equation}{I}_{\mathrm{max}}={T}_{0}\left({Z}_{A}+{U}_{A}\right)={T}_{0}{Z}_{B}={T}_{0}\frac{{S}_{B}}{{n}_{B}}.\end{equation} \tag{ 11 }$$

That means that maximum survivability is achieved by allocating the entire lifetime T₀, uniformly between the nodes of set B. Note also that among the four sets, the ratio $\frac{S}{n}$ is maximal for set B (as was shown Z_D > Z_C, Z_B ⩾ Z_D and Z_B > Z_A). This is the reason for choosing this set to be allocated with the entire lifetime.

The previous result can be presented in another way. According to the former analysis, we get the followings for the sets' lifetimes after the end of the lifetimes transfer

$$\begin{align}\hfill & {t}_{A}=\frac{{T}_{0}}{{n}_{A}}\left(1-{\alpha }_{A}\right),\hfill \\ \hfill & {t}_{B}={\alpha }_{A}\frac{{T}_{0}}{{n}_{B}}\left(1-{\alpha }_{B}\right),\hfill \\ \hfill & {t}_{C}={\alpha }_{A}{\alpha }_{B}\frac{{T}_{0}}{{n}_{C}}\left(1-{\alpha }_{C}\right),\hfill \\ \hfill & {t}_{D}={\alpha }_{A}{\alpha }_{B}{\alpha }_{C}\frac{{T}_{0}}{{n}_{D}}.\hfill \end{align} \tag{ 12 }$$

For example: the final lifetime of set A is the difference between its original lifetime which is $\frac{{T}_{0}}{{n}_{A}}$, and the lifetime was subtracted from it which is ${\alpha }_{A}\frac{{T}_{0}}{{n}_{A}}$, the final lifetime of set B is the difference between its original lifetime which is ${\alpha }_{A}\frac{{T}_{0}}{{n}_{B}}$, and the lifetime was subtracted from it which is ${\alpha }_{B}{\alpha }_{A}\frac{{T}_{0}}{{n}_{A}}$, etc.

Accordingly, we define the following vector of the α's coefficients of the sets' lifetime

$$\begin{equation*}\langle 1-{\alpha }_{A} , {\alpha }_{A}\left(1-{\alpha }_{B}\right) , {\alpha }_{A}{\alpha }_{B}\left(1-{\alpha }_{C}\right) , {\alpha }_{A}{\alpha }_{B}{\alpha }_{C} \rangle .\end{equation*}$$

The first component represents set A lifetime, the second component represents set B lifetime, etc. Since the α's values are 0 or 1, we get that the vector components equal 0, except one component that equals 1 which is the component that related to the set in which the ratio $\frac{S}{n}$ is maximum, and is the only set that should be allocated with lifetime such that the network survivability is maximized. For the previous example – with α_A = 1, α_B = 0 and α_C = 1, the vector is ⟨0, 1, 0, 0⟩, where the second component is the only one that equals 1. This component is related to set B with the maximum ratio of $\frac{S}{n}$ among the four sets A, B, C and D, which is the only set that should be allocated with lifetime in order to maximize the network survivability. The generalization of this presentation for a greater number of sets, is straightforward according to the former analysis.

3.4. Global maximum for survivability function

We present here another aspect of the application of our method.

The choice of four sets A ⊃ B ⊃ C ⊃ D and lifetimes t_A, t_B, t_c and t_D, could be viewed as dividing the network to four disjoint sets with different lifetimes: set A − B with t_A lifetimes units, set B − C witht_A + t_B lifetime units, set C − D with t_A + t_B + t_C lifetime units and set D with t_A + t_B + t_C + t_D lifetime units (there is also the set of nodes that are not received lifetime, but this set contributes nothing to the network survivability and is not considered). Figure 3 illustrates this state.

Zoom In Zoom Out Reset image size

This means that the choice of sets A, B, C and D, is equivalent to a choice of the four disjoint sets A − B, B − C, C − D and D, for lifetime allocation. This description is related to the problem we deal with, as addressed in the 'Model' section: given a lifetime budget for allocating between network's nodes, what are the right sets of nodes for allocation and what is the right way of allocating inside each set, such that the network's survivability is maximized? Let us assume that one chooses four disjoint sets for lifetime allocation, named G₁, G₂, G₃ and G₄. This state is similar to our description of choosing our four disjoint sets. Therefore, we can transforms the sets G₁, G₂, G₃ and G₄ to our model's parameters A − B, B − C, C − D and D, respectively. Then we apply our survivability maximization algorithm—we firstly unify the sets A − B, B − C, C − D and D, and consider the sets A, B, C and D, instead of them. Then we allocate the lifetimes t_A, t_B, t_C and t_D to sets A, B, C and D respectively, and by our algorithm, was described above, we optimize these lifetimes values such that the network's survivability is maximized. Then we use the optimized values in the initial optimization problem of four disjoint sets. That is, if one chooses in advance sets G₁, G₂, G₃ and G₄ to be allocated with lifetime, the maximization of the network's survivablity would be achieved if the optimized t_A, that is the lifetime allocated to set A − B in our model, would be allocated to set G₁, the optimized t_A + t_B, that is the lifetime allocated to set B − C in our model, would be allocated to set G₂, the optimized t_A + t_B + t_C that is the lifetime allocated to set C − D would be allocated to set G₃, and the optimized t_A + t_B + t_C + t_D that is the lifetime allocated to set D would be allocated to set G₄.

However, it is important to note that our algorithm comparison of the ratio $\frac{S}{n}$ between the sets A, B, C and D, is equivalent to a comparison between the sets $\left(A-B\right)\cup \left(B-C\right)\cup \left(C-D\right)\cup D$, $\left(B-C\right)\cup \left(C-D\right)\cup D$, $\left(C-D\right)\cup D$ and D (which are the sets G₁ ∪ G₂ ∪ G₃ ∪ G₄, G₂ ∪ G₃ ∪ G₄, G₃ ∪ G₄ and G₄, respectively). The algorithm does not compare all the possible combinations of the disjoint sets, such as $\left(A-B\right)\cup \left(C-D\right)$, $\left(A-B\right)\cup \left(B-C\right)\cup D$ (which are the combinations G₁ ∪ G₃, G₁ ∪ G₂ ∪ G₄, respectively). Therefore, if the maximum of the ratio $\frac{S}{n}$ is achieved in one of the last sets, it would not be identified by our algorithm. In this case, the set would be chosen by the algorithm would not lead to the global maximum of the survivability function. Nevertheless, we first note that against any nonuniform lifetime allocation between network's nodes, our algorithm identifies a set of nodes such that allocating the entire lifetime uniformly between these nodes, causes the survivability function to be greater than its value with the nonuniform allocation. Second, our algorithm is generalized for any number of finite descending sets with any nonuniform lifetime allocation between them, and specifically for our case is applicable for any replacements of the nodes of sets A − B, B − C, C − D and D (which are the sets G₁, G₂, G₃ and G₄, respectively), among themselves, where in this cases the algorithm will identify the global maximum. For this, we extend the criterion we proved for maximum survivability with four disjoint sets based on comparison between sets A, B, C and D only, to a comparison between all the four disjoint sets combinations. Therefore, the criterion is—choice of the set combined from the four disjoint sets, in which the ratio $\frac{S}{n}$ is maximal, and an allocation of the entire lifetime uniformly between its nodes.

3.5. Conclusion of maximum network survivability

Simulations were implemented on Erdős–Rényi (ER) and scale-free (SF) random networks. For each realization of each simulation of each of the above networks, a budget of lifetime was distributed firstly non-uniformly between the various nodes, due to a distribution rule. Due to that, the sets A, B, C etc, as they are defined above in the 'Theory' section, were identified. Then the network survivability simulation has begun and a time clock was activated, whereby the different sets terminated their life according to their lifetimes t_A, t_B, t_C etc, where these parameters were calculated identically to the definitions of t_A, t_B, t_C etc, in the 'Theory' section. The time duration between two successive sets failures was defined as one stage of the entire network failure. Then, for each of the network failure stages, we calculated the product of the network's giant component size and the stage's time duration—S_At_A for the first stage, S_Bt_B for the second stage, S_Ct_C for the third stage, etc. Then the network survivability was calculated to be the sum of the products—I = S_At_A + S_Bt_B + S_Ct_C + ....

In the second part of each simulation realization, our algorithm was activated. For each set of the network's nodes the ratio $\frac{S}{n}$ was calculated. We chose the set in which this ratio was maximal, and allocated the entire lifetime budget uniformly between this set's nodes. Then the network survivability simulation has begun and a time clock was activated. Obviously, the entire network collapsed after the chosen set's lifetime was passed. The network survivability was calculated to be the product of the chosen set's giant component size by the chosen set's lifetime.

Figures 4(a₁) and (a₂) present simulation results for ER network with N = 10⁴ nodes and mean degree ⟨k⟩ = 2. The nonuniform lifetime allocating rule is—each node receives lifetime with proportion to its degree. Figure 4(a₁) is a graph of the network survivability I vs the time during the network failure, both for the nonuniform lifetime allocation (blue) and the uniform lifetime allocation (red). For the points on the t axis, a bar is drawn whose height represents the value of the accumulated network survivability from the beginning of the network failure until time t, which is ${\int }_{0}^{t}S\left({t}^{\prime }\right)\mathrm{d}{t}^{\prime }$. We see that although in the nonuniform allocation the network life spans a longer time than in the uniform allocation, the total survivability of the uniform allocation (0.97) is greater than of the nonuniform allocation (0.84). This result illustrates that against any proposal of nonuniform lifetime allocation between the network's nodes, a proposal of uniform lifetime allocation can be found, on which the network survivability is greater.

Zoom In Zoom Out Reset image size

For a detailed understanding of the network failure process, a plot of the giant component size vs the time during the network failure, is presented in figure 4(a₂), both for nonuniform lifetime allocation (blue) and for uniform lifetime allocation (red). In the nonuniform lifetime allocation, the network survivability is spanned over four stages, each of them is represented by a blue rectangle. The giant component size at each stage is written above the relevant rectangle, and the time duration of each stage is represented by braces below the t axis, that are spanned over the stage's lifetime, and is written below the braces [In the first stage for example, S_A = 0.79 and ${t}_{A}^{\mathrm{n}\mathrm{u}}=0.49$ (the superscript 'nu' notes nonuniform)]. Set A, in the first stage, includes all the network's nodes (except nodes with degree 0 that obviously are not allocated with lifetime). Set B, in the second stage after the nodes with degree k = 1 (that receive the minimum lifetime) are failed, includes nodes with degrees greater than or equal to 2. Set C, in the third stage, includes nodes with degrees greater than or equal to 3 and set D includes nodes with degrees greater than or equal to 4. The next stages are not considered, since after the termination of the fourth stage where nodes with degree 4 are failed, the network is fragmented and the giant component does not exist in the network. Hence, the contribution of these stages to the network survivability is 0. We get for the network survivability with nonuniform lifetime allocation - $I={S}_{A}{t}_{A}^{\mathrm{n}\mathrm{u}}+{S}_{B}{t}_{B}^{\mathrm{n}\mathrm{u}}+{S}_{C}{t}_{C}^{\mathrm{n}\mathrm{u}}+{S}_{D}{t}_{D}^{\mathrm{n}\mathrm{u}}$.

The uniform lifetime allocation according to our theory is represented by the red rectangle. Our algorithm found that the maximum of the ratio $\frac{S}{n}$ is obtained in set B. This result is shown in the inset of the figure, which is a bar graph with points for the sets A, B, C and D on the horizontal axis, and a bar for each set whose height represents the set's ratio $\frac{S}{n}$. We see that the highest bar belongs to set B with a value of 0.97. Accordingly, the lifetime budget is fully allocated uniformly between set B nodes, and the network fails after one stage that is the failure of set B nodes. The giant component size in this only stage is written above the red rectangle S_B = 0.58, and the time duration of this stage is ${t}_{B}^{\mathrm{u}}=1.68$ (the superscript 'u' notes uniform) and is represented by braces below the t axis. We get for the network survivability with uniform lifetime division - $I={S}_{B}{t}_{B}^{\mathrm{u}}$.

Figures 4(b₁) and (b₂) present simulation results for ER network with N = 10⁴ nodes and mean degree ⟨k⟩ = 2.5. The nonuniform lifetime allocation is implemented according to percentages of the total lifetime, such that 10% of the total lifetime is allocated uniformly between the nodes with degree 1, 15% of the total lifetime is allocated uniformly between the nodes with degrees 2 and 3, and the remained 75% is allocated uniformly between the nodes with degrees greater than or equal to 4. An interesting point is that this allocation causes the lifetime of a single node with degree 1 to be greater than the lifetime of a single node with degree 2 or 3, although the total lifetime of nodes with degree 1 (10%) is less than the total lifetime of nodes with degrees 2 and 3 (15%). This is because the network contains significantly more nodes with degrees 2 and 3 than nodes with degree 1. As a result, set A contains all the network's nodes except nodes with degree 0, set B contains nodes with degree 1 and degrees that are greater than or equal to 4, after the nodes with degrees 2 and 3 of set A − B are failed, and set C contains nodes with degrees greater than or equal to 4. Figure 4(b₁) illustrates again that against the nonuniform lifetime allocation proposal with network survivability value of 0.87, our proposal with uniform lifetime allocation is greater with value of 0.96.

Figures 5(a) and (b) present simulation results for SF network with N = 2.5 × 10⁴ nodes and γ = 2.6. The nonuniform lifetime allocation is implemented according to percentages of the total lifetime. Each of the followings sets—nodes with degree 1, nodes with degree 2, nodes with degrees 3 and 4, nodes with degrees between 5 and 8 and nodes with degrees greater than or equal to 9—is allocated by 20% of the total lifetime budget. Figure 5(b) presents an interesting result, where our algorithm found that maximum survivability is achieved by uniform lifetime allocation on set E that contains the high degrees, where according to SF network properties contains a very small part of the network's nodes. This is explained due to the fact that the probability of all the high degrees nodes of set E to be clustered in one component is very high. Therefore, all, or at least most, of set E nodes are part of its giant component, and the ratio $\frac{{S}_{E}}{{n}_{E}}$ becomes greater than this ratio in the other sets. Another interesting point is the very long time duration of network survivability in this state, that is represented by the very long length of the red rectangle in figure 5(b). This is due to the fact that the very small combination of nodes in set E, receives 20% of the total lifetime, equally to the other sets, such that each node in this set receives a relative high amount of lifetime. Simulations were also implemented on the power-grid real network. See the results in the SI (http://stacks.iop.org/NJP/22/073011/mmedia).

Zoom In Zoom Out Reset image size

In this work we developed a method for maximizing the robustness of a network in the dynamic approach, where the network functionality during the entire nodes removal event is considered, and according to a survivability function was presented in equation (1). Assuming we know the network degree distribution only without knowing the network topology and the links between the nodes, we proved analytically that given a budget of lifetime for allocating between the network's nodes, the way of achieving maximum for the network survivability function, is by a choice of a set of the network's nodes in which the ratio between its giant component size and its size is maximal, and an allocation of the entire lifetime uniformly between the nodes of this set. We hope that these findings could be useful at the stage of network design, as a tool for improving network survivability.