Abstract
Matter-wave interferometry offers insights into fundamental physics and provides a precise tool for sensing. Improving the sensitivity of such experiments requires increasing the time particles spend in the interferometer, which can lead to dephasing in the presence of velocity-dependent phase shifts such as those produced by the Earth's rotation. Here we present a technique to passively compensate for the Coriolis effect using gravity, without the need for any moving components. We demonstrate the technique with fullerenes in a long-baseline molecule interferometer by measuring the gravitational and Coriolis phase shifts and obtaining the maximum visibility one would expect in the absence of the Coriolis effect.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Increasing the interrogation time in matter-wave interferometers is desirable for a range of applications, including the demonstration of macroscopic superpositions [1–3], inertial sensing [4–7], weak equivalence principle tests [8], and precision measurements of the fine-structure constant [9] and the gravitational constant [10]. Long interaction times can be achieved via particle slowing or trapping [11], moving to a free-fall environment [12–14], or increasing the interferometer baseline [3].
A major challenge facing ground-based interferometers is the Coriolis effect, which reduces the interference fringe visibility for slow non-monochromatic beams. Various approaches for compensating the Coriolis force or employing a Sagnac phase as compensation for another dispersive force have been proposed [15, 16] and employed [17–19], for example via mechanical actuation of the gratings. The Coriolis compensation scheme presented here requires no moving components which may induce vibrations nor velocity-resolved measurements which require increased integration times, making it particularly well-suited for long-baseline molecule interferometry.
Gravitational and Sagnac phases were first observed in a series of neutron interferometry experiments [20–22] and later in atom and electron interferometers [23, 24]. Here we use the gravitational phase induced by a tilt of our interferometer to compensate the phase due to the Earth's rotation. We demonstrate this compensation technique with the long-baseline universal matter-wave interferometer (LUMI), a two-meter long Talbot–Lau interferometer which is compatible with both supersonic atomic beams and slow molecular beams. Coriolis compensation is critical for reaching high interference visibilities in the LUMI experiment [3].
1.1. Theory
Talbot–Lau interferometers [3, 25–31] require at least two gratings. The first grating, G1, prepares transverse coherence in the beam, while G2 acts as the diffraction element. The grating structure of G2 is imprinted into the density of the molecular beam in the near field behind the second grating. It is common to employ a third grating, G3, as a transmission mask which is moved transversely to detect these fringes as a sinusoidal variation of the transmitted flux. We use a symmetric scheme, in which the gratings are spaced equidistantly by  and have equal periods
and have equal periods 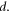
The phase of the interference fringes after traversing such an interferometer subject to a constant transverse acceleration 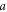 is [32, 33]
is [32, 33]
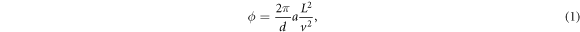
where v is the longitudinal beam velocity.
We define θ as the roll angle of the three gratings around the molecular axis, measured with respect to gravity (see figure 1). We consider 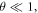 giving a transverse acceleration
giving a transverse acceleration 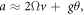 where the first term is due to the Coriolis effect and the second due to gravity. We can therefore express the total phase as
where the first term is due to the Coriolis effect and the second due to gravity. We can therefore express the total phase as
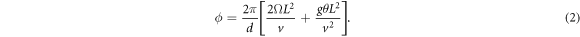
Here,  where
where 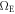 >0 is the rotational frequency of Earth and
>0 is the rotational frequency of Earth and 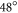 is the geographical latitude of our experiment. We neglect higher order effects such as the contribution of the centrifugal force or the vertical Coriolis shift due to the East–West velocity component.
is the geographical latitude of our experiment. We neglect higher order effects such as the contribution of the centrifugal force or the vertical Coriolis shift due to the East–West velocity component.
Figure 1. The experimental setup, showing the beam passing the three gratings, G1, G2, and G3, under the influence of gravity and the Coriolis force. The adjustable common roll angle θ is defined relative to gravity.
Download figure:
Standard image High-resolution imageVelocity-dependent phase shifts reduce the visibility of the interference pattern when averaged over the velocity distribution of the beam, which is typically broad in molecule interferometry. For a Gaussian velocity distribution 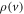 with center velocity
with center velocity  and spread σ, the velocity-averaged fringe visibility
and spread σ, the velocity-averaged fringe visibility 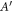 becomes
becomes
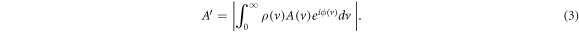
We neglect the negative tail of the Gaussian distribution in the normalization, which is a good approximation for the velocities and spreads we consider. The velocity dependence of the visibility amplitudes  assuming fixed grating open fractions, is given in [34].
assuming fixed grating open fractions, is given in [34].
We define the reduced visibility

as the ratio of the visibility in the presence of gravity and rotation to the visibility without any velocity-dependent phase shifts.
If we set  by aligning the gratings to gravity, only the Coriolis shift contributes in equation (2). In figure 2 the numerically integrated
by aligning the gratings to gravity, only the Coriolis shift contributes in equation (2). In figure 2 the numerically integrated  demonstrates the strong visibility reduction caused by the Coriolis effect alone.
demonstrates the strong visibility reduction caused by the Coriolis effect alone.
Figure 2. The reduced visibility R in LUMI for uncompensated (blue, lower curves) and compensated (red, upper curves) schemes. Solid lines are calculated numerically for a beam of C60 using equations (3) and (4), where  is maximized over θ at each velocity for the compensated case. Dashed lines are the approximate analytic expressions (5) and (7). The two pairs of lines for each scheme correspond to σ/v = 0.1 and 0.2, with the latter corresponding to the lower R values in each case.
is maximized over θ at each velocity for the compensated case. Dashed lines are the approximate analytic expressions (5) and (7). The two pairs of lines for each scheme correspond to σ/v = 0.1 and 0.2, with the latter corresponding to the lower R values in each case.
Download figure:
Standard image High-resolution imageThis can be compensated by choosing a grating roll θ such that the gravitational phase term makes 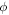 nearly constant over the velocity range of interest. The roll angle which optimizes
nearly constant over the velocity range of interest. The roll angle which optimizes 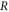 is numerically determined for each velocity, with the improved visibility shown in figure 2.
is numerically determined for each velocity, with the improved visibility shown in figure 2.
Several approximations can be made to obtain analytic forms of the reduced visibility 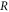 and the optimal roll angle. First, we assume
and the optimal roll angle. First, we assume 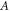 to be constant over the velocity range of interest, such that
to be constant over the velocity range of interest, such that 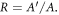
For the  case we expand
case we expand 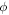 to first order around
to first order around 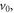 giving
giving
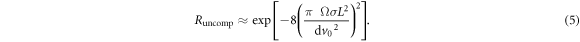
For the compensated case we choose a roll angle  such that
such that 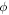 is constant to first order for
is constant to first order for 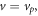 giving
giving
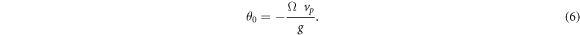
Expanding 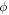 to second order around
to second order around  and setting
and setting  to achieve maximal compensation at each velocity gives
to achieve maximal compensation at each velocity gives
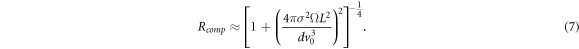
Equations (5) and (7) are plotted as the dashed lines in figure 2 together with the numerically integrated values, showing reasonable agreement especially for small velocity spreads.
1.2. Experimental setup
In the LUMI experiment, the first and third gratings are silicon nitride nano-structures with period 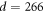 nm, while the center grating is a phase grating formed by a back-reflected 532 nm laser. Such a mixed mechanical-optical grating scheme is advantageous for observing interference of slow beams of highly polarizable molecules [28]. C60 fullerenes were used for these measurements since they form a stable thermal beam and their optical polarizability at 532 nm is known [35]. Detection was via electron impact ionization followed by quadrupole mass selection and ion counting.
nm, while the center grating is a phase grating formed by a back-reflected 532 nm laser. Such a mixed mechanical-optical grating scheme is advantageous for observing interference of slow beams of highly polarizable molecules [28]. C60 fullerenes were used for these measurements since they form a stable thermal beam and their optical polarizability at 532 nm is known [35]. Detection was via electron impact ionization followed by quadrupole mass selection and ion counting.
We studied the Coriolis compensation mechanism by measuring the relative contributions of gravity and the Coriolis force to the phase of the interference fringes as a function of velocity. This was done by modulating the beam with a periodic pseudo-random sequence [36] and cross-correlating the beam signal with the sequence to retrieve the time-of-flight distribution. The third grating was moved transversely and a time-of-flight measurement taken at each position step.
This procedure yields an intensity map of the flux as a function of both transverse grating position and time, such as those shown in figures 4(a)–(c). Each line-cut of the time axis contains a small spread of times determined by the resolution of the time-of-flight measurement. For typical parameters this spread is 3% full-width-at-half-maximum, small enough that velocity averaging over a given line-cut can be safely neglected in the data analysis.
2. Results
Coriolis compensation allows high interference visibility to be retained when interference data is integrated over all velocities in the beam. This is illustrated in figure 3, which shows the improvement in the integrated interference visibility when the gratings are rolled to 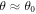 as compared to the uncompensated case of
as compared to the uncompensated case of 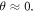 A visibility of 21% for an optical grating power of 7 W would be expected in the absence of the Coriolis effect, while 15% was achieved with compensation, despite a large velocity spread of 0.44
A visibility of 21% for an optical grating power of 7 W would be expected in the absence of the Coriolis effect, while 15% was achieved with compensation, despite a large velocity spread of 0.44 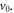 This reduced visibility
This reduced visibility 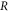 of 0.65 is in reasonable agreement with the predicted value of 0.73 for the given parameters. The lesser degree of experimental compensation compared with theory can likely be explained by a slight relative roll misalignment to which the visibility is very sensitive when working with vertically extended beams [35], as were required for the large velocity spread.
of 0.65 is in reasonable agreement with the predicted value of 0.73 for the given parameters. The lesser degree of experimental compensation compared with theory can likely be explained by a slight relative roll misalignment to which the visibility is very sensitive when working with vertically extended beams [35], as were required for the large velocity spread.
Figure 3. Comparison of the uncompensated (blue) and compensated (red) interference curves, showing the visibility improvement available with the technique. A small downward drift of the counts for the uncompensated case has been corrected. These curves are obtained by integrating the velocity-resolved curves in figures 4(b) and (c) which have a peak velocity of 218 m s−1 and a spread of 95 m s−1.
Download figure:
Standard image High-resolution imageTo analyze the compensation systematically we performed a series of time-resolved interference scans as a function of θ. The roll was adjusted for the three gratings equally in order to maintain their relative alignment while introducing a gravitational phase shift.
A subset of these measurements is shown in figures 4(a)–(c), in which the gravitational phase shift, which dominates at large roll angles, is visible as a shearing of the contours. The power of the optical grating was held fixed at 7 W for these measurements.
Figure 4. (a) Time-resolved interference signal with the common roll of all gratings set to  mrad, where
mrad, where 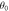 is the roll angle which provides near-optimal compensation for the velocity distribution in these experiments. (b) As (a), but with
is the roll angle which provides near-optimal compensation for the velocity distribution in these experiments. (b) As (a), but with 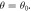 (c) As (a), but with
(c) As (a), but with 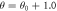 mrad. (d) A zoomed-in plot of the phase versus velocity curve at the optimal roll
mrad. (d) A zoomed-in plot of the phase versus velocity curve at the optimal roll 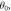 showing a turning point at about 170 m s−1. The shaded region denotes 68% confidence intervals of the fitted phases and the solid line is a fit to equation (2). The absolute phase is arbitrarily set to zero at the starting velocity for visual clarity. (e) Extracted phase for the various roll angles with respect to
showing a turning point at about 170 m s−1. The shaded region denotes 68% confidence intervals of the fitted phases and the solid line is a fit to equation (2). The absolute phase is arbitrarily set to zero at the starting velocity for visual clarity. (e) Extracted phase for the various roll angles with respect to 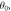 from top to bottom, −1.0, −0.5, 0, +0.5, +1.0 mrad. Solid lines are fits to equation (2), with the various offset angles. Every 20th point is shown for clarity, and error bars are too small to be visible on this scale.
from top to bottom, −1.0, −0.5, 0, +0.5, +1.0 mrad. Solid lines are fits to equation (2), with the various offset angles. Every 20th point is shown for clarity, and error bars are too small to be visible on this scale.
Download figure:
Standard image High-resolution imageTo extract the phase shift as a function of velocity we take horizontal line-cuts of the time-resolved interference signal and fit a sine curve to each of these cuts. This is done first for the optimal-roll setting 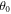 shown in figure 4(b), with the extracted phases shown in figure 4(d). The value of
shown in figure 4(b), with the extracted phases shown in figure 4(d). The value of 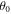 used here was determined by an optimization of the visibility as a function of roll, rather than calculating it via equation (6), since there was some uncertainty regarding the initial grating rolls with respect to gravity.
used here was determined by an optimization of the visibility as a function of roll, rather than calculating it via equation (6), since there was some uncertainty regarding the initial grating rolls with respect to gravity.
The turning point observed at about 170 m s−1 indicates optimal compensation near this velocity. It is also clear evidence that the observed phase shifts are not merely gravitational, as these would be monotonically increasing or decreasing with velocity. We fit equation (2) to the observed phase shifts with an additional constant offset and the roll 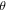 as free parameters. The best-fit value of
as free parameters. The best-fit value of 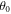 is -0.96 mrad, which provides optimal Coriolis compensation at a velocity of 173 m s−1, as estimated from equation (6).
is -0.96 mrad, which provides optimal Coriolis compensation at a velocity of 173 m s−1, as estimated from equation (6).
The other roll settings of 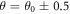 mrad and
mrad and 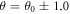 mrad can be similarly analyzed. The results are shown in figure 4(e). With
mrad can be similarly analyzed. The results are shown in figure 4(e). With 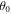 fixed, the only free parameter is the arbitrary constant phase offset. The fits show excellent agreement with the data.
fixed, the only free parameter is the arbitrary constant phase offset. The fits show excellent agreement with the data.
Similar experiments can also be used to measure local gravity or perform equivalence principle tests if 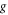 in equation (2) is left as a free parameter.
in equation (2) is left as a free parameter.
3. Conclusion
A passive scheme to compensate for the velocity-dependent Coriolis force is demonstrated in a two-meter long Talbot–Lau molecule interferometer. The scheme uses a grating roll offset to give a gravitational phase shift which compensates the Coriolis shift in the velocity band of interest. The technique provides a simple and robust means to compensate for the Coriolis effect in matter-wave interferometers with non-monochromatic beams.
Acknowledgments
This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (Grant Nr. 320694), the Austrian Science Fund (FWF) within program P-30176 and W1210-N25.







