Abstract
Due to their excellent structural flexibility, low dimensional materials allow to modulate their properties by strain engineering. In this work, we illustrate the phonon calculation of deformed quasi-one dimensional nanostructures involving inhomogeneous strain patterns. The key is to employ the generalized Born–von Karman boundary conditions, where the phonon states are characterized with screw and rotational symmetries. We use wurtzite ZnO nanowire (NW) as a representative to demonstrate the validity and efficiency of the present approach. First, we show the equivalence between the phonon dispersions obtained with this approach and that obtained with standard phonon approach. Next, as an application of the present approach, we study the phonon responses of ZnO NWs to twisting deformation. We find that twisting has more influence on the phonon modes resided in the NW shell than those resided around the NW core. For phonon at the NW shell, the modes polarized along the NW axis is more sensitive to twisting than those polarized in the NW radial dimension. Twisting also induces significant reduction in group velocities for a large portion of optical modes, hinting a non-negligible impact on the lattice thermal conductivity. The present approach may be useful to study the strain-tunable thermal properties of quasi-one dimensional materials.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 4.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Due to their large aspect ratio, quasi-one dimensional nanostructures such as nanotubes (NTs) [1–4], nanoribbons (NRs) [5–9], and nanowires (NWs) [10–13] are usually structurally flexible, and thus can sustain high level of strain. This feature offers a strain way to tailor electronic properties of these materials, which often involves inhomogeneous strain patterns. For example, it was shown that an axial twist could realize metal-to-insulator transition in carbon NTs (CNTs) [14, 15] and graphene NRs (GNRs) [16–18]. On the other hand, in deformed ZnO [19, 20] and other semiconductor NWs [21–23], their fundamental bandgaps could be also tuned to a great extent. Strain can also alter the architecture of the entire electronic spectrum of the system. As a striking example, it was shown that bending [24] or twisting [25] deformation could induce Landau quantization of electronic states. Can thermal behaviors of materials be also effectively modulated by inhomogeneous strains? In essence, this relies on how lattice vibrates at the presence of structural deformations and can be addressed by performing phonon calculations. However, there are difficulties for this purpose, assembly associated with the computational bottleneck.
The standard phonon calculation of crystalline materials within harmonic approximation employs the translational symmetry, and the lattice wave is discretized by imposing the so-called Born–von Karman boundary conditions [26, 27]. For a quasi-one dimensional structure with a unit cell of N0 atoms
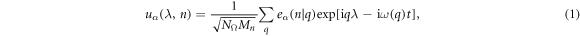
where, uα(λ, n) is the displacement of atom n in λth replica of the unit cell along the α direction. −π < q ≤ π is the wave vector along the axial direction. Mn is mass of atom n. NΩ indicates the size of supercell. ω(q) is q-dependent angular frequency. 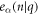 is the normal mode of lattice wave. The motion equations are then obtained as
is the normal mode of lattice wave. The motion equations are then obtained as
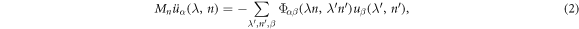
where 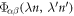 is the harmonic force constant indicating the force on atom n in λth unit cell along the α direction induced by moving atom
is the harmonic force constant indicating the force on atom n in λth unit cell along the α direction induced by moving atom 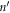 in
in 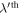 unit cell along the β direction. Note that α, β = x, y, z. Substituting equation (1) into (2) with
unit cell along the β direction. Note that α, β = x, y, z. Substituting equation (1) into (2) with ![${\sum }_{\lambda }\exp [{\rm{i}}(q^{\prime} -q)\lambda ]={N}_{{\rm{\Omega }}}{\delta }_{q^{\prime} q}$](https://content.cld.iop.org/journals/1367-2630/22/2/023004/revision2/njpab6da1ieqn5.gif) , one obtains
, one obtains

where
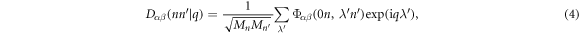
is the dynamical matrix with a dimension of 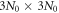 . The angular frequency ω(q) and vibration mode
. The angular frequency ω(q) and vibration mode  are both obtained by diagonalizing
are both obtained by diagonalizing
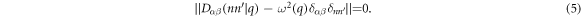
From the above theoretical framework, one sees that in phonon calculations, most computational efforts are devoted to the determination of the harmonic force constant Φαβ(λn, λ'n'), and solving equation (5). For a predictive description of lattice vibration,  is desired to be determined quantum mechanically. This means that one needs to calculate electronic structure by solving the eigenvalue problem with a supercell of
is desired to be determined quantum mechanically. This means that one needs to calculate electronic structure by solving the eigenvalue problem with a supercell of  atoms for each of the
atoms for each of the 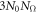 degrees of freedoms. Therefore, the computational expense of phonon calculation is directly related to the size of unit cell. For a system with inhomogeneous strains, such as twisting and bending, the unit cell has a size (N0) same with the size of the distorted motif. As a consequence, phonon calculation of such a large number of atoms with accurate quantum mechanical approach is not within the reach given the state-of-art algorithm.
degrees of freedoms. Therefore, the computational expense of phonon calculation is directly related to the size of unit cell. For a system with inhomogeneous strains, such as twisting and bending, the unit cell has a size (N0) same with the size of the distorted motif. As a consequence, phonon calculation of such a large number of atoms with accurate quantum mechanical approach is not within the reach given the state-of-art algorithm.
In this work, we show that the obstacle can be overcome by adopting a generalization of the Born–von Karman boundary conditions. Using wurtzite ZnO NWs as a representative, we present all the theoretical details and validate the theory by showing the equivalence between the phonon dispersions obtained with the new approach and that obtained with standard method. To showcase the applicability, we study the responses of phonon spectra of ZnO NWs to twisting deformation, which has never been discussed before. Our calculation reveals that phonon modes at different locations along the NW radial dimension exhibit distinct responses to twist. For modes at the NW shell, they usually adopt relatively large thermal shifts; On the contrary, for modes around the NW core, the thermal shifts are small, indeed. We also find that the modes polarized along the NW axis is more sensitive to twisting than those polarized in the NW radial dimension. In addition, twisting also induces significant reduction in group velocities for a large portion of optical modes, hinting a decrease of the lattice thermal conductivity.
2. Method
For a quasi-one dimensional structure, twisting deformation breaks the translational symmetry which the standard phonon calculation approaches rely on. Here we instead make recourse of screw and rotational symmetries to address the problem. As an illustration, we present a structural description of ZnO NWs by exploring the screw and rotational symmetries, and with this, we establish the framework for the phonon calculation.
2.1. Structure of ZnO NWs
We consider wurtzite ZnO NWs grown along [0001] direction with a translation vector T, from which a 48-atom translation unit cell can be identified, see figure 1(a). Besides translation, the NWs also has a three-fold rotational symmetry with a θ2 = 120° rotational angle, figure 1(a) and a screw symmetry, where the screw vector 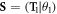 with a translation
with a translation 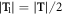 and a rotation θ1 = 60°, figure 1(b). In this way, the NWs can be alternatively described with a primitive motif (heavy-colored atoms in figure 1(a)) containing only 8 atoms using these symmetry components
and a rotation θ1 = 60°, figure 1(b). In this way, the NWs can be alternatively described with a primitive motif (heavy-colored atoms in figure 1(a)) containing only 8 atoms using these symmetry components
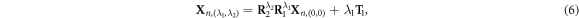
where, Xn, (0,0) denotes the positions of atoms inside the primitive motif. R1 = R1(θ1) is an rotation around the [0001] axis for the angle θ1 and R2 = R2(θ2) is an rotation around the [0001] axis for the angle θ2. λ1 and λ2 are both integers. 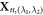 denotes the positions of atoms inside the replica of the primitive motif, indexed by (λ1, λ2).
denotes the positions of atoms inside the replica of the primitive motif, indexed by (λ1, λ2).
Figure 1. (a) Top view (left) and side view (right) for a translational unit cell of a wurtzite ZnO NW containing 48 atoms. The NW has a three-fold rotational symmetry. The 8 atoms in heavy colors constitute the primitive motif considering both screw and rotational symmetries. The balls in gray and red colors denote zinc and oxygen atoms, respectively. (b) Side view of ZnO NW showing the screw vector  with θ1 = 60°. T = 2T1 is translation vector.
with θ1 = 60°. T = 2T1 is translation vector.
Download figure:
Standard image High-resolution image2.2. Phonon calculation
To simplify the eigenvalue problem of phonon, it is highly desirable to fully consider the symmetries explored above. In one dimension, screw and rotation both around the same axis commute with each other, or equivalently, share the same eigenfunctions [28]. The screw  has an eigenvalue of
has an eigenvalue of 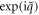 by imposing the helical boundary conditions, and rotation
by imposing the helical boundary conditions, and rotation 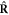 has an eigenvalue of exp(ilθ2) by imposing the cyclic boundary conditions. Note that
has an eigenvalue of exp(ilθ2) by imposing the cyclic boundary conditions. Note that 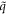 is the helical quantum number with
is the helical quantum number with 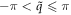 and l is rotational quantum number with l = 0, ..., 2π/θ2 − 1. This way, we have two good quantum numbers,
and l is rotational quantum number with l = 0, ..., 2π/θ2 − 1. This way, we have two good quantum numbers, 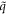 and l to label a phonon state and the atomic displacement due to lattice vibration is now [29–36]
and l to label a phonon state and the atomic displacement due to lattice vibration is now [29–36]
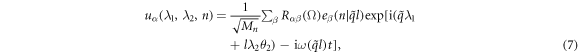
where Rαβ is the rotational matrix elements around the [0001] axis with a rotational angle of Ω = λ1θ1 + λ2θ2. 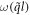 is angular frequency and
is angular frequency and 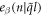 is the eigenvector indicating the vibration of atom n along β direction.
is the eigenvector indicating the vibration of atom n along β direction.  is the symmetry-adapted vector of normal mode (
is the symmetry-adapted vector of normal mode (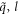 ). Accordingly, the equation of motion reads
). Accordingly, the equation of motion reads
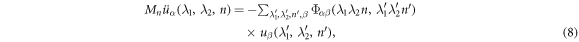
where  is force constant indicating the force in α direction acting on atom n in the replica of primitive motif, indexed by (λ1, λ2) contributed by the motion in β direction of atom
is force constant indicating the force in α direction acting on atom n in the replica of primitive motif, indexed by (λ1, λ2) contributed by the motion in β direction of atom 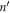 in the replica of the primitive motif indexed by
in the replica of the primitive motif indexed by 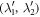 . Substituting equation (7) into (8) gives
. Substituting equation (7) into (8) gives
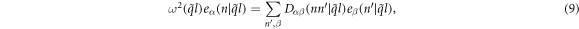
where
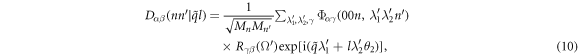
is the dynamical matrix of normal mode (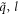 ). Note that
). Note that 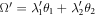 and
and 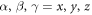 .
.
It can be seen that the harmonic force constant, Φ, is the key quantity to construct the dynamical matrix. Obtaining accurate Φ needs a reliable total energy that can be obtained by carrying out quantum mechanical calculation in general. For crystals with translational symmetry, such calculations are routine now [37, 38]. However, standard methods encounter difficulties in dealing with crystals with screw and rotational symmetries. We indicate that this obstacle can be well overcome by a generalized Bloch scheme [39, 40] that are formulated with these symmetry operations when solving electronic eigenvalue problem.
This way, for a given structure (NT, NR, and NW), the total energy (Etot) is obtained by carrying out electronic structure calculation using the generalized Bloch theorem coupled density-functional tight-binding [41]. With this, Φ is obtained as

To ensure the convergence of the obtained Φ, a supercell with sufficient large size (NΩ) is chosen and the finite difference, equation (11), is evaluated for each atom inside the supercell.
2.3. Phonon spectrum of ZnO NWs
We now use the ZnO NWs shown in figure 1(a) as an example to demonstrate the validity and efficiency of the new approach. Before proceeding, we note that in order to make a direct comparison with standard phonon calculation, a new representation that explicitly accounts for translation is adopted to describe the structure of ZnO NWs
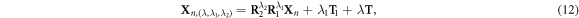
where, T is the translation vector of ZnO NWs. Rotational matrix R1 with rotation angle θ1 is the rotational component of the screw vector S, and T1 is the translation component. R2 is rotational matrix with θ2 for the rotation operation. 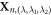 is the replica of the primitive motif Xn. λ1 = 0, 1, λ2 = 0, 1, 2, and
is the replica of the primitive motif Xn. λ1 = 0, 1, λ2 = 0, 1, 2, and 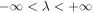 . This way, repeated screw and rotation operations on the primitive motif generate the translational unit cell, and the infinite long NW is obtained by repeatedly applying translation operation T to the translational unit cell. Accordingly, equation (7) of the displacement should be modified slightly as [29–36]
. This way, repeated screw and rotation operations on the primitive motif generate the translational unit cell, and the infinite long NW is obtained by repeatedly applying translation operation T to the translational unit cell. Accordingly, equation (7) of the displacement should be modified slightly as [29–36]
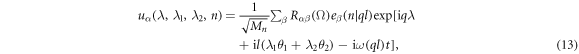
where, quantum number l = 0, 1, ..., 5 and −π < q ≤ π. This way, we have performed phonon calculation of the ZnO NWs with the 8-atom motif. Figure 2 plots the obtained phonon dispersions as function of wave vector q at each quantum number l. We find there are four acoustic phonon branches: two degenerate branches with smaller frequencies at l = 1, 5 and two nondegenerate branches with larger frequencies at l = 0. This result is in good agreement with the previous theoretical model [29] and similar to phononic properties of CNTs [42]. In addition, like bulk wurtzite ZnO [43], there is a large gap among optical phonon branches in phonon dispersions of ZnO NWs, which originates from the difference in the bonding strengths.
Figure 2. Phonon dispersions as function of wave vector q at each quantum number l calculated with the 8-atom motif of the ZnO NWs in figure 1.
Download figure:
Standard image High-resolution imageWhat is interesting is that the phonon dispersion obtained here is equivalent to the one obtained with standard phonon calculation. As a demonstration, we plot these phonon dispersions corresponding to all allowed l on the same graph. One finds that they are identical with the one computed from the 48-atom translational unit cell, see figure 3.
Figure 3. Phonon dispersions of ZnO NWs in figure 1 obtained with the present approach (left) and with standard phonon calculation (right). The colors in the left panel indicate phonon dispersions with different l.
Download figure:
Standard image High-resolution image3. Exemplification: phonon properties of ZnO nanowires under twisting
We now illustrate the applicability of the new method to strain-tunable phonon properties by calculating the phonon dispersions of the wurtzite ZnO NWs under twisting deformation. The diameter of NWs is about 2.42 nm and its primitive motif contains 192 atoms inside the translational unit cell. Twisting breaks the translational symmetry of the NWs. Instead, we describe the twisted structure using screw and the three-fold rotational symmetries with a primitive motif containing a third of atoms inside the translational unit cell (64 atoms), see figure 4(a). Thus, for equation (6), we obtain θ2 = 120°, 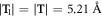 , and θ1 stands for the twist angle. This way, the twist rate is obtained as
, and θ1 stands for the twist angle. This way, the twist rate is obtained as 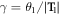 . For each considered twist rate, the NW is fully relaxed using the generalized Bloch theorem [39, 40].
. For each considered twist rate, the NW is fully relaxed using the generalized Bloch theorem [39, 40].
Figure 4. (a) Top view of twisted ZnO NWs at different twist rates: γ = 0 (strain-free) [left], γ = 10°/nm [middle], and γ = 15°/nm [right]. The translational unit cell contains 192 atoms. The primitive motif containing 64 atoms for our calculation is colored in blue. Black dashed lines indicate the structures have three-fold rotational axis. Zinc and oxygen atoms are in gray and red colors, respectively. The atomic positions indexed with n = 1, 2, 3, 4, 5 are on oxygen atoms. (b) Schematic sketch of the four bonds between an oxygen atom and its neighbors in the twisted ZnO NWs (left) and the changes of bond lengths versus position n (right) for the NWs in (a)[middle] with γ = 10°/nm. 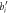 and bi (i = 1, 2, 3, 4) represent bond lengths in twisted and strain-free NWs.
and bi (i = 1, 2, 3, 4) represent bond lengths in twisted and strain-free NWs.
Download figure:
Standard image High-resolution imageDue to the constrain of cyclic boundary conditions, the rotational quantum number l = 0, 1, 2. Therefore, we calculated phonon dispersions of twisted ZnO NWs at each l with several twist rates γ. The outcomes are summarized in figure 5(a), where figure 5(a)[left] plots the phonon dispersions for strain-free ZnO NWs (γ = 0), and figure 5(a)[middle] and [right] plot the phonon dispersions of twisted ZnO NWs with γ = 10°/nm, and γ = 15°/nm, respectively.
Figure 5. (a) Phonon dispersions as function of wave vector 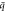 at different quantum numbers l of twisted ZnO NWs at twist rate γ = 0 (strain-free) [left], γ = 10°/nm [middle], and γ = 15°/nm [right]. (b) Group velocity vg, obtained from phonon dispersions in (a), versus frequency.
at different quantum numbers l of twisted ZnO NWs at twist rate γ = 0 (strain-free) [left], γ = 10°/nm [middle], and γ = 15°/nm [right]. (b) Group velocity vg, obtained from phonon dispersions in (a), versus frequency.
Download figure:
Standard image High-resolution imageThe variations are notable. There is a reduction of the phonon gap because that some optical branches below (above) the gap adopt upward (downward) shift, see figures 5(a) and (b). One can also see that some optical branches of highest frequencies (∼500 cm−1) also shift upwards. This indicates that these relatively large thermal shifts are from phonon modes resided at the NW shell, which is illustrated as follows. Figure 6 showcases two phonon branches that resided around the NW core. Under twisting, the thermal shifts of these modes are only of several wave numbers. On the contrary, for those phonon branches that resided at the NW shell as shown in figure 7, the thermal shifts can be large. We attribute the distinct variations of phonon modes to the twist-induced structural distortions. Figure 4(b) shows the bond lengths between the referred atom and its four neighbors for the atom at different atomic sites, n = 1, 2, 3, 4, 5 in a twisted NW. Apparently, for the atomic sites closer to the NW surface, the variations of bond length are more significant, indicating that the atomic structure are significantly distorted; while for the atomic sites near the NW core, the variations of bond length are negligible. This hints that the NW core is less distorted. Further, we also notice that the thermal shifts for phonon modes that are polarized in the NW radial dimension, as shown in figure 7(a) are smaller than those polarized along the NW axis, figure 7(b). This can be also understood by analyzing the structural distortion. A twisting deformation induces an inhomogeneous shear along the NW axis [44], while has little impact on the atomic geometry in the NW radial dimension.
Figure 6. Visualization of axial and radial components of phonon polarization vectors of modes indicated by green dots and triangles at 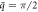 of the phonon dispersions (with l = 0) of twisted ZnO NWs at different twist rates: γ = 0 (strain-free) [left], γ = 10°/nm [middle], and γ = 15°/nm [right].
of the phonon dispersions (with l = 0) of twisted ZnO NWs at different twist rates: γ = 0 (strain-free) [left], γ = 10°/nm [middle], and γ = 15°/nm [right].
Download figure:
Standard image High-resolution imageFigure 7. Visualization of axial and radial components of phonon polarization vectors of modes indicated by (a) green dots and (b) green triangles at 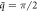 of the phonon dispersions (with l = 0) of twisted ZnO NWs at different twist rates: γ = 0 (strain-free) [left], γ = 10°/nm [middle], and γ = 15°/nm [right].
of the phonon dispersions (with l = 0) of twisted ZnO NWs at different twist rates: γ = 0 (strain-free) [left], γ = 10°/nm [middle], and γ = 15°/nm [right].
Download figure:
Standard image High-resolution imageTwisting also induces a significant lifting of the degeneracy, for example, for these phonon branches with frequencies between 100 and 150 cm−1, figure 5(a). Such disturbance also causes a flattening of the phonon branches, giving rise to a reduction in group velocities, figure 5(b). We note that twisting may also induce a reduction in phonon lifetime because that the twist-induced structural distortion may introduce more phonon-phonon scattering [45, 46]. Overall, these aspects suggest a decrease of the lattice thermal conductivity of the NW according to Peierls-Boltzmann theory [47–49].
4. Conclusions
To summarize, we present the phonon calculation within harmonic approximation of deformed quasi-one dimensional nanostructures with inhomogeneous strain pattern by using twisted ZnO NWs as an example. Because twisting breaks the translational symmetry of NWs, standard phonon calculation approaches encounter difficulty. Here, we instead make recourse of screw symmetry and rotational symmetry. We demonstrate the validity of the present approach by carrying out equivalent calculations of phonon dispersion using this approach and standard phonon approach. We showcase the applicability of this special approach by performing a case study of the phonon properties of ZnO NWs under twisting. Our calculations reveal that twisting has more influence on the phonon modes resided in the NW shell than those resided around the NW core. For phonon at the NW shell, the modes polarized along the NW axis is more sensitive to twisting than those polarized in the NW radial dimension. These variations can be attributed to the twist-induced structural distortion. Twisting also induces significant reduction in group velocities for a large portion of optical modes that should be resided in the NW shell. Therefore, for a twisted ZnO NW, although the twist deformation has little impact on the NW core, it does cause a significant reduction in the lattice thermal conductivity of the NW shell. This hints that the heat transport along the axis of a twisted ZnO NW is better confined around the ultrathin NW core. The present approach may find important applications in the area of the strain-tunable phononic and thermal properties of nanomaterials.
Acknowledgments
ZL thanks Z Zhang and Q Wu for insightful discussions. This work was supported by Ministry of Science and Technology of China under Grant No. 2017YFA0303400, the National Natural Science Foundation of China (NSFC) under Grants Nos. 11674022, 11934003, U1930402, and 41474069. DB-Z was supported by the Fundamental Research Funds for the Central Universities. Computations were carried out at Beijing Computational Science Research Center.










