Abstract
Spin-to-orbital angular momentum conversion (STOC) is a very important fundamental phenomenon governed by the conservation of total angular momentum (TAM). In optics, this conversion is usually associated with the vortex light carrying the orbital angular momentum (OAM). In this paper we demonstrate a new mechanism to achieve STOC via the interaction of an intense circularly polarized (CP) laser pulse with a solid density plasma target. We find that when a laser pulse with relativistic intensity is tightly focused, a longitudinal electric field is induced owing to the finite transverse size and profile of the laser field. Therefore, even for the normally incident CP laser, the induced longitudinal electric field can drive an oscillating vortex plasma surface to emit the vortex harmonics when the laser interacts with the plasma target. Based on simulations and theoretical analysis, we verify this harmonic generation mechanism and reveal the STOC process in the harmonic generation. It is shown that the spin angular momenta of multiple fundamental-frequency photons are converted to the OAM of a single harmonic photon because of the TAM conservation. We also discuss the dynamical symmetries in the harmonic generation process, which physically constrains the harmonic orders, as well as the angular momenta. In addition, if a vortex laser beam or a spiral phase plate is used, the OAM of the harmonic photon becomes more tunable and controllable. This study provides a deep insight into the nature of the spin–orbital interaction in optics.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The total angular momentum (TAM) of light can be separated into the spin and orbital parts of the angular momentum (SAM and OAM). Although the spin and orbital parts themselves are not true angular momenta, they are distinct and physically meaningful [1, 2]. The SAM is associated with the circularly polarized (CP) state. Each photon carries a SAM of  (
( in this paper). The OAM is related to the spatial structure of the wave front. A light beam carrying an OAM, termed a vortex beam [3], has a helical-shaped wave front and can be used as an ideal probing and manipulating tool in many fields, including optical manipulations [4–7], optical communications [8, 9], quantum information and computation [10], super-resolution microscopy [11], and even in astrophysics [12].
in this paper). The OAM is related to the spatial structure of the wave front. A light beam carrying an OAM, termed a vortex beam [3], has a helical-shaped wave front and can be used as an ideal probing and manipulating tool in many fields, including optical manipulations [4–7], optical communications [8, 9], quantum information and computation [10], super-resolution microscopy [11], and even in astrophysics [12].
In the field of optical materials, some optical elements, such as q-plates [13–18], semiconductor microcavities [19], and elements using metasurface [20–23] can be used to realize spin-to-orbital angular momentum conversion (STOC) by flipping the spin direction [24]; however, only 2σ angular momentum can be converted from SAM to OAM with these techniques. STOC can also be induced in free space for nonparaxial light because of the spin–orbit interaction [25, 26]. In this paper, we present a completely different mechanism for achieving tunable and controllable STOC based on high-order harmonic generation (HHG) when an intense CP laser pulse interacts with a solid density plasma target.
According to previous researches [27–29], a CP laser pulse normally irradiating a plasma target cannot generate harmonics, because its ponderomotive force is constant and cannot excite an oscillating current. Here, we demonstrate that it is actually possible to generate the harmonics, as the longitudinal electric field of the CP laser pulse induced by the finite focal size can drive the plasma surface to oscillate rapidly. Essentially, the longitudinal electric field is the derivative of the nonparaxial wave when the laser spot is focused to a small size. We find that the generated harmonics are vortex beams. This is because the SAM of the harmonic photon is only ±1, and the extra SAMs of the fundamental-frequency photons are converted to the OAM due to the TAM conservation. In a similar way, this conversion also exists for the interaction between the vortex beam and the spiral phase plate (SPP), where the OAMs of the harmonic photons can be tuned and controlled. This mechanism provides a deep insight into the nature of the spin and orbital angular momenta and has some potential applications in the fields of extreme ultraviolet optical vortices, optical manipulation, and quantum information.
2. Physical model and simulation results
To reveal the physical mechanism, three-dimensional (3D) Particle-in-Cell (PIC) simulations are performed with the code EPOCH [30]. We used a normalized parameter 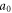 to describe the amplitude of the laser electric field,
to describe the amplitude of the laser electric field,  where E0 is the amplitude of the transverse electric field, me the electron mass, e the electron charge, ω0 is the laser frequency, and c is the speed of light in vacuum. Physically, when
where E0 is the amplitude of the transverse electric field, me the electron mass, e the electron charge, ω0 is the laser frequency, and c is the speed of light in vacuum. Physically, when 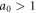 (
( corresponding to the laser intensity
corresponding to the laser intensity 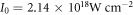 for the wavelength
for the wavelength 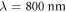 ), the laser-plasma interaction enters the relativistic regime, because the electron quiver in the laser field can reach the relativistic velocity in a laser period.
), the laser-plasma interaction enters the relativistic regime, because the electron quiver in the laser field can reach the relativistic velocity in a laser period.
2.1. The harmonics generated by CP Gaussian laser
We first use a relativistic CP Gaussian laser with wavelength λ = 800 nm and amplitude 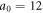 to impinge normally on a solid density plasma target, and the corresponding laser intensity is
to impinge normally on a solid density plasma target, and the corresponding laser intensity is 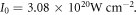 Supposing that the driving laser pulse propagates along the z-axis, its transverse electric field is expressed by
Supposing that the driving laser pulse propagates along the z-axis, its transverse electric field is expressed by ![${\boldsymbol{E}}={a}_{0}\exp \left(-{r}^{2}/{w}^{2}\right)\exp \left[-\,\mathrm{ln}\,2{\left(2\left(t-{k}_{0}z/{\omega }_{0}\right)/\tau \right)}^{2}\right]\left[\cos \left({\omega }_{0}t-{k}_{0}z\right){{\boldsymbol{e}}}_{x}+\sigma \,\sin \left({\omega }_{0}t-{k}_{0}z\right){{\boldsymbol{e}}}_{y}\right].$](https://content.cld.iop.org/journals/1367-2630/22/1/013054/revision2/njpab6873ieqn11.gif) The spot size of the laser pulse is w = 5λ and pulse duration τ = 5 T, where T is the laser period, and
The spot size of the laser pulse is w = 5λ and pulse duration τ = 5 T, where T is the laser period, and ![$\exp \left[-\,\mathrm{ln}\,2{\left(2\left(t-{k}_{0}z/{\omega }_{0}\right)/\tau \right)}^{2}\right]$](https://content.cld.iop.org/journals/1367-2630/22/1/013054/revision2/njpab6873ieqn12.gif) is the carrier envelope. The simulation box is 20λ(x)×20λ(y)×12λ(z) and is divided into 600 × 600 × 720 cells. The plasma target has a density of 10nc and occupies the region of 10λ < z< 12λ, where
is the carrier envelope. The simulation box is 20λ(x)×20λ(y)×12λ(z) and is divided into 600 × 600 × 720 cells. The plasma target has a density of 10nc and occupies the region of 10λ < z< 12λ, where 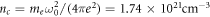 is the critical density for the wavelength of 800 nm. The critical density is defined as the plasma threshold density at which the plasma becomes opaque for an electromagnetic field with frequency
is the critical density for the wavelength of 800 nm. The critical density is defined as the plasma threshold density at which the plasma becomes opaque for an electromagnetic field with frequency 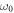 [31].
[31].
When the driving CP Gaussian laser interacts with the target, it drives a vortex plasma surface to oscillate rapidly, and harmonics are generated in the reflected light. In our discussion, we will use the SAM along the z-axis but not the helicity, because the helicity is dependent on the direction of propagation of light. However, the propagation directions are opposite for the incident laser and the emitted harmonics. Therefore, it is not convenient to use the helicity when discussing the angular momentum features. If the driving laser is a CP light beam, the generated harmonics will still be circularly polarized, as shown in figure 1, where the SAM of the driving laser is 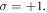 This figure shows the transverse electric fields (Ex and Ey) at the transverse position
This figure shows the transverse electric fields (Ex and Ey) at the transverse position 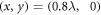 for the first (figure 1(a)), second (figure 1(c)), and third (figure 1(e)) harmonics at t = 24 T. It is found that the harmonics have Gaussian envelopes in longitudinal direction, just as the driving laser pulse. The Ex and Ey fields of the harmonics have nearly identical amplitudes, and their phase difference is π/2 (which is more clearly shown in the embedded figures). This indicates the harmonics are circularly polarized. We also find that the SAM of the harmonic is
for the first (figure 1(a)), second (figure 1(c)), and third (figure 1(e)) harmonics at t = 24 T. It is found that the harmonics have Gaussian envelopes in longitudinal direction, just as the driving laser pulse. The Ex and Ey fields of the harmonics have nearly identical amplitudes, and their phase difference is π/2 (which is more clearly shown in the embedded figures). This indicates the harmonics are circularly polarized. We also find that the SAM of the harmonic is 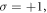 which is equal to the SAM of the incident driving laser. However, for the third harmonic shown in figure 1(e), there is a significant amplitude deviation between Ex and Ey after
which is equal to the SAM of the incident driving laser. However, for the third harmonic shown in figure 1(e), there is a significant amplitude deviation between Ex and Ey after  (marked by the black dashed line). To understand this large deviation, we plot the Ex field in the x–z plane for the harmonics, as shown in figures 1(b), (d) and (f), and find that the third harmonic becomes more and more turbulent after
(marked by the black dashed line). To understand this large deviation, we plot the Ex field in the x–z plane for the harmonics, as shown in figures 1(b), (d) and (f), and find that the third harmonic becomes more and more turbulent after 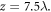 4
Figures 1(a) and (b) indicate that when the turbulent harmonic is being emitted, the main part of the driving laser has been reflected by the plasma surface and the laser intensity acting on the surface is gradually decreasing. Therefore, the current on the plasma surface becomes more and more turbulent at that moment, and the noise is produced to swamp the harmonics. The second harmonic is not affected because of the its higher intensity.
4
Figures 1(a) and (b) indicate that when the turbulent harmonic is being emitted, the main part of the driving laser has been reflected by the plasma surface and the laser intensity acting on the surface is gradually decreasing. Therefore, the current on the plasma surface becomes more and more turbulent at that moment, and the noise is produced to swamp the harmonics. The second harmonic is not affected because of the its higher intensity.
Figure 1. The transverse electric fields of first (a), second (c), and third (e) harmonics driven by the CP Gaussian laser with 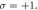 These figures indicate that the harmonic is also circularly polarized and carries the identical SAM with the driving laser. (b), (d) and (f) show the Ex field in the x–z plane of the first, second and third harmonics. It is found that the third harmonic is significantly turbulent after
These figures indicate that the harmonic is also circularly polarized and carries the identical SAM with the driving laser. (b), (d) and (f) show the Ex field in the x–z plane of the first, second and third harmonics. It is found that the third harmonic is significantly turbulent after 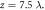
Download figure:
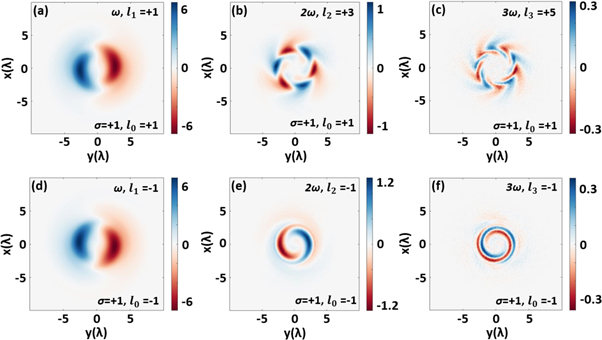
Standard image High-resolution imageFigure 2 shows the y-component of the harmonic electric field, Ey. The fundamental-frequency light is still Gaussian, as shown in figures 2(a) and (d). However, figures 2(b), (c), (e), and (f) indicate that the harmonics have vortex structures. In figures 2(a)–(c), where the driving laser carries the SAM 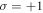 and TAM
and TAM  the OAMs of first to third harmonics are l1 = 0, l2 = +1, and l3 = +2, respectively. In figures 2(d)–(f), where the driving laser beam carries the SAM
the OAMs of first to third harmonics are l1 = 0, l2 = +1, and l3 = +2, respectively. In figures 2(d)–(f), where the driving laser beam carries the SAM 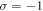 and the TAM
and the TAM 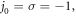 the OAMs of first to third harmonics are l1 = 0, l2 = −1, and l3 = −2. These results can be understood from the point of view of TAM conservation. In the HHG process, multiple angular momenta of fundamental-frequency photons are converted to the angular momentum of one harmonic photon. Therefore, the TAM carried by the nth harmonic photon should be n times that of the driving laser, i.e.
the OAMs of first to third harmonics are l1 = 0, l2 = −1, and l3 = −2. These results can be understood from the point of view of TAM conservation. In the HHG process, multiple angular momenta of fundamental-frequency photons are converted to the angular momentum of one harmonic photon. Therefore, the TAM carried by the nth harmonic photon should be n times that of the driving laser, i.e. 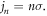 Because the SAM of a photon can only be ±1, the extra SAMs would be converted to OAM so that TAM conservation is ensured, which leads to
Because the SAM of a photon can only be ±1, the extra SAMs would be converted to OAM so that TAM conservation is ensured, which leads to 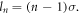 5
5
Figure 2. Transverse electric fields Ey of the harmonics driven by the CP Gaussian laser pulse. (a)–(c) are the first, second, and third harmonics at z = 6λ at 24 T generated by the CP Gaussian laser with 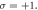 (d)–(f) are the first, second, and third harmonics at z = 6λ at 24 T generated by the CP laser with
(d)–(f) are the first, second, and third harmonics at z = 6λ at 24 T generated by the CP laser with 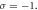
Download figure:
Standard image High-resolution image2.2. The harmonics generated by CP vortex laser
The STOC not only exists in the HHG process driven by a CP Gaussian laser, but also occurs for vortex lasers. A typical vortex laser is the Laguerre-Gaussian (LG) mode, whose transverse electric field is expressed by
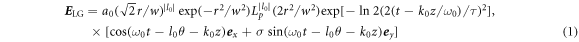
where 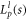 is the associated Laguerre polynomial, l0 is the OAM number, and p is the number of radial nodes in the intensity distribution. The field of the LG mode has a hollow transverse structure (
is the associated Laguerre polynomial, l0 is the OAM number, and p is the number of radial nodes in the intensity distribution. The field of the LG mode has a hollow transverse structure ( at
at  ), and its intensity has a ring-like maximum value. To ensure that the peak intensity of the LG mode is equal to the Gaussian mode above, we set the normalized parameter
), and its intensity has a ring-like maximum value. To ensure that the peak intensity of the LG mode is equal to the Gaussian mode above, we set the normalized parameter 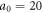 in the simulations here. The SAM of the incident laser is
in the simulations here. The SAM of the incident laser is 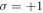 and other parameters are the same as the Gaussian pulse. Figure 3 shows the transverse electric fields, Ex and Ey, at the transverse position
and other parameters are the same as the Gaussian pulse. Figure 3 shows the transverse electric fields, Ex and Ey, at the transverse position 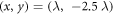 for the first (figure 3(a)), second (figure 3(c)), and third (figure 3(e)) harmonics at t = 24 T, which are driven by a CP LG laser with
for the first (figure 3(a)), second (figure 3(c)), and third (figure 3(e)) harmonics at t = 24 T, which are driven by a CP LG laser with 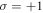 and
and  These figures indicate that the generated harmonics are still CP light carrying the same SAM as the driving laser. We also find the third harmonic becomes turbulent after
These figures indicate that the generated harmonics are still CP light carrying the same SAM as the driving laser. We also find the third harmonic becomes turbulent after 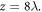
Figure 3. The transverse electric fields of first (a), second (c), and third (e) harmonics driven by the CP LG laser with 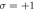 and
and 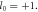 (b), (d) and (f) show the corresponding transverse electric field Ex in the x–z plane. It is found that the third harmonic becomes turbulent after
(b), (d) and (f) show the corresponding transverse electric field Ex in the x–z plane. It is found that the third harmonic becomes turbulent after 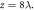
Download figure:
Standard image High-resolution imageFigure 4 illustrates the two groups of harmonics generated by the CP LG lasers with different angular momenta. The electric field components, Ey, of the harmonics plotted in figure 4 show clear vortex structures. In the first case, the driving laser pulse carries the OAM 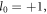 so its TAM is
so its TAM is 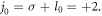 The OAMs of first to third harmonics are
The OAMs of first to third harmonics are 
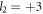 and
and 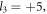 as shown in figures 4(a)–(c). In the second case shown in figures 4(d)–(f), the driving laser pulse carries the OAM
as shown in figures 4(a)–(c). In the second case shown in figures 4(d)–(f), the driving laser pulse carries the OAM 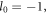 and its TAM is
and its TAM is 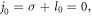 which leads the OAMs of all the harmonics to be
which leads the OAMs of all the harmonics to be 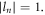 These results can be explained as follows: the driving laser carries the TAM
These results can be explained as follows: the driving laser carries the TAM 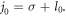 According to the TAM conservation, the TAM of the nth harmonic is given by
According to the TAM conservation, the TAM of the nth harmonic is given by 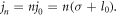 Since the SAM of the nth harmonic photon is still
Since the SAM of the nth harmonic photon is still 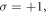 the OAM of the nth harmonic photon is given by
the OAM of the nth harmonic photon is given by 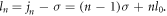 If the OAM of the driving laser is
If the OAM of the driving laser is 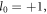 we have
we have 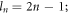 while in the second case the driving laser carries the OAM
while in the second case the driving laser carries the OAM 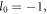 which leads to a constant OAM
which leads to a constant OAM 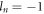 for each order of harmonics.
for each order of harmonics.
Figure 4. Transverse electric fields Ey of the harmonics driven by the CP LG laser pulse with the SAM 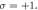 (a)–(c) are the first, second and third harmonics at z = 6λ at 24T generated by the LG laser beam with angular momenta
(a)–(c) are the first, second and third harmonics at z = 6λ at 24T generated by the LG laser beam with angular momenta 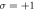 and
and 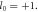 The TAM of the driving laser is
The TAM of the driving laser is 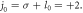 (d)–(f) are the first, second and third harmonics at z = 6λ at 24T generated by the CP LG laser with
(d)–(f) are the first, second and third harmonics at z = 6λ at 24T generated by the CP LG laser with 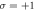 and
and 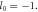 The TAM of the driving laser is
The TAM of the driving laser is 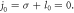
Download figure:
Standard image High-resolution imageTo clearly reveal the structure of the vector vortex of the harmonics, we plot the vector diagrams of the transverse electric fields for the first to third harmonics at the position 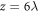 at
at 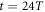 in figure 5. The angular momenta of the driving laser are
in figure 5. The angular momenta of the driving laser are  and
and 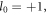 which corresponds to the case shown in figures 4(a)–(c) respectively. The arrows represent the distribution of the electric field vector, and the background color shows the harmonic intensity. The intensity distribution shows a hollow structure just like a donut. The hollow phase derives from the evolution of the phase singularity at the center point on the focal spot plane.
which corresponds to the case shown in figures 4(a)–(c) respectively. The arrows represent the distribution of the electric field vector, and the background color shows the harmonic intensity. The intensity distribution shows a hollow structure just like a donut. The hollow phase derives from the evolution of the phase singularity at the center point on the focal spot plane.
Figure 5. The vector diagrams of the transverse electric fields for the first to third harmonics at the position  at
at 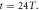 The background color shows the harmonic intensity revealing a hollow structure.
The background color shows the harmonic intensity revealing a hollow structure.
Download figure:
Standard image High-resolution imageFrom the simulation results, it is concluded that since the SAM of a photon can only be +1 or −1, to ensure the TAM conservation, the OAM of the nth harmonic photon should be
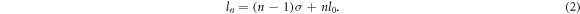
The extra SAMs of the fundamental-frequency photons will be converted to OAMs of the harmonic photons.
2.3. The transverse current on the plasma surface
During the interaction of the intense laser with the plasma, the harmonics are emitted by the transverse current on the plasma surface. To clarify the mechanism of the harmonic generation, let us focus on the details of the evolution of the transverse current. Without loss of generality, we consider the driving laser to carry the angular momenta 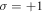 and
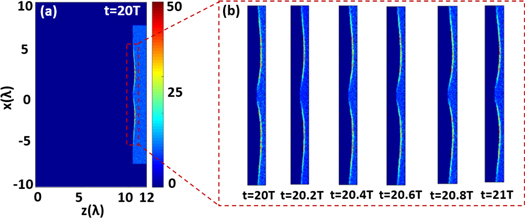
and 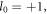 which corresponds to the situation displayed in figures 4(a)–(c). Figure 6 shows the electron density evolution on the plasma surface at the time interval between 20T and 21T. This figure displays a section on the x–z plane. We can see the surface deformation within the skin depth. The electrons are pushed by the light pressure (ponderomotive force) to accumulate on the plasma surface, which forms thin electron shells. The ring-like intensity distribution of the vortex laser drives to form two cambered surfaces shown in figure 6(b).
which corresponds to the situation displayed in figures 4(a)–(c). Figure 6 shows the electron density evolution on the plasma surface at the time interval between 20T and 21T. This figure displays a section on the x–z plane. We can see the surface deformation within the skin depth. The electrons are pushed by the light pressure (ponderomotive force) to accumulate on the plasma surface, which forms thin electron shells. The ring-like intensity distribution of the vortex laser drives to form two cambered surfaces shown in figure 6(b).
Figure 6. The plasma surface deformation within the skin depth at the time interval between 20T and 21T. The ring-like intensity distribution of the incident laser drives to form two cambered surfaces.
Download figure:
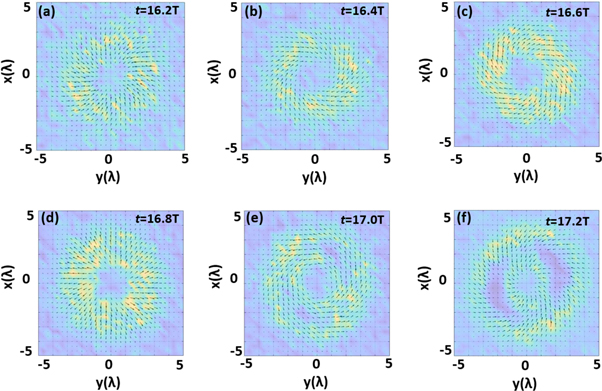
Standard image High-resolution imageFigure 7 shows the formation and evolution of the transverse current in one laser period (from 16.2T to 17.2T) when the laser interacts with the plasma target. This figure displays the current distribution on the surface located at 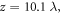 where is the position about 0.1λ depth inside the target. The arrows represent the transverse current vectors, and the background color denotes the electron density distribution. When irradiating the target, the intense laser drives the plasma electrons to produce a rotating and ring-like current first, as shown in figures 7(a)–(c), and then the current evolves into a vortex structure shown in figures 7(d)–(f). Figures 7(e) and (f) show the azimuth-dependent phase structures for the electron density, as well as the current, which are the typical features of the vortex current. This vortex current induces the emission of the vortex harmonics.
where is the position about 0.1λ depth inside the target. The arrows represent the transverse current vectors, and the background color denotes the electron density distribution. When irradiating the target, the intense laser drives the plasma electrons to produce a rotating and ring-like current first, as shown in figures 7(a)–(c), and then the current evolves into a vortex structure shown in figures 7(d)–(f). Figures 7(e) and (f) show the azimuth-dependent phase structures for the electron density, as well as the current, which are the typical features of the vortex current. This vortex current induces the emission of the vortex harmonics.
Figure 7. The formation and evolution of the transverse current on the plasma surface in one laser period (from 16.2T to 17.2T). The driving laser is the LG mode with 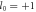 and
and 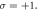 The generated current shows a clear vortex structure shown in (e) and (f).
The generated current shows a clear vortex structure shown in (e) and (f).
Download figure:
Standard image High-resolution image2.4. The spiral phase plates
If the plane plasma target is replaced with a spiral phase plate (SPP) target, more interesting phenomena occur. The SPP is an optical element with a helical surface. The thickness of the component increases smoothly with azimuthal position according to 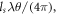 shown in figure 8. When a plane wave laser is reflected on the SPP, it can be converted into a vortex mode with the helical phase
shown in figure 8. When a plane wave laser is reflected on the SPP, it can be converted into a vortex mode with the helical phase  in azimuth [18, 32], where ls is the OAM parameter induced by the SPP. Now, let us use a vortex laser beam to normally irradiate a SPP plasma target. The TAM of the fundamental-frequency light becomes
in azimuth [18, 32], where ls is the OAM parameter induced by the SPP. Now, let us use a vortex laser beam to normally irradiate a SPP plasma target. The TAM of the fundamental-frequency light becomes 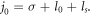 Based on a similar analysis of the above discussion, the OAM of the nth harmonic photon would be
Based on a similar analysis of the above discussion, the OAM of the nth harmonic photon would be
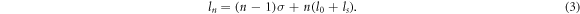
Figure 8. The schematic diagram of the spiral phase plate. The increasing thickness in azimuthal direction introduces a helical phase 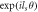 when an incident light is reflected on it. Thus, a plane wave laser can be converted into a vortex mode when it is reflected on the SPP.
when an incident light is reflected on it. Thus, a plane wave laser can be converted into a vortex mode when it is reflected on the SPP.
Download figure:
Standard image High-resolution imageTable 1 shows the simulation results under different conditions. The plane target and Gaussian pulse correspond to  and
and 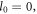 respectively. Obviously, the OAM of the harmonic photon can be tuned and controlled by changing the three parameters: σ, l0 and ls. The simulation results indicate that the OAM of the nth harmonic photon follows equation (3). These results demonstrate that the STOC occurs during the HHG process driven by a CP laser beam. Besides, it should be noted that the increasing target thickness with the azimuthal angle forms a slope structure in the azimuthal direction on the target surface. Then the laser irradiation on the target is equivalent to an oblique incidence at a small angle. It is well known that obliquely incident CP laser can drive the plasma surface to emit the harmonics [28]. So, both the oblique incidence mechanism and longitudinal electric field work to generate harmonics on the SPP target, which enhances the harmonic intensity.
respectively. Obviously, the OAM of the harmonic photon can be tuned and controlled by changing the three parameters: σ, l0 and ls. The simulation results indicate that the OAM of the nth harmonic photon follows equation (3). These results demonstrate that the STOC occurs during the HHG process driven by a CP laser beam. Besides, it should be noted that the increasing target thickness with the azimuthal angle forms a slope structure in the azimuthal direction on the target surface. Then the laser irradiation on the target is equivalent to an oblique incidence at a small angle. It is well known that obliquely incident CP laser can drive the plasma surface to emit the harmonics [28]. So, both the oblique incidence mechanism and longitudinal electric field work to generate harmonics on the SPP target, which enhances the harmonic intensity.
Table 1.
The OAMs of harmonic photons under different conditions. The SPP target with step height 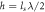 is used to produce an additional phase
is used to produce an additional phase 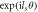 with the OAM ls when the driving laser beam is reflected. This table indicates that the OAM of the nth harmonic is
with the OAM ls when the driving laser beam is reflected. This table indicates that the OAM of the nth harmonic is 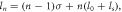 which is universally true in the HHG process.
which is universally true in the HHG process.
| SPP | SAM and OAM of the incident laser pulse | OAMs of harmonic photons | |||
|---|---|---|---|---|---|
| ls | σ | l0 | l1 | l2 | l3 |
| 0 | +1 | 0 | 0 | +1 | +2 |
| 0 | −1 | 0 | 0 | −1 | −2 |
| 0 | +1 | −1 | −1 | −1 | −1 |
| 0 | +1 | +1 | +1 | +3 | +5 |
| +1 | −1 | +1 | +2 | +3 | +4 |
| +1 | +1 | +1 | +2 | +5 | +8 |
| +1 | −1 | −2 | −1 | −3 | −5 |
| +1 | +1 | −2 | −1 | −1 | −1 |
3. Theoretical explanation
3.1. The mechanism of harmonic generation
Physically, STOC is required for the conservation of TAM. The details of how the harmonics are generated are not important when studying the above-mentioned phenomenon. Here, to understand the mechanism how the SAM is converted to OAM in our condition, let us first analyze the HHG induced by the CP laser pulse in theory. Suppose that the target surface is located at 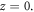 When the CP laser is reflected on the target, a standing wave field is formed outside the plasma target at
When the CP laser is reflected on the target, a standing wave field is formed outside the plasma target at 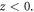 In the Coulomb gauge, the vector potential of the standing wave field can be expressed by
In the Coulomb gauge, the vector potential of the standing wave field can be expressed by

where A0 is the amplitude, 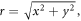 u(r) is the transverse profile and
u(r) is the transverse profile and  describes a Gaussian beam,
describes a Gaussian beam, 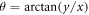 is the azimuth angle,
is the azimuth angle, 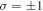 is the SAM, and k0 and ω0 are the wave vector and frequency of the laser, respectively. The corresponding electric field can be derived using
is the SAM, and k0 and ω0 are the wave vector and frequency of the laser, respectively. The corresponding electric field can be derived using 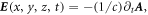
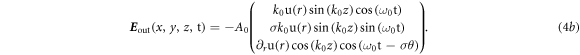
Inside the plasma target ( ), the laser field decays rapidly within a skin layer, and the vector potential is approximated by
), the laser field decays rapidly within a skin layer, and the vector potential is approximated by
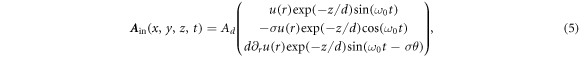
with the skin depth 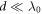 and the amplitude at the surface Ad.
and the amplitude at the surface Ad.
It is well known that the HHG is caused by the transverse current formed owing to the collective oscillating motion of electrons. In the existing HHG theory [27–29], the ponderomotive force of the laser pulse drives the plasma surface oscillation in the longitudinal direction, and the harmonic is emitted by the current on the plasma surface. For linear polarization, the ponderomotive force oscillates at twice the frequency of the driving laser; thus, only odd harmonics are generated when the driving laser impinges normally on the target. However, for circular polarization, the ponderomotive force is constant, and it cannot excite an oscillating plasma surface; therefore, no harmonic is generated.
In our scheme the mechanism of harmonic generation is completely different. When a CP laser pulse is tightly focused, a longitudinal electric field, Ez, is induced due to the finite transverse size and profile of the laser field, as expressed by equations (4) and (5). This longitudinal electric field rapidly oscillates at the frequency equaling the laser frequency, and this drives the plasma surface to oscillate at the same frequency. Consequently, both odd and even harmonics are generated. In addition, Ez has a vortex phase 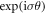 similar to an LG beam with a topological charge of 1 as shown in figure 9. This vortex phase is associated with the SAM of the laser pulse, which produces the angular momentum transfer from the driving laser to plasma surface during the laser-plasma interaction. We notice that Ez is proportional to
similar to an LG beam with a topological charge of 1 as shown in figure 9. This vortex phase is associated with the SAM of the laser pulse, which produces the angular momentum transfer from the driving laser to plasma surface during the laser-plasma interaction. We notice that Ez is proportional to 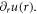 If the focal spot size is much larger than the wavelength, we find
If the focal spot size is much larger than the wavelength, we find 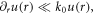 which implies the longitudinal field strength is much smaller than the transverse field, and the intensity of the harmonic is low. However, when the spot size is small and comparable with the laser wavelength, the factor
which implies the longitudinal field strength is much smaller than the transverse field, and the intensity of the harmonic is low. However, when the spot size is small and comparable with the laser wavelength, the factor 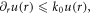 that means Ez can be comparable with the transverse electric field of the driving laser, and the harmonic intensity can be increased. In addition, Ez can also induce longitudinal ponderomotive force. But this ponderomotive force is much smaller than the electric field force,
that means Ez can be comparable with the transverse electric field of the driving laser, and the harmonic intensity can be increased. In addition, Ez can also induce longitudinal ponderomotive force. But this ponderomotive force is much smaller than the electric field force, 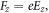 and can be neglected.
and can be neglected.
Figure 9. The longitudinal electric field, Ez, of the CP Gaussian laser beam. (a) the isosurface of Ez. (b) the transverse section of Ez at z = 6λ at 14T.
Download figure:
Standard image High-resolution imageWe know that the harmonics are generated and emitted from the oscillating transverse current, 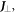 on the plasma surface. The transverse current is generated via the collective transverse quiver of the electrons driven by the transverse laser field [33]. The longitudinal component of the laser field drives the current to oscillate in the longitudinal direction, and then, the harmonics are emitted. The circular polarization makes the current acquire a vortex structure with the phase
on the plasma surface. The transverse current is generated via the collective transverse quiver of the electrons driven by the transverse laser field [33]. The longitudinal component of the laser field drives the current to oscillate in the longitudinal direction, and then, the harmonics are emitted. The circular polarization makes the current acquire a vortex structure with the phase 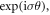 which plays a key role in the angular momentum conversion in the HHG process. To study the details of the harmonic characteristics, we need to solve the nonlinear wave equation
which plays a key role in the angular momentum conversion in the HHG process. To study the details of the harmonic characteristics, we need to solve the nonlinear wave equation
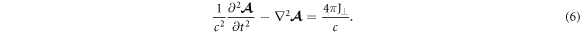
Using the Green function method, the solution to equation (6) can be expressed in an integral form
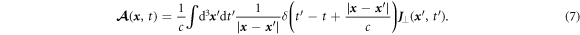
The  integral can be worked out easily by using the delta-function. If we consider that the observation point zobs is far away from the plasma surface in the z-direction and use the paraxial approximation, we get
integral can be worked out easily by using the delta-function. If we consider that the observation point zobs is far away from the plasma surface in the z-direction and use the paraxial approximation, we get 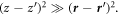 Then, the transverse contribution from
Then, the transverse contribution from 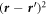 can be neglected, implying that the r-dependent transverse profile of the current is not considered in detail. In the longitudinal direction, the current is sharply localized, say at the position Z(t), with a thin shell on the plasma surface; then, the
can be neglected, implying that the r-dependent transverse profile of the current is not considered in detail. In the longitudinal direction, the current is sharply localized, say at the position Z(t), with a thin shell on the plasma surface; then, the 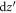 integral can be approximated
integral can be approximated
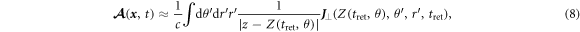
where
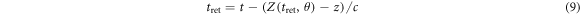
is the retarded time at the observation point 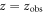 and
and 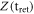 describes the longitudinal oscillation of the current. The transverse current driven by the laser field
describes the longitudinal oscillation of the current. The transverse current driven by the laser field 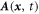 is highly nonlinear and should be described by the nonlinear fluid theory. For simplicity, we neglect some higher order relativistic terms here, and approximate this current as [28]:
is highly nonlinear and should be described by the nonlinear fluid theory. For simplicity, we neglect some higher order relativistic terms here, and approximate this current as [28]:

where 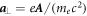 is the normalized transverse vector potential of the CP laser field. The
is the normalized transverse vector potential of the CP laser field. The  and
and  integrals are not important here, because we have neglected the transverse profile of the current in the above approximation. By inserting equations (4) and (10) into (8) we obtain an approximate solution to equation (6):
integrals are not important here, because we have neglected the transverse profile of the current in the above approximation. By inserting equations (4) and (10) into (8) we obtain an approximate solution to equation (6):
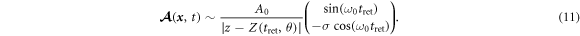
Equation (11) is a quasi-one-dimensional solution, and the transverse profile of the current has been neglected when solving the wave equation. Therefore, this solution is insufficient for explaining all the details of the harmonic features, especially the harmonic intensity and its transverse distribution. However, this theory is sufficient for describing the TAM conservation and the STOC in the HHG process, which is the focus of this work. In addition, the solution (11) indicates that the reflected light has the same polarization as the incident laser.
3.2. Spin-to-orbital angular momentum conversion and TAM conservation
Next, we focus on the physical mechanism of STOC in the HHG process. The oscillation of the plasma surface is driven by the longitudinal laser field, which is a nonlinear process. Here, for the sake of simplicity, we approximate this surface motion as a harmonic oscillation
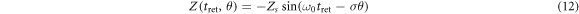
with the oscillation amplitude Zs. Inserting equations (9) into (11) the transverse vector potential of the reflected light takes the form
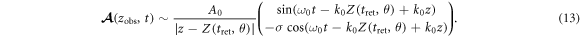
The terms 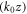 within sine and cosine are not important and can be removed, because we can set the observation point
within sine and cosine are not important and can be removed, because we can set the observation point 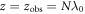 with the integer N. Inserting equations (12) into (13) the vector potential of the reflected light at the observation point is obtained. If the integer
with the integer N. Inserting equations (12) into (13) the vector potential of the reflected light at the observation point is obtained. If the integer 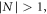 one finds
one finds 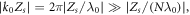 the term
the term 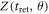 in the denominator of equation (13) is neglectable. For relativistic intensities
in the denominator of equation (13) is neglectable. For relativistic intensities  the amplitude of the plasma surface motion is very small compared with the wavelength of the laser:
the amplitude of the plasma surface motion is very small compared with the wavelength of the laser: 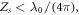 so we have
so we have 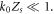 Then the vector potential of the reflected light is approximately derived
Then the vector potential of the reflected light is approximately derived
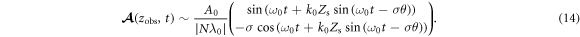
Fourier expansion of equation (14) gives two angular momentum modes of harmonic components,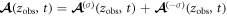
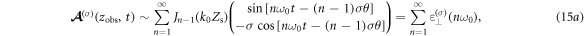
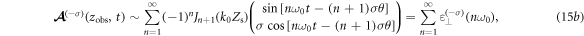
where 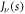 denotes the Bessel function of first kind. Equations (15a) and (15b) represent two different angular momentum modes of harmonics with OAM
denotes the Bessel function of first kind. Equations (15a) and (15b) represent two different angular momentum modes of harmonics with OAM 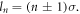 These two modes are closely related to the SAM of the generated harmonics, which can be explained by TAM conservation. Since the driving laser does not carry OAM, its total angular momentum is only determined by SAM,
These two modes are closely related to the SAM of the generated harmonics, which can be explained by TAM conservation. Since the driving laser does not carry OAM, its total angular momentum is only determined by SAM,  During the HHG process, the nth harmonic photon carries the TAM
During the HHG process, the nth harmonic photon carries the TAM 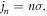 If the harmonic photon carries the same SAM as the incident photons in driving laser, the extra SAMs would be converted to OAM due to the TAM conservation, which leads to
If the harmonic photon carries the same SAM as the incident photons in driving laser, the extra SAMs would be converted to OAM due to the TAM conservation, which leads to 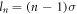 as formulated by mode
as formulated by mode 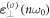 in equation (15a). This result is consistent with equation (2) for
in equation (15a). This result is consistent with equation (2) for 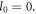 However, there is another case. If the SAM of the harmonic photon flips to
However, there is another case. If the SAM of the harmonic photon flips to 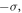 the OAM must be
the OAM must be 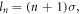 which is expressed by mode
which is expressed by mode 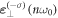 in equation (15b).
in equation (15b).
Since the amplitude of the plasma surface motion is small, 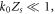 the Bessel function in equation (15) can be expressed by the limiting form:
the Bessel function in equation (15) can be expressed by the limiting form: 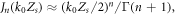 where
where 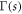 is the Gamma function. Thus, the electric field intensity of the nth harmonic mode
is the Gamma function. Thus, the electric field intensity of the nth harmonic mode 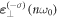 is much lower than the one of the mode
is much lower than the one of the mode 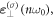 with the ratio
with the ratio 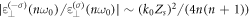
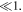 In principle, modes
In principle, modes 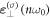 and
and 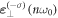 can be distinguished via the OAM spectrum. However, we cannot extract the
can be distinguished via the OAM spectrum. However, we cannot extract the 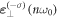 component from the simulations because its intensity is too weak. This is just the reason why the SAM of the harmonic is always the same as the one of the driving laser in our simulations. On the other hand, from figures 1 and 3 we find some small amplitude deviations between Ex and Ey of the second and third harmonics, especially for the LG driving laser. This small amplitude deviation may be a potential evidence that there exists the counter-polarized mode
component from the simulations because its intensity is too weak. This is just the reason why the SAM of the harmonic is always the same as the one of the driving laser in our simulations. On the other hand, from figures 1 and 3 we find some small amplitude deviations between Ex and Ey of the second and third harmonics, especially for the LG driving laser. This small amplitude deviation may be a potential evidence that there exists the counter-polarized mode 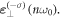 6
Physically, the superposition of modes
6
Physically, the superposition of modes 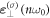 and
and 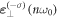 will lead to an elliptic polarization vector, so that Ex and Ey components have different amplitudes.
will lead to an elliptic polarization vector, so that Ex and Ey components have different amplitudes.
If the driving laser pulse is the CP LG beam, the vector potential outside the plasma surface is written as
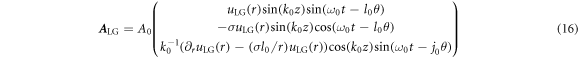
in the Coulomb gauge, where 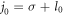 is the TAM,
is the TAM, 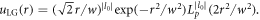 Based on the similar theoretical analysis discussed above, the two angular momentum modes of harmonic components are obtained, with the results
Based on the similar theoretical analysis discussed above, the two angular momentum modes of harmonic components are obtained, with the results
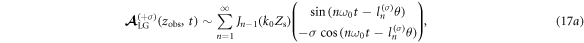

where
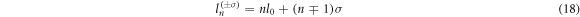
are the OAM of the nth harmonic photons for modes 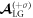 and
and 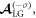 respectively, and they obey the TAM conservation. Equation (18) is well consistent with equation (2) for the mode
respectively, and they obey the TAM conservation. Equation (18) is well consistent with equation (2) for the mode 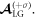 By considering the same reason as the situation of CP Gaussian laser, the harmonic with mode
By considering the same reason as the situation of CP Gaussian laser, the harmonic with mode 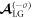 is much weaker than mode
is much weaker than mode 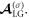 In addition, for the LG laser beam, there is an additional contribution to the longitudinal electric field:
In addition, for the LG laser beam, there is an additional contribution to the longitudinal electric field: 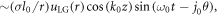 which leads to a higher field strength than the strength of Gaussian laser, especially for large l0. So, the harmonic intensity is higher with LG laser beams than Gaussian laser.
which leads to a higher field strength than the strength of Gaussian laser, especially for large l0. So, the harmonic intensity is higher with LG laser beams than Gaussian laser.
3.3. Dynamical symmetry and selection rules in HHG process
Physically, the conservation laws are closely associated with the symmetries. Regardless of any detailed considerations of the laser-plasma interaction, there are overriding symmetry constraints on the HHG process, and then the selection rules are derived [34, 35]. The electromagnetic field is a vector field, so there are two individual dynamical symmetries (DS): the polarization-dependent DS (related to the SAM conservation) and the spatially dependent DS (related to the OAM conservation). We have known that the harmonics are emitted by the transverse current on the plasma surface. Since the current is driven by the incident laser fields, it obviously has the same symmetry as the driving laser, and then the harmonic response also needs to be invariant under the same symmetry transformations.
We first consider a linearly polarized driving laser. Without loss of generality, we suppose its polarization is along the x axis, and express the vector potential as  where k0, ω0 and l0 are the wave vector, frequency and OAM, respectively. This linearly polarized laser possesses a polarization-dependent DS,
where k0, ω0 and l0 are the wave vector, frequency and OAM, respectively. This linearly polarized laser possesses a polarization-dependent DS, 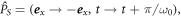 where
where  is the DS operator with eigenvalue +1 when acting on the driving laser field:
is the DS operator with eigenvalue +1 when acting on the driving laser field: 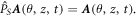 Then the harmonic
Then the harmonic 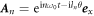 should possess the same symmetry and be invariant under the
should possess the same symmetry and be invariant under the 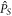 transformation:
transformation: 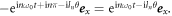 It is satisfied if and only if the harmonic order
It is satisfied if and only if the harmonic order 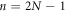 with the integer N, which is the selection rule for the HHG in the linearly polarized laser field. The
with the integer N, which is the selection rule for the HHG in the linearly polarized laser field. The  symmetry implies that the SAM is conserved in the HHG process (here the SAM can be regarded as zero for the linear polarization), and only the odd harmonics are generated. The linearly polarized laser field also possesses a spatially dependent DS,
symmetry implies that the SAM is conserved in the HHG process (here the SAM can be regarded as zero for the linear polarization), and only the odd harmonics are generated. The linearly polarized laser field also possesses a spatially dependent DS, 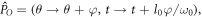 with the eigenvalue +1:
with the eigenvalue +1: 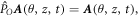 where φ is an arbitrary rotation angle. The invariance of the harmonics under
where φ is an arbitrary rotation angle. The invariance of the harmonics under 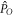 transformation leads to
transformation leads to 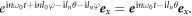 φ is an arbitrary angle, and thus the OAM of the harmonics is derived,
φ is an arbitrary angle, and thus the OAM of the harmonics is derived, 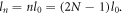 The
The 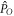 symmetry implies the OAM conservation in the HHG. If the driving laser is a plane wave with
symmetry implies the OAM conservation in the HHG. If the driving laser is a plane wave with 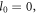 the generated harmonics also do not carry the OAM.
the generated harmonics also do not carry the OAM.
For the case of the CP plane wave, there is a rotation symmetry for the polarization vector. When a polarization-dependent DS operator, 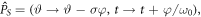 acts on the CP light
acts on the CP light 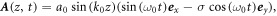 the light field is invariant. Here
the light field is invariant. Here 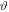 is the azimuthal angle of the polarization vector. It implies that the SAM is conserved in the HHG process, and the harmonics must also be circularly polarized. The invariance of the harmonic,
is the azimuthal angle of the polarization vector. It implies that the SAM is conserved in the HHG process, and the harmonics must also be circularly polarized. The invariance of the harmonic, 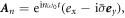 under the same
under the same 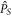 transformation requires
transformation requires 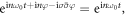 where
where 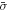 is the SAM of the harmonic photon. It is satisfied if and only if
is the SAM of the harmonic photon. It is satisfied if and only if 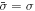 and
and 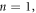 which indicates the harmonics are forbidden by the DS at CP plane wave.
which indicates the harmonics are forbidden by the DS at CP plane wave.
The situation is completely different when the focal spot of the intense CP laser is focused to a small size. The induced longitudinal electric field expressed in equation (4) breaks the dynamical symmetries 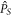 and
and  individually, and both the SAM and OAM are not conserved in HHG. On the other hand, if the combined DS operator,
individually, and both the SAM and OAM are not conserved in HHG. On the other hand, if the combined DS operator, 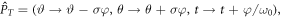 acts on equation (4), the driving laser field is invariant. Therefore, the combined symmetry still holds in this case, and the TAM is conserved in HHG. Under this DS constraint, the harmonic,
acts on equation (4), the driving laser field is invariant. Therefore, the combined symmetry still holds in this case, and the TAM is conserved in HHG. Under this DS constraint, the harmonic, 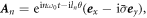 needs to be invariant, which leads to
needs to be invariant, which leads to 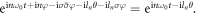 Consequently, both the odd and even harmonics are allowed, and the harmonic photon carries the OAM of
Consequently, both the odd and even harmonics are allowed, and the harmonic photon carries the OAM of 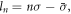 which is consistent with equation (18) for
which is consistent with equation (18) for 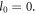
If the driving laser is the CP LG beam expressed in equation (16), the longitudinal field also breaks each individual DS, but the combined DS, 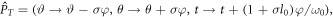 still holds, which ensures the TAM conservation in the HHG process. Then the harmonic
still holds, which ensures the TAM conservation in the HHG process. Then the harmonic  is invariant under this
is invariant under this 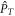 transformation, and we obtain
transformation, and we obtain  Under this DS constraint, the selection rules for the HHG process is derived,
Under this DS constraint, the selection rules for the HHG process is derived, 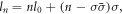 which is also consistent with equation (18).
which is also consistent with equation (18).
4. Conclusion
In conclusion, we present a new mechanism to achieve STOC based on the HHG process when an intense CP laser interacting with a solid density plasma target. Earlier researches indicate that a CP laser normally irradiating a plasma target does not induce the harmonics, because its ponderomotive force cannot drive an oscillating current on the plasma surface. However, in this work, we found that this mechanism works only for the plane wave field and the laser field with a large focal spot. When the focal spot of the intense CP laser is focused to a small size, the situation is completely different. The finite transverse size and profile of the laser field can induce a longitudinal electric field. This longitudinal field drives an oscillating plasma surface at the frequency equaling to the laser frequency. Both odd and even harmonics are emitted from this plasma surface. Moreover, the circular polarization makes the longitudinal electric field acquire a vortex phase, which drives the transverse current to generate a vortex distribution during the laser-plasma interaction. Consequently, the emitted harmonic has a vortex structure and carries the definite OAM. Physically, the generation of OAM harmonics implies an angular momentum conversion from spin to the orbital part, which is an inevitable result of the TAM conservation in the HHG process.
We study the STOC in the HHG process by using the 3D PIC simulation and theoretical analysis. In the simulations, we consider two CP laser modes: the Gaussian mode ( ) and the vortex LG mode (
) and the vortex LG mode (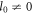 ). We also use the plane target (
). We also use the plane target ( ) and SPP target (
) and SPP target (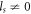 ) to check the angular momentum features. All the results clearly display the angular momentum conversion in the HHG process, and the OAM of the nth harmonic obeys the universal rule:
) to check the angular momentum features. All the results clearly display the angular momentum conversion in the HHG process, and the OAM of the nth harmonic obeys the universal rule: 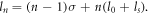 Then, we develop a quasi-1D theory to interpret the revealed phenomena, especially for the STOC mechanism in the HHG process. In our theory, the r-dependent transverse effects are neglected, but the azimuthal angle θ is included, because the rotation and angular momenta along the z-axis are closely related to θ. The theoretical results are well consistent with the simulations.
Then, we develop a quasi-1D theory to interpret the revealed phenomena, especially for the STOC mechanism in the HHG process. In our theory, the r-dependent transverse effects are neglected, but the azimuthal angle θ is included, because the rotation and angular momenta along the z-axis are closely related to θ. The theoretical results are well consistent with the simulations.
We also discuss the symmetric constraint on the solid-density-plasma HHG. For a CP plane light, the polarization-dependent DS ensures the SAM conservation, and this constraint forbids the harmonic generation. However, when the driving laser is focused, the induced longitudinal electric fields breaks the polarization-dependent and spatially dependent dynamical symmetries individually, and only the combined DS still holds. Consequently, both the odd and even harmonic generations are allowed. The TAM conservation produces the STOC, and then the harmonics must come out with vortex structures.
The angular momentum conversion is an importantly fundamental problem in physics, it is governed by the TAM conservation that is a universal rule in various fields. The STOC in the HHG process has some potential applications in many fields, for example the extreme ultraviolet optical vortex, optical manipulation and quantum information. The presented mechanism opens a new window in the study of spin–orbital interaction in optics.
Acknowledgments
We are grateful to Dr Jingwei Wang for many helpful discussions. We gratefully acknowledge the valuable comments of the anonymous referees. This work is supported by the Ministry of Science and Technology of the People's Republic of China (2018YFA0404803 and 2016YFA0401102), the National Natural Science Foundation of China (11674339, 11935008) and Strategic Priority Research Program of the Chinese Academy of Sciences (XDB16). We also thank the support of Innovation Program of Shanghai Municipal Education Commission and Shanghai Supercomputer Center.
Footnotes
- 4
We also check the amplitude deviation at different transverse position, and find this deviation is irregular and looks different at different transverse positions. So, the turbulent part of the harmonic can be regarded as the noise.
- 5
When our revised manuscript was in the second round of the review process, we noticed a paper covering the similar results had been published on line (Wang J. et al, 2019 Nat. Commun. 10 5554). While our submission and the arXiv version (arXiv: 1812.10255) predate that paper, the readers can refer to both papers for the new HHG and STOC mechanisms.
- 6
Objectively, we are not quite sure the small deviations between Ex and Ey must result from the mode
 that is only a possible physical interpretation. The random perturbations or turbulence in laser-plasma interaction, or simulation error, may also induce some small deviation.
that is only a possible physical interpretation. The random perturbations or turbulence in laser-plasma interaction, or simulation error, may also induce some small deviation.