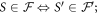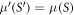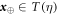Abstract
The seminal idea of quantum money, not forgeable due to laws of Quantum Mechanics, proposed by Stephen Wiesner, has laid the foundations for the Quantum Information Theory in the early '70s. Recently, several other schemes for quantum currencies have been proposed, all, however, relying on the assumption that the quantum source device, acts according to its specification. This makes several known quantum money protocols vulnerable to the so-called hardware Trojan horse attacks. We, therefore, study the following problem: to what extent quantum money schemes can be made independent from the inner working of source and verification-devices used by the honest parties (bank and mint) in creating and processing the quantum money? Drawing inspirations from the semi-device-independent quantum key distribution protocol, we introduce the first scheme of quantum money with this assumption partially relaxed, along with the proof of its unforgeability. Finally, we formulate and discuss a quantum analog of the Oresme–Copernicus–Gresham's law of economy, that may hold in the future.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Quantum Information Science originates from the seminal idea of the scheme of quantum money due to Stephen Wiesner [1]. According to his brilliant concept, the randomly polarized photons could, in principle, represent the banknote, while the Bank's secret key represents the random choices of polarization. During verification, the Bank checks and accepts the banknote if the photons appear to be polarized as they have been designed and rejects otherwise. Although it is rather intuitive that due to quantum no-cloning [2–4] the banknote cannot be forged without disturbing it, this scheme, has been proven to be secure against counterfeiter only recently [5, 6]. Wiesner's scheme bases firmly on the assumption that measurements of the verification are performed according to the specification. Dmitry Gavinsky [7] has designed a protocol powerful enough to drop this assumption. However, the security of the latter relies on the functioning of the device manufacturing banknotes (called here source), which is at the disposal of (otherwise trusted) mint.
1.1. A threat model—hardware Trojan horse attack on quantum money
We go a step further, considering not only the verification device but also the source device as potentially untrusted, implemented by some adversary. This approach involves three parties: mint, bank, and a counterfeiter. They also possess the banknote and several devices. The banknote is a classical-quantum state of physical memory, shared between Bank and counterfeiter's wallet. A source-device (the device which produces a banknote) is at hand of the mint. Verification-device (a measurement device) and software that handles the usage of the devices is at the disposal of the counterfeiter whenever he wants to get a banknote to go through the verification process. The mint is honest, so it delivers the correct number of banknotes at a wish of the Bank according to the specification of the source device. Naturally, the Bank is also considered to be fully honest in all respects. Crucially, we consider the source-device and the verification-device as untrusted. It means that these devices may not work according to official specifications and are manufactured by some adversary in order to produce malformed banknotes. The counterfeiter is untrusted, and we consider that he may be aware of the inner workings of the source and terminal devices. In that, for reducing the number of actors, he can be considered to be an adversary himself. We consider then Bob, who is in the bank, and Frederick, who is the counterfeiter. When describing the honest implementation of the scheme, we also consider Alice as the honest client. When we pass to the proof, with a little abuse of notation, we consider, however, that she might collaborate with Frederick.
1.2. Motivation—the hacker's and cryptanalyst's point of view
Before going into details, it is crucial to ask if the above scenario is indeed a one that can happen in real life, which would yield a direct motivation. At first thought, according to the traditional understanding, the whole mint is trusted, including all machines involved in the process of minting. However, the first thing to note is that the quantum money scheme is, in fact, a cybersecurity-based way of representing cash. We then observe the hidden assumption that mint's devices are honest, need not be practical from the perspective of cybersecurity. Following this, we describe the motivation from both the hacker's and the cryptanalyst's point of view.
First, from the hacker's perspective, considering the mint using the untrusted device is equivalent in cybersecurity language to finding the way to protect the mint (and so the Bank and honest clients) against a Trojan-Horse attack. Indeed, the source-device can be either (i) composed from parts designed with backdoors impossible to check by eye inspection or (ii) designed in a way open to security loopholes. Regarding (i), introducing backdoors in microchips on the physical level of their manufacturing has been recently demonstrated by an attack on random number generator [8]. Regarding (ii) exploiting the loopholes is the new area of successful experimental research aimed at hacking particular implementations of the quantum key distribution devices [9]. With these examples, mentioning the fact that the manufacturing process can be infected by classical viruses seems then unnecessary.
The problem of designing an unforgeable scheme of quantum money belongs to the class of problems from two-party cryptography (the trusted Bank can not trust clients who can be counterfeiters). Moreover, from the cryptoanalyst's perspective, any security proof is based on a set of assumptions. Finding an answer to the question what is the minimal set of assumptions that assure the same functionality? is then a practical application of Ockham's Razor principle commonly adopted in cryptography. Indeed, the quantum (or super quantum) device-independent information processing exemplifies it very well [10, 11]. The first protocol of quantum key distributions trusted all the inner working of the involved devices [12]. However, it turns out that one need not assume that these devices are produced according to specifications. They need not also be tested as being so since one can achieve the same goal (with a small price of lowering the key rate) without these assumptions. It has been demonstrated by the quantum device-independent security proofs [11]. The fewer assumptions a proof bases on, the more independent of the device the proof is. Any proof based on less number of assumptions about the inner working device than the fully device-dependent one is called now a semi-device-independent one [13].
We adopt this approach and terminology to study the problem: to what extent quantum money schemes can be made independent from the inner working of source and verification-devices used by the honest parties (Bank and mint) in creating and processing of the quantum money? As we will see, in the case of the problem presented above, the answer leading to narrowing the assumptions can be provided.
1.3. Results
The main result presented here is a novel money scheme, secure against a broad class of joined attacks of the source quantum device and testing device. It can be viewed as a modification of the testing procedure of the original Wiesner's scheme both in measurement setup, as well as interpretation of the measurement results. We prove the security of the proposed scheme using strictly fewer assumptions than the original one.
To see this more precisely, let us briefly recall what Wiesner's scheme takes for granted. These are (i) dimension of each subsystem of a banknote (register of qubits), (ii) tensor product structure of both the banknote's state and the measurements for testing, (iii) state of each qubit of the banknote is from the set 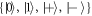 , and the measurements that are done on each of the qubits are projections in either classical
, and the measurements that are done on each of the qubits are projections in either classical 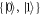 or superposed basis
or superposed basis 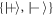 .
.
In our semi-device-independent approach, the assumptions (i)–(ii) are kept. However, we assume neither state of each qubit (each qubit of a banknote's register can be prepared differently), nor the form of measurement (each qubit can be verified due to some unknown measurement strategy, including a POVM). These two relaxations express our lack of trust towards source-device and verification-device, respectively.
An honest implementation of the banknote's state in our scheme is the same as in the original Wiesner's scheme. However, because the source-device is untrusted, an arbitrary state of the form:

shared between the Bank's branch and Alice, that can pass certain test, is a valid banknote. (Here for simplicity a single Bank's branch is shown and we omit the obvious serial number.) The 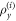 's are arbitrary states of qubits.
's are arbitrary states of qubits.
The idea of the verification in our scheme can be phrased in terms of a game. When Alice wants to get her banknote verified at some Bank's branch, the branch sends a random bit-string of length n to Alice. She should then give a correct answer (i.e. win the game) in as many as possible runs among all n. To this end, she can measure qubits of the banknote (via the tensor product of arbitrary measurements) subsequently and send corresponding answers. If the number of correct answers is high enough, the banknote is accepted as valid.
As a specific choice of a game, we base on the one used in [14], also known as a Random Access Code game [15]. Adapted to the case of our scenario, it is as follows. Alice is asked to guess correctly a randomly chosen bit (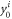 or
or 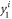 ), out of the two that form the Bank's part of the banknote (for each i ∈ [1, ..., n]). Alice correctly guesses the value of the bit chosen by the Bank's branch as many times as possible. An important aspect of this game is that it encapsulates the so-called dimension witness [16, 17]. It is a test assuring a lower bound on the dimension of the physical system. Enough number of guesses implies, in particular, that the system held by Alice (i.e. quantum part of the banknote) was not classical (excluding thereby trivial vulnerability to forging). Other important consequences of this fact are discussed further.
), out of the two that form the Bank's part of the banknote (for each i ∈ [1, ..., n]). Alice correctly guesses the value of the bit chosen by the Bank's branch as many times as possible. An important aspect of this game is that it encapsulates the so-called dimension witness [16, 17]. It is a test assuring a lower bound on the dimension of the physical system. Enough number of guesses implies, in particular, that the system held by Alice (i.e. quantum part of the banknote) was not classical (excluding thereby trivial vulnerability to forging). Other important consequences of this fact are discussed further.
Crucial to our scheme was to find the threshold number θn of correct answers that imply acceptance. In that we base on a simple idea, that (roughly speaking) a finite-dimensional quantum system can not encode too many logically independent classical bits (call it a dimension constraint). A formal statement with the above meaning, used in [14], originates from [18] (see also [19]). In their case, a qubit can not hold both the value of two independent bits. The threshold θ, we design then to satisfy an inequality:
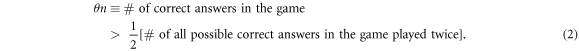
The fact that given the above condition, the same banknote will not get accepted twice comes then from an observation that there are no two disjoint parts of anything containing each more than its half. In our case of the number of correct guesses. We can place a non-trivial bound on the threshold θ, for the following reason. Trying to get accepted a banknote twice, Alice is visiting two different branches (the first one legally, and the second as a forgery called here Frederick). It implies playing the Random Access Code game twice. She would be then asked (with high probability) in half of the times for an answer that requires knowledge of two independent bits, which is, however, impossible due to the mentioned dimension constraint—each answer can be based on a single qubit only. It visualizes how our scheme differs from the original Wiesner's one. We do not require the banknote to be the same as it was manufactured. Instead, the number of correct answers matters, as we do not assume prior knowledge about particular states of each of the qubits of the banknote.
On the one hand, the verification procedure almost coincides with the preamble (testing part of) the SDI QKD protocol of [14] so that one might think, that security of the money scheme should follow from the security of the SDI QKD. However, the relation between the SDI QKD of [14], and the proposed here money scheme is not that direct, due to the difference between the mentioned security scenarios. In the QKD scenario, Bob trusts Alice, and there is also eavesdropper Eve. Contrary to this, the money scheme is a two-party cryptographic scenario: the Bank does not trust Alice (as she can come twice or collaborate with Frederick). To some extent action of Frederick can be viewed as the action of Eve, however only partially, as Alice can freely collaborate with Frederick, which is not the case in the QKD scenario, where she does not help Eve.
The relation between the SDI QKD and the SDI quantum money scheme is rather due to the fact that security proof for both schemes can be based on the same concepts: the dimension constraint and dimension witness. Regarding the idea of dimension witness contained in the Random Access Code game, it implies that the key can not be trivially copied on the way by Eve as the classical key could be, as well as it plays a role in that the banknote can not be trivially forged (as it is not classical). Regarding the dimension constraint, it implies both the proper balance between mutual information functions 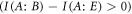 for the key generation and, as we show, a threshold shown in equation (2), which is the base for our money scheme. The latter two facts are otherwise unrelated as it is reflected by the fact that the threshold parameter in our scheme θ ≈ 0.8475 differs from the threshold that enables key generation that approximately equals 0.8415.
for the key generation and, as we show, a threshold shown in equation (2), which is the base for our money scheme. The latter two facts are otherwise unrelated as it is reflected by the fact that the threshold parameter in our scheme θ ≈ 0.8475 differs from the threshold that enables key generation that approximately equals 0.8415.
Straightforward as it is, we find instructive to demonstrate also three malicious source-devices which, along with proper verifying-device, can get a malformed banknote accepted. We show that both Wiesner's and Gavinsky's schemes are vulnerable to all three attacks. We focus on the third attack and prove the security of the presented scheme. Although the assumptions behind our scheme may still be considered as numerous and, therefore, a strong set, they appear to be not too far from optimal. It is because, as it is easy to observe, the fully device-independent security proof of quantum money scheme can not hold. We will discuss it in the latter part of the paper.
Finally, motivated by many proposed quantum currencies, we study a possible consequence of the coexistence of at least two legitimate quantum payment schemes. It is long known that whenever there are two types of money: those with high intrinsic value and those with lower intrinsic value, and both are valid (e.g. as currencies), then people tend to spend the latter ones while keeping the former. This fact was observed and formulated as a law of economy, known today as Gresham's law, stated as follows: 'Bad money drives out good'. We formulate the quantum analog of this statement, which says: 'Bad quantum money drives out good quantum one'. It summarizes the consequences of the attack on the intrinsic value of money, which for historical reasons described further, we call Quantum Oresme–Copernicus–Gresham's law. Whether such law will happen to hold is hard to predict as of now. We propose then, to initiate a discussion on the quantum intrinsic value of the quantum money schemes. It is because the intrinsic value of a quantum currency may be attributed in a much different way than the intrinsic value of a classical one.
The manuscript is organized as follows. In section 2, we review previous quantum money schemes both in private-key and public-key settings. In section 3, we show three different attacks on existing quantum money schemes and briefly discuss that a fully device-independent quantum money scheme cannot exist. In section 4, we present the main results of that work, stating a scheme for semi-device-independent quantum money. In section 5 we discuss a possible quantum analog of the Oresme–Copernicus–Gresham's law. We conclude in section 6 by comparing our scheme to the existing ones (see 6.1), discussing the technological difficulties in possible implementation (see 6.2), and summarizing the paper with some interesting open problems (see 6.3). Additionally, in appendices A–C we present a rigorous security proof of the scheme, show that it is impossible to create fully device-independent quantum money scheme in appendix D, briefly describe honest implementation in appendix E, and discuss the amount of required memory in appendix F.
2. Previous works
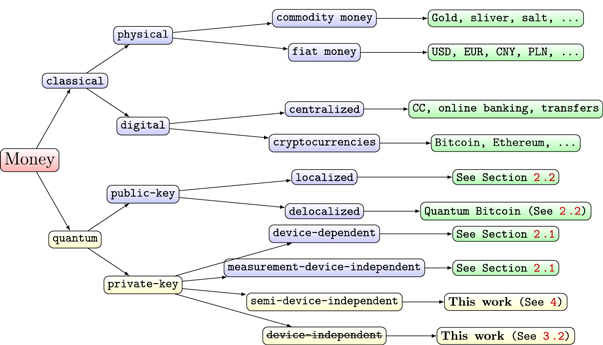
An idea of quantum money proposed by Stephen Wiesner was, to our knowledge, the first application of the quantum effects to the information-theoretic, in fact, cryptographic task. In this section, we will discuss the previous research on this topic using division into private and public-key quantum money suggested by Aaronson [20, 21]. In the private-key quantum money schemes, only the mint itself can verify the banknote. It is worth to notice that in case of private-key quantum money schemes, the Bank and the mint can be treated together as one party. We can do this since the Bank can create money from the secret key needed for verification. On the other hand, in the public-key quantum money schemes, anyone can verify the banknote using publicly available verification procedure, but still, no one, except the mint, cannot copy or create a new banknote. We will conclude by giving (in figure 1) a comprehensive comparison of different classical and quantum money schemes together with their security assumptions.
Figure 1. Types of moneys and their security against forgery: commodity money security is based only on its high intrinsic value. Fiat money's security depends mostly on secret products and procedures used in the money-making process. For example, the paper recipe or the paint chemical composition is kept secret for banknotes. It is worth mentioning that this is against Kerckhoffs's principle. Digital money security follows from hardness assumptions for some computational, probably NP-intermediate, problems. In practice, the RSA algorithm and blockchain techniques are used for which effective attacks, using a quantum computer, were proposed. Also, in case of the public-key quantum money, computational assumptions are necessary, but it is unclear if any concrete scheme remains secure. Finally, the private-key quantum money schemes are information-theoretic secure without any hardness assumptions. Nevertheless, we have to consider real-life implementation using specific, possibly untrusted, both hardware and software.
Download figure:
Standard image High-resolution image2.1. Private-key quantum money
Around 1970 Stephen Wiesner suggested the first scheme of unforgeable quantum money. Unfortunately, his paper was rejected a few times and finally was published in 1983 [1]. Even though Wiesner claimed that the protocol is unconditionally secure, a full proof for the most generalized attacks was presented by Molina et al in 2013 [5].
Because the scheme requires the mint to maintain a massive database for all produced bills, Bennet et al [22] proposed a modification of the protocol, using a cryptographic pseudorandom function, to decrease the needed amount of the memory. The question if it is possible to reduce the database size without imposing any computational assumptions was analyzed by Aaronson [20]. Later he formally proved that the answer is negative and stated the so-called Tradeoff theorem for Quantum Money [23].
Although the above schemes are secure in a regime in which the mint destroys the verified banknote, it is dangerous when we allow to retrieve the bill after verification. So-called interactive attacks were independently proposed by Aaronson [21] and Lutomirski [24]. Even more sophisticated version of the interactive attack, based on the idea of Elitzur–Vaidman bomb tester, was later suggested by Nagaj et al [25].
The scenarios mentioned above require visiting the mint (or at least having a secure quantum channel), so Gavinsky suggested a version of quantum money with classical verification [7]. It is essential to notice that in Gavinsky's scheme, the Bank does not need to trust the measurement device. Such types of schemes are commonly called measurement-device-independent. Another similar scheme was also presented by Georgiou and Kerenidis [26].
Additionally, Pastawski et al [6] and, more recently, Amiri and Arrazola [27] analyze the more realistic scenario in the presence of noise and errors.
It is also worth to mention about fundamentally different approaches aimed at anonymity. Mosca and Stebila [28], (see also Tokunaga et al [29]) proposed quantum coins in such a way that all coins are identical. Their scheme uses a black-box model that makes thorough security analysis difficult.
Furthermore, Selby and Sikora [30] analyzed unforgeable money in the Generalized Probabilistic Theories.
We should also point out experimental results in the quantum money field were presented by three groups of Bartkiewicz et al [31], Bozzio et al [32], and Guan et al [33] respectively. Although the theoretical schemes are secure, in the case of real-life, more practical implementation, new vectors of attack could appear. For example, Jiráková et al [34] show an attack on quantum money implementation.
Soon after the first version of this paper was published on arXiv preprints repository, Bozzio et al [13] presented the result with a similar title 'Semi-device-independent quantum money with coherent states'. Their result requires stronger security assumptions (trusted source device) but is more focused on realistic implementations.
Also, recent paper by Kumar [35] introduces novel quantum money protocol with very high toleration to noise.
Finally, during the review process of our work Radian and Sattath proposed scheme called 'Semi-Quantum Money' [36]. The Authors of the latter article propose the scheme that achieves similar goals by allowing the mint only to perform classical operations. This approach is, however, based on computational assumptions, while in the present article, we focus on what can be achieved without such.
2.2. Public-key quantum money
The biggest drawback of all private-key quantum money schemes is that only the mint can verify the bill. In order to improve this, an idea of public-key quantum money was invented. In that approach, not only the mint but anyone, even untrusted party, could verify the quantum banknote without communication with the mint. General formulation of the public-key quantum money was presented by Aaronson [21], and later, its security was analyzed by Aaronson and Christiano [37].
Following these seminal results, many candidates for the private-key quantum money scheme was presented. The first such scheme, based on stabilizer states, was proposed by Aaronson [21], but it was later broken by Lutomirski et al [38]. There were also some attempts exploring an idea of local Hamiltonian problem that can also be broken using a single-copy tomography presented by Farhi et al [39]. Another idea, based on the knot theory, was proposed by Farhi et al [40]. It remains unbroken, but there is no full security proof.
Until now, more papers concerning the public-key quantum money or an analysis of its security were published that we should point out here [41–43].
In the most recent work, Zhandry [44] proved that if the injective one-way functions and an indistinguishability obfuscator exist, then the scheme of the public-key quantum money exists. Furthermore, he shows how to adapt the Aaronson and Christiano's scheme [37] using these assumptions to get the secure public-key quantum money.
We should also mention ongoing research on the decentralized quantum currencies. First Jogenfors [45] proposed Quantum Bitcoin that connects ideas of quantum money and classical blockchain system like the one used in Bitcoin. Later Ikeda [46] presented another approach called qBitcoin based on quantum teleportation and a quantum chain instead of the classical blocks. Also, Sun et al [47] proposed a cryptocurrency called qulogicoin, based on another version of the quantum blockchain. Recently Adrian Kent proposed a concept of 'S-money' [48], and Kane created a new money scheme based on modular forms [49]. Finally, Andrea Coladangelo proposed a decentralized, blockchain-based, hybrid classical-quantum payment system [50], strengthening the quantum lightning scheme.
3. Motivations
In this section, we first demonstrate simple attacks on some of the private-key quantum money schemes, including Wiesner's and Gavinsky's ones, which are based on the cooperation of the untrusted quantum source device and the counterfeiter. Next, we discuss why it is impossible to make a fully device-independent money scheme in section 3.2.
3.1. Simple joined attacks: when the quantum source device and counterfeiter collaborate
We aim to demonstrate that both the original Wiesner's scheme and that of Gavinsky are vulnerable to the joined attack. Moreover, the attack is general enough to apply to other private-key quantum money schemes, as it bases on dropping important security assumption: the privacy of the key. Before presenting the attacks we recall how an honest source prepare the state:
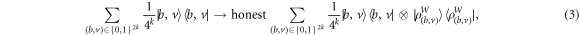
where 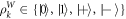 , the bit-string b tells the (random) choice of basis, while v corresponds to outcomes. In the original money, only the system W contains banknote's state.
, the bit-string b tells the (random) choice of basis, while v corresponds to outcomes. In the original money, only the system W contains banknote's state.
Now we are ready to show here three attacks of different types. The first one enlarges the memory of the banknote, the second one uses additional entanglement, and the third makes it a classical state. The first reduces to simple imprinting of the secret key of the Bank directly in banknote's state. It is at the expense of enlarging dimension of its quantum memory:
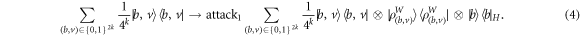
The mistrustfully prepared banknote has an additional 'hidden' register H enabling the attack. This register can be used to generate an unlimited number of identical banknotes via repetitive von Neumann measurement of the system W in the basis indicated by vector  . Allowing for such a strong attack, one can imagine that in principle, the whole string
. Allowing for such a strong attack, one can imagine that in principle, the whole string 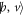 could also be imprinted in money's memory at the price of doubling it. However, imprinting
could also be imprinted in money's memory at the price of doubling it. However, imprinting 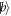 is enough. The operation of copying such a 'banknote' can pass unnoticed from the point of view of the honest Client. From this trivial example, we have then learned that when the dimension of the banknote is unbounded, its security against forgery is compromised.
is enough. The operation of copying such a 'banknote' can pass unnoticed from the point of view of the honest Client. From this trivial example, we have then learned that when the dimension of the banknote is unbounded, its security against forgery is compromised.
The second attack does not require extra memory in the banknote's state but makes use of an additional entanglement between adversary and the untrusted source device. Instead of preparing one from the four honest states 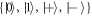 , the source performs locally one from the four Pauli unitaries on a half of a singlet and sends it as a money state. Later the adversary performs global Bell measurement on the whole two-qubit system. That procedure, based on superdense coding [51], allows him to obtain both parts of the secret key and prepare an arbitrary number of valid banknotes.
, the source performs locally one from the four Pauli unitaries on a half of a singlet and sends it as a money state. Later the adversary performs global Bell measurement on the whole two-qubit system. That procedure, based on superdense coding [51], allows him to obtain both parts of the secret key and prepare an arbitrary number of valid banknotes.
In the third one, the untrusted quantum source device and the counterfeiter can attack jointly without increasing the memory of the banknote and without any additional entanglement, by using only classical states (diagonal in a single basis):
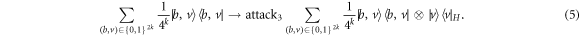
In each run, right before the measurement is physically done, the measurement device is given the type of basis b taking value 0 in case of 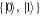 and 1 for
and 1 for 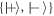 . It can then safely output the value
. It can then safely output the value 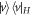 as a good answer. The two bits that cannot be encoded in 1 qubit are split into measurement type (revealed later), and its outcome. In the original Wiesner scheme, the Bank trusts both the production and verification devices. Dropping these assumptions, as we do, with the view of possible hardware Trojan horse attack, we observe that such protocol is vulnerable to forgery. The same holds for the ones by Gavinsky [7] and Molina et al [5].
as a good answer. The two bits that cannot be encoded in 1 qubit are split into measurement type (revealed later), and its outcome. In the original Wiesner scheme, the Bank trusts both the production and verification devices. Dropping these assumptions, as we do, with the view of possible hardware Trojan horse attack, we observe that such protocol is vulnerable to forgery. The same holds for the ones by Gavinsky [7] and Molina et al [5].
In the case of scheme by Wiesner and Molina et al the attack is made as described above. On the other hand to break scheme proposed by Gavinsky one can encode classical values of 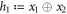 and
and 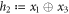 on two qubits. To win the game it is sufficient to output
on two qubits. To win the game it is sufficient to output  and
and 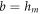 depending on question m. In the above, we use the notation from definition 1 and step 6 of the protocol from [7].
depending on question m. In the above, we use the notation from definition 1 and step 6 of the protocol from [7].
The scheme of money that we propose (see section 4.1), based on the semi-device-independent quantum key distribution protocol, is a partial countermeasure to these three attacks. In the latter protocol, one assumes that there are only qubits sent and no additional entanglement, so the first two attacks (by enlarging memory and superdense coding) are not applicable. On the other hand, the SDI QKD protocol only gets accepted if the data coming from quantum states is observed, i.e. that the systems communicated were not classical bits, disabling thereby the third attack. It, and the fact that the honest implementation of the quantum states processed by the parties in the SDI QKD is Wiesner's money, motivates us to study the security of Wiesner's scheme under the verification of the SDI QKD protocol (as we describe in detail in section 4.1). Before that, in the next section, we will present a minor result, a no-go for device-independent quantum money, which highlights the importance of our money scheme.
3.2. Impossibility of fully device-independent quantum money
In this section, we will show that it is impossible to create a fully device-independent money scheme. We will prove this in a scenario where the Bank has at least two branches that do not communicate during the verification phase. In the device-independent approach, both source and measurement devices are untrusted, and there are no restrictions on state dimension or additional entanglement, as opposed to the semi-device-independent approach that we will present in the next sections. On the other hand, we allow all Bank's branches to have shared randomness that can be used both in the state preparation and verification phases. We also assume that the no-signaling condition is fulfilled, and post-processing is honest, which is the standard approach in most device-independent protocols.
(No-go for device-independent quantum money).Observation 1 It is impossible to create a fully device-independent money scheme with untrusted source and measurement devices that could be produced by an adversary.
Intuitively it is easy to see that we can break any money scheme using appropriate modification of the first attack from the previous section. Indeed, without communication between Bank's branches, a malicious quantum source device can always prepare two copies of the banknote in such a way that both will pass verification in different branches. The only way a branch can verify the banknote is to check correlations with the client's banknote. It is impossible to ensure that the verification will influence, or give knowledge about, correlations of another branch with a different malicious copy of the banknote. To justify these intuitions, we will provide more formal proof of the above theorem in appendix D.
Because of the impossibility result, we can ask how close one can go toward the device-independent approach. We partially answer this question by providing in the next section our main contribution, the semi-device-independent quantum money scheme. It requires weaker assumptions than any previous one. We prove its security against a broad class of essential attacks and conjecture that it is also secure in the general case.
4. Main result
In this section, we present the main result of our work. We first describe the scheme for semi-device-independent quantum money in section 4.1. Next, we compare our money scheme with the corresponding SDI QKD protocol of Pawłowski and Brunner, that we use as a base (see section 4.2). Finally, in section 4.3 we show the idea of the proof, details of which are presented in the appendices.
4.1. Semi-device-independent quantum money protocol
Motivated by the fact that joined attacks can compromise the security of some private-key quantum money schemes, we will show a partial solution to this problem. In this section, we present a scheme for semi-device-independent private-key quantum money. The concept of a semi-device-independent quantum key distribution was discovered by Pawłowski and Brunner [14]. In that scheme, the sender has to trust neither the quantum source nor the measuring device. Instead, there are two nontrivial assumptions about the states sent to the receiver. Firstly, the states have limited dimensions and, secondly, there is no entanglement between the states and the adversary. See figure 2.
Figure 2. Scheme of the semi-device-independent quantum key distribution [14] (SDI QKD).
Download figure:
Standard image High-resolution imageOur scheme of money is similar to the SDI QKD scheme and has the assumption that each state that is sent from the sender to the receiver is qubit (have dimension d = 2). In order to introduce both the concept and notation, it is instructive to recap the semi-device-independent quantum key generation protocol [14] briefly. The key is produced as follows. The sender sets up n pairs of random bits 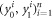 . In each run of the experiment
. In each run of the experiment ![$i\in [n]:= \{1,\ldots ,n\}$](https://content.cld.iop.org/journals/1367-2630/22/2/023007/revision2/njpab6872ieqn21.gif) , upon pressing the correct button sender's device produces an untrusted state
, upon pressing the correct button sender's device produces an untrusted state 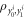 , which is assumed to be a qubit, and sends it to the receiver. The receiver's device is fully untrusted. It measures the state in an arbitrary manner (perhaps knowing state's preparation), yet upon a (random) input xi, it has to output a bit ai, which equals
, which is assumed to be a qubit, and sends it to the receiver. The receiver's device is fully untrusted. It measures the state in an arbitrary manner (perhaps knowing state's preparation), yet upon a (random) input xi, it has to output a bit ai, which equals 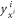 . In the classical case, the maximal success probability of guessing the bits of the sender is only 3/4, while in quantum case, it is
. In the classical case, the maximal success probability of guessing the bits of the sender is only 3/4, while in quantum case, it is 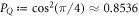 . If the guessing probability is larger than a certain value, the secure key can be established.
. If the guessing probability is larger than a certain value, the secure key can be established.
We are now ready to introduce our money scheme. In the SDI quantum money scheme, one branch of the Bank (mint) plays the role of the sender, while the client Alice is the receiver.
• Money generation protocol. In order to create the money, all k branches of the Bank have to possess common secret randomness (secret key) that is later stored in classical memories of the branches. Each portion of the bits 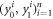 of this key is attached to some serial number of a separate banknote SN in advance. (Note that the secret key can be obtained for example by measurement on the shared
of this key is attached to some serial number of a separate banknote SN in advance. (Note that the secret key can be obtained for example by measurement on the shared 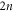 GHZ states [52] or by encrypted classical communication.) To generate a quantum state of the banknote associated to the number SN one branch BS (in practice the closest to Alice branch that can perform the function of the mint, i.e. posses quantum source devices) uses
GHZ states [52] or by encrypted classical communication.) To generate a quantum state of the banknote associated to the number SN one branch BS (in practice the closest to Alice branch that can perform the function of the mint, i.e. posses quantum source devices) uses 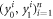 associated with this SN as a sequence of inputs to its untrusted quantum source devices
associated with this SN as a sequence of inputs to its untrusted quantum source devices 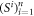 . The latter devices, in turn, generates n qubits (
. The latter devices, in turn, generates n qubits (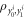 ) that together form the quantum state of the banknote
) that together form the quantum state of the banknote
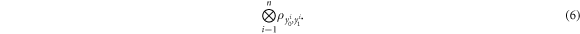
The above state is sent to Alice's wallet (dedicated quantum memory device). In the end, the banknote, i.e. the joined state of k branches of the Bank and Alice's wallet takes the form:
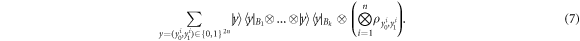
• Money verification protocol at the Bank. In order to verify the money Alice comes to any branch of the Bank denote as Bl. The branch Bl generates a question bit-string 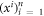 , inputs the bits to the untrusted measurement devices
, inputs the bits to the untrusted measurement devices 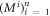 and collects the output bit-string
and collects the output bit-string 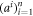 . For a total data represented by a string of tuples:
. For a total data represented by a string of tuples: 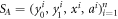 the branch Bl accepts it if the following condition is satisfied:
the branch Bl accepts it if the following condition is satisfied:
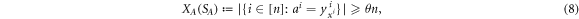
i.e. the number of correct guesses is above the threshold value 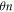 and rejects otherwise.
and rejects otherwise.
Apart from the above scheme, the second main result (see theorem 1) is the proof that 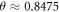 will assure the security of the money scheme within considered set of assumptions. More precisely, in real-life application, one should consider the value of threshold to be a bit larger,
will assure the security of the money scheme within considered set of assumptions. More precisely, in real-life application, one should consider the value of threshold to be a bit larger, 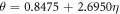 , depending on how small the probability of error, i.e. forgery one would like to tolerate. It is however proven (see theorem 1) to be exponentially small in the length of the banknote, scaling as
, depending on how small the probability of error, i.e. forgery one would like to tolerate. It is however proven (see theorem 1) to be exponentially small in the length of the banknote, scaling as 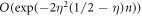 .
.
• Money verification protocol at a distance. Alice establishes an authenticated connection for classical communication with some (arbitrary) branch Bl of the Bank. The Bl gives her random inputs 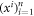 , that she should use together with her quantum state from the memory of her wallet as inputs to the untrusted terminal (her own, or, e.g. the one operated by a seller in a shop). The classical output
, that she should use together with her quantum state from the memory of her wallet as inputs to the untrusted terminal (her own, or, e.g. the one operated by a seller in a shop). The classical output 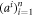 from the device (possibly modified by Alice to
from the device (possibly modified by Alice to 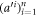 ) is then sent to Bl that checks if the data
) is then sent to Bl that checks if the data 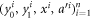 are acceptable if inequality (8) holds, and rejects it otherwise.
are acceptable if inequality (8) holds, and rejects it otherwise.
For the sake of clarity, the whole process of the creation and the verification of the semi-device-independent quantum money is illustrated in figure 3 (for the general scheme with many branches) and figure 4 (for the creation and verification). Generation and verification protocols are also summarized in tables 1 and 2 respectively. We state below certain remarks on the variants of the above approach.
Figure 3. B1 ... Bk represents arbitrary number of Bank's branches that share common randomness 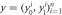 stored in the classical memories. Branch BS inputs the string y into untrusted source device S and sends the generated n quantum systems
stored in the classical memories. Branch BS inputs the string y into untrusted source device S and sends the generated n quantum systems 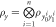 to Alice's memory. When Alice wants to verify the money she visits some branch Bl. This branch generates random binary string
to Alice's memory. When Alice wants to verify the money she visits some branch Bl. This branch generates random binary string 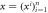 of length n and feeds as an input to untrusted measurement devices of the terminal
of length n and feeds as an input to untrusted measurement devices of the terminal 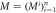 , which generates a string
, which generates a string 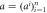 . The branch then count in how many rounds game was won and accepts the banknote as valid or rejects it dependently on whether the condition from equation (8) was met.
. The branch then count in how many rounds game was won and accepts the banknote as valid or rejects it dependently on whether the condition from equation (8) was met.
Download figure:
Standard image High-resolution imageFigure 4. The procedure of generation and verification of a single banknote in the SDI quantum money scheme. The n untrusted source devices independently produce qubit states 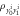 that form in total the banknote that is kept in Alice's wallet and is exposed to the counterfeiting by her or Frederick (or even both). The verification of the banknote is done by n independent (not necessarily identical) untrusted parts of a verification terminal, each checking if
that form in total the banknote that is kept in Alice's wallet and is exposed to the counterfeiting by her or Frederick (or even both). The verification of the banknote is done by n independent (not necessarily identical) untrusted parts of a verification terminal, each checking if 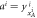 (i.e. if its output is equal to one of the two bits of Bank's note at run i chosen randomly as
(i.e. if its output is equal to one of the two bits of Bank's note at run i chosen randomly as 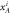 ). The banknote gets accepted if the number of correctly guessed bits exceeds θn with
). The banknote gets accepted if the number of correctly guessed bits exceeds θn with 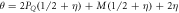 , where
, where 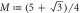 and η depends on n (taking care of possible fluctuations of the number of guesses).
and η depends on n (taking care of possible fluctuations of the number of guesses).
Download figure:
Standard image High-resolution imageTable 1. Summary of semi-device-independent quantum money generation protocol.
| Money generation protocol |
|---|
| Arguments: |
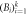 —honest Bank's branches —honest Bank's branches |
| BS—honest mint (Bank's branch that creates the money) |
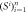 —untrusted source devices (with single qubit outputs) —untrusted source devices (with single qubit outputs) |
| A—possibly dishonest client Alice that posses quantum memory to store money (quantum wallet) |
| SN—serial number of the banknote |
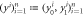 —classical keys of the banknote shared by Bank's branches —classical keys of the banknote shared by Bank's branches |
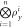 —client's part of the banknote —client's part of the banknote |
| Protocol steps: |
1. Branches Bi generate common classical key string consist of pair of bits 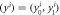 . . |
| 2. Mint BS input strings yiinto untrusted source devices Si. |
3. Devices Si produce states 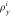 that are sent to the client A together with serial number SN. that are sent to the client A together with serial number SN. |
4. Client A stores states 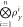 and SN in her quantum wallet. and SN in her quantum wallet. |
Table 2. Summary of semi-device-independent quantum money verification protocol.
| Money verification protocol |
|---|
| Arguments: |
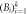 —honest Bank's branches —honest Bank's branches |
| Bl—honest Bank's branch that verifies the money |
| PPl—Bl's honest post-processing unit |
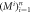 —untrusted measurement devices —untrusted measurement devices |
| V—untrusted verification terminal |
| A—possibly dishonest client Alice that posses quantum memory to store money (quantum wallet) |
| SN—serial number of the banknote |
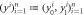 —classical keys of the banknote shared by Bank's branches —classical keys of the banknote shared by Bank's branches |
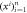 —random questions send by verifying branch —random questions send by verifying branch |
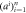 —classical output generated by measurement devices —classical output generated by measurement devices |
 —client's part of the banknote —client's part of the banknote |
| Protocol steps: |
1. Client A inputs her quantum states 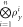 and SN into terminal V. and SN into terminal V. |
2. Bank's branch Bl that have a classical connection with V sends questions 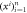 . . |
3. Terminal T, using devices , measures states 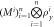 according to questions according to questions 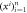 . . |
4. The outputs of measurements 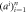 are sent to the branch Bl. are sent to the branch Bl. |
5. The branch counts the number c of correct guesses, i.e. number of i such that  using honest post-processing unit PP. using honest post-processing unit PP. |
| 6. The branch accepts the banknote if c > θn and rejects otherwise. |
Remark 1. One might think that mint could check the quantum source device before its official use. However, one can never exclude the attack based on clock: the quantum device starts misbehaving after it has been (with high probability) tested and treated as honest from that on. Even more importantly, the attack that we show is split between two devices: the quantum source device and the verification device. Since the verification device can also be dishonest, i.e. the honesty of which can again depend on the clock, it is then rather not possible to detect the attack before the money is produced.
Despite this fact, our scheme circumvents a class of attacks of this type by testing each banknote against it during the standard validation procedure. Our scheme can be therefore seen as testing outputs of two not fully trusted devices by inspecting if these outputs possess welcome property.
(The creation of the banknote without communication).Remark 2 The branches can create money without communication. Using synchronized clocks, they can continuously generate new random inputs. When a client arrives, the serial number of her banknote would contain the time that uniquely indicates what remembered randomness verifying branch should use. Additionally, branches should agree among themselves on the allowed generation time to make sure not to generate two bills from the same randomness. A similar idea can also be implemented in some previous money schemes, for example, Wiesner's one.
4.2. Comparison of the SDI QKD and SDI quantum money scheme
We make now an explicit comparison of our protocol with that of the semi-device-independent QKD of Pawłowski and Brunner [14]. Although the honest implementation of two protocols and its assumptions are similar, the proof is fundamentally different. Furthermore, there are three more main differences.
• Memory requirements: A conceptual difference is that we defer the process of measurement and call the collection of states prepared by the source in SDI protocol the banknote. The process of the measurement is identified by us with the verification done later by the terminal. It is of particular convenience that the SDI protocol does not rely on the no-signaling principle, so the measurement of the banknotes can be done any time after they were prepared. In other words, our protocol needs quantum memory, while SDI QKD does not.
• Limited number of runs: A significant practical difference is that the SDI quantum money scheme corresponds to a limited SDI QKD protocol to the creation and the verification procedures without the privacy amplification and information reconciliation part. In particular, in our protocol, the number of runs of the corresponding SDI QKD experiment (i.e. the length of the banknote) is only long enough to enable estimation of the guessing probability which depends only on the possible systematic error in the experiment and the concentration property due to the law of large numbers. It is in contrast with the SDI QKD protocol, which involves as many runs (at least) as the number of key bits needed to be generated. Indeed, we do not aim at creating the secret key because—there is no phase of public reconciliation and privacy amplification. Preparing and verifying a long key is equivalent to creating and verifying a huge number of banknotes.
• An intermediate acceptance threshold: The third difference concerns the acceptance threshold. Acceptable range of the value of the probability of guessing 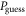 of the string
of the string 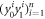 in the SDI QKD protocol varies from the maximal
in the SDI QKD protocol varies from the maximal 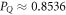 , which implies the highest possible key rate in this scenario, to the minimal
, which implies the highest possible key rate in this scenario, to the minimal 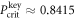 , which implies zero key rate. Let us stress here, that any value between PQ and
, which implies zero key rate. Let us stress here, that any value between PQ and 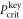 is acceptable, as leading to a non-zero key rate (yet, one aims at the highest). Instead, in the corresponding SDI quantum money scheme one needs the value of this parameter to be larger than
is acceptable, as leading to a non-zero key rate (yet, one aims at the highest). Instead, in the corresponding SDI quantum money scheme one needs the value of this parameter to be larger than 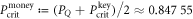 . On the other hand, all money schemes with the acceptance threshold θ in the range
. On the other hand, all money schemes with the acceptance threshold θ in the range ![$({P}_{\mathrm{crit}}^{\mathrm{money}},{P}_{Q}]$](https://content.cld.iop.org/journals/1367-2630/22/2/023007/revision2/njpab6872ieqn77.gif) are protected against forgery given large enough number of qubits of the banknote n.
are protected against forgery given large enough number of qubits of the banknote n.
4.3. Security proof of the SDI quantum money scheme
In this section, we provide the proof of the main result: the SDI quantum money scheme is protected against the qubit-by-qubit forgery. That is, against the case when the source device, the counterfeiter, and the verification terminal possibly created by the counterfeiter cooperate in a manner that each qubit is attacked (prepared, copied and tested) independently. Under some additional necessary assumptions, which we list below, we show that two cooperating clients, Alice and Frederick, cannot get the banknote accepted as valid in two Bank's branches. As we show, the case of many Bank's branches follows from the security in the latter case. The case of a birthday attack of choosing the best pair of branches is then taken care of by the union bound. Indeed let us assume that the number of branches equals 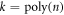 , where n is the length of the banknote, which is a reasonable constraint possible to be satisfied. If for any pair the probability of successful counterfeiting is exponentially small
, where n is the length of the banknote, which is a reasonable constraint possible to be satisfied. If for any pair the probability of successful counterfeiting is exponentially small  , the highest probability of this event for k branches is not higher than
, the highest probability of this event for k branches is not higher than 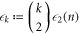 , which is still small (of order
, which is still small (of order 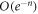 ).
).
- ASM1 Bank's branches have access to a private fully random number generator that they use to generate y's and x's.
- ASM2 Branches of the Bank use honest classical post-processing units in the verification procedure.
- ASM3 The dimension of the state that is produced at the output of the source is bounded, and there is no other information leaking from the source to Alice or Frederick.
- ASM4 The state produced by the source is unentangled from the dishonest parties (Alice and Frederick).
- ASM5 The source devices create the states in an independent way, which also implies that each of the sources has access only to its input (not the inputs of the other sources).
- ASM6 The measurement devices are independent, each measure only its subsystem, and the outputs of Alice and Frederick in each run are independent of the inputs and the outputs from other runs.
It is crucial to notice that our assumptions are strictly weaker than the one used in Wiesner's scheme. Furthermore, all existing quantum money schemes assume that the money state dimension is limited.
In particular case of the presented SDI quantum money scheme, in ASM3 we specify that each of the independent parts of the sources (as specified in ASM5) has output bounded by 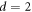 , i.e. the source works by producing independently n qubits (however not necessarily in the same way). What we will prove, our assumptions imply security against the third attack presented above.
, i.e. the source works by producing independently n qubits (however not necessarily in the same way). What we will prove, our assumptions imply security against the third attack presented above.
Now we are ready to formally state main result of our work. Let us define (see appendix C)
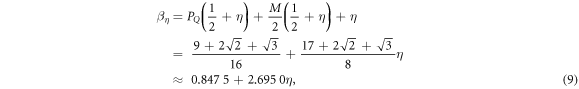
for some small η chosen in such a way that 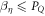 .
.
Theorem 1 Let acceptance threshold θ be larger than 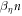 . Then, under Assumptions ASM1–ASM6, where k denotes the number of Bank's branches the probability of a successful forgery
. Then, under Assumptions ASM1–ASM6, where k denotes the number of Bank's branches the probability of a successful forgery 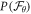 is exponentially small in number of banknote's qubits n and is bounded by
is exponentially small in number of banknote's qubits n and is bounded by
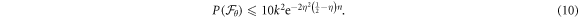
(On the possible weakening of the assumptions).
Remark 3 It seems plausible that the assumption ASM6 could be omitted but, it would complicate the proof. The question of if we can omit the assumption ASM5 is a hard open problem, related to the formulation of the SDI QKD scheme and Random Access Codes [53, 54] in general. On the other hand, all other assumptions are necessary to prove the security of our scheme since rejecting any of them leads to a successful attack.
Let us briefly describe the idea of the proof of the security of the scheme. It is a consequence of two facts: (i) the monogamy inherent to the SDI key generation protocol and (ii) the fact that each Bank's branch queries independently from the other branches during the verification procedure. It will hold for the case when the Bank verifies the banknote via untrusted terminal, i.e. Alice (or Frederick) come to the Bank to get the banknote accepted. We can reduce the case with the communication to the latter, under the assumption that the strategy to lie about the outputs of the devices (which is then at a choice of the dishonest parties) is individual, independent for each of the runs of the protocol (see appendix A). As we discuss in section 6, this a bit unrealistic assumption that can be in principle dropped given the protocol of SDI QKD is proven to be secure against the general, so-called forward signaling attacks.
4.3.1. The case of an attack on a single qubit
Like in Wiesner's scheme, for a banknote to be accepted, its owner has to guess the bits of the Bank correctly. It is instructive to focus on the attack on a single qubit of the banknote to see that two dishonest persons, Alice and Frederick, cannot both pass the verification of our banknote. Suppose Alice and Frederick are trying to 'split' its use to maximize the probability of guessing Pguess in two experiments of some two branches of the Bank. Their joined attack can be described as a conditional probability distribution (a box): 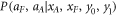 , where y0 and y1 are the secret keys of the Bank which Alice and Frederick are trying to guess, xA and xF are the random inputs, generated by the Bank, send to the verification device.
, where y0 and y1 are the secret keys of the Bank which Alice and Frederick are trying to guess, xA and xF are the random inputs, generated by the Bank, send to the verification device.
For simplicity of description, we will assume that Alice and Frederick come to the Bank, while the Bank sets the input to the devices (we will argue later how to relax this assumption partially). The joined attack aims at generating two bits aA (by Alice), and aF (by Frederick), such that the probability of guessing the xAth bit of  and xFth bit of yB by Frederick are both maximal. The guessing probability for Alice and Frederick respectively read:
and xFth bit of yB by Frederick are both maximal. The guessing probability for Alice and Frederick respectively read:
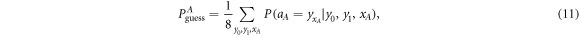
and
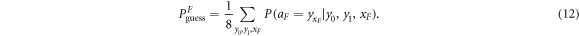
Let us observe first that in the case 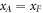 , they can both achieve the maximal possible probability of guessing
, they can both achieve the maximal possible probability of guessing 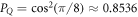 [14]. Indeed, Alice can come first to one branch and behave honestly having the guessing probability
[14]. Indeed, Alice can come first to one branch and behave honestly having the guessing probability 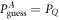 , while Frederick can copy her answer, reaching the same probability of guessing. However, when
, while Frederick can copy her answer, reaching the same probability of guessing. However, when 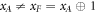 , the dishonest parties need to guess opposite bits: y0 (Alice) and y1 (Frederick) or vice versa (with half probability). However, it is proven in [14] that
, the dishonest parties need to guess opposite bits: y0 (Alice) and y1 (Frederick) or vice versa (with half probability). However, it is proven in [14] that
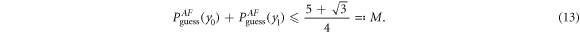
Hence, even if Alice and Frederick were fully collaborating, the sum of the probabilities of guessing of the two bits is bounded.
Since 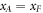 with the probability one half, averaging over the value of
with the probability one half, averaging over the value of 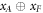 , we conclude that the average number of correctly guessed bits has an upper bound
, we conclude that the average number of correctly guessed bits has an upper bound
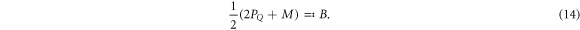
In the next section, we will generalize this bound to the case banknotes that consists of many (n) qubits. Due to the independent nature of the attack, it will suffice to multiply the above bound by n (up to fluctuations around the average). The corresponding bound enlarged by the maximal possible fluctuations reads then 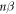 with
with 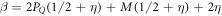 . We will then choose the threshold value θ to be larger than
. We will then choose the threshold value θ to be larger than 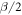 . It will assure that the two dishonest parties cannot get the same banknote accepted in two Bank's branches, as their total sum of the guesses would be larger than
. It will assure that the two dishonest parties cannot get the same banknote accepted in two Bank's branches, as their total sum of the guesses would be larger than 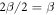 , reaching the desired contradiction.
, reaching the desired contradiction.
4.3.2. Extending the argument to the general case of the qubit-by-qubit attack
We would like to extend this reasoning to the case of the repeated experiment of n runs (n will be relatively small, as short as the length of a usual preamble of the QKD protocols). We assume here that the attack is 'id', i.e. by not necessarily equal however independently distributed random variables, according to the measure:
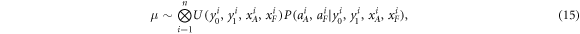
where 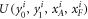 denotes the uniform distribution over its arguments. We then observe that, instead of providing xA to Alice and xF to Frederick, the two branches of the Bank could give xA to Alice and
denotes the uniform distribution over its arguments. We then observe that, instead of providing xA to Alice and xF to Frederick, the two branches of the Bank could give xA to Alice and 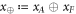 to Frederick. This is because Alice and Frederick are collaborating, so they can compute value of xF from these data in case it is needed. We can, therefore, change the scenario to one in which the parties are given
to Frederick. This is because Alice and Frederick are collaborating, so they can compute value of xF from these data in case it is needed. We can, therefore, change the scenario to one in which the parties are given 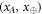 , if the probability measure is changed accordingly to the following one:
, if the probability measure is changed accordingly to the following one:
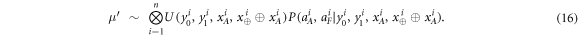
The measure 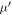 acts on xA and
acts on xA and 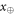 in the same way as μ would act on xA and xF, so in some sense it is undoing the XOR operation. This modification of the scenario does not change the probability of successful forgery, i.e. the probability of an event in which both Alice will get accepted as supposed to have a valid banknote and so will happen to Frederick. To see this, we first note that a set of events (denoted as
in the same way as μ would act on xA and xF, so in some sense it is undoing the XOR operation. This modification of the scenario does not change the probability of successful forgery, i.e. the probability of an event in which both Alice will get accepted as supposed to have a valid banknote and so will happen to Frederick. To see this, we first note that a set of events (denoted as 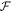 ) leading to a successful forgery reads:
) leading to a successful forgery reads:
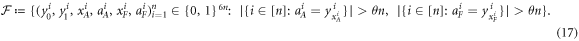
We will also define a strategy S by
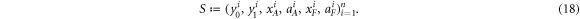
We then prove (see corollary 1) that
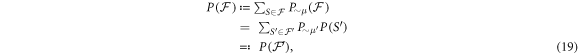
where 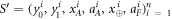 and
and
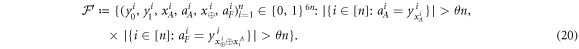
Because 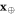 is created from fully random bits that are unknown for adversary during the creation of the money, we have
is created from fully random bits that are unknown for adversary during the creation of the money, we have
We can narrow considerations to the typical 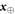 , i.e. those having number of symbol 0 and 1 approximately
, i.e. those having number of symbol 0 and 1 approximately 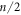 times. More formally the set of typical sequences is defined as
times. More formally the set of typical sequences is defined as
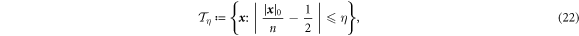
where 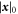 is the number of positions with symbol 0 in a bitstring
is the number of positions with symbol 0 in a bitstring 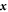 . All sequences of the length n (given n is large enough) are with high probability typical (i.e. with a probability
. All sequences of the length n (given n is large enough) are with high probability typical (i.e. with a probability 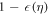 for
for 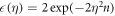 ). We have therefore
). We have therefore
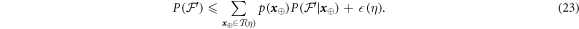
We then see that one can fix a typical 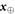 , and prove that for any such
, and prove that for any such 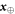 , the probability of acceptance is low. We will assure it by setting an appropriate θ, so that with a high probability over the conditional measure
, the probability of acceptance is low. We will assure it by setting an appropriate θ, so that with a high probability over the conditional measure 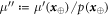 the strings
the strings 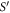 emerging from the attack will be rejected as having too small number of guessed bits of
emerging from the attack will be rejected as having too small number of guessed bits of 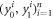 .
.
In more detail, we first note that for a fixed 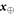 , on average, over n runs with respect to the measure
, on average, over n runs with respect to the measure 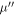 , there are no more guessed inputs than
, there are no more guessed inputs than  with B given in equation (14). It remains to take into account the fact that the observed number of the guessed inputs need not be equal to its average. However,
with B given in equation (14). It remains to take into account the fact that the observed number of the guessed inputs need not be equal to its average. However, 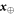 is typical, hence the number of runs will be at least
is typical, hence the number of runs will be at least 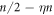 , so we can use the fact that the attack is performed in an independent manner. Due to Hoeffding's inequality, we obtain that the observed number of guessed inputs is with a high probability bounded from above by:
, so we can use the fact that the attack is performed in an independent manner. Due to Hoeffding's inequality, we obtain that the observed number of guessed inputs is with a high probability bounded from above by:
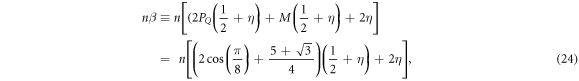
where η takes care of the maximal possible fluctuations.
Before we explicitly control these fluctuations, we first define four random variables describing the guessing at the ith run of the verification procedure by Alice and Frederick as
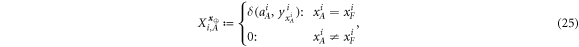
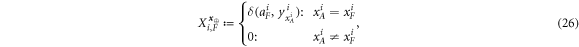
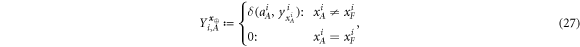
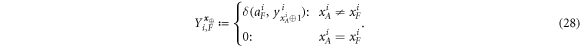
Now we can get back to describing deviations from the average of the 4 random variables: 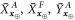 and
and 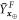 that are the sums over
that are the sums over ![$i\in [n]$](https://content.cld.iop.org/journals/1367-2630/22/2/023007/revision2/njpab6872ieqn124.gif) for the variables described above. The values of
for the variables described above. The values of 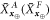 are the numbers of bits of
are the numbers of bits of 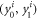 correctly guessed by Alice (Frederick) from the positions i satisfying
correctly guessed by Alice (Frederick) from the positions i satisfying 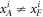 . Analogously,
. Analogously, 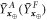 describe the number of correct guesses for i such that
describe the number of correct guesses for i such that 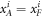 . Details are given in lemma 2 and corollary 2 (see also appendix B for an explicit definition of random variables, their sum and expected values).
. Details are given in lemma 2 and corollary 2 (see also appendix B for an explicit definition of random variables, their sum and expected values).
The last argument follows from a simple observation. Namely, if the total fraction of the correctly guessed positions by two persons is less than β, the minimum of the fractions of the correct guesses by each of them separately is not greater than  . Setting the acceptance threshold θ large enough that the minimum of the numbers of guesses is below θ, we assure that for each typical
. Setting the acceptance threshold θ large enough that the minimum of the numbers of guesses is below θ, we assure that for each typical 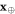 the banknote is rejected with the high probability in at least one branch. In particular, for any
the banknote is rejected with the high probability in at least one branch. In particular, for any 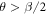 this probability is at least
this probability is at least 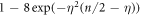 , where for every typical
, where for every typical 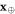 the error
the error 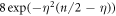 upper bounds the probability of event that at least one of the 4 random variables
upper bounds the probability of event that at least one of the 4 random variables 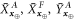 ,
, 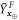 is far from its respective average.
is far from its respective average.
Taking into account equations (23) and (19), we obtain finally
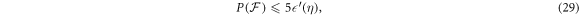
with 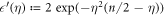 .
.
5. Quantum Oresme–Copernicus–Gresham's law
One of the famous laws of the economy is:
• Bad money drives out good.
This law states, colloquially speaking, that if certain money is cheaper to produce, then it will eventually subside the one that is more expensive to produce, where expensive is understood not in terms of face value but in terms of intrinsic value. Although it was named after Sir Gresham, it has been observed by others, even much earlier. The two most cited authors are Oresme [55] and Nicolaus Copernicus [56], so that the law is also referred to as Copernicus', or the Oresme–Copernicus–Gresham's law (OCG law). However, the first known appearance of a similar statement is in the comedy 'The Frogs', written by the Ancient Greek playwright Aristophanes around 405 BC [57]. For an overview of the law, see, e.g. [58].
From the perspective of the economy, the concept of money is a matter of a social agreement and properties of a given material/procedure used to produce a coin or a banknote. So it might appear that there is no need to consider a quantum variant of Gresham's law per se because one can apply the OCG law to the new method of mining—from quantum states. This is what happens to classical crypto-currencies. Instead, formulating quantum analog of the OCG law, we would like to stimulate a discussion on the intrinsic value of quantum currencies. This quantum intrinsic value is much different from one used in the case of classical money. For example, we can treat quantum money states as a source of randomness. Furthermore, we can also take into account how hard it is to implement different quantum money schemes. This is because one could choose a 'cheaper' way to produce money—from quantum states that are 'cheaper' to obtain whatever means 'cheaper' to quantum technology at a given moment of development. We, therefore, would like to introduce and discuss a version of Quantum Gresham's law in the following way:
• Bad quantum money drives out good quantum one.
Deciding whether to keep a given quantum currency or not may be a complex process, depending on various mutually dependent parameters, the importance of which varies over a change of preferences of particular individuals or societies. It is therefore too early and hence too hard to foresee the behavior of the quantum currency flow between the schemes provided they happen to be realized experimentally. Nevertheless, we can exemplify a possible in real life situation, which may cause the quantum OCG law to hold. In that, we will restrict ourselves to show the interplay between the two different, yet both legible representations of quantum banknotes, of the same type of currency—the one which we introduce in this manuscript.
Example 1. For the presented SDI quantum money scheme, to be unforgeable in a qubit-by-qubit way, it is enough that the source of the banknote (if it can produce a large number of banknotes) manages to produce SDI key at a rate  . It is, however, not demanded that
. It is, however, not demanded that  , i.e. that the source would be able to produce money equivalent to the small number of runs of the SDI key generation experiment with the maximal possible rate PQ.
, i.e. that the source would be able to produce money equivalent to the small number of runs of the SDI key generation experiment with the maximal possible rate PQ.
Suppose that some provider PI can produce the SDI quantum money which passes the acceptance threshold 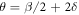 for some
for some 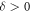 . Next, suppose that some other provider PII can produce a reliable SDI quantum money with the lower acceptance threshold
. Next, suppose that some other provider PII can produce a reliable SDI quantum money with the lower acceptance threshold 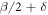 . As we have proved in theorem 1, banknotes of both providers are valid and cannot be forged under the same set of assumptions. However, the banknote of the provider PI can be attributed with a larger quantum commodity value defined as the SDI key rate of a source which produced the banknote. From the perspective of banknote's holder, this key rate implies a nonzero rate of the min-entropy of banknote's quantum state and hence the nonzero rate of the private randomness. An additional reason to keep the PI type money and spend more often PII type is that the first one could be more robust to noise. Indeed, even decrease by δ of the observed fraction of the correct guesses will not invalidate the banknote.
. As we have proved in theorem 1, banknotes of both providers are valid and cannot be forged under the same set of assumptions. However, the banknote of the provider PI can be attributed with a larger quantum commodity value defined as the SDI key rate of a source which produced the banknote. From the perspective of banknote's holder, this key rate implies a nonzero rate of the min-entropy of banknote's quantum state and hence the nonzero rate of the private randomness. An additional reason to keep the PI type money and spend more often PII type is that the first one could be more robust to noise. Indeed, even decrease by δ of the observed fraction of the correct guesses will not invalidate the banknote.
We make then the following observation:
Observation 2. If the Quantum Oresme–Copernicus–Gresham's law applies, the SDI quantum money with a lower acceptance threshold θ will drive out the SDI quantum money with a higher θ. (We note here, that we have implicitly assumed that the hardware parameters of the realization by PI and PII are comparable. Otherwise, a realization of the banknote according to type PII' receipt can be simply too expensive, e.g. in energy spent on keeping them in a quantum wallet).
The above example is minimal, as it concerns different ways of realization of the same money scheme (i.e. currency). It is however plausible that if the quantum version of the OCG law turns out to be accurate, the individuals will tend to keep the most secure, cheapest to produce and to store money of the highest commodity value (in the sense of its use for quantum information processing), and will spend the other currencies more often. Going a bit further, one can consider monies in a theory T (for such a general approach see [30]), and have a 'T Oresme–Copernicus–Gresham's law', a theory-dependent version describing the flow of currencies valid in theory T. An interesting particular case would be the 'multi-theory OCG law' that could govern the flow of currencies between different sub-theories. A natural example of the latter would be Classical-Quantum Oresme–Copernicus–Gresham's law, expressing the behavior of classical currencies and the quantum ones on the same footing. In this case, we can treat quantumness itself as an intrinsic value. It is because it can prevent some kinds of attacks.
6. Discussion
6.1. A comparison of the money schemes
In table 3, we present the comparison of different protocols, including the original protocol of Stephen Wiesner [1] and that of Dimitry Gavinsky [7], and show which parties and devices have to be trusted by the Bank in order to maintain security.
Table 3. Table of the Bank's trust.
| Protocol | Classical scheme | Wiesner's scheme [1] | Gavinsky's scheme [7] | SDI[this work] | DI[this work] |
|---|---|---|---|---|---|
| Source device | Yes | Yes | Yes | No | No |
| Alice's measurement | N/A | Yesa | No | No | No |
| System dimension | No | No | No | Yes | No |
| Number of branches | 1 | unlimited | unlimited | unlimited | unlimited |
aThe measurement of Alice's subsystem can be performed in Bank's branch or inside the partially trusted terminal (for example, in a shop).
6.2. How close we are to practice?
A fundamental obstacle in the realization of the presented one and many other money schemes is the fact that it relies on the existence of a reliable and long-time living quantum memory. It is hard to foresee when (if ever) such memories would be available. However, there are works in this direction. As an example of a recent substantial experimental progress in developing the quantum memory, we can invoke the paper by Wang et al [59], presenting a single-qubit quantum memory that exceeds coherence time of ten minutes. Furthermore, Harper and Flammia [60] demonstrated the first implementation of the error-correcting codes on a real quantum computer. It may indicate that the error-correcting codes can become useful in the near future quantum memories.
We want to emphasize here that the tasks of universal fault-tolerant quantum computing [61] and of a reliable quantum repeater [62] (for latest discovery see [63] and references therein) are both different from that of a fault-tolerant quantum storage (QS). The memory of the quantum computer need not be stable for a long time, because it is needed only for the time when the gates of the quantum algorithm are done, while the QS needs to be stable for a long time. However, operations on the QS are far from being universal [64], reduced to measurements in two bases (at least in the considered SDI quantum money scheme).
Although there is no physical law that bounds from above the time of coherence of a qubit state, achieving a reliable QS appears to be an arduous task, because of quantum decoherence, which is usually happening very fast. This is the reason why the very first idea (of QS needed for money schemes) that appear in theory may become the last one (after quantum computer and quantum Internet) to be realized in practice. It may also happen because, in contrast to quantum computing or secure quantum communication, the money scheme requires to be widely implemented in order to be useful.
It is also worth to notice that, recently, the first experimental implementation of quantum money schemes were performed [31–33]. It indicates that real-life implementation of quantum money could potentially be achievable using near-future technologies.
6.3. Conclusions
In this article, we have presented an alternative testing method for the original Wiesner's banknotes—a semi-device-independent quantum money scheme. To our knowledge, this is the first attempt to provide the quantum money scheme unforgeability of which would not entirely rely on trusting quantum source device and the inner workings of the verifying terminal at the same time.
Furthermore, we provide impossibility results for a fully device-independent quantum money scheme. It shows that our semi-device-independent approach is close to the strongest possible money scheme. To clarify, by the strongest, we mean here that we maximally reduce trust in the inner working of all quantum devices that are used in all stages of money production and verification.
We have provided a protocol of quantum money, which has relaxed assumptions with respect to Wiesner's protocol and is at the same time immune to a broader class of attacks.
Considered attacks and the aspect of classicality of the money have not been considered so far. The attacks are, in fact, hardware Trojan horse attacks that can exploit modification of both the production and verification process.
It is plausible that the proposed scheme inherits the security of the underlying, in our case, the original semi-device-independent quantum key distribution protocol. Given the full proof of security of the SDI QKD against a forward signaling adversary, as it is the case for the DI QKD [65] (see [66] for the latest breakthrough), it may follow that our suitably modified scheme is fully unforgeable. Sufficient modification concerns the communication in the verification procedure. The counterfeiter would need to give the answer(s)  after getting inputs
after getting inputs 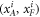 , but before learning next inputs
, but before learning next inputs 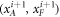 . In such a case, each possible history-dependent lie can be treated safely as a part of the attack of the device and hence would not affect the model. The rest of the proof would follow from similar arguments as above with proper use of the concentration of martingales. It is, therefore, important to verify if the SDI protocol is fully secure. An intermediate step would be to extend the security proof the presented SDI quantum money scheme to its variant given in [67] proves there to be secure against collective attacks.
. In such a case, each possible history-dependent lie can be treated safely as a part of the attack of the device and hence would not affect the model. The rest of the proof would follow from similar arguments as above with proper use of the concentration of martingales. It is, therefore, important to verify if the SDI protocol is fully secure. An intermediate step would be to extend the security proof the presented SDI quantum money scheme to its variant given in [67] proves there to be secure against collective attacks.
One might think that we could have used the scheme of the device-dependent key secure against the quantum adversary [65] directly, avoiding thereby unnatural assumption that the terminal can change (lie about) output values only in an independent manner during verification procedure. It is indeed straightforward to extend the idea presented here for a single Bank's branch with much weaker assumptions. However, it needs suitable modifications leading to a novel scheme, in order to be extended to the case with multiple Bank's branches. This approach, therefore, results in a scheme fundamentally different from the original one and its follow-ups like the presented SDI quantum money scheme.
In general, SDI QKD and the SDI quantum money scheme are connected by the honest implementation and underlying game as well as by the common concepts that assure their security. However, they are also different, as we have discussed, in that, in particular, they have different thresholds for the number of correct guesses in the random access code game. It is because the conditions leading to security thresholds does not coincide, reflecting difference in security scenarios. It is important here to note that the moderate error threshold opens the possibility to some robustness to noise, which is important to study further (see in this context recent article [68]). It is also important to ask if other games than the random access code game, can lead to similar schemes via our concept of 'winning in more than half of possible times' as we exposed in equation (2). Considering other setups can lead possibly to weakening of the assumptions much in the same way as the assumptions of SDI QKD has been to some extent relaxed in [68] for private randomness certification.
Given a more promising for practical realization variant of this scheme exists, one should consider its robust version that can be realized in the laboratory, including all side effects that may potentially open it for the attacks of hackers. This aspect of the SDI QKD has been recently studied in [35, 67, 69–71].
Another important direction of development would be checking if the proposed scheme could be treated as an option for a user of the original Wiesner's scheme or its other extensions like Gavinsky's protocol. The resulting scheme would give higher protection against Trojan horse attacks, matching the best of two approaches. In the presented scheme, the banknotes (even in case of the honest client Alice) are inevitably lost during verification. It seems natural (like it is done by Gavinsky [7]) to extend our scheme to the case of the transactions, which we also defer to the future work.
Finally, in a bit speculative way, we have put forward a hypothesis called the Quantum Oresme–Copernicus–Gresham's law: an analog of the classical law of the economy, also known as Gresham's law. We have supported the possible validity of this hypothetical law based on different realizations of the SDI quantum money scheme, corresponding to the different values of the threshold leading to the acceptance of money. These speculations need further, more formal, exploration with examples based on more types of currencies, as well as an extension (what appears to be straightforward) to the case of resources within the paradigm of [72].
Acknowledgments
The work is supported by the grant Sonata Bis 5 no. 2015/18/E/ST2/00327 from the National Science Centre, Poland. KH acknowledges partial support by the Foundation for Polish Science (IRAP project, ICTQT, contract no. 2018/MAB/5, co-financed by EU via Smart Growth Operational Programme).
The authors would like to thank Anubhav Chaturvedi, Ryszard P Kostecki, Sergii Strelchuk, and Marek Winczewski for useful comments. MS thanks Or Sattath for the enlightening discussion about relating results presented as a poster at the 8th International Conference on Quantum Cryptography (QCrypt 2018) Shanghai, China, 27–31 August 2018.
Author Contributions: All authors researched, collated, and wrote this paper.
Competing interests: The authors declare that there are no competing interests.
Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.
Appendix A.: Preliminary definitions
We will start by defining two crucial constants M and PQ, which come from [14],
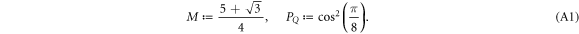
It is easy to see that 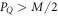 .
.
Lets us now define the notation used in the rest of the paper. By y's we denote the inputs used by the Bank in order to create the money, x's stand for the questions that the branches verifying Alice and Frederick ask them, 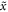 represents real value that Alice and Frederick input into the devices, and we use a's for Alice's and Frederick's outputs. Furthermore, i in an upper index denotes the ith run of the protocol that acts on the ith quantum subsystem. The general attack performed in a qubit-by-qubit manner (see Assumptions ASM5 and ASM6) can be described by a probability measure on the data used in the verification protocol. The Bank generates part of the data (inputs to the verification procedure). On the other hand, Alice and Frederick generates the outputs aA and aF according to their choice of the conditional distribution. The total joint distribution of the inputs and outputs reads
represents real value that Alice and Frederick input into the devices, and we use a's for Alice's and Frederick's outputs. Furthermore, i in an upper index denotes the ith run of the protocol that acts on the ith quantum subsystem. The general attack performed in a qubit-by-qubit manner (see Assumptions ASM5 and ASM6) can be described by a probability measure on the data used in the verification protocol. The Bank generates part of the data (inputs to the verification procedure). On the other hand, Alice and Frederick generates the outputs aA and aF according to their choice of the conditional distribution. The total joint distribution of the inputs and outputs reads
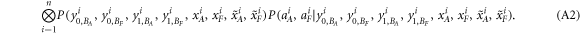
In what follows we will simplify it due to certain assumptions. We know, from the definition of money generating protocol, that if Frederick wants to verify the same banknote as Alice, then y's are the same for all branches, so we can omit variables for each branch and write just 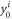 and
and 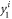 . Furthermore, if Bank's branches input appropriate bits to the devices themselves, than we are sure that
. Furthermore, if Bank's branches input appropriate bits to the devices themselves, than we are sure that 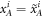 and
and 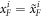 , obtaining
, obtaining
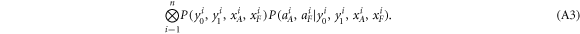
Observation 3. Our scheme remains secure if we allow Alice and Frederick to set device inputs, under the assumption that they do independently in each run. Any run-independent cheating strategy where Alice or Frederick uses inputs 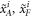 that are different from
that are different from 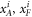 provided by the Bank can be incorporated into the inner working of the untrusted devices so we can also omit it.
provided by the Bank can be incorporated into the inner working of the untrusted devices so we can also omit it.
Since we assume that y's and x's generated by Bank are fully random, what is possible due to Assumption ASM1, we can rewrite the above formula as
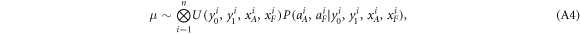
where U, here and in all measures defined later, stands for the uniform distribution over appropriate variables.
Now we can define the set describing successful forgery, meaning that both Alice and Frederick are accepted using the same banknote.
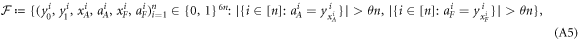
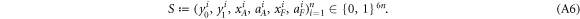
We also define sequences
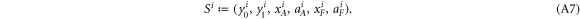
Now we can make the following observation that is an easy consequence of the security proof of [14]. It is important to notice that we need here Assumptions ASM1, ASM2, ASM3, and ASM4 since there are also necessary in [14] For clarity, we change notation by substituting B and E by A and F, respectively.
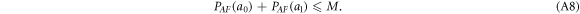
Proof. From equation (12) of [14] and the comment that follows the equation we know that
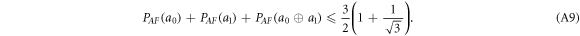
Using equation (13) of [14],
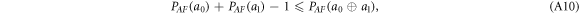
we obtain
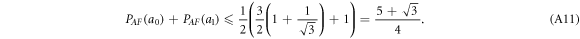
The right side is equal to M, which completes the proof. 
Appendix B.: Main lemmas
We will use numerously the concentration property of a distribution of independently distributed n random variables on ![$[0,1]$](https://content.cld.iop.org/journals/1367-2630/22/2/023007/revision2/njpab6872ieqn156.gif) due to Hoeffding, of the form
due to Hoeffding, of the form
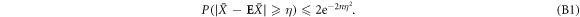
where 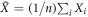 .
.
For a bitstring x of length n we will denote by  the number of occurrences of symbol 0 in x (analogously
the number of occurrences of symbol 0 in x (analogously 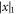 will denote the number of 1s in x). Thus,
will denote the number of 1s in x). Thus,
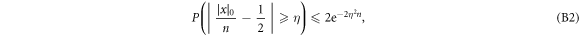
where  . Due to the above concentration, probability mass function is concentrated on the so-called η-typical sequences, defined as the values of x satisfying
. Due to the above concentration, probability mass function is concentrated on the so-called η-typical sequences, defined as the values of x satisfying 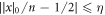 . In other words, for a set
. In other words, for a set
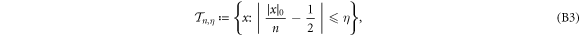
there is,
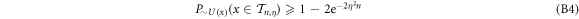
where the probability is taken from a uniform distribution U(x) of sequences 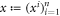 over
over  . In particular, for two sequences xA and xF drawn independently at random from
. In particular, for two sequences xA and xF drawn independently at random from 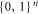 ,
,
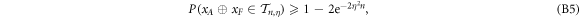
where by  we mean the bit-wise XOR operation on the bits of xA and xF. Indeed, for any fixed xA the distribution of
we mean the bit-wise XOR operation on the bits of xA and xF. Indeed, for any fixed xA the distribution of 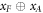 is uniform if such was that of xF. Then we can use the typicality argument and average over
is uniform if such was that of xF. Then we can use the typicality argument and average over 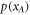 .
.
At the expense of small error, one can deal only with such as S that have η-typical inputs xA and xF. Such S will be called η-typical:
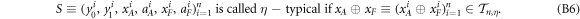
The set of η-typical S will be denoted as 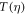 .
.
In what follows, we will show that the probability of acceptance of a banknote twice, i.e. 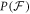 , is equal to the probability accepting it twice in a different scenario (the XOR scenario). In the latter, Alice gets xA while Frederick obtains
, is equal to the probability accepting it twice in a different scenario (the XOR scenario). In the latter, Alice gets xA while Frederick obtains  . Even though it will not be the case in real life, this transformation of the scenario (and the corresponding probability measure) will simplify our considerations.
. Even though it will not be the case in real life, this transformation of the scenario (and the corresponding probability measure) will simplify our considerations.
The XOR scenario is obtained from the original one by the following map on the events S:
We will refer to the transformed event as the one having 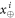 on the position where
on the position where  is in S:
is in S:
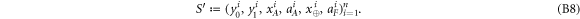
We define the set of all forged  in a way analogous to the definition of the set
in a way analogous to the definition of the set  :
:
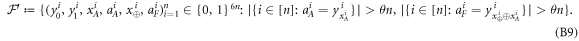
A new probability measure 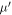 defined on the set of events
defined on the set of events  is defined as
is defined as
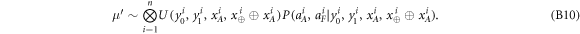
- 1.is bijective and involutive;
- 2.satisfies
 and
and - 3.satisfies
 .
.
Proof. The bijectivity follows directly from the fact that  is bijectively mapped to
is bijectively mapped to  . The first input is preserved, while the second one can be reconstructed uniquely by XORing inputs. It is also easy to see that π is an involution, since
. The first input is preserved, while the second one can be reconstructed uniquely by XORing inputs. It is also easy to see that π is an involution, since 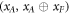 is mapped back to
is mapped back to 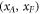 .
.
We show now Property 2. Let  . This happens if and only if
. This happens if and only if
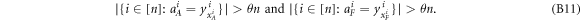
The event 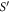 equals
equals 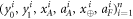 . By definition of
. By definition of 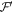 , we have that
, we have that 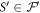 if and only if
if and only if
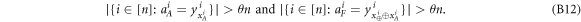
Since the left conditions are identical, we only have to prove equality of the right conditions. By definition of a map  , we obtain
, we obtain
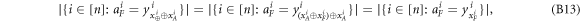
what proves an appropriate equality and implies that  .
.
Finally, we argue that the Property 3 also holds. Let us fix arbitrary S. Hence, 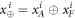 in definition of
in definition of 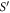 , and
, and
where  above denotes that equality follows from the properties of the inverse of map π, which due to involution property is equal to π.
above denotes that equality follows from the properties of the inverse of map π, which due to involution property is equal to π.

Alice, as before, gets bit 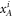 , but Frederick obtains XOR of bits
, but Frederick obtains XOR of bits 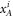 and
and 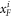 . Despite this, 'original' box, due to 'wirings', receives
. Despite this, 'original' box, due to 'wirings', receives 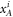 and
and  . We have then an important corollary that we can focus now on the XOR scenario because the probability of forgery in the latter equals the probability of forgery in the former.
. We have then an important corollary that we can focus now on the XOR scenario because the probability of forgery in the latter equals the probability of forgery in the former.
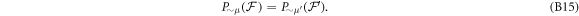
One can focus on the typical sequences S, i.e. those for which 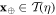 , at the expense of exponentially small inaccuracy in estimating the probability of forgery due to measure
, at the expense of exponentially small inaccuracy in estimating the probability of forgery due to measure  .
.
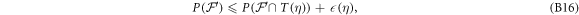
with 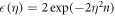 .
.
Proof. With a little abuse of notation we will mean by  the properly ordered sequence of tuples
the properly ordered sequence of tuples  , where
, where  , and by analogy the same for other symbols.
, and by analogy the same for other symbols. 
We will show first a sequence of (in)equalities:
We have used the fact that the distribution of  is the same (uniform) irrespectively of a particular attack. This is because the distributions of xA and xF with respect to the measure μ are uniform and independent from the attack. It follows from the fact that there are being prior to the attack. Similarly,
is the same (uniform) irrespectively of a particular attack. This is because the distributions of xA and xF with respect to the measure μ are uniform and independent from the attack. It follows from the fact that there are being prior to the attack. Similarly, 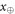 has the distribution of
has the distribution of  according to the definition of a measure
according to the definition of a measure 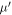 . In the last inequality, we have used the typicality argument from equation (B5).
. In the last inequality, we have used the typicality argument from equation (B5).
Due to the random nature of variable  ,
,
The advantage of the measure  is that we can easily divide the set of each run i according to the values of the
is that we can easily divide the set of each run i according to the values of the 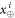 . Technical as it sounds, it will simplify the argument. In the runs where
. Technical as it sounds, it will simplify the argument. In the runs where  , the best strategy achieves quantum value PQ for both Alice and Frederick. However, for
, the best strategy achieves quantum value PQ for both Alice and Frederick. However, for 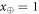 , they are in a position of Alice guessing the opposite bit to the one which Frederick is at the same time in this run i to guess. Hence, they are limited, as it is shown in the original paper by Pawłowski and Brunner [14].
, they are in a position of Alice guessing the opposite bit to the one which Frederick is at the same time in this run i to guess. Hence, they are limited, as it is shown in the original paper by Pawłowski and Brunner [14].
From now on, we will fix 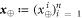 and prove a common bound on guessing for all of its typical values. We can then define new conditional measure
and prove a common bound on guessing for all of its typical values. We can then define new conditional measure 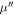 that depends on
that depends on 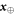 as
as
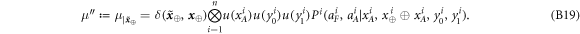
We will now show that, on average, the forgeries Alice and Frederick have the total number of correctly guessed bits of  bit-strings bounded from above by particular value. Let us first define the set of indexes
bit-strings bounded from above by particular value. Let us first define the set of indexes
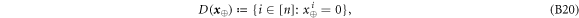
and its complement  . It is important to notice that, for runs in the set
. It is important to notice that, for runs in the set 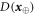 , Alice and Frederick will be asked about the same Bank's bit and in the case of
, Alice and Frederick will be asked about the same Bank's bit and in the case of 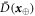 they will have to guess two different bits of the Bank.
they will have to guess two different bits of the Bank.
Then we can consider four types of random variables defined on 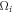 , each depending on the value of the
, each depending on the value of the 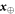 . It is important to notice that these variables describe the probabilities of guessing appropriate bits in ith run, by Alice and Frederick respectively and furthermore have a strong connection with the definition of
. It is important to notice that these variables describe the probabilities of guessing appropriate bits in ith run, by Alice and Frederick respectively and furthermore have a strong connection with the definition of 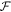 .
.
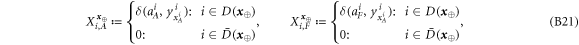
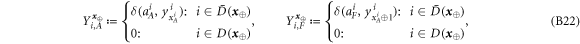
where the sample space is defined as
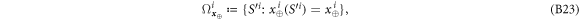
while 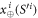 denotes taking a variable with a label
denotes taking a variable with a label 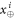 from the sequence
from the sequence 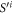 . We will also define sums
. We will also define sums
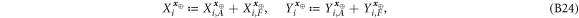
and the random variables built from Xi and Yi, that is their sums:
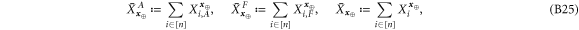
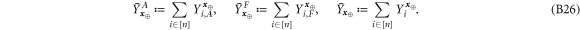
From equation (B19) we know that the measure  is a product of measures
is a product of measures
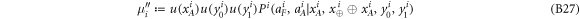
what implies that 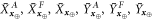 are described by Poisson distribution.
are described by Poisson distribution.
The respective averages over the measure  read
read
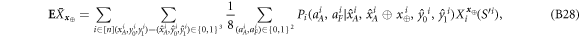
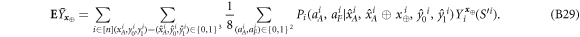
Although the above averages are defined on the whole range ![$[n]$](https://content.cld.iop.org/journals/1367-2630/22/2/023007/revision2/njpab6872ieqn231.gif) , they depend only on their respective subsets:
, they depend only on their respective subsets:
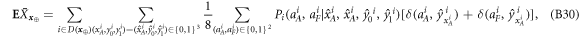
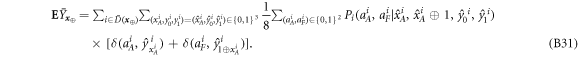
We will prove now that the above averages are bounded if the attack is made in a qubit-by qubit manner, and adversaries are quantum (see Assumptions ASM3–ASM6).
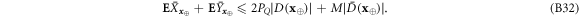
Proof. We will separately prove that the first term of lhs is bounded by the first term of rhs, and later that the second term of lhs is bounded by the second term of rhs. The best quantum strategy for a single person (say, Alice) in a single run of experiment is upper bounded by PQ, while the other party is asked to guess the same bit as Alice was asked, so can copy her answer. We have
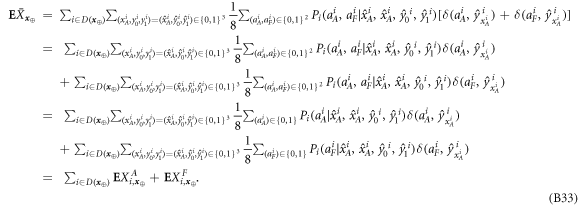
Now, for each  , there is:
, there is:
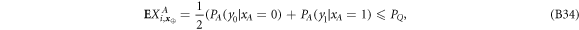
where we here used equation (7) of [14] (note the change of notation: our  correspond to
correspond to  there, respectively). Analogously, for
there, respectively). Analogously, for  ,
,
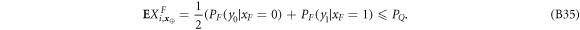
Summing the above inequalities over  we obtain
we obtain 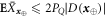 .
.
More elaborative is relating the second terms of (B32). We begin analogously:
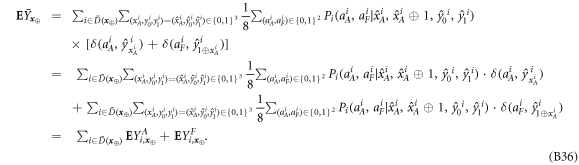
For each 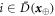 ,
,
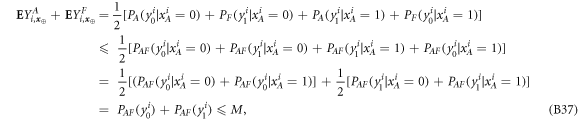
where in the pre-last inequality we have used the fact, that Alice and Frederick can collaborate. This can only increase the average probability of guessing. In the last inequality we have rephrased the results of [14] as in Observation 4. Summing up over 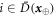 , we obtain
, we obtain
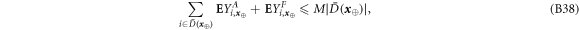
as it was claimed.

We have shown above that the average number of guessed bits has an upper bound. We are going now to argue about the concentration properties of the random variables involved in the process.
We assume here that 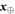 is fixed, and results in the well defined sets
is fixed, and results in the well defined sets  and
and 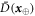 . For brevity, we will sometimes omit
. For brevity, we will sometimes omit 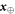 from the notation of D. We will also define subsequences
from the notation of D. We will also define subsequences 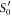 and
and  of particular realization of strategy
of particular realization of strategy  ,
,
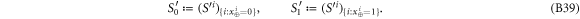
In the spirit of the above technical lemma, we will consider four random variables, each reporting the distance between the theoretical average value of a number of guessed inputs and the observed number of guessed inputs for the respective dishonest party on the respective set (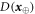 or
or 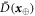 ),
),
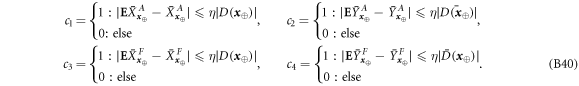
Due to the concentration property given in equation (B1) on the total measure  , that is product of measures
, that is product of measures  (see equation (B27)), base on which the joined distribution of
(see equation (B27)), base on which the joined distribution of  random variables defined above, we can bound the probability of 0's as follows:
random variables defined above, we can bound the probability of 0's as follows:
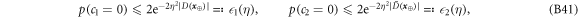
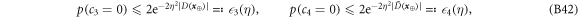
where the probability of the above measures is taken over the measure  .
.
Now, thanks to the union bound, we obtain:
Corollary 2. For any 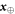 , there is
, there is
The above rather technical results are summarized below in the upper bound on the total number of guesses. Namely, we will show that for a fixed  , and an attack defining the measure
, and an attack defining the measure  , the random variable of the total number of guesses defined as a function of
, the random variable of the total number of guesses defined as a function of 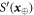 sampled from
sampled from 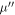 is bounded from above with high probability, as it is close to the sum of averages that are bounded. Indeed, let us define the random variable of the total number of guesses,
is bounded from above with high probability, as it is close to the sum of averages that are bounded. Indeed, let us define the random variable of the total number of guesses,
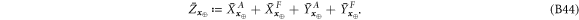
We additionally define two other useful variables,
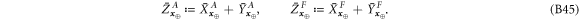
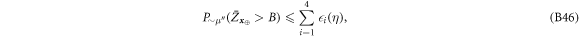
where
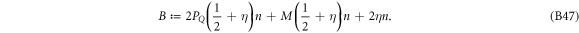
Proof. From the corollary 2, omitting the modulus, we obtain a sequence of inequalities
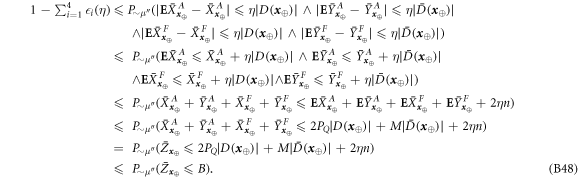
In the second inequality we have used lemma 2. In the next one we have used definition of  , and then we have used the typicality of
, and then we have used the typicality of 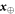 , which implies upper bounds on the power of sets
, which implies upper bounds on the power of sets 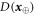 and
and 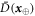 . This implies
. This implies
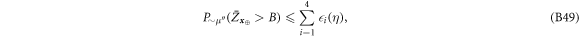
as we have claimed.

Let us recall now definition of 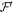 from equation (B9)
from equation (B9)
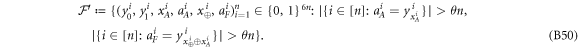
In what follows for clarity we will explicitly show dependence on θ using notation  .
.
Observation 6. Let the acceptance threshold be 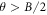 . Then
. Then
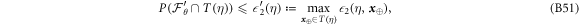
where 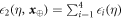 .
.
Proof. Let us fix 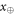 . Then there is
. Then there is
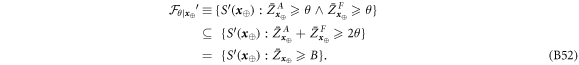
The above fact is consequences of the sequence of implications, where the last follows from 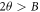 . We now invoke equation (B18) and note immediately a bound:
. We now invoke equation (B18) and note immediately a bound:
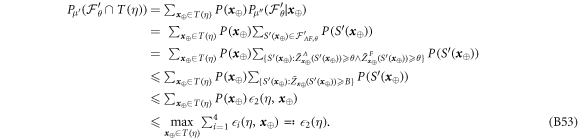
In the pre-last inequality we have used lemma 3 with 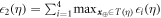 .
. 
Appendix C.: Proof of main theorem 1
Finally, after presenting all necessary definitions and lemmas, we are ready to proof theorem 1. For convenience of the reader we will first restate the theorem. Let
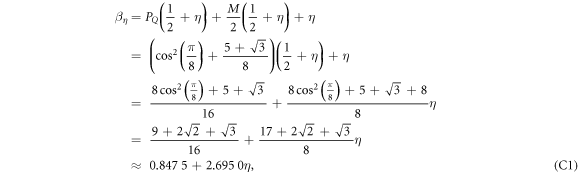
for some small η chosen in such a way that 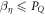 .
.
Theorem 2 Let acceptance threshold 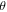 be larger than
be larger than 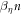 . Then, under Assumptions ASM1–ASM6, where k denotes the number of Bank's branches the probability of a successful forgery
. Then, under Assumptions ASM1–ASM6, where k denotes the number of Bank's branches the probability of a successful forgery 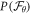 is exponentially small in number of banknote's qubits n and is bounded by
is exponentially small in number of banknote's qubits n and is bounded by
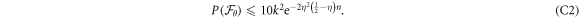
Proof. Using corollary 1, lemma 1, and Observation 6 we obtain the following bound on 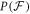
Since there are many Bank's branches, collaborating Alice and Frederick can use birthday attack in order to choose two branches that have the biggest common set D. For k branches, we apply union bound obtaining another factor k2 what finalizes the proof. 
Appendix D.: Proof of No-go for device-independent quantum money
In this section, we will provide more formal proof of Observation 1.
Proof. We will follow the standard proof technique used in device-independent scenarios. Since all of the quantum devices are untrusted, the only way for Bank's branches to verify the money is to use classical statistics of inputs and outputs from quantum black boxes. Without loss of generality, we can assume a four-partite scenario with two Bank's branches B1, B2, Alice A, and Frederick F that all share some nonlocal box. We will denote the device's inputs as I and outputs as O with appropriate subscript denoting the party. The general scenario can be modeled by the probability distribution of the form
In the verification phase, Alice tries to pass verification with branch B1, while Frederick tries with branch B2. Since Bank's branches cannot communicate, they have access only to the part of outputs. Therefore, the only way is to check correlations from distribution
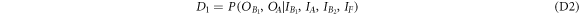
for the branch B1 and
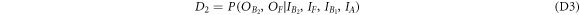
for the branch B2. We assume here that Alice and Frederick can freely talk during the verification stage. In order to be secure, the money scheme has to disallow both Alice and Frederick to pass verification. Furthermore, the conditions for passing verification have to be the same for all branches. Since there must exist a honest quantum implementation (see appendix E) for Alice with distribution H1, then Frederick could also pass verification using the same distribution 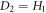 . To obtain such a result, Adversary, controlling the source and measurement devices, can prepare joined devices with distribution D simply as
. To obtain such a result, Adversary, controlling the source and measurement devices, can prepare joined devices with distribution D simply as 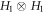 . Such preparation of state and measurement will always break any device-independent money scheme and cannot be detected by the Bank in any way without communication between the branches of the Bank.
. Such preparation of state and measurement will always break any device-independent money scheme and cannot be detected by the Bank in any way without communication between the branches of the Bank. 
Appendix E.: Honest implementation
In this appendix we will present honest implementation based on Semi-Device-independent Quantum Key Distribution [14]. Let, for all runs i, the honest source prepare all states 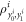 in the following way
in the following way
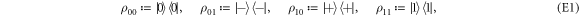
where 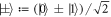 . Let us also choose an appropriate measurement
. Let us also choose an appropriate measurement  , depending on the branch's question xi,
, depending on the branch's question xi,
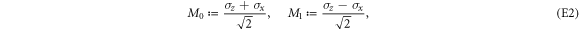
where  and
and  are Pauli matrices
are Pauli matrices
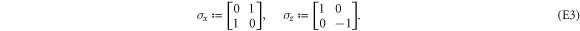
It turns out, as shown in [14], that, using these states and measurements, the optimal guessing probability equals 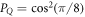 .
.
Remark 4 In the honest implementation of our scheme, we use the same states as in the original Wiesner's scheme. On the other hand, the measurement settings have to be different since, from [14], we know that Wiesner's cannot be used in the semi-device-independent approach.
Appendix F.: Required number of qubits
This appendix establishes the relation between the number of qubits and the upper bounds on the probability of forgery. Since from the equation (C1) we know that 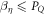 we can calculate that the maximal allowed value of η equals
we can calculate that the maximal allowed value of η equals
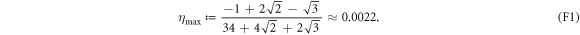
When we put that value into equation (10), for the trivial case of the single Bank without any additional branches, we obtain that
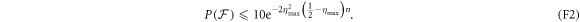
It is easy to calculate numerically that this bound becomes trivial when the number of qubits n is smaller than 463018. Furthermore, when we demand that the probability of forgery is smaller than some security parameter and we want to assume a more realistic scenario the number of required qubits grows significantly.
Although one cannot expect that such a large number of qubits will be available in quantum memories soon, let us emphasize that the bounds used in the proof of theorem 1 are not tight, and there is some room for improvement. What is more important, we expect that using more complex random access codes, i.e. ones with more inputs and outputs, can lead to a significant decrease in the number of required qubits as it is discussed in section 6.