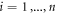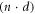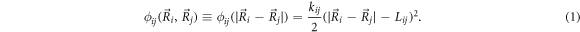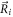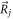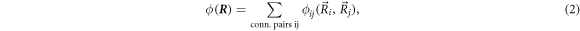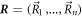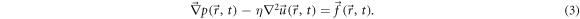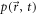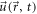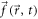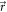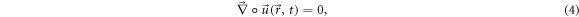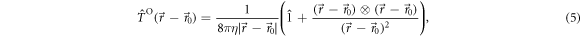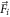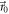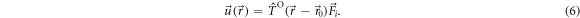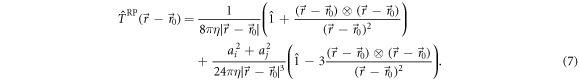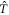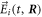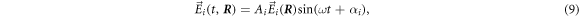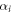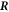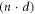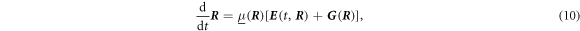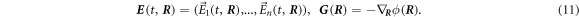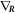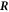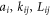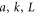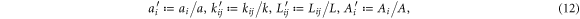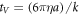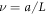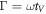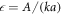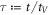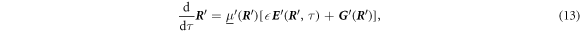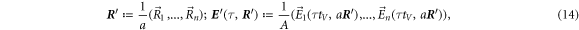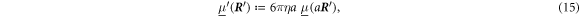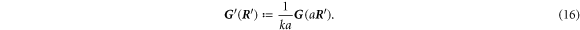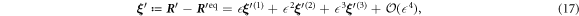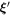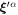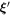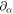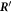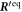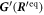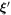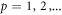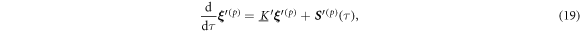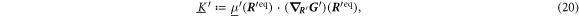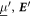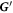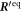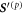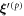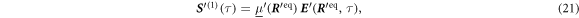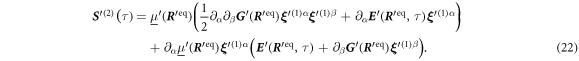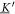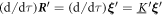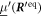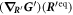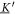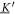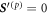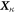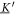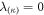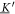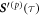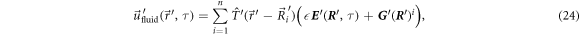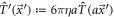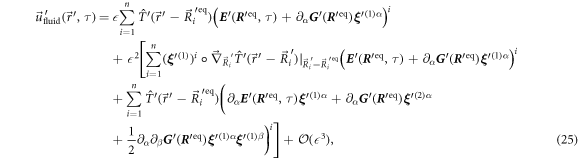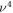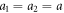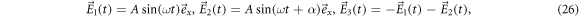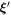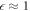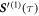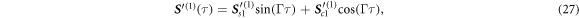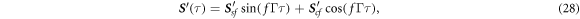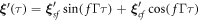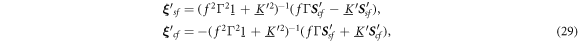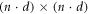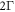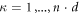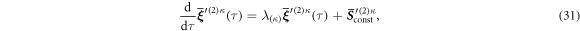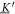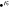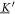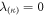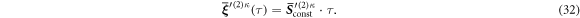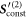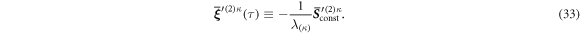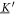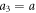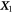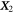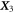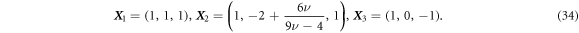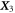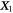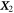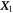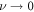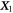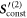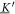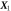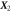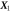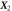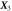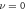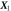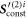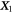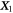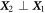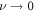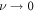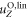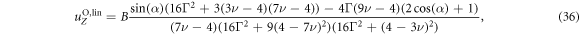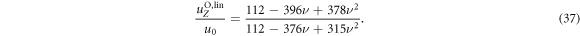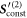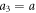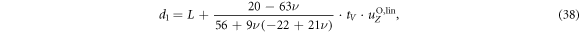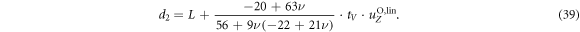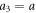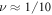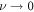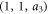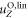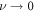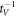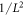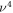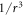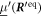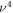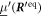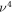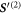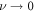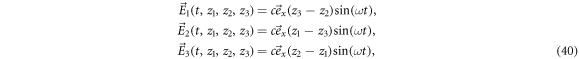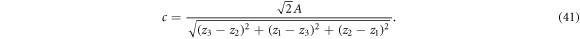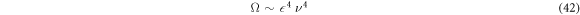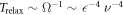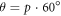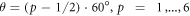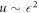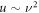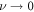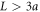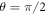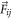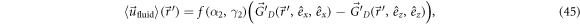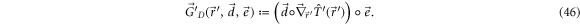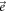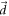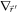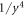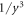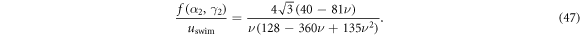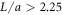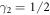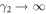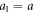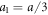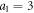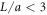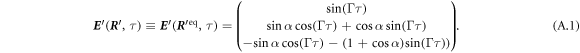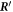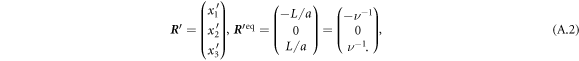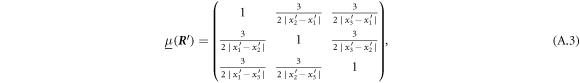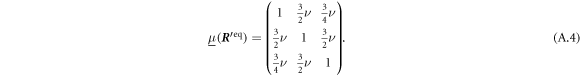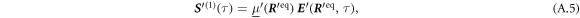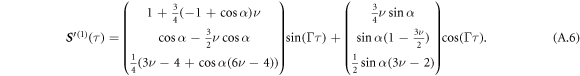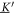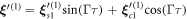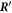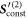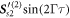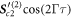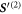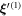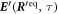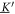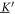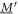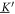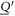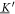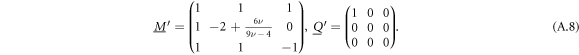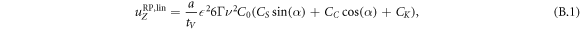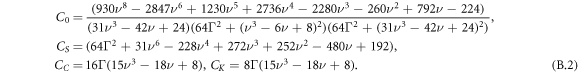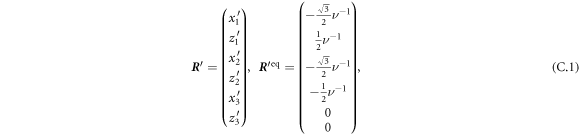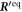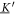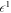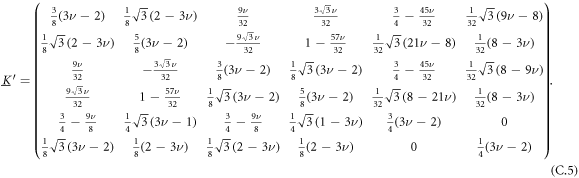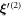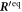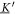A general perturbative approach for bead-based microswimmers reveals rich self-propulsion phenomena

The locomotion of swimmers at small scales has been an active area of research in recent years [1], with a variety of microswimmer models being proposed, both experimental [2–11] and theoretical [12–21]. A number of these models aims at understanding the propulsion mechanisms of small organisms such as bacteria or algae cells, or at designing artificial microswimmers. Due to the time-independence of the Stokes equation, modeling microswimmers has turned out to be a tradeoff between as little degrees of freedom as possible and enough degrees to break the time-reversal symmetry [22].

A milestone in the field has been the minimalistic swimmer consisting of three spherical beads arranged in a linear fashion, introduced by Najafi and Golestanian [12]. In their model, each neighbouring pair of beads is connected by an extendible arm of a length that is prescribed as a function of time. Calculating the swimming velocity to leading order in the extension of the arms gives rise to a simple intuition for the swimmer's speed: the displacement of the swimmer corresponding to one swimming stroke is proportional to the area enclosed by the swimmer's trajectory in the conformation space [13]. This model has been used to investigate the hydrodynamic properties of microswimmers, including the flow fields they produce and their mutual interaction [23–25], as well as the interaction of a swimmer with a wall [26, 27].

Despite its immense usefulness, this model suffers from the constriction of all internal degrees of freedom by the swimming stroke, namely the internal dynamical behavior of the swimmer cannot react to its surrounding. This was overcome by replacing the arms with springs and prescribing the forces acting on the beads rather than the stroke itself [28, 20]. Importantly, the responsive elastic degree of freedom, which is typically associated with the swimmer design, but which could also be in the fluid, is responsible for several interesting phenomena. For example, it is the source of the optimal driving frequency in the overdamped regime [29] and it promotes swimming based on the minimization of drag or enhancement of hydrodynamic interactions [20]. Furthermore, it is also responsible for the existence of a viscosity maximising the swimming velocity [30] and synchronization effects of the stroke [20]. Similar findings have been reported in investigations of bead-based swimmers in a visco-elastic fluid [31, 32]. Recently, an altered version of the bead-spring model has been proposed, where the swimmer was driven by periodic changes in the equilibrium lengths of the springs [33, 34].

The boundedness of the linear swimmer to one dimension is broken in a triangular swimmer geometry, allowing for translational as well as rotational motion [35, 14, 16]. This geometry has also been used to model Chlamydomonas reinhardtii and investigate in particular the synchronization between the beating of its two flagella [18, 36, 19]. Experimentally, a triangular swimmer with intrinsic elasticity has been realized by placing ferromagnetic beads subject to an oscillating magnetic field at a water–air interface [10, 9] and a similar system has been investigated by means of lattice Boltzmann simulations [29]. The full controllability of a triangular swimmer in the 2D space has recently been shown analytically [21], expanding on the use of the bead-spring model [20]. However, the perturbative calculations in [20, 30, 21] hold only in the limit of very large bead separations where the swimming velocity becomes extremely small. Especially since this limit is inaccessible in experiments (see [5, 9]) as external disturbances become exuberant and can break the swimmer, an investigation of swimmers with smaller bead separations is required and still lacking.

In this paper, we fill this gap by presenting a general perturbative framework to calculate the full behavior of arbitrarily shaped bead-spring swimmers, i.e. not only their stroke and swimming velocity, but also the average deformation and the produced flow field. The accuracy of the results in terms of the bead separation is tuned by the choice of the mobility matrix, whereas the precision in terms of the actuation strength is controlled by the perturbation order. This is essentially different from previous calculations [28, 30, 21] as we split the equation of motion by orders of the driving force and systematically solve the long-term limit of each order, while the assumption of very large bead separation is not made within the perturbation scheme, but is imposed by the hydrodynamic model. Consequently, given a sufficiently precise mobility matrix, the presented method provides arbitrarily precise results for the swimming velocity. However, even within the same approximation for the mobility matrix as used in previous approaches, our systematic perturbative scheme provides some corrections. The latter are small for the symmetric linear swimmer, but grow strongly when the swimmer becomes asymmetric or is no longer linear. As an example of the latter, we choose a triangular swimmer for which, besides an accurate swimming velocity, we find a transient phase of rotation towards a purely translational stable steady state. Interestingly, under these conditions the swimmer produces a dipolar flow field, which has not been reported for the triangular bead-spring swimmer so far to our knowledge.

The remainder of the article is structured as follows: in the next section we introduce the general model of bead-spring microswimmers. We proceed by analyzing the equation of motion by means of perturbation theory and present the calculation of the swimmer's velocity, flow field and the beads's trajectories step by step in section 3. Subsequently, in section 4, we apply this framework to the linear swimmer as a benchmark. Finally, in section 5, we use it to investigate the triangular swimmer in both external and internal driving. Section 6 contains the discussion and conclusion.

We consider a microswimmer composed of n spherical beads of respective radius a_i ($i=1,...,n$) in the d-dimensional space. Throughout the paper, vectors and matrices on the d-dimensional configuration space of a single bead will be denoted with arrows and hats respectively. For vectors and matrices on the $(n\cdot d)$-dimensional configuration space of all beads, we use bold and underlined symbols respectively. Latin indices run from 1 to n, greek indices from 1 to n · d. Some pairs of beads are connected by linear springs which we assume here to be harmonic corresponding to the interaction potential

$$\begin{eqnarray}&&{\phi }_{{ij}}({\vec{R}}_{i},{\vec{R}}_{j})\equiv {\phi }_{{ij}}(| {\vec{R}}_{i}-{\vec{R}}_{j}| )=\displaystyle \frac{{k}_{{ij}}}{2}{\left(| {\vec{R}}_{i}-{\vec{R}}_{j}| -{L}_{{ij}}\right)}^{2}.\end{eqnarray} \tag{ 1 }$$

Here, ${\vec{R}}_{i}$ and ${\vec{R}}_{j}$ are the positions of the beads, k_ij the stiffness and L_ij the length of the spring connecting bead i and j in the swimmer's mechanical equilibrium. Our approach can also easily be adopted to more complex interaction potentials, e.g. magneto-capillary potentials (see [37]). Note that the springs are not tied to a certain direction but can freely rotate as the beads move in the fluid. The total spring potential of the device is given by

$$\begin{eqnarray}&&\phi ({\boldsymbol{R}})=\displaystyle \sum _{\mathrm{conn}.\,\mathrm{pairs}\,\mathrm{ij}}{\phi }_{{ij}}({\vec{R}}_{i},{\vec{R}}_{j}),\end{eqnarray} \tag{ 2 }$$

where we sum over all pairs of beads that are connected and define ${\boldsymbol{R}}=({\vec{R}}_{1},...,{\vec{R}}_{n})$ as a vector with n · d components.

We assume that the Reynolds number of the beads in the fluid is small and that the relaxation of the fluid takes place sufficiently fast [38] such that the fluid dynamics can be described by the Stokes equation

$$\begin{eqnarray}&&\vec{{\rm{\nabla }}}p(\vec{r},t)-\eta {{\rm{\nabla }}}^{2}\vec{u}(\vec{r},t)=\vec{f}(\vec{r},t).\end{eqnarray} \tag{ 3 }$$

Here, $p(\vec{r},t)$ denotes the pressure in the fluid, $\vec{u}(\vec{r},t)$ the velocity of the fluid, $\vec{f}(\vec{r},t)$ the force density applied to the fluid and η its dynamic viscosity. $\vec{r}$ and t denote position vector and time respectively. The fluid is assumed to be incompressible:

$$\begin{eqnarray}&&\vec{{\rm{\nabla }}}\,\circ \,\vec{u}(\vec{r},t)=0,\end{eqnarray} \tag{ 4 }$$

with ◦ denoting the scalar product. Forces ${\vec{F}}_{i}$ applied to all particles induce an instantaneous fluid flow field $\vec{u}(\vec{r})$. This flow field gives rise to hydrodynamic interactions between the particles in the fluid. The mathematical complexity associated with the description of those hydrodynamics interactions increases greatly as the typical distance between the particles decreases. In this article, to illustrate the precision and efficiency of our method, we will restrict ourselves to the two simplest expressions for the hydrodynamic interaction. Nevertheless, any expression can be used in our model, which does not suffer from any restriction regarding the hydrodynamic interactions considered. The simplest approximation is given by the Oseen tensor and reads

$$\begin{eqnarray}&&{\hat{T}}^{{\rm{O}}}(\vec{r}-{\vec{r}}_{0})=\displaystyle \frac{1}{8\pi \eta | \vec{r}-{\vec{r}}_{0}| }\left(\hat{1}+\displaystyle \frac{(\vec{r}-{\vec{r}}_{0})\otimes (\vec{r}-{\vec{r}}_{0})}{{\left(\vec{r}-{\vec{r}}_{0}\right)}^{2}}\right),\end{eqnarray} \tag{ 5 }$$

with ⨂  the tensor product and $\hat{1}$ the d-dimensional unity matrix. It describes two-body interactions only, where the flow field resulting from a force ${\vec{F}}_{i}$ acting on a bead located at position ${\vec{r}}_{0}$ is given by

$$\begin{eqnarray}&&\vec{u}(\vec{r})={\hat{T}}^{{\rm{O}}}(\vec{r}-{\vec{r}}_{0}){\vec{F}}_{i}.\end{eqnarray} \tag{ 6 }$$

For a large separation between two beads in terms of their radii, the Oseen tensor is a sufficient description for their interaction. For a more precise modeling of the hydrodynamic interactions, we make use of the Rotne–Prager approximation [39], which is given by

$$\begin{eqnarray}\begin{array}{rcl}{\hat{T}}^{\mathrm{RP}}(\vec{r}-{\vec{r}}_{0}) & = & \displaystyle \frac{1}{8\pi \eta | \vec{r}-{\vec{r}}_{0}| }\left(\hat{1}+\displaystyle \frac{(\vec{r}-{\vec{r}}_{0})\otimes (\vec{r}-{\vec{r}}_{0})}{{\left(\vec{r}-{\vec{r}}_{0}\right)}^{2}}\right)\\ & & +\displaystyle \frac{{a}_{i}^{2}+{a}_{j}^{2}}{24\pi \eta | \vec{r}-{\vec{r}}_{0}{| }^{3}}\left(\hat{1}-3\displaystyle \frac{(\vec{r}-{\vec{r}}_{0})\otimes (\vec{r}-{\vec{r}}_{0})}{{\left(\vec{r}-{\vec{r}}_{0}\right)}^{2}}\right).\end{array}\end{eqnarray} \tag{ 7 }$$

Investigations of the hydrodynamic interactions inside a two-bead system have shown that the Rotne–Prager approximation does deviate by less then 5% from the complete hydrodynamic interaction as long as L_ij/a_i > 3 [40]. Hence, we expect the Rotne–Prager approximation to be sufficient in this parameter range. More accurate expressions are available in the literature [38, 41] and can be employed similarly for the subsequent calculation. Under the Oseen and Rotne–Prager approximations, the mobility matrix of an ensemble of n spheres is a $(n\cdot d)\times (n\cdot d)$ matrix defined in terms of d × d blocks as

$$\begin{eqnarray}\underline{\mu }({\boldsymbol{R}})\equiv \underline{\mu }(({\vec{R}}_{1},...,{\vec{R}}_{n}))=\left\{\begin{array}{lr}\hat{1}/(6\pi \eta {a}_{i}), & \mathrm{for}\ i=j\\ \hat{T}({\vec{R}}_{i}-{\vec{R}}_{j}), & \mathrm{for}\ i\ne j\end{array}\right.,\end{eqnarray} \tag{ 8 }$$

with $\hat{T}$ either the Oseen or the Rotne–Prager tensor. In (8), we account for both, the Stokes drag as well as the interaction of the beads due to the fluid. Note that more accurate approximations for the hydrodynamic interaction [38, 41] do affect both diagonal and off-diagonal components of the mobility matrix. The springs are assumed to be not interacting with the fluid.

An oscillating force ${\vec{E}}_{i}(t,{\boldsymbol{R}})$ with fixed frequency ω is acting on each bead i as

$$\begin{eqnarray}&&{\vec{E}}_{i}(t,{\boldsymbol{R}})={A}_{i}{\vec{E}}_{i}({\boldsymbol{R}})\sin (\omega t+{\alpha }_{i}),\end{eqnarray} \tag{ 9 }$$

with A_i encoding the amplitude of the driving for each bead i and ${\alpha }_{i}$ the phase shift associated with each bead. The vector ${\vec{E}}_{i}({\boldsymbol{R}})$ is dimensionless and subject to a suitable normalization that will be chosen specifically for each geometry and driving protocol. As indicated above, we allow for a dependence of the driving forces on the current configuration of the swimmer ${\boldsymbol{R}}$. This is required if e.g. the driving forces result from spatially dependent magnetic or electric fields, or if certain demands to the driving protocol shall be fulfilled, like a constantly zero total torque for an effectively rotating swimmer.

The temporal evolution of the system is governed by the constitutive equation of the mobility matrix on the $(n\cdot d)$-dimensional configuration space of the beads as

$$\begin{eqnarray}&&\displaystyle \frac{{\rm{d}}}{{\rm{d}}{t}}{\boldsymbol{R}}=\underline{\mu }({\boldsymbol{R}})[{\boldsymbol{E}}(t,{\boldsymbol{R}})+{\boldsymbol{G}}({\boldsymbol{R}})],\end{eqnarray} \tag{ 10 }$$

with

$$\begin{eqnarray}&&{\boldsymbol{E}}(t,{\boldsymbol{R}})=({\vec{E}}_{1}(t,{\boldsymbol{R}}),...,{\vec{E}}_{n}(t,{\boldsymbol{R}})),\ {\boldsymbol{G}}({\boldsymbol{R}})=-{{\rm{\nabla }}}_{{\boldsymbol{R}}}\phi ({\boldsymbol{R}}).\end{eqnarray} \tag{ 11 }$$

${{\rm{\nabla }}}_{{\boldsymbol{R}}}$ denotes the gradient of a function with respect to all n · d components of ${\boldsymbol{R}}$. We furthermore omit the explicit t-dependence of ${\boldsymbol{R}}$ in our notation for the sake of clarity.

In view of the rescaling of the equations of motion, we introduce for each family of parameters ${a}_{i},{k}_{{ij}},{L}_{{ij}}$ and A_i a characteristic value ($a,k,L$ and A, respectively) and define dimensionless parameters by

$$\begin{eqnarray}&&{a}_{i}^{{\prime} }:= {a}_{i}/a,{k}_{{ij}}^{{\prime} }:= {k}_{{ij}}/k,{L}_{{ij}}^{{\prime} }:= {L}_{{ij}}/L,{A}_{i}^{{\prime} }:= {A}_{i}/A,\end{eqnarray} \tag{ 12 }$$

which become 1 in the case of equal parameters of one type.

To calculate how the swimmer behaves around a stable mechanical equilibrium, we develop a perturbative approach that allows to split the equation of motion by orders of the driving force. We firstly rescale the equation of motion using the characteristic length a and the characteristic time ${t}_{V}=(6\pi \eta a)/k$ [30], denoted as viscous time. The latter describes the time scale emerging from the interplay of viscous drag and the spring force acting on a bead. Any event taking place on a period much larger than t_V will correspond to a quasi-static process during which the system relaxes at every time step toward equilibrium. On the contrary, short lived events compared to t_V give small responses from the system because of high viscous dissipation.

From the previous definitions, we find the effective parameters to be $\nu =a/L$ the aspect ratio between bead radius and separation, and ${\rm{\Gamma }}=\omega {t}_{V}$ the rescaled driving frequency, comparing the time scale set by the external driving to the viscous one. Finally, $\epsilon =A/({ka})$ denotes the rescaled driving force amplitude, which in essence quantifies the swimmer deformation by describing the strength of the actuation force A relative to force needed to extend the reference spring by one bead radius, namely ka. Small values of therefore correspond to small swimmer deformations and are used for the development of the perturbative scheme. Depending on the precision required, more terms corresponding to higher orders can be used in the perturbation scheme. Rescaled variables are marked with an additional dash and the rescaled time is $\tau := t/{t}_{V}$. The equation of motion can then be re-expressed as

$$\begin{eqnarray}&&\displaystyle \frac{{\rm{d}}}{{\rm{d}}\tau }{\boldsymbol{R}}^{\prime} =\underline{\mu }^{\prime} ({\boldsymbol{R}}^{\prime} )[\epsilon {\boldsymbol{E}}^{\prime} ({\boldsymbol{R}}^{\prime} ,\tau )+{\boldsymbol{G}}^{\prime} ({\boldsymbol{R}}^{\prime} )],\end{eqnarray} \tag{ 13 }$$

with

$$\begin{eqnarray}&&{\boldsymbol{R}}^{\prime} := \displaystyle \frac{1}{a}({\vec{R}}_{1},...,{\vec{R}}_{n});{\boldsymbol{E}}^{\prime} (\tau ,{\boldsymbol{R}}^{\prime} ):= \displaystyle \frac{1}{A}({\vec{E}}_{1}(\tau {t}_{V},a{\boldsymbol{R}}^{\prime} ),...,{\vec{E}}_{n}(\tau {t}_{V},a{\boldsymbol{R}}^{\prime} )),\end{eqnarray} \tag{ 14 }$$

$$\begin{eqnarray}&&\underline{\mu }^{\prime} ({\boldsymbol{R}}^{\prime} ):= 6\pi \eta a\,\underline{\mu }(a{\boldsymbol{R}}^{\prime} ),\end{eqnarray} \tag{ 15 }$$

and

$$\begin{eqnarray}&&{\boldsymbol{G}}^{\prime} ({\boldsymbol{R}}^{\prime} ):= \displaystyle \frac{1}{{ka}}{\boldsymbol{G}}(a{\boldsymbol{R}}^{\prime} ).\end{eqnarray} \tag{ 16 }$$

The equation of motion (13) can be solved with a perturbative approach in the vicinity of  = 0. Therefore, we employ a suitable power series ansatz in for the displacement out of the equilibrium

$$\begin{eqnarray}&&{\boldsymbol{\xi }}^{\prime} := {\boldsymbol{R}}^{\prime} -{{\boldsymbol{R}}}^{{\prime} \mathrm{eq}}=\epsilon {{\boldsymbol{\xi }}}^{{\prime} (1)}+{\epsilon }^{2}{{\boldsymbol{\xi }}}^{{\prime} (2)}+{\epsilon }^{3}{{\boldsymbol{\xi }}}^{{\prime} (3)}+{ \mathcal O }\left({\epsilon }^{4}\right),\end{eqnarray} \tag{ 17 }$$

where ${{\boldsymbol{R}}}^{{\prime} \mathrm{eq}}$ is the rescaled equilibrium configuration of the swimmer. We also omit in our notation the explicit time-dependence of ${\boldsymbol{\xi }}^{\prime}$. A Taylor expansion of all ${\boldsymbol{R}}^{\prime}$-dependent parts of (13) around ${{\boldsymbol{R}}}^{{\prime} \mathrm{eq}}$ yields

$$\begin{eqnarray}\begin{array}{rcl}\displaystyle \frac{{\rm{d}}}{{\rm{d}}\tau }({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}}+{\boldsymbol{\xi }}^{\prime} ) & = & \left[\underline{\mu }^{\prime} ({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}})+{\partial }_{\alpha }\underline{\mu }^{\prime} ({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}}){{\boldsymbol{\xi }}}^{{\prime} \alpha }+\displaystyle \frac{1}{2}{\partial }_{\alpha }{\partial }_{\beta }\underline{\mu }^{\prime} ({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}}){{\boldsymbol{\xi }}}^{{\prime} \alpha }{{\boldsymbol{\xi }}}^{{\prime} \beta }\,+...\right]\\ & & \times \left[\left(\epsilon {\boldsymbol{E}}^{\prime} ({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}},\tau )+\epsilon {\partial }_{\alpha }{\boldsymbol{E}}^{\prime} ({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}},\tau ){{\boldsymbol{\xi }}}^{{\prime} \alpha }+\displaystyle \frac{\epsilon }{2}{\partial }_{\alpha }{\partial }_{\beta }{\boldsymbol{E}}^{\prime} ({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}},\tau ){{\boldsymbol{\xi }}}^{{\prime} \alpha }{{\boldsymbol{\xi }}}^{{\prime} \beta }\,+...\right)\ \right.\\ & & \left.+\left({\boldsymbol{G}}^{\prime} ({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}})+{\partial }_{\alpha }{\boldsymbol{G}}^{\prime} ({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}}){{\boldsymbol{\xi }}}^{{\prime} \alpha }+\displaystyle \frac{1}{2}{\partial }_{\alpha }{\partial }_{\beta }{\boldsymbol{G}}^{\prime} ({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}}){{\boldsymbol{\xi }}}^{{\prime} \alpha }{{\boldsymbol{\xi }}}^{{\prime} \beta }+...\right)\right].\end{array}\end{eqnarray} \tag{ 18 }$$

$\alpha ,\beta$ are summed over when appearing as a pair of upper and lower indices and go from 1 to n · d, ${{\boldsymbol{\xi }}}^{{\prime} \alpha }$ denotes the αth component of ${\boldsymbol{\xi }}^{\prime}$, and ${\partial }_{\alpha }$ the derivative with respect to the αth component of ${\boldsymbol{R}}^{\prime}$. '×' highlights that a matrix-vector-multiplication is performed on the line break. The τ-derivative of ${{\boldsymbol{R}}}^{{\prime} \mathrm{eq}}$ is zero as well as the spring forces evaluated in the equilibrium ${\boldsymbol{G}}^{\prime} ({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}})$.

We proceed by replacing ${\boldsymbol{\xi }}^{\prime}$ in (18) by its power series in (17). Ordering and splitting the resulting equation by powers of yields a vectorial equation for each order $p=1,2,...$ in . One finds that each of them is of the generic form

$$\begin{eqnarray}&&\displaystyle \frac{{\rm{d}}}{{\rm{d}}\tau }{{\boldsymbol{\xi }}}^{{\prime} (p)}=\underline{K}^{\prime} {{\boldsymbol{\xi }}}^{{\prime} (p)}+{{\boldsymbol{S}}}^{{\prime} (p)}(\tau ),\end{eqnarray} \tag{ 19 }$$

with

$$\begin{eqnarray}&&\underline{K}^{\prime} := \underline{\mu }^{\prime} ({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}})\cdot ({{\boldsymbol{\nabla }}}_{{\boldsymbol{R}}^{\prime} }{\boldsymbol{G}}^{\prime} )({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}}),\end{eqnarray} \tag{ 20 }$$

where '·' denotes the matrix multiplication and $({{\boldsymbol{\nabla }}}_{{\boldsymbol{R}}^{\prime} }{\boldsymbol{G}}^{\prime} )({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}})$ is the Jacobian matrix of the spring forces, evaluated at the swimmer's equilibrium. ${{\boldsymbol{S}}}^{{\prime} (p)}$ is a term that only depends on the displacements ${{\boldsymbol{\xi }}}^{{\prime} (1)},...,{{\boldsymbol{\xi }}}^{{\prime} (p-1)}$ and on the derivatives (of first and higher order) of $\underline{\mu }^{\prime} ,{\boldsymbol{E}}^{\prime}$ and ${\boldsymbol{G}}^{\prime}$, evaluated at ${{\boldsymbol{R}}}^{{\prime} \mathrm{eq}}$. Since ${{\boldsymbol{S}}}^{{\prime} (p)}$ does not depend on ${{\boldsymbol{\xi }}}^{{\prime} (p)}$, it can be considered as a source term that is known assuming (19) are solved in ascending order in p. The first two source terms read

$$\begin{eqnarray}&&{{\boldsymbol{S}}}^{{\prime} \left(1\right)}\left(\tau \right)=\underline{\mu }^{\prime} \left({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}}\right)\,{\boldsymbol{E}}^{\prime} \left({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}},\tau \right),\end{eqnarray} \tag{ 21 }$$

$$\begin{eqnarray}\begin{array}{rcl}{{\boldsymbol{S}}}^{{\prime} \left(2\right)}\left((,\tau \right) & = & \underline{\mu }^{\prime} \left({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}}\right)\left(\displaystyle \frac{1}{2}{\partial }_{\alpha }{\partial }_{\beta }{\boldsymbol{G}}^{\prime} \left({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}}\right){{\boldsymbol{\xi }}}^{{\prime} \left(1\right)\alpha }{{\boldsymbol{\xi }}}^{{\prime} \left(1\right)\beta }+{\partial }_{\alpha }{\boldsymbol{E}}^{\prime} \left({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}},\tau \right){{\boldsymbol{\xi }}}^{{\prime} \left(1\right)\alpha }\right)\\ & & +{\partial }_{\alpha }\underline{\mu }^{\prime} \left({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}}\right){{\boldsymbol{\xi }}}^{{\prime} \left(1\right)\alpha }\left((,{\boldsymbol{E}}^{\prime} \left({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}},\tau \right)+{\partial }_{\beta }{\boldsymbol{G}}^{\prime} \left({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}}\right){{\boldsymbol{\xi }}}^{{\prime} \left(1\right)\beta }\right).\end{array}\end{eqnarray} \tag{ 22 }$$

The matrix $\underline{K}^{\prime}$ maps the displacement vector ${\boldsymbol{\xi }}^{\prime}$ to the velocity vector $({\rm{d}}/{\rm{d}}\tau ){\boldsymbol{R}}^{\prime} =({\rm{d}}/{\rm{d}}\tau ){\boldsymbol{\xi }}^{\prime} =\underline{K}^{\prime} {\boldsymbol{\xi }}^{\prime}$ that emerges from the displacement in the situation of zero external forces. We assume the mobility matrix $\underline{\mu }^{\prime} ({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}})$ to be positive definite and symmetric. The Jacobian of the spring forces, $({{\boldsymbol{\nabla }}}_{{\boldsymbol{R}}^{\prime} }{\boldsymbol{G}}^{\prime} )({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}})$, has to be negative semi-definite due to the stability of the swimmer's equilibrium and symmetric as it is the Hessian of the spring potential. For the latter matrix, we distinguish between eigenvalues being zero, associated with translations and rotations of the whole swimmer, and negative eigenvalues, associated with deformations of the swimmer. Given this, one can also show that the matrix $\underline{K}^{\prime}$ is diagonalizable and has only non-positive eigenvalues with zero eigenvalues associated with translations/rotations and negative eigenvalues associated with internal degrees of freedom [42].

The explicit way to solve a set of differential equations like (19), accounting for certain initial conditions, is to split the initial conditions by orders of , find the full solution for each order, and adjust it to these initial conditions by a suitable choice of the parameters in the homogeneous solution. Knowing that $\underline{K}^{\prime}$ has only non-positive eigenvalues λ_(κ), the solution to the homogeneous counterpart to (19) (${{\boldsymbol{S}}}^{{\prime} (p)}=0$) can be written as

$$\begin{eqnarray}&&{{\boldsymbol{\xi }}}_{{\rm{\hom }}}^{{\prime} (p)}=\displaystyle \sum _{\kappa =1}^{n\cdot d}{{\boldsymbol{X}}}_{\kappa }\exp ({\lambda }_{(\kappa )}\tau ),\end{eqnarray} \tag{ 23 }$$

with ${{\boldsymbol{X}}}_{\kappa }$ a suitably scaled eigenvector of $\underline{K}^{\prime}$ corresponding to the eigenvalue λ_(κ). For translational and rotational degrees of freedom, one has ${\lambda }_{(\kappa )}=0$ and hence a constant solution. The displacements corresponding to the internal degrees of freedom are exponentially decaying and hence go to zero for large τ. Therefore, the homogeneous solution describes the relaxation of the swimmer in the absence of driving from arbitrary initial conditions. Consequently, all solutions to the inhomogeneous equations (${{\boldsymbol{S}}}^{{\prime} (p)}\ne 0$) differ only by the constant homogeneous solution for large τ. It suffices to find a single arbitrary solution to the full equation (19) in order to determine the swimming velocity and the deformation of the swimmer. For a fixed source term, the swimmer's behavior is hence independent of the initial conditions for large τ. The eigenvalues of $\underline{K}^{\prime}$ corresponding to internal degrees of freedom are of the order of 1, such that the displacements corresponding to the internal degrees of freedom decay exponentially with a characteristic time of the order of t_V. In the following calculations, we are interested in the behavior of the swimmer after a few t_V, when the swimmer's stroke has equilibrated. Therefore, we will neglect all terms decaying exponentially at time scale t_V arising from the initial conditions in the displacements ${{\boldsymbol{\xi }}}^{{\prime} (1)},...,{{\boldsymbol{\xi }}}^{{\prime} (p-1)}$ when calculating the source term of each order p.

We point out here that if the system is not invariant under the translational or rotational degree of freedom, e.g. because the driving forces are not invariant under these transformations, the source term ${{\boldsymbol{S}}}^{{\prime} (p)}(\tau )$ explicitly depends on those degrees of freedom. Via that pathway, the initial conditions may actually have an impact on the swimmer's behavior. This will be the case for the triangular swimmer in external driving as it will be discussed in section 5.1.

The rescaled flow field ${\vec{u}}_{\mathrm{fluid}}^{{\prime} }(\vec{r}^{\prime} )$ generated by the swimmer, expressed in dependence of the rescaled position $\vec{r}^{\prime}$, is given by

$$\begin{eqnarray}&&{\vec{u}}_{\mathrm{fluid}}^{{\prime} }(\vec{r}^{\prime} ,\tau )=\displaystyle \sum _{i=1}^{n}\hat{T}^{\prime} (\vec{r}^{\prime} -{\vec{R}}_{i}^{{\prime} }){\left((,\epsilon {\boldsymbol{E}}^{\prime} ({\boldsymbol{R}}^{\prime} ,\tau )+{\boldsymbol{G}}^{\prime} ({\boldsymbol{R}}^{\prime} \right)}^{i}),\end{eqnarray} \tag{ 24 }$$

with $\hat{T}^{\prime} (\vec{x}^{\prime} ):= 6\pi \eta a\hat{T}(a\vec{x}^{\prime} )$ the rescaled Oseen/Rotne–Prager tensor and ${\left(\bullet \right)}^{i}$ the ith part in a decomposition of • into n partial vectors of length d, i.e. the components associated with the ith bead. Given the solutions of (19) up to order p, the flow field can be calculated up to the same order p in by expanding (24). We here state the explicit expression up to the second order in

$$\begin{eqnarray}\begin{array}{rcl}{\vec{u}}_{\mathrm{fluid}}^{{\prime} }(\vec{r}^{\prime} ,\tau ) & = & \epsilon \displaystyle \sum _{i=1}^{n}\hat{T}^{\prime} (\vec{r}^{\prime} -{\vec{R}}_{i}^{{\prime} \mathrm{eq}}){\left((,{\boldsymbol{E}}^{\prime} ({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}},\tau )+{\partial }_{\alpha }{\boldsymbol{G}}^{\prime} ({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}}){{\boldsymbol{\xi }}}^{{\prime} (1)\alpha }\right)}^{i}\\ & & +\,{\epsilon }^{2}\left[\displaystyle \sum _{i=1}^{n}{\left({{\boldsymbol{\xi }}}^{{\prime} \left(1\right)}\right)}^{i}\,\circ \,{\vec{{\rm{\nabla }}}}_{{\vec{R}}_{i}^{{\prime} }}\hat{T}^{\prime} (\vec{r}^{\prime} -{\vec{R}}_{i}^{{\prime} }){| }_{{\vec{R}}_{i}^{{\prime} }={\vec{R}}_{i}^{{\prime} \mathrm{eq}}}{\left((,{\boldsymbol{E}}^{\prime} ({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}},\tau )+{\partial }_{\alpha }{\boldsymbol{G}}^{\prime} ({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}}){{\boldsymbol{\xi }}}^{{\prime} (1)\alpha }\right)}^{i}\right.\\ & & +\,\displaystyle \sum _{i=1}^{n}\hat{T}^{\prime} (\vec{r}^{\prime} -{\vec{R}}_{i}^{{\prime} \mathrm{eq}})\left(\Space{0ex}{3.0ex}{0ex}{\partial }_{\alpha }{\boldsymbol{E}}^{\prime} ({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}},\tau ){{\boldsymbol{\xi }}}^{{\prime} (1)\alpha }+{\partial }_{\alpha }{\boldsymbol{G}}^{\prime} ({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}}){{\boldsymbol{\xi }}}^{{\prime} (2)\alpha }\right.\\ & & +\,\left.{\left.\displaystyle \frac{1}{2}{\partial }_{\alpha }{\partial }_{\beta }{\boldsymbol{G}}^{\prime} ({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}}){{\boldsymbol{\xi }}}^{{\prime} (1)\alpha }{{\boldsymbol{\xi }}}^{{\prime} (1)\beta }\right)}^{i}\right]+{ \mathcal O }\left({\epsilon }^{3}\right),\end{array}\end{eqnarray} \tag{ 25 }$$

with ${{\rm{\nabla }}}_{{\vec{R}}_{i}^{{\prime} }}$ the gradient with respect to ${\vec{R}}_{i}^{{\prime} }$ and ${\vec{R}}_{i}^{{\prime} \mathrm{eq}}$ the equilibrium position of bead i. Note that having solved for the displacements in advance, we simply need to insert them into (25) to obtain the flow fields produced by the swimmer.

It is worth noticing that our method, given the very general assumptions being made, does not suffer from restrictions expected from multi-scale approaches. More specifically, the system is characterized by the viscous time t_V and the time scale associated with the frequency of driving. Both time scales can be arbitrarily large or small compared to another one without impairing our method. However, the competition between these two time scales yields interesting phenomena, including the increase of the swimming velocity with the increase of viscosity [30] and the non-monotonous frequency response [29]. The main limitation of the perturbative scheme is related to the separation between the beads, as set by the choice of the model for the hydrodynamic interactions.

The simplest one-dimensional bead-spring swimmer able to swim at low Reynolds number is the linear three-bead swimmer (figure 1). A swimmer with two beads comes with only one internal degree of freedom which is not sufficient to break the time-reversal symmetry [22]. The linear three-bead swimmer has been studied in detail in previous analytical works [28, 20, 30], where two similar perturbative calculations were performed. In the latter works [20, 30], the results for the swimming velocity were expanded and truncated in orders of ν. With the precision of the Oseen tensor, this calculation does not allow for a predictive result at higher order than the leading order ν².

Zoom In Zoom Out Reset image size

We will show that the result of our approach for the swimming velocity employing the Oseen tensor is correct up to order ν³ and that using the Rotne–Prager tensor hydrodynamics has an impact at orders ${\nu }^{4}$ and higher. The Rotne–Prager calculation thereby reproduces the results from the Oseen approximation up to order ν³, showing the consistency of our calculation scheme. Furthermore, we find that our approach coincides at leading order ν² to the aforementioned previous results [28, 20, 30], but differs at order ν³, explaining why our results also hold at order ν³. We verify this outcome by comparison to numerical solutions to the governing equations of motion, which are independent of the choice of perturbation scheme. We find a very accurate agreement to our analytical results.

The swimmer consists of three beads for which we choose radii ${a}_{1}={a}_{2}=a$ and a₃ respectively [28]. The beads are connected by two identical harmonic springs of stiffness k and equilibrium length L. The driving forces ${\vec{E}}_{i}(t)$, specified as

$$\begin{eqnarray}&&{\vec{E}}_{1}(t)=A\sin (\omega t){\vec{e}}_{x},{\vec{E}}_{2}(t)=A\sin (\omega t+\alpha ){\vec{e}}_{x},{\vec{E}}_{3}(t)=-{\vec{E}}_{1}(t)-{\vec{E}}_{2}(t),\end{eqnarray} \tag{ 26 }$$

act on the beads, ensuring that the total force vanishes. ${\vec{e}}_{x}$ denotes the unit vector in x-direction. The second derivative of ${\boldsymbol{G}}^{\prime} ({\boldsymbol{R}}^{\prime} )$ vanishes, because the swimmer is restricted to one dimension. Furthermore, the driving forces are not spatially dependent and hence all their spatial derivatives vanish too.

We here calculate the displacement ${\boldsymbol{\xi }}^{\prime}$ up to second order in , pointing out that the displacement to higher order can be obtained analogously. Numerical investigations show that the second order is a good approximation up to $\epsilon \approx 1$. The source term ${{\boldsymbol{S}}}^{{\prime} (1)}(\tau )$ from (21) composes of purely oscillating contributions with frequency Γ

$$\begin{eqnarray}&&{{\boldsymbol{S}}}^{{\prime} (1)}(\tau )={{\boldsymbol{S}}}_{s1}^{{\prime} (1)}\sin ({\rm{\Gamma }}\tau )+{{\boldsymbol{S}}}_{c1}^{{\prime} (1)}\cos ({\rm{\Gamma }}\tau ),\end{eqnarray} \tag{ 27 }$$

with the indices s1 and c1 denoting first the correspondence to sin or cos and second indicating the argument of the trigonometric function in multiples of Γτ. To safe efforts later, we calculate here the solution for a more general source term given by

$$\begin{eqnarray}&&{\boldsymbol{S}}^{\prime} (\tau )={{\boldsymbol{S}}}_{{sf}}^{{\prime} }\sin (f{\rm{\Gamma }}\tau )+{{\boldsymbol{S}}}_{{cf}}^{{\prime} }\cos (f{\rm{\Gamma }}\tau ),\end{eqnarray} \tag{ 28 }$$

with f an arbitrary positive integer. Given the linear nature of (19), a suitable ansatz for the displacement is ${\boldsymbol{\xi }}^{\prime} (\tau )={{\boldsymbol{\xi }}}_{{sf}}^{{\prime} }\sin (f{\rm{\Gamma }}\tau )+{{\boldsymbol{\xi }}}_{{cf}}^{{\prime} }\cos (f{\rm{\Gamma }}\tau )$. The resulting solutions to (19) read

$$\begin{eqnarray}\begin{array}{rcl}{\boldsymbol{\xi }}{{\prime} }_{{sf}} & = & {\left({f}^{2}{{\rm{\Gamma }}}^{2}\underline{1}+\underline{K}{{\prime} }^{2}\right)}^{-1}(f{\rm{\Gamma }}{{\boldsymbol{S}}}_{{cf}}^{{\prime} }-\underline{K}^{\prime} {{\boldsymbol{S}}}_{{sf}}^{{\prime} }),\\ {\boldsymbol{\xi }}{{\prime} }_{{cf}} & = & -{\left({f}^{2}{{\rm{\Gamma }}}^{2}\underline{1}+\underline{K}{{\prime} }^{2}\right)}^{-1}(f{\rm{\Gamma }}{{\boldsymbol{S}}}_{{sf}}^{{\prime} }+\underline{K}^{\prime} {{\boldsymbol{S}}}_{{cf}}^{{\prime} }),\end{array}\end{eqnarray} \tag{ 29 }$$

with $\underline{1}$ the $(n\cdot d)\times (n\cdot d)$ unit matrix. These results are in full agreement with [28].

Having calculated the first order displacement in , we proceed by calculating the second order source term (22). We find that it contains oscillating terms of the frequency $2{\rm{\Gamma }}$ and a constant contribution:

$$\begin{eqnarray}&&{{\boldsymbol{S}}}^{{\prime} (2)}(\tau )={{\boldsymbol{S}}}_{s2}^{{\prime} (2)}\sin (2{\rm{\Gamma }}\tau )+{{\boldsymbol{S}}}_{c2}^{{\prime} (2)}\cos (2{\rm{\Gamma }}\tau )+{{\boldsymbol{S}}}_{{\rm{const}}}^{{\prime} (2)}.\end{eqnarray} \tag{ 30 }$$

Again, the linearity of (19) allows us to calculate its solution for each summand in (30) separately and to add up the results to obtain a full solution. Firstly, the oscillating parts in the source term yield oscillating contributions to the ²-displacement (see (28), (29)), which contribute to the stroke of the swimmer. Secondly, (19) with the constant source term alone can be easily solved by expressing the source term in the eigenbasis of $\underline{K}^{\prime}$, where this matrix becomes diagonal and the equations separate. We find for each eigenvalue λ_(κ), $\kappa =1,...,n\cdot d$:

$$\begin{eqnarray}&&\displaystyle \frac{{\rm{d}}}{{\rm{d}}\tau }{\overline{{\boldsymbol{\xi }}}}^{{\prime} (2)\kappa }(\tau )={\lambda }_{(\kappa )}{\overline{{\boldsymbol{\xi }}}}^{{\prime} (2)\kappa }(\tau )+{\overline{{\boldsymbol{S}}}}_{{\rm{const}}}^{{\prime} (2)\kappa },\end{eqnarray} \tag{ 31 }$$

with the overline indicating the expression of a vector in the eigenbasis of $\underline{K}^{\prime}$ and ${\bullet }^{\kappa }$ the κth of the n · d components of •. For the translational and rotational degrees of freedom with respect to $\underline{K}^{\prime}$ we have ${\lambda }_{(\kappa )}=0$ and the solution is a linear function in time τ plus a constant which we neglect here, as it is determined by the choice of initial conditions:

$$\begin{eqnarray}&&{\overline{{\boldsymbol{\xi }}}}^{{\prime} (2)\kappa }(\tau )={\overline{{\boldsymbol{S}}}}_{{\rm{const}}}^{{\prime} (2)\kappa }\cdot \tau .\end{eqnarray} \tag{ 32 }$$

Hence, the second order swimming velocity and angular velocity are obtained from the components of ${{\boldsymbol{S}}}_{{\rm{const}}}^{{\prime} (2)}$ associated with the translational and rotational degrees of freedom respectively. A detailed step-by-step calculation is presented in appendix A. For the internal degrees of freedom, ${\lambda }_{(\kappa )}\lt 0$, the solution to (31) is constant in time plus an exponentially decaying term that we neglect since we are only interested in the limit of $t\gg {t}_{V}$:

$$\begin{eqnarray}&&{\overline{{\boldsymbol{\xi }}}}^{{\prime} (2)\kappa }(\tau )\equiv -\displaystyle \frac{1}{{\lambda }_{(\kappa )}}{\overline{{\boldsymbol{S}}}}_{{\rm{const}}}^{{\prime} (2)\kappa }.\end{eqnarray} \tag{ 33 }$$

In effect, this describes a deformation of the swimmer such that the beads do not oscillate around their mechanical equilibrium but around a different, deformed configuration.

Analyzing the eigensystem of $\underline{K}^{\prime}$, we find that the linear three-bead spring swimmer with equal radii (${a}_{3}=a$) and restricted to one dimension has one translational mode ${{\boldsymbol{X}}}_{1}$ and two internal eigenmodes ${{\boldsymbol{X}}}_{2}$ and ${{\boldsymbol{X}}}_{3}$ (see figure 2(a)) with

$$\begin{eqnarray}&&{{\boldsymbol{X}}}_{1}=(1,1,1),{{\boldsymbol{X}}}_{2}=\left(1,-2+\displaystyle \frac{6\nu }{9\nu -4},1\right),{{\boldsymbol{X}}}_{3}=(1,0,-1).\end{eqnarray} \tag{ 34 }$$

The mode ${{\boldsymbol{X}}}_{3}$ is orthogonal (with respect to the standard scalar product) to ${{\boldsymbol{X}}}_{1}$ and ${{\boldsymbol{X}}}_{2}$. The modes ${{\boldsymbol{X}}}_{1}$ and ${{\boldsymbol{X}}}_{2}$ are in general not orthogonal to each other, but become orthogonal for $\nu \to 0$. In our calculation, the swimming velocity can be read off from the component parallel to ${{\boldsymbol{X}}}_{1}$ in the decomposition of ${{\boldsymbol{S}}}_{{\rm{const}}}^{{\prime} (2)}$ in terms of the eigenvectors of $\underline{K}^{\prime}$ (green arrow in figure 2(a)).

Zoom In Zoom Out Reset image size

In a previous work [28], the swimming velocity was effectively calculated as

$$\begin{eqnarray}&&{\vec{u}}_{0}^{{\prime} }=\displaystyle \frac{1}{{\displaystyle \sum }_{p}{a}_{p}}\displaystyle \sum _{i}{a}_{i}{\left({{\boldsymbol{S}}}_{{\rm{const}}}^{{\prime} (2)}\right)}^{i},\end{eqnarray} \tag{ 35 }$$

with ${{\boldsymbol{S}}}_{{\rm{const}}}^{{\prime} (2)i}$ being the part of the constant source term associated with bead i. In the case of equal bead radii, this calculation is equivalent to an orthogonal projection of the source term onto the vector ${{\boldsymbol{X}}}_{1}$ and reading off the velocity from the projected source term in multiples of ${{\boldsymbol{X}}}_{1}$ (blue arrow in figure 2(a)). Due to ${{\boldsymbol{X}}}_{2}\perp {{\boldsymbol{X}}}_{1}$ for $\nu \to 0$, the axis projected onto is in this limit orthogonal to the two internal modes and both the projection and the decomposition of the source term yield the same result for the swimming velocity. This explains why both calculations agree for $\nu \to 0$, but also why they differ for finite values of ν. This can also be seen in the explicit ratio between our result ${u}_{Z}^{{\rm{O}},\mathrm{lin}}$ (with the superscript denoting Oseen approximation and linear swimmer), given by

$$\begin{eqnarray}&&{u}_{Z}^{{\rm{O}},\mathrm{lin}}=B\displaystyle \frac{\sin (\alpha )\left(16{{\rm{\Gamma }}}^{2}+3(3\nu -4)(7\nu -4,),)\right)-4{\rm{\Gamma }}(9\nu -4)(2\cos (\alpha )+1)}{(7\nu -4)\left(16{{\rm{\Gamma }}}^{2}+9{\left(4-7\nu \right)}^{2}\right)\left(16{{\rm{\Gamma }}}^{2}+{\left(4-3\nu \right)}^{2}\right)},\end{eqnarray} \tag{ 36 }$$

with $B=(a/{t}_{V})\,{\epsilon }^{2}{\rm{\Gamma }}{\nu }^{2}\,(9\nu (21\nu -22)+56)$, and the result u₀ stated in [28]. This ratio (37) converges to 1 for $\nu \to 0$:

$$\begin{eqnarray}&&\displaystyle \frac{{u}_{Z}^{{\rm{O}},\mathrm{lin}}}{{u}_{0}}=\displaystyle \frac{112-396\nu +378{\nu }^{2}}{112-376\nu +315{\nu }^{2}}.\end{eqnarray} \tag{ 37 }$$

The differences discussed above stem in part from the fact that the original perturbative approach [28] calculates the oscillations of the beads around the undisturbed swimmer shape. In contrast, in the current scheme, the swimmer's average shape and the oscillations of the beads around it are obtained simultaneously. Actually, both the mean deformation and the swimming velocity arise from the constant contribution to the second order source term ${{\boldsymbol{S}}}_{{\rm{const}}}^{{\prime} (2)}$ (30). The distances d₁ between bead 1 and 2 and d₂ between bead 2 and 3 in the swimmer's mean configuration, around which the beads oscillate harmonically, are given up to order ² and for ${a}_{3}=a$ by

$$\begin{eqnarray}&&{d}_{1}=L+\displaystyle \frac{20-63\nu }{56+9\nu (-22+21\nu )}\cdot {t}_{V}\cdot {u}_{Z}^{{\rm{O}},\mathrm{lin}},\end{eqnarray} \tag{ 38 }$$

and

$$\begin{eqnarray}&&{d}_{2}=L+\displaystyle \frac{-20+63\nu }{56+9\nu (-22+21\nu )}\cdot {t}_{V}\cdot {u}_{Z}^{{\rm{O}},\mathrm{lin}}.\end{eqnarray} \tag{ 39 }$$

Hence, the ratio between deformation and swimming velocity, both of order ², is a simple geometrical factor. Also, the amplitude of the deformation obeys a similar frequency dependence as the swimming velocity itself and decays similarly as 1/L² for large bead separations (see below).

The comparison to numerical calculations, done by numerically integrating the equation of motion (13), shows a very neat agreement between our result and the numerics with errors below 0.1% (figure 2(b)). Comparing our result with the one obtained in [28], we find for ${a}_{3}=a$ (i.e. equal bead radii) and $\nu \approx 1/10$ small differences in the range of percents, but the difference increases drastically for increasing values of a₃ (figure 2(b)), i.e. when the swimmer becomes asymmetric. We observe that for ${a}_{3}\ne a$, all pairs of eigenvectors are in general no more orthogonal, even in the limit $\nu \to 0$. Also, (35) describes no more a projection onto ${{\boldsymbol{X}}}_{1}$ but onto $(1,1,{a}_{3})$. This explains why the difference between u₀ and ${u}_{Z}^{{\rm{O}},\mathrm{lin}}$ grows for increasing a₃ in figure 2(b), yet in the limit $\nu \to 0$ both still agree independently of a₃.

Despite this quantitative difference to previous results [28], we recover the typical dependencies for bead-spring swimmers which have been reported previously [28, 20, 30, 29]: the swimming velocity scales with the square of the driving forces for small amplitudes, the swimming speed becomes maximal in the vicinity of ${t}_{V}^{-1}$ and decays as $1/{L}^{2}$ for large bead separations.

The Rotne–Prager approximation (appendix B) has only an impact onto the swimming velocity at orders ${\nu }^{4}$ and higher: using the Rotne–Prager tensor instead of the Oseen tensor yields an additional term to the mobility matrix scaling as $1/{r}^{3}$ (see (7)), with r the distance between the beads. This results in additional terms to $\underline{\mu }^{\prime} ({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}})$ and ${\partial }_{\alpha }\underline{\mu }^{\prime} ({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}})$, scaling with ν³ and ${\nu }^{4}$ respectively. A closer investigation of the second order source term (22) shows that the factor multiplied to $\underline{\mu }^{\prime} ({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}})$ is zero, such that the additional term due to the Rotne–Prager extension has an impact at order ${\nu }^{4}$ and higher on the source term ${{\boldsymbol{S}}}^{{\prime} (2)}$ and likewise on the swimming velocity.

5.1. External driving

Triangular bead-spring swimmers have been studied in detail recently [21, 43], where the employed driving protocol prescribes forces on each bead parallel to the adjoining sides of the triangle. By varying the amplitudes of and the phase shifts between the driving forces, the swimmer can be steered on arbitrary trajectories. Both, translational and rotational motion were shown to scale with the square of the driving force. Also here, the perturbative approach used in [21] does only hold in the limit $\nu \to 0$.

The triangular swimmer is composed of three spherical beads, each of radius a, connected by identical springs of equilibrium length L and spring constant k. All beads are placed in the x–z-plane with orientation θ the angle between the connection of bead 3 to the middle between bead 1 and 2 and the x-axis (figure 3). Numerous experimental realizations of microswimmers rely on an external field, commonly an electric or magnetic one [11, 5, 2]. Therefore, we first consider here a toy model swimmer that is subject to an external force field which shall act in one direction only (without restriction of generality the x-direction) for the sake of simplicity. For the swimmer to be self-propelled, we demand that all forces acting on the three beads sum up to zero and also have vanishing total torque. We determine the remaining degree of freedom by prescribing that the sum of the squares of all forces is equal to a constant, 2 A², such that the forces explicitly are given by

$$\begin{eqnarray}\begin{array}{rcl}{\vec{E}}_{1}(t,{z}_{1},{z}_{2},{z}_{3}) & = & c{\vec{e}}_{x}({z}_{3}-{z}_{2})\sin (\omega t),\\ {\vec{E}}_{2}(t,{z}_{1},{z}_{2},{z}_{3}) & = & c{\vec{e}}_{x}({z}_{1}-{z}_{3})\sin (\omega t),\\ {\vec{E}}_{3}(t,{z}_{1},{z}_{2},{z}_{3}) & = & c{\vec{e}}_{x}({z}_{2}-{z}_{1})\sin (\omega t),\end{array}\end{eqnarray} \tag{ 40 }$$

with

$$\begin{eqnarray}&&c=\displaystyle \frac{\sqrt{2}A}{\sqrt{{\left({z}_{3}-{z}_{2}\right)}^{2}+{\left({z}_{1}-{z}_{3}\right)}^{2}+{\left({z}_{2}-{z}_{1}\right)}^{2}}}.\end{eqnarray} \tag{ 41 }$$

With this definition, all three beads are treated on an equal basis, experiencing forces that depend explicitly on the configuration of the swimmer, in order to satisfy the force-free and torque-free condition throughout the whole swimming stroke. Moreover, at a given orientation of the swimmer, the three driving force amplitudes can be scaled by the same factor, yet the force- and the torque-free conditions will still be fulfilled. Furthermore, setting the square of all three driving force amplitudes equal to a constant allows us to keep the power input at the same order of magnitude, as the power input is known to scale with the square of the force for a bead in the viscous regime [20]. Later in this section, we apply our method to the driving protocol used in [21, 43] for comparison. Throughout the whole section on triangular swimmers, we make use of the Oseen approximation for the hydrodynamic interactions of the beads.

Zoom In Zoom Out Reset image size

In numerical studies, we observe that the swimmer typically undergoes a transient phase during which it both rotates and translates. It finally reaches a steady state in which the motion is purely translational (figure 4(a)). A closer numerical investigation shows that the angular velocity of the swimmer averaged over one stroke depends in sinusoidal fashion on the instantaneous orientation of the swimmer (figure 4(b)). The rotational dynamics of the externally driven triangular swimmer hence is equivalent to the one of an overdamped pendulum. Perturbation theory and numerics consistently show that the angular velocity Ω at fixed angle scales as

$$\begin{eqnarray}&&{\rm{\Omega }}\sim {\epsilon }^{4}\,{\nu }^{4}\end{eqnarray} \tag{ 42 }$$

and attains its maximum for driving frequencies close to the inverse viscous time, similarly to the translational velocity. The time scale of the rotational relaxation hence can be estimated as ${T}_{{\rm{relax}}}\sim {{\rm{\Omega }}}^{-1}\sim {\epsilon }^{-4}\,{\nu }^{-4}$. In the parameter range for which the perturbation approach applies, this time scale is several orders of magnitude larger than t_V.

Zoom In Zoom Out Reset image size

We find stable steady states of the swimmer at $\theta =p\cdot 60^\circ$ and unstable steady states at $\theta =(p-1/2)\cdot 60^\circ ,p\,=\,1,...,6$ (see figure 4(c)). Obviously, the swimmer in external driving is invariant under a 3-fold rotation. Furthermore, a 180° rotation inverts the swimming direction but does not affect the stroke in internal coordinates, showing that the stability of states is invariant under a 6-fold rotation. Hence, all stable steady states can be considered equivalent and likewise all unstable states. The swimmer is found to always rotate towards the stable steady state closest to the initial orientation as shown in figure 4(b). The existence of stable and unstable steady states results from prescribing the driving forces with respect to the laboratory frame compared to their prescription in the swimmer's frame of reference [21]. In the latter protocol, the forces are held constant in the internal coordinates throughout the rotation of the swimmer and hence the swimmer undergoes constant translation and rotation.

In the steady states of the externally driven swimmer, we find for the swimming velocity in the Oseen approximation the following expression

$$\begin{eqnarray}&&{u}_{x}^{{\rm{O}},\mathrm{tri}}=-\displaystyle \frac{a}{{t}_{V}}\displaystyle \frac{12\sqrt{3}{\epsilon }^{2}{{\rm{\Gamma }}}^{2}{\nu }^{2}\left(2835{\nu }^{3}-8640{\nu }^{2}+5568\nu -1024\right)}{(9\nu -8)\left(64{{\rm{\Gamma }}}^{2}+9{\left(8-15\nu \right)}^{2}\right)\left(256{{\rm{\Gamma }}}^{2}+9{\left(8-9\nu \right)}^{2}\right)}.\end{eqnarray} \tag{ 43 }$$

A detailed calculation is presented in appendix C. Performing an expansion and truncation of (43) to leading order of ν shows that this result is in agreement with the result presented in [21]. We recover the typical $u\sim {\epsilon }^{2}$ dependence for small force amplitudes and $u\sim {\nu }^{2}$ in the limit $\nu \to 0$, which seem characteristic for bead-spring swimmers. We can understand the latter dependence from the fact that swimming emerges from the interplay between the hydrodynamic interaction of parts of the swimmer and variations in their distance, suggesting a swimming speed scaling with the gradient of the hydrodynamic interaction and hence with ν². In the range of $L\gt 3a$, we find that expression (43) is negative meaning that the swimmer swims towards the base (with respect to the symmetry) of the triangle (see figure 5(a)). For sufficiently small amplitudes of the driving, we observe that the beads 1 and 2 move on ellipsoidal trajectories that are tilted towards the middle axis of the swimmer. In the orientation $\theta =\pi /2$, exemplaric for the unstable steady states, the swimmer swims at the same speed as in a stable state (43). We point out that this property is sensitive to the way the normalization of the forces is done (see (40)), i.e. it holds only if the sum of the squares is fixed. In contrast to the stable states, the swimming direction is here pointing towards the tip of the triangle and also the trajectories of the beads 1 and 2 are in this case tilted towards the base of the triangle (figure 5(b)).

Zoom In Zoom Out Reset image size

Analysis of the analytically computed flow fields shows that in contrast to previous works, which reported that triangular swimmers produce in average neutral flow fields at second order in the driving force [21, 43], we here find a non-vanishing average dipolar flow field at order ² in both states (see figures 5(c), (d)). Going from stable to the unstable state comes with an exact inversion of the flow field, transforming the puller-like swimmer in the stable state into a pusher-like swimmer in the unstable one.

5.2. Internal driving and flow field

In order to provide deeper insights into the swimmer's pusher or puller character, we repeat the calculation of the flow field for a purely translational driving protocol defined in the swimmer's frame of reference, presented similarly in [21]. The swimmer is oriented symmetrically with respect to the z-axis with bead 1 at the top and bead 2 and 3 defining the base of the swimmer. The center of mass of the swimmer is located at the origin of the coordinate system. The forces ${\vec{F}}_{{ij}}$ that act between each pair of beads i, j are defined as

$$\begin{eqnarray}&&{\vec{F}}_{12}(t)=A\sin (\omega t){\vec{e}}_{12},{\vec{F}}_{13}(t)=A\sin (\omega t){\vec{e}}_{13},{\vec{F}}_{23}(t)={\gamma }_{2}A\sin (\omega t+{\alpha }_{2}){\vec{e}}_{23},\end{eqnarray} \tag{ 44 }$$

with ${\vec{e}}_{{ij}}$ the unit vector connecting bead i to bead j. The application of the perturbative approach presented here and the analysis of the resulting average flow field shows that the fields at order ² (in dependence of the rescaled position $\vec{r}^{\prime}$) can be approximated to leading order as a superposition of two force dipoles

$$\begin{eqnarray}&&\langle {\vec{u}}_{\mathrm{fluid}}\rangle (\vec{r}^{\prime} )=f({\alpha }_{2},{\gamma }_{2})\left((,{\vec{G^{\prime} }}_{D}(\vec{r}^{\prime} ,{\hat{e}}_{x},{\hat{e}}_{x})-{\vec{G^{\prime} }}_{D}(\vec{r}^{\prime} ,{\hat{e}}_{z},{\hat{e}}_{z},)\right),\end{eqnarray} \tag{ 45 }$$

with

$$\begin{eqnarray}&&{\vec{G^{\prime} }}_{D}(\vec{r}^{\prime} ,\vec{d},\vec{e}):= \left((,\vec{d}\circ {\vec{{\rm{\nabla }}}}_{\vec{r}^{\prime} }\hat{T}^{\prime} (\vec{r}^{\prime} ,)\right)\,\circ \,\vec{e}.\end{eqnarray} \tag{ 46 }$$

$\vec{e}$ denotes the direction in which the forces act, $\vec{d}$ the separation vector of the two forces of the dipole and ${{\rm{\nabla }}}_{\vec{r}^{\prime} }$ the gradient with respect to rescaled coordinates. In the direction orthogonal to the swimmer plane, the two force dipoles cancel up to order $1/{y}^{4}$, such that in this direction only the quadrupolar flow field, scaling as $1/{y}^{3}$, remains. Investigation of the magnitude of the dipolar flow field shows that a swimmer can be tuned from pusher to puller by changing α₂ and γ₂ (figure 6, black curve).

Zoom In Zoom Out Reset image size

Comparison of the strength of the force dipole $f({\alpha }_{2},{\gamma }_{2})$ produced by the swimmer and the swimming velocity u_swim in z-direction shows that their ratio is a function of ν only:

$$\begin{eqnarray}&&\displaystyle \frac{f({\alpha }_{2},{\gamma }_{2})}{{u}_{{\rm{swim}}}}=\displaystyle \frac{4\sqrt{3}(40-81\nu )}{\nu \left(128-360\nu +135{\nu }^{2}\right)}.\end{eqnarray} \tag{ 47 }$$

This ratio is positive for $L/a\gt 2.25$, associating a swimming motion towards the tip of the triangle with a pusher flow field and motion towards the base with a puller flow field. For ${\gamma }_{2}=1/2$ and ${\alpha }_{2}=\pi$, we recover the driving of the stable steady state, showing that the swimmer behaves as a puller. The unstable steady state is recovered for ${\gamma }_{2}\to \infty$ making the corresponding swimmer a pusher. Plots of the average ²-flow fields in the swimmer plane and in the orthogonal plane through the symmetry axis of the swimmer (figures 5(c)–(f)) illustrate the dipolar character of the flow in the plane of the swimmer and its fast decay orthogonal to the swimmer plane.

The complexity of the flow field at order ² increases when the radius of bead 1 is chosen differently, in particular the form (45) does not hold and the fast decay of the magnitude in y-direction is lost. Also the curve determining the pusher/puller behavior in dependence of α₂ and γ₂ is sensitive to changes in the parameter a₁ (figure 6). Still, the labels of the pusher and puller area are positioned such that they do not only hold for ${a}_{1}=a$ (solid line) but also for ${a}_{1}=a/3$ (dotted–dashed line) and ${a}_{1}=3$ (dashed line).

We presented a general perturbative approach to calculate the trajectories, internal dynamics and the flow fields of swimmers consisting of beads interacting by harmonic potentials and hydrodynamic interactions, organized in an arbitrary geometry and subject to a force protocol of choice. To illustrate and address the efficiency and precision of our method, two descriptions of the hydrodynamics interactions were considered, namely the Oseen and Rotne–Prager approximation.

We first applied our perturbation method to the linear swimmer as a benchmark. Comparison to previous results showed that our approach, combined with the Oseen tensor, yields a swimming velocity that is correct up to order ν³, whereas previous approaches are only correct up to order ν². This is due to the different ways of extracting the swimming velocity from the constant contribution to the source term. The current formulation maintains consistency and provides corrections that were to the best of our knowledge unaccounted for in previous perturbation schemes. The consequences of these terms are negligible in the case of the symmetric swimmer for which the swimming modes are orthogonal. However, since the deviations from orthogonality increase with enhancing the asymmetry of the linear design, important quantitative differences can be observed in the swimming velocity.

We further investigated the dynamics of an externally driven triangular swimmer with equal bead radii and discovered the existence of stable and unstable rotational steady states. We showed that the swimmer propagates at the same speed in both states, but in opposite directions with respect to the symmetry axis of the swimmer. In contrast to previous results [21], the average flow field produced by the swimmer was shown to be puller- or pusher-like, depending on the forces driving the swimmer. Actually, the character of the dipolar flow field for the internal driving can be directly associated with the swimming direction, which is, unlike in the stroke-based models, a consequence of the driving. Interestingly, the average flow field of the triangular swimmer with equal bead radii is strong near the swimmer plane, but shows a quick decay in the direction orthogonal to the swimmer plane, in contrast to the linear swimmer which produces a rotationally symmetric flow field. This may prove to be important when considering assemblies of swimmers.

To demonstrate that our perturbation model can be coupled with any choice of approximation for the hydrodynamic interactions, we moreover investigate the changes in the swimming velocity when employing the Rotne–Prager mobility matrix. Naturally, we reproduce the result of the Oseen calculation up to order ν³ demonstrating the consistency of our approach, and furthermore capture the swimming velocity at the next higher order in the inverse bead separation. In this context, we do lift the restriction of very large bead separations, which previous approaches came with. Actually, the current perturbation scheme can yield arbitrarily precise results for the swimming velocity, by improving the accuracy of the mobility matrix.

In the light of the above discussion, a natural next step is to investigate the accuracy of our analytical results at small bead separations, when near field effects play a role. From the analysis of the two-bead mobility matrix ([44, 40]) and the comparison of the perturbative calculations for three-sphere swimmers with lattice Boltzmann simulations ([30, 39]), this regime is expected at separations of $L/a\lt 3$. Notably, the near field corrections were recently addressed in the context of the stroke-based three-sphere swimmer [45]. Indeed, previous perturbative approaches, based on perturbation around the rest shape of the swimmer, allowed for a full mapping between the stroke and force based protocols [39]. However, this cannot be done in the current case since our model predicts a deformation of the swimmer's average shape due to acting forces. Hence, addressing near field corrections in modeling the hydrodynamic interactions requires the development of a new force-based numerical framework, which is an interesting research direction to pursue in future. Such a scheme could be particularly useful for studies of complex microsystems, where the accurate modeling of many-body interactions may be imperative.

Our perturbative approach, moreover, may be also applied in a three-dimensional setting, both in the context of a single swimmer design or when considering an ensemble of interacting microswimmers. With small reformulations, our approach allows for a calculation of relative and absolute translational and angular velocities of a swimmer in the presence of an arbitrary configuration of other ones. The model is, therefore, well suited to provide a comprehensive study of the mechanisms underlying the interaction of microswimmers. While this issue has been addresed in part for dumbbell-shaped swimmers [46, 47], the stroke-based linear swimmer [24, 25] and recently, for a force-based linear swimmer [34], a full discussion of the interaction between bead-based microswimmers is still pending. The tools presented herein can be used as the foundation of such analysis, which is a task that we intend to address in future work.

The authors acknowledge founding by the European Research Council through the grant MembranesAct ERC Stg 2013-337283 and by the DFG Priority Programme 'Microswimmers—From Single Particle Motion to Collective behavior' (SPP 1726). We also thank Alexander Sukhov, Galien Grosjean, Oleg Trosman and Jayant Pande for valuable discussions.

We provide a step-by-step calculation of the swimming velocity of the linear three-sphere swimmer with equal bead radii in the Oseen approximation. We use n = 3 and d = 1 as the system is confined to a one-dimensional subspace. The calculations presented here were done with Mathematica [48]. From (26), we find the rescaled driving forces

$$\begin{eqnarray}&&{{\boldsymbol{E}}}^{{\prime} }({{\boldsymbol{R}}}^{{\prime} },\tau )\equiv {{\boldsymbol{E}}}^{{\prime} }({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}},\tau )=\left(\begin{array}{c}\sin ({\rm{\Gamma }}\tau )\\ \sin \alpha \cos ({\rm{\Gamma }}\tau )+\cos \alpha \sin ({\rm{\Gamma }}\tau )\\ -\sin \alpha \cos ({\rm{\Gamma }}\tau )-(1+\cos \alpha )\sin ({\rm{\Gamma }}\tau ))\end{array}\right).\end{eqnarray} \tag{ A.1 }$$

For this swimmer, the driving forces do not depend on the positions of the beads ${{\boldsymbol{R}}}^{{\prime} }$, so all spatial derivatives thereof are zero. With

$$\begin{eqnarray}&&{{\boldsymbol{R}}}^{{\prime} }=\left(\begin{array}{c}{x}_{1}^{{\prime} }\\ {x}_{2}^{{\prime} }\\ {x}_{3}^{{\prime} }\end{array}\right),{{\boldsymbol{R}}}^{{\prime} \mathrm{eq}}=\left(\begin{array}{c}-L/a\\ 0\\ L/a\end{array}\right)=\left(\begin{array}{c}-{\nu }^{-1}\\ 0\\ {\nu }^{-1}.\end{array}\right),\end{eqnarray} \tag{ A.2 }$$

we find the rescaled mobility matrix from (5), (8) and (15) as

$$\begin{eqnarray}\underline{\mu }({{\boldsymbol{R}}}^{{\prime} })=\left(\begin{array}{ccc}1 & \tfrac{3}{2| {x}_{2}^{{\prime} }-{x}_{1}^{{\prime} }| } & \tfrac{3}{2| {x}_{3}^{{\prime} }-{x}_{1}^{{\prime} }| }\\ \tfrac{3}{2| {x}_{1}^{{\prime} }-{x}_{2}^{{\prime} }| } & 1 & \tfrac{3}{2| {x}_{3}^{{\prime} }-{x}_{2}^{{\prime} }| }\\ \tfrac{3}{2| {x}_{1}^{{\prime} }-{x}_{3}^{{\prime} }| } & \tfrac{3}{2| {x}_{2}^{{\prime} }-{x}_{3}^{{\prime} }| } & 1\end{array}\right),\end{eqnarray} \tag{ A.3 }$$

which can be easily evaluated for ${{\boldsymbol{R}}}^{{\prime} \mathrm{eq}}$:

$$\begin{eqnarray}\underline{\mu }({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}})=\left(\begin{array}{ccc}1 & \tfrac{3}{2}\nu & \tfrac{3}{4}\nu \\ \tfrac{3}{2}\nu & 1 & \tfrac{3}{2}\nu \\ \tfrac{3}{4}\nu & \tfrac{3}{2}\nu & 1\end{array}\right).\end{eqnarray} \tag{ A.4 }$$

The source term ${{\boldsymbol{S}}}^{{\prime} (1)}(\tau )$ is calculated according to (21) as

$$\begin{eqnarray}&&{{\boldsymbol{S}}}^{{\prime} (1)}(\tau )=\underline{\mu }^{\prime} ({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}})\,{\boldsymbol{E}}^{\prime} ({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}},\tau ),\end{eqnarray} \tag{ A.5 }$$

where we perform a matrix-vector multiplication. We separate the resulting terms by $\sin ({\rm{\Gamma }}\tau )$ and $\cos ({\rm{\Gamma }}\tau )$ and find

$$\begin{eqnarray}&&{{\boldsymbol{S}}}^{{\prime} (1)}(\tau )=\left(\begin{array}{c}1+\tfrac{3}{4}(-1+\cos \alpha )\nu \\ \cos \alpha -\tfrac{3}{2}\nu \cos \alpha \\ \tfrac{1}{4}(3\nu -4+\cos \alpha (6\nu -4))\end{array}\right)\sin ({\rm{\Gamma }}\tau )+\left(\begin{array}{c}\tfrac{3}{4}\nu \sin \alpha \\ \sin \alpha (1-\tfrac{3\nu }{2})\\ \tfrac{1}{2}\sin \alpha (3\nu -2)\end{array}\right)\cos ({\rm{\Gamma }}\tau ).\end{eqnarray} \tag{ A.6 }$$

For the linear swimmer, the matrix ${\underline{K}}^{{\prime} }$ is given by

$$\begin{eqnarray}{\underline{K}}^{{\prime} }=\left(\begin{array}{ccc}-1+\tfrac{3}{2}\nu & 1-\tfrac{9}{4}\nu & \tfrac{3}{4}\nu \\ 1-\tfrac{3}{2}\nu & -2+3\nu & 1-\tfrac{3}{2}\nu \\ \tfrac{3}{4}\nu & 1-\tfrac{9}{4}\nu & -1+\tfrac{3}{2}\nu \end{array}\right).\end{eqnarray} \tag{ A.7 }$$

Via (29) with f = 1 we are able to calculate the first order displacements of the beads, which are purely oscillatory ${{\boldsymbol{\xi }}}^{{\prime} (1)}={{\boldsymbol{\xi }}}_{s1}^{{\prime} (1)}\sin ({\rm{\Gamma }}\tau )+{{\boldsymbol{\xi }}}_{c1}^{{\prime} (1)}\cos ({\rm{\Gamma }}\tau )$ and too lengthy to be printed here explicitly.

We proceed with calculating the second order source term ${{\boldsymbol{S}}}^{{\prime} (2)}(\tau )$ given by (22). Each derivative ∂ applied to a tensorial quantity increases its order by one. In each product a summation is performed over pairwise appearing upper and lower indices α and β, both running from 1 to n · d. In the case of the linear three-sphere swimmer, the first summand of (22) vanishes because the second derivative of the spring forces is zero and because the driving forces do not depend on ${\boldsymbol{R}}^{\prime}$. The second summand yields a lengthy result which is not shown here. Next, the obtained result for the second order source term has to be separated into its constant part ${{\boldsymbol{S}}}_{\mathrm{const}}^{{\prime} (2)}$ and into oscillating contributions of the form ${{\boldsymbol{S}}}_{s2}^{{\prime} (2)}\sin (2{\rm{\Gamma }}\tau )$ and ${{\boldsymbol{S}}}_{c2}^{{\prime} (2)}\cos (2{\rm{\Gamma }}\tau )$. This can be done after explicitly calculating ${{\boldsymbol{S}}}^{{\prime} (2)}$, or before by separating all appearing factors ${{\boldsymbol{\xi }}}^{{\prime} (1)}$ and ${{\boldsymbol{E}}}^{{\prime} }({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}},\tau )$ by their τ-dependence and combining them according to common trigonometric rules.

The final task is to extract from the constant second order source term the actual swimming velocity. We therefore need to decompose the constant source term with respect to the eigenbasis of ${\underline{K}}^{{\prime} }$ and keep only the components associated with the translational degree of freedom. From the eigenmodes of ${\underline{K}}^{{\prime} }$, given by (34), we construct the change of basis $\underline{M}^{\prime}$ (given below) transforming vectors expressed in the eigensystem of ${\underline{K}}^{{\prime} }$ into vectors expressed in standard coordinates. Furthermore, ${\underline{Q}}^{{\prime} }$ selects the first component of a vector and can hence be used to obtain from the source term expressed in the eigensystem of $\underline{K}^{\prime}$ the part associated with the translational degree of freedom.

$$\begin{eqnarray}\underline{M}^{\prime} =\left(\begin{array}{ccc}1 & 1 & 1\\ 1 & -2+\tfrac{6\nu }{9\nu -4} & 0\\ 1 & 1 & -1\end{array}\right),{\underline{Q}}^{{\prime} }=\left(\begin{array}{ccc}1 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\end{array}\right).\end{eqnarray} \tag{ A.8 }$$

We then calculate the swimming velocity (in standard coordinates) as

$$\begin{eqnarray}&&{\boldsymbol{u}}^{\prime} =\underline{M}^{\prime} \cdot {\underline{Q}}^{{\prime} }\cdot {\underline{M}}^{{\prime} -1}\cdot {{\boldsymbol{S}}}_{\mathrm{const}}^{{\prime} (2)}.\end{eqnarray} \tag{ A.9 }$$

This vector ${\boldsymbol{u}}^{\prime}$ composes of n similar copies of the velocity vector $\vec{u}^{\prime}$ of the swimmer in real space. As d = 1, this vector only has one component and gives directly rise to (36).

The result for the swimming velocity of the linear swimmer in the Rotne–Prager approximation is given by

$$\begin{eqnarray}&&{u}_{Z}^{\mathrm{RP},\mathrm{lin}}=\displaystyle \frac{a}{{t}_{V}}{\epsilon }^{2}6{\rm{\Gamma }}{\nu }^{2}{C}_{0}\left({C}_{S}\sin (\alpha )+{C}_{C}\cos (\alpha )+{C}_{K}\right),\end{eqnarray} \tag{ B.1 }$$

with

$$\begin{eqnarray}\begin{array}{rcl}{C}_{0} & = & \displaystyle \frac{\left(930{\nu }^{8}-2847{\nu }^{6}+1230{\nu }^{5}+2736{\nu }^{4}-2280{\nu }^{3}-260{\nu }^{2}+792\nu -224\right)}{\left(31{\nu }^{3}-42\nu +24\right)\left(64{{\rm{\Gamma }}}^{2}+{\left({\nu }^{3}-6\nu +8\right)}^{2}\right)\left(64{{\rm{\Gamma }}}^{2}+{\left(31{\nu }^{3}-42\nu +24\right)}^{2}\right)},\\ {C}_{S} & = & \left(64{{\rm{\Gamma }}}^{2}+31{\nu }^{6}-228{\nu }^{4}+272{\nu }^{3}+252{\nu }^{2}-480\nu +192\right),\\ {C}_{C} & = & 16{\rm{\Gamma }}\left(15{\nu }^{3}-18\nu +8\right),{C}_{K}=8{\rm{\Gamma }}\left(15{\nu }^{3}-18\nu +8\right).\end{array}\end{eqnarray} \tag{ B.2 }$$

We present the explicit calculation of the swimming velocity of the equilateral triangular swimmer in the external driving in the stable steady state θ = 0. We use the Oseen tensor and set n = 3 and d = 2. The calculation follows the same steps as in the case of the linear swimmer. The vector ${\boldsymbol{R}}^{\prime}$ and the swimmer's equilibrium configuration ${{\boldsymbol{R}}}^{{\prime} \mathrm{eq}}$ are

$$\begin{eqnarray}&&{\boldsymbol{R}}^{\prime} =\left(\begin{array}{c}{x}_{1}^{{\prime} }\\ {z}_{1}^{{\prime} }\\ {x}_{2}^{{\prime} }\\ {z}_{2}^{{\prime} }\\ {x}_{3}^{{\prime} }\\ {z}_{3}^{{\prime} }\end{array}\right),\ {{\boldsymbol{R}}}^{{\prime} \mathrm{eq}}=\left(\begin{array}{c}-\tfrac{\sqrt{3}}{2}{\nu }^{-1}\\ \tfrac{1}{2}{\nu }^{-1}\\ -\tfrac{\sqrt{3}}{2}{\nu }^{-1}\\ -\tfrac{1}{2}{\nu }^{-1}\\ 0\\ 0\end{array}\right),\end{eqnarray} \tag{ C.1 }$$

where bead 3 has been placed in the origin of the coordinate system. The driving forces (40) are given in the manuscript and evaluate to

$$\begin{eqnarray}&&{\boldsymbol{E}}^{\prime} ({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}},\tau )=\left(\begin{array}{c}\tfrac{1}{\sqrt{3}}\\ 0\\ \tfrac{1}{\sqrt{3}}\\ 0\\ -\tfrac{2}{\sqrt{3}}\\ 0\end{array}\right)\sin ({\rm{\Gamma }}\tau ).\end{eqnarray} \tag{ C.2 }$$

We directly give the mobility matrix for the equilibrium configuration ${{\boldsymbol{R}}}^{{\prime} \mathrm{eq}}$, as the unevaluated expression becomes too lengthy:

$$\begin{eqnarray}\underline{\mu }^{\prime} ({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}})=\left(\begin{array}{cccccc}1 & 0 & \tfrac{3}{4}\nu & 0 & \tfrac{21}{16}\nu & -\tfrac{3\sqrt{3}}{16}\nu \\ 0 & 1 & 0 & \tfrac{3}{2}\nu & -\tfrac{3\sqrt{3}}{16}\nu & \tfrac{15}{16}\nu \\ \tfrac{3}{4}\nu & 0 & 1 & 0 & \tfrac{21}{16}\nu & \tfrac{3\sqrt{3}}{16}\nu \\ 0 & \tfrac{3}{2}\nu & 0 & 1 & \tfrac{3\sqrt{3}}{16}\nu & \tfrac{15}{16}\nu \\ \tfrac{21}{16}\nu & -\tfrac{3\sqrt{3}}{16}\nu & \tfrac{21}{16}\nu & \tfrac{3\sqrt{3}}{16}\nu & 1 & 0\\ -\tfrac{3\sqrt{3}}{16}\nu & \tfrac{15}{16}\nu & \tfrac{3\sqrt{3}}{16}\nu & \tfrac{15}{16}\nu & 0 & 1\end{array}\right).\end{eqnarray} \tag{ C.3 }$$

From this, the first order source term is

$$\begin{eqnarray}&&{{\boldsymbol{S}}}^{{\prime} (1)}(\tau )=\left(\begin{array}{c}\tfrac{1}{\sqrt{3}}-\tfrac{5\sqrt{3}}{8}\nu \\ \tfrac{3}{8}\nu \\ \tfrac{1}{\sqrt{3}}-\tfrac{5\sqrt{3}}{8}\nu \\ -\tfrac{3}{8}\nu \\ -\tfrac{2}{\sqrt{3}}+\tfrac{7\sqrt{3}}{8}\nu \\ 0\end{array}\right)\sin ({\rm{\Gamma }}\tau ).\end{eqnarray} \tag{ C.4 }$$

The matrix $\underline{K}^{\prime}$ needed for the calculation of the ${\epsilon }^{1}$-displacements reads

$$\begin{eqnarray}\underline{K}^{\prime} =\left(\begin{array}{cccccc}\tfrac{3}{8}(3\nu -2) & \tfrac{1}{8}\sqrt{3}(2-3\nu ) & \tfrac{9\nu }{32} & \tfrac{3\sqrt{3}\nu }{32} & \tfrac{3}{4}-\tfrac{45\nu }{32} & \tfrac{1}{32}\sqrt{3}(9\nu -8)\\ \tfrac{1}{8}\sqrt{3}(2-3\nu ) & \tfrac{5}{8}(3\nu -2) & -\tfrac{9\sqrt{3}\nu }{32} & 1-\tfrac{57\nu }{32} & \tfrac{1}{32}\sqrt{3}(21\nu -8) & \tfrac{1}{32}(8-3\nu )\\ \tfrac{9\nu }{32} & -\tfrac{3\sqrt{3}\nu }{32} & \tfrac{3}{8}(3\nu -2) & \tfrac{1}{8}\sqrt{3}(3\nu -2) & \tfrac{3}{4}-\tfrac{45\nu }{32} & \tfrac{1}{32}\sqrt{3}(8-9\nu )\\ \tfrac{9\sqrt{3}\nu }{32} & 1-\tfrac{57\nu }{32} & \tfrac{1}{8}\sqrt{3}(3\nu -2) & \tfrac{5}{8}(3\nu -2) & \tfrac{1}{32}\sqrt{3}(8-21\nu ) & \tfrac{1}{32}(8-3\nu )\\ \tfrac{3}{4}-\tfrac{9\nu }{8} & \tfrac{1}{4}\sqrt{3}(3\nu -1) & \tfrac{3}{4}-\tfrac{9\nu }{8} & \tfrac{1}{4}\sqrt{3}(1-3\nu ) & \tfrac{3}{4}(3\nu -2) & 0\\ \tfrac{1}{8}\sqrt{3}(3\nu -2) & \tfrac{1}{8}(2-3\nu ) & \tfrac{1}{8}\sqrt{3}(2-3\nu ) & \tfrac{1}{8}(2-3\nu ) & 0 & \tfrac{1}{4}(3\nu -2)\end{array}\right).\end{eqnarray} \tag{ C.5 }$$

The resulting displacement ${{\boldsymbol{\xi }}}^{{\prime} (2)}$ is calculated from (29).

We proceed with the calculation of the second order source term (22), where the second derivative of the spring forces (a rank 3 tensor which we do not state explicitly) and the spatial derivatives of the driving forces both do not vanish in the case of the triangular swimmer. Evaluated at ${{\boldsymbol{R}}}^{{\prime} \mathrm{eq}}$, the latter one reads

$$\begin{eqnarray}{{\rm{\nabla }}}_{{\boldsymbol{R}}^{\prime} }{\boldsymbol{E}}^{\prime} ({{\boldsymbol{R}}}^{{\prime} \mathrm{eq}},\tau )=\left(\begin{array}{cccccc}0 & -\tfrac{\nu }{\sqrt{3}} & 0 & -\tfrac{\nu }{\sqrt{3}} & 0 & \tfrac{2\nu }{\sqrt{3}}\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & \tfrac{\nu }{\sqrt{3}} & 0 & \tfrac{\nu }{\sqrt{3}} & 0 & -\tfrac{2\nu }{\sqrt{3}}\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0\end{array}\right)\sin ({\rm{\Gamma }}\tau ).\end{eqnarray} \tag{ C.6 }$$

To obtain the swimming velocity, we separate constant and oscillating parts of the source term as before. The eigensystem of $\underline{K}^{\prime}$ decomposes into two translational modes (in x and z-direction), one rotational mode and three internal (deformation) modes. The corresponding change of basis and the corresponding matrix $\underline{Q}^{\prime}$, selecting only translational and rotational components, read

$$\begin{eqnarray}\underline{M}^{\prime} =\left(\begin{array}{cccccc}0 & 1 & -\tfrac{\sqrt{3}}{2} & \tfrac{\sqrt{3}(9\nu -8)}{8(3\nu -2)} & \tfrac{8-15\nu }{4(3\nu -4)} & -\tfrac{1}{2}\\ 1 & 0 & -\tfrac{1}{2} & \tfrac{8-3\nu }{8(3\nu -2)} & \tfrac{\sqrt{3}(8-9\nu )}{4(3\nu -4)} & \tfrac{\sqrt{3}}{2}\\ 0 & 1 & \tfrac{\sqrt{3}}{2} & \tfrac{\sqrt{3}(8-9\nu )}{8(3\nu -2)} & \tfrac{8-15\nu }{4(3\nu -4)} & -\tfrac{1}{2}\\ 1 & 0 & -\tfrac{1}{2} & \tfrac{8-3\nu }{8(3\nu -2)} & \tfrac{\sqrt{3}(9\nu -8)}{4(3\nu -4)} & -\tfrac{\sqrt{3}}{2}\\ 0 & 1 & 0 & 0 & 1 & 1\\ 1 & 0 & 1 & 1 & 0 & 0\end{array}\right),\ \underline{Q}^{\prime} =\left(\begin{array}{cccccc}1 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0\end{array}\right).\end{eqnarray} \tag{ C.7 }$$

The swimming velocity is again calculated by (A.9). Only its x-component is non-zero, giving rise to (43).