Abstract
Open quantum systems with chiral interactions can be realized by coupling atoms to guided radiation modes in photonic waveguides or optical fibers. In their steady state these systems can feature intricate many-body phases such as entangled dark states, but their detection and characterization remains a challenge. Here we show how such collective phenomena can be uncovered through monitoring the record of photons emitted into the guided modes. This permits the identification of dark entangled states but furthermore offers novel capabilities for probing complex dynamical behavior, such as the coexistence of a dark entangled and a mixed phase. Our results are of direct relevance for current optical experiments, as they provide a framework for probing, characterizing and classifying classical and quantum dynamical features of chiral light–matter systems.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The ability to interface quantum emitters with optical systems opens novel routes for investigating non-equilibrium phenomena in open condensed matter physics [1] and provides, potentially, a platform to perform quantum information processing [2–7]. In recent years, the open quantum dynamics of chiral systems, where the emission of photons into a waveguide presents a broken left-right symmetry, has been the object of intense investigation [8–15]. This propagation-direction-dependent light–matter interaction has been observed in a variety of systems, for instance atoms coupled to the evanescent field of a waveguide [16] or a photonic crystal [17–19], and quantum dots in photonic nano-structures [20]. From the quantum many-body physics perspective, it has been demonstrated that chiral coupling induces steady state entanglement between emitters. In particular, when a chain of spins is coupled to a waveguide, under precise conditions, peculiar phases of matter can form, among them pure entangled many-body dark states that are protected from decoherence [21, 22]. Such dark states find applications in quantum information processing, e.g. as a platform for the realization of quantum memories [23] and logical gates [24]. However, it still remains an experimental challenge to realize the specific conditions required for the creation of these entangled dark states. Furthermore, it is generally a difficult task to detect and characterize such states once created. This poses obstacles for exploring and using of the rich variety of quantum states and many-body phases for practical purposes, e.g. in optical quantum computing protocols [25].
In this work, we show that the counting statistics of the photons emitted into the photonic waveguide provides a means to detect and characterize the many-body state of a chiral atom chain. Our approach exploits that the guided photons do not only induce interactions between the emitters, but also carry information about their quantum state [26, 27]. For example, measuring the output field of the waveguide thus allows to infer the occurrence of dark steady states. More generally, this perspective allows to probe intricate dynamical phenomena such as transitions and the coexistence between dynamical phases in the steady state. In the latter case, entangled states may occur as fluctuations in an intermittent dynamics and are heralded through characteristic features of the time-resolved photon count signal. To establish this correspondence on a formal level we utilize the scaled cumulant generating function (SCGF) formalism together with the large deviation principle [28, 29]. This does not only allow to develop an understanding of the dynamical non-equilibrium behavior of a chirally coupled atom chain, but also permits to systematically assess the effect of inevitable imperfections, such as the emission of photons into unguided modes.
2. Atoms on a chiral photonic waveguide
The setting under consideration is shown in figure 1. The atoms are coupled both to the left and right propagating guided modes of the waveguide as well as to the unguided modes of the electromagnetic field outside the waveguide. Two photon detectors are placed at the extremes of the waveguide which allows in principle to resolve the photons emitted into both directions. Under the Born–Markov approximation, the open quantum dynamics of the atoms can be described by a Lindblad master equation:
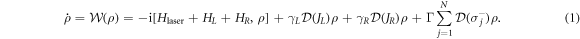
Here, HL and HR describe induced coherent dipole–dipole interactions due to the coupling between the atom chain and the left and right propagating modes of the waveguide, respectively. They read

with k being the propagation constant of the waveguide [30]. The incoherent collective spin decay into the guided modes is described by the dissipators 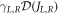 , where
, where 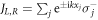 are jump operators describing the emission of a photon into the guided modes, and
are jump operators describing the emission of a photon into the guided modes, and 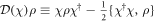 . The last term of equation (1) represents the coupling of the atoms to the modes of the free (unguided) electromagnetic field with rate Γ3
.
. The last term of equation (1) represents the coupling of the atoms to the modes of the free (unguided) electromagnetic field with rate Γ3
.
Figure 1. Atom chain with chiral interactions. A chain of two-level atoms, separated from each other by a distance a, is placed at a distance d from the center of a waveguide. The system is driven homogeneously via a laser field, with Rabi frequency Ω and detuning δ. The photons emitted into the left and right guided modes of the waveguide with rates γL and γR, respectively, are collected by two detectors placed at the ends of the waveguide. Emission of unguided photons into unguided modes occurs at a rate Γ.
Download figure:
Standard image High-resolution imageIn the remainder of the paper we assume, for concreteness, that the spacing between the atoms, a, is commensurate with the wavelength of the laser field: 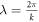 , such that kxj = 2πn with n = 1, 2, ...for all j = 1,..., N. Under these conditions, the master equation (1) simplifies considerably and takes the form
, such that kxj = 2πn with n = 1, 2, ...for all j = 1,..., N. Under these conditions, the master equation (1) simplifies considerably and takes the form
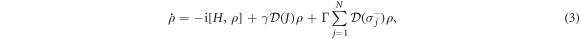
with γ = γR + γL and
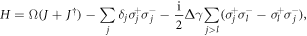
where  and Δγ = γR − γL. For now (we will return to this at a later stage) we also neglect decay into the unguided modes, i.e. we consider Γ = 0.
and Δγ = γR − γL. For now (we will return to this at a later stage) we also neglect decay into the unguided modes, i.e. we consider Γ = 0.
We are here particularly interested in the case of chiral interactions, i.e. when the couplings with the left and the right propagating modes are not symmetric and hence 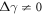 . This is realized by an appropriate choice of the laser polarization and transition dipole moment of each atom: as shown in [32], the dipole moments are required to have a real and imaginary part (elliptically polarized light) in order for the coupling to the guided modes to acquire a chiral character. Note that, in the non-chiral case, i.e. when Δγ = 0, equation (3) with Γ = 0 describes a fully symmetric Dicke model [33]. In this sense, the breaking of chiral symmetry, which induces an effective coupling between the emitters, is crucial to observe any interesting quantum many-body phases.
. This is realized by an appropriate choice of the laser polarization and transition dipole moment of each atom: as shown in [32], the dipole moments are required to have a real and imaginary part (elliptically polarized light) in order for the coupling to the guided modes to acquire a chiral character. Note that, in the non-chiral case, i.e. when Δγ = 0, equation (3) with Γ = 0 describes a fully symmetric Dicke model [33]. In this sense, the breaking of chiral symmetry, which induces an effective coupling between the emitters, is crucial to observe any interesting quantum many-body phases.
3. Photon detection and cumulant generating function
The statistics of the photon count at the two detectors (see figure 1) carries information about the state of the atom chain as well as its dynamical behavior [34]. The counting statistics is fully characterized by the cumulants (e.g. the mean value, the fluctuations, etc), which are encoded in the SCGF. We first briefly summarize how to obtain the SCGF associated to the emission of a generic open quantum system. To this extend, let us consider a quantum system weakly coupled to a reservoir in the Markovian regime. The evolution of its density matrix ρ(t) is described by a master equation:
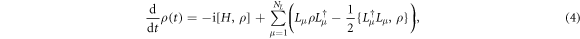
where Lμ and 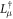 are the Lindblad operators. The detection, i.e. the time record of projection events associated with the emission of photons, can be regarded as a quantum jump trajectory of the system [35]. The probability to observe K events after time t is given by
are the Lindblad operators. The detection, i.e. the time record of projection events associated with the emission of photons, can be regarded as a quantum jump trajectory of the system [35]. The probability to observe K events after time t is given by
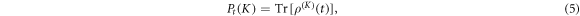
where  is a reduced density matrix obtained by projecting the full density matrix onto the subspace containing K photons. The large deviation assumption comes into play when considering the long time expression of the probability distribution: for long times, i.e. times much longer than any microscopic time scale of the dynamics, Pt(K) acquires the form [28]:
is a reduced density matrix obtained by projecting the full density matrix onto the subspace containing K photons. The large deviation assumption comes into play when considering the long time expression of the probability distribution: for long times, i.e. times much longer than any microscopic time scale of the dynamics, Pt(K) acquires the form [28]:
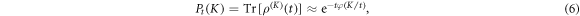
where the large deviation function φ(k) (k ≡ K/t) encloses the statistical information about the probability of K at long times. The statistics of K is encoded in the generating function, together with its associated large deviation form:
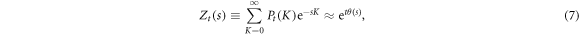
where the function θ(s) is the SCGF of the photon counts. It is possible to establish a formal correspondence between the large deviation functions, φ(k) and θ(s), defined in the space of quantum jump trajectories, and the entropy density and free energy density in the configurations space in equilibrium statistical mechanics, respectively. Within this correspondence, s plays the role of the conjugate field to the dynamical order parameter K: they are related by a Legendre transform, ![$\theta (s)=-{\min }_{k}\left[\varphi (k)+{ks}\right]$](https://content.cld.iop.org/journals/1367-2630/21/11/113021/revision2/njpab4f50ieqn9.gif) . In analogy with the free-energy in statistical mechanic, any anomalous dependence of θ(s) on the s field, indicates non-trivial change of behavior in the trajectories space. Moreover, discontinuities in the derivatives of θ(s) have been found to correspond to phase transitions in the dynamical ensembles of trajectories [29].
. In analogy with the free-energy in statistical mechanic, any anomalous dependence of θ(s) on the s field, indicates non-trivial change of behavior in the trajectories space. Moreover, discontinuities in the derivatives of θ(s) have been found to correspond to phase transitions in the dynamical ensembles of trajectories [29].
In practice, the large-deviation function θ(s) may be found from a generalized master equation: first we define a density matrix which is s-biased
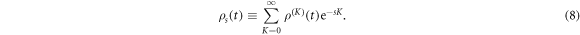
Then, the large deviation form of the SCGF, θ(s), is given by the largest real eigenvalue of the biased dynamical generator:
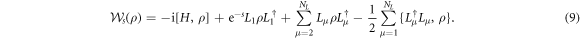
Here, L1 is the Lindblad operator which produces the quantum jumps we count.
The operator Ws is not describing a physical dynamics and in first instance it can be regarded simply as a means to obtain the SCGF. However, it is important to note that albeit its seemingly non-physical nature Ws contains important information on dynamical phase structure of an open quantum system. For 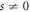 it describes a biased dynamics whose unraveling generates trajectories with a biased probability weight
it describes a biased dynamics whose unraveling generates trajectories with a biased probability weight 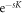 . Moreover, derivatives of the SCGF taken away from s = 0 permit the calculation of the photon count rate (and also higher moments) of this biased trajectory ensemble, e.g.:
. Moreover, derivatives of the SCGF taken away from s = 0 permit the calculation of the photon count rate (and also higher moments) of this biased trajectory ensemble, e.g.:
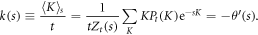
We will later see that this perspective becomes particularly useful when the open system displays phase coexistence (manifesting in a strongly intermittent photon emission). In this situation the tuning of s provides an elegant way to access and characterize the coexisting phases individually.
We now apply the theoretical formalism discussed above to find the SCGF of the photon emitted by the atomic chain system in (1). Let us consider the density matrix 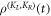 , which represents the state of the atomic system at time t conditioned to the detection of exactly KL and KR photons on the left and right detector, respectively. The corresponding photon detection probability is thus given by
, which represents the state of the atomic system at time t conditioned to the detection of exactly KL and KR photons on the left and right detector, respectively. The corresponding photon detection probability is thus given by ![${P}_{t}({K}_{L},{K}_{R})={\rm{Tr}}\left[{\rho }^{({K}_{L},{K}_{R})}(t)\right]$](https://content.cld.iop.org/journals/1367-2630/21/11/113021/revision2/njpab4f50ieqn13.gif) and its generating function is calculated via the two-dimensional Laplace transform
and its generating function is calculated via the two-dimensional Laplace transform 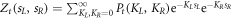 . In the limit of long times its large deviation form is:
. In the limit of long times its large deviation form is: 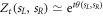 . The SCGF is here given by θ(sL, sR), the largest real eigenvalue of the transformed doubly-biased master operator [29]:
. The SCGF is here given by θ(sL, sR), the largest real eigenvalue of the transformed doubly-biased master operator [29]:
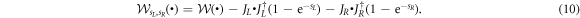
This permits a direct calculation of the SCGF associated with the left/right photon emission, whose derivatives with respect to sL and sR, taken at 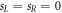 , yield the moments of the photon number distribution. For example, the average number of photons emitted into the left propagating mode is given by
, yield the moments of the photon number distribution. For example, the average number of photons emitted into the left propagating mode is given by 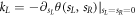 , while the corresponding fluctuations are given by
, while the corresponding fluctuations are given by  . Hence, a sudden change of the structure of the SCGF in the vicinity of sL = sR = 0 is concomitant with large cumulants, e.g. strong fluctuations, which is a manifestation of the occurrence of non-trivial dynamical behavior [36, 37].
. Hence, a sudden change of the structure of the SCGF in the vicinity of sL = sR = 0 is concomitant with large cumulants, e.g. strong fluctuations, which is a manifestation of the occurrence of non-trivial dynamical behavior [36, 37].
4. Intermittent entangled dark states
To be more concrete we consider a system of N = 6 atoms in the chiral regime (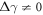 ), described by the master equation (3) with Γ = 0. All atoms are driven by a laser field with spatially uniform detunings δj = δ. To simplify things further, we count the total emission K = KL + KR into both detectors, without resolving the left and right photons separately
), described by the master equation (3) with Γ = 0. All atoms are driven by a laser field with spatially uniform detunings δj = δ. To simplify things further, we count the total emission K = KL + KR into both detectors, without resolving the left and right photons separately 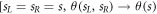 ]. The resulting SCGF is displayed in figure 2(a) as a function of the laser Rabi frequency Ω. For sufficiently large Ω, θ(s) shows a sudden change around s = 0. This signals a sharp increase of the fluctuations in the number of photons arriving at the detectors per unit of time.
]. The resulting SCGF is displayed in figure 2(a) as a function of the laser Rabi frequency Ω. For sufficiently large Ω, θ(s) shows a sudden change around s = 0. This signals a sharp increase of the fluctuations in the number of photons arriving at the detectors per unit of time.
Figure 2. Intermittent entangled dark states. Chain of N = 6 atoms, with Δγ = 2γ/3 and spatially uniform detuning δj = δ = γ/10. (a) Scaled cumulant generating function (SCGF), θ(s), as function of the Rabi frequency Ω. In the inset, a cut for Ω/γ = 1.4 (white dashed line in the main panel) shows that the SCGF undergoes a sharp change at s ≈ 0. (b) Associated photon count k(s), which shows a steep jump at s = 0 for sufficiently large Ω, more noticeable in the inset for Ω/γ = 1.4. (c) Purity of the conditioned state ρs. The state is generally mixed except in a region at large Ω and s > 0 (delimited by a fine white line). (d) Concurrence of the reduced two-body conditioned density matrix 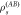 for the atom pairs shown above the panel. (e) (Conditioned/biased) time-resolved photon emission record calculated at
for the atom pairs shown above the panel. (e) (Conditioned/biased) time-resolved photon emission record calculated at 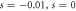 and s = 0.01 for Ω/γ = 1.4 (time is in units of 1/γ) obtained via a quantum-Jump Monte Carlo simulation.
and s = 0.01 for Ω/γ = 1.4 (time is in units of 1/γ) obtained via a quantum-Jump Monte Carlo simulation.
Download figure:
Standard image High-resolution imageWe show below that this is a consequence of the fact that the stationary state for large Ω is actually one where two states (or phases) with drastically different dynamical properties coexist. To analyze the nature of this phenomenon, let us come back to the generating function of the photon count distribution function:
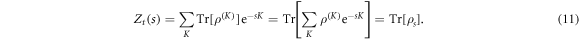
According to this formula, Zt(s) is given as the trace of a biased (unnormalized) density matrix ρs: For s < 0, it is biased towards conditional states, ρ(K), with large numbers of photon count K, while for s > 0 the states with low K are the ones dominantly contributing to ρs. Note that ρs can in practice be found as the eigenstate of the dynamical generator given by equation (10) corresponding to the largest eigenvalue θ(s).
The fact that the SCGF changes quickly in the vicinity of s = 0, as seen in figure 2(a), therefore signals that the biased state ρs changes drastically when s is varied across zero. In the case at hand the steady state turns out to be characterized by the coexistence of a dark state with zero photon count K (inactive phase) and a bright (active) phase with large K. This is seen in figure 2(b), where we show the (biased) mean number of emitted photons per unit time, k(s)4 .
Analyzing the biased state ρs for positive and negative values of s provides direct access to the properties of the two phases that coexist in the steady state. The inactive phase (ρs for s > 0) is characterized by the absence of photon emission into the waveguide. It is expected to be a so-called dark state [38], which is pure and in which 'photons are trapped' in the atomic system due to quantum interference such that the steady state is virtually uncoupled from the modes of the waveguide. Indeed, calculating the purity of the biased state, 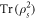 (see figure 2(c)), shows that for large Ω and s > 0 a pure state is assumed. Conversely, a mixed state is found for s < 0. Interestingly, the dark state is entangled in a very peculiar way: in figure 2(d) we show the concurrence [39]
(see figure 2(c)), shows that for large Ω and s > 0 a pure state is assumed. Conversely, a mixed state is found for s < 0. Interestingly, the dark state is entangled in a very peculiar way: in figure 2(d) we show the concurrence [39] 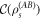 of the two-atom reduced (and biased) density matrix
of the two-atom reduced (and biased) density matrix 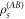 for the AB-pairs shown above the panel. Note, that other pairs are not entangled, i.e. this inactive phase is one of highly entangled dimers.
for the AB-pairs shown above the panel. Note, that other pairs are not entangled, i.e. this inactive phase is one of highly entangled dimers.
Figure 2 nicely illustrates the strength of the applied analysis method: large fluctuations, i.e. a steep change of the photon count rate k(s) at s = 0, are indeed the consequence of two coexisting phases in the steady state. Experimentally, this manifests itself in a highly intermittent photon count, as shown in figure 2(e) (middle panel). However, the theoretical investigation of the biased states ρs reveals much more. It shows that with increasing Ω the steady state of the chiral atom chain is at first unimodal and enters a mixed entangled phase from an unentangled pure (product) state. Increasing Ω further, the steady state acquires an at first highly suppressed (only appearing at large negative s) component of a mixed phase. The weight of this phase increases until it coexists with the entangled phase, which has in turn become a pure dark state.
We now turn briefly to a case which was recently investigated in [22]. Here the atoms are excited with a laser field whose detuning is alternating, 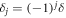 . This may be challenging to achieve experimentally but has the advantage that the steady state can be calculated analytically: it is a dark state formed by dimers, which takes the form
. This may be challenging to achieve experimentally but has the advantage that the steady state can be calculated analytically: it is a dark state formed by dimers, which takes the form 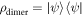 , where
, where 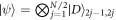 and
and 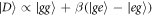 with
with 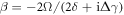 . The corresponding SCGF, the biased photon emission rate as well as the purity of the biased state are shown in figure 3. The plots are similar to the situation depicted in figure 2, i.e. there is an inactive (dark state) phase and an active (mixed) phase that is closing in as Ω is increased. However, unlike in the previous case, both phases cannot be brought into coexistence, i.e. the mixed phase always remains strongly suppressed. For an initial state in which all atoms are in their ground state
. The corresponding SCGF, the biased photon emission rate as well as the purity of the biased state are shown in figure 3. The plots are similar to the situation depicted in figure 2, i.e. there is an inactive (dark state) phase and an active (mixed) phase that is closing in as Ω is increased. However, unlike in the previous case, both phases cannot be brought into coexistence, i.e. the mixed phase always remains strongly suppressed. For an initial state in which all atoms are in their ground state  it is only visible in the transient behavior of the photo current, as shown in figure 3(d). Notice here that the photo current in figure 3(d) is obtained via a quantum Jump Monte Carlo simulation: the transition from a non-zero emission to a dark state is sharp, rather than being exponential, precisely because we consider a single trajectory.
it is only visible in the transient behavior of the photo current, as shown in figure 3(d). Notice here that the photo current in figure 3(d) is obtained via a quantum Jump Monte Carlo simulation: the transition from a non-zero emission to a dark state is sharp, rather than being exponential, precisely because we consider a single trajectory.
Figure 3. Steady state dark states. The system parameters are the same as in figure 2, but the detuning is alternating, 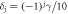 . (a) SCGF, θ(s), as a function of the Rabi frequency Ω. In the inset, a cut for Ω/γ = 1.4 (white dashed line in the main panel) shows that the SCGF has a sharp change this time at s < 0, i.e. active and inactive phase do not coexist. (b) (Biased) steady state photon count rate k(s) and cut taken at Ω/γ = 1.4. (c) Purity of the biased state ρs. The dark entangled state ρdimer is the stationary state of the system for all Ω. (d) The photo current I(t), obtained as a single quantum-Jump Monte Carlo trajectory, shows that the dark state is indeed reached after a (Ω-dependent) transient period. The initial state chosen here is one where all atoms are in their ground state
. (a) SCGF, θ(s), as a function of the Rabi frequency Ω. In the inset, a cut for Ω/γ = 1.4 (white dashed line in the main panel) shows that the SCGF has a sharp change this time at s < 0, i.e. active and inactive phase do not coexist. (b) (Biased) steady state photon count rate k(s) and cut taken at Ω/γ = 1.4. (c) Purity of the biased state ρs. The dark entangled state ρdimer is the stationary state of the system for all Ω. (d) The photo current I(t), obtained as a single quantum-Jump Monte Carlo trajectory, shows that the dark state is indeed reached after a (Ω-dependent) transient period. The initial state chosen here is one where all atoms are in their ground state 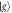 and the time is in units of 1/γ.
and the time is in units of 1/γ.
Download figure:
Standard image High-resolution image5. Emission into unguided modes
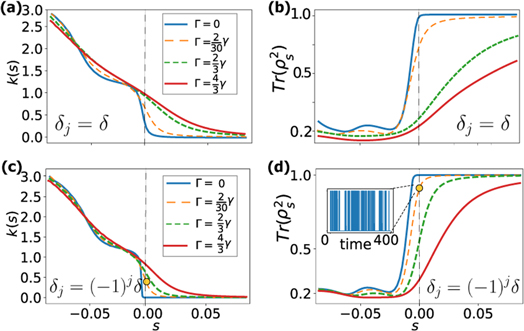
In an experiment, photons are inevitably emitted also into unguided modes at a finite rate Γ [17]. We investigate this in figure 4 for the two detuning patterns discussed in figure 2 ![$[{\delta }_{j}=\delta ]$](https://content.cld.iop.org/journals/1367-2630/21/11/113021/revision2/njpab4f50ieqn34.gif) and figure 3
and figure 3 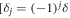 ], respectively. We find that in both cases increasing the value of Γ smooths the sharp features found for
], respectively. We find that in both cases increasing the value of Γ smooths the sharp features found for  in the (biased) emission rate k(s). In the case of homogeneous detuning, the s = 0 line lies precisely at the dynamical phase transition point both for Γ = 0 and
in the (biased) emission rate k(s). In the case of homogeneous detuning, the s = 0 line lies precisely at the dynamical phase transition point both for Γ = 0 and 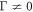 (figures 4(a), (b)). Hence, the dynamics in this case is affected only qualitatively by the presence of the unguided modes. However, the situation changes drastically in the alternating detuning case (figures 4(c), (d)). Here, when Γ = 0 the steady state is exactly the dark state (heralded by k(s = 0) = 0 and purity equal to one). However, for any
(figures 4(a), (b)). Hence, the dynamics in this case is affected only qualitatively by the presence of the unguided modes. However, the situation changes drastically in the alternating detuning case (figures 4(c), (d)). Here, when Γ = 0 the steady state is exactly the dark state (heralded by k(s = 0) = 0 and purity equal to one). However, for any 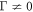 the steady state becomes a mixture between the dark state and a mixed phase. This results in an intermittent photon emission dynamics which is no longer transient, as is shown in the inset of figure 4(d). I.e. just like in figure 2, the unguided modes remove the pure dimerized steady state, which now is probed dynamically through fluctuations, like in the homogeneous detuning scenario.
the steady state becomes a mixture between the dark state and a mixed phase. This results in an intermittent photon emission dynamics which is no longer transient, as is shown in the inset of figure 4(d). I.e. just like in figure 2, the unguided modes remove the pure dimerized steady state, which now is probed dynamically through fluctuations, like in the homogeneous detuning scenario.
Figure 4. Emission into unguided modes. (a) (Biased) Photon emission rate k(s) for the same system as discussed in figure 2 ![$[{\delta }_{j}=\delta ]$](https://content.cld.iop.org/journals/1367-2630/21/11/113021/revision2/njpab4f50ieqn39.gif) at Ω/γ = 1.4. Increasing the emission rate Γ into unguided modes smooths out the sharp features of the SCGF. (b) Purity of the biased state ρs. Increasing Γ moves the steady state into a mixed phase. (c) (Biased) Photon emission rate k(s) for the same system as discussed in figure 3
at Ω/γ = 1.4. Increasing the emission rate Γ into unguided modes smooths out the sharp features of the SCGF. (b) Purity of the biased state ρs. Increasing Γ moves the steady state into a mixed phase. (c) (Biased) Photon emission rate k(s) for the same system as discussed in figure 3 ![$[{\delta }_{j}={(-1)}^{j}\delta ]$](https://content.cld.iop.org/journals/1367-2630/21/11/113021/revision2/njpab4f50ieqn40.gif) at Ω/γ = 1.4. (d) Purity of the biased state ρs. Inset: unbiased photon emission record (for Γ = 2γ/30) showing intermittent behavior due to phase coexistence.
at Ω/γ = 1.4. (d) Purity of the biased state ρs. Inset: unbiased photon emission record (for Γ = 2γ/30) showing intermittent behavior due to phase coexistence.
Download figure:
Standard image High-resolution imageFinally we remark, that the coupling strength between the quantum emitters and the guided modes can be controlled by employing a cavity, as showed in [40], or by considering a photonic crystal waveguide integrated with solid-state emitters, as shown in [41]. Here, the chiral interaction is obtained in presence of slow-light, together with a strong Purcell enhancement.
6. Conclusion
The counting statistics of photons emitted into guided modes yields direct insights into the steady state dynamics of chiral atom chains. Not only does this connection allow the inference of the emergence of dark state phases, it also provides in situ access to dynamical properties and fluctuations. We demonstrated this by focusing on a regime of coexistence between an entangled dark state and a mixed bright phase. Our approach also shows the conceptual strength of the SCGF method and the usefulness of the correspondingly biased quantum state for unraveling complex dynamical behavior in open quantum systems which go beyond the chiral atom chain. For example, the method is applicable with minor modifications to experimental situations where quantum dots, superconducting qubits and cold atoms are coupled to waveguides and photonic nanostructures or crystals [42–45]. In the future it would be interesting to explore other photon detection protocols and the possibility to directly create the biased quantum state via post-selection [46, 47] or a 'deformed dynamics' [48]. The latter is particularly relevant when considering the emission into unguided modes, where dark entangled phases merely emerge as a fluctuation in the steady state dynamics.
Acknowledgments
We thank Dario Cilluffo and all members of the ErBeStA consortium for fruitful discussions. The research leading to these results has received funding from the European Research Council under the European Union's Seventh Framework Programme (FP/2007-2013) [ERC Grant Agreement No. 335266 (ESCQUMA)] and from the European Union's H2020 research and innovation programme [Grant Agreement No. 800942 (ErBeStA)]. Funding was also received from the EPSRC [Grant No. EP/M014266/1]. IL gratefully acknowledges funding through the Royal Society Wolfson Research Merit Award. BO was supported by the Royal Society and EPSRC [Grant No. DH130145].
Footnotes
- 3
Note, that this expression is only valid when the separation between the atoms is sufficiently large, ka ≫ 1. When ka < 1, the emission into the unguided modes becomes collective instead of local, and the exchange of virtual photons gives rise to coherent interactions between the atoms [31].
- 4
Note here that, for s < 0, we find another crossover in k(s): this is a finite-size effect as we confirmed by numerical analysis.