Abstract
Vortex shedding from a moving obstacle potential in a two-component Bose–Einstein condensate is investigated numerically. For a miscible two-component condensate composed of 23Na and 87Rb atoms, in the wake of obstacle, the Kármán vortex street is discovered in one component, while the Kármán-like vortex street named 'half-quantum vortex street' is formed in another component. The other patterns of vortex shedding, such as the vortex dipoles, V-shaped vortex pairs and corresponding 'half-quantum vortex shedding', can also be found. The drag force acting on obstacle potential is calculated and discussed. The parameter region for various vortex patterns and critical velocity for vortex emission are presented. In addition, a 85Rb–87Rb mixture is also considered, where the Kármán vortex street and other typical patterns exist in both components. Finally, we provide an experimental protocol for the above realization and observation.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The phenomenon of periodic vortex shedding from a symmetrical bluff body and the formation of vortices in a street are of vital significance to both theoreticians and experimenters [1]. In the classical physics, this work has been greatly triggered by von Kármán in 1912, who not only analyzed the stability of vortex street configuration, but also established a theoretical link between the vortex street structure and the drag on the body, so the periodic anti-symmetric double-row vortex street was named as Kármán vortex street [1, 2]. Looking for this quantum vortex pattern in the superfluids is one way that physicists can gain a deeper understanding of the relationship between classical and quantum fluids.
Nowadays, Bose–Einstein condensate (BEC) has provided a clean testing ground for the microscopic physics of vortex shedding. Numerical simulations based on the Gross–Pitaevskii equation (GPE) have shown that the vortex dipoles or vortex–antivortex pairs can be nucleated when a superfluid moves past an obstacle faster than the critical velocity, above which vortex shedding induces the drag force [3–8]. Moreover, the vortex dipoles can also be generated by the moving Gaussian potential [9, 10], the oscillating Gaussian potential [11] in a condensate, the circular motion of a Gaussian potential stirring the condensate [12], or the moving circular potential in the plane-wave state of a pseudospin-1/2 BEC with Rashba spin–orbit coupling [13]. In the reported experiment [14], the vortex dipoles have been nucleated by causing a highly oblate BEC to move past a repulsive Gaussian obstacle, and the critical velocity for vortex dipole shedding has been measured.
In 2010, the Kármán vortex street in a single-component BEC, in which an obstacle potential moves, has been first investigated via numerical calculations by Sasaki et al [15]. Subsequently, for a strong phase-separated two-component BEC, in which a bubble of one component moves through the other component, the vortex street is also formed in the wake of moving bubble [16]. Soon after, an elliptical obstacle moving through the BEC also generates the wake of quantum vortices, which resembles the Kármán vortex street, and the role of ellipticity is to facilitate the interaction of vortices nucleated by obstacle [17, 18]. In particular, in a strongly correlated superfluid system, i.e. superfluid 4He at zero temperature, when two-dimensional flow moves past an infinitely long cylinder of nanoscopic radius, the onset of dissipation is characterized by vortex–antivortex pair shedding from the periphery of moving cylinder, while vortex pairs with the same circulation are occasionally emitted in the form of dimers, which constitute the building blocks for the Kármán vortex street structure [19]. On the other hand, through a series of experiments [20–22], in a highly oblate BEC, the vortex shedding from a moving obstacle, which is formed by focusing a repulsive Gaussian laser beam, is investigated by Kwon et al Finally, in 2016, they have reported on the experimental observation for the first time, where the shedding of vortex clusters each consisting of the two like-sign vortices is generated to form a regular configuration in a periodic and stagger manner, like the Kármán vortex street [23].
In the two-component BEC, a variety of dynamical properties have been observed and reported [24–29], and the tunable inter-component interaction has been realized experimentally by using the Feshbach resonance technology [30, 31]. Especially, the quantized vortices have been created and studied [32–39]. For instance, a vortex dipole can not only penetrate the interface between the two components, but also disappear or disintegrate at the interface, depending on its velocity and the interaction parameters [40]. However, as far as we know, there has been little work on studying the vortex shedding from a moving obstacle in a two-component BEC.
In this paper, we investigate the vortex shedding from a moving obstacle potential in a two-component BEC. Here, we systematically perform the numerical simulations to solve the coupled GPEs. First, we consider a miscible two-component condensate which is composed of 23Na and 87Rb atoms at length. The results show that, in the 87Rb component, the Kármán vortex street is discovered in the wake of obstacle potential; in the 23Na component, the Kármán-like vortex street named 'half-quantum vortex street', which is formed for 'half-quantum vortices', is also discovered. The various patterns of vortex shedding, such as no vortex, vortex dipoles, V-shaped vortex pairs, irregular vortices, and corresponding 'half-quantum vortex shedding', can also be found. The drag force acting on the moving obstacle potential is calculated, which depends upon the radius and velocity of obstacle. Also shown is the contribution to the drag force from vortex shedding. The parameter region for all kinds of vortex patterns and the fitting curve of critical velocity for vortex emission are presented. The critical velocity is related to the geometry of obstacle and the speed of sound waves. In addition, a dual-species 85Rb–87Rb condensate is also considered, and there exist the Kármán vortex street and other typical patterns in both components. The drag force, parameter region and critical velocity are also presented. In particular, in the 23Na–87Rb mixture, the absence of vortices in one component could be related to the different sound velocity with respect to the 85Rb–87Rb mixture. Finally, we offer a protocol to realize and observe the above dynamics in future experiments.
2. Formulation of the problem
Considering a two-component BEC within the framework of zero-temperature mean-field theory, the dynamics of system can be well described by the coupled GPEs [16, 41, 42]:
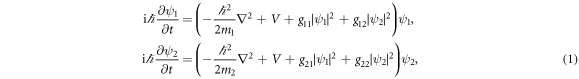
where ψj denotes the macroscopic wave function, mj is the atomic mass of the jth component (j = 1, 2), and V is the external potential. The number of the jth atoms is 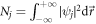 . The intra- and inter-component interaction coefficients can be written as
. The intra- and inter-component interaction coefficients can be written as 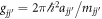 [16] with
[16] with 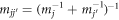 being the reduced mass and
being the reduced mass and  being the s-wave scattering length between atoms in the jth and
being the s-wave scattering length between atoms in the jth and 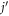 th components, which can be controlled by Feshbach resonance technology [30, 31]. In the experiments, the condensates are generally confined in a harmonic potential
th components, which can be controlled by Feshbach resonance technology [30, 31]. In the experiments, the condensates are generally confined in a harmonic potential 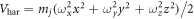 with ωx, ωy, and ωz being the x-, y-, and z-directions trapping frequencies [43]. Here a Gaussian obstacle potential with peak strength V0 and radius d is employed, which moves in the −x direction at a velocity υ [15]
with ωx, ωy, and ωz being the x-, y-, and z-directions trapping frequencies [43]. Here a Gaussian obstacle potential with peak strength V0 and radius d is employed, which moves in the −x direction at a velocity υ [15]
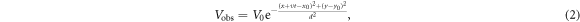
where (x0, y0) is the center position of obstacle potential at t = 0. In the experiments, this moving obstacle potential can be produced by a repulsive Gaussian laser beam along the z direction [9, 14, 15, 20–23].
Here, the system can be reduced to quasi-two-dimensional by considering a very strong confinement along z axis, i.e. ℏωz being much larger than any other energy scale [42–46], which is easily realized in the experiments, e.g. the experiments of Kwon et al [20–23]. It is reasonable that the wave function can be expressed as  , and the motion of atoms along the z-direction is frozen into the ground state
, and the motion of atoms along the z-direction is frozen into the ground state 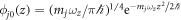 . Then, we can choose
. Then, we can choose 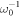 and
and 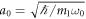 to be the temporal and spatial characteristic quantities, where ω0 = min[ωx, ωy]. One can now obtain the dimensionless coupled GPEs as
to be the temporal and spatial characteristic quantities, where ω0 = min[ωx, ωy]. One can now obtain the dimensionless coupled GPEs as
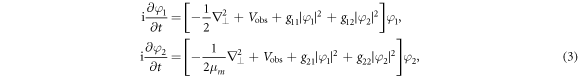
where  is the 2D Laplacian operator and μm = m2/m1. The corresponding dimensionless interaction parameters read
is the 2D Laplacian operator and μm = m2/m1. The corresponding dimensionless interaction parameters read  with
with 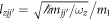 , where n0 is a given particle density. There is an assumption that the moving obstacle potential Vobs is the same for both components. In general, one can take the maximum particle density as n0 (but this is not necessary). The number of the jth atoms is expressed by
, where n0 is a given particle density. There is an assumption that the moving obstacle potential Vobs is the same for both components. In general, one can take the maximum particle density as n0 (but this is not necessary). The number of the jth atoms is expressed by 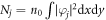 . The speed of sound waves can be written as
. The speed of sound waves can be written as 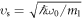 . The various physical quantities in equation (3) are normalized according to
. The various physical quantities in equation (3) are normalized according to
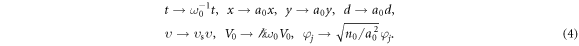
3. Vortex shedding from the obstacle
In order to study the vortex shedding from obstacle, we consider a two-component BEC composed of 23Na and 87Rb atoms. Here, in order to simplify the problem without loss of generality, the interaction parameters can be taken as g11 = g22 = 1.0 and g12 = g21 = 0.5 to satisfy the condition 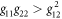 and
and 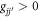 , so that the two components are miscible and stable [38, 39]. This situation can be easily realized in the experiments and it will be discussed later in detail. When the numerical calculations are performed, [−256, 256] ⨂ [−64, 64] spatial domain will be discretized into 2048×512 grids. First, we find the ground state of equation (3) by the imaginary-time propagation approach [43] with υ = 0 and initial condition φ1 = φ2 = 1. Then, the time-splitting spectral method [47–49] is employed to make the nonlinear dynamical evolution with periodic boundary condition, where the initial condition is adopted as the ground state obtained above plus a small amount of noise to break the symmetry of system. The Gaussian obstacle potential Vobs with V0 = 100 and (x0, y0) = (128, 0) will begin to move along the −x direction at a velocity υ for t > 0.
, so that the two components are miscible and stable [38, 39]. This situation can be easily realized in the experiments and it will be discussed later in detail. When the numerical calculations are performed, [−256, 256] ⨂ [−64, 64] spatial domain will be discretized into 2048×512 grids. First, we find the ground state of equation (3) by the imaginary-time propagation approach [43] with υ = 0 and initial condition φ1 = φ2 = 1. Then, the time-splitting spectral method [47–49] is employed to make the nonlinear dynamical evolution with periodic boundary condition, where the initial condition is adopted as the ground state obtained above plus a small amount of noise to break the symmetry of system. The Gaussian obstacle potential Vobs with V0 = 100 and (x0, y0) = (128, 0) will begin to move along the −x direction at a velocity υ for t > 0.
Figures 1 and 2 display the main results of this study. In a miscible two-component BEC composed of 23Na (component 1) and 87Rb (component 2) atoms, it is obvious that there are no quantized vortices in component 1, as shown in figures 1(a) and (b), while there are quantized vortices in component 2, as shown in figures 1(c) and (d). In component 2, it is significant that the two point quantized vortices in a pair, which shed from the moving obstacle potential at a time, have the same circulation. The quantized vortex is the topological defect of order parameter and the circulation is quantized to h/mj [9, 40] with h being the Planck's constant. Here, the symbols + and − denote the clockwise and counterclockwise circulations of quantized vortices. Hence, the circulation of top row is +h/m, while that of bottom row is −h/m. Note that, the two point quantized vortices having the same circulation in a pair rotate around their center without changing distance between vortex and vortex and between pair and pair. As a result, the vortex shedding will form a periodic anti-symmetric double-row vortex street in the wake of moving obstacle potential, this is the signature of quantum analog of the Kármán vortex street. Here we have also measured the distance between two vortex rows being b ≈ 4.38a0 and that between two vortex pairs in the one vortex row being l ≈ 15.88a0 on average, and hence b/l ≈ 0.28. This ratio is in good agreement with the stability condition of Kármán vortex street arrangement 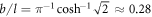 [1, 2, 15]. Correspondingly, in component 1, there exists the Kármán-like vortex street formed for the 'half-quantum vortices'. One can see from figures 1(e) and (f) that, 23Na atoms fill into the 'pits' in component 2 but the 'pits' are not full-filled, and the position of a density peak in component 1 is the center position of a vortex in component 2. The density peak is a part of vortex structure in the two-component BEC, so that this density distribution structure in component 1 can be named as 'half-quantum vortex street'. Figure 2 shows the dynamics of the Kármán vortex street and 'half-quantum vortex street' formation from the moving obstacle potential in detail. The used parameters are the same as those in figure 1. It is obvious that the two point quantized vortices having the same circulation and corresponding 'half-quantum vortices' are periodically and alternately shed from the moving obstacle potential. The pairs of quantized vortices or 'half-quantum vortices' are released obliquely backward left and right with alternate circulations. Eventually, in the wake of moving obstacle potential, the Kármán vortex street and 'half-quantum vortex street' are formed in the component 2 and component 1, respectively.
[1, 2, 15]. Correspondingly, in component 1, there exists the Kármán-like vortex street formed for the 'half-quantum vortices'. One can see from figures 1(e) and (f) that, 23Na atoms fill into the 'pits' in component 2 but the 'pits' are not full-filled, and the position of a density peak in component 1 is the center position of a vortex in component 2. The density peak is a part of vortex structure in the two-component BEC, so that this density distribution structure in component 1 can be named as 'half-quantum vortex street'. Figure 2 shows the dynamics of the Kármán vortex street and 'half-quantum vortex street' formation from the moving obstacle potential in detail. The used parameters are the same as those in figure 1. It is obvious that the two point quantized vortices having the same circulation and corresponding 'half-quantum vortices' are periodically and alternately shed from the moving obstacle potential. The pairs of quantized vortices or 'half-quantum vortices' are released obliquely backward left and right with alternate circulations. Eventually, in the wake of moving obstacle potential, the Kármán vortex street and 'half-quantum vortex street' are formed in the component 2 and component 1, respectively.
Figure 1. Density distributions,  ,
, 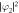 ,
, 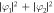 ,
,  , and phase distributions, arg φ1, arg φ2, of the vortex shedding from a moving obstacle potential in the 23Na–87Rb mixture. The potential radius and velocity are d = 1.0 and υ = 0.25. The dotted arrow indicates the direction in which the obstacle potential moves and the solid curved arrow indicates the direction in which a pair of two point quantized vortices or two point 'half-quantum vortices' rotates. The symbols + and − denote the clockwise and counterclockwise circulations of quantized vortices. The density is normalized by n0. The field of view is 64 × 32 in dimensionless units.
, and phase distributions, arg φ1, arg φ2, of the vortex shedding from a moving obstacle potential in the 23Na–87Rb mixture. The potential radius and velocity are d = 1.0 and υ = 0.25. The dotted arrow indicates the direction in which the obstacle potential moves and the solid curved arrow indicates the direction in which a pair of two point quantized vortices or two point 'half-quantum vortices' rotates. The symbols + and − denote the clockwise and counterclockwise circulations of quantized vortices. The density is normalized by n0. The field of view is 64 × 32 in dimensionless units.
Download figure:
Standard image High-resolution imageFigure 2. Serial snapshots of density distributions,  ,
, 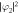 , and phase distributions, arg φ1, arg φ2, of the vortex shedding from a moving obstacle potential in the 23Na–87Rb mixture at different time. The used parameters are the same as those in figure 1, the radius and velocity (d, υ) = (1.0, 0.25). The dotted arrow indicates the direction in which the obstacle potential moves and the solid curved arrow indicates the direction in which a pair of two point quantized vortices or two point 'half-quantum vortices' rotates. The symbols + and − denote the clockwise and counterclockwise circulations of quantized vortices. The density is normalized by n0. The time interval is 40/ω0. The field of view is 32 × 32 in dimensionless units.
, and phase distributions, arg φ1, arg φ2, of the vortex shedding from a moving obstacle potential in the 23Na–87Rb mixture at different time. The used parameters are the same as those in figure 1, the radius and velocity (d, υ) = (1.0, 0.25). The dotted arrow indicates the direction in which the obstacle potential moves and the solid curved arrow indicates the direction in which a pair of two point quantized vortices or two point 'half-quantum vortices' rotates. The symbols + and − denote the clockwise and counterclockwise circulations of quantized vortices. The density is normalized by n0. The time interval is 40/ω0. The field of view is 32 × 32 in dimensionless units.
Download figure:
Standard image High-resolution imageFigures 3 and 4 show the other typical patterns of vortex shedding shed from a moving obstacle potential with the different radius d and velocity υ. As shown in figures 3(a)–(d), when the velocity υ exceeds the critical velocity, that we shall characterize later, the vortex dipoles and 'half-quantum vortex dipoles' will begin to be periodically and symmetrically shed from the obstacle potential. The vortex dipole consists of two point quantized vortices having the opposite circulation, +h/m and −h/m. If the radius d or velocity υ are further increased, the vortex–antivortex pairs and 'half-quantum vortex–antivortex pairs' will be periodically and alternately generated. Since a symmetric double row of vortices is unstable, the vortex–antivortex pairs and 'half-quantum vortex–antivortex pairs' will drift along the +y or −y direction, eventually forming the vortex pattern of V-shaped vortex pairs and 'half-quantum vortex pairs', as shown in figures 3(e)–(h). Especially, as indicated by the solid arrows in figures 3(a), (c), (e) and (g), a pair of two point quantized vortices or 'half-quantum vortices' moves in the direction perpendicular to a line between the pair. For a sufficiently small radius d or velocity υ, the flow around the obstacle is a steady laminar flow and there is no quantized vortex and 'half-quantum vortex' for two components, as shown in figures 4(a)–(d). Conversely, if the radius d or velocity υ is too large, the shedding of quantized vortices and 'half-quantum vortices' will no longer have obvious periodicity and begin to be irregular, as shown in figures 4(e)–(h).
Figure 3. Density distributions, 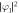 ,
, 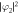 , and phase distributions, arg φ1, arg φ2, of the vortex shedding from a moving obstacle potential with different potential radius d and velocity υ in the 23Na–87Rb mixture. The radius and velocity (d, υ) are (0.4, 0.27) in (a)–(d) and (0.4, 0.29) in (e)–(h). The dotted arrow indicates the direction in which the obstacle potential moves and the solid straight arrow indicates the direction in which a pair of two point quantized vortices or two point 'half-quantum vortices' moves. The symbols + and − denote the clockwise and counterclockwise circulations of quantized vortices. The density is normalized by n0. The field of view is 64 × 32 in dimensionless units.
, and phase distributions, arg φ1, arg φ2, of the vortex shedding from a moving obstacle potential with different potential radius d and velocity υ in the 23Na–87Rb mixture. The radius and velocity (d, υ) are (0.4, 0.27) in (a)–(d) and (0.4, 0.29) in (e)–(h). The dotted arrow indicates the direction in which the obstacle potential moves and the solid straight arrow indicates the direction in which a pair of two point quantized vortices or two point 'half-quantum vortices' moves. The symbols + and − denote the clockwise and counterclockwise circulations of quantized vortices. The density is normalized by n0. The field of view is 64 × 32 in dimensionless units.
Download figure:
Standard image High-resolution imageFigure 4. Density distributions, 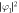 ,
, 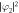 , and phase distributions, arg φ1, arg φ2, of the vortex shedding from a moving obstacle potential with different potential radius d and velocity υ in the 23Na–87Rb mixture. The radius and velocity (d, υ) are (0.4, 0.25) in (a)–(d) and (1.0, 0.29) in (e)–(h). The dotted arrow indicates the direction in which the obstacle potential moves. The symbols + and − denote the clockwise and counterclockwise circulations of quantized vortices. The density is normalized by n0. The field of view is 64 × 32 in dimensionless units.
, and phase distributions, arg φ1, arg φ2, of the vortex shedding from a moving obstacle potential with different potential radius d and velocity υ in the 23Na–87Rb mixture. The radius and velocity (d, υ) are (0.4, 0.25) in (a)–(d) and (1.0, 0.29) in (e)–(h). The dotted arrow indicates the direction in which the obstacle potential moves. The symbols + and − denote the clockwise and counterclockwise circulations of quantized vortices. The density is normalized by n0. The field of view is 64 × 32 in dimensionless units.
Download figure:
Standard image High-resolution imageFigure 5 shows the normalized drag force acting on the moving obstacle potential, which is given by 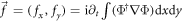 with Φ = (φ1, φ2)T, where T denotes transpose. Corresponding to the situation of no quantized vortex and 'half-quantum vortex' (figures 4(a)–(d)), it is obvious that both fx and fy are about zero, as shown in figure 5(a). However, when the vortex dipoles and 'half-quantum vortex dipoles' are created periodically and symmetrically (figures 3(a)–(d)), fx begin to have an clear periodicity, as shown in figure 5(b). For the vortex patterns of V-shaped vortex pairs and 'half-quantum vortex pairs' (figures 3(e)–(h)) or Kármán vortex street and 'half-quantum vortex street' (figures 1(a)–(d)), both fx and fy are almost periodic, while the periodicity of fx is only half that of fy, as shown in figures 5(c) and (d). It is due to that the vortex emission are not only periodic but also alternate, just as the quantized vortex and 'half-quantum vortex' are released obliquely backward left and right with alternate circulations (see in figure 2). When the shedding of quantized vortices and 'half-quantum vortices' are irregular (figures 4(e)–(h)), both fx and fy will have no obvious periodicity, as shown in figure 5(e). To deeply understand the dependence of drag force acting on the moving obstacle potential, we calculate the normalized time-averaged drag force which can be given by
with Φ = (φ1, φ2)T, where T denotes transpose. Corresponding to the situation of no quantized vortex and 'half-quantum vortex' (figures 4(a)–(d)), it is obvious that both fx and fy are about zero, as shown in figure 5(a). However, when the vortex dipoles and 'half-quantum vortex dipoles' are created periodically and symmetrically (figures 3(a)–(d)), fx begin to have an clear periodicity, as shown in figure 5(b). For the vortex patterns of V-shaped vortex pairs and 'half-quantum vortex pairs' (figures 3(e)–(h)) or Kármán vortex street and 'half-quantum vortex street' (figures 1(a)–(d)), both fx and fy are almost periodic, while the periodicity of fx is only half that of fy, as shown in figures 5(c) and (d). It is due to that the vortex emission are not only periodic but also alternate, just as the quantized vortex and 'half-quantum vortex' are released obliquely backward left and right with alternate circulations (see in figure 2). When the shedding of quantized vortices and 'half-quantum vortices' are irregular (figures 4(e)–(h)), both fx and fy will have no obvious periodicity, as shown in figure 5(e). To deeply understand the dependence of drag force acting on the moving obstacle potential, we calculate the normalized time-averaged drag force which can be given by 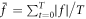 with T being total time. As shown in figure 6, it is obvious that the drag force depends upon the radius d and velocity υ of the moving obstacle potential. With the increase of radius and velocity, the drag force
with T being total time. As shown in figure 6, it is obvious that the drag force depends upon the radius d and velocity υ of the moving obstacle potential. With the increase of radius and velocity, the drag force 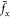 and
and 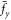 raises gradually while there are some fluctuations. In particular, when velocity is more than the critical velocity, the drag force
raises gradually while there are some fluctuations. In particular, when velocity is more than the critical velocity, the drag force 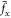 will increase substantially. Also shown is the contribution to the drag force from vortex shedding, namely the vortex shedding induces drag force.
will increase substantially. Also shown is the contribution to the drag force from vortex shedding, namely the vortex shedding induces drag force.
Figure 5. Time evolution of the normalized drag force acting on the moving obstacle potential in the 23Na–87Rb mixture. The blue solid and red dashed lines show fx and fy. The parameters used in (a)–(e) are the same as those in figures 4(a)–(d), 3(a)–(d), (e)–(h), 1(a)–(d) and 4(e)–(h), namely the vortex shedding of no vortex, vortex dipoles, V-shaped vortex pairs, Kármán vortex street, irregular vortices and corresponding no 'half-quantum vortex', 'half-quantum vortex dipoles', V-shaped 'half-quantum vortex pairs', 'half-quantum vortex street', irregular 'half-quantum vortices', respectively.
Download figure:
Standard image High-resolution imageFigure 6. The normalized time-averaged drag force acting on the moving obstacle potential with different radius d depending upon the velocity υ in the 23Na–87Rb mixture. The red, green and blue solid lines show 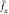 in radius d = 0.5, 1.0 and 1.5, respectively. The orange, cyan and purple dashed lines show
in radius d = 0.5, 1.0 and 1.5, respectively. The orange, cyan and purple dashed lines show  in radius d = 0.5, 1.0 and 1.5, respectively. The black dot marked in the curve is where the critical velocity is located.
in radius d = 0.5, 1.0 and 1.5, respectively. The black dot marked in the curve is where the critical velocity is located.
Download figure:
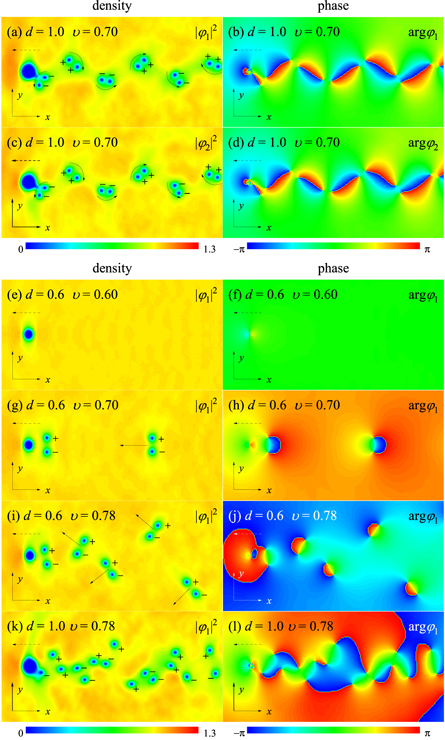
Standard image High-resolution imageThe numerical simulations for the various values of normalized radius d and velocity υ are systematically performed and kinds of the typical patterns of vortex shedding are carefully classified in figure 7. These patterns are the vortex shedding of no vortex (figures 4(c) and (d)), vortex dipoles (figures 3(c) and (d)), V-shaped vortex pairs (figures 3(g) and (h)), Kármán vortex street (figures 1(c) and (d)), irregular vortices (figures 4(g) and (h)) and corresponding no 'half-quantum vortex' (figures 4(a) and (b)), 'half-quantum vortex dipoles' (figures 3(a) and (b)), V-shaped 'half-quantum vortex pairs' (figures 3(e) and (f)), 'half-quantum vortex street' (figures 1(a) and (b)), irregular 'half-quantum vortices' (figures 4(e) and (f)), respectively. Obviously, with the variation of radius d or velocity υ, the pattern of vortex shedding changes from one to another. In particular, compared with the other vortex patterns, the region of vortex street is rather restricted. In figure 7, the white curve is the fitting curve of dimensionless critical velocity for vortex emission 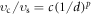 with c ≈ 1/4.79 and p ≈ 1/3.71 in the 23Na–87Rb mixture. It is obvious that the dimensionless critical velocity υc/υs depends on the geometry of moving obstacle potential and shows a 1/dp dependence with p < 1, which is in good agreement with the result in the experiments which the vortex shedding is produced by a repulsive Gaussian laser beam moving through a highly oblate BEC [21] and is also the case in a strongly correlated superfluid 4He system which a two-dimensional flow past an infinitely long cylinder of nanoscopic radius [19]. Besides, the critical velocity υc is also related to the speed of sound waves υs in the BEC.
with c ≈ 1/4.79 and p ≈ 1/3.71 in the 23Na–87Rb mixture. It is obvious that the dimensionless critical velocity υc/υs depends on the geometry of moving obstacle potential and shows a 1/dp dependence with p < 1, which is in good agreement with the result in the experiments which the vortex shedding is produced by a repulsive Gaussian laser beam moving through a highly oblate BEC [21] and is also the case in a strongly correlated superfluid 4He system which a two-dimensional flow past an infinitely long cylinder of nanoscopic radius [19]. Besides, the critical velocity υc is also related to the speed of sound waves υs in the BEC.
Figure 7. Dependence of the typical patterns of vortex shedding on the dimensionless radius d and velocity υ of moving obstacle potential in the 23Na–87Rb mixture. The purple, blue, green, orange and red regions correspond to the patterns shown in figures 4(a)–(d), 3(a)–(d), (e)–(h), 1(a)–(d) and 4(e)–(h), namely the vortex shedding of no vortex, vortex dipoles, V-shaped vortex pairs, Kármán vortex street, irregular vortices and corresponding no 'half-quantum vortex', 'half-quantum vortex dipoles', V-shaped 'half-quantum vortex pairs', 'half-quantum vortex street', irregular 'half-quantum vortices', respectively. The white curve is the fitting curve of dimensionless critical velocity for vortex emission υc/υs = c(1/d)p with c ≈ 1/4.79 and p ≈ 1/3.71 as a function of radius d.
Download figure:
Standard image High-resolution imageIn addition to the 23Na–87Rb mixture discussed before, we consider another two-component BEC composed of 85Rb and 87Rb atoms. The interaction parameters are taken as g11 = g22 = 1.0, g12 = g21 = 0.9 to satisfy the miscible condition. Figure 8 displays the main results, unlike the situation of 23Na–87Rb mixture, it is in the both components of 85Rb–87Rb mixture that the quantized vortices exist. It is obvious that the Kármán vortex street has been formed in the wake of a moving obstacle potential in both components, as shown in figures 8(a)–(d). Here the ratio is also b/l ≈ 0.28 with b ≈ 5.63a0 and l ≈ 20.13a0 on average, which satisfies the stability condition. The other typical patterns of vortex shedding are also created by a moving obstacle potential with the different radius d and velocity υ. Only the density distribution 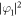 and phase distribution arg φ1 are shown, because they are similar in both components. There also exist the vortex shedding of no vortex (figures 8(e) and (f)), vortex dipoles (figures 8(g) and (h)), V-shaped vortex pairs (figures 8(i) and (j)), and irregular vortices (figures 8(k) and (l)), respectively. As shown in figure 9, both the drag force fx and fy have similar characteristics and periodicity, such as both fx and fy are almost periodic but the periodicity of fx is half that of fy for the vortex shedding of V-shaped vortex pairs and Kármán vortex street. Since vortices are generated in both components, the amplitude of drag force in figure 9 is greater than that in figure 5. For the 85Rb–87Rb mixture, the parameter regions for the various patterns of vortex shedding are also presented in figure 10. By comparison with the 23Na–87Rb mixture, the region of vortex street becomes wider distinctly in the 85Rb–87Rb mixture. Here, the fitting curve of the dimensionless critical velocity is υc/υs = c(1/d)p with c ≈ 1/1.70 and p ≈ 1/3.89 in the 85Rb–87Rb mixture. In particular, the absence of quantized vortices in the 23Na component of the 23Na–87Rb mixture could be related to the different sound velocity υs with respect to the 85Rb–87Rb mixture.
and phase distribution arg φ1 are shown, because they are similar in both components. There also exist the vortex shedding of no vortex (figures 8(e) and (f)), vortex dipoles (figures 8(g) and (h)), V-shaped vortex pairs (figures 8(i) and (j)), and irregular vortices (figures 8(k) and (l)), respectively. As shown in figure 9, both the drag force fx and fy have similar characteristics and periodicity, such as both fx and fy are almost periodic but the periodicity of fx is half that of fy for the vortex shedding of V-shaped vortex pairs and Kármán vortex street. Since vortices are generated in both components, the amplitude of drag force in figure 9 is greater than that in figure 5. For the 85Rb–87Rb mixture, the parameter regions for the various patterns of vortex shedding are also presented in figure 10. By comparison with the 23Na–87Rb mixture, the region of vortex street becomes wider distinctly in the 85Rb–87Rb mixture. Here, the fitting curve of the dimensionless critical velocity is υc/υs = c(1/d)p with c ≈ 1/1.70 and p ≈ 1/3.89 in the 85Rb–87Rb mixture. In particular, the absence of quantized vortices in the 23Na component of the 23Na–87Rb mixture could be related to the different sound velocity υs with respect to the 85Rb–87Rb mixture.
Figure 8. Density distributions, 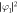 ,
, 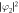 and phase distributions, arg φ1, arg φ2, of the vortex shedding from a moving obstacle potential in the 85Rb–87Rb mixture. The potential radius and velocity are d = 1.0 and υ = 0.25. The dotted arrow indicates the direction in which the obstacle potential moves, the solid straight arrow and the solid curved arrow indicate the direction in which a pair of two point vortices moves and rotates, respectively. The symbols + and − denote the clockwise and counterclockwise circulations of vortices. The density is normalized by n0. The field of view is 64 × 32 in dimensionless units.
and phase distributions, arg φ1, arg φ2, of the vortex shedding from a moving obstacle potential in the 85Rb–87Rb mixture. The potential radius and velocity are d = 1.0 and υ = 0.25. The dotted arrow indicates the direction in which the obstacle potential moves, the solid straight arrow and the solid curved arrow indicate the direction in which a pair of two point vortices moves and rotates, respectively. The symbols + and − denote the clockwise and counterclockwise circulations of vortices. The density is normalized by n0. The field of view is 64 × 32 in dimensionless units.
Download figure:
Standard image High-resolution imageFigure 9. Time evolution of the normalized drag force acting on the moving obstacle potential in the 85Rb–87Rb mixture. The blue solid and red dashed lines show fx and fy. The parameters used in (a)–(e) are the same as those in figures 8(e) and (f), (g) and (h), (i) and (j), (a)–(d), (k) and (l), namely the vortex shedding of no vortex, vortex dipoles, V-shaped vortex pairs, Kármán vortex street, irregular vortices, respectively.
Download figure:
Standard image High-resolution imageFigure 10. Dependence of the typical patterns of vortex shedding on the dimensionless radius d and velocity υ of moving obstacle potential in the 85Rb–87Rb mixture. The purple, blue, green, orange and red regions correspond to the patterns shown in figures 8(e) and (f), (g) and (h), (i) and (j), (a)–(d), (k) and (l), namely the vortex shedding of no vortex, vortex dipoles, V-shaped vortex pairs, Kármán vortex street, irregular vortices, respectively. The white curve is the fitting curve of dimensionless critical velocity for vortex emission υc/υs = c(1/d)p with c ≈ 1/1.70 and p ≈ 1/3.89 as a function of radius d.
Download figure:
Standard image High-resolution imageFinally, we provide an experimental protocol for the realization of above Kármán vortex street and the dynamics of quantized vortices can be observed by the destructive imaging technique [14, 42]. To do so, we consider a miscible two-component BEC composed of 23Na and 87Rb atoms, which are prepared in the 23Na 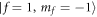 hyperfine state and 87Rb
hyperfine state and 87Rb 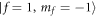 hyperfine state [50] with m1 = 0.38 × 10−25 kg, m2 = 1.45 × 10−25 kg, μm = m2/m1 ≈ 3.78 and the numbers of atoms N1 ≈ 6.55 × 106, N2 ≈ 6.38 × 106 (n0 = 100). Here, the condensate is confined in a harmonic potential
hyperfine state [50] with m1 = 0.38 × 10−25 kg, m2 = 1.45 × 10−25 kg, μm = m2/m1 ≈ 3.78 and the numbers of atoms N1 ≈ 6.55 × 106, N2 ≈ 6.38 × 106 (n0 = 100). Here, the condensate is confined in a harmonic potential 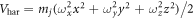 with (ωx, ωy, ωz) = 2π × (4, 4, 235) Hz, so that ω0 = 2π × 4 Hz and a0 = 10.46 μm. The s-wave scattering lengths are
with (ωx, ωy, ωz) = 2π × (4, 4, 235) Hz, so that ω0 = 2π × 4 Hz and a0 = 10.46 μm. The s-wave scattering lengths are 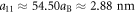 (for 23Na) and a22 ≈ 100.40aB ≈ 5.31 nm (for 87Rb) [51], with aB being the Bohr radius. With an inter-species Feshbach resonance which is realized by Wang et al [51], the inter-species scattering length can be tuned to
(for 23Na) and a22 ≈ 100.40aB ≈ 5.31 nm (for 87Rb) [51], with aB being the Bohr radius. With an inter-species Feshbach resonance which is realized by Wang et al [51], the inter-species scattering length can be tuned to 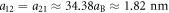 , which leads to the dimensionless quantities g11 = g22 ≈ 1 and g12 = g21 ≈ 0.5 in equation (3). Then, the moving obstacle potential is produced by a repulsive Gaussian laser beam [9, 14, 15, 20–23] along the z direction with peak strength V0 = 2.65 × 10−31 J and radius d = 10.46 μm, which is initially located at (x0, y0) = (1.34,0) mm at t = 0, and moves in the −x direction at a velocity
, which leads to the dimensionless quantities g11 = g22 ≈ 1 and g12 = g21 ≈ 0.5 in equation (3). Then, the moving obstacle potential is produced by a repulsive Gaussian laser beam [9, 14, 15, 20–23] along the z direction with peak strength V0 = 2.65 × 10−31 J and radius d = 10.46 μm, which is initially located at (x0, y0) = (1.34,0) mm at t = 0, and moves in the −x direction at a velocity  for t > 0, corresponding to the parameters used in figure 1.
for t > 0, corresponding to the parameters used in figure 1.
For the 85Rb–87Rb mixture, which are prepared in the 85Rb 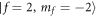 hyperfine state and 87Rb
hyperfine state and 87Rb 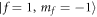 hyperfine state [31] confined in harmonic potential Vhar with (ωx, ωy, ωz) = 2π × (2, 2, 65) Hz. The parameters corresponding to figure 8 can be taken as m1 = 1.42 × 10−25 kg, m2 = 1.45 × 10−25 kg, μm = 1.02, N1 ≈ 3.28 × 106, N2 ≈ 3.27 × 106, n0 = 50, ω0 = 2π × 2 Hz, a0 = 7.70 μm, V0 = 1.32 × 10−31 J, (x0, y0) = (0.98,0) mm, d = 7.70 μm,
hyperfine state [31] confined in harmonic potential Vhar with (ωx, ωy, ωz) = 2π × (2, 2, 65) Hz. The parameters corresponding to figure 8 can be taken as m1 = 1.42 × 10−25 kg, m2 = 1.45 × 10−25 kg, μm = 1.02, N1 ≈ 3.28 × 106, N2 ≈ 3.27 × 106, n0 = 50, ω0 = 2π × 2 Hz, a0 = 7.70 μm, V0 = 1.32 × 10−31 J, (x0, y0) = (0.98,0) mm, d = 7.70 μm, 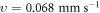 , a11 ≈ 99.24aB ≈ 5.25 nm,
, a11 ≈ 99.24aB ≈ 5.25 nm, 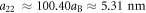 , and
, and 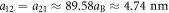 (the corresponding dimensionless quantities g11 = g22 ≈ 1 and g12 = g21 ≈ 0.9 in equation (3)), respectively. Here, both a11 and a12 are assumed to be controlled simultaneously (using some unknown method).
(the corresponding dimensionless quantities g11 = g22 ≈ 1 and g12 = g21 ≈ 0.9 in equation (3)), respectively. Here, both a11 and a12 are assumed to be controlled simultaneously (using some unknown method).
4. Conclusion
In summary, we have numerically investigated the vortex shedding from a moving obstacle potential in a two-component BEC by solving a coupled GPEs. We consider two kinds of miscible two-component condensate, one is composed of 23Na and 87Rb atoms , the other is composed of 85Rb and 87Rb atoms. In the 23Na–87Rb mixture, the Kármán vortex street is discovered in the 87Rb component, while the Kármán-like vortex street named 'half-quantum vortex street', which is formed for 'half-quantum vortices', is discovered in the 23Na component. The various patterns of vortex shedding, such as no vortex, vortex dipoles, V-shaped vortex pairs, irregular vortices, and corresponding 'half-quantum vortex shedding', can also be found. In the 85Rb–87Rb mixture, there exist the Kármán vortex street and other typical patterns in both components. The drag force acting on the moving obstacle potential is calculated, which depends upon the radius and velocity of obstacle. Also shown is the contribution to the drag force from vortex shedding. The parameter region for all kinds of vortex patterns and the fitting curve of critical velocity for vortex emission are presented. The critical velocity is related to the geometry of obstacle and the speed of sound waves. In particular, in the 23Na–87Rb mixture, the absence of vortices in the 23Na component could be related to the different sound velocity with respect to the 85Rb–87Rb mixture. We also provide a protocol for the above realization and observation in future experiments. Finally, we hope that these results can stimulate the further investigation of the vortex shedding in BEC.
Acknowledgments
This work is supported by the National Natural Science Foundation of China under Grant No. 11565021 and the Scientific Research Foundation of Northwest Normal University under Grant Nos. NWNU-LKQN-16-3, NWNU2019KT232.