Frequency measurement of the ${}^{1}{{\rm{S}}}_{0},F=5/2\,\leftrightarrow {}^{3}{{\rm{P}}}_{1},F=7/2$ transition of 27Al+ via quantum logic spectroscopy with 40Ca+

M Guggemos; M Guevara-Bertsch; D Heinrich; O A Herrera-Sancho; Y Colombe; R Blatt; C F Roos

doi:10.1088/1367-2630/ab447a

1. Introduction

Narrow atomic transitions in the optical frequency domain can serve as extremely accurate frequency references with the potential to determine the atomic transition frequency with an uncertainty as low as one part in 10¹⁸ [1]. Over the last decade, optical atomic clocks [2] probing narrow transitions in neutral atoms or trapped ions have been developed that are rapidly approaching this ambitious goal. Through the interrogation of a large number of atoms, frequency standards based on neutral atoms held in optical lattices, achieve excellent short-term instabilities [3, 4]. Frequency standards interrogating only a single ion suffer from larger short-term instabilities but have the advantage to facilitate the control over systematic frequency shifts. Both, single-ion and lattice clocks, have demonstrated a control of systematic frequency uncertainties at the level of 10⁻¹⁸ [5–9]. Thus, they surpass the performance of Cs clocks as testified by frequency ratio measurements between different clocks with an uncertainty of about 5 · 10⁻¹⁷ [3, 10].

Single-ion frequency standards based on Hg⁺, Ca⁺, Sr⁺, or Yb⁺ have demonstrated systematic uncertainties below 10⁻¹⁶ [7, 11–13]. These ions species are attractive since relativistic frequency shifts can be made small by laser-cooling the ions to sub-millikelvin temperatures and their clock transition can be measured using the electron shelving technique, which enables the detection of an ion's quantum state with an efficiency close to 100%. They require, however, a careful evaluation of systematic frequency shifts such as electric quadrupole, ac-Stark or black-body radiation-induced shifts.

From this perspective, the ${}^{1}{{\rm{S}}}_{0}\leftrightarrow {}^{3}{{\rm{P}}}_{0}$ clock transition in Al⁺ (see figure 1) has very attractive features, combining an extremely narrow linewidth of about 8 mHz at 267.4 nm, which gives rise to a high Q factor of ν/Δν ≈ 10¹⁷, with high immunity to perturbations by external fields. The transition has a low dc second-order Zeeman shift, a very small black-body radiation shift, and a negligibly small electric quadrupole shift. The total contribution of these shifts to the total systematic relative uncertainty of the clock has been reported with values below Δν/ν ≈ 8 × 10⁻¹⁸ [10, 14, 15] . For this reason, there are ongoing efforts in several laboratories for constructing an optical frequency standard based on ²⁷Al⁺ [16–19]. In addition, singly charged aluminium ions are a promising candidate for the construction of a transportable optical clock with low fractional systematic uncertainties [20].

Figure 1. Refer to the following caption and surrounding text. — **Figure 1.** Lowest energy levels of the ${}^{27}{\mathrm{Al}}^{+}$ and ${}^{40}{\mathrm{Ca}}^{+}$ . (a) ${}^{27}{\mathrm{Al}}^{+}$ : there are three transitions to the triplet P states, namely the hyperfine-induced clock transition at 267.4 nm, the intercombination transition at 267.0 nm and the magnetic quadrupole transition at 266.1 nm. Hyperfine interaction splits the ³P₁ level into three components. Excitation of the intercombination line on the ${}^{1}{{\rm{S}}}_{0}\,\leftrightarrow {}^{3}{{\rm{P}}}_{1},F=7/2$ transition enables one to prepare the ion in a single Zeeman ground state and to detect whether the ion was excited to the ${}^{3}{{\rm{P}}}_{0}$ state by a laser pulse probing the clock transition. In a magnetic field that lifts the degeneracy of the Zeeman states, the frequency of the intercombination line can be determined by probing the two stretched transitions indicated in the plot by black arrows. (b) ${}^{40}{\mathrm{Ca}}^{+}$ : the ${{\rm{S}}}_{1/2}\leftrightarrow {{\rm{D}}}_{5/2}$ electric quadrupole transition at 729 nm constitutes a frequency standard that can be interrogated by exciting two or more of the ten available Zeeman transition. All transitions denoted by solid lines can be probed by lasers that are available in our experimental setup. For further details, see main text.
Download figure:
Standard image High-resolution image

**Figure 1.** Lowest energy levels of the ${}^{27}{\mathrm{Al}}^{+}$ and ${}^{40}{\mathrm{Ca}}^{+}$ . (a) ${}^{27}{\mathrm{Al}}^{+}$ : there are three transitions to the triplet P states, namely the hyperfine-induced clock transition at 267.4 nm, the intercombination transition at 267.0 nm and the magnetic quadrupole transition at 266.1 nm. Hyperfine interaction splits the ³P₁ level into three components. Excitation of the intercombination line on the ${}^{1}{{\rm{S}}}_{0}\,\leftrightarrow {}^{3}{{\rm{P}}}_{1},F=7/2$ transition enables one to prepare the ion in a single Zeeman ground state and to detect whether the ion was excited to the ${}^{3}{{\rm{P}}}_{0}$ state by a laser pulse probing the clock transition. In a magnetic field that lifts the degeneracy of the Zeeman states, the frequency of the intercombination line can be determined by probing the two stretched transitions indicated in the plot by black arrows. (b) ${}^{40}{\mathrm{Ca}}^{+}$ : the ${{\rm{S}}}_{1/2}\leftrightarrow {{\rm{D}}}_{5/2}$ electric quadrupole transition at 729 nm constitutes a frequency standard that can be interrogated by exciting two or more of the ten available Zeeman transition. All transitions denoted by solid lines can be probed by lasers that are available in our experimental setup. For further details, see main text.
Download figure:
Standard image High-resolution image

Experiments with Al⁺ are complicated by the fact that the dipole-allowed transition ${}^{1}{{\rm{S}}}_{0}\leftrightarrow {}^{1}{{\rm{P}}}_{1}$ that could be used for detecting the quantum state of the ion via state-dependent fluorescence measurements and for preparing the ion in a desired initial state has a wavelength of 167 nm. This makes the operation of Al⁺ clocks technically more challenging than the one of other ion clocks. Moreover, its linewidth of about 220 MHz is rather large so that Doppler cooling on this transition would lead to minimum temperatures that are a magnitude above the ones reached when Doppler cooling Ca⁺, Sr⁺, Hg⁺ or Yb⁺ ions [21]. The problem of detecting the quantum state of the aluminium ion is overcome by quantum logic spectroscopy [22], a technique that enables detecting the quantum state of a trapped atomic or molecular ion [16, 23–27] by transferring the information to a co-trapped ion that can be easily read out.

Excitation of Al⁺ ions on their ${}^{1}{{\rm{S}}}_{0}\leftrightarrow {}^{3}{{\rm{P}}}_{1}$ intercombination line at 267 nm by coherent laser pulses is a technique that enables a set of useful tools for the construction of an optical frequency standard. As the ³P₁ state has a lifetime of ${{\tau }_{{}^{3}{{\rm{P}}}_{1}}}_{}=305(10)\,\mu {\rm{s}}$ [28], the intercombination line can be used for initialising the ion in a pure electronic state by optical pumping, and, even more importantly, for high-fidelity state detection after probing its clock transition by repetitive quantum non-demolition measurements based on quantum logic spectroscopy [29]. Despite the importance of this transition, to our knowledge, a measurement of its transition frequency has only been carried out once before and reported in a conference abstract [30].

In the present paper, we describe quantum logic spectroscopy experiments with a two-ion crystal composed of an ²⁷Al⁺ ion and a ⁴⁰Ca⁺ ion. We use ⁴⁰Ca⁺ as the logic ion primarily because of its similar mass and a relatively narrow cooling transition, which enables efficient sympathetic cooling [31]. Moreover, the ${{\rm{S}}}_{1/2}\leftrightarrow {{\rm{D}}}_{5/2}$ quadrupole transition can be used for a direct clock comparison. Using a frequency comb, we measure the transition frequency of the ${}^{1}{{\rm{S}}}_{0}\leftrightarrow {}^{3}{{\rm{P}}}_{1}$ line in ²⁷Al⁺ by interleaving probing of this transition with probing of the ${{\rm{S}}}_{1/2}\leftrightarrow {{\rm{D}}}_{5/2}$ quadrupole transition in ⁴⁰Ca⁺, which is used as a frequency reference. As a test for systematic errors in the measurement of our ⁴⁰Ca⁺ frequency reference, its transition frequency is compared to the ones measured in two other ⁴⁰Ca⁺ experiments, which are located in neighbouring laboratories. In addition, we also determine the g-factor of the ${}^{3}{{\rm{P}}}_{1},F=7/2$ level.

The paper is organised as follows: the experimental apparatus is described in section 2. In section 3, we describe the preparation of the mixed ⁴⁰Ca⁺–²⁷Al⁺ ion crystal, the quantum logic spectroscopy protocol, and relative frequency measurements of the quadrupole transition in ⁴⁰Ca⁺. In section 4, we describe the absolute frequency measurement of the ${}^{1}{{\rm{S}}}_{0}\leftrightarrow {}^{3}{{\rm{P}}}_{1}$ transition, including a discussion of relevant systematic frequency shifts. We conclude the paper by a brief discussion of the results and preliminary measurements of the ${}^{1}{{\rm{S}}}_{0}\leftrightarrow {}^{3}{{\rm{P}}}_{0}$ clock transition.

2. Experimental apparatus

The experimental apparatus that we designed for quantum logic experiments with Ca⁺ and Al⁺ ions has been previously described in detail in the [32]. In the following, we provide a brief summary of its main features. Ions are stored in a blade-style linear ion trap mounted in an ultra-high vacuum chamber at a residual gas pressure of roughly 10⁻¹¹ mbar. A magnetic field of about 4 G, which defines the quantisation axis along the symmetry axis of the trap, is created by a pair of coils driven by a current source with a long-term fractional current stability of about $| {\rm{\Delta }}I/I| \sim 3\cdot {10}^{-6}$ . Singly charged Al and Ca ions are created via two-step photoionisation from neutral atoms obtained by short-pulse ablation from two different targets. For Doppler cooling and detecting the Ca⁺ ions, we use the light of a frequency-doubled extended-cavity diode laser at 397 nm resonant with the ${{\rm{S}}}_{1/2}\leftrightarrow {{\rm{P}}}_{1/2}$ transition (see figure 1). Two extended-cavity diode lasers, one emitting at 866 nm and the other at 854 nm are used as repumpers. The fluorescence emitted by calcium ions at 397 nm is recorded by a photomultiplier tube and an electron-multiplying CCD camera.

Figure 2 shows the laser setup used for probing and measuring the narrow transitions in ${\mathrm{Ca}}^{+}$ and ${\mathrm{Al}}^{+}$ . For coherent manipulation of the electronic and motional state of the calcium ion, the ${{\rm{S}}}_{1/2}\leftrightarrow {{\rm{D}}}_{5/2}$ quadrupole transition at 729 nm is excited by a titanium-sapphire laser locked to a high-finesse cavity yielding a spectral linewidth on the order of 1 Hz on the time scale of a few seconds; the fibre-induced noise between the laser and the cavity is suppressed by using a similar arrangement as in [33]. The transition frequency can simultaneously be compared with frequency measurements obtained in two other ⁴⁰Ca⁺ experiments in nearby laboratories, designated from now on in the paper as IQOQI lab 1 and University lab (see figure 2). The experiment setups of both laboratories are described in [24, 34], respectively. The fibres connecting different laboratories have optical path lengths that are interferometrically stabilised. Laser light can be sent from one lab to the other by optical fibres that are path-length stabilised by fibre noise cancellation [33], too.

Figure 2. Refer to the following caption and surrounding text. — **Figure 2.** Overview of the optical setup used for probing and measuring the narrow transitions in ⁴⁰Ca⁺ and ²⁷Al⁺ in *IQOQI lab2*. For interrogation of the ²⁷Al⁺ transition, a diode laser at 1068 nm is stabilised to a high-finesse cavity and frequency-quadrupled to 267 nm. The frequency of the 1068nm laser is constantly measured by a frequency comb whose repetition rate is locked to the frequency of the ultrastable laser at 729 nm located in *IQOQI lab1*. A fraction of this laser's output is amplified in a tapered amplifier (TA) and delivered to the ion trap in *IQOQI lab2*. An optical fibre linking the *IQOQI labs* to the *University lab*, which houses an independent frequency-stable Ti:Sa laser at 729 nm, enables a performance evaluation of the two 729 nm laser systems and probing of systematic frequency shifts of the quadrupole transition in Ca⁺ by a simultaneous interrogation of Ca⁺ ions in three different ion traps. To keep the diagram simple, we sketch only *IQOQI lab2*'s acousto-optic modulators (AOMs), which are used for frequency-shifting and intensity-switching the laser beams.
Download figure:
Standard image High-resolution image

For excitation of the ${(3{s}^{2})}^{1}{{\rm{S}}}_{0}\leftrightarrow \,{(3s3p)}^{3}{{\rm{P}}}_{1},F=7/2$ transition in ²⁷Al⁺ a frequency-quadrupled extended-cavity diode laser is used, with a maximum output power of 20 mW at 267.0 nm. The fundamental radiation at 1068 nm of this laser system is stabilised to a high finesse cavity ( ${ \mathcal F }=300\,000$ ). Additionally, a frequency-quadrupled fibre laser is available for excitation of the clock transition at 267.4 nm. Beat measurements between the two lasers (tuned to the same wavelength) reveal a linewidth of 1.6 Hz FWHM or less at 4 s at the fundamental frequency of the lasers. In order to guide the 267.0 nm light to the ion, we implemented a solid-core photonic crystal fibre made from fused silica [35]. This arrangement has the advantage of providing a clean beam profile, thus minimising the amount of UV light that could illuminate the trap electrodes giving rise to the emission of undesired photo-electrons. The Al⁺/Ca⁺ two-ion crystal is illuminated by approximately 200 μW of 267.0 m light by a laser beam parallel to the weak axis of the trap with a beam diameter of ∼65 μm. During the quantum logic spectroscopy experiments the frequency of the 1068nm laser is measured with a femtosecond frequency comb whose repetition rate is locked to the frequency of the ultrastable laser at 729 nm located at IQOQI lab1.

3. Experimental results

Our experiments start by loading a single Ca⁺ ion into the trap and optimising its cooling and fluorescence measurements. Typical oscillation frequencies of a single Ca⁺ ion are 820 kHz along the weak axial direction of the trap and about 1.5 MHz along the radial directions. Micromotion caused by residual electric stray fields is detected by probing the micromotion sidebands of the S_1/2 to D_5/2 transition. It is compensated by applying additional voltages to two compensation electrodes shifting the ion in the radial plane of the linear trap and by unbalancing the dc-voltages applied to the tip electrodes providing the axial confinement. Modulation indices of less than 10⁻² on the transition used for micromotion compensation are obtained at the end of the procedure.

3.1. Trapping, cooling and motional analysis of two-ion Ca⁺/Al⁺ crystals

As described in [32], a ${\mathrm{Ca}}^{+}/{\mathrm{Al}}^{+}$ ion crystal is created by loading an Al⁺ via laser ablation. In experiments probing the intercombination line, mixed ion crystal lifetimes of several hours are typically observed, limited by background gas collisions leading to ion loss or chemical reactions giving rise to conversion of atomic ions to unwanted molecular ions.

A second tool for investigating the collective motion of the two-ion crystal is provided by measurements of absorption sideband spectra on the quadrupole transition in Ca⁺. Figure 3 shows a part of an absorption spectrum obtained by a laser beam with overlap with all six collective modes of motion, which give rise to upper and lower vibrational sidebands of the carrier transition shown in the centre of the plot.

Figure 3. Refer to the following caption and surrounding text. — **Figure 3.** Excitation spectrum of a calcium ion probed at 729 nm in a mixed Al⁺/Ca⁺ ion crystal at typical trapping conditions. The centre peak represents the ${\mathrm{Ca}}^{+}\,{S}_{1/2},{m}_{J}=1/2\leftrightarrow \,{D}_{5/2},{m}_{J}=5/2$ carrier transition with its red and blue motional sidebands of the mixed crystal symmetrically placed to the left and right, respectively. The axial in- and out-of-phase modes are visible at ν_z,i = 888 kHz and ν_z,0 = 1.596 MHz respectively. The degeneracy of the radial potential is lifted by a dc-voltage applied to a pair of blade electrodes so that the radial modes are observed at approximately ν_y,o = 1.25 MHz, ν_x,o = 1.1 MHz, ν_x,i = 1.9 MHz, and ν_y,i = 2.1 MHz. Other peaks appearing correspond to second-order sidebands.
Download figure:
Standard image High-resolution image

**Figure 3.** Excitation spectrum of a calcium ion probed at 729 nm in a mixed Al⁺/Ca⁺ ion crystal at typical trapping conditions. The centre peak represents the ${\mathrm{Ca}}^{+}\,{S}_{1/2},{m}_{J}=1/2\leftrightarrow \,{D}_{5/2},{m}_{J}=5/2$ carrier transition with its red and blue motional sidebands of the mixed crystal symmetrically placed to the left and right, respectively. The axial in- and out-of-phase modes are visible at ν_z,i = 888 kHz and ν_z,0 = 1.596 MHz respectively. The degeneracy of the radial potential is lifted by a dc-voltage applied to a pair of blade electrodes so that the radial modes are observed at approximately ν_y,o = 1.25 MHz, ν_x,o = 1.1 MHz, ν_x,i = 1.9 MHz, and ν_y,i = 2.1 MHz. Other peaks appearing correspond to second-order sidebands.
Download figure:
Standard image High-resolution image

For carrying out the quantum logic spectroscopy protocol described further below (section 3.3), one common vibrational mode of the crystal has to be cooled to its ground state. We observe heating rates of the axial in-phase (z_in) and out-of-phase (z_out) mode of ≈70 phonons s⁻¹ and ≈0.8 phonons s⁻¹, respectively. Due to its lower heating rate, the z_out mode was chosen as the bus mode for the quantum state transfer. Possible dispersive frequency shifts by cross-mode coupling to other collective modes [36] are at the level of a few Hertz and thus too small to be relevant for the experiments described in this paper. In our experiments, we cool both axial vibrational modes to mean phonon numbers below 0.05 by sideband cooling the calcium ion, in order to minimise coupling strength fluctuations when resonantly exciting sideband transitions in Al⁺ or Ca⁺.

3.2. Preparation of the Al⁺ ion in a specific Zeeman ground state

The Al⁺ ion is initialised in a pure electronic state by optical pumping on the intercombination line. In our current experiment, there is only a single laser beam available for exciting the ion from a direction that is parallel to the quantisation axis set by the magnetic field. By making its polarisation circular, it is used to populate either one of the m = ±5/2 stretched Zeeman states using a series of carrier π-pulses exciting the five $m\leftrightarrow m\pm 1$ Zeeman transitions that can be used for pumping out the undesired Zeeman states.

We also tested whether frequency-resolved optical pumping to the stretched states could be achieved by making the beam's polarisation linear. This approach comes with the prospect of being able to optically pump into any Zeeman state or to rapidly switch between populating one or the other stretched state by optical pumping without resetting the beam's polarisation. This approach enabled us to excite all available ${\sigma }_{+}({\sigma }_{-})$ Zeeman transitions using the protocol described below. We found, however, that the pumping worked less reliably as compared to the one by a circularly polarised beam. We attribute these difficulties to coherent population trapping and ac-Stark shifts by the unwanted polarisation component as adjacent Zeeman ground states have energy shifts of less than 10 kHz at a magnetic field of 4 G. From this perspective, it seems more promising to add fast polarisation control or a second laser beam with a different polarisation to the experimental setup.

3.3. Quantum logic spectroscopy of the ${}^{1}{{\rm{S}}}_{0},F=5/2\leftrightarrow {}^{3}{{\rm{P}}}_{1},F=7/2$ transition

Quantum logic spectroscopy experiments probing the intercombination line in Al⁺ are carried out by using the following steps for quantum state initialisation, excitation, and probing:

(i)
Logic ion initialisation. The ion crystal is prepared in the Lamb–Dicke regime by 5 ms of Doppler cooling on the ${{\rm{S}}}_{1/2}\leftrightarrow {{\rm{P}}}_{1/2}$ transition of Ca⁺ at 397 nm. Light at 866 and 854 nm is used to optically pump out the metastable D_3/2 and D_5/2 states of the logic ion. A circularly polarised beam at 397 nm oriented in the direction of the quantisation axis initialises the calcium ion in one of the S_1/2 ground states.
(ii)
Spectroscopy ion initialisation. The Al⁺ ion is optically pumped into either one of the two stretched m_F = ±5/2 Zeeman states of the ¹S₀ ground state by exciting the ${}^{1}{{\rm{S}}}_{0},F=5/2$ to ${}^{3}{{\rm{P}}}_{1},F=7/2$ intercombination line with a circularly polarised beam at 267 nm counterpropagating to the circularly polarised beam at 397 nm. A series of laser pulses driving the five ${m}_{F}\leftrightarrow {m}_{{F}^{{\prime} }}\pm 1$ Zeeman transitions ( $-5/2\leqslant {m}_{F}\lt 5/2$ ) with pulse areas of π followed by a waiting time of 300 μs pushes the population towards the target state. This sequence of pulses is repeated 10 times in order to populate the stretched Zeeman state.
(iii)
Ground-state cooling and logic ion preparation. Both axial modes are sideband-cooled close to the ground state by two laser pulses on the quadrupole transition at 729 nm with a total duration of 7 ms. To minimise the average vibration quantum number of the out-of-phase mode used for the quantum logic state transfer, the in-phase-mode is cooled prior to cooling the out-of-phase mode. Finally, a carrier π-pulse transfers the Ca⁺ ion into the D_5/2 state.
(iv)
Spectroscopy ion probing. The ${| }^{1}{{\rm{S}}}_{0},F=5/2,{m}_{F}=\pm 5/2\rangle \leftrightarrow \,{| }^{3}{{\rm{P}}}_{1},F=7/2,{m}_{{F}^{{\prime} }}=\pm 7/2\rangle$ carrier transition is probed by either a single pulse or in a Ramsey experiment by a pair of π/2 pulses separated by a waiting time.
(v)
Quantum state transfer. For state mapping to the logic ion, a π-pulse of the upper motional sideband of the out-of-phase mode on the ${| }^{1}{{\rm{S}}}_{0},F=5/2,{m}_{F}=\pm 5/2\rangle \leftrightarrow \,{| }^{3}{{\rm{P}}}_{1},F=7/2,{m}_{{F}^{{\prime} }}=\pm 7/2\rangle$ transition adds a phonon to the system if the previous carrier excitation was unsuccessful. The phonon is mapped to a change of the electronic state in Ca⁺ by a consecutive π-pulse on the upper motional sideband of the same mode on the ${{\rm{S}}}_{1/2}\leftrightarrow \,{{\rm{D}}}_{5/2}$ transition, which returns the calcium ion to its electronic ground state. As a result, the calcium ion is found in D_5/2 if the aluminium ion was excited to the metastable state by the carrier excitation pulse of step (iv).
(vi)
Quantum state detection. The quantum state of Ca⁺ is measured via electron shelving.

Figure 4 shows an application of this protocol that was used for recording Rabi oscillations on the blue sideband and the carrier transition of the ${| }^{1}{{\rm{S}}}_{0},F=5/2,{m}_{F}=5/2\rangle \leftrightarrow | {}^{3}{{\rm{P}}}_{1},F=7/2,{m}_{{F}^{{\prime} }}=7/2\rangle$ transition. Note, that in the former case, we omit step (iv) and vary the duration of the sideband pulse in step (v). It demonstrates that π-pulses can be realised on the sideband with a fidelity of about 95% and that the Al⁺ ion can be coherently excited to the metastable state by a carrier π-pulse with a duration of about 4 μs. On the carrier transition, the loss of contrast versus time is predominantly caused by high-frequency phase noise of the quadrupled diode laser system , leading to an exponential damping of Rabi oscillations. This assumption is corroborated by the fact that the ratio γ/Ω between the damping rate γ of the oscillations and the carrier Rabi frequency Ω is not constant but increases with Ω in qualitative agreement with the measured spectral phase noise of the laser. On the sideband, the contrast loss is due to laser phase noise and loss of population from the upper state by spontaneous emission.

Figure 4. Refer to the following caption and surrounding text. — **Figure 4.** (a) Rabi oscillations on the blue sideband (z_out) of the ${(3{s}^{2})}^{1}{{\rm{S}}}_{0},{m}_{F}=-5/2\leftrightarrow \,{(3s3p)}^{3}{{\rm{P}}}_{1},F\,=\,7/2,{m}_{F}=-7/2$ transition of the Al⁺ ion detected by quantum logic spectroscopy. After 15 μs approximately 95% of the population is transferred to the excited state. The imperfections of this π-pulse give rise to the baseline in the Ramsey patterns. The fidelity is limited by high frequency noise of the laser and temperature fluctuations of the axial in-phase mode. The error bars are determined from quantum projection noise. The red curve, an exponentially decaying sine function including a constant offset, is fitted to the experimental data. (b) Rabi oscillations on the carrier transition for identical parameters. The signal is obtained by adding a carrier excitation pulse of variable length to the pulse sequence prior to the blue-sideband π-pulse. Again, the data is fitted by an exponentially damped harmonic oscillation.
Download figure:
Standard image High-resolution image

**Figure 4.** (a) Rabi oscillations on the blue sideband (z_out) of the ${(3{s}^{2})}^{1}{{\rm{S}}}_{0},{m}_{F}=-5/2\leftrightarrow \,{(3s3p)}^{3}{{\rm{P}}}_{1},F\,=\,7/2,{m}_{F}=-7/2$ transition of the Al⁺ ion detected by quantum logic spectroscopy. After 15 μs approximately 95% of the population is transferred to the excited state. The imperfections of this π-pulse give rise to the baseline in the Ramsey patterns. The fidelity is limited by high frequency noise of the laser and temperature fluctuations of the axial in-phase mode. The error bars are determined from quantum projection noise. The red curve, an exponentially decaying sine function including a constant offset, is fitted to the experimental data. (b) Rabi oscillations on the carrier transition for identical parameters. The signal is obtained by adding a carrier excitation pulse of variable length to the pulse sequence prior to the blue-sideband π-pulse. Again, the data is fitted by an exponentially damped harmonic oscillation.
Download figure:
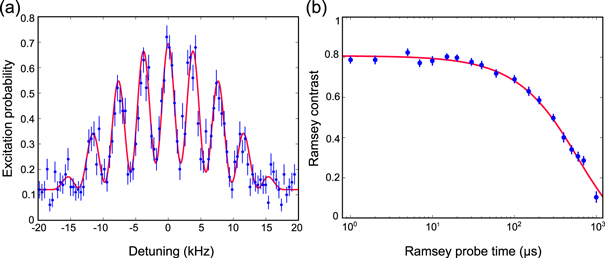
Standard image High-resolution image

For a further investigation of the coherence time on the intercombination line, Ramsey experiments on the carrier transition were carried out using the quantum logic spectroscopy protocol for state read-out. Figure 5(a) shows the Ramsey signal as a function of laser detuning, whereas figure 5(b) shows the Ramsey contrast as a function of the waiting time between the π/2-pulses. At short waiting times a Ramsey contrast of 0.81(1) is obtained which is limited by imperfect π/2 and state mapping pulses. At longer waiting times, the contrast decays exponentially with time, in agreement with an exponential loss of contrast with a decay time of τ = 2τ_3P1 as expected from spontaneous decay of the ³P₁ state. Contrast loss by magnetic field noise is insignificant as compared to the effect of amplitude-damping.

Figure 5. Refer to the following caption and surrounding text. — **Figure 5.** (a) Ramsey experiment on the ²⁷Al⁺ ${(3{s}^{2})}^{1}{{\rm{S}}}_{0},{m}_{F}=-5/2\leftrightarrow {(3s3p)}^{3}{{\rm{P}}}_{1},F=7/2,{m}_{{F}^{{\prime} }}=-7/2$ carrier transition: measured excitation as a function of laser detuning (blue points) for Ramsey pulses of 50 μs duration and a waiting time of 200 μs. The data is fitted by a numerical integration of the master equation describing the Ramsey experiment (solid line), including spontaneous decay of the ³P₁ level. The resulting excitation probability is adjusted for a frequency offset, an excitation baseline and a reduction in contrast. (b) Ramsey contrast versus waiting time on the same transition. Fitting an exponential decay curve to the data yields a contrast of 0.81(1) for very short Ramsey times and a decay time of τ = 598(20) μs that agrees within its error bar with twice the lifetime of the ³P₁ level.
Download figure:
Standard image High-resolution image

**Figure 5.** (a) Ramsey experiment on the ²⁷Al⁺ ${(3{s}^{2})}^{1}{{\rm{S}}}_{0},{m}_{F}=-5/2\leftrightarrow {(3s3p)}^{3}{{\rm{P}}}_{1},F=7/2,{m}_{{F}^{{\prime} }}=-7/2$ carrier transition: measured excitation as a function of laser detuning (blue points) for Ramsey pulses of 50 μs duration and a waiting time of 200 μs. The data is fitted by a numerical integration of the master equation describing the Ramsey experiment (solid line), including spontaneous decay of the ³P₁ level. The resulting excitation probability is adjusted for a frequency offset, an excitation baseline and a reduction in contrast. (b) Ramsey contrast versus waiting time on the same transition. Fitting an exponential decay curve to the data yields a contrast of 0.81(1) for very short Ramsey times and a decay time of τ = 598(20) μs that agrees within its error bar with twice the lifetime of the ³P₁ level.
Download figure:
Standard image High-resolution image

3.4. Probing the ${{\rm{S}}}_{1/2}\leftrightarrow {{\rm{D}}}_{5/2}$ transition in ⁴⁰Ca⁺

The ${{\rm{S}}}_{1/2}\leftrightarrow \,{{\rm{D}}}_{5/2}$ transition in ⁴⁰Ca⁺ was used as a stable and calibrated frequency [13, 34, 37] for the 729 nm laser and as a magnetic field sensor. In order to keep track of any frequency drift Δf of the 729 nm laser or any magnetic field fluctuations ΔB we probed two different Zeeman transitions, $| {{\rm{S}}}_{1/2},m=\pm 1/2\rangle \leftrightarrow \,| {{\rm{D}}}_{5/2},{m}^{{\prime} }=\pm 3/2\rangle$ , as illustrated in figure 1, with Ramsey experiments composed of π/2-pulses of 50 μs duration that were separated by a 2 ms waiting time. The frequency shift of the laser Δf is given by the arithmetic mean of the measured detunings from the two transitions. As the g-factors of the electronic states are well-known [34, 38], the frequency splitting of the Zeeman transitions provides also a measure of the absolute value of the dc-magnetic field fluctuations ΔB. Choosing two opposite Zeeman transitions has the advantage of cancelling not only the first-order dc-Zeeman shift but also possible ac-Zeeman shifts caused by currents oscillating at the trap drive frequency.

To ensure that systematic frequency shifts do not cause any significant error in the determination of the frequency of the intercombination line in Al⁺, a direct comparison of the calcium transition frequency measured in three different laboratories was made. The frequency measured in our experimental setup (IQOQI lab 2) was compared to the frequency measured in two similar experimental setups (see figure 2). The setups of IQOQI lab1 and IQOQI lab 2 share the same 729 nm laser while the University lab has its own independent laser setup. Laser beat measurements show, after subtraction of a linear frequency drift, that the two lasers differ by no more than 10 Hz over the course of several hours. For the frequency comparison, two Zeeman transitions, ${{\rm{S}}}_{1/2},m=\pm 1/2\leftrightarrow \,{{\rm{D}}}_{5/2},{m}^{{\prime} }=\pm 3/2$ , were probed with Ramsey experiments of 3 ms duration during a period of five hours. Here, the laser frequency was not locked to the ion's transition frequency; instead, the slow linear drift (∼50 mHz s⁻¹) of the high-finesse cavity's reference frequency, which the laser was locked to, was further reduced by a feed-forward on the laser frequency. The data was subsequently binned into one-minute intervals and the frequency difference between two setups was evaluated. Figure 6 shows histograms of the measured frequency differences with the other two setups.

Figure 6. Refer to the following caption and surrounding text. — **Figure 6.** Comparison of the measured frequency differences of the ${{\rm{S}}}_{1/2}\leftrightarrow \,{{\rm{D}}}_{5/2}$ transition of a single Ca⁺ ion in the present setup (*IQOQI lab* 2) with two similar experimental setups, (a) *IQOQI lab* 1, and (b) *University lab*. For this histogram, the data was binned into one-minute time intervals. For a detailed description of the measurement scheme, see section 3.4. A Gaussian fit of the histogram distribution (red line) in both cases yields line widths of 2.77(0.15) Hz and 2.33(0.11) Hz, respectively, which are consistent with measurement uncertainties caused by quantum projection noise.
Download figure:
Standard image High-resolution image

**Figure 6.** Comparison of the measured frequency differences of the ${{\rm{S}}}_{1/2}\leftrightarrow \,{{\rm{D}}}_{5/2}$ transition of a single Ca⁺ ion in the present setup (*IQOQI lab* 2) with two similar experimental setups, (a) *IQOQI lab* 1, and (b) *University lab*. For this histogram, the data was binned into one-minute time intervals. For a detailed description of the measurement scheme, see section 3.4. A Gaussian fit of the histogram distribution (red line) in both cases yields line widths of 2.77(0.15) Hz and 2.33(0.11) Hz, respectively, which are consistent with measurement uncertainties caused by quantum projection noise.
Download figure:
Standard image High-resolution image

The frequency measured in the IQOQI lab 2 experimental setup differed by 1.3(2) Hz from the value measured in IQOQI lab 1, and by 1.2(2) Hz from the value found in University lab. We attribute the offsets between the labs mainly to different electric quadrupole shifts due to different axial trapping confinements and stray electric field gradients, and to a lesser degree to AC Stark shifts caused by stray light (see also table 1). A detailed investigation of the systematic frequency shift of a single Ca⁺ ion clock can be found in [34]. After subtraction of known systematic shifts, the frequencies agree with each other to better than 1 Hz.

Table 1. Systematic frequency shifts and measurement uncertainties of the two transitions probed in ${\mathrm{Ca}}^{+}$ and ${\mathrm{Al}}^{+}$ . For the determination of the intercombination line frequency, the systematic shifts of the calcium transition enter the error budget after having been multiplied by the frequency ration ν_Al/ν_Ca.

Effect	Ca shift (uncertainty)(Hz)	Al shift (uncertainty) (Hz)
${S}_{1/2}-{D}_{5/2}$ frequency	0 (4)	—
Electric quadrupole shift	2.7(0.1)	−7.4
2nd order Zeeman shift	2.8	−2.1
Ramsey probe time dependence	—	0 (85)
Statistics	—	0 (8.8)

Total shift	5.5(4.0)	−9.5 (85.5)

4. Frequency measurement of the intercombination transition

The remainder of the paper is about frequency measurements in Al⁺. In the following, we will describe how we infer the absolute frequency of the intercombination line from the measurement results we obtained when probing the transition and discuss the corresponding error budget.

4.1. Measurement results

For a measurement of the ${(3{s}^{2})}^{1}{{\rm{S}}}_{0}\leftrightarrow {(3s3p)}^{3}{{\rm{P}}}_{1},F=7/2$ transition, we probe the Al⁺ ion with Ramsey experiments as described in section 3.3. The fundamental frequency of the laser probing the transition is recorded with the frequency comb whose repetition rate is locked to the frequency of the ultrastable laser at 729 nm. The frequency of the latter is monitored by Ramsey experiments on Ca⁺ that are interleaved with experiments probing the Al⁺ ion. In this way, the frequency of the intercombination line can be determined with respect to the well-known ${{\rm{S}}}_{1/2}\leftrightarrow \,{{\rm{D}}}_{5/2}$ transition frequency of ${}^{40}{\mathrm{Ca}}^{+}$ . The comb measurements show that frequency fluctuations of the light probing the intercombination line in Al⁺ are typically about 60 Hz over the course of fifteen minutes.

We interrogated the ${| }^{1}{{\rm{S}}}_{0},F=5/2,{m}_{F}=5/2\rangle \leftrightarrow \,{| }^{3}{{\rm{P}}}_{1},F=7/2,{m}_{{F}^{{\prime} }}=7/2\rangle$ Zeeman transition with Ramsey experiments composed of π/2-pulses of 50 μs duration separated by a waiting time of either 100 or 200 μs. The phase ϕ of the second π/2-pulse was shifted with respect to the first one by either 0, ± π/2, or π, in order to extract both the laser-ion detuning and the contrast of the Ramsey fringe. For each setting of ϕ, the experiment was repeated 100 times. Next, another four sets of 100 experiments were carried out probing two Zeeman ${{\rm{S}}}_{1/2}\leftrightarrow \,{{\rm{D}}}_{5/2}$ transitions in ${}^{40}{\mathrm{Ca}}^{+}$ as described in section 3.4, with the phase of the second Ramsey pulse shifted by ϕ = ±π/2, for a measurement of the detuning of the laser at 729 nm from the atomic transition and the magnetic bias field, with an uncertainty of 4.5 μG. This cycle of eight different experiments was repeated fifty times followed by a recalibration of experimental parameters. The same type of experiment was also carried out for a measurement of the ${| }^{1}{{\rm{S}}}_{0},F=5/2,{m}_{F}=-5/2\rangle \leftrightarrow \,{| }^{3}{{\rm{P}}}_{1},F=7/2,{m}_{{F}^{{\prime} }}=-7/2\rangle$ Zeeman transition. The absolute value of the transition frequency is obtained with respect to the transition frequency of the ${S}_{1/2}\leftrightarrow {D}_{5/2}$ transition in ${}^{40}{\mathrm{Ca}}^{+},{\nu }_{\mathrm{Ca}}=411\,042\,129\,776\,398(4)$ Hz, where we took the weighted average of the frequency measurements reported by three different groups in [13, 34, 37].

Our evaluation of the ${}^{1}{{\rm{S}}}_{0},F=5/2\leftrightarrow {}^{3}{{\rm{P}}}_{1},F=7/2$ transition frequency is based on a total of n = 18 sets of measurements. For each set, the uncertainty of the measured average deviation of the laser frequency from the atomic transition is predominantly given by quantum projection noise. For the probed Zeeman transitions, the transition frequency f at non-zero magnetic field B is related to the transition frequency f₀ at zero magnetic field by $f={f}_{0}+\tfrac{{\mu }_{B}}{h}\left(\tfrac{7}{2}{g}_{{}^{3}{P}_{1},{F}^{{\prime} }=7/2}-\tfrac{5}{2}{g}_{{}^{1}{S}_{0}}\right){s}_{\pm }B$ where ${s}_{\pm }=\pm 1$ depending on which of the two stretched state transitions is probed, with μ_B the Bohr magneton and h Planck's constant. For each measurement set, we determine the magnetic field strength by measuring the frequency splitting of the two Zeeman transitions probed in Ca⁺ with an uncertainty of about 1 μGauss. We plot the measured frequency f_i as a function of ${s}_{\pm }B$ and fit a straight line to the data in order to extract f₀ and the g-factor of the ${}^{3}{{\rm{P}}}_{1},{F}^{{\prime} }=7/2$ state. This procedure yields a transition frequency at B = 0 of ${f}_{0}=1122\,842\,857\,334\,711\,\mathrm{Hz}$ . The residuals of the fit are shown in figure 7 with error bars accounting for the standard deviation of the fifty frequency measurements per data set and errors in the determination of the magnetic field. Under the assumption of normally distributed residuals, we estimate their standard deviation to be σ = 36.4 Hz which results in a statistical error of the transition frequency f₀ of $\sigma /\sqrt{n-1}=8.8\,\mathrm{Hz}$ .

Figure 7. Refer to the following caption and surrounding text. — **Figure 7.** Residuals of the 18 frequency measurements of the Al⁺ transition from the linear fit. Data points 1–8 were taken with the frequency comb's repetition rate locked to a stable quartz oscillator. Data points 9–18 were recorded with a comb line locked to the frequency of the laser at 729 nm. Measurements of the $m=5/2\leftrightarrow m=7/2$ transition are denoted by squares, measurements of the $m=-5/2\leftrightarrow m=-7/2$ transition are denoted by circles. The colour indicates whether the duration of the Ramsey experiments was 100 μs (blue) or 200 μs (red). Dashed lines indicate the means of the residuals with the corresponding colour.
Download figure:
Standard image High-resolution image

**Figure 7.** Residuals of the 18 frequency measurements of the Al⁺ transition from the linear fit. Data points 1–8 were taken with the frequency comb's repetition rate locked to a stable quartz oscillator. Data points 9–18 were recorded with a comb line locked to the frequency of the laser at 729 nm. Measurements of the $m=5/2\leftrightarrow m=7/2$ transition are denoted by squares, measurements of the $m=-5/2\leftrightarrow m=-7/2$ transition are denoted by circles. The colour indicates whether the duration of the Ramsey experiments was 100 μs (blue) or 200 μs (red). Dashed lines indicate the means of the residuals with the corresponding colour.
Download figure:
Standard image High-resolution image

The scatter of the data points is somewhat bigger than what one would expect given that half of the individual data points have residuals that are larger than their individual 1σ-error bars. Moreover, the measurements with free Ramsey durations of 200 μs yield a frequency estimate differing by δν = 40 Hz from the measurement based on Ramsey experiments of 100 μs duration. To evaluate the statistical significance of this finding, we test the null hypothesis H that the determined frequency is independent of the duration of the Ramsey experiment. Under this hypothesis, the difference ${\rm{\Delta }}=2/N{\sum }_{i=1}^{N/2}({X}_{i}^{(200)}-{X}_{i}^{(100)})$ (with ${ \mathcal N }(0,{\sigma }_{r}^{2})$ -distributed Gaussian random variable ${X}_{i}^{(T)}$ describing the outcome of the ith measurement with Ramsey duration T) is itself a Gaussian random variable with a distribution given by ${ \mathcal N }(0,{\sigma }^{2})$ with $\sigma =\sqrt{4/N}{\sigma }_{r}=17\,\mathrm{Hz}$ . Then, the probability of finding a difference of δ or larger is given by $p=P(| {\rm{\Delta }}| \geqslant | \delta | | H)=1-{\rm{erf}}(\delta /(\sqrt{2}\sigma ))\approx 0.02$ . This rather small p-value makes it seem unlikely that there was no systematic shift present in the experiment. It could be the result of a rather unlikely statistical fluctuation or caused by an undetected systematic shift in the experiment. However, no such shift was detected in subsequent control experiments probing the transition by alternating between Ramsey experiments of 100 and 200 μs duration.

From the variation of the magnetic-field-induced splitting ${\rm{\Delta }}\nu /B=\tfrac{{\mu }_{B}}{h}\left(\tfrac{7}{2}{g}_{{}^{3}{{\rm{P}}}_{1},{F}^{{\prime} }=7/2}-\tfrac{5}{2}{g}_{{}^{1}{{\rm{S}}}_{0}}\right)\,=2.100\,056(9)$ MHz/G on the known magnetic field and the knowledge of ${g}_{{}^{1}{{\rm{S}}}_{0}}$ [23], we determine the Landé g-factor of the excited state to be ${g}_{{}^{3}{{\rm{P}}}_{1},{F}^{{\prime} }=7/2}=0.428\,133(2)$ , where the error bar represents the statistical uncertainty due to the finite number of measurements.

4.2. Evaluation of systematic frequency shifts and measurement uncertainties

For the evaluation of the ${}^{1}{{\rm{S}}}_{0}{\leftrightarrow }^{3}{{\rm{P}}}_{1}$ transition frequency, both systematic frequency shifts in Al⁺ and Ca⁺ need to be taken into consideration. The scatter of the frequency measurements shown in figure 7 suggests that an unexpected systematic shift might have been present when these measurements were taken. Even though it seems unlikely, the frequency shift of 40 Hz between the measurements taken with 100 μs (200 μs) Ramsey time could have been caused by an ac-Stark down-shifting the transition frequency during the π/2-pulses. This effect would vanish in the limit of infinitely long Ramsey experiments and lead to a systematic shift of −85 Hz in the frequency measurement. Conversely, an ac-Stark shift upshifting the transition frequency only during the period of free time evolution could explain the observed 40 Hz discrepancy and would lead to a systematic shift of +85 Hz. As we cannot rule out the existence of such ac-Stark, nor the existence of a shift of the same magnitude but opposite sign, or other shifts (even though we do not know any mechanism producing a shift of the required magnitude), we added an uncertainty of 85 Hz to our error budget and calculate the absolute error of the frequency measurement by adding this uncertainty and the statistical error in quadrature.

The electric quadrupole moment of the ${}^{3}{{\rm{P}}}_{1}$ level of the ${}^{27}{\mathrm{Al}}^{+}$ ion couples to any static electric field gradients in the trap. The dominant electric field gradient is caused by the quadrupolar static electric potential confining ions axially and by the electric field gradient of the co-trapped ${}^{40}{\mathrm{Ca}}^{+}$ ion. These field gradients will shift the energy of the stretched ${}^{3}{{\rm{P}}}_{1},F=7/2,{m}_{F}=\pm 7/2$ levels by ${\rm{\Delta }}E=\tfrac{1}{2\sqrt{30}}\langle {nJ}| | {Q}_{2}| | {nJ}\rangle \tfrac{{\partial }^{2}{\rm{\Phi }}}{\partial {z}^{2}}$ . Following the prescription of [15, 31] for calculating the second derivative of the potential for a mixed ion crystal with 888 kHz axial in-phase oscillation frequency, one obtains a frequency shift of −7.4 Hz for the stretched Zeeman states where we used the reduced matrix element $\langle {nJ}| | {Q}_{2}| | {nJ}\rangle$ calculated in [15] for the estimation of the shift.

The fine-structure mixing effect of a non-zero magnetic field gives rise to a small second-order Zeeman shift of the ${| }^{3}{{\rm{P}}}_{1},F=7/2,{m}_{F}=\pm 7/2\rangle$ states via a coupling to the ${}^{3}{{\rm{P}}}_{2}$ states with the same magnetic quantum number. Using second-order perturbation theory, the quadratic Zeeman shift can be approximated by ${\rm{\Delta }}{E}_{J,M}^{(2)Z}{(}^{3}{{\rm{P}}}_{1})=-\tfrac{1}{2}{\zeta }_{{nLS}}{\left(B/{B}_{\mathrm{fs}}\right)}^{2}$ , [39, 40] where ${B}_{\mathrm{fs}}\equiv {\zeta }_{{nLS}}J^{\prime} /{\mu }_{B}^{{\prime} }$ is the fine-structure crossover field, with ${\mu }_{B}^{{\prime} }\equiv ({g}_{s}-{g}_{J}){\mu }_{B}\cong {\mu }_{B}$ , and ${\zeta }_{{nLS}}=1.859\,1\,\mathrm{THz}$ the coupling constant. For the ³P₂–³P₁ fine-structure splitting we have L = 1, S = 1, J' = 2 and B_fs = 265.344 × 10⁴ G. We calculate for the quadratic frequency shift of the J = M = 1 level that ${{\rm{d}}}^{2}\nu /{{\rm{d}}{B}}^{2}=-263.74\,\mathrm{mHz}\,{{\rm{G}}}^{-2}$ . For a magnetic field of approximately 4 G the systematic shift amounts to only −2.109(5) Hz.

In ${}^{40}{\mathrm{Ca}}^{+}$ , the D_5/2 state has an electric quadrupole moment of ${\rm{\Theta }}(D,5/2)=1.83(1){{ea}}_{0}^{2}$ [41] where e is the elementary charge and a₀ the Bohr radius. The interaction of the electric quadrupole moment with the static electric field gradient of the linear ion trap (i.e. the dominant field gradient in our experiments) upshifts the m = ±3/2 Zeeman states by 2.83 Hz. Additionally, there is a second-order Zeeman shift by the magnetic field that couples the Zeeman levels of the D_5/2 state to the levels of the D_3/2 state having the same magnetic quantum number. A field of 4 G causes a frequency shift of the D_5/2, m = ±3/2 levels of 2.79 Hz. Both shifts taken together result in a 15.1(3) Hz correction of the transition frequency in Al⁺. Other sources of frequency shifts such as black-body radiation, time-dilation shifts by excess micromotion or non-zero secular motion are expected to be no bigger than 1 Hz. This claim is supported by the absence of any large frequency shifts in the comparison with other Ca⁺ experiments (section 3.4).

The systematic frequency shifts discussed above are summarised in table 1. Taking them into consideration leads to a correction of 24.5 Hz of the transition frequency f₀, which was obtained by extrapolating the measured frequencies of the stretched state transitions to zero magnetic field, and results in a transition frequency of ν_Al = 1122 842 857 334 736(93) Hz.

Systematic frequency shifts also need to be considered for the determination of the ${}^{3}{{\rm{P}}}_{1}$ state's g-factor. Electric quadrupole shifts and second-order Zeeman shifts do not affect the g-factor determination as they shift both stretched Zeeman states by the same amount. Ac-Zeeman shifts, magnetic field gradients and ac-Stark shifts, however, need to be considered.

The ion trap drive generates an ac-magnetic field, whose component ${B}_{{\rm{ac}},\perp }$ that is perpendicular to the dc-magnetic field off-resonantly couples neighbouring Zeeman states and gives rise to a level shift that scales as ${B}_{{\rm{ac}},\perp }^{2}\,m$ , where m is the magnetic quantum number. This perpendicular field has a peak amplitude of 62(8) mG at 1 Watt of applied rf-power as inferred from measurements of the frequency splitting of the $| {{\rm{S}}}_{1/2},m=\pm 1/2\rangle \leftrightarrow | {{\rm{D}}}_{5/2},m=\pm 3/2\rangle$ transitions as a function of the rf-power. For rf-confinement used in the experiments, the ac-Zeeman shift reduces the splitting of the transition frequencies of the $| {{\rm{S}}}_{1/2},m\,=\pm 1/2\rangle \leftrightarrow | {{\rm{D}}}_{5/2},m=\pm 3/2\rangle$ Zeeman transitions in Ca⁺ by 2 · 9.7(1.2) Hz. Our determination of the dc-magnetic field based on these transitions take this effect into account, which gives rises to a fractional correction of 2.2 · 10⁻⁶ of the field value. In Al⁺, due to the smaller splitting of the Zeeman levels, the ac-magnetic field shift amounts to only ±1.4(2) Hz, which changes the Zeeman splitting of the stretched transitions by a factor of (1–2) · 10⁻⁷ that is irrelevant for our determination of ${g}_{{}^{3}{{\rm{P}}}_{1},{F}^{{\prime} }=7/2}$ .

The static magnetic field gradient of 30 μG m⁻¹ causes only a negligible magnetic field difference in the two ion locations and can thus be neglected. Ac-Stark shifts on the ${}^{1}{{\rm{S}}}_{0}\leftrightarrow {}^{3}{{\rm{P}}}_{1}$ transition that arise from off-resonant coupling to the axial out-of-phase sideband transitions or to Δm = 0, ± 1 transitions induce fractional errors in the g-factor determination of well below 10⁻⁶. Therefore, we conclude that systematic shifts do not alter the measured g-factor value of ${g}_{{}^{3}{{\rm{P}}}_{1},{F}^{{\prime} }=7/2}=0.428\,133(2)$ and that its measurement uncertainty is largely dominated by the statistical errors.

5. Discussion and conclusion

Using the ${{\rm{S}}}_{1/2}\leftrightarrow$ D_5/2 quadrupole transition of ⁴⁰Ca⁺ as a frequency reference, we have employed quantum logic spectroscopy for a measurement of the (3s²)¹S ${}_{0}\leftrightarrow (3$ s3p)³P₁, F = 7/2 intercombination transition in ²⁷Al⁺ with an uncertainty of tilde 1 00 Hz. Our results are consistent with previous measurements of the transition [30] and improve the uncertainty by one order of magnitude. While the transition itself is not particularly interesting as a frequency standard, its coherent excitation is an enabling technology for detecting population in the ³P₀ state when exciting the highly relevant ${}^{1}{{\rm{S}}}_{0}\leftrightarrow {}^{3}{{\rm{P}}}_{0}$ clock transition.

Recently, we have also probed the ${}^{1}{{\rm{S}}}_{0}\leftrightarrow {}^{3}{{\rm{P}}}_{0}$ clock transition. Figure 8 shows a spectrum of the $(m=-5/2)\leftrightarrow (m=-3/2)$ Zeeman transition with a probe-time limited width of about 1 kHz.

Figure 8. Refer to the following caption and surrounding text. — **Figure 8.** Excitation of the ${| }^{1}{{\rm{S}}}_{0},{m}_{F}=-5/2\rangle \leftrightarrow | {}^{3}{{\rm{P}}}_{0},{m}_{{F}^{{\prime} }}=-3/2\rangle$ transition of Al⁺ with a laser pulse of 1 ms duration. The excitation probability is inferred by measuring the probability of the ion to undergo a change of its electronic state from one experiment to the next. For probing the transition, the measurement protocol described in section 3.3 is modified by probing the clock transition instead of the intercombination line in step (iv) and repeating the quantum logic steps (v) and (vi) twice. In this way, errors arising from imperfect state mapping from Al⁺ to Ca⁺ are suppressed.
Download figure:
Standard image High-resolution image

${| }^{1}{{\rm{S}}}_{0},{m}_{F}=-5/2\rangle \leftrightarrow | {}^{3}{{\rm{P}}}_{0},{m}_{{F}^{{\prime} }}=-3/2\rangle $ — **Figure 8.** Excitation of the ${| }^{1}{{\rm{S}}}_{0},{m}_{F}=-5/2\rangle \leftrightarrow | {}^{3}{{\rm{P}}}_{0},{m}_{{F}^{{\prime} }}=-3/2\rangle$ transition of Al⁺ with a laser pulse of 1 ms duration. The excitation probability is inferred by measuring the probability of the ion to undergo a change of its electronic state from one experiment to the next. For probing the transition, the measurement protocol described in section 3.3 is modified by probing the clock transition instead of the intercombination line in step (iv) and repeating the quantum logic steps (v) and (vi) twice. In this way, errors arising from imperfect state mapping from Al⁺ to Ca⁺ are suppressed.
Download figure:
Standard image High-resolution image

Efforts to obtain spectrally narrower lines are hampered by two experimental shortcomings, namely frequency drifts of the frequency-quadrupled fibre laser probing the clock transition and creation of molecular ions by reaction background gas molecules. In experiments where the aluminium ion spends about half the time in the ³P₀ clock state, we observe that Al⁺ ions are replaced by molecular ions of mass m = 28u on a time scale of about 15 min. While we cannot unambiguously identify the ion species, it seems likely that Al⁺ reacts with H₂ background gas molecules to form AlH⁺ [42, 43]. The resulting short time span for probing the clock transition in Al⁺, in combination with long ${\mathrm{Al}}^{+}$ reloading times [32], prevented us from investigating the clock transition more thoroughly. This will be subject to future work once the apparatus has been improved.

Acknowledgements

We acknowledge funding by the European Space Agency (contract number 4000102396/10/NL/SFe) and by the European Commission via the integrated project SIQS, and by the Institut für Quanteninformation GmbH. We would also like to thank J Walraven and K Beloy for helpful insights in the calculation of systematic shifts.

Frequency measurement of the {}^{1}{{\rm{S}}}_{0},F=5/2\,\leftrightarrow {}^{3}{{\rm{P}}}_{1},F=7/2 transition of 27Al+ via quantum logic spectroscopy with 40Ca+

Author notes

Author notes

Notes

Article metrics

Share this article

Dates

Abstract