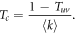Abstract
Our understanding of how diseases spread has greatly benefited from advances in network modeling. However, despite of its importance for disease contagion, the directionality of edges has rarely been taken into account. On the other hand, the introduction of the multilayer framework has made it possible to deal with more complex scenarios in epidemiology such as the interaction between different pathogens or multiple strains of the same disease. In this work, we study in depth the dynamics of disease spreading in directed multilayer networks. Using the generating function approach and numerical simulations of a stochastic susceptible-infected-susceptible model, we calculate the epidemic threshold of synthetic and real-world multilayer systems and show that it is mainly determined by the directionality of the links connecting different layers, regardless of the degree distribution chosen for the layers. Our findings are of utmost interest given the ubiquitous presence of directed multilayer networks and the widespread use of disease-like spreading processes in a broad range of phenomena such as diffusion processes in social and transportation systems.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Directionality in contact networks has often been disregarded, either because of the lack of data or in order to simplify theoretical approaches [1]. This is the case of disease spreading models, which usually consider the underlying networks as undirected [2, 3]. However, there are scenarios in which directionality has been found to be a key feature. Relevant examples are the case of meerkats in which transmission varies between groomers and groomees [4] and the transmission of HIV between humans, with male-to-female transmission being 2.3 times greater than female-to-male transmission [5]. Similarly, when addressing the problem of diseases that can be transmitted among different species, it is important to account for the fact that they might be able to spread from one type of host to the other, but not the other way around. For example, the bubonic plague can be endemic in rodent populations and spread to humans and other animals under certain conditions. If it evolves to the pneumonic form, it may then spread from human to human [6]. Analogously, Andes virus usually spreads within rodent populations, but it can be transmitted to humans and then spread via person-to-person contacts [7]. These types of interspecies contagions and other similar cases can be studied using multilayer networks, in which the network of each species is encoded in the layers and the possible interspecies interactions are given by the links that connect the layers [8].
Human behavior by itself can also introduce asymmetric patterns of disease spreading, either via the transmission mechanisms or via asymmetries in social mixing [9]. For instance, vaccination might induce asymmetric interactions among vaccinated and unvaccinated individuals [10]. Similarly, large-scale cooperation [11] can hinder disease spreading via peer punishment (e.g. prohibiting traveling if infected) and peer rewarding (e.g. free medical treatment from organizations). Both peer punishment and peer rewarding would deviate individual interactions far from symmetry, also inducing directionality in disease contagion. Even more, the own dynamics of the entities producing the diseases might be asymmetrical. For example, the interplay between cancer and the immune system can show asymmetric relationships [12]. There are also diseases with long latent periods that induce complicated dynamics between individuals who develop further the disease and those who do not, such as the interaction between individuals in the primary infection phase of Tuberculosis and those in the active state [13, 14]. For those cases, multilayer networks might be able to help disentangling dynamics that would be otherwise hidden.
The use of directed multilayer networks is not constrained to diseases that can infect human populations. Indeed, analogous scenarios can be found in the interface between wildlife and livestock, with diseases being endemic in one of them and then being transmitted unidirectionaly to the other [15]. This directionality is particularly relevant in the surveillance of diseases within the livestock industry, where the direction of the livestock interchange between farms can uncover structural changes that would be otherwise hidden [16]. Even more, the recent introduction of high resolution data of face-to-face interactions has also renewed the interest in using directed networks both in human and animal populations [17, 18]. This data can be used to build temporal multilayer networks in which the connections between layers, i.e. different time frames, have to be necessarily directed in order to preserve the causality induced by time ordering [19].
In this work, we aim at characterizing the spreading of diseases in directed multiplex networks. We focus on investigating how the epidemic threshold is influenced by the directionality of both interlayer and intralayer links. In particular, we consider multiplex networks composed by two layers with either homogeneous or heterogeneous degree distributions in the layers. Besides, we analyze several combinations of directionality: (i) Directed layer—Undirected interlinks—Directed layer (DUD); (ii) Directed layer—Directed interlinks—Directed layer (DDD); and (iii) Undirected layer—Directed interlinks—Undirected layer (UDU). For the sake of comparison, we also include the standard scenario, namely, (iv) Undirected layer—Undirected interlinks—Undirected layer (UUU). We then implement a susceptible-infected-susceptible (SIS) model on these networks and study the evolution of the epidemic threshold as a function of the directionality and the coupling strength between layers. In addition, we analytically derive the epidemic thresholds using generating functions, which allows to provide theoretical insights on the underlying mechanisms driving the dynamics of these systems. Our results show that the presence of directed links results in larger epidemic thresholds with respect to the case of undirected networks, and that the system is more resilient when the interlayer links are directed. Therefore, our conclusions are in line with previous works [20, 21] in that directionality is a key topological feature that should not be disregarded as it can lead to new phenomenology and sizable dynamical effects.
2. The model
Multilayer networks are an extension of classical contact networks in which nodes are assigned to a given layer, u, and can be connected to nodes in the same layer or in other layers. As a result, it is possible to distinguish two types of links: intralayer links, which connect pairs of nodes in the same layer, and interlayer links, which connect pairs of nodes in different layers. This formulation is used to encode features that characterize the nodes or the links that would be otherwise hidden, such as different types of interactions in protein networks or the multiple transportation modes present in mass transit systems [8]. In particular, in this work we focus on two-layer directed multiplex networks. That is, networks composed by two layers in which links, either within layers or to other layers, can be directed. Furthermore, the term multiplex, in contrast to multilayer, implies that a node can only be connected to its counterpart in the other layer. In other words, it is not possible to have more than one link in each node going to the other layer [22].
First, we implement SIS dynamics on two layer multiplex networks. In this model, nodes can be either susceptible or infected. The latter spread the disease to the former if they are in contact with a given probability. One of the main characteristics of multiplex networks is the existence of several types of links. Thus, it is possible to associate different spreading probabilities to each of these links [23]. In our model, we assume two spreading probabilities: the interlayer spreading probability, γ, and the intralayer spreading probability, β. Hence, an infected node transmits the disease with probability β to those susceptible neighbors of the same layer and with probability γ to those located in other layers. This distinction implies that it is possible to find a critical value of β for each value of γ and vice versa. Thus, henceforth we will define the epidemic threshold as βc and explore its value as a function of γ.
In the simulations, all the nodes in the system are initially susceptible. The spreading starts when one node is set to the infectious state. Then, at each time step, each infected node spreads the disease through each of its links with probability β if the link is contained in a layer and with probability γ if the link connects nodes in different layers. Besides, each infected node recovers with probability μ at each time step. The simulation runs until a stationary state for the number of infected individuals is reached.
To determine the epidemic threshold we fix the value of γ and run the simulation over multiple values of β, repeating 103 times the simulation for each of those values. The minimum value of β at which, on average, the number of infected individuals in the steady state is greater than one determines the value of the epidemic threshold, βc/μ. This procedure is then repeated for several values of γ to obtain the dependency of βc with the spreading across layers. Lastly, this dependency is evaluated for 102 realizations of each network considered in the study and their βc(γ) curves are averaged.
2.1. General analytical derivation of the epidemic threshold
In order to obtain insights into the mechanisms driving the spreading process on directed multiplex networks, we analytically derive the epidemic threshold for all the configurations considered in this work. To this end, we extend the generating function formalism, which has been used previously in the context of directed monolayer networks [24] and interdependent directed networks [25], to multiplex networks.
Within the generating function formalism, a node has an in-degree j, out-degree l and inter-degree m with probability pjlm, being the first two related to the links contained in each layer and the latter to links connecting nodes in different layers. The generating function for the degree distribution of a node is then defined as
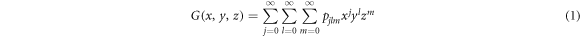
so that in order to describe a particular network it is sufficient to set pjlm to the degree distribution of the network. Indeed, with this function it is possible to characterize several properties of the network such as the excess degree which is the main quantity that is needed for the derivation of the epidemic threshold. The excess degree of a node is defined as the number of links of a node reached by following a randomly chosen link, without including the incoming link. Hence, the distribution of excess degree of a node that is reached by following a directed link in its direction is generated by
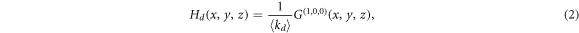
where  is the average directed degree and the superscript
is the average directed degree and the superscript  refers to partial derivation with respect to x. Similar expressions can be obtained for the excess degree of a node reached via the reverse direction of the same directed link and via an undirected link (see appendix).
refers to partial derivation with respect to x. Similar expressions can be obtained for the excess degree of a node reached via the reverse direction of the same directed link and via an undirected link (see appendix).
The size of an outbreak, as well as the epidemic threshold, can be obtained by computing the fraction of occupied links in the network. In this context, occupied link refers to a link through which the disease was transmitted. This can be accounted for by incorporating the transmissibility, i.e. the mean probability of transmission between individuals [26], to the previous equations so that
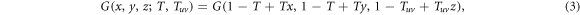
where T and Tuv denote the transmissibility within a layer and across layers, respectively.
In the SIS epidemic model, an infected individual at time t might recover from the disease or might spread it to its direct neighbors. We assume both the recovering process and the spreading process are independent Poisson processes with rate μ and β, respectively. The time, denoted as τi, that an infected node i remains infected is a random variable, whose distribution follows an exponential distribution with rate μ.
The probability  that the disease will not transmit from an infected node i to a susceptible node j is
that the disease will not transmit from an infected node i to a susceptible node j is  . As τi is a random variable, the probability Tij of disease transmission is also a random variable. When assuming a homogeneous recovering rate for each node, the average of disease transmission probability between infected and susceptible individuals is the average over the distribution of infectious time, which follows
. As τi is a random variable, the probability Tij of disease transmission is also a random variable. When assuming a homogeneous recovering rate for each node, the average of disease transmission probability between infected and susceptible individuals is the average over the distribution of infectious time, which follows
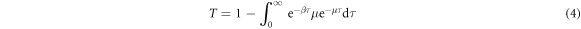
from which we obtain

Analogously, the average transmission probability of individuals between different layers reads, given that the spreading rate between layers is γ,

Hence, the generating function for the distribution of the size of an outbreak can be expressed as
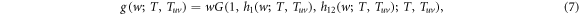
where h1 and h12 are recursive functions that generate the distribution of the size of an outbreak starting at a link connecting nodes in layer 1 and at a link connecting nodes in layer 1 and 2 respectively. The average size of an outbreak will be then given by the derivative with respect to w of g(w; T, Tuv) evaluated at w = 1. The said derivative goes to infinity when its denominator equals 0, which characterizes a phase transition from a phase in with only small size outbreaks to one characterized by the occurrence of macroscopic outbreaks. Thus, the epidemic threshold can be obtained from the equality
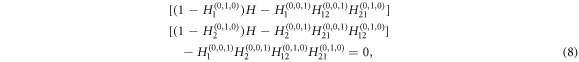
where  and Hi refers to transmission within layer i and Hij to transmission from layer i to layer j.
and Hi refers to transmission within layer i and Hij to transmission from layer i to layer j.
The above expression is general enough as to be used in the calculation of the epidemic threshold for each of the cases considered in this work. To this end, the only step that is left is to substitute Hi by Hd if the links in layer i are directed or, conversely, by Hu if they are undirected (see appendix).
3. Results
We first present results of numerical simulations of a stochastic SIS model. The SIS dynamics is implemented on directed multiplex networks composed by two layers. As previously stated, we explore four different configurations of directionality denoted as DUD, DDD, UDU and UUU. Furthermore, to define the degree distribution in the layers we use power-law and Poisson distributions, which correspond respectively to Scale-Free (SF) and Erdős–Rényi (ER) network models. In figure 1 we show the evolution of the epidemic threshold, βc, as a function of γ for the configurations with undirected interlinks, UUU and DUD, both for ER (1A) and SF (1B) networks, for two different average degrees  .
.
Figure 1. Epidemic threshold for the spread of a disease within layers, βc, as a function of the probability of interlayer contagion, γ. Panels (A) and (B) show results for the UUU and DUD configurations with ER (A) and SF (B) degree distributions in the layers. In all cases μ = 0.1, the number of nodes is N = 2 × 104 and for each directionality configuration there are two sets of networks: in the ER case one with  in both layers and another one with
in both layers and another one with  in both layers; in the SF case one with kmin = 4 and α = 2.7 (average degree
in both layers; in the SF case one with kmin = 4 and α = 2.7 (average degree  ) and another one with kmin = 10 and α = 2.8 (average degree
) and another one with kmin = 10 and α = 2.8 (average degree  ). In panels (C) and (D) we compare the analytical values of βc with corresponding results from the numerical simulations for the same networks and directionality configurations shown in panels (A) and (B).
). In panels (C) and (D) we compare the analytical values of βc with corresponding results from the numerical simulations for the same networks and directionality configurations shown in panels (A) and (B).
Download figure:
Standard image High-resolution imageFor the cases in which the interlinks are directed, we need to define how many links point from one layer u to another layer v, either in the  direction or in the opposite one,
direction or in the opposite one,  . Indeed, if we set all interlinks to have the same direction, the epidemic threshold would be trivially the one of the source layer and thus the multiplex structure would play no role. For this reason, for each directed link connecting layers u and v we set the directionality to be
. Indeed, if we set all interlinks to have the same direction, the epidemic threshold would be trivially the one of the source layer and thus the multiplex structure would play no role. For this reason, for each directed link connecting layers u and v we set the directionality to be  with probability p and
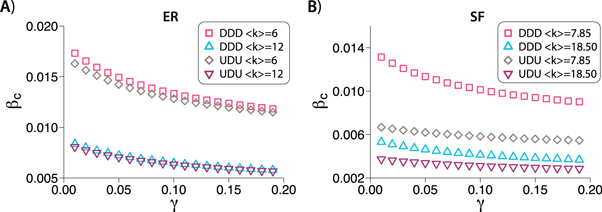
with probability p and  with probability (1 − p). Consequently, in networks with directed interlinks the epidemic threshold will be given as a function of this probability p. We refer to this procedure of generating interlinks as the p-model. The same dependence of the critical threshold depicted in figure 1 is shown in figure 2 for DDD and UDU configurations built using the p-model. The dependency of the results with the value of p is shown in figure 3.
with probability (1 − p). Consequently, in networks with directed interlinks the epidemic threshold will be given as a function of this probability p. We refer to this procedure of generating interlinks as the p-model. The same dependence of the critical threshold depicted in figure 1 is shown in figure 2 for DDD and UDU configurations built using the p-model. The dependency of the results with the value of p is shown in figure 3.
Figure 2. Critical value of the within-layer spreading rate, βc, as a function of the spreading rate across layers, γ, in DDD and UDU configurations built up using the p-model with ER (A) and SF (B) degree distributions in the layers. In all cases p = 0.5, μ = 0.1, the number of nodes is N = 2 × 104 and for each directionality configuration there are two sets of networks: in the ER case one with  in both layers and another one with
in both layers and another one with  in both layers; in the SF case one with kmin = 4 and α = 2.7 (average degree
in both layers; in the SF case one with kmin = 4 and α = 2.7 (average degree  ) and another one with kmin = 10 and α = 2.8 (average degree
) and another one with kmin = 10 and α = 2.8 (average degree  ).
).
Download figure:
Standard image High-resolution imageFigure 3. Epidemic threshold for two-layered multiplex networks for different values of p with: (A) directed layers with ER degree distribution and directed interlinks; (B) directed layers with SF degree distribution and directed interlinks; (C) undirected layers with ER degree distribution and directed interlinks; (D) undirected layers with SF degree distribution and directed interlinks. In both ER cases the average degree is 12 and in the SF cases the minimum degree is 10 and the exponent is 2.8, resulting in an average degree of 18.50.
Download figure:
Standard image High-resolution imageIt is also possible to study scenarios in which each interlink does not only have one possible directionality, either  or
or  , but instead are bi-directional. This is achieved by setting two independent probabilities—one for each direction—, thus allowing for the coexistence of single directionality and bi-directionality in the interlinks. This situation, which we denote as the pq-model, is further analyzed in the supplementary material, which is available online at stacks.iop.org/NJP/21/093026/mmedia.
, but instead are bi-directional. This is achieved by setting two independent probabilities—one for each direction—, thus allowing for the coexistence of single directionality and bi-directionality in the interlinks. This situation, which we denote as the pq-model, is further analyzed in the supplementary material, which is available online at stacks.iop.org/NJP/21/093026/mmedia.
In what follows, we present the analytical results obtained for the thresholds after considering directionality (or lack thereof) and different network topologies.
3.1. ER networks
In ER networks the degree distribution follows a Poisson distribution. If we consider an UUU network with nodes in both layers following said degree distribution, the generating function, (1), is
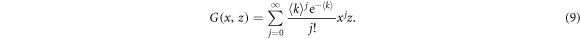
Inserting this expression in (8), the epidemic threshold can be expressed as (the full derivation is presented in supplementary material).

Henceforth, to facilitate readability and unless otherwise stated, we provide expressions for the epidemic threshold in terms of the average transmission probability through intralinks, T, and the average transmission probability through interlinks, Tuv. Nevertheless, the thresholds can be easily rewritten in terms of βc in a straightforward way using (5) and (6). For this case, we can rewrite the above equation and explicitly express the value of βc as,
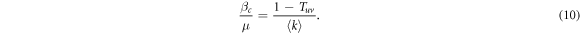
Note that if we set γ = 0 in (6) so that the spreading from one layer to the other is completely removed, Tuv = 0 and (10) is simplified to  , which is the classical value of the epidemic threshold in single layer ER networks [27].
, which is the classical value of the epidemic threshold in single layer ER networks [27].
In a DUD network with nodes in both layers following a Poisson degree distribution, with the same average degree for both incoming and outgoing links, the generating function (1) is
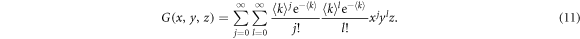
Again, by inserting this expression in (8) we obtain
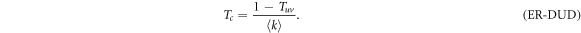
On the other hand, using the p-model previously described, the epidemic threshold in DDD configurations as a function of p is
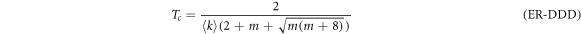
with  and in the UDU configuration is
and in the UDU configuration is
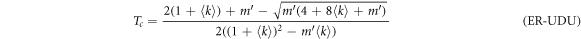
with  . In figure 4(A) we compare the behavior of these four configurations plotting βc as a function of γ.
. In figure 4(A) we compare the behavior of these four configurations plotting βc as a function of γ.
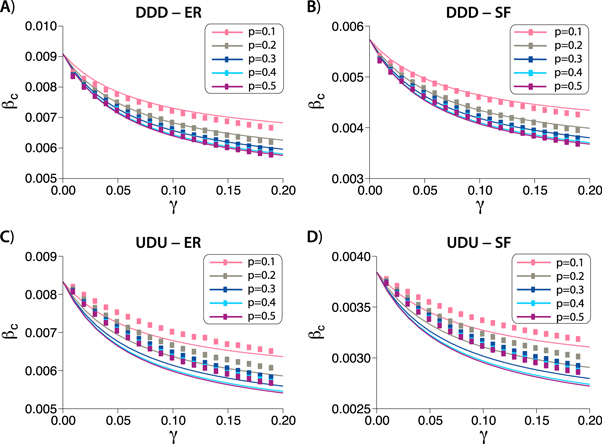
Figure 4. Comparison of the analytically derived epidemic thresholds for each network configuration UXU or DXD (X = U or D) and different degree distributions for the networks in the layers. (A) ER networks with  and p = 0.5. (B) SF networks with kmin = 3, α = 2.6, resulting in the theoretical average degree
and p = 0.5. (B) SF networks with kmin = 3, α = 2.6, resulting in the theoretical average degree  and p = 0.5.
and p = 0.5.
Download figure:
Standard image High-resolution image3.2. SF networks
In SF networks the degree distribution follows a power-law of the form  . Thus, the epidemic thresholds are
. Thus, the epidemic thresholds are

for the UUU configuration,

for the DUD configuration,
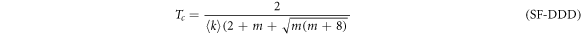
with  for the DDD configuration and
for the DDD configuration and
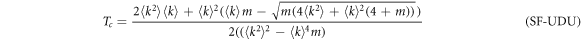
with  for the UDU configuration. The full derivation can be found in the supplementary material. As in the ER case, the explicit dependence of βc with γ is shown in figure 4(B).
for the UDU configuration. The full derivation can be found in the supplementary material. As in the ER case, the explicit dependence of βc with γ is shown in figure 4(B).
4. Discussion
Our results show that directionality is a key factor in the spreading of epidemics in multiplex networks. Even more, these findings suggest that its effects cannot be trivially generalized as the consequences of changing the directionality of some links are completely different for Scale-Free and ER networks. In particular, in figure 1(A), we can see that for networks with  the epidemic threshold is very similar in both UUU and DUD configurations. This effect is again seen for denser networks,
the epidemic threshold is very similar in both UUU and DUD configurations. This effect is again seen for denser networks,  , implying that it is the directionality of the interlinks, and not the one of the links contained within layers, the main driver of the epidemic in these networks. On the other hand, in figure 1(B) we can see that this behavior is not replicated for SF networks. Certainly, there is a large difference between the curves of the UUU and DUD configurations, implying that the directionality of intralinks is much more important in this type of networks. In agreement with these observations, when the interlinks are those that are directed, we found the same difference between ER and SF networks. As can be observed in figure 2(A), the evolution of the epidemic threshold as a function of γ is again quantitatively similar for both DDD and UDU configurations. Conversely, in figure 2(B), a difference between these configurations arises again for SF networks. Besides, in all the cases considered so far, figures 1 and 2, the epidemic threshold is always lower for those configurations with undirected links within the layers, compared to those in which those links are directed, given the same interlink directionality.
, implying that it is the directionality of the interlinks, and not the one of the links contained within layers, the main driver of the epidemic in these networks. On the other hand, in figure 1(B) we can see that this behavior is not replicated for SF networks. Certainly, there is a large difference between the curves of the UUU and DUD configurations, implying that the directionality of intralinks is much more important in this type of networks. In agreement with these observations, when the interlinks are those that are directed, we found the same difference between ER and SF networks. As can be observed in figure 2(A), the evolution of the epidemic threshold as a function of γ is again quantitatively similar for both DDD and UDU configurations. Conversely, in figure 2(B), a difference between these configurations arises again for SF networks. Besides, in all the cases considered so far, figures 1 and 2, the epidemic threshold is always lower for those configurations with undirected links within the layers, compared to those in which those links are directed, given the same interlink directionality.
To get further insights into the mechanisms driving the behavior observed previously, we rely on the analytically derived thresholds and explore the evolution of βc as a function of γ for the whole range of possible values of the latter parameter. Results are shown in figure 4. In this case, we can see that the value of the epidemic threshold of the DUD configuration in SF networks tends to the value of the UUU case for large values of the spreading probability across layers, mimicking the behavior of ER networks. Thus, when  we reach the state in which both networks exhibit the same properties, namely: (i) the epidemic threshold in DUD and UUU configurations is the same; (ii) XDX (X = U or D) configurations are almost not affected by the value of γ, except for the weakly coupled regime (i.e. small values of γ). Hence, in general, one can conclude that the directionality (or lack of) of the interlinks is the main driver of the epidemic spreading process. The exception is the limit of small spreading from layer to layer, as in this scenario, the directionality of interlinks makes SF networks much more resilient, see the dashed–dotted line in figure 4(B). Altogether, the general conclusion is that directionality reduces the impact of disease spreading in multilayer systems.
we reach the state in which both networks exhibit the same properties, namely: (i) the epidemic threshold in DUD and UUU configurations is the same; (ii) XDX (X = U or D) configurations are almost not affected by the value of γ, except for the weakly coupled regime (i.e. small values of γ). Hence, in general, one can conclude that the directionality (or lack of) of the interlinks is the main driver of the epidemic spreading process. The exception is the limit of small spreading from layer to layer, as in this scenario, the directionality of interlinks makes SF networks much more resilient, see the dashed–dotted line in figure 4(B). Altogether, the general conclusion is that directionality reduces the impact of disease spreading in multilayer systems.
It is important to note that these results are not only relevant for the situations described in the introduction of this paper. First, because even though a system might be commonly presented as a monolayer network, it may be possible to detect different types of links in the network that would allow for the construction of a multiplex network. If this is done, as we have shown in this paper, the definition of the directionality of the interlinks is far from trivial as it can have dramatic consequences on the dynamics. In particular, the epidemic threshold can change by up to a factor of two depending on the directionality of the interlinks. Even more, these results are not restricted only to epidemic modeling, as these kind of diffusion processes can be applied to a broad range of systems. For example, the generating function approach has been proposed as a tool to identify influential spreaders in social networks [28].
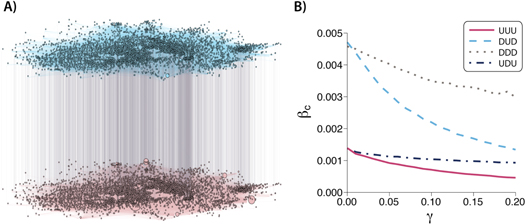
One particularly interesting and open challenge is to quantify the effects that the interplay between different social networks could have on spreading dynamics. The theoretical framework developed here is particularly suitable to study this and similar challenges related to the spreading of information in social networks. On the one hand, because social relations are, by default, directed: a user is not necessarily followed by her followings, i.e. social relations are not always reciprocal [29]. On the other hand, disease-like models have been widely used to study information dissemination, or in other words, simple social contagion [30, 31]. We have analyzed the dependence of the epidemic threshold with the inter-spreading rate in a real social network composed by two layers, see figure 5(A). The first layer of the multilayer systems is made up by the directed set of interactions in a subset of users of the now defunct FriendFeed platform, whereas the second layer is defined by the directed set of interactions of those same users in Twitter. Even though this multiplex network originally corresponds to a DUD configuration, we have also explored the other possible configurations for the directionality of the links. Note that in contrast with the synthetic networks studied in the previous section, in this network the layers have different average degrees. In particular, the FriendFeed layer has 4768 nodes and 29 501 directed links, resulting in an average out-degree of 6.19, and the Twitter layer is composed by 4768 nodes and 40 168 directed links, with an average out-degree of 8.42. Nevertheless, their degree distributions are both heavy tailed, although the maximum degree in the FriendFeed network is much larger than in the Twitter network. For details on how this network was obtained, we refer the reader to the original source of the data [32].
Figure 5. Epidemic threshold measured in a multiplex network composed by users of two different social platforms: friendfeed and twitter. The original network (A) has directed intralinks and undirected interlinks, thus it corresponds to the DUD configuration. Nevertheless, to explore the effects of directionality, the four configurations studied in this paper are considered (B). For those configurations with directed interlinks we used the p-model to generate them, setting p = 0.5.
Download figure:
Standard image High-resolution imageThe results, figure 5(B), confirm our findings for synthetic networks. In particular, for the range of γ under consideration, the configurations with some directionality are always more resilient against the disease. These results would imply that information travels much more easily in undirected systems than in directed systems. For instance, one could build up a directed multiplex network using Instagram and Twitter data, either in a DUD configuration if it is assumed that the likelihood of someone sharing the information from one platform to the other is independent of the source or in a DDD configuration if the likelihood of sending it from Instagram to Twitter is deemed to be different than from Twitter to Instagram. On the other hand, undirected social platforms such as Facebook and WhatsApp should be modeled using UDU or UUU configurations. According to our results, information would spread more easily through these platforms, which could be worrisome as they have recently been identified as one of the main sources of misinformation spreading [33].
Lastly, it would be possible to build similar directed multiplex networks in transportation systems [34]. In these systems, the interlinks can be modeled as undirected or directed, depending on the purpose of the study. If one is interested in taking into account the fact that, for example, a metro station can be overcrowded in the incoming direction but not in the outgoing direction, such as during the morning peak time, or the other way around, during the evening peak time, it would be necessary to use directed links. On the other hand, if congestion is not relevant for the study, those links could be regarded as undirected.
In summary, we have developed a framework that allows studying disease-like processes in multilayer networks. This represents an important step towards the characterization of diffusion and spreading processes in interdependent multilevel complex systems. Our results show that directionality has a positive impact on the system's resistance to disease propagation and that the way in which interdependent (social) networks are coupled could determine their ability to spread information. Our results could be applied to a plethora of systems and show that more emphasis should be put in studying the role of interlinks in diffusion processes that take place on top of them.
Acknowledgments
XW acknowledges the support of the research program complexity in logistics (No. 439.16.107) from NWO and the project 'PCL Future Regional Network Facilities for Large-scale Experiments and Applications (PCL2018KP001)'. AA acknowledges the support of the FPI doctoral fellowship from MINECO and its mobility scheme (grant FIS2014-55867-P). DL acknowledges support from the China Scholarship Council though a PhD fellowship. YM acknowledges partial support from the Government of Aragón, Spain through a grant to the group FENOL (E36-17R), by MINECO and FEDER funds (grant FIS2017-87519-P) and by Intesa Sanpaolo Innovation Center. The funders had no role in study design, data collection and analysis, or preparation of the manuscript.
: Appendix. Full derivation of the epidemic threshold
Consider a directed multiplex network consisting of two layers interconnected by interlinks. The directed contact between an infective individual to a susceptible individual can be within the same layer, or across different layers or a mix of both. Depending on the directionality of links within layers and the directionality of links interconnecting different layers, we analyze all possible combinations in which directionality is the same in both layers, namely: (i) directed layers and undirected interlinks, denoted as DUD, (ii) directed layers and directed interlinks, denoted as DDD, (iii) undirected layers and directed interlinks, denoted as UDU and (iv) undirected layers and undirected interlinks, denoted as UUU.
For a general directed multilayer network, a node has an in-degree j, out-degree k and inter-degree m with probability pjkm. The generating function for the degree distribution of a node is defined as
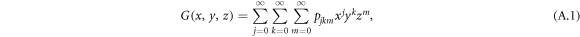
where  satisfying the probability property.
satisfying the probability property.
Another quantity related to the nodal degree distribution is called the excess degree distribution, which is the distribution of degrees of nodes reached by following a randomly chosen link. The probability to reach a node is biased by nodal degrees because nodes with a higher degree have a higher probability to be chosen. The probability to reach a node by following the direction of a randomly chosen link, i.e. in-link of the reached node, is  . The corresponding generating function for the excess in-degree j − 1, out-degree k and inter-degree m reads
. The corresponding generating function for the excess in-degree j − 1, out-degree k and inter-degree m reads
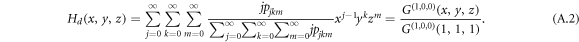
Analogously, the generating function for a node reached by following the reverse direction of a randomly chosen directed link, i.e. out-link of the reached node, follows
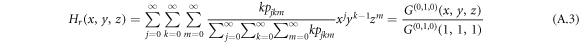
and similarly, the generating function for a node reached by following an undirected inter-link reads
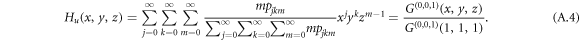
To account for the probability of a link being infected by a disease that is transmitted from an infective individual to a susceptible individual, we further modify the generating functions. Denote  as the average probability that a susceptible individual will be infected by an infectious individual in the same layer. Denote Tuv as the average probability that an infectious individual from layer u will transmit the disease to a susceptible individual in layer v. We omit the subscript of Ti when there is no ambiguity. The generating function for the distribution of the number of infected links of a randomly chosen node is obtained by incorporating the probability of disease transmission in the generating function of degree distribution, G(x, y, z, T, Tuv), which reads
as the average probability that a susceptible individual will be infected by an infectious individual in the same layer. Denote Tuv as the average probability that an infectious individual from layer u will transmit the disease to a susceptible individual in layer v. We omit the subscript of Ti when there is no ambiguity. The generating function for the distribution of the number of infected links of a randomly chosen node is obtained by incorporating the probability of disease transmission in the generating function of degree distribution, G(x, y, z, T, Tuv), which reads
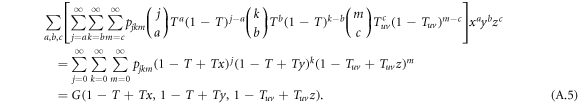
Analogously, we derive the generating functions for the distribution of the number of infected links of a node reached by following a randomly chosen directed link in the designed direction, as
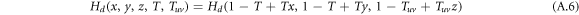
and similarly of a node reached by following a randomly chosen undirected inter-link, as

A number of nodes can be infected starting from a single infected node within the directed multilayer network. Due to the randomness of disease spreading and the variability of contacts, the size of a disease outbreak is a random variable. To eventually determine the epidemic threshold, we first investigate the distribution of the size of an outbreak starting from a single infected node and its corresponding generating function.
Denote ![$\Pr [S=s]$](https://content.cld.iop.org/journals/1367-2630/21/9/093026/revision2/njpab3dd0ieqn35.gif) as the probability of the size s of an outbreak starting from a single infected node. The generating function for the size distribution is defined as
as the probability of the size s of an outbreak starting from a single infected node. The generating function for the size distribution is defined as ![$g(w,T,{T}_{{uv}})={\sum }_{s}\Pr [S=s]{w}^{s}$](https://content.cld.iop.org/journals/1367-2630/21/9/093026/revision2/njpab3dd0ieqn36.gif) . To solve the average size of an outbreak, we further define the generating function for the size of an outbreak starting from a node reached by a randomly chosen directed link in the designed direction, which denotes as
. To solve the average size of an outbreak, we further define the generating function for the size of an outbreak starting from a node reached by a randomly chosen directed link in the designed direction, which denotes as ![$h(w,T,{T}_{{uv}})={\sum }_{t}\Pr [S=t]{w}^{t}$](https://content.cld.iop.org/journals/1367-2630/21/9/093026/revision2/njpab3dd0ieqn37.gif) . By adding subscript u or uv to the generating function h(w, T, Tuv), we distinguish a randomly chosen link within a layer u, u = 1, 2, and a randomly chosen interlink uv connecting layers u and v.
. By adding subscript u or uv to the generating function h(w, T, Tuv), we distinguish a randomly chosen link within a layer u, u = 1, 2, and a randomly chosen interlink uv connecting layers u and v.
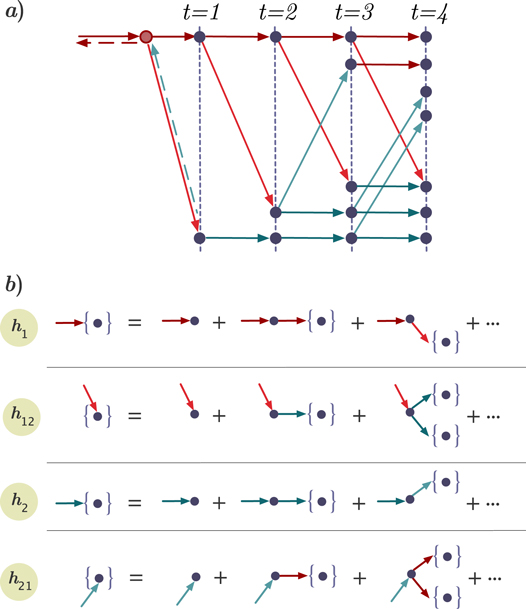
Starting from a single infected node reached by following a randomly chosen intra-link (links within layers), the possible ways of future transmission are: the disease spreads along an intra-link in the same layer, it spreads along an inter-link to the opposite layer, it spreads along two intra-links, it spreads along one intra-link and one inter-link, etc. The transmission diagram is shown in figure A1. To account for all the transmission possibilities, we construct a recursive relation in the generating functions. Without loss of generality, we assume the disease spreading starting from an infected node in layer 1, the generating function satisfies a recursive relation
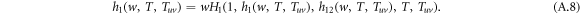
The generating function for the distribution of the size of an outbreak w along a randomly chosen interlink satisfies a recursive relation
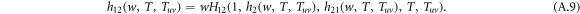
Analogously, the spreading in layer 2 itself satisfies a recursive relation

and
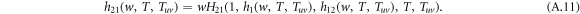
The recursive relation of the generating functions is shown in figure A1. Similarly, the generating function for the distribution of the size of an outbreak along a randomly chosen node in layer 1 reads
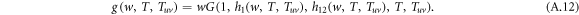
The average size E[S] of an outbreak starting from a randomly chosen node thus can be calculated by
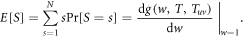
Performing the derivative with respect to w on both sides of equation (A.8)–(A.12), the derivatives for generating functions hu, huv and g read
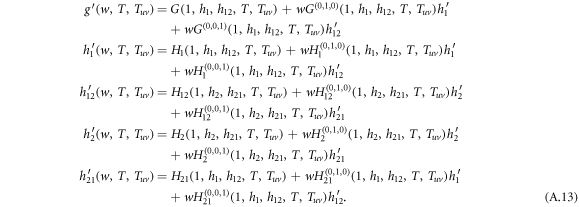
Figure A1. Panel (a) shows the future transmission diagram starting from a single infected node reached by following the direction of a randomly chosen link. Solid lines represent the disease transmission on directed links and dashed lines depict the bidirectional disease transmission on undirected links. Panel (b) shows the recursive relation of generating functions for the size distribution of outbreaks by following four types of links which are (i) intralink in layer 1, (ii) interlink pointing from layer 1 to layer 2, (iii) intralink in layer 2 and (iv) interlink pointing from layer 2 to layer 1 .
Download figure:
Standard image High-resolution imageFor w = 1, the derivatives of generating functions are simplified as
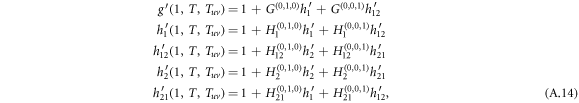
where the arguments of a function in the right side of the equation are omitted for readability, for example  is denoted as G(0,1,0) .
is denoted as G(0,1,0) .
Now, we can express the average size E[s] of an outbreak in terms of the generating functions as
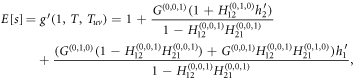
where
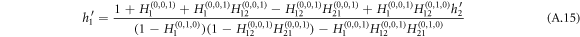
and

The expression for E[s] goes to infinity when the denominator equals zero, which characterizes a phase transition from small size of outbreaks with tree-like structure to the occurrence of large-scale outbreaks. Therefore, the critical equation that determines the epidemic threshold reads
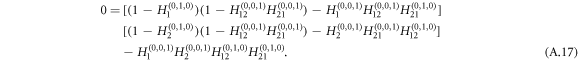
A.1. Epidemic threshold for ER networks
In this subsection, we elaborate on the derivation of epidemic threshold for coupled ER networks with DUD configuration.
DUD: Consider a directed multilayer network consisting of two directed graphs that are interconnected by undirected links. We employ Poisson degree distributions as an example to illustrate the derivation of the epidemic threshold. If both the in-degree and out-degree follow a Poisson distribution with the same average degree  , the generating function for the excess degree Hd follows
, the generating function for the excess degree Hd follows
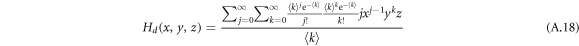
from which we derive the partial derivative with respect to y evaluated at the point x = y = z = 1 as
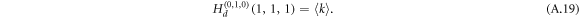
Since intralinks in the configuration of DUD are directed, the generation function H1 for layer 1 is substituted by Hd which reads
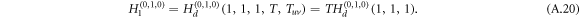
The derivatives of the generating function H1 for layer 1, and similarly H2 for layer 2, thus follow
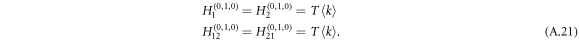
As two layers of graphs are connected by undirected or bidirected interlinks, the disease thus can be transmitted with probability Tuv from layer 1 to layer 2 and, meanwhile, with probability Tuv to be transmitted from layer 2 to layer 1 . The bidirectionality for disease transmission of undirected interlinks is reflected by the generating functions
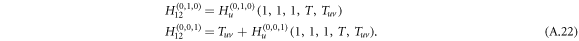
The extra added term Tuv incorporates the spreading from layer 2 to layer 1 due to the bi-directionality of an undirected interlink. With  for a Poisson degree distribution and
for a Poisson degree distribution and  for zero extra undirected interlink (apart from the interlink we come along), we arrive at
for zero extra undirected interlink (apart from the interlink we come along), we arrive at
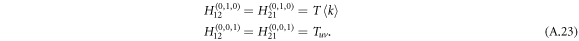
Substituting generating functions (A.21) and (A.23) into the equation (A.17), which characterizes the critical point of phase transition, we derive the epidemic threshold for DUD as