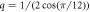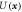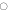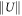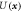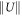Abstract
Soft matter systems have been observed to self-assemble, over a range of system parameters, into quasicrystalline structures. The resulting quasicrystals (QCs) may minimize the free energy, and be in thermodynamic coexistence with the liquid state. At such state points, the likelihood of finding the presence of spatially localized states with quasicrystalline structure within the liquid is increased. Here we report the first examples of metastable spatially localized QCs of varying sizes in both two and three dimensions. Implications of these results for the nucleation of quasicrystalline structures are discussed. Our conclusions apply to a broad class of soft matter systems and more generally to continuum systems exhibiting quasipatterns.
1. Introduction
Soft matter is capable of organising into complex structures even when the underlying interactions between the individual constituents are simple. These structures can be described by the phase field crystal (PFC) model [1]. The PFC model represents a simplification [2–4] of the more accurate density functional theory (DFT) approach [5–7] and has proved useful in understanding the formation and properties of soft matter crystals under various conditions. Our work analyses structure formation in a PFC model of a broad class of soft matter systems, such as dendrimers or block copolymer micelles, but is relevant more generally to the field of pattern formation. Such macromolecules can interact through an effective pair potential that is isotropic, i.e. a potential that depends on the distance between the centres of the particles and not their relative orientation [8, 9]. When the constituents have two inherent length scales, DFT shows that density modulations with two distinct length scales feature strongly [10–13].
We analyse structure formation in such soft matter systems using a PFC approach, which consists of a gradient expansion of the DFT, equivalent to a Taylor expansion of the pair direct correlation function in Fourier space [14, 15]. In earlier work, it was shown that the presence of two length scales in the interactions promotes the formation of quasicrystals (QCs), i.e. structures with rotation symmetries on average but no translation symmetries, and a dense point diffraction spectrum [10–13, 16–19]. QCs are formed when the ratio of the two length scales is near particular values specified below. Two length scales can arise in other pattern forming soft matter systems due to the interaction of particles with short-range attraction and long-range repulsion [20, 21] or other forms of frustration in the interactions [22]. Just as in the QC-forming systems of interest here, the liquid state static structure factor S(k) in the above systems has two distinct peaks, corresponding to the two different length scales, but their ratio is different from the values required for QC formation.
Soft matter QCs are often dodecagonal in two dimensions (2D) and icosahedral in three dimensions (3D). QCs have been found in nanoparticle [23] and polymeric [24–28] soft matter systems. Our earlier work [18] shows that QCs can be in thermodynamic coexistence with the liquid, suggesting the possibility of finding spatially localized QCs [29]. Of course, a localized structure cannot, strictly speaking, be a QC. In the following we use this terminology to refer to localized structures that have the dodecagonal or icosahedral symmetry of a QC, but do not fill the domain completely. Such states can be thermodynamically stable, metastable or unstable. In this paper, we show that spatially localized QCs not only exist but can be thermodynamically metastable. These metastable spatially localized QCs come in a variety of sizes, which change continuously from one to another, via unstable states, when one of the system parameters varies.
The relative simplicity of the PFC approach means that it is increasingly widely used to model systems in which more precise treatments are difficult or impossible, for example, liquid–solid transitions, colloid patterning and liquid crystals (see [1] and references therein). In adopting a PFC model, we make a simplification of the physics of dendrimer interactions. As a result, our model provides a generic description of the crystallization of soft matter into QCs, but no comparison can be made with any specific material. Nonetheless, the results in our work provide a proof of concept, focusing on the most important aspects in the problem, namely the interaction of density modulations on two length scales and thermodynamic coexistence of QCs with the liquid. Moreover, the simplicity of the model implies that it may be considered to be a generic model for pattern formation in systems with two length scales, an energy (or free energy) minimization principle and conserved dynamics.
The PFC model is a theory for a scalar density-like order parameter with grand potential (Landau free energy) functional . Minimizers of with nonconstant are identified with the solid phase, while those with constant correspond to the liquid phase. The simplest PFC model takes the form of the conserved Swift–Hohenberg equation and the steady states of this model have been studied in detail in 1D, 2D and 3D [30]. The model exhibits coexistence between the liquid state and various crystalline states over a range of temperatures [1, 14]. In this regime one also finds thermodynamic equilibria corresponding to spatially localized structures that bifurcate from the periodic crystal, and exhibit homoclinic snaking [29–31]. Suitably modified to allow interaction between two different spatial scales [18, 32] the PFC model also forms spatially extended QCs. Both dodecagonal QCs in 2D [32] and icosahedral QCs in 3D [18] have been identified and these can be thermodynamically stable under appropriate conditions, that is, at these state points, they are global minima of the grand potential free energy Ω. In contrast, the localized QCs that we have found are only metastable, i.e. they correspond to local minima of Ω. Note that throughout this work, we do not refer to the localized QCs that we find as either 'grains' or 'clusters', since this word is associated with various different meanings in the context of QCs. For further discussion on this point, see the appendix. Instead, we use the word 'motif' to refer to the aperiodically repeating local arrangements of density peaks observed in our QCs.
2. Model and numerical details
Our model describes the space–time evolution of a dimensionless scalar field that specifies the location and magnitude of density perturbations from a homogeneous state [1]. The system is described by the Helmholtz free energy
The time evolution of U conserves mass, i.e. is fixed, where D is the system volume, and follows
The linear operator is chosen to promote the growth of density modulations at two wave numbers, hereafter k = 1 and k = q < 1. This choice of is aimed at modelling generic soft matter systems where the liquid state static structure factor S(k) is isotropic, i.e. S(k) depends only on the magnitude of the wave vector . The structure factor is an important quantity in the present context, since it is proportional to the Fourier transform of the linear density response function [5]. Moreover, for an equilibrium liquid, the structure factor also determines the dispersion relation that specifies the growth or decay rate σ(k) of infinitesimal sinusoidal density perturbations with wave number k: [33].
For dendrimers or any other such soft particles with isotropic effective pair interaction potentials and two inherent length scales, density modulations with two distinct length scales can feature strongly [10–13]. This important qualitative property is captured by the generic choice (see figure 1 in [18])
We adopt the choice and as in [18, 34] and use the two temperature-dependent parameters r1 and rq to control the linear growth rates of the modes with k = 1 and k = q. In addition, the parameter σ0 < 0 controls the sharpness of the peaks in the growth rate at these two wave numbers. Our model allows independent control of these three quantities, in contrast to models based on the Lifshitz–Petrich free energy [32, 35].
In general, when the temperature decreases, both r1 and rq increase. In the following, we vary r1, plotting results for fixed rq, as a function of r1. In particular, when , modes with wave number decay as . When or there are additional terms in σ(k) and when the growth rate σ(k) is also influenced by the parameter Q [18]. This important parameter also controls the strength of three-wave interactions. With appropriate choice of q, such as or , the model promotes the formation of dodecagonal QCs in 2D (d = 2) or icosahedral QCs in 3D (d = 3), respectively [18, 35].
In view of equation (2), the evolution of the free energy with time is given by
where we have used the functional chain rule and an integration by parts, assuming no boundary contributions. This result implies that the free energy decreases monotonically with time, until it reaches a local or global minimum. Thus at equilibrium , implying that the quantity is constant. This quantity is the chemical potential. The equilibrium states of the dynamical system (2) therefore satisfy
In the following we characterize equilibrium structures in terms of the grand potential
whose minima correspond to metastable states. The global minimum amongst all equilibrium states corresponds to the thermodynamically stable state. All results presented here are computed at μ = 0, so states that minimize Ω also minimize . For a given value of μ, there can be several possible bulk extended equilibria; we focus on the one with lowest Ω. With μ = 0, the only homogeneous equilibrium for our parameter values is the liquid state with and Ω = 0, in which case σ(1) = r1 and .
2D direct numerical simulations of equation (2) are carried out in a periodic square domain of side 60π. In the 3D calculations, we used a periodic cubic domain of size 32π chosen in a similar fashion to [18]. These choices of the domain size allow the formation of extended (but still approximate) QCs [36]. In our pseudospectral approach we use FFTW [37] employing 256 Fourier modes in each direction in 2D (192 in 3D), and time-step using second-order exponential time differencing (ETD2) [38]. Starting from smoothed random initial conditions, we find (in 2D) several qualitatively distinct equilibria: the liquid state, lamellae (lam) and hexagons (hex) at each of the two possible wavelengths (2π and 2π/q), and a dodecagonal QC. In 3D, we find in addition body-centred cubic crystals and body-centred icosahedral QC. These equilibria are then used as initial conditions for numerical continuation of equation (5) using pseudo-arclength continuation [39] employing a biconjugate gradient stabilized method [40] and an induced dimension reduction method [41] to solve the large linear systems that arise in the Newton iteration up to an accuracy of . This procedure allows us to trace out connected branches of equilibria with the same μ (but different ) as r1 varies and to explore the space of possible equilibria of the model irrespective of their dynamical stability.
3. Results
3.1. Spatial localization of a 3D icosahedral QC
In [18], we showed that minima of the grand potential Ω in 3D domains correspond to periodic structures such as lamellae, columnar hexagons, and body-centred cubic crystalline phases, as well as a body-centred icosahedral QC such as that shown in figure 1(a). These extended states fill the domain, but for parameter values where the homogeneous liquid phase and the icosahedral QC state are both linearly stable, we also find states that minimize Ω and correspond to spatially localized QCs, i.e. states in which the QC phase fills only part of the domain. Figure 1(b) shows one such state. This metastable state retains icosahedral symmetry and the slice is chosen to reveal its (approximate) 5-fold symmetry. One may think of such localized QC structures as a QC with a superposed envelope that locally picks out a particular motif from the QC and suppresses the pattern further away.
Figure 1. The 3D density sliced perpendicular to the 5-fold symmetry axis for (a) a thermodynamically stable extended icosahedral QC and (b) a metastable localized quasicrystal at the same parameters: r1 = rq = −0.51, , Q = 2, σ0 = −100 and chemical potential μ = 0. See the supplementary information, available at stacks.iop.org/njp/20/122002/mmedia, for more details on the structure of the extended and spatially localized QCs.
Download figure:
Standard image High-resolution imageSuch spatially localized equilibria lie on a continuous solution branch along which the size of the region occupied by the QC phase changes. The solution branch can be found using numerical continuation techniques that minimize and more generally find stationary solutions, while varying parameters. These include r1 and rq, which determine the peak growth rates of wave numbers 1 and q, and the chemical potential μ. Analogous behaviour is present in 2D, and since most soft matter QCs are planar, we focus on 2D dodecagonal QCs in the remainder of the paper.
3.2. Phase diagram for 2D dodecagonal QCs
Figure 2(a) shows the (r1, rq) parameter plane for μ = 0, indicating the global minimum of the grand potential Ω at each point. When both r1 and rq are strongly negative, the liquid state is the global minimum. When r1 or rq increase we obtain hexagons with lattice spacing 2π[1-hex] or 2π/q (q-hex, figure 2(b)) and a region of q-lamellae when both are positive. Of particular interest is a substantial region in the third quadrant with stable dodecagonal QCs (figure 2(c)). In this region the liquid state is linearly stable, as r1 and rq are both negative, albeit metastable with respect to the QC. Parameter values where the grand potentials of two different states are equal, i.e. the Maxwell points, separate the different regions (solid lines in figure 2(a)). Maxwell points are ideal starting parameter combinations for locating spatially localized states consisting of a patch of one state embedded in a background of another.
Figure 2. (a) Thermodynamically stable 2D structures in the (r1, rq) plane, computed as global minima of the grand potential Ω when the chemical potential vanishes, μ = 0. The dashed lines indicate the axes. The dotted line represents a path corresponding to rq = −0.412 explored in detail in subsequent plots. Panels (b) and (c) show stable states along this path, q-hex at r1 = −0.6181 and QC at r1 = −0.3112, respectively. The remaining parameters are: , Q = 2 and σ0 = −10. The colour scale indicates the value of the order parameter in panels (b)–(c).
Download figure:
Standard image High-resolution image3.3. Branches of spatially extended and localized states
In order to investigate the effect of varying r1, we set rq = −0.412 and μ = 0 (dotted line in figure 2(a)) and study the bifurcation behaviour of the system. Figure 3(a) shows the specific grand potential Ω/A (A is the area of the domain) as a function of r1 for spatially extended states: liquid (black line), 1-lam (brown line), 1-hex (blue line), q-hex (green line), the dodecagonal QC (red line) and a branch of spatially localized QC states with dodecagonal symmetry (magenta line). The 1-lam, 1-hex and QC structures originate at the spinodal (threshold for linear instability of the liquid state) point, r1 = 0. The hexagonal and the QC states arise via transcritical bifurcations and so are found on either side of r1 = 0. However, linearly stable states are only found along parts of the branches below the prominent cusps in panel (a).
Figure 3. (a) Specific grand potential Ω/A as a function of r1 (dotted line in figure 2(a)), with μ = 0 and rq = −0.412. The remaining parameters are as in figure 2. (b) Norm of the state as a function of r1 for the same parameters as in (a). In both figures, spatially extended states include the liquid (black line), 1-lam (brown line), 1-hexagons (blue line), q-hexagons (green line), the QC state (red line), while the magenta line indicates a branch of spatially localized QC states with dodecagonal symmetry. The portions of this line where localized states are metastable are indicated with arrows. These portions correspond to the lower parts of the 'swallow-tails' in (a), which are displayed in greater detail in figure 4(a).
Download figure:
Standard image High-resolution imageFigure 4(a) shows a magnification of a portion from figure 3(a) in the vicinity of the coexistence between the QC states (red line) and the liquid (black line). The QC and liquid are in thermodynamic coexistence at the crossing point of these lines at r1 ≈ −0.6. Spatially localized QC states, shown by the magenta line, are found nearby. In figure 4(a), dashed magenta lines indicate linearly unstable spatially localized QCs while solid magenta lines indicate metastable spatially localized QC states. Panels (b) and (c) show zoomed-in views of two of the swallow-tails.
Figure 4. (a) Zoom of figure 3(a) showing the dependence of the specific grand potential Ω/A on the parameter r1. In addition to the spatially extended states shown in black (liquid state), blue (1-hexagons) and red (QC state), the magenta line indicates the branch of spatially localized QC states with dodecagonal symmetry. The solid line indicates regions of metastability while dashed lines indicate unstable equilibria. Further zoomed-in views of the swallow-tail behaviour close to (b) r1 = −0.62 and (c) r1 = −0.415, corresponding to the states shown in panels (d) and (f), respectively, are also shown. (d)–(f) Metastable localized QC states on each swallow-tail at the locations indicated by in the inset in panel (a), corresponding to r1 = −0.5954, −0.4926 and −0.4151, respectively. (g) Unstable localized state at r1 = −0.14. The remaining parameters are as in figure 2.
Download figure:
Standard image High-resolution imagePanels (d)–(g) of figure 4 show sample solutions along this branch at the locations indicated in the inset of panel (a). These states arise via long wavelength modulational instabilities [42], in which long wavelength modulations suppress the QC amplitude in different parts of the spatial domain. States (e)–(g) do not depend on domain size: identical states are found in boxes of size 164π. With increasing r1, the branch of localized states undergoes fold bifurcations creating three 'swallow-tails' close to locations (d)–(f), before connecting to the unstable small amplitude extended QC branch close to the QC spinodal, near location (g).
Panel (d) shows an example of a spatially modulated QC, where the QC structure is suppressed in the vicinity of the four corners of the domain. The state shown is metastable and is organized around a dodecagonal structure at its centre. As one follows the branch of modulated QC states (magenta line) to the next swallow-tail, these holes deepen, suppressing the QC structure further and leaving a spatially localized QC in a background liquid state. Panel (e) shows a metastable state of this type. As r1 increases from the left fold close to (e), the structure starts to lose the outer ring of 12 peaks. This process is almost complete by location (f), where there is only one ring of 12 peaks surrounding a single central peak. This state is also metastable. With further increase in r1, the state gradually decreases in amplitude, while the interface becomes more diffuse, as the spatially modulated structure approaches an unstable low amplitude but spatially extended QC solution near the spinodal. Panel (g) shows an example of an unstable localized state just prior to the merger with the unstable extended QC state at r1 = −0.11.
Metastable localized states are found only on the lower branch in each of the three swallow-tail regions, and these regions are a reflection of slanted snaking that is expected of localized structures in mass-conserving systems [30, 43, 44]. Indeed, if we replot the data shown in figure 3(a) in terms of the L2 norm of the order parameter U(x) we find a slanted snaking diagram (figure 3(b)) of the type that is present in other conserved system such as the conserved Swift–Hohenberg equation [30] and binary fluid convection in a porous medium [45], a system in which temperature gradients and fluid flow redistribute a conserved amount of solute [46]. Moreover, [30] shows that if the slanted snaking data from the one-dimensional Swift–Hohenberg equation are replotted as a function of the chemical potential μ the snake is 'straightened out' and an upright snaking bifurcation diagram is recovered. For structures confined in two or more spatial dimensions the snaking behaviour is not as clear owing to the greater number of ways the structure may grow but the same relation between swallow-tails, slanted snaking and upright snaking is expected. In figure 3(b) we indicate the location of the solutions that correspond to local energy minima and hence the swallow-tails in figure 3(a). This correspondence in turn shows that the number of swallow-tails will grow as the localized QC or quasicrystalline patch grows following the solution branch. In the numerical continuation the ultimate size of such a patch is of course determined by the size of the computational domain. We find that both the size of the patch and the behaviour of the corresponding solution branch are insensitive to the domain size (and the conditions applied at its boundary) provided the pattern does not grow so large as to come within several wavelengths 2π/q of the boundary. Weak effects of the square symmetry of the domain can in fact be detected for smaller patches—these are present because of exponentially weak interactions with 'image' patches outside the depicted domain—but do not fundamentally alter our conclusions.
We anticipate therefore that in larger domains the number of swallow-tails in figure 3(a) will be greater since each is associated with the appearance of a new layer of structure around the central dodecagonal motif. Similar spatially localized but crystalline structures are associated with the periodic structures also shown in figure 2. Thus patches of hexagons, etc are also present, as is the case in non-conserved systems [31].
3.4. Spatially localized states with reduced symmetry
The dodecagonal symmetry about the central peak visible in figures 4(b)–(e) is retained all along the branch of localized QC shown by the magenta line in figure 4(a). Additional branches of localized QC with reduced symmetry are also present. Figures 5(b), (e) show two such equilibria with hexagonal and square central motifs, for r1 values near where the associated localized states merge with the unstable extended QC state. In general the growth of these structures with decreasing r1 does not maintain the symmetry of the central motif—these states are, after all, quasicrystalline and hence aperiodic—unless enforced by the shape of the domain. We show examples of equilibria that have broken the (approximate) hexagonal or square symmetry of the central motif in figures 5(c), (d), (f), (g).
Figure 5. (a) Specific grand potential Ω/A as a function of r1. In addition to branches of spatially extended solutions (black, blue and red lines) and the symmetric spatially localized states (magenta line) from the inset in figure 4(a), we show a branch of localized states with hexagonal central motif (dashed–dotted dark grey line), and a branch of localized states with square central motif (dashed mustard line). The line decorations in this figure serve only to distinguish the different branches and are not indicative of stability. The profiles corresponding to (b) r1 = −0.2388, (c) r1 = −0.4926 and (d) r1 = −0.5954 are on the dashed–dotted dark grey line with hexagonal central motif while (e) r1 = −0.2937, (f) r1 = −0.3495 and (g) r1 = −0.4859 are on the dashed mustard line with square central motif. The remaining parameters are as in figure 2.
Download figure:
Standard image High-resolution imageThe branches of localized solutions associated with each of the symmetry-broken motifs also display swallow-tails, as shown in figure 5(a). The numbers and parameter ranges of the swallow-tails along each branch differ. Among the branches of localized solutions, the branch with hexagonal motif has the lowest grand potential Ω over most of its range.
4. Concluding remarks
We have shown that localized patches of QCs surrounded by bulk liquid can be metastable both in 2D and 3D. In 2D these structures are located on the swallow-tails in figures 3–5 and we expect similar behaviour in 3D. As shown in figure 3(b), the swallow-tails in figure 3(a) (zoomed in view shown in figure 4(a)) correspond to slanted snaking when replotted in terms of the norm . This applies to regular crystals as well, although in both cases the overall snaking structure becomes more complex as one goes from 1D to 2D and then to 3D, with the 'wiggles' in the snake becoming less regular [29–31]. This is because with increasing dimensionality there is an increase in the number of sites around a localized structure where new peaks can appear as the size of the structure grows along a solution branch. In the case of QCs (as opposed to hexagons) this complexity is greater, owing to the variety of different ways the additional density peaks can be placed and removed. Interestingly, we find that as the symmetric localized QC (figure 4) increases in size, the growth leads to a snaking with fewer wiggles than one might expect. The growth is more akin to that observed for circularly symmetric 'target' patterns than the growth of hexagonal localized states [31], presumably because the energy to locate a new peak on the surface of the localized QC depends very little on its location on the surface. Note also that in figure 3(b) the lower two wiggles in the localized QC branch are smoother than the higher wiggles because these are for localized states that do not interact with the domain boundary. Once the localized QC approaches the boundary and starts to interact with its images, the wiggling becomes more complex.
The fact that some of these spatially localized QCs are metastable (i.e. local minima of the free energy) has significant consequences: their stability will make these structures longer lived in an environment with thermal fluctuations. One should therefore expect that some of these will play the role of 'stepping-stones' on the path through phase space either side of the critical nucleus and on towards forming the bulk QC phase, thereby greatly influencing the rate of QC nucleation. In other words, the existence of these localized QC will lead to the timescale for forming the bulk QC to be shorter than it might otherwise be, thereby enabling the QC, for some parameter values, to out-compete the regular crystal in the race to form from the liquid. In this manner, these structures will suppress the formation of the regular hexagonal crystal [47]. Moreover, since they have a different symmetry from the regular crystal, the latter is unlikely to form in any region of the liquid containing a localized QC. We expect this to be very much akin to the role played by the so-called locally favoured structures (LFS) discussed, e.g. in [48–50]. In 3D, icosahedral LFS are believed to be linked to dynamic arrest [50], i.e. the avoidance of crystallization, because these LFS do not have the symmetry of the crystalline phase. Indeed, based on the large spatial extent of some of the stable localized structures we find, we conjecture that in general quite large LFS may be present in systems of this kind.
Acknowledgments
We are grateful to Daniele Avitabile and Laurette Tuckerman for assistance and discussions of the biconjugate gradient method and to Joe Firth for technical support. This work was supported in part by a L'Oréal UK and Ireland Fellowship for Women in Science (PS), by the EPSRC under grants EP/P015689/1 (AJA) and EP/P015611/1 (AMR), by the Leverhulme Trust (RF-2018-449/9, AMR) and by the NSF under grant DMS-1613132 (EK).
: Appendix. Terminology
In this appendix we briefly comment on several uses and concepts in the literature relating to the word 'cluster' [51]. (i) Some soft matter systems freeze into a so-called cluster crystal, in which each density peak corresponds to the average location of the centres of mass of several polymeric macromolecules [9, 52]. The soft matter systems we consider here are of this type. (ii) Finite collections of attracting particles in a vacuum can minimize their potential energy by forming clusters, and for certain small numbers of particles, these clusters have icosahedral symmetry [53, 54]. Our metastable localized QCs are, in contrast, states that minimize the free energy and are surrounded by the liquid. (iii) In simple one-length scale molecular potential systems, icosahedral structures can be the minimal energy structures in small finite size collections of simple molecules [53–55]. However, as the number of particles increases, the icosahedral minimum energy states generally first transform into anti-Mackay clusters for intermediate numbers of particles, and finally transform into close-packed fcc or hcp structures for large particle numbers. In contrast, the localized states we observe retain the QC symmetry over a range of sizes, until they fill the entire domain and form a QC. (iv) In the QC context, the word 'cluster' is often used to denote a particular arrangement of atoms or molecules that is regularly repeated throughout the system [51]. We instead refer to aperiodically repeating arrangements within our QCs as 'motifs'. (v) Icosahedral clusters of atoms in some supercooled liquids are known to influence the process of crystallization [47]. Our work is relevant to this; see section 4. (vi) Other authors speak of spatially localized grains. For example, in [56] such grains are fabricated by manipulating nanoparticles, e.g. by stirring. However, in this system the particles are polydisperse and the quasicrystalline grains that form are the result of different sized particles. In contrast, in our system all particles are identical. In order to prevent confusion between these various uses of the words cluster and grain (or patch in 2D), we avoid the use of these terms altogether.





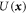
![${\rm{\Omega }}[U({\boldsymbol{x}})]$](https://content.cld.iop.org/journals/1367-2630/20/12/122002/revision2/njpaaf3bdieqn2.gif)
![${\rm{\Omega }}[U({\boldsymbol{x}})]$](https://content.cld.iop.org/journals/1367-2630/20/12/122002/revision2/njpaaf3bdieqn3.gif)
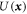
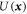
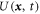

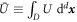


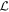
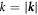
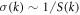
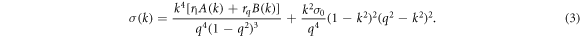
![$A(k)=[{k}^{2}({q}^{2}-3)-2{q}^{2}+4]{({q}^{2}-{k}^{2})}^{2}{q}^{4}$](https://content.cld.iop.org/journals/1367-2630/20/12/122002/revision2/njpaaf3bdieqn12.gif)
![$B(k)=[{k}^{2}(3{q}^{2}-1)+2{q}^{2}-4{q}^{4}]{(1-{k}^{2})}^{2}$](https://content.cld.iop.org/journals/1367-2630/20/12/122002/revision2/njpaaf3bdieqn13.gif)
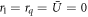
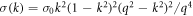
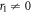
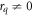
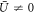
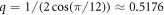
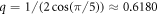
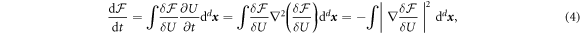
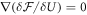
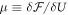
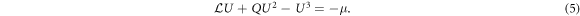
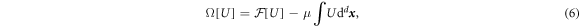
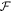
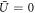
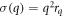

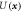
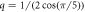
![${\rm{\Omega }}[U({\boldsymbol{x}})]$](https://content.cld.iop.org/journals/1367-2630/20/12/122002/revision2/njpaaf3bdieqn32.gif)