Abstract
We propose an optomechanical setup allowing quantum mechanical correlation, entanglement and steering of two ultrashort optical pulses. The protocol exploits an indirect interaction between the pulses mediated optomechanically by letting both interact twice with a highly noisy mechanical system. We prove that significant entanglement can be reached in the bad cavity limit, where the optical decay rate exceeds all other damping rates of the optomechanical system. Moreover, we demonstrate that the protocol generates a quantum non-demolition interaction between the ultrashort pulses which is the basic gate for further applications.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
According to the rules of quantum theory, a quantum state can be swapped between physical systems of the same dimension without any limitation. Such transduction between different physical platforms opens the full operation space for quantum technology [1]. Many different systems, however, do not interact directly and transduction can be realized only through a mediator. Mechanical systems are very good candidates for such mediators, interconnecting electromagnetic radiation of different or same frequencies and building universal transducers [2–5], as they can couple to various quantum systems including spins, cold atoms, Bose–Einstein condensates and photons of a wide range of frequencies. The interaction of light with mechanical oscillators is the subject of the special field of optomechanics. The principle of interconnecting radiation fields with help of a mechanical mediator has been demonstrated in a number of experiments connecting optical and microwave fields [6–10]. Experiments have been reported connecting optical to optical [11–13] and microwave to microwave [14] fields. Theoretical proposals for building transducers connecting light and microwave radiation in the continuous-wave regime [15–21] have also been put forward.
To be fully compatible with modern hybrid quantum optics [22–25], pulsed versions of quantum optomechanics have been initiated in two regimes: exponentially modulated pulses with duration significantly exceeding the mechanical period [26] and high-intensity pulses which are very short compared to the mechanical period [27]. The former has been used to demonstrate Gaussian entanglement between microwave field and mechanical oscillator [28], quantum state transfer [29, 30], non-classical photon–phonon correlations [31, 32], entanglement between distant mechanical oscillators [33], and also motivated other theoretical ideas [34–36]. Likewise, the latter approach, also known as stroboscopic, has stimulated a number of experimental [37] and theoretical [38, 39] works. Recently, quantum transducers based on geometric phase effect have been proposed [40] and analysed in the regime of long pulses [41]. There it was shown that by proper optimization an entangling quantum non-demolition (QND) interaction [27, 42] can be established between two systems mediated by a mechanical oscillator, without the need to cool the latter close to the ground state. The idea has been applied to generate entanglement between optical and microwave field [28]. Such a scheme requires high-Q cavity systems, resolved-sideband regime, and intensive two-tone driving to eliminate the destructive free mechanical evolution and thereby reach nearly ideal performance. It, however, still remains unclear, whether the geometric phase effect will be sufficient to obtain a robust transducer in the stroboscopic regime with ultrashort pulses without entering the sideband resolved regime, and potentially without cavity. Such a proposal will stimulate a much broader class of feasible quantum transducers mediated by mechanical systems.
In this paper we propose a pulsed stroboscopic quantum transducer based on the geometric phase effect, which generates a QND coupling between optical fields of possibly different frequencies. We show that for state-of-the-art optomechanical systems the proposed scheme performs very well under the influence of different decoherence processes and for an almost arbitrarily noisy mechanical mediator. We also analyse the gradual build-up of non-classical correlations, entangling power and quantum steering after different numbers of sequential pulses, demonstrating that even simplified versions of the protocol produce quantum correlations. It allows for a verification of its performance in the middle of the transducer protocol. In addition we prove that this protocol is also efficient in a system which does not contain an optical cavity.
2. Protocol
We propose a setup allowing to entangle two optical modes (possibly of different wavelengths), A and B, applying sequential interactions with a mechanical oscillator. We start by considering a mechanical mode of the optomechanical cavity (as in figure 1), although the protocol can be extended to a system without the cavity (see section 8). The optomechanical cavity is typically a system consisting of two modes, an optical and a mechanical one. In the presence of a strong classical optical pump at the cavity resonance, the inherently nonlinear optomechanical interaction [43] can be linearized. In the frame rotating with the pump frequency the Hamiltonian of the system including this linearized interaction, reads [44]
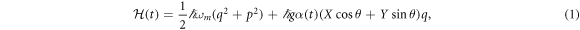
where the first summand describes the free evolution of the mechanical mode and the second one describes the optomechanical coupling of the optical mode with quadratures (X,Y) and the mechanical mode with dimensionless displacement q and momentum p, such that ![$[X,Y]=[q,p]=i$](https://content.cld.iop.org/journals/1367-2630/20/8/083042/revision2/njpaadbb7ieqn1.gif) . Here g is the single-photon optomechanical coupling rate, ωm is the mechanical frequency and θ is the optical quadrature phase. The mean intracavity amplitude α(t) induced by the pump is assumed to have constant value
. Here g is the single-photon optomechanical coupling rate, ωm is the mechanical frequency and θ is the optical quadrature phase. The mean intracavity amplitude α(t) induced by the pump is assumed to have constant value 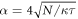 over the pulse duration τ, where κ is the energy decay rate of the cavity. This amplitude is normalized in such a way that the average number of photons in the corresponding pulse is N = α2τκ/16 . If the interaction time is short compared to the mechanical period, as, for instance, in the experiment [37], the free evolution of the mechanical mode can approximately be ignored, so that only the second (coupling) term in the Hamiltonian (1) remains. Numerical estimations prove that the free mechanical evolution during the pulsed interaction does indeed not influence the entanglement of the modes significantly. This step significantly simplifies the resonant optomechanical interaction, because we can reach two different QND interactions associated with θ = 0, π/2 in (1), without any change in the non-demolition variables X, q and Y, q.
over the pulse duration τ, where κ is the energy decay rate of the cavity. This amplitude is normalized in such a way that the average number of photons in the corresponding pulse is N = α2τκ/16 . If the interaction time is short compared to the mechanical period, as, for instance, in the experiment [37], the free evolution of the mechanical mode can approximately be ignored, so that only the second (coupling) term in the Hamiltonian (1) remains. Numerical estimations prove that the free mechanical evolution during the pulsed interaction does indeed not influence the entanglement of the modes significantly. This step significantly simplifies the resonant optomechanical interaction, because we can reach two different QND interactions associated with θ = 0, π/2 in (1), without any change in the non-demolition variables X, q and Y, q.
Figure 1. (a) The block-scheme of the transducer. Optical modes of possibly different wavelengths A and B interact sequentially with the mechanical system M by four QND interactions with Hamiltonians  . Between these interactions the mechanical mode undergoes free evolution through one quarter of the mechanical period while interacting with the mechanical environment (
. Between these interactions the mechanical mode undergoes free evolution through one quarter of the mechanical period while interacting with the mechanical environment ( ) and the optical modes are subject to optical losses (η). ti denote corresponding interaction end moments. (b) A possible experimental implementation of the protocol. The mirror (dashed) is optional. Optical modes A and B interact alternately with the mechanical system M. DL—delay lines. (c) Path of the mechanical mode of the transducer in phase-space. The mechanical system starts in the first quadrant. Then the momentum kick by the mode A occurs (red vertical arrow). After that the mechanical system evolves freely per one quarter of the mechanical period, ending up in the second quadrant (purple arrow). Subsequently the interaction with the mode B occurs. The procedure is repeated until the system reaches the 'end' point. In the ideal case the trajectory of the mechanical mode in the phase space is closed and this mode appears to be effectively decoupled from the optical ones.
) and the optical modes are subject to optical losses (η). ti denote corresponding interaction end moments. (b) A possible experimental implementation of the protocol. The mirror (dashed) is optional. Optical modes A and B interact alternately with the mechanical system M. DL—delay lines. (c) Path of the mechanical mode of the transducer in phase-space. The mechanical system starts in the first quadrant. Then the momentum kick by the mode A occurs (red vertical arrow). After that the mechanical system evolves freely per one quarter of the mechanical period, ending up in the second quadrant (purple arrow). Subsequently the interaction with the mode B occurs. The procedure is repeated until the system reaches the 'end' point. In the ideal case the trajectory of the mechanical mode in the phase space is closed and this mode appears to be effectively decoupled from the optical ones. 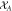 and
and 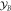 stand for amplitude and phase quadratures of systems A and B, respectively, and χ is the interaction strength.
stand for amplitude and phase quadratures of systems A and B, respectively, and χ is the interaction strength.
Download figure:
Standard image High-resolution imageOur proposed protocol consists of four sequential pulsed QND interactions (two for each of the optical modes) separated by a quarter of the period of the free mechanical evolution during which there is no interaction with any of the optical modes (see figure 1(c)). Between the optomechanical interactions with the mechanical oscillator, each of the optical modes is directed to the delay line. The Hamiltonians of the individual pulsed interactions read (the quadratures of modes A and B are labelled with corresponding subscript)
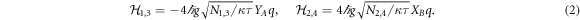
Each of the QND interactions shift the momentum of the mechanical mode and also one of the quadratures of the corresponding optical mode. Combined with the precisely timed free evolutions of the mechanical mode that effectively swap the mechanical quadratures  this ideally allows the mechanical mode to follow a closed path in phase space (figure 1 (c)). The geometric phase induced by this closed path enables coupling of the optical modes while keeping the mechanical mode decoupled from those.
this ideally allows the mechanical mode to follow a closed path in phase space (figure 1 (c)). The geometric phase induced by this closed path enables coupling of the optical modes while keeping the mechanical mode decoupled from those.
For the QND interaction with Hamiltonian 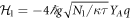 (for the phase θ = 0) the quantum Langevin equations take the following form [3, 45]:
(for the phase θ = 0) the quantum Langevin equations take the following form [3, 45]:
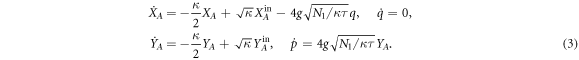
Here 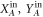 are the quadratures of the input optical fluctuations with commutator
are the quadratures of the input optical fluctuations with commutator ![$[{X}^{\mathrm{in}}(t),{Y}^{\mathrm{in}}(t^{\prime} )]={\rm{i}}\delta (t-t^{\prime} )$](https://content.cld.iop.org/journals/1367-2630/20/8/083042/revision2/njpaadbb7ieqn10.gif) .
.
We assume the optical decay rate κ to be much larger than other characteristic rates of the system—inverse pulse duration τ−1, mechanical frequency ωm and the enhanced optomechanical coupling strength 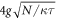 which is well justified in certain experiments [46, 47]. This corresponds to the adiabatic regime where the optical mode reacts instantaneously to influences. This allows us to set
which is well justified in certain experiments [46, 47]. This corresponds to the adiabatic regime where the optical mode reacts instantaneously to influences. This allows us to set 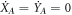 in (3). Thus with the help of the input–output relations [48] in the form
in (3). Thus with the help of the input–output relations [48] in the form
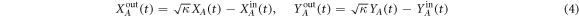
we can write down the solution of (3):
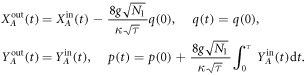
Now we introduce new optical modes with quadratures 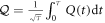 and QND interaction strength
and QND interaction strength  , and integrate the equations for
, and integrate the equations for 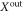 and
and 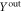 over the duration of the first pulsed interaction. We then obtain the standard QND form [49] of interaction:
over the duration of the first pulsed interaction. We then obtain the standard QND form [49] of interaction:
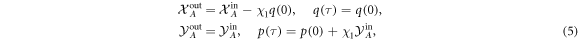
valid when 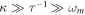 . Equations (5) describe the ideal unitary coupling between the new temporal modes which are not affected by decoherence during the short period of the pulse. We apply the same approach for the remaining interactions.
. Equations (5) describe the ideal unitary coupling between the new temporal modes which are not affected by decoherence during the short period of the pulse. We apply the same approach for the remaining interactions.
3. Decoherence processes
In this section we describe the model of the decoherence processes in the system. The most fundamental decoherence processes are that of mechanical decoherence due to the coupling to the thermal environment and optical losses.
3.1. Mechanical thermal noise
Since the pulsed optomechanical interactions in our scheme are very short compared to the mechanical period ( ) and the thermal decoherence time (
) and the thermal decoherence time ( ), it is safe to neglect the free evolution of the mechanical mode for the time of the interaction. Between the interactions, however, the mechanical mediator is subject to damped harmonic oscillations that last for a quarter of mechanical period (
), it is safe to neglect the free evolution of the mechanical mode for the time of the interaction. Between the interactions, however, the mechanical mediator is subject to damped harmonic oscillations that last for a quarter of mechanical period (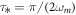 ). This evolution is described by the following equations of motion
). This evolution is described by the following equations of motion
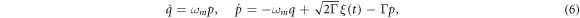
where Γ is the mechanical damping coefficient, ξ(t) is the thermal noise operator that obeys the autocorrelation 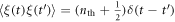 with
with 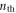 being the mean occupation number of the mechanical bath.
being the mean occupation number of the mechanical bath.
We can formally solve the equations (6) and find the transformation of the mechanical mode for a high-Q mechanical oscillator that satisfies Γ ≪ ωm:
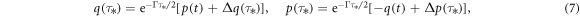
with Δ q, Δ p being mechanical noise operators defined as:
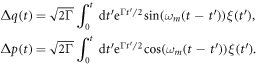
These operators have the following properties:
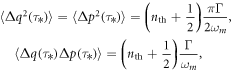
which resembles standard Markovian noise [50].
3.2. Optical losses
The optical losses in the system stem from imperfect coupling to the optomechanical cavity, mismatch of modes, propagating photon losses etc. Importantly, all these processes are linear and this leads to admixture of vacuum. Therefore the effect of losses on an optical mode with quadratures Q can be modelled as a beamsplitter with vacuum in the unused port. The corresponding phase-insensitive transformations of quadratures Q read
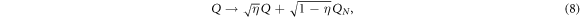
with QN being the quadrature of the optical vacuum noise (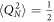 ) and η, the transmittance of the beamsplitter. For example, when η = 1 there are no optical losses in the system.
) and η, the transmittance of the beamsplitter. For example, when η = 1 there are no optical losses in the system.
We introduce the optical loss after the first QND interaction for the optical mode A and after the second QND interaction for the optical mode B (see figure 1(a) for reference). The optical losses before the first and after the last interactions are not taken into account since they may be considered as not being inherent in the protocol itself and may be easily added to the final results if needed.
We have now described each of the evolution blocks constituting figure 1 in terms of input–output relations for the quadratures of the modes affected. Sequentially applying this formalism, we can obtain expressions for the quadratures at a certain instant of time, from which we can evaluate the required parameters, in particular, the covariance matrices.
4. Generalized squeezing, conditional squeezing, Gaussian entanglement and Gaussian quantum steering
A zero-mean Gaussian state  of a bipartite system A + B with the quadratures forming a vector f = (XA, YA, XB, YB) can be completely described by the covariance matrix [51, 52] with elements
of a bipartite system A + B with the quadratures forming a vector f = (XA, YA, XB, YB) can be completely described by the covariance matrix [51, 52] with elements ![${V}_{{ij}}=\tfrac{1}{2}\mathrm{Tr}[\hat{\rho }({f}_{i}{f}_{j}+{f}_{j}{f}_{i})]$](https://content.cld.iop.org/journals/1367-2630/20/8/083042/revision2/njpaadbb7ieqn25.gif) . This matrix has the block structure
. This matrix has the block structure
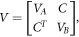
where VA, VB and C are the 2 × 2 matrices describing individual variances and co-variances correspondingly. Superscript T means transposition.
The mathematical formalism for Gaussian states allows us to investigate different signatures of quantum mechanical correlations between two modes [53]. We will use four suitable Gaussian quantifiers: generalized squeezing, conditional squeezing, entanglement and steering. They have gradually higher demand on quantity of quantum correlations between A and B.
Generalized squeezing [54] specifies squeezing available in the system by global passive transformations. It is also the signature that the covariance matrix corresponds to a non-classical state. This quantity is defined as the minimal eigenvalue of the covariance matrix.
Conditional squeezing procedure may be described in the following way [55]. Let us perform homodyne detection of the amplitude quadrature of mode B. After this procedure the covariance matrix of system A is transformed in the following way:
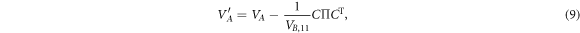
with 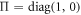 . The conditional squeezing is possible when the smallest eigenvalue of
. The conditional squeezing is possible when the smallest eigenvalue of 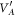 (which we will later refer to as conditional variance and which in the simple case of diagonal
(which we will later refer to as conditional variance and which in the simple case of diagonal 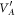 corresponds to the variance of amplitude or phase quadrature of system A) is smaller than the shot-noise variance, established by the Heisenberg's uncertainty principle. An analogous procedure can be applied to check for the possibility of obtaining conditional squeezing of system B. Conditional squeezing justifies that generalized squeezing can be, at least partially, induced in one mode by a measurement of the other one.
corresponds to the variance of amplitude or phase quadrature of system A) is smaller than the shot-noise variance, established by the Heisenberg's uncertainty principle. An analogous procedure can be applied to check for the possibility of obtaining conditional squeezing of system B. Conditional squeezing justifies that generalized squeezing can be, at least partially, induced in one mode by a measurement of the other one.
The state 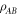 of a bipartite system is called an entangled state if it cannot be presented in the form
of a bipartite system is called an entangled state if it cannot be presented in the form 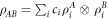 with
with 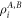 being the states of the first and second systems correspondingly and ci being the probabilities. A measure of entanglement is the logarithmic negativity defined for Gaussian states as follows [53]:
being the states of the first and second systems correspondingly and ci being the probabilities. A measure of entanglement is the logarithmic negativity defined for Gaussian states as follows [53]:
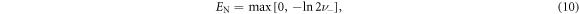
where ν− is the smallest symplectic eigenvalue of the covariance matrix of the partially transposed state. This eigenvalue can be calculated in the following way:
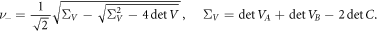
The modes A and B are entangled when 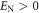 .
.
The logarithmic negativity constitutes an upper bound to the distillable entanglement, and is a proper entanglement monotone that can be easily evaluated provided a covariance matrix and does not require complicated optimization. Therefore we prefer it to other entanglement measures, including Duan's criterion [51]. The latter could be used as well, but it requires a proper optimization of the combination of the quadratures of the subsystems A and B.
The state 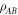 is A→B steerable if after performing measurements on subsystem A, it is possible to predict the measurement results of system B with an accuracy better than for a pure separable minimum uncertainty state. To quantify the steering of bipartite Gaussian systems we use the steerability [56]:
is A→B steerable if after performing measurements on subsystem A, it is possible to predict the measurement results of system B with an accuracy better than for a pure separable minimum uncertainty state. To quantify the steering of bipartite Gaussian systems we use the steerability [56]:
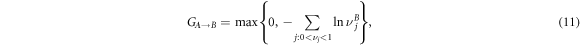
where 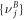 are the orthogonal eigenvalues of the matrix
are the orthogonal eigenvalues of the matrix 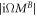 with
with 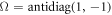 and
and 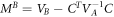 . The steerability in opposite direction from party B to party A may be calculated by replacing matrices VA and VB.
. The steerability in opposite direction from party B to party A may be calculated by replacing matrices VA and VB.
5. Basic quantum transducer
To understand the process of building quantum correlations and entanglement, we will analyse the correlations after output of each step of the protocol. After only two QND interactions the transducer is capable of building correlations sufficient for conditional squeezing of at least one optical mode. The presence of this non-classical aspects of correlations would be a demonstration of the feasibility of the basic protocol.
We consider a sequence of interactions, where mode A first interacts with the mediator M with Hamiltonian 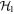 , then the mechanical system evolves quarter of a mechanical period and after that mode B interacts with the mediator with Hamiltonian
, then the mechanical system evolves quarter of a mechanical period and after that mode B interacts with the mediator with Hamiltonian  (see figure 1(a)). We start with the simplest case when there is no decoherence in the system and all individual QND interaction strengths are equal to χ. The optical modes are initially in vacuum, and the mechanical mode in a thermal state with occupation n0. When each of the two optical modes have interacted with the mediator, the transformations of quadratures are as follows:
(see figure 1(a)). We start with the simplest case when there is no decoherence in the system and all individual QND interaction strengths are equal to χ. The optical modes are initially in vacuum, and the mechanical mode in a thermal state with occupation n0. When each of the two optical modes have interacted with the mediator, the transformations of quadratures are as follows:
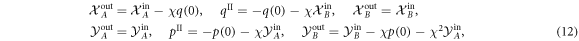
where q(0) and p(0) are the mechanical quadratures before the first optomechanical interaction.
After homodyning an arbitrary quadrature 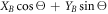 of system B, the covariance matrix of system A takes the form:
of system B, the covariance matrix of system A takes the form: 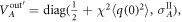 where
where
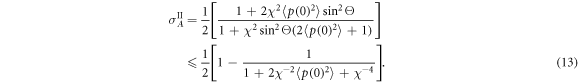
The diagonal elements of the covariance matrix of a Gaussian system (in the diagonal form) show uncertainties in its quadratures. When one of the elements is below the shot noise level, the system is squeezed. Therefore, homodyne detection on system B is capable of squeezing the mode of system A. This is already a nontrivial aspect of Gaussian quantum correlations build-up achieved using the mechanical mediator. The possibility of squeezing can be understood from the equations (12). Homodyne measurement of 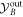 effectively reduces its variance to zero. Since the quadrature
effectively reduces its variance to zero. Since the quadrature 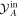 constitutes a part of this quadrature, its variance could as well be reduced as a result of this measurement, that is it will become squeezed. To achieve significant squeezing, however, one needs the coupling to be strong enough to secure
constitutes a part of this quadrature, its variance could as well be reduced as a result of this measurement, that is it will become squeezed. To achieve significant squeezing, however, one needs the coupling to be strong enough to secure 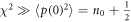 , so that the dominant term in the expression for
, so that the dominant term in the expression for 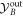 is provided by fluctuations in
is provided by fluctuations in  and not by the initial mechanical fluctuations in p(0). Formally this amounts to the need to decrease the denominator of the fraction in (13). This means that for realistic values of the coupling χ ≤ 10, squeezing can be observed for a mechanical occupancy of n0 ≈ 100. Cooling the phonon number to this level is achievable within the sideband unresolved regime using different techniques such as active feedback cooling [58], hybrid systems [59], optomechanically induced transparency [46] or dissipative optomechanics [60]. Experimentally, feedback cooling has allowed for an occupancy of n0 = 5 of a mechanical oscillator [61, 62] which can be improved to yield ground state cooling using a higher detection efficiency or using squeezed state probing [63]. These experiments on near ground state cooling have been performed in a 4 K cryostat, but with the development of new high-Q mechanical oscillators [64–66], ground state cooling in a room temperature environment is within reach.
and not by the initial mechanical fluctuations in p(0). Formally this amounts to the need to decrease the denominator of the fraction in (13). This means that for realistic values of the coupling χ ≤ 10, squeezing can be observed for a mechanical occupancy of n0 ≈ 100. Cooling the phonon number to this level is achievable within the sideband unresolved regime using different techniques such as active feedback cooling [58], hybrid systems [59], optomechanically induced transparency [46] or dissipative optomechanics [60]. Experimentally, feedback cooling has allowed for an occupancy of n0 = 5 of a mechanical oscillator [61, 62] which can be improved to yield ground state cooling using a higher detection efficiency or using squeezed state probing [63]. These experiments on near ground state cooling have been performed in a 4 K cryostat, but with the development of new high-Q mechanical oscillators [64–66], ground state cooling in a room temperature environment is within reach.
To determine the full dynamics, including mechanical decoherence and optical losses, we resort to numerical estimations. The results are presented in figure 2(a). The good correspondence between the lossless solution and the one with losses should be noted. This indicates that the approximate model captures the system really well and that the initial occupation is the main source of decoherence.
Figure 2. Generalized and conditional squeezing after two (a), three (b) and four (c) QND interactions as a function of the initial mechanical occupation (note different axis range in (a) and (b), (c)). Corresponding generalized (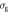 ) and conditional variances (
) and conditional variances ( ) after the phase quadrature of the system B (A) was homodyned as the function of initial occupation of the mechanical mode M for different values of the QND coupling strength. Darker colours denote conditional squeezing and lighter colours denote generalized one. Solid lines stand for the case including all the decoherence processes, dotted ones stand for ideal cases without any decoherence and lines with markers are responsible for the optimized values. Conditional squeezing coincides with generalized one for every case except the case of χ = 1 in (b) and (c). Parameters used are the following:
) after the phase quadrature of the system B (A) was homodyned as the function of initial occupation of the mechanical mode M for different values of the QND coupling strength. Darker colours denote conditional squeezing and lighter colours denote generalized one. Solid lines stand for the case including all the decoherence processes, dotted ones stand for ideal cases without any decoherence and lines with markers are responsible for the optimized values. Conditional squeezing coincides with generalized one for every case except the case of χ = 1 in (b) and (c). Parameters used are the following:  ,
, 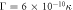 , g = 4 × 10−7 κ, τ = 16/κ what corresponds to the recent experiment [57]. We also assume
, g = 4 × 10−7 κ, τ = 16/κ what corresponds to the recent experiment [57]. We also assume 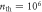 and η = 0.9.
and η = 0.9.
Download figure:
Standard image High-resolution imageOur estimations show that in the case of two QND interactions conditional squeezing σA is identical to the generalized one  meaning that the former reaches the maximal possible value of squeezing in this system (darker and lighter lines coincide in figure 2(a)).
meaning that the former reaches the maximal possible value of squeezing in this system (darker and lighter lines coincide in figure 2(a)).
Conditional squeezing of mode B is, however, not possible as no information about B is written into A after only two QND interactions.
Our analytical and numerical estimates of the logarithmic negativity and the steerability show that there is no entanglement between modes A and B and that steering is not possible in either direction.
6. Advanced quantum transducer
We now proceed to consider 3 interactions and investigate different measures of quantum correlations between the optical modes. In the ideal case without decoherence when the interaction strengths are equal, the transformations of quadratures take the following form:
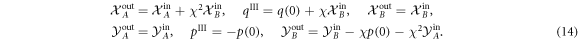
System B is not affected by the third interaction, thereby the measurement performed on it will provide the same squeezing of mode A as after only the two interactions. As we see from these equations the initial state of the mechanical oscillator is completely traced out from system A, and now quadrature 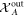 contains information about
contains information about 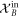 . From this we conclude that by homodyning system A in this ideal case one can perform squeezing of system B and the amount of squeezing does not depend on the initial occupation of the mechanical oscillator. The conditional variance in this case is expressed as
. From this we conclude that by homodyning system A in this ideal case one can perform squeezing of system B and the amount of squeezing does not depend on the initial occupation of the mechanical oscillator. The conditional variance in this case is expressed as 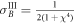 and is defined only by the value of the QND coupling strength.
and is defined only by the value of the QND coupling strength.
When there are optical losses in the system, the conditional variance becomes dependent on the initial occupation of the mechanical system and may be approximated for small losses by:
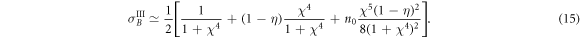
The optimization of σB with respect to unequal individual QND interaction strengths χ1,2,3 allows us to partially compensate for the influence of optical losses and to make σB independent of n0 and equal to 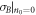 . The presence of the mechanical bath defines the maximal achievable amount of squeezing and cannot be compensated by the optimization. In the case of a high mechanical quality factor Q = ωm / Γ the conditional variance takes the following form:
. The presence of the mechanical bath defines the maximal achievable amount of squeezing and cannot be compensated by the optimization. In the case of a high mechanical quality factor Q = ωm / Γ the conditional variance takes the following form:
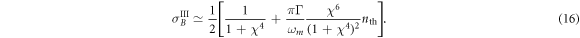
The reasoning above proves that the major impediment to successful performance is the initial thermal occupation n0. In the lossless case it is automatically balanced out by the equal QND gains, and when the losses break the balance, the proper combination of unequal gains can help to alleviate the influence of n0. Numerical estimations for the full dynamics including mechanical bath and optical losses are presented in the figure 2(b). The upper bound of the range of initial occupation, n0 = 106, corresponds to the equilibrium occupation of a mechanical oscillator with frequency ωm = 2π × 100 kHz at temperature of 5 K.
Comparison of the conditional squeezing with the generalized one shows that for the case of low QND coupling strengths (χ ≲ 1) the amount of squeezing produced by conditional measurement does not reach the maximal possible one (in both cases of the idealized dynamics without any decoherence and in the case of full model). To attain the maximally available squeezing the value χ should be increased. See figure 2(b) for details.
We now investigate the entanglement generated in this system. From (14) we conclude that logarithmic negativity should be sensitive to the initial occupation of the mechanical mode as the term −χ p(0) enters the expression for 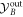 . In the ideal case, the logarithmic negativity is a monotonically increasing function of χ. Optical losses break this monotonicity. This is related to the fact that losses modify the trajectory of the mechanical system in phase space, displacing it away from the optimal final point, most pronounced for higher QND gains. Optimization with respect to QND couplings of individual interactions χ1,2,3 partially compensates the optical losses and makes the logarithmic negativity a monotonic function again. The presence of the mechanical bath imposes a limit on the maximal achievable amount of entanglement. The optimization with respect to unequal QND strengths partially compensates the influence of the mechanical bath and allows higher values of entanglement to be reached, compared to the non-optimized case. This is represented in the figure 3(a) together with estimates for non-optimized values.
. In the ideal case, the logarithmic negativity is a monotonically increasing function of χ. Optical losses break this monotonicity. This is related to the fact that losses modify the trajectory of the mechanical system in phase space, displacing it away from the optimal final point, most pronounced for higher QND gains. Optimization with respect to QND couplings of individual interactions χ1,2,3 partially compensates the optical losses and makes the logarithmic negativity a monotonic function again. The presence of the mechanical bath imposes a limit on the maximal achievable amount of entanglement. The optimization with respect to unequal QND strengths partially compensates the influence of the mechanical bath and allows higher values of entanglement to be reached, compared to the non-optimized case. This is represented in the figure 3(a) together with estimates for non-optimized values.
Figure 3. Entanglement and steerability after three interactions. (a) Logarithmic negativity as a function of the initial occupation of the mechanical mode n0 for different values of the mechanical bath occupation number 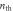 and for χ = 1. Inset: logarithmic negativity as a function of the QND coupling strength χ for different values of the mechanical bath occupation number
and for χ = 1. Inset: logarithmic negativity as a function of the QND coupling strength χ for different values of the mechanical bath occupation number  , n0 = 0 and pulse photon numbers 0 ≤ N ≤ 1013. (b) Steering
, n0 = 0 and pulse photon numbers 0 ≤ N ≤ 1013. (b) Steering 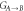 and
and 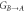 as a function of the QND coupling χ for different values of the mechanical initial occupation n0 and Γ/κ = 3 × 10−10. Dashed red lines represent the ideal case without any decoherence, whereas the solid lines represent the case with all decoherence processes included. Lines with markers indicate optimized parameter values. Parameters which are not mentioned separately are the same as in figure 2.
as a function of the QND coupling χ for different values of the mechanical initial occupation n0 and Γ/κ = 3 × 10−10. Dashed red lines represent the ideal case without any decoherence, whereas the solid lines represent the case with all decoherence processes included. Lines with markers indicate optimized parameter values. Parameters which are not mentioned separately are the same as in figure 2.
Download figure:
Standard image High-resolution imageThe steerability properties are very similar to the ones of logarithmic negativity—optical losses break the monotonicity whereas the mechanical bath is responsible for limiting the maximal value of steerability. The optimization of this quantity with respect to χ1,2,3 partially compensates these two decoherence effects (see figure 3(b)). There is, however, a threshold value of optomechanical coupling necessary to achieve steering. For 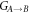 , in absence of the decoherence processes, it is defined by the value of n0. The joint impact of optical losses and mechanical bath makes this threshold higher. In contrast,
, in absence of the decoherence processes, it is defined by the value of n0. The joint impact of optical losses and mechanical bath makes this threshold higher. In contrast,  does not demonstrate such a threshold in the ideal case, and only the presence of decoherence processes causes this limitation.
does not demonstrate such a threshold in the ideal case, and only the presence of decoherence processes causes this limitation.
7. Full quantum transducer
In this section we finally consider the complete scheme of four sequential QND interactions (figure 1(a)). As above, we study different signatures of quantum correlations. In the idealized symmetric adiabatic case without decoherence the transformation of quadratures takes the following form:
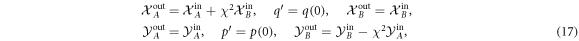
describing the QND interaction between the modes A and B with the Hamiltonian:

As can be seen from (17) the mechanical mediator is finally traced out from the optical modes. This is a manifestation of the geometric phase effect.
We start by estimating the amount of conditional squeezing. System A is not involved in the fourth interaction, therefore measuring A yields the same conditional variance 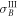 as after only three interactions, as analysed in section 6. System B does not contain any influence of the mechanical momentum and in the ideal case, the conditional variance
as after only three interactions, as analysed in section 6. System B does not contain any influence of the mechanical momentum and in the ideal case, the conditional variance 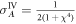 is a function of only the QND coupling strength. The optical losses modify the trajectory of the mechanical system in phase-space and make it non-closed. As a consequence,
is a function of only the QND coupling strength. The optical losses modify the trajectory of the mechanical system in phase-space and make it non-closed. As a consequence, 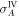 becomes dependent on n0 and for small losses, it takes the following form:
becomes dependent on n0 and for small losses, it takes the following form:
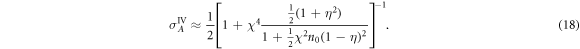
Optimization with respect to individual QND couplings χi allows to bring this phase-space trajectory as close to the ideal one (figure 1(c)) as possible. The optimized value of σA becomes equal to 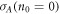 . The mechanical bath defines the maximal achievable value of conditional squeezing and its influence cannot be compensated in this case. The corresponding conditional variance for high mechanical quality factor Q approximately reads:
. The mechanical bath defines the maximal achievable value of conditional squeezing and its influence cannot be compensated in this case. The corresponding conditional variance for high mechanical quality factor Q approximately reads:
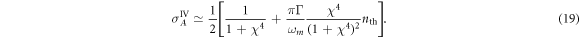
It is clear that the influence of n0 is the major encumbrance for good protocol performance. In the absence of optical losses in the system, n0 is automatically traced out from the equations by proper combination of QND gains. Once losses are introduced, they break this balance. This can be compensated by the optimization of unequal QND gains, which is presented in the figure 2(c).
Analogous to the case of three QND interactions, conditional squeezing coincide with the generalized one for large enough values of χ. For experimentally attainable values χ < 1 the amount of conditional squeezing is lower than maximally possible one (see figure 2(c)).
We now study the entanglement and steerability. In the ideal case the logarithmic negativity and steerability are defined only by the value of the QND coupling χ. Optical losses modify them in a way that they become dependent on n0. In the region of weak QND couplings and for small optical losses the eigenvalues defining the quantities (10), (11) can be approximately expressed by:
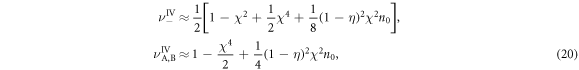
demonstrating that the optical losses are responsible for the appearance of the summand proportional to n0. The influence of the mechanical bath is expressed by the additional term independent from n0 and defining the maximal achievable entanglement and steerability. In the region of weak QND couplings and for high mechanical quality factor the eigenvalues are expressed as:

It follows from the analysis above that n0 is the main obstacle for the entanglement and steerability generation. The influence of optical losses and mechanical bath may be partially compensated by the optimization of individual unequal QND gains χ1,2,3,4. For the case of a cold mechanical bath and weak QND gains, the optimized values of logarithmic negativity and steerability tend to 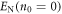 and
and 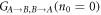 correspondingly. It is worthwhile to note that decoherence effects are responsible for the appearance of a threshold value of the QND coupling χ required to reach non-zero steerability. The numerical estimations for the full dynamics are presented in the figure 4.
correspondingly. It is worthwhile to note that decoherence effects are responsible for the appearance of a threshold value of the QND coupling χ required to reach non-zero steerability. The numerical estimations for the full dynamics are presented in the figure 4.
Figure 4. Entanglement and steerability after four interactions. (a): Logarithmic negativity as a function of QND coupling χ for different values of the mechanical bath occupation number  . Inset: logarithmic negativity as a function of the initial occupation of the mechanical mode for different values of mechanical bath occupation number
. Inset: logarithmic negativity as a function of the initial occupation of the mechanical mode for different values of mechanical bath occupation number 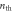 and χ = 1. (b) Steerability
and χ = 1. (b) Steerability 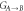 and
and 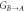 as a function of the initial occupation for χ = 1. Inset: steerability as a function of QND interaction strength for n0 = 10. Red dashed line shows the ideal case without any decoherence included, while the solid lines show the full dynamics. Lines with markers represent the case of optimized parameters. Mean photon number is varied in the region 0 ≤ N ≤ 1015. Other parameters are the same as in the figure 2.
as a function of the initial occupation for χ = 1. Inset: steerability as a function of QND interaction strength for n0 = 10. Red dashed line shows the ideal case without any decoherence included, while the solid lines show the full dynamics. Lines with markers represent the case of optimized parameters. Mean photon number is varied in the region 0 ≤ N ≤ 1015. Other parameters are the same as in the figure 2.
Download figure:
Standard image High-resolution image8. Transducer without a cavity
The so-called bad cavity regime (κ ≫ ωm) is advantageous for our transducer, because a cavity with higher decay rate does not distort the shape of pulses significantly, which allows us to consider the system in the adiabatic regime. Therefore a natural next step is to consider the transducer without the optical cavity, where the mechanical mode is coupled directly to the propagating light fields. The transducer without the cavity does not face the problem of mode matching between the propagating light and cavity so it does not need delicate cavity operation which is beneficial for the experiment. In this section we estimate the achievable amounts of entanglement and quantum steering for such a transducer.
The optomechanical system without a cavity may be presented by figure 1(b) without the mirror in a dashed box. We still consider four sequential QND interactions with the mechanical mediator as depicted in the figure 1(a). The transformations of the quadratures in the ideal case without any decoherence effects included take the same form as (17) with replacement  [37] where
[37] where  is the amplitude of zero-point fluctuations with m being the mass of the mechanical oscillator and λ—the optical wavelength.
is the amplitude of zero-point fluctuations with m being the mass of the mechanical oscillator and λ—the optical wavelength.
The dynamics of the system without the cavity is completely equivalent to the one with the cavity, and the numerical estimation results replicate of figure 4 after the replacement 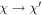 . Parameters used are the same with addition λ = 1064 nm, m = 10−12 kg and 0 ≤ N ≤ 1016. The system without the cavity does not have the advantage of resonant enhancement of the circulating power. Therefore, to achieve the same performance as in the system with the cavity, one has to supply the input power approximately
. Parameters used are the same with addition λ = 1064 nm, m = 10−12 kg and 0 ≤ N ≤ 1016. The system without the cavity does not have the advantage of resonant enhancement of the circulating power. Therefore, to achieve the same performance as in the system with the cavity, one has to supply the input power approximately 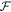 times higher, where
times higher, where 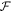 is the finesse of the cavity.
is the finesse of the cavity.
9. Conclusion
In this paper we explored the pulsed optomechanical transducer operating beyond the sideband resolved regime. This transducer allows to interconnect two optical modes A and B via a sequence of interactions with the same noisy mechanical mediator, which can be an element of an optomechanical cavity or just be coupled to freely propagating pulses. An advantage of the proposed scheme is that it is suitable for, in principle, arbitrary wavelengths of radiation, therefore it is capable of creating quantum correlations of pulses at different frequencies that would not interact otherwise.
We studied non-classical correlations after any number of sequential QND interactions in the adiabatic regime. We have shown that two QND interactions are enough to create conditional squeezing at least in one direction. Three sequential interactions allow conditional squeezing in both directions, entanglement between optical modes and quantum steering in both directions, provided that the mechanical mode is cooled close to its ground state. Finally, the full transducer with four sequential QND interactions is capable of producing sufficient values of conditional squeezing of both optical modes, entanglement and steerability in both directions at almost an arbitrary initial occupation of the mechanical mode.
The three negative effects that can degrade the performance of the transducer are the initial thermal occupation of the mechanical mode, its thermal environment and the losses in the modes of radiation. We have shown that the initial occupation is the most significant impediment to quantum correlations, until it is traced out from the optical modes by a proper combination of QND gains. The presence of optical losses breaks this balance and makes quantum correlations sensitive to the initial occupation again, whereas the interaction with the mechanical bath defines the maximally achievable amount of quantum correlations. Remarkably, the optimization of unequal gains of individual QND interactions allows to substantially compensate these two unwanted effects.
Thus, we have shown that the geometric phase effect allows for realizing an optomechanical transducer in the stroboscopic regime outside the sideband resolved limit for the systems with low-Q cavity, potentially without cavity. We have also demonstrated that it is feasible in the context of state-of-the-art optomechanical experiments. This investigation may stimulate further researches in the area of quantum transducers based on mechanical mediators.
Acknowledgments
NV, AAR and RF acknowledge the support of the project GB14-36681G of the Czech Science Foundation. AAR and RF have received national funding from the MEYS under grant agreement No. 731473 and from the QUANTERA ERA-NET cofund in quantum technologies implemented within the European Union's Horizon 2020 Programme (project TheBlinQC). AAR acknowledges support by the Development Project of Faculty of Science, Palacky University and COST Action CA15220 'QTSpace'. UBH and ULA acknowledge support from the Danish National Research Foundation (bigQ DNRF142) and the Villum foundation (grant no. 13300).








