Abstract
We theoretically investigate the optical response of many cold atoms within a pair of identical planar lattices mostly in a dense regime using microscopic electrodynamics numerical simulations. We find cooperative optical properties of the double atomic lattices to a normal incidence of low-intensity radiation at particular ranges of sample parameters. The main findings are that resonance shifts, linewidths, and transmittance could be engineered by varying layer-to-layer distance, lattice constant, and parameters for incident light. We also propose a bilayer atomic lattice could be modeled as two effective superatoms. Simulation results qualitatively agree with the ones from an isotropic infinite lattice model in the ranges of external parameters for which a mean-field approximation is not valid. Hopefully, our bilayer lattice samples might be exploited for implementing an optical switch and a photonic device in quantum computing.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Owing to advances in trapping techniques [1] for laser or evaporatively cooled atoms, a sample of effectively stationary atoms is experimentally manipulated and engineered to explore light–matter interaction at the most fundamental level. Moreover, there is a growing interest in light propagation through a nanometer-size sample of homogeneously broadened (i.e. low-temperature) atoms with a sufficiently high number density due to potential applications in the areas of efficient light transport [2], quantum information processing [3], metamaterials [4], integrated optical devices [5], and nano-optics [6]. Recently realized experiments [7–11] for cold dense atoms motivate theoretical investigations [12–24] of light propagation at the microscopic level. Even if responses of a single two-level atom to the incident radiation have been fairly well known, optical behaviors of an aggregation of two-level atoms are far more elusive. In particular, for a homogeneously broadened sample in close proximity, atoms move distances on the order of the resonant wavelength over the time for internal state to relax to steady-state. The total field on each atom is then expressed by the field scattered from the other atoms as well as the incident field. Consequently, sample atoms are strongly correlated and their behaviors can be explained by solving highly coupled dynamics that is self-consistently described.
Prior studies developed theoretical formalisms for a two-dimensional (2D) cold atom lattice driven by external radiation [16]. In this study, we extend the formalism to a pair of coupled 2D lattices in the high density regime. Light pressure and effects of photon recoils of the steady-state atoms are all neglected. Furthermore, low light intensity is considered so that the atomic lattices driven by the external light are well approximated as dipoles with fixed positions and described by the coupled-dipole equations [12–17, 22]. We obtain local fields seen by dipoles at their positions by solving the coupled-dipole equations. For a two-atom sample we present analytical solutions for transmittance and optical thickness. Exact solutions for many-atom lattices are obtained numerically for cooperative resonance shifts, linewidths, and optical spectra. Our main finding is that cooperative optical responses of bilayer samples such as splitting of the absorption lines, which are observed at a high atomic density of the monolayer plane [16] or a small plane-to-plane distance, cannot be explained by the standard optics theory based on an electrodynamics of a polarizable medium (EDPM) [25]. In fact, the EDPM is the effective-medium mean-field theory (MFT) which approximates the local fields of atoms to be the same everywhere, so it cannot properly describe the physics of a sample with a nanometric size. Therefore, we need to resort to large-scale simulations as a way to understand the optical behaviors of cold dense many-atom samples.
In the regime of high atomic density and small interlayer separation, we validate our theoretical approaches and numerical simulations by comparing line shifts with analytical results for a two-atom sample and for an isotropic and infinite lattice model. In the low atomic density regime, standard optics theory confirms the validity of simulation results. It is predicted that under certain conditions, the transmittance of cold dense atoms in a regular array can be reduced to near-zero. This suggests that a bilayer lattice formed by cold dense atoms can realize on- and off-states and therefore is a candidate system for a photonic device in quantum computing [13, 17]. Finally, we discuss that each monolayer of a bilayer lattice could be modeled as an effective superatom acting as a mirror [26] with amplitude reflection and transmission coefficients [27] which makes it convenient for applying a Fabry–Pérot interferometer.
2. Microscopic electrodynamics simulation
Our approach is based on earlier quantum-field theory [28] of light propagation through dipolar medium where field operators describe ground-state and excited-state atoms coupled to the quantized electromagnetic field via the dipole interaction. In the limit of low light intensity for a particular atomic transition from the ground-level angular momentum Jg = 0 to the excited-level one Je = 1, the resulting approximate evolution for the polarization P at a position r1 reads
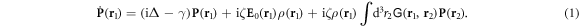
Here Δ = ω − ω0 is the detuning of the incident light with angular frequency ω with respect to the atomic transition frequency ω0, γ is the HWHM linewidth of the optical transition, E0 the electric field in the absence of matter, and ρ the atomic density. 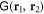 represents the monochromatic dipole field propagator [16] such that
represents the monochromatic dipole field propagator [16] such that 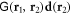 expresses the electric field at r1 due to an oscillating dipole moment d at r2. We also define
expresses the electric field at r1 due to an oscillating dipole moment d at r2. We also define  in which the reduced dipole matrix element
in which the reduced dipole matrix element 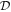 is related to the transition linewidth γ and the wavenumber k0 = 2π/λ0 = ω0/c of resonant light with wavelength λ0 by
is related to the transition linewidth γ and the wavenumber k0 = 2π/λ0 = ω0/c of resonant light with wavelength λ0 by
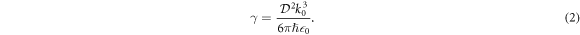
With the solution of equation (1) given, the expectation value of the electric field is expressed as
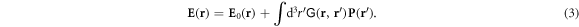
In the present theoretical scheme we do not include the motion of the atoms, light pressure, and effects of photon recoil. Equation (1) is obtained under assumption that there are no correlations between the positions and dipole moments of the atoms so that it is a mean-field equation for atomic density and polarization. In such a mean-field approximation polarization is treated as a continuous field. As a result, the information about the precise atomic positions and light-mediated correlations are all lost.
A prescription from a microscopic electrodynamics now enters into the theoretical scheme in order to fix its mean-field nature: we assign the positions of all two-level atoms in a pair of identical and parallel 2D square lattices with N sites each filled with one point-like cold atom. Positions of the atoms  within the sample are generated deterministically such that light-mediated correlations are not initially built in the sample. Therefore, our simulation with fixed atomic positions differs from stochastic coupled-dipole numerical simulations [14, 15, 18, 22, 29] with random atomic positions. We assume that atoms in the lattice sites are in a steady-state and do not tunnel into the other sites, leading to the dipole moments of the atoms
within the sample are generated deterministically such that light-mediated correlations are not initially built in the sample. Therefore, our simulation with fixed atomic positions differs from stochastic coupled-dipole numerical simulations [14, 15, 18, 22, 29] with random atomic positions. We assume that atoms in the lattice sites are in a steady-state and do not tunnel into the other sites, leading to the dipole moments of the atoms
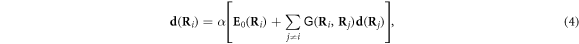
where
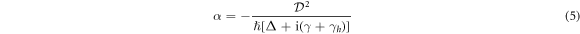
is the polarizability of a two-level atom valid at low light intensity. Here γh denotes the HWHM linewidth of homogeneous broadening. Formalism extended to multistate atomic transitions is presented in [11]. The total electric field driving the dipole at the position Ri then reads
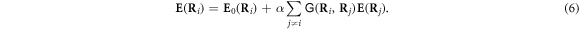
Crux of the simulations is to solve numerically such closed inhomogeneous sets of linear equations. The total electric field is then given by
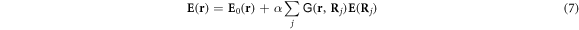
at any field point r except the positions of the atoms, where the dipolar kernel 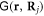 diverges. Our numerical simulations use the units below
diverges. Our numerical simulations use the units below
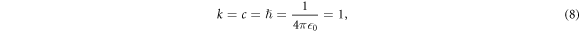
where k = 2π/λ = ω/c is the wavenumber of the incident light with wavelength λ. The unit of length is k−1 and the units of quantities related with length are determined accordingly. Unless explicitly mentioned otherwise, all quantities are obtained in these units. We also express the detuning Δ and the linewidth of homogeneous broadening γh in the unit of linewidth γ
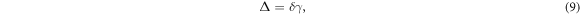
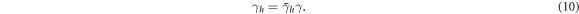
Following our conventions, dipole matrix element and the polarizability are given below:
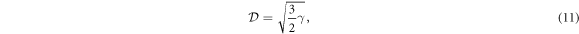
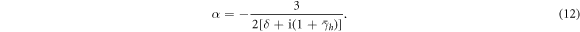
At any field point the magnetic field is
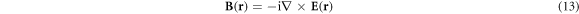
and Poynting vector is
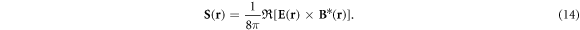
Let us briefly describe setup and quantities to be evaluated in the numerical experiments. The sample embedded into a free space is illuminated by a plane monochromatic light linearly polarized along the y direction and propagating in the z direction at normal incidence. Each of 2D square lattices has an interatomic separation a and lies on the xy plane with their centers at z = −h/2 and z = h/2 such that monolayer lattice is described by the area-number density σ = a−2 and the total number of atoms within the bilayer sample is 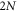 . Our sample system with N = 25 is illustrated in figure 1. The primary quantity to be calculated numerically is the optical depth (thickness or density) of the
. Our sample system with N = 25 is illustrated in figure 1. The primary quantity to be calculated numerically is the optical depth (thickness or density) of the 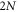 -atom samples at a far-field point
-atom samples at a far-field point 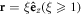 expressed by
expressed by
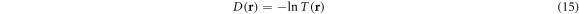
for the transmittance
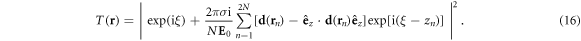
Detailed derivations have been given in our previous works [16, 22] and in the other group's study [30] for different purposes. Equation (16) is obtained in the limit of large lateral size of the 2D planar lattice so that simulation result would be accurate for a sample with a large enough value of 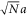 compared with a. Calculation of dipole moments in equation (16) involves a task of finding local fields experienced by atoms at all lattice sites as a backaction to the incident radiation. We then should deal with the dipole propagator which is not absolutely convergent either at small or large interatomic spacing a. Increasing a from zero, we encounter such a divergence for the first time at a = 2π (λ in SI units) due to Bragg scattering [31]. When nontrivial Bragg scattering is possible for
compared with a. Calculation of dipole moments in equation (16) involves a task of finding local fields experienced by atoms at all lattice sites as a backaction to the incident radiation. We then should deal with the dipole propagator which is not absolutely convergent either at small or large interatomic spacing a. Increasing a from zero, we encounter such a divergence for the first time at a = 2π (λ in SI units) due to Bragg scattering [31]. When nontrivial Bragg scattering is possible for 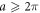 , Bragg scattered waves transport energy to a direction other than the direction of the incident light, leading to energy loss manifesting as R(r) + T(r) < 1 for the reflectance R(r). In order to use a relation R(r) + T(r) = 1 such that there is no energy loss due to Bragg scattered waves, we restrict lattice constants in the range of a < 2π in the present numerical simulations.
, Bragg scattered waves transport energy to a direction other than the direction of the incident light, leading to energy loss manifesting as R(r) + T(r) < 1 for the reflectance R(r). In order to use a relation R(r) + T(r) = 1 such that there is no energy loss due to Bragg scattered waves, we restrict lattice constants in the range of a < 2π in the present numerical simulations.
Figure 1. The geometry of a sample for our numerical experiment is illustrated: bilayer square lattices of cold dense atoms are perpendicularly illuminated by a linearly polorized plane wave light beam. Lattice constant is denoted by a, and two identical 2D planar lattices are separated by a distance h along the light propagation direction z. Electric field of the light beam is illustrated by a blue curved line with a y-axis directed polarization.
Download figure:
Standard image High-resolution image3. Two-atom samples
We illustrate the fundamental concepts of light propagation through a two-atom sample by solving equation (6) analytically. For simplicity we do not include the linewidth of homogeneous broadening γh. We consider the simplest model in which two atoms positioned at 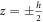 are illuminated by a plane wave linearly polarized in the y direction and propagating along the z direction. For the incident light and the positions of the two dipoles
are illuminated by a plane wave linearly polarized in the y direction and propagating along the z direction. For the incident light and the positions of the two dipoles
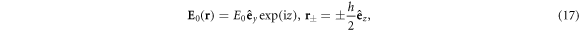
the radiation fields at the positions of two dipoles as solved from equation (6) are
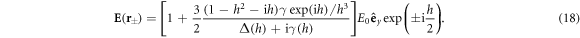
Here
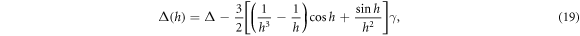
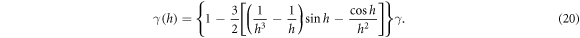
Equations (19) and (20) manifest themselves as cooperative resonance shift and broadened linewidth of the atoms, respectively, which can be explained as a result of altered vacuum field at the position of one dipole in the vicinity of the other coherently radiating dipole. The modification of vacuum field arises from the light-mediated dipole–dipole interactions owing to repeated exchange of photons between the two atoms, so-called recurrent scattering. Moreover, the h dependence of cooperative resonance shift Δ(h) and linewidth γ(h) evidently reveals the propagation of light from one atom to the other and its effect on cooperative response of atoms. In the limit of  we obtain the shift of the resonance and the linewidth
we obtain the shift of the resonance and the linewidth
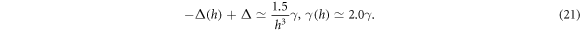
The shift of the resonance line depends on h−3, which clearly indicates the near-field dipole–dipole interactions between the atoms. On the other hand, the cooperative linewidth is independent of h and doubles in the small interatomic separation limit. Refer to [22] for analytical calculations of Δ(a) and γ(a) in case when two atoms are separated by a distance a along the direction of the linear light polarization. This suggests that collective resonance shifts and linewidths can be controlled in an aggregation of many cold atoms in different geometries for designing an artificial optical transition [32]. Recent experiment [33] reports cooperative radiation of two neutral atoms strongly coupled to the single-mode field of an optical cavity. Experiment on two trapped ions has also been reported [34]. The expression of dimensionless detuning for which Δ(h) = 0 is satisfied reads

At these detunings the radiation field is on the resonance. We use equation (22) as a way to predict detunings for cooperative resonances in numerical simulation of optical spectra.
We also obtain the transmittance and optical depth for the two-atom sample by considering light-induced dipole correlations as follows:

and
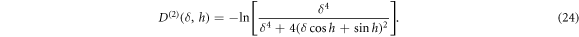
We have provided details for the calculation of equations (23) and (24) as described by equations (A.9) and (A.10) in appendix A. When the two-atom transmittance from equation (23) is plotted as a function of a dimensionless detuning δ, narrow Fano resonances are observed with a shift corresponding to
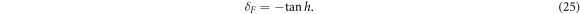
The spectral lines are broadened as h increases in the range of ![$[m\pi ,\left(m+\tfrac{1}{2}\right)\pi ]$](https://content.cld.iop.org/journals/1367-2630/20/8/083012/revision2/njpaad614ieqn14.gif) and as h decreases in the range of
and as h decreases in the range of ![$(\left(m+\tfrac{1}{2}\right)\pi ,(m+1)\pi ]$](https://content.cld.iop.org/journals/1367-2630/20/8/083012/revision2/njpaad614ieqn15.gif) for m = 0, 1, 2, .... In two different two-atom samples with atomic separations h1 and h2 under condition of h1 + h2 = m π (m = 1, 2, 3, ...), Fano resonances occur at detunings δ = ±δF due to a π-periodicity of tangent function. For an example, figure 2 demonstrates the transmittance and optical depth of two-atom samples with h1 = 0.15π (dashed and solid lines) and h2 = 0.85π (dotted and dotted–dashed lines), where Fano resonance lineshapes are symmetric around zero detuning. We see that such a behavior is clue for red- and blue-detuned shifts in the spectral response of 3D dense atomic layers to be numerically simulated. Fano resonances in the transmittance correspond to narrow dips in the optical depth at δF. It is evident that lineshapes of optical spectra can be tailored by varying the interatomic distance. In particular, narrow Fano resonances [35] emerge at specific atomic separations. If h is an integer multiple of π/2 (λ/4 in SI units), the Fano resonances vanish. For an atomic separation a bit smaller or larger than integer multiples of π/2, Fano resonances become sharpest, and transmittances reach almost zero. The similar spectral features for light propagation have been demonstrated for atoms confined in a one-dimensional waveguide [23]. Main feature of a cooperative two-atom response is the modification of optical responses by adjusting the atomic separation; such a feature will be exploited for a collection of cold dense atoms whose optical properties are to be investigated by numerical simulations. For different aspects of cooperativity and ways to control it, refer to [36]. In contrast to the correlated-atom cases, the independent-atom transmittance in the MFT without dipole correlations reads
for m = 0, 1, 2, .... In two different two-atom samples with atomic separations h1 and h2 under condition of h1 + h2 = m π (m = 1, 2, 3, ...), Fano resonances occur at detunings δ = ±δF due to a π-periodicity of tangent function. For an example, figure 2 demonstrates the transmittance and optical depth of two-atom samples with h1 = 0.15π (dashed and solid lines) and h2 = 0.85π (dotted and dotted–dashed lines), where Fano resonance lineshapes are symmetric around zero detuning. We see that such a behavior is clue for red- and blue-detuned shifts in the spectral response of 3D dense atomic layers to be numerically simulated. Fano resonances in the transmittance correspond to narrow dips in the optical depth at δF. It is evident that lineshapes of optical spectra can be tailored by varying the interatomic distance. In particular, narrow Fano resonances [35] emerge at specific atomic separations. If h is an integer multiple of π/2 (λ/4 in SI units), the Fano resonances vanish. For an atomic separation a bit smaller or larger than integer multiples of π/2, Fano resonances become sharpest, and transmittances reach almost zero. The similar spectral features for light propagation have been demonstrated for atoms confined in a one-dimensional waveguide [23]. Main feature of a cooperative two-atom response is the modification of optical responses by adjusting the atomic separation; such a feature will be exploited for a collection of cold dense atoms whose optical properties are to be investigated by numerical simulations. For different aspects of cooperativity and ways to control it, refer to [36]. In contrast to the correlated-atom cases, the independent-atom transmittance in the MFT without dipole correlations reads
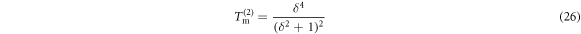
as derived by equation (A.15) in appendix A. Because the repeated photon exchanges between the two atoms are all ignored, the independent-atom transmittance 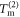 cannot be modified by varying the interatomic separation. The MFT applies to a many-atom sample of randomly distributed positions at low atomic densities [18].
cannot be modified by varying the interatomic separation. The MFT applies to a many-atom sample of randomly distributed positions at low atomic densities [18].
Figure 2. Optical depth D(2) (solid and dotted–dashed lines) and transmittance T(2) (dashed and dotted lines) of a two-atom sample versus light-emitter detuning δ from analytical calculation for two atomic separations h1 = 0.15 π (solid and dashed lines) and h2 = 0.85 π (dotted–dashed and dotted lines). In two bilayer lattice samples whose atomic separations satisfy h1 + h2 = m π (m = 1, 2, 3, ...), Fano resonances occur at δ = ±δF. Narrow spectral lines created by a Fano resonance in the transmittance correspond to dips in the optical thickness at δF.
Download figure:
Standard image High-resolution image4. Simulation results
We primarily explore conditions under which an aggregation of homogeneously broadened atoms on a bilayer atomic lattice will cooperatively respond to a driving radiation field using numerical simulation. We focus on a simple transition 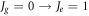 in the limit of low light intensity such that the classical simulations provide an exact solution for the atomic lattices coupled to the incident radiation.
in the limit of low light intensity such that the classical simulations provide an exact solution for the atomic lattices coupled to the incident radiation.
The dependence of optical depth D on number density σ of a monolayer lattice within the 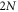 -atom bilayer samples is represented by a set of graphs of D as a function of light-emitter detuning δ, as illustrated in figure 3. Samples under our investigation have a fixed layer-to-layer distance h = 0.32 and different total numbers of dipoles
-atom bilayer samples is represented by a set of graphs of D as a function of light-emitter detuning δ, as illustrated in figure 3. Samples under our investigation have a fixed layer-to-layer distance h = 0.32 and different total numbers of dipoles  162 (thin), 578 (dashed), 1058 (red), and 1458 (dotted–dashed). The interatomic separations are set to
162 (thin), 578 (dashed), 1058 (red), and 1458 (dotted–dashed). The interatomic separations are set to 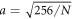 such that the monolayer area A = N a2 remains constant as
such that the monolayer area A = N a2 remains constant as 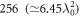 at the HWHM linewidth of homogeneous broadening γh = 5.00. The criterion
at the HWHM linewidth of homogeneous broadening γh = 5.00. The criterion  (
(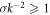 in SI units), which defines the 'dense sample' is satisfied for the cases with
in SI units), which defines the 'dense sample' is satisfied for the cases with 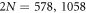 , and 1458 where respective densities are σ = 1.13, 2.07, and 2.85, while the
, and 1458 where respective densities are σ = 1.13, 2.07, and 2.85, while the 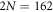 sample with σ = 0.32 is not. It is evident that three-dimensional (3D) lattice geometry formed by two planar lattices gives rise to optical responses of emitters that are quite different from those for 2D lattices [16, 17], and significantly modifies absorption line shapes at special sample parameters. First, we find that cooperative resonance shifts of the bilayer atomic lattices are exhibited both at positive and negative detunings as already demonstrated in figure 2 for the two-atom cases. On the other hand, resonance lines from monolayer square lattices [16] were shifted only to negative detunings, which is plotted as a gray line in figure 3 for a N = 1024 monolayer lattice of a = 0.71. Secondly, cooperative resonance shifts of the bilayer lattices, which for monolayer lattices are proportional to the atomic density σ, are reduced as σ increases; the bilayer lattice of
sample with σ = 0.32 is not. It is evident that three-dimensional (3D) lattice geometry formed by two planar lattices gives rise to optical responses of emitters that are quite different from those for 2D lattices [16, 17], and significantly modifies absorption line shapes at special sample parameters. First, we find that cooperative resonance shifts of the bilayer atomic lattices are exhibited both at positive and negative detunings as already demonstrated in figure 2 for the two-atom cases. On the other hand, resonance lines from monolayer square lattices [16] were shifted only to negative detunings, which is plotted as a gray line in figure 3 for a N = 1024 monolayer lattice of a = 0.71. Secondly, cooperative resonance shifts of the bilayer lattices, which for monolayer lattices are proportional to the atomic density σ, are reduced as σ increases; the bilayer lattice of  atoms exhibits least resonance shift as shown in figure 3. Such an aspect is seemingly against the fact that the size of shift is proportional to the area density: this may be interpreted as an outcome of a cooperative optical response. Therefore, a 3D lattice structure might be used for the elimination of resonance shifts, which is crucial in order to improve spectroscopic accuracy in 3D optical lattice clocks [37]. Moreover, enhanced optical response of the bilayer samples is distinctly shown in comparison of the 1024-atom monolayer plot with the 1058-atom bilayer one; a pair of identical N-atom planar lattices with the same number density σ exhibits greater maximum values and linewidths of optical spectrum than for a monolayer lattice of
atoms exhibits least resonance shift as shown in figure 3. Such an aspect is seemingly against the fact that the size of shift is proportional to the area density: this may be interpreted as an outcome of a cooperative optical response. Therefore, a 3D lattice structure might be used for the elimination of resonance shifts, which is crucial in order to improve spectroscopic accuracy in 3D optical lattice clocks [37]. Moreover, enhanced optical response of the bilayer samples is distinctly shown in comparison of the 1024-atom monolayer plot with the 1058-atom bilayer one; a pair of identical N-atom planar lattices with the same number density σ exhibits greater maximum values and linewidths of optical spectrum than for a monolayer lattice of 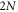 atoms with the same σ. We emphasize such enhanced responses of the bilayer samples furthermore by presenting analytical expression of the optical depth for a planar lattice of independent 1024 atoms:
atoms with the same σ. We emphasize such enhanced responses of the bilayer samples furthermore by presenting analytical expression of the optical depth for a planar lattice of independent 1024 atoms:
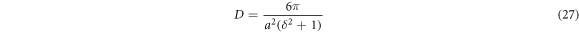
plotted as a dotted line in figure 3. Equation (27) is obtained from independent-dipole scattering theory [7] that does not include dipole–dipole interactions of the planar lattice. In homogeneously broadened samples in figure 3, correlations between the dipoles are important and for these samples interactions between dipoles are cooperative. Such correlations originate from a recurrent scattering of photons between atoms, because each of sample atoms has the same resonance frequency.
Figure 3. Optical depth D of bilayer samples versus light-emitter detuning δ from numerical simulations for a fixed separation h = 0.32 between two identical planar square lattices. The total numbers of dipoles on the samples are 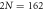 (thin), 578 (dashed), 1058 (red), and 1458 (dotted–dashed) with the fixed monolayer area of A = 256. Separation between two resonance lines is reduced as total atom number (area density) of lattice increases. For a monolayer square lattice with N = 1024 dipoles and lattice constant a = 0.71, gray line exhibits a numerical simulation and dotted line a collective independent-dipole scattering theory.
(thin), 578 (dashed), 1058 (red), and 1458 (dotted–dashed) with the fixed monolayer area of A = 256. Separation between two resonance lines is reduced as total atom number (area density) of lattice increases. For a monolayer square lattice with N = 1024 dipoles and lattice constant a = 0.71, gray line exhibits a numerical simulation and dotted line a collective independent-dipole scattering theory.
Download figure:
Standard image High-resolution imageWe also find two resonances of the absorption line in figure 3. As the total number of atoms is increased so that the number density of monolayer lattice is increased, resonant optical thicknesses of the samples are strengthened with their increased linewidths, and two peaks are placed closer: the separations between two resonance lines are 92.4, 86.8, 77.6, and 70.0 in our unit of frequency for the samples of 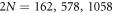 , and 1458, respectively. Number and density dependence of linewidths manifest itself and they are proportional to a degree of cooperative optical responses of the atoms, which arises from all the repeated photon exchanges between the sample atoms. Cooperative linewidths are modified by varying the total number of atoms and lattice constant such that a collective superadiant or subradiant [38–40] emission can be engineered in a pair of planar atomic lattices in the optical frequency domain.
, and 1458, respectively. Number and density dependence of linewidths manifest itself and they are proportional to a degree of cooperative optical responses of the atoms, which arises from all the repeated photon exchanges between the sample atoms. Cooperative linewidths are modified by varying the total number of atoms and lattice constant such that a collective superadiant or subradiant [38–40] emission can be engineered in a pair of planar atomic lattices in the optical frequency domain.
We understand that two resonances are reminiscent of Fano resonances of optical depth illustrated in figure 2 as dips for a two-atom sample. Such resonance shifts on the absorption line manifest themselves as a cooperative feature [15] that cannot be predicted by equation (B.1) in appendix B from an EDPM. They are attributed to collective resonance shifts Δ± associated with two collective linewidths Γ±, which originate from imaginary part of the sum over left- and right-propagating fields along the ±z directions from one lattice plane to the other and vacuum field. Therefore, in the far-field sample dipoles radiatively decay into three modes: left- and right-propagating modes and vacuum mode. Markedly different broadenings of the optical spectra at maximum and second peaks reveal imbalance between Γ+ and Γ− at given densities and interlayer separations where the ratio Γ+/Γ− ≈ 50. As illustrated in figure 2 for a two-atom case, Γ+/Γ− varies at different layer-to-layer distance h. Evidently, both resonance shifts and radiative decay rates of many-atom sample can be tailored by adjusting spatial arrangement of atoms. An analogous phenomenon, which exhibits two resonances in the absorption spectrum as sample atomic density varies, has been displayed in the monolayer kagome lattices in the previous work [16]. Presumably, two collective modes corresponding to left- and right-propagating modes for the bilayer lattices arise from two emitters of different dipole moments as for the case with each primitive unit cell of kagome lattice. We surmise that bilayer atomic lattices are two effective superatoms separated by h along the propagation direction of incident radiation. Similar superatom model [41] for a planar lattice of atoms is used to understand light propagation through stacks of planar lattices. Numerical resonance shifts are in good agreement with analytical results from an infinite and isotropic lattice model which has been introduced for calculating resonance shift of monolayer lattices [16]. We will present detailed and quantitative analysis regarding superatom analogy with bilayer atomic lattice.
We discuss dependence of resonance shifts and line shapes on interatomic and interlayer separations. The absorption line shape is altered significantly by varying h alone and keeping a and 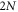 fixed as shown in figure 4, where h = 0.25 (gray line), 1.00 (dotted), and 2.00 (blue) are used for bilayer square lattices with a = 1.00 and
fixed as shown in figure 4, where h = 0.25 (gray line), 1.00 (dotted), and 2.00 (blue) are used for bilayer square lattices with a = 1.00 and  atoms. Such a feature is also a cooperative effect that has no parallels in EDPM, because according to equation (B.1) in appendix B, it is absolutely impossible to modify a shift of the resonance line by varying interlayer distance alone. Relatively large lattice constants within h = 1.00 and h = 2.00 samples allow the dipoles on the front layer to interact weakly with those on the back, leading to the absence of second peak and narrower line shapes. In particular, relative phases of the periodically ordered dipoles within a pair of square lattices give rise to large Bragg reflection such that above 99% reflectances are exhibited for h = 1.00 and h = 2.00 samples at nearly δ ≈ 0. At particular lattice constants satisfying conditions for zero transmittance, radiation incident to the samples at exact atomic resonance frequency is completely reflected. Such a resonant suppression of the transmission is the main feature of the Fano resonance [35], and similar characteristic 2D features were obtained for 2D arrays of resonant ultracold atoms loaded into optical lattices [21] and of artificial atoms in the solid-state context [13]. Further numerical simulations reveal that the absorption line is not split into two in a regime of interlayer separation
atoms. Such a feature is also a cooperative effect that has no parallels in EDPM, because according to equation (B.1) in appendix B, it is absolutely impossible to modify a shift of the resonance line by varying interlayer distance alone. Relatively large lattice constants within h = 1.00 and h = 2.00 samples allow the dipoles on the front layer to interact weakly with those on the back, leading to the absence of second peak and narrower line shapes. In particular, relative phases of the periodically ordered dipoles within a pair of square lattices give rise to large Bragg reflection such that above 99% reflectances are exhibited for h = 1.00 and h = 2.00 samples at nearly δ ≈ 0. At particular lattice constants satisfying conditions for zero transmittance, radiation incident to the samples at exact atomic resonance frequency is completely reflected. Such a resonant suppression of the transmission is the main feature of the Fano resonance [35], and similar characteristic 2D features were obtained for 2D arrays of resonant ultracold atoms loaded into optical lattices [21] and of artificial atoms in the solid-state context [13]. Further numerical simulations reveal that the absorption line is not split into two in a regime of interlayer separation 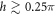 for samples used in figures 3 and 4. This is reasonable, because dipoles are more weakly correlated in this regime than in the opposite regime for h. Therefore, to a good approximation, optical responses of the bilayer atomic lattices with
for samples used in figures 3 and 4. This is reasonable, because dipoles are more weakly correlated in this regime than in the opposite regime for h. Therefore, to a good approximation, optical responses of the bilayer atomic lattices with 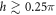 used in figures 3 and 4 can be explained by standard optics.
used in figures 3 and 4 can be explained by standard optics.
Figure 4. Optical depth D of 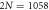 bilayer lattices with atomic separation a = 1.00 versus light-emitter detuning δ. Layer-to-layer distances are h = 0.25 (gray line), 1.00 (dotted), and 2.00 (blue), respectively.
bilayer lattices with atomic separation a = 1.00 versus light-emitter detuning δ. Layer-to-layer distances are h = 0.25 (gray line), 1.00 (dotted), and 2.00 (blue), respectively.
Download figure:
Standard image High-resolution imageWe now further investigate effects of the interlayer separation on the absorption line shape. Figure 5 shows maximum values of the optical depth of a 512-atom bilayer sample as a function of interlayer separation h for lattice constants a = 0.870 (cross), 1.00 (circle), 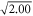 (gray), and 1.10π (black). We collect maximum values of the optical depth from the plots of D versus δ for various interlayer separations at each of four lattice constants. To validate simulation schemes, we compare the results for
(gray), and 1.10π (black). We collect maximum values of the optical depth from the plots of D versus δ for various interlayer separations at each of four lattice constants. To validate simulation schemes, we compare the results for 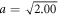 and 1.10π with analytical approximation by modeling each monolayer lattice as a single superatom acting as a mirror with the amplitude reflection and transmission coefficients ri and ti (i = 1, 2). From the Fabry–Pérot transmittance, the corresponding optical depth reads
and 1.10π with analytical approximation by modeling each monolayer lattice as a single superatom acting as a mirror with the amplitude reflection and transmission coefficients ri and ti (i = 1, 2). From the Fabry–Pérot transmittance, the corresponding optical depth reads
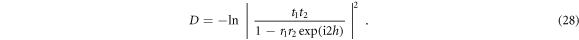
Analytical calculations of optical depth from equation (28) are shown as dashed and dotted lines for 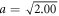 and 1.10π in figure 5. The simulation result for
and 1.10π in figure 5. The simulation result for 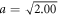 is plotted as a gray line and coefficients t1 = t2 = 45.0% and r1 = r2 = 55.0% are used to fit the simulation. A black line in the bottom shows the simulation result for a = 1.10π with fitted coefficients t1 = t2 = 86.4% and r1 = r2 = 13.6%. Exact calculations of r1(2) and t1(2) using quantum-mechanical framework have been presented in [27], where a pair of two-level atoms within a one-dimensional (1D) waveguide is considered as a model system. Deviation from numerical simulation is substantial for a small
is plotted as a gray line and coefficients t1 = t2 = 45.0% and r1 = r2 = 55.0% are used to fit the simulation. A black line in the bottom shows the simulation result for a = 1.10π with fitted coefficients t1 = t2 = 86.4% and r1 = r2 = 13.6%. Exact calculations of r1(2) and t1(2) using quantum-mechanical framework have been presented in [27], where a pair of two-level atoms within a one-dimensional (1D) waveguide is considered as a model system. Deviation from numerical simulation is substantial for a small 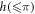 as shown in figure 5, while it is negligible for a large
as shown in figure 5, while it is negligible for a large 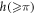 . Such a deviation is plausible because dipoles are strongly correlated in the limit of
. Such a deviation is plausible because dipoles are strongly correlated in the limit of 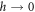 than in the one of
than in the one of 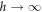 . For two dilute samples with
. For two dilute samples with 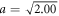 and 1.1π, sinusoidal behavior of optical spectra with a π-periodicity qualitatively agrees with results for an optical cavity-like system, which is predicted by standard optics. This spatial periodicity of absorption spectrum is also exhibited for samples with lattice constants
and 1.1π, sinusoidal behavior of optical spectra with a π-periodicity qualitatively agrees with results for an optical cavity-like system, which is predicted by standard optics. This spatial periodicity of absorption spectrum is also exhibited for samples with lattice constants 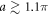 . On the other hand, as demonstrated in figure 5, dense samples interact with light quite differently in that peaks of the sample with a = 1.00 are split into two at
. On the other hand, as demonstrated in figure 5, dense samples interact with light quite differently in that peaks of the sample with a = 1.00 are split into two at 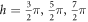 , and the optical depth is abruptly increased by varying interlayer separation slightly from h ≈ 9.82 (1.56λ0) to h ≈ 10.0 (1.59λ0). Similar splitting of the peaks and abrupt changes in optical depth are also observed for the sample with a = 0.860 at different h. In particular, the transmittances are almost zero at interlayer distances for which peak values of the optical depth are obtained so that periodic occurrences of zero transmittances are displayed by varying the interlayer separation of the bilayer lattice. Presumably, optical spectra of our bilayer atomic lattices are tailored by adjusting the lattice parameters. For example, tailored transmittance at proper lattice constant
, and the optical depth is abruptly increased by varying interlayer separation slightly from h ≈ 9.82 (1.56λ0) to h ≈ 10.0 (1.59λ0). Similar splitting of the peaks and abrupt changes in optical depth are also observed for the sample with a = 0.860 at different h. In particular, the transmittances are almost zero at interlayer distances for which peak values of the optical depth are obtained so that periodic occurrences of zero transmittances are displayed by varying the interlayer separation of the bilayer lattice. Presumably, optical spectra of our bilayer atomic lattices are tailored by adjusting the lattice parameters. For example, tailored transmittance at proper lattice constant  and interlayer separation h may be used to implement on- and off-states for a high-fidelity logic gate in quantum computing. The similar theoretical findings were reported earlier on an array of resonant dipoles in the solid-state context [13] and for the light propagation through a triangular 2D array of N = 102 interacting atoms [17]. More theoretical investigations of 2D lattice samples of atoms interacting with light can be found in [13, 21, 24, 42, 43]. Refer to [44] and references therein for recent theories on plasmonic nanoparticles formed by 2D planar lattices.
and interlayer separation h may be used to implement on- and off-states for a high-fidelity logic gate in quantum computing. The similar theoretical findings were reported earlier on an array of resonant dipoles in the solid-state context [13] and for the light propagation through a triangular 2D array of N = 102 interacting atoms [17]. More theoretical investigations of 2D lattice samples of atoms interacting with light can be found in [13, 21, 24, 42, 43]. Refer to [44] and references therein for recent theories on plasmonic nanoparticles formed by 2D planar lattices.
Figure 5. Maximum optical depth D as a function of interlayer separation h for a 512-atom bilayer sample of square lattices with atomic separations a = 0.870 (red cross), 1.00 (blue circle), 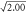 (gray), and 1.10π (black). Comparisons with analytical results are presented for
(gray), and 1.10π (black). Comparisons with analytical results are presented for 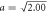 (dashed line) and 1.10π (dotted).
(dashed line) and 1.10π (dotted).
Download figure:
Standard image High-resolution imageOne of candidate systems to realize our numerical simulation scheme experimentally is an optical lattice in a Mott-insulator state in which the atomic positions in each site fluctuate due to the vacuum fluctuations in the ground state. These atomic position fluctuations vary depending on the confinement strength of the atoms to the optical lattice potential. The greater the confinement strength is, the less the position fluctuations are anticipated. In large-scale simulations of homogeneously broadened atomic gases, we should not neglect the effects of the atomic position fluctuations on the optical spectra to be measured. However, realistic large-scale simulations require longer computation time, because we need to compute the ensemble averages after stochastically sampling the positions of atoms in each individual 2D lattice site from a position distribution of interest. Therefore, we consider a case of tight confinement of atoms to the optical lattice. The effects of the fluctuations of the atomic positions was recently investigated for the numerical simulations of an array of atoms in a 1D waveguide [23]. The other experimental issue to be resolved is to reduce photon loss, which may be substantially reduced in atoms confined in a photonic crystal [45].
5. Conclusion
We have discussed that cooperative response is a fundamental concept of light propagation through a pair of identical 2D square lattices of homogeneously broadened dense atoms. Cooperativity originates from light-induced strong correlation between atoms and its major application predicted is the modification of optical spectra by adjusting lattice constant and interlayer distance of the bilayer lattices. In particular, bilayer atomic lattices could be manipulated such that they reflect all of a driving radiation field at properly selected lattice parameters and cancel density-dependent resonance shifts at specific polarization and propagation direction of the probing light. We semiclassically perform numerical simulations of steady-state point-like dipoles within a nanometer-scale sample coupled to low-intensity light by solving the coupled-dipole equation. We elucidate that there exists a strongly correlated regime of sample parameters in which cooperative phenomena occur. In the other regimes, positions and dipole moments of the atoms are weakly correlated so that analysis from standard optics can explain collective behaviors of the samples. One instance is to use the Fabry–Pérot transmittance to explain plots of optical depth as a function of interlayer separation in the low-density regime using the superatom analogy of the bilayer lattices. In the strongly correlated regime, simulation results are in qualitative agreement with predictions from an isotropic infinite lattice model. Nonetheless, there remains hosts of cooperative features yet to be explained both from a new electrodynamics theory pertinent to nanometric samples and a phenomenological method using large-scale numerical simulations.
A bilayer atomic lattice might be exploited to engineer collective resonance shifts, HWHM linewidths of the optical transition, and transmittances by tuning system parameters. Such a lattice could find applications in on- and off-states for an optical switch and a photonic device. Numerical simulations with computer clusters for total number of atoms as large as 140 000 will shed lights on this issue.
Acknowledgments
This work is supported by the Hongik University new faculty research support fund and dedicated to the memory of my Father, Won S. Yoo, who always believed in my ability to be successful in the research area. We thank the Korea Institute for Advanced Study for providing computing resources (KIAS Center for Advanced Computation Abacus4) for this work. We especially thanks J Javanainen for enlightening discussions and supports for stays at University of Connecticut during the 2015 and 2016 summers, Sun Mok Paik at Kangwon National University, Jaewan Kim at KIAS, and Young Soon Kim at Myongji University for advices and encouragemenent for manuscript preparation.
Funding
Hongik University (new faculty research support fund).
Appendix A.: Analytical optical spectra for a two-atom sample
In appendix A we derive optical spectra for a two-atom sample as shown in equations (23)–(26) using the transfer matrix method originating from the Fresnel equations [46]. We follow a formalism [23] previously introduced for light propagation through an array of cold atoms confined in a 1D waveguide. Here we do not consider radiative losses out of the sample. The slowly varying picture has been used to describe the time-dependent classical quantities, so 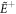 denotes the positive frequency component of electric field. For a coupled sample of light traveling along the +z-direction and a single point-like atom positioned at z1, the transmission amplitude
denotes the positive frequency component of electric field. For a coupled sample of light traveling along the +z-direction and a single point-like atom positioned at z1, the transmission amplitude 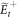 in the region of z > z1 is obtained in terms of the incident and reflected field amplitudes
in the region of z > z1 is obtained in terms of the incident and reflected field amplitudes 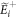 and
and 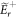 in z < z1 as follows:
in z < z1 as follows:
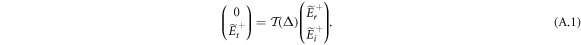
Here a transfer matrix 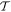 as a function of detuning Δ reads
as a function of detuning Δ reads

The transmission and reflection amplitudes are respectively obtained as
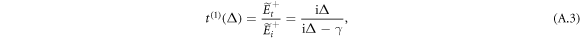
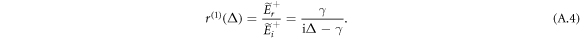
For two identical atoms placed at z1 and z2 we should consider the propagation phases of the light from zi to zi+1, which is expressed by the matrix

Two positions to the left and to the right of the two-atom sample are denoted by z0 and z3, and a composite transfer matrix 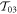 is
is
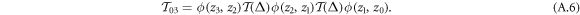
The incident and reflected amplitudes are then described by
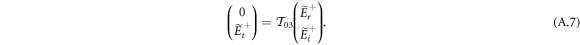
The transmission amplitude is then
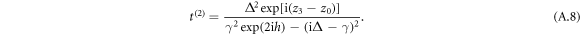
It would be worth addressing what the expression for t(2) implies: 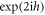 (with h = z2 − z1) in the denominator is a propagation phase for a single oscillation of the light between the positions of atoms 1 and 2. From the double-angle identities of trigonometry, we obtain the two-atom transmittance and optical depth:
(with h = z2 − z1) in the denominator is a propagation phase for a single oscillation of the light between the positions of atoms 1 and 2. From the double-angle identities of trigonometry, we obtain the two-atom transmittance and optical depth:
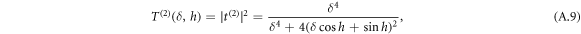

Resonance of the transmittance in equation (A.9) occurs at a particular detunig δF expressed by

At the detuning δ = δF the two-atom transmittance equals 1. In a case when the linewidth of homogeneous broadening is included, we obtain
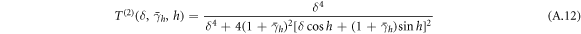
from which resonance detuning is given by
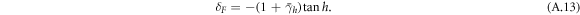
Finally, if light-induced correlations are neglected, each atom in the sample conveys the same amount of light. Then the MFT two-atom transmission amplitude  would be constructed by the product of the single-atom transmission amplitudes equation (A.3):
would be constructed by the product of the single-atom transmission amplitudes equation (A.3):
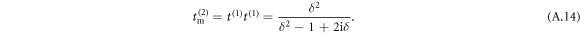
We then obtain the MFT transmittance
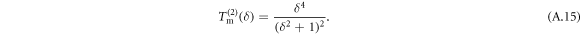
For nonzero linewidth of homogeneous broadening we obtain
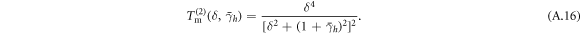
Note that the MFT optical spectra may be valid in the limit of low density for atomic ensembles with stochastically distributed positions.
Appendix B.: Electrodynamics of a bilayer of dielectrics
If light is normally incident from free space to the double identical slabs of depth d and the index of refraction n, which are separated by distance h, the optical depth calculated from standard optics [46] reads
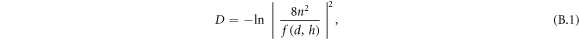

EDPM introduces the local-field corrections so that all atoms see the effective field, leading to the refraction index of the slabs with the same number density ρ written as
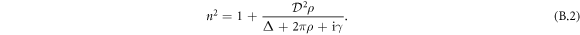
Even if this analytical result cannot be exactly applied to samples in our numerical simulation because of zero depth, it qualitatively explains aspects regarding resonance shifts. Clearly, standard optics predicts that absorption lineshape has one peak and resonance lines are shifted only to negative detunings. Furthermore, we can figure out the interferences of light propagating along six different paths within a bilayer sample from the denominator of equation (B.1).









