Abstract
The generalized tight-binding model, being based on the spin-dependent sublattices, is developed to explore the magnetic quantization of monolayer bismuthene. The sp3 orbital hybridizations, site energies, nearest and next-nearest hopping integrals, spin–orbital interactions and magnetic field (Bz 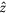 ) are taken into account simultaneously. There exist three groups of low-lying Landau levels (LLs), in which they are mainly from the (6px, 6py, 6pz) orbitals, and only the first group belongs to the unoccupied conduction states. Furthermore, each group is further split into the spin-up- and spin-down-dominated subgroups. The six subgroups present the rich and unique Bz-dependent LL energy spectra, covering the specific or arc-shaped Bz-dependences, the normal/irregular spin–split energies, and the non-crossing/crossing/anti-crossing behaviors. Specially, the second group of valence LLs near the Fermi level can create the frequent inter-subgroup LL anti-crossings since the main and side modes are comparable. The main features of energy spectra can create the special structures in density of states.
) are taken into account simultaneously. There exist three groups of low-lying Landau levels (LLs), in which they are mainly from the (6px, 6py, 6pz) orbitals, and only the first group belongs to the unoccupied conduction states. Furthermore, each group is further split into the spin-up- and spin-down-dominated subgroups. The six subgroups present the rich and unique Bz-dependent LL energy spectra, covering the specific or arc-shaped Bz-dependences, the normal/irregular spin–split energies, and the non-crossing/crossing/anti-crossing behaviors. Specially, the second group of valence LLs near the Fermi level can create the frequent inter-subgroup LL anti-crossings since the main and side modes are comparable. The main features of energy spectra can create the special structures in density of states.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
The monoelemental 2D materials have stirred a lot of experimental and theoretical researches since the first discovery of graphene in 2004 by the mechanical exfoliation [1]. They are very suitable for studying the diverse physical, chemical and material properties. Up to now, the successfully synthesized group-IV and group-V systems cover few-layer/multilayer graphene [1–3], silicene [4, 5], germanene [6, 7], tinene [8], phosphorene [9, 10], antimonene [11, 12], and bismuthene [13–18]. Specifically, layered bismuthenes are epitaxially grown on the 3D Bi2Te3(111)/Bi2Se3(111)/Si(111) substrates [13–17]. Also they could be directly obtained from the mechanical exfoliation [18]. Besides, monolayer bismuthene, with a planar/sp2 honeycomb lattice, is epitaxially deposited on the specific SiC substrate [19]. There exist very prominent chemical bondings between Bi atoms and the substrate, which causes the fully planar configuration of the honeycomb layer. There are various Hamiltonians, being sensitive to the planar/buckled structures, lattice symmetries, layer numbers, stacking configurations, single- or multi-orbital hybridizations, site energies, spin–orbital couplings (SOCs), and external electric and magnetic fields. How to solve new Hamiltonians is one of the main-stream topics in physics science. This work is focused on the unique quantization of monolayer bismuthene in a uniform perpendicular magnetic field (Bz 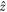 ) by using the generalized tight-binding model.
) by using the generalized tight-binding model.
For few-layer bismuthene, there are some studies on geometric structures [15, 20–23], electronic structures [20–23] and transport properties [18]. Bi atoms could form 2D honeycomb lattice with a highly buckled structure, as clearly identified from the measurements of scanning tunneling microscopy and high-resolution electron diffraction [15, 16, 22]. The angle-resolved photoemission spectroscopy has confirmed the unusual low-lying energy bands with the cone-like, parabolic, and sombrero-shaped dispersions centered at the Γ point [13–17]. The similar band structures are revealed in the theoretical calculations using the first-principles method [20–23] and the tight-binding model [21]. They are deduced to be dominated by the geometric structure, the multi-orbital chemical bondings, the distinct site energies and the strong SOC. Such critical factors are responsible for a 3D rhombohedral Bi semimetal [24, 25]. The combination with a magnetic field is expected to create the diversified Landau levels (LLs) in terms of the Bz-dependent energy spectra and the quantum oscillation modes of the spatial probability distributions. This is worthy of a systematic investigation.
We utilize the generalized tight-binding model to investigate magneto-electronic properties of monolayer bismuthene. All the significant interactions and the various external fields are included in the calculations simultaneously. The magnetic Hamiltonian matrix elements, being related to the sp3 bondings and site energies, SOC and Bz 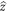 , are calculated from the tight-binding functions in an enlarged unit cell due to vector potential. The orbital-, spin- and sublattice-decomposed wave functions are delicately evaluated to characterize the dominating oscillation modes and determine the quantum numbers of LLs. The dependences of the LL energies and wave functions on the field strength are explored in detail, especially for the neighboring LL energy spacings, the spin–split energies, and the non-crossing/crossing/anti-crossing behaviors. The LL anti-crossings will be examined from the probability transfer between the main and side modes, as well as the change of spin configurations. The van Hove singularities in creating the special structures of DOS are also discussed.
, are calculated from the tight-binding functions in an enlarged unit cell due to vector potential. The orbital-, spin- and sublattice-decomposed wave functions are delicately evaluated to characterize the dominating oscillation modes and determine the quantum numbers of LLs. The dependences of the LL energies and wave functions on the field strength are explored in detail, especially for the neighboring LL energy spacings, the spin–split energies, and the non-crossing/crossing/anti-crossing behaviors. The LL anti-crossings will be examined from the probability transfer between the main and side modes, as well as the change of spin configurations. The van Hove singularities in creating the special structures of DOS are also discussed.
2. Methods
Bismuthene is composed of buckled hexagonal lattices in which two equivalent A and B sublattices are, respectively, located at two parallel planes with a separation of Δz = 1.81 Å. The primitive unit vectors are indicated by a1 and a2 with a lattice constant of a = 4.33 Å (Figure 1(a)), and the buckled structure is associated with the angle between the Bi–Bi bond and the z-axis, θ = 126° (figure 1(b)). The generalized tight-binding model [26, 27] is utilized to explore the electronic properties under external fields, in which all the critical interactions are taken into account simultaneously. The strong sp3 orbital hybridizations, the distinct site energies and the significant SOC will dominate the essential properties near the Fermi level. In the bases of {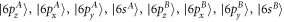 }
}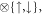 the Hamiltonian is expressed as
the Hamiltonian is expressed as

where  (
(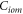 ), i, o, and m stand for the creation (annihilation) operator, lattice site, atomic orbital, and spin, respectively. The first term is the site energy, and Eo of the 6s and 6p orbitals are set to be −9.643 eV and −0.263 eV, respectively [25]. The second term is the nearest-neighbor hopping integral (
), i, o, and m stand for the creation (annihilation) operator, lattice site, atomic orbital, and spin, respectively. The first term is the site energy, and Eo of the 6s and 6p orbitals are set to be −9.643 eV and −0.263 eV, respectively [25]. The second term is the nearest-neighbor hopping integral (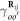 ) which depends on the type of atomic orbitals, the translation vector of the nearest-neighbor atom (
) which depends on the type of atomic orbitals, the translation vector of the nearest-neighbor atom (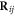 ), and θ. The various interactions are characterized by the sp3 chemical bondings: Vppπ = −0.679 eV, Vppσ = 2.271 eV, Vspσ = 1.3 eV and Vssσ = −0.703 eV [25], as clearly indicated in figure 1(c). For the next-nearest-neighbor atoms, the hopping integral in the third term is independent of θ, since such atoms are located at the same plane. It is related to Vppπ = 0.004 eV, Vppσ = 0.303 eV, Vspσ = 0.065 eV and
), and θ. The various interactions are characterized by the sp3 chemical bondings: Vppπ = −0.679 eV, Vppσ = 2.271 eV, Vspσ = 1.3 eV and Vssσ = −0.703 eV [25], as clearly indicated in figure 1(c). For the next-nearest-neighbor atoms, the hopping integral in the third term is independent of θ, since such atoms are located at the same plane. It is related to Vppπ = 0.004 eV, Vppσ = 0.303 eV, Vspσ = 0.065 eV and 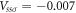 eV. The last term represents the intra-atomic SOC Vsoc =
eV. The last term represents the intra-atomic SOC Vsoc = 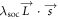 with
with 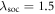 eV. α, β and γ denote the
eV. α, β and γ denote the 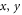 or z direction, and σ is the Pauli spin matrix.
or z direction, and σ is the Pauli spin matrix. 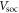 can also be expressed as
can also be expressed as 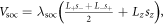 where L± and s± are the ladder operators for the angular momentum and spin. The SOC is vanishing for the same orbital. It could induce the change of spin configurations between the 6pz and (6px, 6py) orbitals and the 6px and 6py orbitals.
where L± and s± are the ladder operators for the angular momentum and spin. The SOC is vanishing for the same orbital. It could induce the change of spin configurations between the 6pz and (6px, 6py) orbitals and the 6px and 6py orbitals.
Figure 1. (a) The x − y projections of monolayer bismuthene with an enlarged rectangular unit cell in Bz  , (b) the buckled structure, (c) the various orbital hybridizations; (d) the Brillouin zone of the hexagonal lattice with the high-symmetry points and the reduced first Brillouin zone. a1 and a2 in (a) are lattice vectors, and the subscript of Ai corresponds to the ith Bi atom.
, (b) the buckled structure, (c) the various orbital hybridizations; (d) the Brillouin zone of the hexagonal lattice with the high-symmetry points and the reduced first Brillouin zone. a1 and a2 in (a) are lattice vectors, and the subscript of Ai corresponds to the ith Bi atom.
Download figure:
Standard image High-resolution imageThe periodical Peierls phases, being created by a uniform perpendicular magnetic field, can modulate the hopping integral as 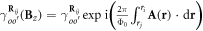 and induce an enlarged unit cell. Φ0 (hc/e) is the flux quantum. Under the Landau gauge A = (0, Bzx, 0), a rectangular unit cell covers 4RB (
and induce an enlarged unit cell. Φ0 (hc/e) is the flux quantum. Under the Landau gauge A = (0, Bzx, 0), a rectangular unit cell covers 4RB (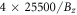 ) Bi atoms (figure 1(a)), where RB is the ratio of Φ0 versus magnetic flux through a hexagon. The area of a reduced Brillouin zone (a small rectangle in figure 1(d)) is
) Bi atoms (figure 1(a)), where RB is the ratio of Φ0 versus magnetic flux through a hexagon. The area of a reduced Brillouin zone (a small rectangle in figure 1(d)) is 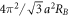 . The magnetic Hamiltonian is built from the space spanned by the
. The magnetic Hamiltonian is built from the space spanned by the 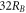 tight-binding functions {
tight-binding functions { }, where
}, where 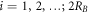 . By the detailed analytic calculations, this Hermitian matrix could be transferred into the band-like form to solve LL energies and wave functions more efficiently. When a uniform electric field is applied along the z-axis, it can create a Coulomb potential Vz/2 (
. By the detailed analytic calculations, this Hermitian matrix could be transferred into the band-like form to solve LL energies and wave functions more efficiently. When a uniform electric field is applied along the z-axis, it can create a Coulomb potential Vz/2 (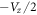 ) on the site energy of the A (B) sublattice. The generalized tight-binding model could be further developed to comprehend the magnetic quantization in other layered systems with complex orbital bondings and spin configurations under composite fields.
) on the site energy of the A (B) sublattice. The generalized tight-binding model could be further developed to comprehend the magnetic quantization in other layered systems with complex orbital bondings and spin configurations under composite fields.
Up to now, there are two kinds of theoretical models to investigate the diverse magnetic quantization phenomena, namely, the generalized tight-binding model and the low-energy elective-mass approximation. Concerning the low-energy perturbation method [28–34], the zero-field Hamiltonian matrix elements are expanded about the high-symmetry points (e.g., the Γ point in monolayer bismuthene, and the K point in layered graphene). And then, the magnetic quantization is further made from an approximate Hamiltonian matrix. That is to say, the zero-field and magnetic Hamiltonian matrices have the same dimension. However, some interlayer hopping integrals in layered graphene will create much difficulty in the study of magnetic quantization. Some of them are usually ignored in the effective-mass approximation. Consequently, certain unique and diverse magnetic quantization phenomena are lost by using this method, e.g., the anti-crossing phenomenon in ABC-stacked trilayer graphene, and the extra magneto-absorption selection rules [27]. In general, the perturbation method cannot deal with the low-symmetry systems with multi-constant-energy loops, as observed in bismuthene.
3. Results and discussion
Monolayer bismuthene exhibits a feature-rich electronic structure due to the significant multi-orbital bondings, site energies and SOC. The low-lying electronic properties are mainly determined by three energy bands near the Γ point (figure 1(d)), as clearly shown in figure 2. Each electronic state is doubly degenerate for the spin degree of freedom. The first conduction band (c1) has parabolic energy dispersion centered at the Γ point. The second valence band (v2) presents the valley-like dispersion except a slightly rounded structure near the Γ point. Specially, the first valence band (v1) reveals the sombrero-shaped structure with the non-monotonic wave-vector dependence, in which the extreme points deviate from the Γ point. There coexist two constant-energy loops within a certain energy range, being expected to induce the complicated magnetic quantization under their strong competitions. Apparently, the lowest unoccupied state in the c1 band and the highest occupied states in the v1 band (the outer constant-energy loop) have the different wave vectors and thus lead to an indirect energy gap of 0.293 eV. It should also be noted that the low-energy electronic structure is consistent with the first-principle calculations, which means that the low-energy electronic properties could be properly described by the tight-binding method [21–23].
Figure 2. Energy bands of bismuthene along the high-symmetry points. Also shown are the 3D band structures near the Γ point.
Download figure:
Standard image High-resolution imageBismuthene exhibits three groups of low-lying LLs with distinct characteristics, as clearly shown in figures 3 and 4. The valence and conduction LLs are asymmetric about the Fermi level. The first, the second, and the third groups are associated with the magnetic quantization of the 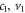 and v2 energy bands, respectively. Each LL group is further split into two spin-dependent LL subgroups because the cooperation of SOC and magnetic field destroys the spin degeneracy. For any (
and v2 energy bands, respectively. Each LL group is further split into two spin-dependent LL subgroups because the cooperation of SOC and magnetic field destroys the spin degeneracy. For any (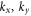 ) states, these LLs are doubly degenerate owing to the mirror symmetry about the z-axis. For example, at (kx = 0, ky = 0), the two degenerate wave functions have equivalent spatial distributions, but are localized near the 0 and 1/2 positions of the enlarged unit cell, respectively. The 1/2-localization-center states are chosen to illustrate the main features of LL wave functions (figures 3(b) and 4(b)). Each LL state is characterized by the spatial probability density on the A and B sublattices with sp3 orbitals and two spin configurations. This distribution might have a normal zero-point number and present the symmetric/anti-symmetric mode about the localization center, as revealed in a harmonic oscillator (2D electron gas). As a result of the hexagonal lattice, the A and B sublattices possess the same oscillation mode after magnetic quantization.
) states, these LLs are doubly degenerate owing to the mirror symmetry about the z-axis. For example, at (kx = 0, ky = 0), the two degenerate wave functions have equivalent spatial distributions, but are localized near the 0 and 1/2 positions of the enlarged unit cell, respectively. The 1/2-localization-center states are chosen to illustrate the main features of LL wave functions (figures 3(b) and 4(b)). Each LL state is characterized by the spatial probability density on the A and B sublattices with sp3 orbitals and two spin configurations. This distribution might have a normal zero-point number and present the symmetric/anti-symmetric mode about the localization center, as revealed in a harmonic oscillator (2D electron gas). As a result of the hexagonal lattice, the A and B sublattices possess the same oscillation mode after magnetic quantization.
Figure 3. (a) The spin-dependent LL energies for the first and the third groups at Bz = 30 T; (b) the orbital-projected probability distributions in the 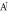 ,
,  ,
, 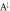 and
and 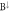 sublattices.
sublattices.
Download figure:
Standard image High-resolution imageFigure 4. Similar plot as figure 3, but shown for the second group of LLs.
Download figure:
Standard image High-resolution imageFor the first group, the 6px- and 6py-decomposed probability distributions present an identical oscillation mode in the 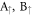 ,
, 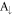 and
and 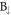 sublattices (red and green curves in figure 3(b)). Furthermore, they dominate the oscillation modes of the spin–split LLs, in which the number of zero points can serve as a quantum number (
sublattices (red and green curves in figure 3(b)). Furthermore, they dominate the oscillation modes of the spin–split LLs, in which the number of zero points can serve as a quantum number (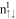 ). The
). The 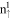 and
and 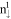 LLs, respectively, have the
LLs, respectively, have the  - and
- and 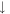 -dominated components. The splitting of the
-dominated components. The splitting of the 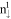 and
and  subgroups are, respectively, shown in figure 3(a) by the solid and dashed blue lines. At Bz = 30 T, the first three conduction LLs belong to the
subgroups are, respectively, shown in figure 3(a) by the solid and dashed blue lines. At Bz = 30 T, the first three conduction LLs belong to the 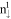 LLs and then the
LLs and then the 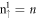 and
and 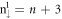 LLs appear alternatively. The energy spacing between two neighboring LLs in the same subgroup is almost uniform. This directly reflects the magnetic quantization of the parabolic c1 band (figure 2), as observed in 2D electron gas. Furthermore, the spin–split energy between two different subgroups is about 37 meV regardless of the state energy. The third group is very different from the first group in terms of energy spacing, split energy; orbital and spin components. The LL spacing is non-uniform because of the valley-like energy dispersion. The spin–split energy declines in the increase of state energy, as shown by the dashed and solid red lines in figure 3(a). The dominating orbitals cover 6pz, 6px and 6py (black, red and green curves in the lower half part of figure 3(b)). They have the same quantum mode, while the former and the latter two present the opposite spin configurations. The 6pz or 6px/6py component is suitable for serving as the dominating quantum mode (n3), and the latter is chosen to illustrate the diversified properties among three groups of LLs. For the
LLs appear alternatively. The energy spacing between two neighboring LLs in the same subgroup is almost uniform. This directly reflects the magnetic quantization of the parabolic c1 band (figure 2), as observed in 2D electron gas. Furthermore, the spin–split energy between two different subgroups is about 37 meV regardless of the state energy. The third group is very different from the first group in terms of energy spacing, split energy; orbital and spin components. The LL spacing is non-uniform because of the valley-like energy dispersion. The spin–split energy declines in the increase of state energy, as shown by the dashed and solid red lines in figure 3(a). The dominating orbitals cover 6pz, 6px and 6py (black, red and green curves in the lower half part of figure 3(b)). They have the same quantum mode, while the former and the latter two present the opposite spin configurations. The 6pz or 6px/6py component is suitable for serving as the dominating quantum mode (n3), and the latter is chosen to illustrate the diversified properties among three groups of LLs. For the ![${n}_{\uparrow }^{3}[{n}_{\downarrow }^{3}]$](https://content.cld.iop.org/journals/1367-2630/20/6/062001/revision2/njpaaca24ieqn43.gif) LLs, there are, respectively,
LLs, there are, respectively,  and
and 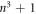 [n3 − 1 and n3] zero points in the 6px/6py-dependent (A
[n3 − 1 and n3] zero points in the 6px/6py-dependent (A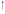 ,
,  ) and (A
) and (A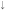 ,B
,B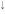 ) sublattices. The similar zero-point numbers are revealed in the
) sublattices. The similar zero-point numbers are revealed in the 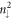 LLs (figure 4(b)).
LLs (figure 4(b)).
Specially, the second group of LLs exhibits an abnormal ordering (figure 4(a)) and the highly asymmetric probability distributions (figure 4(b)). The quantum number 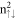 is determined from the 6px/6py-dependent oscillation mode even if its probability density is lower than that of the 6pz orbital. The spatial probability density does not present the well-behaved symmetric distribution about the localization center except for the
is determined from the 6px/6py-dependent oscillation mode even if its probability density is lower than that of the 6pz orbital. The spatial probability density does not present the well-behaved symmetric distribution about the localization center except for the 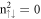 and/or 1 LLs. This suggests the superposition of the main and side oscillation modes (the distinct normal modes) in each
and/or 1 LLs. This suggests the superposition of the main and side oscillation modes (the distinct normal modes) in each 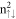 LL. Apparently, the LL energy spacing and the spin–split energy do not have the specific relations with state energy, as shown by the dashed (
LL. Apparently, the LL energy spacing and the spin–split energy do not have the specific relations with state energy, as shown by the dashed (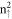 ) and solid (
) and solid (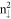 ) black lines in figure 4(a). The unusual LL energy spectrum, being sensitive to the magnetic field strength, is related to the sombrero-shaped energy dispersion (figure 2). At
) black lines in figure 4(a). The unusual LL energy spectrum, being sensitive to the magnetic field strength, is related to the sombrero-shaped energy dispersion (figure 2). At 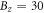 T, the
T, the 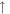 -dominated (
-dominated (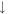 -dominated) LL energies have the ordering of
-dominated) LL energies have the ordering of 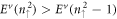 for
for 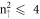 (
(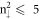 ), and then the inverse ordering for others. This clearly reflects the small-
), and then the inverse ordering for others. This clearly reflects the small-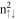 LLs arising from the inner valley centered at the Γ point (figure 2), the
LLs arising from the inner valley centered at the Γ point (figure 2), the  -dependent energy ordering similar to the wave-vector dependence of energy band, and the strong competitions between the inner and outer constant-energy loops.
-dependent energy ordering similar to the wave-vector dependence of energy band, and the strong competitions between the inner and outer constant-energy loops.
The low-lying LLs exhibit the rich and unique Bz-dependent energy spectra, as clearly illustrated in figures 5 and 6(a). The conduction LLs have no intra-subgroup and inter-subgroup crossings/anti-crossings (the dashed and solid blue curves in figure 5(a)). Each LL energy exhibits the linear Bz-dependence, in which the neighboring LL spacing and the spin–split energy are proportional to the field strength. These are directly reflected from the monotonous wave-vector dependence of a parabolic conduction band. The third- and second group LLs coexist in the deeper valence energy spectrum (the red and black curves in figure 5(b)). They frequently cross each other because of the well-behaved spatial distributions without the same quantum mode. The former roughly have the 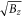 -dependent energies, especially for the larger
-dependent energies, especially for the larger 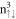 or the stronger Bz. This is associated with the quasi-linear valence band.
or the stronger Bz. This is associated with the quasi-linear valence band.
Figure 5. The Bz-dependent LL energy spectra for the first, second and third groups (the blue, black and red curves) in the absence/presence of crossings.
Download figure:
Standard image High-resolution imageFigure 6. (a) The crossing and anti-crossing energy spectra due to the spin-up- and spin-down-dominated second group of LLs, (b) the 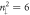 and
and 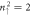 LL anti-crossing within a certain range of Bz; the variations of probability distributions along the (c) higher- and (d) lower-energy paths.
LL anti-crossing within a certain range of Bz; the variations of probability distributions along the (c) higher- and (d) lower-energy paths.
Download figure:
Standard image High-resolution imageThe LL energy spectrum of the second group, as shown in figure 6(a), is in sharp contrast with those of the first and third groups (figures 5(a) and (b)). All the LLs present the arc-like Bz-dependence except that the 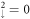 LL energy monotonously declines with the increasing Bz. Their energies agree with that of the Γ point (−0.222 eV) in the sombrero-shaped band (figure 2(a)) when Bz approaches zero. This clearly indicates that the magnetic quantization is initiated from electronic states near the Γ point. For very large
LL energy monotonously declines with the increasing Bz. Their energies agree with that of the Γ point (−0.222 eV) in the sombrero-shaped band (figure 2(a)) when Bz approaches zero. This clearly indicates that the magnetic quantization is initiated from electronic states near the Γ point. For very large 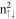 (
(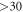 ), the LL energies grow quickly as Bz slightly increases from zero. The n
), the LL energies grow quickly as Bz slightly increases from zero. The n and n
and n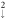 LLs reach the maximum energy (−0.146 eV), being nearly identical at
LLs reach the maximum energy (−0.146 eV), being nearly identical at 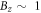 T. This energy corresponds to the highest level of the outer constant-energy loop. With the increase of Bz , the spin-dependent two subgroups start to separate, in which the n
T. This energy corresponds to the highest level of the outer constant-energy loop. With the increase of Bz , the spin-dependent two subgroups start to separate, in which the n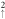 LLs exhibit more drastic changes. As a result, there exist very frequent inter-subgroup crossings and anti-crossings, depending on whether the neighboring
LLs exhibit more drastic changes. As a result, there exist very frequent inter-subgroup crossings and anti-crossings, depending on whether the neighboring 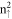 and
and  LLs have the same oscillation modes.
LLs have the same oscillation modes.
The anti-crossings between two spin-dominated subgroups deserve a closer examination. They mainly arise from the n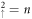 and
and 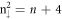 LLs, as illustrated by the red rectangles in figure 6(a). In addition to the major mode with n zero points, these two LLs also possess the side modes with different zero-point numbers. The latter are due to the cooperation of the intrinsic interactions and the magnetic field. Such modes are examined to have
LLs, as illustrated by the red rectangles in figure 6(a). In addition to the major mode with n zero points, these two LLs also possess the side modes with different zero-point numbers. The latter are due to the cooperation of the intrinsic interactions and the magnetic field. Such modes are examined to have 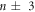 zero points by the detailed numerical calculations. For example, the
zero points by the detailed numerical calculations. For example, the  LL strongly anti-crosses with the
LL strongly anti-crosses with the 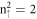 LL in the range of 60 T < Bz < 70 T (figure 6(b)). When Bz increases from 50 T along the higher-energy path (the solid blue arrow), the n = 6 main mode in the
LL in the range of 60 T < Bz < 70 T (figure 6(b)). When Bz increases from 50 T along the higher-energy path (the solid blue arrow), the n = 6 main mode in the  /
/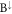 sublattice declines quickly (figure 6(c)), and the n = 3 side mode in the same sublattice grows rapidly. Furthermore, the main and side modes, respectively, with 5 and 2 zero points in the
sublattice declines quickly (figure 6(c)), and the n = 3 side mode in the same sublattice grows rapidly. Furthermore, the main and side modes, respectively, with 5 and 2 zero points in the 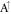 /
/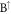 sublattice behave similarly. These two modes are comparable near the critical magnetic field (∼65 T). Their roles are interchanged in the further increase of field strength. For example, at
sublattice behave similarly. These two modes are comparable near the critical magnetic field (∼65 T). Their roles are interchanged in the further increase of field strength. For example, at  T, the spatial distribution is dominated by the oscillation mode with 2 zero points in the
T, the spatial distribution is dominated by the oscillation mode with 2 zero points in the 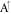 and
and 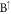 sublattices (the first row in figure 6(c)). That is, the
sublattices (the first row in figure 6(c)). That is, the 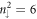 LL is changed into the
LL is changed into the  LL during the variation of Bz. The probability transfer between the spin-up and spin-down components is driven by the critical SOC. The similar anti-crossing process is revealed in the inverse transformation along the lower-energy path (the dashed blue arrow).
LL during the variation of Bz. The probability transfer between the spin-up and spin-down components is driven by the critical SOC. The similar anti-crossing process is revealed in the inverse transformation along the lower-energy path (the dashed blue arrow).
The van Hove singularities in the energy-wave-vector space can create the special structures in DOS, being sensitive to the effective dimensions. DOS is defined as
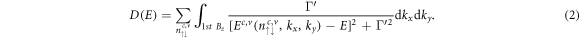
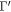 (=0.1 meV) in the calculations is the broadening parameter. At zero-field, the 2D band structure exhibits three shoulder structures (the red dashed circles) and one strong asymmetric peak in the square-root form (the red solid circle), as shown in figures 7(a) and (b). The first, second and third shoulders situated at E = 0.148 eV,
(=0.1 meV) in the calculations is the broadening parameter. At zero-field, the 2D band structure exhibits three shoulder structures (the red dashed circles) and one strong asymmetric peak in the square-root form (the red solid circle), as shown in figures 7(a) and (b). The first, second and third shoulders situated at E = 0.148 eV, 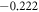 eV and −0.396 eV are, respectively due to the band-edge states (the extreme points) in the parabolic conduction band, the rounded inner constant-energy loop centered at the Γ point, and the rounded valley-like valence band (figure 2(a)). The latter comes from the outer constant-energy loop with the highest level in the first valence band, since it could be regarded as a 1D parabolic band. Band gap is energy difference between the first shoulder of the conduction states (figure 7(a)) and the prominent asymmetric peak. Under the magnetic quantization, the delta-function-like peaks arising from the zero-dimensional LLs come to exist. Their intensities are proportional to the number of LLs. The first group, as shown by the black solid curves in figure 7(a) at Bz = 30 T, presents a lot of uniform symmetric peaks, being composed of the
eV and −0.396 eV are, respectively due to the band-edge states (the extreme points) in the parabolic conduction band, the rounded inner constant-energy loop centered at the Γ point, and the rounded valley-like valence band (figure 2(a)). The latter comes from the outer constant-energy loop with the highest level in the first valence band, since it could be regarded as a 1D parabolic band. Band gap is energy difference between the first shoulder of the conduction states (figure 7(a)) and the prominent asymmetric peak. Under the magnetic quantization, the delta-function-like peaks arising from the zero-dimensional LLs come to exist. Their intensities are proportional to the number of LLs. The first group, as shown by the black solid curves in figure 7(a) at Bz = 30 T, presents a lot of uniform symmetric peaks, being composed of the  - and
- and 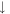 -dominated ones. This further illustrates the absence of crossing and anti-crossing. Specially, the initial three conduction peaks nearest to EF are associated with the
-dominated ones. This further illustrates the absence of crossing and anti-crossing. Specially, the initial three conduction peaks nearest to EF are associated with the 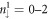 LLs (the blue circles), indicating the specific energy spacing between two neighboring LLs. For the higher-energy peaks, they could be utilized to identify the separate contributions of the
LLs (the blue circles), indicating the specific energy spacing between two neighboring LLs. For the higher-energy peaks, they could be utilized to identify the separate contributions of the 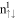 LLs. As to the valence LLs, they exhibit many double-peak structures and some single peaks (figure 7(b)). The former are induced by the frequent crossings and anti-crossings between the
LLs. As to the valence LLs, they exhibit many double-peak structures and some single peaks (figure 7(b)). The former are induced by the frequent crossings and anti-crossings between the 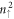 and
and 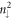 LLs, and the similar crossings between the
LLs, and the similar crossings between the  and
and 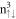 LLs. The higher-energy valence peaks before the strong asymmetric peak are due to the
LLs. The higher-energy valence peaks before the strong asymmetric peak are due to the 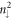 LLs. Their energies and numbers could be tuned by the magnetic field strength. The threshold peak energy will, respectively, approach to −0.148 and −0.222 eV (energies of the asymmetric peak and the second shoulder), when Bz is reduced to 1 and ∼0 T.
LLs. Their energies and numbers could be tuned by the magnetic field strength. The threshold peak energy will, respectively, approach to −0.148 and −0.222 eV (energies of the asymmetric peak and the second shoulder), when Bz is reduced to 1 and ∼0 T.
Figure 7. The low-energy density of states of monolayer bismuthene under 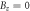 and 30 T for (a) conduction and (b) valence states.
and 30 T for (a) conduction and (b) valence states.
Download figure:
Standard image High-resolution imageDOSs are very useful in understanding the essential properties, e.g., band structureoptical spectra, and transport properties. The van Hove singularities in DOSs will create the strong responses after the various external perturbations. They dominate the physical properties, such as, the prominent absorption intensity arising from the inter-Landau level transitions (the occupied LLLs to the unoccupied ones). The magneto-optical excitations are under the current investigations. The theoretical magnetic/non-magnetic DOSs could be examined by the STS measurements, further revealing the diverse magnetic quantization/energy bands. Up to now, STS has successfully served as a powerful experimental method for investigating the magnetically quantized energy spectra in layered graphenes. The measured tunneling differential conductance directly reflects the form, energy, number and degeneracy of the LL prominent peaks. Part of the theoretical predictions on the LL energy spectra are consistent with the experimental examinations, covering the 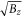 -dependent LL energies of monolayer graphene [35–39], the linear Bz-dependence in bilayer AB stacking [40–42], the coexistent square-root and linear Bz-dependences of trilayer ABA-stacked graphene [40], and the 3D and 2D characteristics of the Landau subbands in 3D Bernal graphite [43, 44].
-dependent LL energies of monolayer graphene [35–39], the linear Bz-dependence in bilayer AB stacking [40–42], the coexistent square-root and linear Bz-dependences of trilayer ABA-stacked graphene [40], and the 3D and 2D characteristics of the Landau subbands in 3D Bernal graphite [43, 44].
4. Conclusion
The diverse magnetic quantization phenomena of monolayer bismuthene are explored in detail using the generalized tight-binding model. The main features of LLs are determined by the multi-orbital chemical bondings, the distinct site energies, the nearest and next-nearest hopping integrals, the significant SOCs and the magnetic field. The theoretical model could be further developed to solve new Hamiltonians in emerging 2D materials under the uniform/non-uniform external fields, e.g., the magnetic Hamiltonians with various interactions in few-layer bismuthene, antimonene [11, 12], phosphorene [9, 10] and arsenene [21, 45, 46]. Moreover, the generalized tight-binding model could combine with the single- and many-particle theories to study the other essential physical properties, such as magneto-optical spectra [47], magnetoplasmons [48], and quantum transports [49].
The low-energy electronic structure covers the parabolic conduction band, the sombrero-shaped valence band (the inner and outer constant-energy loops) and the rounded valley-like valence band, with an indirect gap of 0.293 eV. Such energy bands are closely related to three groups of (6px, 6py, 6pz)—created LLs, in which each group is split into the 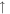 - and
- and 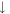 -dominated subgroups. The dominating oscillation mode of the 6px/6py-projected probability distribution could provide a good quantum number. The first and third groups possess the well-behaved wave functions, while the second group might have the main and side modes in the
-dominated subgroups. The dominating oscillation mode of the 6px/6py-projected probability distribution could provide a good quantum number. The first and third groups possess the well-behaved wave functions, while the second group might have the main and side modes in the  LLs. The former two do not present the anti-crossing behavior in the Bz-dependent energy spectra. However, the frequent anti-crossings occur between the
LLs. The former two do not present the anti-crossing behavior in the Bz-dependent energy spectra. However, the frequent anti-crossings occur between the 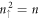 and
and 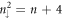 LLs. The LL energies of the first, second and third groups, respectively, exhibit the linear, arc-shaped and square-root-form Bz-dependences. Furthermore, the normal spin–split energies are only revealed in the first group. The van Hove singularities in parabolic bands, the outer constant-energy loop and LLs, respectively, lead to shoulders, a prominent asymmetric peak and many delta-function-like peaks. The predicted electronic energy spectra could be examined by STS measurements.
LLs. The LL energies of the first, second and third groups, respectively, exhibit the linear, arc-shaped and square-root-form Bz-dependences. Furthermore, the normal spin–split energies are only revealed in the first group. The van Hove singularities in parabolic bands, the outer constant-energy loop and LLs, respectively, lead to shoulders, a prominent asymmetric peak and many delta-function-like peaks. The predicted electronic energy spectra could be examined by STS measurements.
Monolayer bismuthene exhibits the electronic properties that are easily tuned by the geometric symmetry, intrinsic interactions, SOCs; electric and magnetic fields. Energy gaps have a strong effect on the temperature-dependent transport currents, so that this system could serve as a field-effect transistor. Optical gaps determine the threshold absorption spectra and thus are available in detectors. Moreover, the LLs might belong to the spin–split states, being useful in spintronic devices. That is, a new research field/direction, which covers the magneto-electronic properties, optical/magneto-optical absorption spectra, novel quantum Hall transports, and magneto-Coulomb electronic excitations, will be created under the full theoretical framework, since the magnetic quantization is clearly identified to reveal the diverse phenomena.
Acknowledgments
This work was supported by the MOST of Taiwan, under Grant No. MOST 105-2112-M-006-002-MY3 and MOST 106-2112-M-022-001.










