Abstract
We study phase imprinting on Bose–Einstein condensates (BECs) with the fast-forward scaling theory revealing a nontrivial scaling property in quantum dynamics. We introduce a wave packet with uniform momentum density (WPUM) which has peculiar properties but is short-lived. The fast-forward scaling theory is applied to derive the driving potential for creation of the WPUMs in a predetermined time. Fast manipulation is essential for the creation of WPUMs because of the instability of the state. We also study loading of a BEC into a predetermined Bloch state in the lowest band from the ground state of a periodic potential. Controlled linear potential is not sufficient for creation of the Bloch state with large wavenumber because the change in the amplitude of the order parameter is not negligible. We derive the exact driving potential for creation of predetermined Bloch states using the obtained theory.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
To find suitable driving fields for tailoring a quantum system to generate a target state from a given initial state is challenging in general. Naive numerical trial-and-error methods are time- and resource-consuming. Therefore, to deepen the understanding of relevant quantum dynamics is desirable to find useful control schemes. Furthermore, the obtained knowledge on the quantum dynamics can be used cooperatively with numerical schemes to reduce the required time and resources.
The fast-forward scaling theory can be used to derive the driving potential which accelerates or decelerates a reference dynamics [1]. The driving potential is explicitly represented as a functional of the wave function of the reference dynamics. Thus, infinite number of different dynamics (slow dynamics and fast dynamics) are continuously related to each other [2].
This fast-forward scaling property may considerably decrease the difficulty of control problems. Let us consider a problem such as 'find a driving field which generates a target state at time T from a given initial state'. The fast-forward scaling property reduces the problem to 'find a driving field which generates the target state from a given initial state' removing the constraint on time. It is because once we have a single dynamics which evolves from the initial state to the target state, we can derive the driving potential to generate the target state at any desired time T by accelerating or decelerating the original dynamics.
Adiabatic controls are widely used for manipulation of quantum systems. However the decoherence degrades the efficiency of the control in the long time manipulation. The fast-forward scaling theory was extended to accelerate adiabatic dynamics, and the formula of the driving potential was derived [3, 4]. The driving potential realizes the target state at desired time, which is originally supposed to be achieved after infinitely long time.
The fast-forward scaling theory was extended to many-body systems [5] and discrete systems [6, 7], and applications to manipulations of Bose–Einstein condensates (BECs) [1, 3, 5, 8], charged particles [9] and molecular vibrational states [10–13] were proposed. Protection of quantum states from the disturbance due to fluctuating background potential with the sequential manipulation [14] and sorting of trapped ions [12] were proposed using the fast-forward driving potential. A scheme encompassing quantum, classical and stochastic dynamics was proposed utilizing flow fields providing compact expressions for counter-diabaitc Hamiltonians and fast-forward potentials [15]. Recently a scheme of fast-forward of adiabatic control of stationary tunneling states has been proposed, which allows the acceleration of both the amplitude and phase of wave functions throughout the fast-forward time range. The scheme realizes the fast-forward observation of the transport coefficients under the adiabatically changing barrier with the fixed energy of an incoming particle [16].
Shortcuts-to-adiabaticity (STA) or assisted adiabatic transformation protocols have been developed to generate the same target state as reference adiabatic dynamics, with overall weaker driving fields and/or in a shorter time [2, 17]. Various schemes of STA have been proposed, e.g., the counter-diabatic [18], fast-forward [3] and invariant-based engineering protocols [19]. Applications of STA protocols have been proposed and implemented for manipulations of, e.g., atoms and molecules [10, 18, 20–25], BECs [3–5, 8, 19, 26, 27], spin systems [28–34] including electron spin of a single nitrogen-vacancy center in diamond [35, 36], various STIRAP systems [11, 18, 20, 37, 38] and also for creation of entangled states [39, 40] and nonlocal two-qubit gate operations in a quantum dot array [41]. Transition probability generating function was studied from a point of view of STA [42]. STA for classical systems and quantum–classical correspondence of STA have been studied [23, 43, 44].
In this paper, we study phase imprinting on the order parameter of BECs with the fast-forward scaling theory showing the nontrivial scaling property. In contrast to the various phase imprinting protocols previously proposed or demonstrated, e.g., [45–56], our phase imprinting protocol is based on the nontrivial scaling property of quantum dynamics. The theory is applied to derive the driving potential for creation of a peculiar state, a wave packet with uniform momentum density (WPUM), which is introduced in this paper. Mathematically the state has infinite expectation value of the momentum and finite energy in an ideal condition but is short-lived due to imperfection of potential in actual physical systems. Fast manipulation is essential for the creation of WPUMs because of the instability of the state.
We also study loading of a BEC in the ground state of a periodic potential into a predetermined Bloch state in the lowest band. Controlling a linear potential is not sufficient for creation of the Bloch state when the target wavenumber is large because the change in the amplitude of the order parameter is not negligible. We exactly show the required modification of the driving potential from the time-dependent linear potential.
This paper is organized as follows. In section 2, we introduce the WPUMs. In section 3, we obtain the driving potential for phase imprinting for the case where the amplitude of the wave function is unchanged during the control. The result is applied to the creation of the WPUM. In section 4, we extend the theory to the case that the amplitude of the wave function is time-dependent during the phase imprinting. The theory is applied to loading of the BEC into a predetermined Bloch state. Section 5 is devoted to discussion and summary.
2. Wave packet with uniform momentum density (WPUM)
Here, we introduce an interesting state: a WPUM density, which has the peculiar properties summarized below. We consider a particle under potential V in the one-dimensional system. The following theory is straightforwardly extended to the two- and the three-dimensional systems and also to the Gross–Pitaevskii (GP) equation which describes BECs.
We assume that the particle is in an energy eigenstate, and the phase of the wave function is space-dependent but time-independent except for the dynamical phase. The wave function is represented as
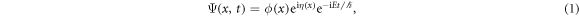
where ϕ(x) are η(x) are real-valued functions and E is the energy. We assume that 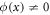 . Here, Ψ in equation (1) satisfies time-independent Schrödinger equation
. Here, Ψ in equation (1) satisfies time-independent Schrödinger equation

We compare the imaginary parts of the both sides of equation (2) after dividing them by  to obtain
to obtain
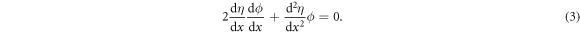
Solving equation (3), phase η is represented in terms of ϕ as
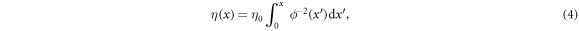
where η0 is an arbitrary constant. Using equation (2), the potential, which maintains the state in equation (1), is obtained as
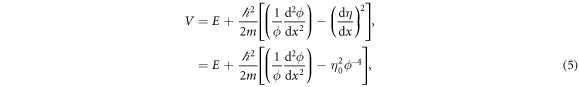
where we used
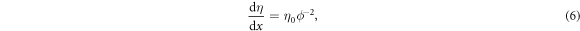
which is obtained from equation (4), in the last line of equation (5). We refer equations (4) and (6) as the phase-amplitude relation hereafter. The last term in equation (5) is the modification of the potential due to phase η, while the second term corresponds to the spatial dependence of ϕ.
The properties of the WPUM and the potential in equation (5) are summarized as follows: (A) the WPUM is a nonequilibrium steady state with a uniform current, (dη/dx)ϕ2 = η0; (B) the expectation value of the momentum 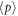 diverges because of the uniform momentum density while the energy E is finite; (C) the phase diverges at the tails of the wave function where ϕ asymptotically approaches to zero; (D) the potential diverges to negative infinity at the tails; (E) the state is short-lived in actual systems because of the imperfection of the physically feasible potential.
diverges because of the uniform momentum density while the energy E is finite; (C) the phase diverges at the tails of the wave function where ϕ asymptotically approaches to zero; (D) the potential diverges to negative infinity at the tails; (E) the state is short-lived in actual systems because of the imperfection of the physically feasible potential.
The uniform current is the consequence of the phase-amplitude relation in equation (6), which shows that space derivative of the phase is inversely proportional to the square of the amplitude of the wave function, and it is a manifestation of steady states. The reason why the amplitude of the wave function remains constant in time is that the current is space independent. The reason of the finite energy in spite of the infinite momentum is the potential diverging to negative infinity at the tails of the wave function.
3. Creation of WPUM
Now we consider creation of the WPUMs in equation (1). We assume that the particle in potential V0 is in the ground state at the initial time. The amplitude of the wave function ϕ(x) satisfies
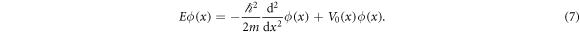
We aim to derive the potential which drives the initial state to the WPUMs. In this section we consider the case where ϕ(x) is unchanged during the phase imprinting. We discuss the case where the amplitude changes in the latter sections.
3.1. Driving potential
We use the wave function ansatz given by

where R changes monotonically from 0 to 1 with time. We typically choose the time dependence of R as [8]

so that the particle is in the ground state, ϕ, at t = 0 and becomes the target WPUM at t = T. The time dependence of R is arbitrary as long as it satisfies conditions 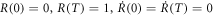 , although we use the particular form in equation (9) for the present study for concreteness. Conditions R(0) = 0 and R(T) = 1 guarantee that the state is in the given initial state at t = 0 and the target state at t = T, respectively. The reason of the conditions:
, although we use the particular form in equation (9) for the present study for concreteness. Conditions R(0) = 0 and R(T) = 1 guarantee that the state is in the given initial state at t = 0 and the target state at t = T, respectively. The reason of the conditions: 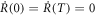 is explained below in this section.
is explained below in this section.
The time-dependent Schrödinger equation is represented as
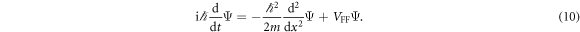
We divide equation (10) by Ψ and compare the real parts of the both sides to obtain the driving potential
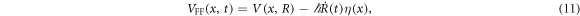
where 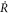 is the time derivative of R, and
is the time derivative of R, and 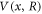 is defined by
is defined by
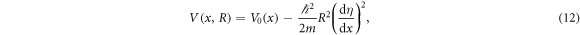
with V0, the initial trapping potential, given by
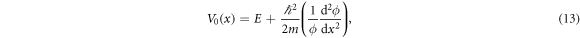
which is obtained by dividing equation (7) by 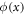 . Note that the imaginary part vanishes because of equation (3). Here, V(x, R) is the potential which can maintain the WPUM in equation (8) for a fixed R. The second term in equation (11), which vanishes when
. Note that the imaginary part vanishes because of equation (3). Here, V(x, R) is the potential which can maintain the WPUM in equation (8) for a fixed R. The second term in equation (11), which vanishes when 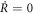 , is for the non-adiabatic driving of the state. As seen in equation (9),
, is for the non-adiabatic driving of the state. As seen in equation (9), 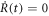 for t < 0 and t > T. Therefore the driving potential in equation (11) continuously changes from V0 to
for t < 0 and t > T. Therefore the driving potential in equation (11) continuously changes from V0 to 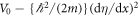 .
.
3.2. Scaling property of dynamics
The results obtained in section 3.1 reveal the scaling property of the quantum dynamics. Once a pair of ϕ and η is found, we obtain the driving potential which realizes the state in equation (8) for any time dependence of R because the form of the driving potential in equation (11) is independent of the form of R. (Note that R does not have to start from 0 nor to become 1 at t = T for the validity of the scaling property.)
A pair composed of the dynamics of the system and the corresponding driving potential, {Ψ[R], VFF[R]} , are characterized by R, a function of time. We can consider the ensemble composed of such infinite number of pairs. The ensemble can be represented by one of Ψ[R]. Thus, infinite number of the pairs of the dynamics and the potential corresponding to different R are related to each other. The scaling property is explained in detail for a more general case in the following section.
Due to the scaling property, the final state of an adiabatic dynamics with 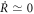 can be realized for any finite time T. As mentioned, this fast-forwarding of the dynamics is important for the creation of the target WPUM because WPUMs are short-lived under a finite potential.
can be realized for any finite time T. As mentioned, this fast-forwarding of the dynamics is important for the creation of the target WPUM because WPUMs are short-lived under a finite potential.
3.3. Example
As an example we apply the driving potential in equation (11) to a BEC of 87Rb in a harmonic trap to create a WPUM. The dynamics is governed by the GP equation
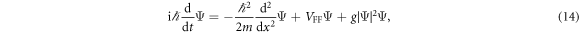
where m is the mass of the atom, g the coupling constant and Ψ the condensate order parameter. For simplicity we consider the case of g = 0. (The form of the driving potential for finite g is the same as equation (11) because 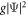 can be regarded as a part of the potential, although the driving potential differs from the one for g = 0 because of the dependence of ϕ on g [8].) We assume that the initial state is the ground state of the harmonic trap, of which the condensate order parameter is ϕ. We take the initial harmonic potential as
can be regarded as a part of the potential, although the driving potential differs from the one for g = 0 because of the dependence of ϕ on g [8].) We assume that the initial state is the ground state of the harmonic trap, of which the condensate order parameter is ϕ. We take the initial harmonic potential as
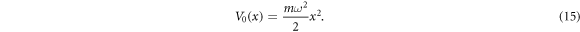
The target state is given in equation (1) with the phase in equation (4).
Figure 1 shows the phase η(x) of the target WPUM and the final potential V in equation (12) for a parameter set: ω/(2π) = 500 Hz and η0 = 2.1 × 106 (m−2). The real part of the order parameter oscillates with respect to x due to the phase change. The potential diverges to negative infinity where the amplitude of the order parameter is small.
Figure 1. (a) The purple solid curve shows the phase η(x). The green dotted curve shows the real part of the order parameter in equation (1). (b) The purple solid curve shows x-dependence of the potential at the final time T. The inset is for a small interval around x = 0. The dashed green curve represents the approximate potential that we employ in our numerical simulation.
Download figure:
Standard image High-resolution imageNow we simulate evolution of the state driven from the ground state in the harmonic potential in equation (15) to a WPUM for the same ω and η0 as in figure 1. In the following simulation we use the approximate potential of which 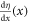 is set to
is set to 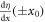 for x > x0 (=0.72 μm) and x < −x0, respectively, as exhibited in figure 1(b) to avoid drastic change in potential with respect to x and t. Figure 2(a) shows approximate VFF during the control for T = 32 μs. (Hereafter we simply refer the approximate potential as VFF instead of approximate VFF.) The potential is tilted to imprint a phase η, which is asymmetric, generating positive momentum (see the potential for t = T/4 and T/2). At the end of the control, t = T, the potential coincides with the one represented by the dashed line in figure 1(b).
for x > x0 (=0.72 μm) and x < −x0, respectively, as exhibited in figure 1(b) to avoid drastic change in potential with respect to x and t. Figure 2(a) shows approximate VFF during the control for T = 32 μs. (Hereafter we simply refer the approximate potential as VFF instead of approximate VFF.) The potential is tilted to imprint a phase η, which is asymmetric, generating positive momentum (see the potential for t = T/4 and T/2). At the end of the control, t = T, the potential coincides with the one represented by the dashed line in figure 1(b).
Figure 2. (a) VFF at the times indicated in the panel, where T = 32 μs. The initial harmonic potential represented by the black solid curve is much smaller in amplitude in this scale than the potential at different times represented by colored curves. (b) Fidelity as a function of T. The dashed line is a guide for eyes.
Download figure:
Standard image High-resolution imageFigure 2(b) shows the fidelity, as a function of T, defined as the amplitude of the overlap between the state at t = T and the target state in equation (1). The fidelity decreases with the increase of T because of the imperfection of the approximate potential. Therefore, fast control is essential for creation of the target state.
Figure 3 shows the initial and the final profiles of the square of the amplitude of the order parameter for T = 32 μs and T = 191 μs. For longer control the order parameter moves to the x-direction because of the imperfect potential. In the numerical simulation there are hard walls at x = ±4.8 μm, which reflect the order parameter. The oscillation in the order parameter for T = 191 μs is due to the interference of the order parameter with the one reflected by the hard walls, while for T = 32 μs, the order parameter approximately keeps its initial form. It might not be very obvious why the distortion of the order parameter is reduced at the final time of the creation, t = T, when T is sufficiently short and the approximated potential is sufficiently closer to the exact one in spite of the asymmetry of the potential. It is because that the target WPUM has the spatially uniform current of the amplitude of order parameter. Because the current is independent of x, the amplitude of the order parameter is stationary in the ideal case. Due to the current flowing to the x-direction, the order parameter is reflected back by the hard wall at x = 4.8 μm in the both cases for T = 32 and 192 μs. However t = 32 μs is so short that the major part of the order parameter has not been reflected yet at that time. This is the reason why the oscillation due to interference is not clearly seen at t = 32 μs.
Figure 3. Square of the amplitude of the order parameter at the initial and final times of the control for T = 32 μs and T = 191 μs.
Download figure:
Standard image High-resolution image3.4. Dynamics in free space
Suppose we release the order parameter in equation (1) by putting V = 0 at t = 0. The pattern of the order parameter is distinct from that without phase η. Thus, observation of the amplitude of the BEC after releasing can be used for an indirect measurement of the WPUMs.
Evolution of 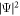 in free space is shown in figure 4(a) as a function of t and x. The spatial oscillation of
in free space is shown in figure 4(a) as a function of t and x. The spatial oscillation of  is clearly seen. The fringe pattern is moving toward positive direction of x, and the intervals between the peaks increase. Such fringe pattern is not observed with the ground state order parameter which is simply broaden. This pattern of the order parameter which resembles an expanded wing of birds is a manifestation of the spatially changing phase. Figure 4(b) shows the amplitude of the Fourier transform of Ψ at the initial time. Note that there is a fringe pattern in the Fourier transform of the order parameter in k > 0, and this initial distribution of the order parameter in the k-space is attributed to the pattern of the released order parameter in figure 4(a). Detailed study on this pattern such as the correlation between η0 and the peak intervals is beyond the scope of the present paper and will be conducted elsewhere.
is clearly seen. The fringe pattern is moving toward positive direction of x, and the intervals between the peaks increase. Such fringe pattern is not observed with the ground state order parameter which is simply broaden. This pattern of the order parameter which resembles an expanded wing of birds is a manifestation of the spatially changing phase. Figure 4(b) shows the amplitude of the Fourier transform of Ψ at the initial time. Note that there is a fringe pattern in the Fourier transform of the order parameter in k > 0, and this initial distribution of the order parameter in the k-space is attributed to the pattern of the released order parameter in figure 4(a). Detailed study on this pattern such as the correlation between η0 and the peak intervals is beyond the scope of the present paper and will be conducted elsewhere.
Figure 4. (a) 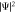 evolving in free space is shown as a function of t and x for ω/(2π) = 500 Hz and η0 = 2.1 × 106 (m–2). (b) Amplitude of the Fourier transform of the wave function at the initial time.
evolving in free space is shown as a function of t and x for ω/(2π) = 500 Hz and η0 = 2.1 × 106 (m–2). (b) Amplitude of the Fourier transform of the wave function at the initial time.
Download figure:
Standard image High-resolution image4. Phase imprinting with time-dependent amplitude of wave function
In the previous section we considered the case in which the amplitude of the wave function is time-independent during the phase imprinting. Now we consider the case in which the amplitude evolves as well as the phase. The result is applied to loading of a BEC to a predetermined Bloch state.
We consider a state represented as
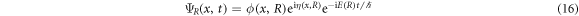
which is an instantaneous eigenstate with energy E(R) under the potential given by
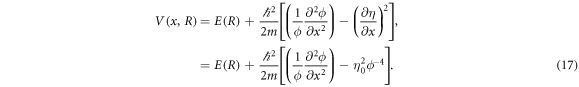
Note that ϕ is R-dependent. We call ΨR for R = 0 and ΨR for  the initial state and the target state, respectively. Here, η is given in equation (4) in terms of ϕ, and satisfies equation (3).
the initial state and the target state, respectively. Here, η is given in equation (4) in terms of ϕ, and satisfies equation (3).
4.1. Fast-forward scaling theory
Now we derive the driving potential which generates the target state. We assume that the wave function during the creation of the target state is represented as
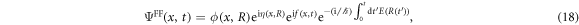
where R is a time-dependent parameter, which starts from 0 and becomes 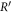 at t = T. In the intermediate wave function in equation (18), an additional phase f is introduced. The time-dependent Schrödinger equation is represented as
at t = T. In the intermediate wave function in equation (18), an additional phase f is introduced. The time-dependent Schrödinger equation is represented as
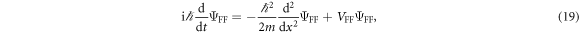
with the driving potential VFF.
We divide equation (19) by the phase factor of ΨFF and substitute equation (18), and compare the imaginary and the real parts of the both sides of the equation. Using the phase-amplitude relation in equation (3), the imaginary part leads to the equation for additional phase f as
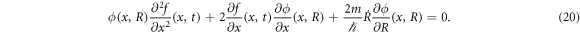
Equation (20) is to be solved to obtain f(x, t). A solution of ∂ f/∂ x is given as
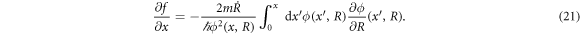
Thus, we obtain the additional phase by integrating equation (21). 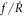 is explicitly given by
is explicitly given by
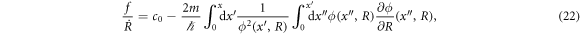
where c0 is a constant. On the other hand, the real part gives rise to the driving potential
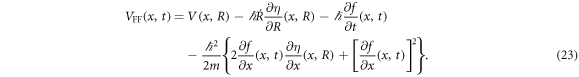
Once we set the time dependence of R, the additional phase and the driving potential are calculated using equations (22) and (23). Importantly, the additional phase vanishes at the initial time and the final time by imposing 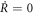 at those times as seen from equation (22). Thus we are guaranteed to obtain the target state from the initial state at predetermined time. The form of the driving potential for finite g is the same as equation (23), although the driving potential differs from the one for g = 0 because of the dependence of ϕ on g.
at those times as seen from equation (22). Thus we are guaranteed to obtain the target state from the initial state at predetermined time. The form of the driving potential for finite g is the same as equation (23), although the driving potential differs from the one for g = 0 because of the dependence of ϕ on g.
4.2. Scaling property
It is seen, from equation (20) or (22), that 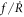 depends on R and x but not explicitly on t because ϕ depends explicitly only on R and x. This reveals that if we have the additional phase for a particular function for R, say R1(t), the additional phase for a different function R2(t) is obtained using a simple relation between the phases. (Note that we do not have an analytical form of f for higher dimensions in general.)
depends on R and x but not explicitly on t because ϕ depends explicitly only on R and x. This reveals that if we have the additional phase for a particular function for R, say R1(t), the additional phase for a different function R2(t) is obtained using a simple relation between the phases. (Note that we do not have an analytical form of f for higher dimensions in general.)
For example, we assume that the additional phase is f1 for R1 and f2 for R2. Then we have the relation

if R1(t1) = R2(t2) because the both sides of the above equation do not depend on t explicitly. (We assume that there exists t2 such that R2(t2) = R1(t1) for any t1.) Thus we obtain
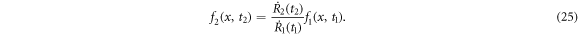
The driving potential in equation (23) is a functional of f and R. Therefore the driving potential for R2 is easily obtained if we have additional phase f1 for R1.
As in the previous section, this theory can be regarded as providing a shortcut to adiabaticity protocol because it shows the connection between the adiabatic dynamics corresponding to the  limit and accelerated dynamics with finite
limit and accelerated dynamics with finite  . However, we emphasize that this theory covers wider concept because it uncovers the connection between infinite number of non-adiabatic dynamics characterized by different R.
. However, we emphasize that this theory covers wider concept because it uncovers the connection between infinite number of non-adiabatic dynamics characterized by different R.
Equation (25) leads to
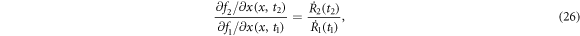
which can be interpreted as follows. The left hand side is the ratio of the currents of the probability density at x for the dynamics corresponding to R1 to that for R2 because the current is proportional to  , and we have ϕ(R1(t1), x) = ϕ(R2(t2), x). This ratio is the same as the ratio between
, and we have ϕ(R1(t1), x) = ϕ(R2(t2), x). This ratio is the same as the ratio between 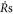 (right hand side) because it determines the ratio between the rates of the change in the probability density.
(right hand side) because it determines the ratio between the rates of the change in the probability density.
4.3. Loading to a Bloch state
Study on the motion of a particle in a spatially periodic potential has revealed interesting features of the system such as acceleration theorem formulated by Bloch [57]. The dynamics of a particle under a periodic potential and an additional linear potential has been extensively studied, e.g., asymptotic expression of Bloch oscillators in the limit of weak electric field [58] and numerical study of the dynamics of Bloch oscillation [59]. Dynamics of a particle in a periodically driven lattice potential has been also studied [60, 61]. However, to the best of our knowledge, no explicit form of the driving potential, which can load a particle into a predetermined Bloch state, has been presented.
We apply the result obtained in the above subsection to derive the driving potential without tight binding approximation, which generates a predetermined Bloch state in the lowest band from the ground state as depicted in figure 5(a).
Figure 5. (a) Energy diagram in the first Brillouin zone. The arrow indicates the driving from k = 0 state to a state with finite k. (b) Square of the amplitude of the order parameter for different values of k for 0 ≤ k ≤ 0.96π/L in a single period of the lattice potential for L = 0.8 μm. The order parameter is normalized in the single period of the potential. The arrows indicate the directions in which the order parameter changes as the wavenumber increases. (c) ϕ2(x, k) as a function of t and x for k(t) defined in equation (32). (d) Additional phase f as a function of x and t. The parameters used are the same as those used for (c).
Download figure:
Standard image High-resolution imageWe consider a BEC in an optical lattice potential

with period L and potential height V0. The order parameter of a Bloch state in Vp is represented as

with the amplitude of the order parameter ϕ(x, k) and the energy E(k). Here, k is the wavenumber. Phase η can be separated as

where Δη(x, k) is periodic with respect to x with period L as well as ϕ, that is, Δη(x + L) = Δη(x) and ϕ(x + L) = ϕ(x). Note that the profile of ϕ(x, k) depends on k as shown in figure 5(b). Note also that η satisfies the phase-amplitude relation in equation (6) because Ψk is an instantaneous energy eigenstate.
As in the previous subsections, the order parameter ansatz is written as
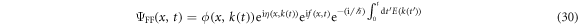
with the additional phase f. The additional phase is given by
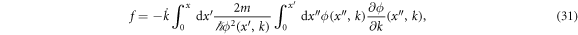
where we used equation (22) with c0 = 0 without loss of generality.
For concreteness we consider k defined by
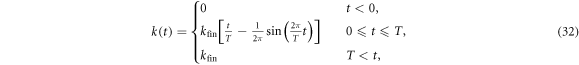
where kfin is the final (target) wavenumber. We use the parameter set: L = 0.8 μm, kfin = 0.96π/L and T = 67.5 μs. m is the mass of a 87Rb atom. V0 = 0.14 ER, where ER is defined by  with kL = π/L. Figure 5(c) shows ϕ2(x, k) as a function of t and x for k(t) defined in equation (32).
with kL = π/L. Figure 5(c) shows ϕ2(x, k) as a function of t and x for k(t) defined in equation (32).
The driving potential is given by
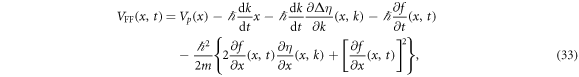
where we used equations (23) and (29). Since dk/dt = 0 for t ≤ 0 and t ≥ T the additional phase f disappears and the potential VFF coincides with the original potential Vp because f and ∂f/∂t vanish as seen from equation (31). The first and the second terms in equation (33) are the original periodic potential and the time-dependent linear potential, respectively. The linear potential corresponds to imprinting the linear phase kx. The third term corresponds to the periodic phase Δη. Other terms are attributed to the change of the profile of the amplitude of the order parameter with respect to k. There is no divergence in phase η and driving potential VFF because the amplitude of the order parameter of Bloch states in the lowest band has no node.
The driving potential in equation (33) is shown as a function of x and t in figure 6(a). In figure 6(b), simpler potential composed of the original and the linear potentials, 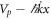 , is plotted for comparison. We refer this potential as the simple potential. The left panels in figures 6(a) and (b) are for 0 ≤ t ≤ T/2, while the right panels are for T/2 < t ≤ T. The difference between the two cases is apparent for t ≥ T/2 when ϕ(x, k) for
, is plotted for comparison. We refer this potential as the simple potential. The left panels in figures 6(a) and (b) are for 0 ≤ t ≤ T/2, while the right panels are for T/2 < t ≤ T. The difference between the two cases is apparent for t ≥ T/2 when ϕ(x, k) for 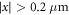 changes rapidly as shown in figure 5(c). In figures 6(c) and (d) the evolution of
changes rapidly as shown in figure 5(c). In figures 6(c) and (d) the evolution of  is shown for the potentials in figures 6(a) and (b), respectively. The fidelity, which is defined as the amplitude of the overlap between the state at t = T and the target state in equation (28), is 0.99 for the control with VFF and 0.95 for the control with the simple potential. Infidelity (decrease of the fidelity) of the control with VFF is attributed to numerical error. The evolutions of
is shown for the potentials in figures 6(a) and (b), respectively. The fidelity, which is defined as the amplitude of the overlap between the state at t = T and the target state in equation (28), is 0.99 for the control with VFF and 0.95 for the control with the simple potential. Infidelity (decrease of the fidelity) of the control with VFF is attributed to numerical error. The evolutions of 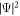 driven by the potentials exhibit clear difference although the difference of the fidelities is not significant. The evolution of
driven by the potentials exhibit clear difference although the difference of the fidelities is not significant. The evolution of 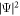 is almost the same as the ideal one shown in figure 5(c). On the other hand, the evolution of
is almost the same as the ideal one shown in figure 5(c). On the other hand, the evolution of  in figure 6(d) clearly differs from the one in figure 5(c) due to the lack of the potential which supports the change in the amplitude of the order parameter.
in figure 6(d) clearly differs from the one in figure 5(c) due to the lack of the potential which supports the change in the amplitude of the order parameter.
Figure 6. (a) The driving potential VFF normalized by ER as a function of x and t. (b) 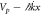 normalized by ER as a function of x and t. (c) Square of the amplitude of the order parameter driven by VFF and (d) the simple potential,
normalized by ER as a function of x and t. (c) Square of the amplitude of the order parameter driven by VFF and (d) the simple potential, 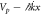 .
.
Download figure:
Standard image High-resolution image5. Summary and discussion
We have introduced phase imprinting on the order parameter of BECs with the fast-forward scaling theory uncovering the nontrivial scaling property of quantum dynamics. The form of the driving potential for the phase imprinting has been explicitly derived. The obtained scaling property reveals the connection between infinite number of the pairs composed of the dynamics (including adiabatic dynamics) and the corresponding potential. Due to the scaling property the final state of an adiabatic dynamics can be realized for any desired finite time. Thus, it can be regarded as a shortcut to adiabaticity. Moreover, we emphasize that this theory covers wider concepts because it uncovers the connection between infinite number of non-adiabatic dynamics.
The theory has been applied to derive the driving potential for creation of WPUMs density, which are introduced in this paper. The state has infinite expectation value of the momentum and finite energy in ideal condition but is short-lived due to imperfection of potential in actual systems. (The state cannot be stable after creation because of imperfection of the driving and the final stationary potentials.) Thus, fast manipulation is essential for the creation of the WPUMs because of the instability of the state. The driving potential to create the WPUMs has been derived.
We have also studied the loading of a BEC, which is in the ground state of a periodic potential initially, into a predetermined Bloch state in the lowest band. Controlling a linear potential is not sufficient for the creation of the Bloch state when the target wavenumber is large because the change in the amplitude of the order parameter is not negligible. We have exactly shown the required modification of the driving potential from the time-dependent linear potential extending the theory to the case that the amplitude of the order parameter changes as well as the phase.
Acknowledgments
SM acknowledges the support from JST ERATO (Grant No. JPMJER1601). MN is grateful to JSPS for partial support from a Grants-in-Aid for Scientific Research (Grant No. 17K05554).









