Abstract
Contrary to traditional thinking and driver intuition, here we show that there is no benefit to ground vehicles increasing their packing density at stoppages. By systematically controlling the packing density of vehicles queued at a traffic light on a Smart Road, drone footage revealed that the benefit of an initial increase in displacement for close-packed vehicles is completely offset by the lag time inherent to changing back into a 'liquid phase' when flow resumes. This lag is analogous to the thermodynamic concept of the latent heat of fusion, as the 'temperature' (kinetic energy) of the vehicles cannot increase until the traffic 'melts' into the liquid phase. These findings suggest that in situations where gridlock is not an issue, drivers should not decrease their spacing during stoppages in order to lessen the likelihood of collisions with no loss in flow efficiency. In contrast, motion capture experiments of a line of people walking from rest showed higher flow efficiency with increased packing densities, indicating that the importance of latent heat becomes trivial for slower moving systems.
Export citation and abstract BibTeX RIS

Original content from this work may be used under the terms of the Creative Commons Attribution 3.0 licence. Any further distribution of this work must maintain attribution to the author(s) and the title of the work, journal citation and DOI.
1. Introduction
Any driver knows the unspoken rule that vehicles should increase their packing density at stoppages such as red lights or traffic jams. However, this 'liquid-to-solid' phase transition can be a source of accidents. For instance, rear-end crashes are the most common accident at work zones, due to the tailgating inherent to the frequent stop-and-go phase transitions [1, 2]. More generally, it was estimated that over a quarter of all car crashes were rear-end collisions, which almost always occur due to short headways between vehicles [3]. Given the increased safety risk, close-packing at queues can only be justified if it significantly improves the efficiency of traffic flow; it is therefore surprising that there have been virtually no studies on the effects of spacing on the efficiency of group motion from rest. It is not necessarily a given that inducing phase transitions at stoppages increases flow efficiency, as reverting back into the liquid phase when motion is resumed is analogous to the input of 'latent heat,' which produces significant lag.
Various types of non-physical systems including traffic and granular flows or economic, social, and biological systems have been modeled by employing statistical physics, nonlinear dynamics, and thermodynamical considerations [4–9]. Similar modeling techniques have also been used to model the social interactions and collective behavior of various animal species [10–13]. For the specific context of vehicular traffic flow, several models have been developed that are macroscopic (fluid dynamics) [14, 15], microscopic (follow-the-leader) [16, 17], or mesoscopic (Lattice gas automata) [18, 19].
Perhaps the most impactful traffic model is the optimal velocity model (OVM) pioneered by Bando et al, where the acceleration and deceleration forces of each individual car are a function of the spacing between cars, the speed limit of the road, and the sensitivity of the drivers [16, 17, 20–24]. The OVM has been correlated with experiments of single-lane traffic on circuits [25, 26] or freeways [27–31], but nearly always in the context of beginning with flow in the liquid phase and identifying critical conditions for jamming to occur. To the best of our knowledge, the reverse situation of cars moving from rest has not been considered, aside from some brief mentions in purely theoretical implementations of OVM [32, 33].
Weber and Mahnke have recently expanded the OVM to develop expressions for the internal energy and kinetic energy of the traffic system [34]. This thermodynamical approach was used to calculate the theoretical change in energy for a liquid-to-solid phase transition [35]. While these works were an important first step toward conceptualizing the thermodynamics of phase transitions, no experiments were done to test the model and only the liquid-to-solid phase transition was considered, not the reverse case of solid-to-liquid.
The dynamics of pedestrian traffic are analogous to vehicles, except that flow is two-dimensional and the preferred direction of the pedestrians has to be considered [36]. As with traffic studies, most models of pedestrians focus on beginning with the liquid phase and identifying bottlenecks that cause jamming [37–41], not the latent heat associated with motion from rest.
Here, for the first time we show both experimentally and theoretically how the physics of group motion from rest are governed by the thermodynamic concept of latent heat. Two different types of experiments were conducted: one with ten cars stopped at a red light and a second with pedestrians queued in a single-file line, where the initial separation between each car/person was varied and the resulting movement through the intersection/line was captured with a drone/motion-capture. Correlating the results to the OVM revealed a universal trend that the interaction potential of a group at rest must go to zero in order for group motion to fully resume, resulting in the latent heat (lag time) inherent to group motion from rest. For the slow-moving pedestrian system, the intuition to close-pack in a queue is correct, as the increase in lag time is minor relative to the savings in displacement. However, the importance of latent heat for vehicles was profound: the time required for cars to cross the intersection did not vary even as the initial spacing between cars was increased by a factor of 20. Hence, the current rule of thumb that vehicles should become close-packed at stoppages does not appear to be sensible, as safer spacings can be maintained with no reduction in the departure flow rate.
2. Car motion through a traffic light
2.1. Smart Road experiments
Ten volunteer drivers conducted a study on the closed-circuit Smart Road located at the Virginia Tech Transportation Institute (figure 1(A)). Each driver was provided a Chevy Impala (LS Sedan 4D, 2011-2012) of identical dimensions that was rented from Virginia Tech Fleet Services and insured for the study. The Smart Road includes a traffic light located in the middle of a flat, straight road with single lanes and a speed limit of 35 mph (15.6 m s−1). The traffic light was initially set to red and all ten volunteer drivers were instructed to line up in a queue. Using radio transmitters and approved safety protocols (IRB #15-484, see appendix A), each driver came to a stop at a fixed bumper-to-bumper spacing ( ) from the car ahead. Spacings were measured by fixing a tape measure between two tall traffic cones; one cone was placed at the rear bumper of a car already stopped in 'Park', while another car was instructed to slowly approach the second cone until its front bumper made contact. For any given trial, all cars in the queue exhibited an identical value of
) from the car ahead. Spacings were measured by fixing a tape measure between two tall traffic cones; one cone was placed at the rear bumper of a car already stopped in 'Park', while another car was instructed to slowly approach the second cone until its front bumper made contact. For any given trial, all cars in the queue exhibited an identical value of  , which was varied to be either 1.25 ft (0.38 m), 3 ft (0.91 m), 6 ft (1.8 m), 12 ft (3.6 m), 25 ft (7.6 m), or 50 ft (15 m). Once all ten cars were queued at the red light with the appropriate spacing, a drone helicopter (DJI Inspire 1) was programmed to hover over the intersection at a fixed elevation of 200 ft (61 m) with respect to the road. The drone included a digital video camera attached to a gimbal (DJI Zenmuse X3) to obtain controlled bird's-eye-view footage of the traffic. All drivers could see the traffic signal and they were instructed to accelerate in a normal and comfortable fashion up to the road's speed limit of 35 mph when the light turned green. It was strongly emphasized that the bumper-to-bumper spacing initially imposed at the red light does not need to be maintained once flow resumed. Three trials were captured for each car spacing, with the order of the drivers changing for each trial. For consistency, the three different driver orders chosen for the three trials were kept the same for all six car spacings. When the cars and drone were all in place, the drivers were instructed to put their cars in 'Drive' and proceed through the intersection when the light turned green. Once all drivers confirmed via radio that they were idling and ready to go, the traffic light was turned to green using a Smart phone interfaced with the Smart light.
, which was varied to be either 1.25 ft (0.38 m), 3 ft (0.91 m), 6 ft (1.8 m), 12 ft (3.6 m), 25 ft (7.6 m), or 50 ft (15 m). Once all ten cars were queued at the red light with the appropriate spacing, a drone helicopter (DJI Inspire 1) was programmed to hover over the intersection at a fixed elevation of 200 ft (61 m) with respect to the road. The drone included a digital video camera attached to a gimbal (DJI Zenmuse X3) to obtain controlled bird's-eye-view footage of the traffic. All drivers could see the traffic signal and they were instructed to accelerate in a normal and comfortable fashion up to the road's speed limit of 35 mph when the light turned green. It was strongly emphasized that the bumper-to-bumper spacing initially imposed at the red light does not need to be maintained once flow resumed. Three trials were captured for each car spacing, with the order of the drivers changing for each trial. For consistency, the three different driver orders chosen for the three trials were kept the same for all six car spacings. When the cars and drone were all in place, the drivers were instructed to put their cars in 'Drive' and proceed through the intersection when the light turned green. Once all drivers confirmed via radio that they were idling and ready to go, the traffic light was turned to green using a Smart phone interfaced with the Smart light.
Figure 1. (A) Schematic of the experiment performed on a Smart Road, where ten volunteer drivers with identical Chevy Impalas (length  m) were queued at a red light with a controlled bumper-to-bumper spacing (
m) were queued at a red light with a controlled bumper-to-bumper spacing ( ) (see supplementary movie S1 available online at stacks.iop.org/NJP/19/113034/mmedia). When the light turned green, a drone flying overhead captured the acceleration of the cars through the intersection as a function of
) (see supplementary movie S1 available online at stacks.iop.org/NJP/19/113034/mmedia). When the light turned green, a drone flying overhead captured the acceleration of the cars through the intersection as a function of  . (B) Drone footage revealed that it takes more time for cars to begin to move for small values of
. (B) Drone footage revealed that it takes more time for cars to begin to move for small values of  compared to larger values, which can be conceptualized as the latent heat of transitioning from a solid phase to a liquid phase (see supplementary movie S2). Time zero for all figures corresponds to the leading car's onset of motion, as the drone could not see exactly when the light turned green.
compared to larger values, which can be conceptualized as the latent heat of transitioning from a solid phase to a liquid phase (see supplementary movie S2). Time zero for all figures corresponds to the leading car's onset of motion, as the drone could not see exactly when the light turned green.
Download figure:
Standard image High-resolution imageThe drone footage showed that it takes more time for cars to begin to accelerate with decreasing  (figure 1(B)). For example, when
(figure 1(B)). For example, when  m (top images), the third car in the queue is not moving even after 6 s from when the first car began to accelerate through the intersection. This is because of the long delay time required for each car to regain a safe distance to the car ahead before readily accelerating (latent heat). In contrast, when
m (top images), the third car in the queue is not moving even after 6 s from when the first car began to accelerate through the intersection. This is because of the long delay time required for each car to regain a safe distance to the car ahead before readily accelerating (latent heat). In contrast, when  m, the latent heat is reduced and even the fifth car is able to move within the initial 6 s.
m, the latent heat is reduced and even the fifth car is able to move within the initial 6 s.
An open-source software (Tracker) was used to convert the drone footage to displacement plots for each car. Solid lines in figure 2 show the displacements of the front bumpers of all ten cars over time for each value of  , with all values being averaged from the 3 separate trials to mitigate effects of driver variability. Remarkably, the time required for all ten cars to cross the intersection remained fixed at 23.0 ± 1.1 s for all spacings ranging from
, with all values being averaged from the 3 separate trials to mitigate effects of driver variability. Remarkably, the time required for all ten cars to cross the intersection remained fixed at 23.0 ± 1.1 s for all spacings ranging from  m up to
m up to  m (figure 3(A)), even though in the latter case
m (figure 3(A)), even though in the latter case  is larger by a factor of 20 and the vehicles are traveling twice as far to cross the intersection (figure 2(A), (E)). This balance between reduced lag and increased displacement is eventually lost, but only for the extreme case where
is larger by a factor of 20 and the vehicles are traveling twice as far to cross the intersection (figure 2(A), (E)). This balance between reduced lag and increased displacement is eventually lost, but only for the extreme case where  exceeds the minimum spacing required for comfortable driving (analogous to a 'gas phase'). For example, the cars required a slightly larger time of 27 ± 3 s for
exceeds the minimum spacing required for comfortable driving (analogous to a 'gas phase'). For example, the cars required a slightly larger time of 27 ± 3 s for  m (figure 3(A)). Moreover, as it is depicted in figure C1(A), the time required for each car to cross the intersection was found independent of the static bumper-to-bumper spacing as
m (figure 3(A)). Moreover, as it is depicted in figure C1(A), the time required for each car to cross the intersection was found independent of the static bumper-to-bumper spacing as  varies from 0.38 to 7.6 m.
varies from 0.38 to 7.6 m.
Figure 2. Experimental (solid lines) and theoretical (dashed lines) displacements of ten cars driving from rest through a traffic light. The initial location of the lead car's front bumper is defined as  and each vehicle effectively clears the intersection upon reaching
and each vehicle effectively clears the intersection upon reaching  m. The initial bumper-to-bumper spacings of the cars was (A)
m. The initial bumper-to-bumper spacings of the cars was (A)  ft (0.38 m), (B)
ft (0.38 m), (B)  ft (0.91 m), (C)
ft (0.91 m), (C)  ft (1.8 m), (D)
ft (1.8 m), (D)  ft (3.6 m), (E)
ft (3.6 m), (E)  ft (7.6 m), (F)
ft (7.6 m), (F)  ft (15 m). Experimental lines represent an average of 3 trials and the alternating blue and green colors are to help guide the eye. The black dashed lines represent the optimal velocity model, where bf is a fitting parameter representing the inflection point of the optimal velocity function that will be discussed fully in section 2.2. For visualization purposes, the y-axis is not scaled the same for graphs (A)–(F).
ft (15 m). Experimental lines represent an average of 3 trials and the alternating blue and green colors are to help guide the eye. The black dashed lines represent the optimal velocity model, where bf is a fitting parameter representing the inflection point of the optimal velocity function that will be discussed fully in section 2.2. For visualization purposes, the y-axis is not scaled the same for graphs (A)–(F).
Download figure:
Standard image High-resolution imageFigure 3. (A) Mean total time required for all ten cars to drive through the intersection. Time zero corresponds to when the lead car begins to move. The hashed region depicts the start-up lost time, which by convention is the time for the first four cars to pass the intersection. Error bars show one standard deviation between the three trials. The effect of condition is statistically significant for the total time and start-up lost time, using two one-way ANOVAs (JMP Pro 11 software,  for significance). Conditions sharing the same letters are not significantly different in terms of Tukey post hoc tests (
for significance). Conditions sharing the same letters are not significantly different in terms of Tukey post hoc tests ( ). There is no statistically significant difference in the start-up lost time for all six spacings, despite a variance in the bumper-to-bumper spacing by a factor of 40; only the conditions with smallest and largest initial spacings show statistically significant differences for the total time. (B) Displacement versus time of the last (tenth) car in the line for different static bumper-to-bumper spacings. (C) Drone imaging of the vehicular flow dynamics for all the six spacings at
). There is no statistically significant difference in the start-up lost time for all six spacings, despite a variance in the bumper-to-bumper spacing by a factor of 40; only the conditions with smallest and largest initial spacings show statistically significant differences for the total time. (B) Displacement versus time of the last (tenth) car in the line for different static bumper-to-bumper spacings. (C) Drone imaging of the vehicular flow dynamics for all the six spacings at  , 10 s, and the time when the last car crosses the finished-line. (D), (E) Non-dimensionalized interaction potential and kinetic energy of the system versus time.
, 10 s, and the time when the last car crosses the finished-line. (D), (E) Non-dimensionalized interaction potential and kinetic energy of the system versus time.
Download figure:
Standard image High-resolution imageFigure 4. (A) Experiments with queues of pedestrians used motion-capture facilities to characterize the flow out of a line as a function of initial packing densities. (B) Mean total time required for the first 16 pedestrians to exit the line increased with increasing spacings, revealing that latent heat is not as important for pedestrians as for vehicles, see supplementary movie S3. The hashed region shows the start-up lost time required for the fourth pedestrian to exit the line. Error bars show one standard deviation between the three trials. The effect of condition is statistically significant for the total time and start-up lost time, using two one-way ANOVAs (JMP Pro 11 software,  ). Conditions sharing the same letters are not significantly different in terms of Tukey post hoc tests (
). Conditions sharing the same letters are not significantly different in terms of Tukey post hoc tests ( ). Both the start-up lost time and the total evacuation time are increasing with larger initial spacings by a statistically significant amount, with possible overlap between adjacent values of
). Both the start-up lost time and the total evacuation time are increasing with larger initial spacings by a statistically significant amount, with possible overlap between adjacent values of  . (C) Displacement versus time of the last last person in the line for each spacing. (D), (E) Non-dimensionalized interaction potential and kinetic energy of the pedestrian traffic.
. (C) Displacement versus time of the last last person in the line for each spacing. (D), (E) Non-dimensionalized interaction potential and kinetic energy of the pedestrian traffic.
Download figure:
Standard image High-resolution imageIt is already well known that the saturation flow rate of vehicles passing through a green light is generally fixed around 1500–1800 vphg (vehicles per hour of green) over a wide variety of natural driving conditions [42–44]. However, this is because the saturation flow rate only considers the steady-state case of cars that are already crossing the intersection with a constant liquid-phase headway (figure C2(A)) [45–47], thus ignoring the initial start-up lost time where the solid-to-liquid transition actually occurs. Our focus here is therefore not on the saturation flow rate, but on the start-up lost time (i.e. departure flow rate) which considers the time required for the first four cars in the queue to cross the intersection when the light first turns green. By breaking up the total time required for all 10 cars to cross the intersection into the transient and steady times, we observe that both the departure flow rate and the saturation flow rate are insensitive to  for all solid and liquid-phase packing densities (figures 3(A), C2(B)). By definition, it is obvious that the saturation flow rate is independent of
for all solid and liquid-phase packing densities (figures 3(A), C2(B)). By definition, it is obvious that the saturation flow rate is independent of  , so we emphasize that our surprising finding is that even the start-up lost time is invariant with
, so we emphasize that our surprising finding is that even the start-up lost time is invariant with  due to the effect of latent heat. Previous reports have characterized how the start-up lost time can be affected by inclement weather [48], countdown timers [49, 50], the time of day or speed limit [51], and distracted drivers [52, 53]. However, to our knowledge there are no reports where the effects of the initial (static) car spacing on the start-up lost time were investigated, which is the novelty of our present work.
due to the effect of latent heat. Previous reports have characterized how the start-up lost time can be affected by inclement weather [48], countdown timers [49, 50], the time of day or speed limit [51], and distracted drivers [52, 53]. However, to our knowledge there are no reports where the effects of the initial (static) car spacing on the start-up lost time were investigated, which is the novelty of our present work.
2.2. Theoretical model
The above results show the pronounced effect of latent heat on group motion from rest, which will now be examined analytically using the OVM. The development of a theoretical model will be especially useful for extrapolating the displacement curves of the experiments done with large spacings ( m), where the drone's field-of-view could not capture the initial position and acceleration of several cars at the back of the queue (see figures 2(D)–(F) and movie S2). Recall that the OVM is a semi-empirical microscopic model and can be used to develop theoretical displacement curves to match the experiments. The equation of motion for the i-th car with mass M and velocity vi is [32]:
m), where the drone's field-of-view could not capture the initial position and acceleration of several cars at the back of the queue (see figures 2(D)–(F) and movie S2). Recall that the OVM is a semi-empirical microscopic model and can be used to develop theoretical displacement curves to match the experiments. The equation of motion for the i-th car with mass M and velocity vi is [32]:
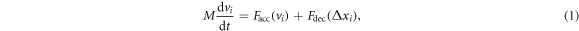
where  and
and  are the acceleration and deceleration forces acting on the car, respectively, and
are the acceleration and deceleration forces acting on the car, respectively, and  is the headway distance between the
is the headway distance between the  th and ith cars (
th and ith cars ( ).
).
The acceleration and deceleration functions are defined as:
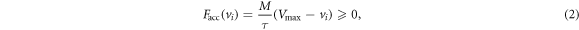
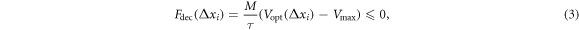
where τ is the delay time and defined as the inverse of drivers' sensitivity ( ). The higher the sensitivity of a driver, the faster the driver will accelerate or decelerate to reach the optimal velocity. The value of a is typically chosen to fit the model to the experimental displacement curves; here, a constant value of a = 0.15 s−1 was assigned to all drivers. The Vmax term in equation (2) corresponds to the speed limit of the road (15.6 m s−1). In equation (3),
). The higher the sensitivity of a driver, the faster the driver will accelerate or decelerate to reach the optimal velocity. The value of a is typically chosen to fit the model to the experimental displacement curves; here, a constant value of a = 0.15 s−1 was assigned to all drivers. The Vmax term in equation (2) corresponds to the speed limit of the road (15.6 m s−1). In equation (3),  represents the optimal velocity desired by each car at any moment in time as a function of the headway distance, and is represented by the optimal velocity function (OVF) [16]:
represents the optimal velocity desired by each car at any moment in time as a function of the headway distance, and is represented by the optimal velocity function (OVF) [16]:
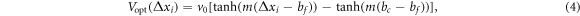
where the four parameters v0, m, bf and bc are constants obtained from the experiments. Specifically, v0 is a velocity term solved from boundary conditions, m is a fitting parameter, bf is the inflection point in the OVF, and bc is the critical lower limit of the headway distance that represents jamming. Note that while there are alternate expressions for the OVF in the literature [24, 34], we found that equation (4) resulted in the best fit with the experimental data.
To obtain the value of bc, let us define the actual length of the car as lc, which is approximately 5 m for the Chevy Impalas used in this study. Obviously, even in traffic jams each driver must maintain a headway distance larger than the actual car length to avoid crashing. Therefore the effective length of each car (bc) must include a minimal bumper-to-bumper spacing (typically  m), such that
m), such that  m. Note that for the controlled experiments performed here, the parameter space deliberately included
m. Note that for the controlled experiments performed here, the parameter space deliberately included  (by virtue of using traffic cones and spotters) to probe the full extent of latent heat. A solution for v0 can be obtained by considering the limiting case of
(by virtue of using traffic cones and spotters) to probe the full extent of latent heat. A solution for v0 can be obtained by considering the limiting case of  , where the optimal velocity of each car will simply be the speed limit (
, where the optimal velocity of each car will simply be the speed limit ( ) and
) and  . This simplifies equation (4) to
. This simplifies equation (4) to ![${v}_{0}={V}_{\max }/[1-\tanh (m({b}_{c}-{b}_{f}))]$](https://content.cld.iop.org/journals/1367-2630/19/11/113034/revision1/njpaa95f0ieqn51.gif) , where here
, where here  m−1 for each spacing. Finally, the inflection point of the OVF is defined as
m−1 for each spacing. Finally, the inflection point of the OVF is defined as  in which
in which  and B is a fitting parameter to be determined from the experimental data. In equation (3), the deceleration force reaches to its maximum value when
and B is a fitting parameter to be determined from the experimental data. In equation (3), the deceleration force reaches to its maximum value when  and it goes to zero as
and it goes to zero as  goes to infinity. In summary, we utilize a constant value for τ,
goes to infinity. In summary, we utilize a constant value for τ,  , lc,
, lc,  , bc, and m for all trials, such that only B and by extension bf and v0 are varying with
, bc, and m for all trials, such that only B and by extension bf and v0 are varying with  . For a given trial, all of these terms are the same for all ten drivers. Despite the fact that
. For a given trial, all of these terms are the same for all ten drivers. Despite the fact that  for some of the experiments here (
for some of the experiments here ( m and
m and  m), fitting B to the experimental data ensures that
m), fitting B to the experimental data ensures that  over the entire parameter space even when modeling the initial motion from rest (figure C3).
over the entire parameter space even when modeling the initial motion from rest (figure C3).
The governing differential equations of the system can be found by substituting equations (2) and (3) into equation (1) [16]:

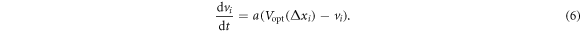
We have used Mathematica to integrate the coupled equations of motion, equations (5) and (6), in order to determine the position and velocity of each car at every moment of time. The dashed black lines in figure 2 show the theoretical displacement curves, which agree with their experimental counterparts within the experimental uncertainty for all times (figure C4). Therefore, we can use the theoretical solution to extract all of the velocity and acceleration curves for each spacing (figures C5 and C6). Note that minor differences in the initial positions of the cars are due to imperfections in aligning the cars experimentally compared to the perfectly consistent values of  used in the model.
used in the model.
By plotting the theoretical displacement curves of the final (tenth) car in the line for each value of  , it can be seen that the increased travel distance required for liquid phase queues is perfectly compensated for by a reduced lag in acceleration compared to solid phase queues (figure 3(B)). This is also evident by looking at the drone footage for each value of
, it can be seen that the increased travel distance required for liquid phase queues is perfectly compensated for by a reduced lag in acceleration compared to solid phase queues (figure 3(B)). This is also evident by looking at the drone footage for each value of  (figure S3 and movie S2). As mentioned before, the time required to clear the intersection does finally increase for the largest ('gas phase') spacing of
(figure S3 and movie S2). As mentioned before, the time required to clear the intersection does finally increase for the largest ('gas phase') spacing of  m, where the increase in required displacement finally becomes greater than the reduction in lag. The theoretical time required for each of the ten cars to cross the intersection is in excellent agreement with the experimental results (figure C1).
m, where the increase in required displacement finally becomes greater than the reduction in lag. The theoretical time required for each of the ten cars to cross the intersection is in excellent agreement with the experimental results (figure C1).
As  increases, the delay time required until each vehicle begins to move with respect to the car in front of it will be decreased (figures C5 and C6). For example, 20 s after the first car begins to move, the average velocity of the tenth car increased by 49% when comparing
increases, the delay time required until each vehicle begins to move with respect to the car in front of it will be decreased (figures C5 and C6). For example, 20 s after the first car begins to move, the average velocity of the tenth car increased by 49% when comparing  m to
m to  m.
m.
To characterize the lag of vehicular motion in terms of the concept of latent heat, we first need to develop an expression for the internal energy of the system. The total interaction potential of the vehicles is [34]:
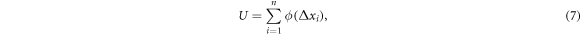
where  is the interaction potential function which represents the interaction between the
is the interaction potential function which represents the interaction between the  th car and the ith car ahead. The interaction potential function can be obtained from the integration of the deceleration force function with respect to
th car and the ith car ahead. The interaction potential function can be obtained from the integration of the deceleration force function with respect to  :
:
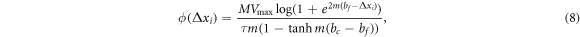
with the boundary condition  (see the appendi B for the full derivations). Figure 3(D) plots the total non-dimensionalized interaction potential,
(see the appendi B for the full derivations). Figure 3(D) plots the total non-dimensionalized interaction potential,  , versus time for each value of
, versus time for each value of  . As expected, the interaction potential of the system is dramatically larger with decreasing
. As expected, the interaction potential of the system is dramatically larger with decreasing  , for example the potential for
, for example the potential for  m (smallest spacing) is nearly three times larger than for
m (smallest spacing) is nearly three times larger than for  m (biggest spacing). Interestingly, the interaction potential is completely reduced to zero well before the cars are able to cross the intersection, which reveals that drivers do not feel comfortable reaching even moderate velocities under the presence of internal energy. This explains the significant lag time of close-packed queues of vehicles upon resumption of flow, where the interaction potentials are dramatically increased relative to loose-packed systems. We therefore define the latent heat of fusion as equivalent to the queue's total interaction potential at rest. To our knowledge, this is the first such definition of latent heat with regards to group motion from rest.
m (biggest spacing). Interestingly, the interaction potential is completely reduced to zero well before the cars are able to cross the intersection, which reveals that drivers do not feel comfortable reaching even moderate velocities under the presence of internal energy. This explains the significant lag time of close-packed queues of vehicles upon resumption of flow, where the interaction potentials are dramatically increased relative to loose-packed systems. We therefore define the latent heat of fusion as equivalent to the queue's total interaction potential at rest. To our knowledge, this is the first such definition of latent heat with regards to group motion from rest.
The total kinetic energy of the system is:
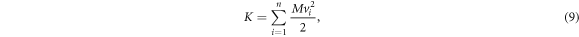
which can be non-dimensionalized by the maximum kinetic energy( ) and plotted versus time for each car spacing (figure 3(E)). Looking at figures 3(D), (E) together, one can conclude that the kinetic energy of the system cannot come close to its maximum value until the interaction potential goes to zero. Trying to accelerate cars packed in a solid-phase is somewhat analogous to trying to heat a bucket of ice water. Just as the energy input into the ice water cannot be converted to sensible heat until all ice has melted by the latent heat of fusion, the cars cannot readily increase their 'temperature' (kinetic energy) until the solid phase has 'melted' into the liquid phase.
) and plotted versus time for each car spacing (figure 3(E)). Looking at figures 3(D), (E) together, one can conclude that the kinetic energy of the system cannot come close to its maximum value until the interaction potential goes to zero. Trying to accelerate cars packed in a solid-phase is somewhat analogous to trying to heat a bucket of ice water. Just as the energy input into the ice water cannot be converted to sensible heat until all ice has melted by the latent heat of fusion, the cars cannot readily increase their 'temperature' (kinetic energy) until the solid phase has 'melted' into the liquid phase.
3. Pedestrians emptying a line
3.1. Motion-capture experiments
It is now clear that latent heat plays a major role in the dynamics of vehicular motion starting from rest. But how general are these findings? In the preceding section, we defined the latent heat as equivalent to the total interaction potential of the queue at rest:  . According to the OVM model, the value of Ui is dependent upon system parameters such as the maximum speed (Vmax) and the sensitivity (
. According to the OVM model, the value of Ui is dependent upon system parameters such as the maximum speed (Vmax) and the sensitivity ( ) of each moving body (equations (7), (8)). Therefore it is possible that, for systems where moving bodies are slow and/or able to quickly accelerate, the latent heat becomes less significant and it may no longer be desirable to avoid phase transitions at stoppages. To test this hypothesis, a second set of experiments were performed to study the effects of latent heat on the group motion of pedestrians, who move slowly and accelerate quickly relative to vehicles. The experiment was performed at the Moss Arts Center at Virginia Tech in a motion-capture room called 'The Cube'. Using approved protocols (IRB #14-914), a group of 27 volunteers were asked to form a one-dimensional line that was defined by plastic chains suspended between stanchions (figures 4(A) and C7). As with the vehicles, the spacing between pedestrians at rest in the line was systematically varied and 3 trials were performed for each spacing. In one set of experiments the subjects were instructed to pack together as close as possible (average period of 0.37 m), while subsequent experiments fixed the person-to-person spacing at 3 ft (0.91 m), 6 ft (1.8 m), and 12 ft (3.6 m).
) of each moving body (equations (7), (8)). Therefore it is possible that, for systems where moving bodies are slow and/or able to quickly accelerate, the latent heat becomes less significant and it may no longer be desirable to avoid phase transitions at stoppages. To test this hypothesis, a second set of experiments were performed to study the effects of latent heat on the group motion of pedestrians, who move slowly and accelerate quickly relative to vehicles. The experiment was performed at the Moss Arts Center at Virginia Tech in a motion-capture room called 'The Cube'. Using approved protocols (IRB #14-914), a group of 27 volunteers were asked to form a one-dimensional line that was defined by plastic chains suspended between stanchions (figures 4(A) and C7). As with the vehicles, the spacing between pedestrians at rest in the line was systematically varied and 3 trials were performed for each spacing. In one set of experiments the subjects were instructed to pack together as close as possible (average period of 0.37 m), while subsequent experiments fixed the person-to-person spacing at 3 ft (0.91 m), 6 ft (1.8 m), and 12 ft (3.6 m).
The person at the front of the line was adjacent to a detachable rope, which was removed to initiate group motion once all 27 pedestrians were in place. The volunteers were instructed in advance to proceed from the line into an adjacent open space by walking at a normal pace without any passing. Each pedestrian wore a black hat containing a white motion-capture tracer bead, whose displacement was captured using 24 synchronized cameras surrounding the walls that were interfaced to a software package (Qualisys, see supplementary movie S3). Analogous to the Smart Road study, the Tracker software was used to generate the displacement plots (solid lines in figures C8(A)–(D)). Displacements were only analyzed for the first 16 pedestrians in the line, as this was the maximum number of people who were able to fit inside of the line for the largest spacing.
In contrast to the vehicular flows, figure 4(B) shows that the required time for all pedestrians to empty the line increases significantly with increasing  . Note that for the minimal value of
. Note that for the minimal value of  tested, the pedestrians were instructed to pack as close together as possible, so our observation of increasing flow rates with decreasing
tested, the pedestrians were instructed to pack as close together as possible, so our observation of increasing flow rates with decreasing  held true even for the maximal possible amount of latent heat.
held true even for the maximal possible amount of latent heat.
3.2. Theoretical model
The one-dimensional configuration of the pedestrian flow enables the use of the OVM to quantify these findings in a manner similar to the vehicular study. The maximum velocity of the pedestrian traffic was measured to be approximately  m s−1, in agreement with the literature [40]. The actual length of each person has been assumed as lc ≈ 0.24 m. The jamming length of
m s−1, in agreement with the literature [40]. The actual length of each person has been assumed as lc ≈ 0.24 m. The jamming length of  m was found from the trials where the volunteers were instructed to pack together as comfortably as possible. To fit the model to the experiments, the sensitivity of the pedestrians was found to be
m was found from the trials where the volunteers were instructed to pack together as comfortably as possible. To fit the model to the experiments, the sensitivity of the pedestrians was found to be  s−1 and
s−1 and  for all spacings. Dashed lines in figures C8(A)–(D) show the theoretical displacement versus time for different static spacings which have a good agreement with the experimental data. Moreover, the velocity and acceleration of all individuals were extrapolated from the x-t plot (figures C8(E), (F) and C9).
for all spacings. Dashed lines in figures C8(A)–(D) show the theoretical displacement versus time for different static spacings which have a good agreement with the experimental data. Moreover, the velocity and acceleration of all individuals were extrapolated from the x-t plot (figures C8(E), (F) and C9).
Analogous to the vehicular motion, we have also found the departure versus saturation flow rates of the pedestrian motion (figure C10). Both the departure flow rate and saturation flow rate decrease as  increases, in sharp contrast to the vehicular experiments. This confirms our hypothesis that for systems with low velocities and fast accelerations, it now becomes favorable to change to a solid phase at stoppages. This is because the lag time due to latent heat of the close-packed system is now minor relative to the benefit of the increased initial displacement.
increases, in sharp contrast to the vehicular experiments. This confirms our hypothesis that for systems with low velocities and fast accelerations, it now becomes favorable to change to a solid phase at stoppages. This is because the lag time due to latent heat of the close-packed system is now minor relative to the benefit of the increased initial displacement.
Figure 4(C) graphs the modeled displacement of the last (16th) person in line; the required time for this last person to exit the line increases significantly with increasing  . There is still some latent heat, for example the last person is able to begin moving nearly 10 s earlier for
. There is still some latent heat, for example the last person is able to begin moving nearly 10 s earlier for  m compared to
m compared to  m. However, the last pedestrian required only 5 s of walking for
m. However, the last pedestrian required only 5 s of walking for  m compared to roughly 40 s of walking for
m compared to roughly 40 s of walking for  m, more than offsetting the comparatively minor lag of the latent heat. This can be more explicitly quantified by again considering the system's interaction potential, which can be dissipated considerably faster than with the vehicular traffic (figure 3(D) and 4(D)). When comparing the minimum
m, more than offsetting the comparatively minor lag of the latent heat. This can be more explicitly quantified by again considering the system's interaction potential, which can be dissipated considerably faster than with the vehicular traffic (figure 3(D) and 4(D)). When comparing the minimum  of the pedestrians to the vehicles, Ui was dissipated after only 9 s for pedestrians while requiring 16 s for the vehicles, which is 78% longer. Finally, note that for the largest pedestrian spacing (
of the pedestrians to the vehicles, Ui was dissipated after only 9 s for pedestrians while requiring 16 s for the vehicles, which is 78% longer. Finally, note that for the largest pedestrian spacing ( m) the interaction potential was completely negligible, compared to a much larger spacing with vehicles (
m) the interaction potential was completely negligible, compared to a much larger spacing with vehicles ( m) which still exhibited a non-zero potential.
m) which still exhibited a non-zero potential.
4. Conclusions
Using a drone camera and drivers queued at a red light on a Smart Road, we have shown that vehicles jamming into a 'solid phase' at stoppages do not increase the efficiency of resumed flow due to the latent heat inherent to the reverse phase-transition back to the 'liquid phase.' Counterintuitively, the larger bumper-to-bumper spacings that cars maintain when driving at speed can therefore be largely preserved at stoppages to minimize the risk of rear-end collisions with no loss in travel efficiency. Latent heat becomes less important when considering slow moving systems such as pedestrian traffic, as demonstrated by motion-capture experiments where lines of people could empty more efficiently with increasing packing density. As a queue's packing density is increased, we conclude that how the cost of the lag time (latent heat) compares with the savings of increased initial displacement depends upon the optimal velocity and sensitivity of the system.
Our findings with the Smart Road experiments suggest that future policy should discourage close-packing for vehicles during certain stop-and-go scenarios. Because gridlock is often a concern for traffic intersections and city driving, these findings are expected to be more relevant for stop-and-go traffic on highways. A practical challenge is the difficulty of changing the entrenched habit of drivers to induce phase transitions at stoppages. Another open question is whether the dangers of high packing densities at queues will eventually be removed via advances in adaptive cruise control and autonomous vehicles. We hope that our study will inspire the analysis of other aspects of latent heat on traffic, for example on lane merges/splits on a freeway.
Acknowledgments
The authors would like to acknowledge startup funds from the Department of Biomedical Engineering and Mechanics at Virginia Tech and a grant from the Institute for Creativity, Arts, and Technology to JBB and NA. We thank Jared Bryson, Julie Cook, Suzie Lee, and Leonore Nadler for assistance with coordinating the VTTI Smart Road experiments and Kriz Andrew and Jennifer Tomlin for piloting the drone camera. We thank Tanner Upthegrove for assistance with coordinating the motion-capture experiments in the Cube and Hollins Exposition Services for providing the stanchions and chains. Finally, we are thankful to Saurabh Nath for helpful discussions.
SFA and JBB designed research; all authors performed research; SFA and JBB analyzed data; and SFA and JBB wrote the paper.
Appendix A.: IRB approval and recruiting procedure
Since this research involved human subjects, the protocols of the study (for both the vehicular and pedestrian traffic) were reviewed and approved by the Institutional Review Board (IRB #15-484 for vehicular experiments and IRB #14-914 for pedestrians). After receiving IRB approval, volunteers were recruited for the pedestrian experiment by on-campus advertising (flyers and class announcements), while volunteers for the vehicular experiment were recruited by both on-campus and off-campus advertising (flyers). Each volunteer read and signed the informed consent form which provided the study procedures, risks, compensations, etc. To avoid any risk of bias in the participants' behavior, volunteers were not told the hypothesis of the studies. For the vehicular experiment, all participants had a background check of their driving record by the Department of Human Resources and were required to pass vision and hearing tests at the consent signing. All vehicles used were rented from the Virginia Tech Fleet Services Department with insurance to cover the study.
Appendix B.: Derivation
The analytical form of the interaction potential equation was shown in equation (8). Here our derivation of this function is shown step by step. The interaction potential function can be found from the deceleration force as:
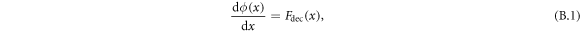
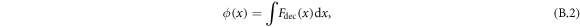
where the deceleration force ( ) is defined as:
) is defined as:

Recall that  is the optimal velocity function, which is defined as:
is the optimal velocity function, which is defined as:
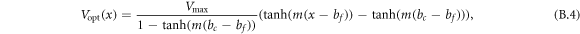
and the terms on the right-hand side of equation (B.4) are already defined in the main paper. Substituting (B.3) and (B.4) into (B.2) yields:
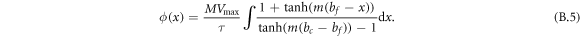
To find the analytical solution of (B.5) let us define  so that
so that  . Using the trigonometric identity
. Using the trigonometric identity
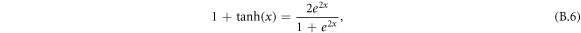
(B.5) is simplified to:

whose integration yields the following solution:

where C is the constant of the integration. Using the boundary condition of  as
as  , the interaction potential energy between two particles is found as:
, the interaction potential energy between two particles is found as:
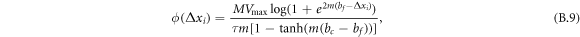
which is equation (8) which was used to calculate the interaction potential of the system in conjunction with equation (7).
Appendix C.: Supporting figures
Figure C1. Experimental (A) and theoretical (B) time required for each vehicle to pass the intersection versus vehicle posion in the queue for different static bumper-to-bumper spacings. Error bars show one standard deviation between the three trials.
Download figure:
Standard image High-resolution imageFigure C2. (A) Departure headway versus vehicle position in the queue for different static bumper-to-bumper spacings ( ). The saturation headway is the steady-state headway which was (approximately) obtained after the fourth car in the queue, and was about 2 s for all cases except the 'gas phase' of
). The saturation headway is the steady-state headway which was (approximately) obtained after the fourth car in the queue, and was about 2 s for all cases except the 'gas phase' of  m. Values are based off the theoretical model that was best-fit to the experimental results; the departure headway for the first car is artificially low because the reaction time of the driver to the light turning green was not included. (B) Experimental departure and saturation flow rates for different values of
m. Values are based off the theoretical model that was best-fit to the experimental results; the departure headway for the first car is artificially low because the reaction time of the driver to the light turning green was not included. (B) Experimental departure and saturation flow rates for different values of  , in terms of the vehicles per hour of green light (vphg) that cross the intersection. The departure flow rate corresponds to the start-up lost time of the first four vehicles crossing the intersection during the initial transient, while the saturation flow rate corresponds to steady-state headway conditions.
, in terms of the vehicles per hour of green light (vphg) that cross the intersection. The departure flow rate corresponds to the start-up lost time of the first four vehicles crossing the intersection during the initial transient, while the saturation flow rate corresponds to steady-state headway conditions.
Download figure:
Standard image High-resolution imageFigure C3. (A) Dimensionalized and (B) non-dimensionalized optimal velocity function (OVF) versus headway distance for all of the static bumper-to-bumper spacings. The horizontal red line corresponds to the speed limit of 15.6 m s−1. Even for the highly packed case of  = 0.38 m, it can be seen that the OVF is zero until the headway distance becomes larger than bc to ensure safe driving. The OVF is either zero or positive over the entire parameter space, showing that the non-physical case of a negative velocity does not occur.
= 0.38 m, it can be seen that the OVF is zero until the headway distance becomes larger than bc to ensure safe driving. The OVF is either zero or positive over the entire parameter space, showing that the non-physical case of a negative velocity does not occur.
Download figure:
Standard image High-resolution imageFigure C4. Experimental (solid green lines) and theoretical (dashed black lines) displacements of the even numbered cars driving from rest through a traffic light. The shaded region about each experimental line represents the standard deviation of the three trials and the odd numbered cars are omitted for visual clarity. The initial location of the lead car's front bumper is defined as  0 and each vehicle effectively clears the intersection upon reaching
0 and each vehicle effectively clears the intersection upon reaching  5 m. The initial bumper-to-bumper spacings of the cars were: (A)
5 m. The initial bumper-to-bumper spacings of the cars were: (A)  1.25 ft(0.38 m), (B)
1.25 ft(0.38 m), (B)  3 ft(0.91 m), (C)
3 ft(0.91 m), (C)  6 ft(1.8 m), (D)
6 ft(1.8 m), (D)  12 ft(3.6 m), (E)
12 ft(3.6 m), (E)  25 ft(7.6 m), and (F)
25 ft(7.6 m), and (F)  50 ft(15 m). It can be seen that the OVM displacement curves agree with the real-life values within experimental uncertainty, with the exception of some minor disagreement in initial locations which was due to imperfections in lining up cars on the Smart Road.
50 ft(15 m). It can be seen that the OVM displacement curves agree with the real-life values within experimental uncertainty, with the exception of some minor disagreement in initial locations which was due to imperfections in lining up cars on the Smart Road.
Download figure:
Standard image High-resolution imageFigure C5. Theoretical velocities of ten cars driving from rest through a traffic light for: (A)  0.38 m, (B)
0.38 m, (B)  0.91 m, (C)
0.91 m, (C)  1.8 m, (D)
1.8 m, (D)  3.6 m, (E)
3.6 m, (E)  7.6 m, and (F)
7.6 m, and (F)  15 m. The red line represents the speed limit (
15 m. The red line represents the speed limit ( 15.6 m s−1).
15.6 m s−1).
Download figure:
Standard image High-resolution imageFigure C6. Theoretical accelerations of ten cars driving from rest through a traffic light for: (A)  0.38 m, (B)
0.38 m, (B)  0.91 m, (C)
0.91 m, (C)  1.8 m, (D)
1.8 m, (D)  3.6 m, (E)
3.6 m, (E)  7.6 m, and (F)
7.6 m, and (F)  15 m.
15 m.
Download figure:
Standard image High-resolution imageFigure C7. Snapshots of the experiment in the motion-capture room which shows the motion of pedestrians exiting a line when the initial period between people is  1.8 m. As it is shown in figure 4 of the main paper, the required time for the 16th person to exit the line is about 25.5 s.
1.8 m. As it is shown in figure 4 of the main paper, the required time for the 16th person to exit the line is about 25.5 s.
Download figure:
Standard image High-resolution imageFigure C8. Experimental (solid lines) and theoretical (dashed lines) displacements of 16 pedestrians' motion from rest through an assigned line. The initial location of the lead person is defined as  0 and each person effectively exits the line upon reaching
0 and each person effectively exits the line upon reaching  1 m. The initial spacing (period) between each person was: (A) close-packed (
1 m. The initial spacing (period) between each person was: (A) close-packed ( 0.13 m), (B)
0.13 m), (B)  0.67 m, (C)
0.67 m, (C)  1.6 m, (D)
1.6 m, (D)  3.4 m. Experimental lines represent an average of 3 trials and the alternating blue and green colors are to help guide the eye. The theoretical velocity (E) and acceleration (F) curves of all 16 pedestrians walking from rest were identical for
3.4 m. Experimental lines represent an average of 3 trials and the alternating blue and green colors are to help guide the eye. The theoretical velocity (E) and acceleration (F) curves of all 16 pedestrians walking from rest were identical for  3.4 m, showing the complete lack of latent heat at sufficiently large spacings. The red line in (E) shows the maximum speed achieved by pedestrians in the study (
3.4 m, showing the complete lack of latent heat at sufficiently large spacings. The red line in (E) shows the maximum speed achieved by pedestrians in the study ( 1.37 m s−1).
1.37 m s−1).
Download figure:
Standard image High-resolution imageFigure C9. Theoretical velocities of the 16 pedestrians in the line walking from rest for: (A) close-packed ( = 0.13 m), (B)
= 0.13 m), (B)  = 0.67 m, and (C)
= 0.67 m, and (C)  1.6 m. The red line shows the maximum speed achieved by pedestrians in the study (Vmax = 1.37 m s−1). Theoretical accelerations of the 16 pedestrians walking from rest for: (D) close-packed (
1.6 m. The red line shows the maximum speed achieved by pedestrians in the study (Vmax = 1.37 m s−1). Theoretical accelerations of the 16 pedestrians walking from rest for: (D) close-packed ( = 0.13 m), (E)
= 0.13 m), (E)  = 0.67 m, and (F)
= 0.67 m, and (F)  1.6 m.
1.6 m.
Download figure:
Standard image High-resolution imageFigure C10. (A) Departure headway for each pedestrian in the queue for different gap spaces between pedestrians at rest ( ), obtained from the OVM model best-fit to the experiments. As with the vehicular traffic, the saturation headway is defined as the steady-state departure headway occurring from the fourth person in the queue onward. The saturation headway is increased by a factor of 3 as
), obtained from the OVM model best-fit to the experiments. As with the vehicular traffic, the saturation headway is defined as the steady-state departure headway occurring from the fourth person in the queue onward. The saturation headway is increased by a factor of 3 as  varies from 0.13 to 3.4 m. (B) Experimental departure and saturation flow rates for different spacings, in terms of the number of people who depart the line per hour of 'green' (pphg). Both the transient (departure) flow rate and the saturation flow rate decrease with increasing spacing, showing that the effects of latent heat are minor for pedestrian traffic.
varies from 0.13 to 3.4 m. (B) Experimental departure and saturation flow rates for different spacings, in terms of the number of people who depart the line per hour of 'green' (pphg). Both the transient (departure) flow rate and the saturation flow rate decrease with increasing spacing, showing that the effects of latent heat are minor for pedestrian traffic.
Download figure:
Standard image High-resolution image

















